Tree metrics and edge-disjoint $S$-paths

Abstract

Given an undirected graph $G=(V,E)$ with a terminal set $S \subseteq V$, a weight function on terminal pairs, and an edge-cost $a: E \rightarrow \mathbf{Z}_+$, the $\mu$-weighted minimum-cost edge-disjoint $S$-paths problem ($\mu$-CEDP) is to maximize $\sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(P)$ over all edge-disjoint sets $\mathcal{P}$ of $S$-paths, where $s_P,t_P$ denote the ends of $P$ and $a(P)$ is the sum of edge-cost $a(e)$ over edges $e$ in $P$. Our main result is a complete characterization of terminal weights $\mu$ for which $\mu$-CEDP is tractable and admits a combinatorial min–max theorem. We prove that if $\mu$ is a tree metric, then $\mu$-CEDP is solvable in polynomial time and has a combinatorial min–max formula, which extends Mader’s edge-disjoint $S$-paths theorem and its minimum-cost generalization by Karzanov. Our min–max theorem includes the dual half-integrality, which was earlier conjectured by Karzanov for a special case. We also prove that $\mu$-EDP, which is $\mu$-CEDP with $a = 0$, is NP-hard if $\mu$ is not a truncated tree metric, where a truncated tree metric is a weight function represented as pairwise distances between balls in a tree. On the other hand, $\mu$-CEDP for a truncated tree metric $\mu$ reduces to $\mu '$-CEDP for a tree metric $\mu '$. Thus our result is best possible unless P = NP. As an application, we obtain a good approximation algorithm for $\mu$-EDP with “near” tree metric $\mu$ by utilizing results from the theory of low-distortion embedding.

1 Introduction

Let $G$ be an undirected graph with vertex set $V = V(G)$ and edge set $E=E(G)$. We are given a specified set $S$ of vertices, called terminals. An $S$-path is a path connecting distinct terminals in $S$. Let $a: E \rightarrow \mathbf{Z}_+$ be a nonnegative integral edge-cost, and let be a nonnegative integral terminal weight defined on the set of all (unordered) pairs of $S$. One $(s,t)$-path $P$ has the value $\mu (s,t)$ as well as the cost $a(P) := \sum \nolimits _{e \in E} a(e)$. We want to find an edge-disjoint set $\mathcal{P}$ of $S$-paths having a high value and a low cost. Motivated by this, we consider the $\mu$-weighted minimum-cost edge-disjoint $S$-paths problem ($\mu$-CEDP):

$$\begin{aligned} \mu \hbox {-CEDP:}&\text{ Maximize } \displaystyle \sum \limits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(P) \\&\text{ over } \text{ all } \text{ edge-disjoint } \text{ sets }\, \mathcal{P} \,\hbox {of}\, S\hbox {-paths in}\, G, \end{aligned}$$

where $s_P,t_P$ denote the terminals which $P$ connects. Let $\mathop {\mathrm{val}}(\mu ;G,a)$ denote the optimal value of $\mu$-CEDP.

In general, $\mu$-CEDP is NP-hard. To see this, let $S =\{s,t,s',t'\}$ and define weight $\mu _\mathrm{2com}$ by $\mu _\mathrm{2com}(u,v) := 1$ if $\{u,v\} = \{s,t\}$ or $\{s',t'\}$, and $\mu _\mathrm{2com}(u,v) := 0$ otherwise. Then $\mu _\mathrm{2com}$-CEDP with $a = 0$ is the integer version of the 2-commodity flow maximization problem [20]. This problem is known to be NP-hard [10].

However, there is an instance of terminal weights $\mu$ such that $\mu$-CEDP is tractable, admits a nice combinatorial min–max theorem, and is not reducible to minimum-cost (single commodity) flow problem. The case of $(\mu ,a) = (1,0)$ is fundamental, where $1$ denotes the all one function and $0$ denotes the all zero function. In this case, $\mu$-CEDP is nothing but the edge-disjoint $S$-paths packing problem. Mader [34] proved the following combinatorial min–max theorem for this problem:

$$\begin{aligned} \mathop {\mathrm{val}}(1; G,0) = \frac{1}{2} \min \left( \sum \limits _{s \in S} |\delta X_s| - \kappa \right) , \end{aligned}$$

(1.1)

where the minimum is taken over all families of disjoint node subsets $X_s\;(s \in S)$ with $s \in X_s$, and $\delta X$ denotes the set of edges joining $X$ and $V {\setminus } X$, and $\kappa$ denotes the number of connected components $K$ in $G - \bigcup _{s \in S} X_s$ such that $|\delta V(K)|$ is odd. Moreover edge-disjoint $S$-paths attaining the maximum $\mathop {\mathrm{val}}(1; G,0)$ can be found in polynomial time by Lovasz’s (linear) matroid matching algorithm [31, 32] or by the ellipsoid method [28]; see [43, Section 73.1].

In the 1990s, Karzanov [24, 26] studied $\mu$-CEDP for $\mu = p 1\;(p > 0)$ and an arbitrary cost $a$. If $p$ is large enough, then any optimal solution is a maximum edge-disjoint set of $S$-paths with the minimum total cost. He gave a min–max theorem together with a combinatorial polynomial time algorithm. A proof outline was given in [26]. However the full proof [24] takes over 60 pages, is rather complicated, and has not yet been submitted to any journal.

Our main result is a complete characterization of terminal weights $\mu$ for which $\mu$-CEDP is tractable and admits a combinatorial min–max theorem, extending the edge-disjoint $S$-paths theorem by Mader and its min-cost generalization by Karzanov. To state the main result, let us introduce some notions. A tree metric is a weight function that can be represented as distances among points in a (weighted) tree. More precisely, a weight $\mu$ is called a tree metric if there exist a tree $\varGamma$, a positive $\gamma >0$, and a family of nodes $\{p_s\}_{s \in S} \subseteq V({\varGamma })$ indexed by $S$ such that $\mu (s,t) = \gamma d_{{\varGamma }}(p_s,p_t)$ for $s,t \in S$, where $d_{{\varGamma }}$ denotes the shortest path metric of $\varGamma$ with respect to unit edge-length. Triple $({\varGamma }, \{p_s\}_{s \in S}; \gamma )$ is called a tree realization of $\mu$. Here $\gamma$ is always taken as $1/2$ if $\mu$ is an integer-valued tree metric. Indeed, by definition, a tree metric $\mu$ is also represented as the shortest path metric among node subset $\{p_s\}_{s \in S}$ in some weighted tree $\varGamma$ of edge-weight $l: E \rightarrow \mathbf{R}_+$. We can assume that for each vertex $v$ of degree at most two there is $s \in S$ with $v = p_s$. Then each edge-length $l(e)$ is half-integral since $l(e)$ is equal to is $(\mu (s,u) + \mu (t,v) + \mu (s,v) + \mu (t,u) - \mu (s,t)- \mu (u,v) )/2$ for some $s,t,u,v \in S$. Hence, by edge-subdivision, we get a realization of $\mu$ with $\gamma = 1/2$.

Let $G = (V,E)$ be a graph with terminal set $S$. A node in $V {\setminus } S$ is called an inner node. $G$ is said to be inner Eulerian if every inner node has an even degree. An inner-odd-join is an edge subset $F \subseteq E$ for which $G - F = (V, E {\setminus } F)$ is inner Eulerian. For a tree $\varGamma$ and a map $\rho : V \rightarrow V(\varGamma )$, let $d_{\varGamma } \cdot \rho$ denote a function on $E$ defined by $(d_{\varGamma } \cdot \rho ) (e) = d_{\varGamma }(\rho (x),\rho (y))$ for $e = xy$. We are now ready to state our main theorem:

Theorem 1.1

Let $\mu$ be an integer-valued tree metric realized by $({\varGamma },\{p_s\}_{s \in S}; 1/2)$. Then we have

$$\begin{aligned} \displaystyle \mathop {\mathrm{val}}(\mu ; G,a) = \min _{\rho } \max _{F} \left( \frac{1}{2} d_{\varGamma } \cdot {\rho } - a\right) (E {\setminus } F), \end{aligned}$$

(1.2)

where the maximum is taken over inner-odd-joins $F$ and the minimum is taken over maps $\rho : V \rightarrow V(\varGamma )$ satisfying $\rho (s) = p_s$ for $s \in S$. Moreover there exists a polynomial time algorithm to find an edge-disjoint set of $S$-paths attaining $\mathop {\mathrm{val}}(\mu ; G,a)$.

Relation to Mader’s min–max formula. Mader’s formula (1.1) can be deduced from our formula (1.2) as follows. First, observe that, in (1.1), the minimum is always attained by $\{X_s\}$ with the following property:

$$\begin{aligned} \hbox {Each}\; x \in X_s\; \hbox {is reachable from}\; s\; \hbox {in the subgraph of}\; G\; \hbox {induced by}\; X_s. \end{aligned}$$

(1.3)

Indeed, delete such nonreachable nodes from $X_s$. Then $\sum |\delta X_s| - \kappa$ does not increase. Next consider our formula (1.2). Let $\mu = 1$, and let $\varGamma$ be a star with $|S|$ leaves $p_{s}\;(s \in S)$ and center $p_0$. Then $({\varGamma }, \{p_s\}_{s \in S}; 1/2)$ realizes $\mu$. A map $\rho : V \rightarrow V(\varGamma )$ satisfying $\rho (s) = p_s$ is identified with a set $\{X_s\}_{s \in S}$ of disjoint sets with $s \in X_s$ by correspondence $X_s \leftrightarrow \rho ^{-1}(p_s)$. Then $(d_{\varGamma } \cdot {\rho })(E) = \sum \nolimits _{s \in S} |\delta X_s|$. Also in (1.2) the minimum is always attained by a map $\rho$ with the property (1.3) (under the correspondence $X_s \leftrightarrow \rho ^{-1}(p_s)$). To see this, consider a map $\rho '$ obtained from $\rho$ by replacing $\rho (x)$ with $p_0$ for all such nonreachable nodes $x$. Then the inner maximum does not increase. Indeed, take an inner-odd-join $F'$ attaining $\max _F (d_{\varGamma } \cdot {\rho '})(E{\setminus } F)$. Since $(d_{\varGamma } \cdot {\rho '})(e) \le (d_{\varGamma } \cdot {\rho })(e)\;(e \in E)$ by the construction, we have $(d_{\varGamma } \cdot {\rho '})(E {\setminus } F') \le (d_{\varGamma } \cdot {\rho }) (E {\setminus } F') \le \max _{F} (d_{\varGamma } \cdot {\rho })(E{\setminus } F)$. Next we estimate $\min _F (d_{\varGamma } \cdot {\rho })(F)$ under property (1.3). Let $Y_1,Y_2,\ldots , Y_{m}$ be the node sets of connected components of $G - \bigcup _{s \in S} X_s$. Any inner-odd-join $F$ meets at least one edge in $\delta Y_i$ if $|\delta Y_i|$ is odd; hence $\min _F (d_{\varGamma } \cdot {\rho })(F) \ge \kappa$. Conversely, taking one edge from each $\delta Y_i$ with $|\delta Y_i|$ odd, we obtain an edge set $F$ with $(d_{\varGamma } \cdot {\rho })(F) = \kappa$. By (1.3), we can greedily add edges $e$ with $(d_{\varGamma } \cdot {\rho })(e) = 0$ to $F$, and extend $F$ to an inner-odd-join of $G$. This means $\min _F (d_{\varGamma } \cdot {\rho })(F) = \kappa$. Hence Theorem 1.1 implies Mader’s min–max formula (1.1).

Dual half-integrality of min-cost edge-disjoint $S$-paths problem. As mentioned already, our result includes Karzanov’s min-cost edge-disjoint $S$-paths theorem for a special case of $\mu = p1$. Therefore this paper includes a relatively simpler proof of his result. Furthermore our min–max formula includes half-integrality of dual. Indeed, it will turn out that the inner maximization is a minimum-cost $T$-join problem. Although edge-cost $c := (d_{\varGamma } \cdot \rho )/2 - a$ is half-integral, the sum of $c(e)$ along every cycle is an integer (since tree $\varGamma$ is bipartite). By Seymour’s odd-cut packing theorem [45] for bipartite graphs, the inner maximization is dualized to a half-integral odd-cut packing problem. This dual half-integrality affirmatively resolves a question raised by Karzanov [26, Section 6, (2)] as the special case; see Sect. 6.4 for detail.

Tractability classification of terminals weights. By considering $a = 0$ we get an important special case $\mu$-EDP of $\mu$-CEDP:

$$\begin{aligned} \mu \text{-EDP: } \quad \text{ Maximize } \displaystyle \sum \limits _{P \in \mathcal{P}} \mu (s_P,t_P) \text{ over } \text{ all } \text{ edge-disjoint } \text{ sets }\; \mathcal{P} \;\hbox {of}\; S\hbox {-paths in}\; G. \end{aligned}$$

A terminal weight $\mu$ is said to be EDP-tractable if $\mu$-EDP is solvable in polynomial time for every graph containing terminal set $S$. The all-one weight 1 is EDP-tractable. By our result, every tree metric is EDP-tractable. However, a slightly more general class of weights is EDP-tractable. A weight $\mu$ is said to be a truncated tree metric if it can be represented as distances between balls in a weighted tree, or equivalently, if there are a tree metric $\bar{\mu }$ and a nonnegative function (radius) $r$ on $S$ such that

$$\begin{aligned} \mu (s,t) = \max \left( \bar{\mu }(s,t) -r(s) -r(t), 0\right) \quad (s,t \in S). \end{aligned}$$

(1.4)

Corollary 1.2

Every truncated tree metric is EDP-tractable.

Indeed, suppose that $\mu$ is a truncated tree metric represented as (1.4) for a tree metric $\bar{\mu }$ and radius $r$. Then $\mu$-EDP reduces to $\bar{\mu }$-CEDP as follows. First, for each terminal $s$, add a new inner node $s'$, and replace each edge $sx$ incident to $s$ by two edges $ss'$ and $s'x$. Clearly the problem does not change. Next define cost $a$ as: $a(e) = r(s)$ if $e = ss'$ for a terminal $s$ and $a(e) = 0$ otherwise. Consider $\bar{\mu }$-CEDP for this graph with this cost. Then value $\bar{\mu }(s,t) - a(P)$ of any $(s,t)$-path $P$ is equal to $\bar{\mu }(s,t) - a(s) - a(t) (\le \mu (s,t))$. Therefore the optimal value of the $\bar{\mu }$-CEDP is at most that of the original $\mu$-EDP. Conversely, from an optimal solution in the $\mu$-EDP, we can delete all paths $P$ with $\mu (s_P,t_P) = 0$ to obtain a solution in the $\bar{\mu }$-CEDP of the same objective value. Note that the same idea also reduces $\mu$-CEDP to $\bar{\mu }$-CEDP. We further prove that this result is best possible in the following sense:

Theorem 1.3

If $\mu$ is not a truncated tree metric, then $\mu$-EDP is NP-hard.

This hardness result implies that EDP-tractable weights are exactly truncated tree metrics unless P = NP.

Application: Approximating edge-disjoint $S$-paths for “near” tree metric. Finding a good approximation for $\mu$-EDP (with general $\mu$) is a great challenge in the area of approximation algorithms [47]; the current best is an $O(\sqrt{|V|})$-approximation due to Chekuri et al. [4].

The following observation suggests a possible use of our result to the design of approximation algorithms for $\mu$-EDP:

If we can choose some EDP-tractable weight $\mu ^*$ with $\mu \le \mu ^* \le \alpha \mu$ for some $\alpha \ge 1$, then any optimal solution for $\mu ^*$-EDP is an $\alpha$-approximate solution for $\mu$-EDP.

An $\alpha$-approximate solution is a solution having the objective value at least $1/\alpha$ times the optimal value. In the case of metric weights, this problem—finding a good embedding into a tree metric—falls into the area of the low-distortion embedding; see [33]. For two metric spaces $(X,d)$ and $(Y,d')$, a map $\phi : X \rightarrow Y$ is an embedding with distortion $\alpha$ if $d(x,y) \le d'(\phi (x),\phi (y)) \le \alpha d(x, y)$ for $x,y \in X$. Given a metric $\mu$ (metric space $(S,\mu )$), let $\alpha ^*$ denote the minimum distortion of an embedding into a tree metric (the metric space on a tree). Finding a tree metric achieving $\alpha ^*$ for a given metric $\mu$ is NP-hard. Consider the case where the input metric $\mu$ is a graph metric, i.e., $\mu = d_{H}$ for some graph $H$ with $S = V(H)$. Bădoiu et al. [2] gave a polynomial time algorithm to find an embedding into some tree metric with distortion $O(\alpha ^*)$. Later, Chepoi et al. [6] gave a polynomial time algorithm to find a tree embedding with distortion $6 \alpha ^*$. Thus we have the following.

Corollary 1.4

Let $\mu$ be a graph metric that can be embedded into a tree metric with distortion $\alpha ^*$. Then there exists a $6 \alpha ^*$-approximation algorithm for $\mu$-EDP.

Unfortunately, this approach does not improve the approximation ratio (for general graph metrics) since the minimum distortion of general metrics into tree metrics is $\Omega (|S|)$ [40]. (Note that Bartal’s probabilistic embedding [1] does not work since our problem is a maximization problem.) Also the assumption that $\mu$ is a metric is rather restrictive, and not natural. The most prominent case in the literature is the case where $\mu$ is a weight on a $2k$ element terminal set $S = \{s_1,s_2, \ldots ,s_k, t_1,t_2,\ldots ,t_k\}$ taking a nonzero value only on $s_it_i\;(1 \le i \le k)$; such a weight is far from being a metric. Nevertheless, we hope that our results and techniques will provide tools to approximation algorithms for $\mu$-EDP/CEDP.

Multicommodity flows. A natural fractional relaxation of $\mu$-EDP—$\mu$-weighted maximum multiflow problem—has been well-studied in the literature. Hu [20] proved the existence of a half-integral optimal solution for the 2-commodity flow maximization problem (the case of $\mu = \mu _\mathrm{2com}$). Lovász [30] and Cherkassky [5] independently proved the existence of a half-integral optimal solution for all-one weight $\mu = 1$. However the 3-commodity flow does not have such a property. Namely, there is no integer $k > 0$ such that every 3-commodity flow problem has a $1/k$-integral optimal solution. Such phenomena of the (non-)existence of an optimal solution with bounded denominator lead to another kind of a weight classification problem, called the fractionality problem. The fractionality problem [22, 23] asks the classification of weights $\mu$ for which every $\mu$-weighted multiflow problem has a $1/k$-integral optimal multiflow for some integer $k$. Recent works [16–18] by Hirai gave a solution to the fractionality problem. He [19] also gave a solution to the node-capacitated variation as: $\mu$ has bounded fractionality for node-capacitated $\mu$-weighted maximum multiflow problems if and only if $\mu$ can be represented as the distance between subtrees (not necessarily balls!) in a tree. This work is influenced by these developments.

Discrete minimax relation. The formula (1.2) can be seen as a discrete minimax relation, a minimax relation on a discrete domain, as follows. It is shown in [27] that if $G$ is inner Eulerian and $\mu$ is an integer-valued tree metric realized by $({\varGamma },\{p_s\}_{s \in S};1/2)$, then the $\mu$-weighted maximum (fractional) multiflow problem has an integral optimal multiflow with value

$$\begin{aligned} \min _{\rho } \frac{1}{2} (d_{\varGamma } \cdot \rho ) (E), \end{aligned}$$

where the minimum is taken over all maps $\rho :V \rightarrow V(\varGamma )$ with $\rho (s) =p_s$ for $s \in S$; see Sect. 3.1. Since the complement of the union of edge-disjoint $S$-paths is an inner-odd-join, for a graph $G = (V,E)$ (not necessarily inner Eulerian) we have

$$\begin{aligned} \mathrm{val}(\mu ; G,a)&= \max _F \left( \mathrm{val}(\mu ; G-F,0) - a(E {\setminus } F)\right) \\&= \max _F \min _{\rho } \left( \frac{1}{2} d_{\varGamma } \cdot \rho - a\right) (E {\setminus } F). \end{aligned}$$

Hence our formula (1.2) implies a minimax theorem stating that “max” and “min” are interchangeable. (In particular, the weak duality of (1.2) can be seen by the general relation $\max _{x} \min _{y} f(x,y) \le \min _{y} \max _{x} f(x,y)$.) An interesting point is that this minimax theorem is on a discrete structure, and seems not to be explained by Euclidean convexity.

Organization. The first goal is the proof of Theorem 1.1, and the second goal is the proof of Theorem 1.3. We construct an LP-relaxation of $\mu$-CEDP/EDP according to the observation: the union of $S$-paths is an inner Eulerian graph, and hence the complement is an inner-odd-join. Thus, $\mathop {\mathrm{val}}(\mu ; G,a) = \max _{F} \mathop {\mathrm{val}}(\mu ; G-F,0) - a(E {\setminus } F)$ holds. Next relax inner-odd-joins into points in the convex hull of the incidence vectors of inner-odd-joins (inner-odd-join polytope), and relax edge-disjoint paths into multiflows in a natural way. This LP-relaxation was used in [3, 26, 28] (implicitly or explicitly). Note that the inner-odd-join polytope is a $T$-join polytope, and therefore a polynomial time separation oracle exists; see, e.g., [36]. Hence this LP-relaxation can be solved in polynomial time by the ellipsoid method [13]. We prove that if $\mu$ is a tree metric, then this LP-relaxation has an integral optimal solution. This extends a result of Keijsper et al. [28] for $(\mu ,a) = (1, 0)$. Although their proof assumes Mader’s theorem (1.1), our proof does not, and is purely polyhedral, i.e., it consists only of LP-based techniques. Therefore our paper gives a new proof of Mader’s edge-disjoint path theorem.

In Sect. 2, we describe a high-level idea of how to prove the integrality of this LP-relaxation. In Sect. 3, we give preliminary arguments including the polyhedral description of inner-odd-join polytope. In Sect. 4, we prove the first part of Theorem 1.1, which consists of three steps. The first step is to represent the dual of the LP-relaxation as a facility location problem on a tree. The second step is to show that a dual optimum is always attained by a nice structured combinatorial solution, and the optimal value coincides with the right hand side in the min–max formula (1.2). In the third step, we analyze the stability of dual combinatorial solutions under edge deletion; we see an unexpected application of the polynomial uncrossing process [26]. We then prove by induction the existence of an integral optimal solution. In Sect. 5, we prove the polynomial solvability (the second part of Theorem 1.1) and NP-hardness (Theorem 1.3). The polynomial solvability is almost proved by the argument in Sect. 4. The proof of the NP-hardness result is based on an interesting connection between a reduction to an integer 2-commodity flow feasibility problem and 4-point characterization of truncated tree metrics. As is well known, a metric $\mu$ is a tree metric if and only if there is no quadruple $(s,t,s',t')$ (violating quadruple) satisfying $\mu (s,t) + \mu (s',t') > \max \{\mu (s,s')+ \mu (t,t'), \mu (s',t) + \mu (s,t')\}$; see [44]. We prove a similar 4-point characterization for truncated tree metrics. From a violating quadruple $(s,t,s',t')$, we can reduce a version of the integer 2-commodity flow feasibility problem, which is NP-hard, to $\mu |_{S'}$-EDP on the four terminal $S' = \{s,t,s',t'\}$. In Sect. 6, we discuss related issues and raise future research directions.

Notation. Let $\mathbf{R}$ and $\mathbf{R}_+$ denote the sets of reals and nonnegative reals, respectively, and let $\mathbf{Z}$ and $\mathbf{Z}_+$ denote the sets of integers and nonnegative integers, respectively. For a set $X$, let $\mathbf{R}^X$ and $\mathbf{R}^X_+$ denote the sets of functions from $X$ to $\mathbf{R}$ and from $X$ to $\mathbf{R}_+$, respectively. For a function $f: X \rightarrow \mathbf{R}$, let $\mathcal{D}^+ f$ and $\mathcal{D}^- f$ denote the sets of elements $x \in X$ with $f(x) > 0$ and $f(x) < 0$, respectively. Let $f^+, f^-$, and $|f|$ denote the functions defined by $f^+(x) = \max (0,f(x)), f^-(x) = \min (0, f(x))$, and $|f|(x) = \max (-f(x),f(x))$, respectively. Let $\Vert f\Vert$ denote the $l_{\infty }$-norm of $f$; $\Vert f\Vert := \max _{x \in X} |f(x)|$. For a subset $Y \subseteq X$, let $f(Y)$ denote the sum of $f(y)$ over all $y \in Y$. The all-one function is denoted by $1$, and the zero function is denoted by 0.

By a metric on a set $V$, we mean a function $d: V \times V \rightarrow \mathbf{R}_+$ satisfying $d(x,x) = 0, d(x,y) = d(y,x)$, and triangle inequalities $d(x,y) + d(y,z) \ge d(x,z)$ for $x,y,z \in V$. For a subset $X \subseteq V$, the cut metric $\delta _X$ is defined by $\delta _{X} (x,y) = 1$ if $| X \cap \{x,y\}| = 1$ and $\delta _{X} (x,y) = 0$ otherwise.

Let $G = (V,E)$ be a graph with possible parallel edges and loops. For an edge $e$, we write $e = xy$ if $e$ joins nodes $x,y$. For a node subset $X \subseteq V$, let $\delta X = \delta ^G X$ denote the set of edges joining $X$ and $V {\setminus } X$. For two functions $f,g$ on $E$, let $f \cdot g$ denote the inner product $\sum \nolimits _{e \in E} f(e) g(e)$. We regard a metric $d$ on $V$ as a function on $E$ by $d(e) := d(x,y)$ for $e = xy \in E$. In particular, $\delta _X \cdot \xi = \xi (\delta X)$ for $\xi \in \mathbf{R}^E$.

2 High-level idea for the proof of Theorem 1.1

The aim of this section is to explain the high-level idea behind the proof of Theorem 1.1. In Sect. 2.1, we introduce an LP-relaxation of $\mu$-CEDP; our goal is to show that this LP is exact. In Sect. 2.2, taking a special case of $(\mu ,a) = (1,0)$, we illustrate a basic idea to prove the existence of an integral optimal solution. In Sect. 2.3, we explain how to extend this idea to general $(\mu ,a)$, with giving an outline of Sects. 3 and 4.

Let $G = (V,E)$ be an undirected graph with terminal set $S \subseteq V, \mu$ a terminal weight, and $a$ an edge-cost.

2.1 LP relaxation

Recall that an inner-odd-join is an edge subset $F$ for which $G -F$ is inner Eulerian. Our starting point is the following relation:

$$\begin{aligned} \mathop {\mathrm{val}}(\mu ; G,a) = \max _F \left( \mathop {\mathrm{val}}(\mu ; G - F, 0) - a(E {\setminus } F)\right) , \end{aligned}$$

(2.1)

where the maximum is taken over all inner-odd-joins $F$ in $G$. To see this, let $\mathcal{P}^*$ be an edge-disjoint set of $S$-paths attaining $\mathop {\mathrm{val}}(\mu ; G,a)$, and let $F^*$ be the complement of the union of $\mathcal{P}^*$. Then $F^*$ is an inner-odd-join, and $\mathop {\mathrm{val}}(\mu ; G,a) = \sum \nolimits _{P \in \mathcal{P}^*}\mu (s_P,t_P) - a(E {\setminus } F^*) \le \mathop {\mathrm{val}}(\mu ; G-F^*, 0) - a(E {\setminus } F^*)$. Conversely, for any inner-odd-join $F$ and any edge-disjoint set $\mathcal{P}$ of $S$-paths in $G-F$, we have $\sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(E {\setminus } F) \le \sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(P) \le \mathop {\mathrm{val}}(\mu ;G,a)$, where we use the nonnegativity of $a$ in the first inequality.

Motivated by (2.1), we consider the following linear programming relaxation:

$$\begin{aligned} \text{ Max. }&\sum \limits _{P \in {\varPi }} \mu (s_P,t_P) f(P) - a(E) + \sum \limits _{e \in E} a(e) \xi (e) \nonumber \\ \text{ s. } \text{ t. }&\xi (e) + \sum \limits _{P \in {\varPi }: e \in P} f(P) \le 1 \quad (e \in E), \nonumber \\&\xi \in Q,\ f: {\varPi } \rightarrow \mathbf{R}_+. \end{aligned}$$

(2.2)

Here $Q = Q_{G,S}\subseteq \mathbf{R}^E_+$ denotes the convex hull of the incidence vectors of all inner-odd-joins in $G$, and ${\varPi } = {\varPi }_{G,S}$ denotes the set of all $S$-paths in $G$. The maximum value of (2.2) is denoted by $\overline{\mathop {\mathrm{val}}}(\mu ;G,a)$. Obviously $\mathop {\mathrm{val}}(\mu ;G,a) \le \overline{\mathop {\mathrm{val}}}(\mu ;G,a)$. We are going to show that if $\mu$ is a tree metric, then (2.2) has an integral optimal solution, and the LP-dual of (2.2) has an optimal solution of a special combinatorial interpretation, which gives the formula (1.2).

2.2 Case $(\mu ,a) = (1,0)$: a fractional approach to Mader’s theorem

To illustrate a basic idea behind the proof of the formula (1.2), we consider the special case of $(\mu , a) = (1, 0)$, i.e., the case of Mader. Let us introduce a slightly different formulation of the minimization problem of RHS in Mader’s formula (1.1).

A partition $\mathcal{X}$ of $V$ is said to be feasible (with respect to $G$ and $S$) if it satisfies:

• (1) for every $X \in \mathcal{X}$ we have $|X \cap S| \le 1$.

• (2) for every distinct $X,Y \in \mathcal{X}$ with $|X \cap S| = |Y \cap S| = 0$ there is no edge between $X$ and $Y$.

For a feasible partition $\mathcal{X}$, denote by $\mathcal{X}_{S}$ the set of subsets $X$ in $\mathcal{X}$ with $|X \cap S| = 1$, and define $\tau (\mathcal{X}) (= \tau ^{G}(\mathcal{X}))$ by

$$\begin{aligned} \tau (\mathcal{X}) := \frac{1}{2} \left( \sum \limits _{X \in \mathcal{X}_S} |\delta X| - \sum \limits _{Z \in \mathcal{X} {\setminus } \mathcal{X}_{S}} (|\delta Z| \ \mathrm{mod}\ 2)\right) , \end{aligned}$$

(2.3)

where $(n \ \mathrm{mod} \ 2) = 1$ if $n$ is odd, and $=0$ if $n$ is even. It is not difficult to see that $\tau$ is an upper bound of $\overline{\mathop {\mathrm{val}}}$. Thus we have

$$\begin{aligned} \mathop {\mathrm{val}}(1;G,0) \le \overline{\mathop {\mathrm{val}}} (1; G, 0) \le \min _\mathcal{X} \tau (\mathcal{X}). \end{aligned}$$

(2.4)

Observe that $\min _\mathcal{X} \tau (\mathcal{X})$ is equal to the RHS of (1.1). Mader’s theorem asserts that the inequalities (2.4) hold in equality.

Our fractional approach proves Mader’s theorem by establishing the following:

• Dual Integrality: $\overline{\mathop {\mathrm{val}}} (1; G, 0) = \min \tau (\mathcal{X})$.

• Primal Integrality: $\mathop {\mathrm{val}}(1;G,0) = \overline{\mathop {\mathrm{val}}} (1; G, 0)$.

• Edge-deletion Property: For an optimal solution $(f,\xi )$ in (2.2) and an edge $e$ with $\xi (e) > 0$, we have $\overline{\mathop {\mathrm{val}}} (1; G-e, 0) = \overline{\mathop {\mathrm{val}}} (1; G,0)$.

In fact, the dual integrality implies two other properties:

Edge-deletion Property $\Rightarrow$ Primal Integrality. For an optimal solution $(f,\xi )$, if $\xi = 0$, then $G$ is necessarily inner Eulerian, and by Lovász–Cherkassky theorem [5, 30] there is an integral optimal solution. If $\xi (e) > 0$, then by the induction and the edge-deletion property we have $\mathop {\mathrm{val}}(1; G,0) \le \overline{\mathop {\mathrm{val}}} (1; G, 0) = \overline{\mathop {\mathrm{val}}}(1; G-e, 0) = \mathop {\mathrm{val}}(1; G - e,0) \le \mathop {\mathrm{val}}(1; G,0)$, which implies $\mathop {\mathrm{val}}(1; G,0) = \overline{\mathop {\mathrm{val}}} (1; G, 0)$. $\square$

Dual Integrality $\Rightarrow$ Edge-deletion Property [sketch]. Let $(f,\xi )$ be an optimal solution in (2.2). Take an edge $e = xy \in E$ with $\xi (e) > 0$. Suppose indirectly $\overline{\mathop {\mathrm{val}}} (1;G - e,0) < \overline{\mathop {\mathrm{val}}} (1;G,0)$. In the following, we use simplified notation: $\tau ' := \tau ^{G - e}$, and $\delta ' := \delta ^{G-e}$. We are going to show:

• $(\clubsuit )$ If an optimal partition $\mathcal{X}$ of $G$ is a nonoptimal feasible partition of $G - e$, then there exists a feasible partition $\mathcal{X'}$ for $G -e$ with $\tau '(\mathcal{X}') < \tau ' (\mathcal{X})$ such that $\mathcal{X}'$ or its small modification $\tilde{\mathcal{X}}'$ is optimal to $G$.

Then, by applying the complementary slackness condition for $(f, \xi )$ and $\mathcal{X}'$ (or $\tilde{\mathcal{X}}'$), we can obtain an information of $\xi (e)$, and derive a contradiction.

Take an optimal feasible partition of $\mathcal{X}$ of $G$. Obviously $\mathcal{X}$ is feasible to $G - e$. By edge-subdivision, we can assume that $x$ and $y$ belong to a common set in $\mathcal{X}$. Then we have $\tau '(\mathcal{X}) = \tau (\mathcal{X}) = \overline{\mathop {\mathrm{val}}} (1; G,0) > \overline{\mathop {\mathrm{val}}} (1; G - e,0)$. This means that $\mathcal{X}$ is nonoptimal feasible partition of $G'$. Hence there is a feasible partition $\mathcal{X}'$ of $G - e$ with $\tau '(\mathcal{X}') < \tau '(\mathcal{X})$.

Take $X,Y \in \mathcal{X}'$ such that $x \in X$ and $y \in Y$. Consider the case where $X, Y \in \mathcal{X}' {\setminus } \mathcal{X}'_S$ Then $X \ne Y$. Otherwise $\mathcal{X}'$ is also feasible to $G$ with $\tau (\mathcal{X}') = \tau ' (\mathcal{X}') < \tau (\mathcal{X}')$; a contradiction. Although $\mathcal{X}'$ is not feasible to $G$, a partition $\tilde{\mathcal{X}}' := \mathcal{X} {\setminus } \{X,Y\} \cup \{X \cup Y\}$ is feasible to $G$. If at least one of $|\delta ' X|$ and $|\delta ' Y|$ is even, then $\tau (\tilde{\mathcal{X}}') = \tau ' (\mathcal{X}')$, and $\tau (\mathcal{X}) \le \tau (\tilde{\mathcal{X}}') = \tau ' (\mathcal{X}') < \tau (\mathcal{X})$; a contradiction. So suppose that both $|\delta ' X|$ and $|\delta ' Y|$ are odd. Then $|\delta (X \cup Y)| (= |\delta ' (X \cup Y) \cup \{e\}|)$ is even, and the second term in the RHS in (2.3) decreases by $2$. Thus $\tau (\tilde{\mathcal{X}}') = \tau '(\mathcal{X}') + 1$. Observe that $\tau$ is integer-valued. Hence we have $\tau (\mathcal{X}) \le \tau (\tilde{\mathcal{X}}') = \tau '(\mathcal{X}') + 1 \le \tau (\mathcal{X})$, and $\tilde{\mathcal{X}}'$ is optimal to $G$; now we arrive at a situation of $(\clubsuit )$. By the complementary slackness condition obtained from $\tau (\tilde{\mathcal{X}}') - \sum f(P) = 0$, we have $\xi (\delta (X \cup Y)) = (|\delta (X \cup Y)|\ \mathrm{mod}\ 2) = 0$, which implies $\xi = 0$ on $\delta (X \cup Y) = (\delta X \cup \delta Y) {\setminus } \{e\}$. Decompose $\xi$ into a convex combination of the incidence vectors of inner-odd-joins $F_1,F_2,\ldots ,F_m$. Each $F_i$ cannot meet $\delta X {\setminus } \{e\}$. On the other hand, every inner-odd-join must meet an even number of edges of $\delta X$ (since $|\delta X|$ is even). Necessarily each $F_i$ does not meet $e$, implying $\xi (e) = 0$; a contradiction to the first assumption. In this way, one can derive a contradiction for all the other cases. $\square$

Thus the remaining task is to prove the dual integrality. This needs a thorough analysis of the LP-dual of (2.2) (even when $(\mu ,a) = (1,0)$), which is the central subject of Sects. 3 and 4.

2.3 Outline

Let us now return the general situation. One can see that a large part of the argument in Sect. 2.2 is applicable to the general $(\mu ,a)$, provided one establishes that $\overline{\mathop {\mathrm{val}}}(\mu ;G,a)$ is equal to the minimum of a certain discrete optimization problem.

We first formulate the LP-dual as a continuous optimization problem over a certain space $\mathcal{C}$ with objective function $\tau$. In Sects. 3.2 and 3.4, we introduce several notions to describe $\mathcal{C}$ and $\tau$. In Sect. 4.2 we establish the duality relation:

$$\begin{aligned} \overline{\mathop {\mathrm{val}}}(\mu ;G,a) = \min _{\mathcal{X} \in \mathcal{C}} \tau (\mathcal{X}). \end{aligned}$$

(2.5)

We will define a discrete subset $\mathcal{B} \subseteq \mathcal{C}$, which represents special combinatorial solutions; the relation between $\mathcal{B}$ and $\mathcal{C}$ is analogous to that between $\mathbf{Z}$ and $\mathbf{R}$. In Sect. 4.3, we show that the minimum of $\tau$ is attained by an element in $\mathcal{B}$.

• Dual Integrality: $\displaystyle \min _{\mathcal{X} \in \mathcal{B}} \tau (\mathcal{X}) = \min _{\mathcal{X} \in \mathcal{C}} \tau (\mathcal{X}) \quad (= \overline{\mathop {\mathrm{val}}}(\mu ;G,a) )$.

However the dual integrality itself is not enough to prove the edge-deletion property and the primal integrality. In the proof of the dual integrality $\Rightarrow$ the edge-deletion property above, $(\clubsuit )$ was essential. To establish $(\clubsuit )$, we need the following property, which we call the dual stability:

• Dual Stability: If $\mathcal{X} \in \mathcal{B}$ is not optimal, then there exists $\mathcal{X}' \in \mathcal{B}$ such that $\tau (\mathcal{X}') < \tau (\mathcal{X})$ and $\mathcal{X}'$ belongs to a certain neighborhood of $\mathcal{X}$ in $\mathcal{C}$.

The precise statement is Lemma 4.7. In the case of $(\mu , a) = (1,0)$ above, we can take a relatively small space as $\mathcal{C}$, and the dual stability is automatically satisfied.

We will establish the dual integrality/stability by the following way. After establishing (2.5) (Lemma 4.1 in Sect. 4.2), we also prove the following (Lemma 4.2):

• (A) If $\mathcal{X} \in \mathcal{C}$ is not optimal, then there exists $\mathcal{X}' \in \mathcal{C}$ such that $\tau (\mathcal{X}') < \tau (\mathcal{X})$ and $\mathcal{X}'$ belongs to an arbitrary small neighborhood of $\mathcal{X}$ in $\mathcal{C}$.

In Euclidean convex optimization, the property (A) is obvious. The space $\mathcal{C}$, however, is not a Euclidean space because the formulation of $\mathcal{C}$ involves laminar solutions of the LP-dual of the minimum-cost $T$-join (inner-odd-join) problem; notice that the set of laminar solutions is not convex. In Sect. 3.3, we establish a stability property (Lemma 3.6) of laminar solutions of the LP-dual of the minimum-cost $T$-join problem, as a consequence of Karzanov’s polynomial uncrossing process. In Sect. 4.3, we prove the following (Theorem 4.5):

• (B) For $\mathcal{X} \in \mathcal{C}$ there exists $\mathcal{X}^* \in \mathcal{B}$ such that $\tau (\mathcal{X}^*) \le \tau (\mathcal{X})$ and $\mathcal{X}^*$ belongs to a certain neighborhood of $\mathcal{X}$ in $\mathcal{C}$.

Property (B) includes dual integrality. Combining with (A), we can establish the dual stability in the following way. Suppose that $\mathcal{X} \in \mathcal{B}$ is not optimal (over $\mathcal{B}$), Then this is not optimal over $\mathcal{C}$ by (B). By (A) there is $\tilde{\mathcal{X}}$ in an arbitrary small neighborhood of $\mathcal{X}$ with $\tau (\tilde{\mathcal{X}}) < \tau (\mathcal{X})$. By (B), there exists $\mathcal{X}' \in \mathcal{B}$ such that $\tau (\mathcal{X}') \le \tau (\tilde{\mathcal{X}}) (< \tau (\mathcal{X}))$ and $\mathcal{X}'$ belongs to a neighborhood of $\tilde{\mathcal{X}}$ and of $\mathcal{X}$.

Once one establishes dual integrality and stability, one can prove the primal integrality along the same line of Sect. 2.2, the formal details of which is given in Sect. 4.4.

3 Preliminaries

3.1 Laminar locking theorem

In the case where $G$ is inner Eulerian and $a= 0$, our problem becomes easier; we may put $\xi = 0$ in (2.2). So (2.2) coincides with the natural LP-relaxation of $\mu$-EDP. We will use the following fact as the base case of our inductive argument:

Lemma 3.1

If $\mu$ is a tree metric, $G$ is inner Eulerian, and $a = 0$, then there exists an integral optimal solution $(\xi ^*,f^*)$ in (2.2) with $\xi ^* = 0$.

This is a special case of the multiflow locking theorem due to Karzanov–Lomonosov [27]; see [43, Section 77.3c]. The multiflow locking theorem says that if a family $\mathcal{F} \subseteq 2^S$ has no pairwise crossing triple and $G$ is inner Eulerian, then there exists an integral multiflow $f$ being simultaneously a maximum (single-commodity) $(A, S {\setminus } A)$-flow for all $A \in \mathcal{F}$. Here a pair of sets $X,Y \subseteq S$ is said to be crossing if $X \cap Y, X {\setminus } Y, Y{\setminus } X$, and $S {\setminus } (X \cup Y)$ are all nonempty. A pair of two sets $X,Y \subseteq V$ is said be intersecting if $X \cap Y, X {\setminus } Y$, and $Y {\setminus } X$ are all nonempty. A family of sets without intersecting pairs is called laminar. One can easily see that such a multiflow $f$ is a maximum multiflow with respect to a terminal weight $\mu = \sum \nolimits _{X \in \mathcal{F}} \beta (X) \delta _{X}$ for any $\beta : \mathcal{F} \rightarrow \mathbf{R}_+$. As is well-known, a tree metric is just a nonnegative sum of cut metrics for a laminar family; see Sect. 3.4 below.

A simpler and shorter proof of the multiflow locking theorem is available at [11], and a faster algorithm finding an integer optimal solution is given by [21].

3.2 $T$-joins and inner-odd-joins

Let $G = (V,E)$ be an undirected graph, and let $T$ be a node subset $T \subseteq V$ having an even cardinality. For an edge subset $F \subseteq E$, let $\mathrm{odd}(F)$ denote the set of nodes incident to an odd number of edges in $F$. An edge subset $F$ is called a $T$-join if $\mathrm{odd}(F) = T$. See [29, Chapter 12] and [43, Chapter 29] for basics on $T$-joins. Let $S$ be a terminal subset of $V$. An inner-odd-join is an edge subset $F$ such that $G - F$ is inner-Eulerian. Let $G/S$ be the graph obtained from $G$ by identifying $S$ into one node. Hence $E(G/S)$ is naturally identified with $E$. We observe the following relation between $T$-joins and inner-odd-joins.

Lemma 3.2

$F$ is an inner-odd-join in $G$ with terminal set $S$ if and only if $F$ is an $\mathrm{odd}(E)$-join in $G/S$.

Thus any argument for inner-odd-joins falls into the theory of $T$-joins. We are interested in the minimum cost inner-odd-join problem with a cost vector $w: E \rightarrow \mathbf{R}$. Let $h[w] = h^G[w]$ be a set function on $V {\setminus } S$ defined by

$$\begin{aligned} h[w](X) := \left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm{if}\ | \delta X {\setminus } \mathcal{D}^- w|\; \text{ is } \text{ odd }, \\ 0 &{} \mathrm{if}\ | \delta X {\setminus } \mathcal{D}^- w|\; \text{ is } \text{ even }, \end{array}\right. \quad (X \subseteq V {\setminus } S). \end{aligned}$$

(3.1)

Lemma 3.3

For $w: E \rightarrow \mathbf{R}$, the following values are equal:

• (1) $\min \{w(F) \mid F: \text{ inner-odd-join } \}$.

• (2) $w^-(E) + \min \left\{ |w| \cdot \xi \mid \ \xi \in \mathbf{R}_+^E,\ \delta _{X} \cdot \xi \ge h[w](X) \ (X \subseteq V {\setminus } S)\right\}$.

• (3) $w^-(E) + \max \left\{ \sum \nolimits _{X} \pi (X) h[w] (X) \big | \sum \nolimits _{X} \pi (X) \delta _{X} \le |w|,\ \pi :{2^{V {\setminus } S} \rightarrow \mathbf{R}_+}\right\}$.

Proof

(2) $\equiv$ (3) follows from LP-duality. We show (1) $\equiv$ (2). By a well-known trick [43, Section 29.1] and [29, Section 12.2], we first reduce (1) to a minimum cost $T$-join problem for a nonnegative cost vector $|w|$. Observe that, for $F,H \subseteq E$, symmetric difference $H \triangle F$ is an $\mathrm{odd}(E)$-join if and only if $F$ is an $\mathrm{odd}(E {\setminus } H)$-join. Therefore, by taking $\mathcal{D}^- w$ as $H$, we obtain

$$\begin{aligned}&\min \{w(F) \mid F: \text{ inner-odd-join } \} = \min \{w(F) \mid F: \mathrm{odd}(E)\text{-join } \text{ in } G/S \}\nonumber \\&\quad = \min \{w(F' \triangle \mathcal{D}^{-}w) \mid F': \mathrm{odd}(E {\setminus } \mathcal{D}^-w)\text{-join } \text{ in }\; G/S \} \nonumber \\&\quad = \min \{w(F') + w(\mathcal{D}^{-}w) - 2 w(F'\cap \mathcal{D}^{-}w) \mid F': \mathrm{odd}(E {\setminus } \mathcal{D}^-w)\text{-join } \text{ in }\; G/S\} \nonumber \\&\quad = w^-(E) + \min \{|w|(F') \mid F': \mathrm{odd}(E {\setminus } \mathcal{D}^- w)\text{-join } \text{ in }\; G/ S \}. \end{aligned}$$

(3.2)

Since $|w|$ is nonnegative, the second term of the last equation is equivalent to a linear minimization over the uphull $P + \mathbf{R}_+^E$ of the $T$-join polytope $P$ for $G/S$ with $T := \mathrm{odd}(E {\setminus } \mathcal{D}^- w)$. By the Edmonds–Johnson theorem [9], the uphull $P + \mathbf{R}^E$ is the set of points $\xi$ satisfying

$$\begin{aligned} \xi (e) \ge 0&(e \in E), \nonumber \\ \xi (\delta ^{G/S} X) \ge 1&(X \subseteq V(G/S),\ |X \cap T|: \text{ odd }). \end{aligned}$$

(3.3)

A node subset in $G/S$ is identified with a node subset $X$ in $G$ with $X \subseteq V {\setminus } S$ or $S \subseteq X$; clearly $\delta ^G X = \delta ^{G/S}X$. Moreover, for $H \subseteq E, |X \cap \mathrm{odd}(H)|$ is odd if and only if $| \delta X \cap H |$ is odd. By substituting (3.3) to the last equation in (3.2), and using $h[w]$, we obtain (1) $\equiv$ (2). $\square$

The explicit inequality description of inner-odd-join polytope $Q$ is also given as

$$\begin{aligned}&0 \le \xi (e) \le 1 \quad (e \in E), \nonumber \\&\xi (\delta X {\setminus } F) + (1 - \xi )(\delta X \cap F) \ge h[- 1_{F}](X) \quad (X \subseteq V {\setminus } S,\ F \subseteq E), \end{aligned}$$

(3.4)

where $1_{F}$ denotes the incidence vector of $F$. This is also a consequence of Lemma 3.2 and the Edmonds–Johnson theorem.

We end this subsection by noting the following fundamental properties of $h = h[w]$, which immediately follow from the definition.

Lemma 3.4

For $X,Y \subseteq V {\setminus } S$, we have the following.

• (1) If $X \cap Y = \emptyset$, then $h(X \cup Y) \equiv h(X) + h(Y) \mod 2.$

• (2) If $h(X)= h(Y) = 1$, then $h(X \cap Y)= h(X \cup Y) = 1$ or $h(X {\setminus } Y) = h(Y \setminus X) = 1$.

3.3 Polynomial uncrossing process

In this subsection, we study the following cut packing program arising from (3) in Lemma 3.3, where we denote $h[w]$ by $h$.

$$\begin{aligned} \text{ Max. } \ \sum \limits _{X} \pi (X) \quad \text{ s.t. } \sum \limits _{X} \pi (X) \delta _X \le |w|,\ \pi : \mathcal{D}^+ h \rightarrow \mathbf{R}_+. \end{aligned}$$

(3.5)

We are interested in a feasible solution $\pi$ of (3.5) such that support $\mathcal{D}^+ \pi$ is laminar. Such a feasible solution is called laminar.

We are given an arbitrary feasible function $\pi$ of (3.5). Consider the following process, called an uncrossing process.

• Step 0: If $\mathcal{D}^+ \pi$ is laminar, then stop.

• Step 1: Choose an intersecting pair $X,Y \in \mathcal{D}^+ \pi$ and let $\alpha := \min (\pi (X),\pi (Y))$.

• Step 2: Choose $(X',Y') \in \{(X \cup Y, X \cap Y), (X {\setminus } Y, Y{\setminus } X)\}$ with $X',Y' \in \mathcal{D}^+ h$, decrease $\pi$ by $\alpha$ on $X,Y$ and increase $\pi$ by $\alpha$ on $X',Y'$. Go to step 0.

Here the existence of $X',Y'$ in step 2 is guaranteed by Lemma 3.4 (2). The operation in step 2 is called an uncrossing. By an arbitrary choice of $X,Y,X',Y'$ in each iteration, this process terminates after finitely many iterations. So we can make any feasible solution $\pi$ laminar, keeping the feasibility and the objective value. In particular the maximum of (3.5) is always attained by a laminar solution.

In [25], Karzanov proved that, by an appropriate choice of $X,Y,X',Y'$, the uncrossing process for $\pi$ terminates so that the number of uncrossings is bounded by a polynomial of $|V|$ and $|\mathcal{D}^+ \pi | \le |2^{V}|$. The important point is that this bound does not depend on the bit size representing the numerical values of $\pi$. Hence we have the following.

Theorem 3.5

[25] There exists a function $p:\mathbf{Z}_+ \rightarrow \mathbf{Z}_+$ such that for every feasible solution $\pi$ in (3.5) some uncrossing process to $\pi$ terminates after at most $p(|V|)$ uncrossings.

This result has an unexpected application about a stability of laminar feasible solutions in (3.5); recall that $\Vert \cdot \Vert$ is the $l_{\infty }$-norm.

Lemma 3.6

Let $\pi$ be a function on $\mathcal{D}^+ h$ having a laminar support. For a sufficiently small $\epsilon > 0$, suppose that there exists a feasible solution $\pi '$ with $\Vert \pi - \pi '\Vert \le \epsilon$. Then there exists a laminar feasible solution $\pi ^*$ such that $\Vert \pi - \pi ^*\Vert \le (2^{p(|V|)} - 1) \epsilon$ and the objective value of $\pi ^*$ is not less than that of $\pi '$.

Proof

Since $\epsilon$ is small, we can assume

$$\begin{aligned} \epsilon < \frac{\min \nolimits _{X \in \mathcal{D}^+ \pi } \pi (X)/2}{2^{p(|V|)+1} -1}. \end{aligned}$$

Apply Karzanov’s uncrossing process to $\pi '$. Then we get a laminar feasible solution $\pi ^*$ having an objective value not less than that of $\pi '$. By $\epsilon < \min _{X \in \mathcal{D}^+ \pi } \pi (X)$, we have $\mathcal{D}^+ \pi \subseteq \mathcal{D}^+ \pi '$. Therefore each uncrossing step chooses $X,Y$ so that at least one of $X,Y$ does not belong to $\mathcal{D}^+ \pi$. In each iteration $\alpha$ takes a value (of current $\pi '$) on $\mathcal{D}^+ h {\setminus } \mathcal{D}^+ \pi$, and the change in the uncrossing is bounded by the maximum value on $\mathcal{D}^+ h {\setminus } \mathcal{D}^+ \pi$. Moreover, by Theorem 3.5, the number of uncrossings is bounded by $p(|V|)$. From this we have

$$\begin{aligned} \Vert \pi - \pi ^* \Vert \le \Vert \pi - \pi ' \Vert + \Vert \pi ' - \pi ^* \Vert \le \epsilon + \sum \limits _{k=1}^{p(|V|)} 2^k \epsilon = (2^{p(|V|)+1} -1) \epsilon .\quad \end{aligned}$$

(3.6)

$\square$

3.4 Trees and laminar families

A metric-tree $\mathcal{T}$ is a metric space isometric to a $1$-dimensional contractible complex endowed with the length metric. The metric function is denoted by $d_\mathcal{T}$. For a point $p \in \mathcal{T}$ and nonnegative $\epsilon \ge 0$, the closed ball $B(p,\epsilon )$ and the open ball $B^{\circ }(p,\epsilon )$ are defined as the subsets of points $q \in \mathcal{T}$ with $d_\mathcal{T}(p,q) \le \epsilon$ and with $d_\mathcal{T}(p,q) < \epsilon$, respectively. For two points $p,q$, the closed interval $[p,q]$ is defined as the set of points $t$ with $d_\mathcal{T}(p,q) = d_\mathcal{T}(p,t) + d_\mathcal{T}(t,q)$. The open interval $(p,q)$ is defined as $[p,q] {\setminus } \{p,q\}$. A vertex of $\mathcal{T}$ is a point $q$ such that, for every $\epsilon > 0$, the open ball $B^{\circ }(q,\epsilon )$ is not an open interval. A metric-tree of two vertices is called a segment. In the case where $\mathcal{T}$ is endowed with a special point $r \in \mathcal{T}$, called a root, we can define a partial order $\preceq$ by $p \preceq q \Leftrightarrow [r,p] \subseteq [r,q]$. By $p \prec q$ we mean $[r,p] \subset [r,q]$ (proper inclusion).

Let $\varGamma$ be a tree (in the graph-theoretical sense). From $\varGamma$ we can construct a metric-tree as follows. For each edge $e = uv \in E(\varGamma )$, consider segment $F_e$ with two vertices $p_{e,u},p_{e,v}$ and unit length $d_{F_e}(p_{e,u},p_{e,v}) = 1$. Then consider the disjoint union $\bigcup _{e \in E} F_e$, and for each node $u \in V(\varGamma )$, identify points $p_{e,u}$ for all edges $e$ incident to $u$; the image of $p_{e,u}$ is denoted by $p_u$. The resulting metric-tree is denoted by $\bar{\varGamma }$. Then $(V(\varGamma ), d_{\varGamma })$ isometrically embeds into $(\bar{\varGamma },d_{\bar{\varGamma }})$ by $v \mapsto p_v$. Hence we can identify $v$ and $p_v$, and can assume $V(\varGamma ) \subseteq \bar{\varGamma }$.

Let $\varphi$ be a map from $V$ to a metric-tree $\mathcal{T}$ (with root $r$). We use the following notation:

• Let ${d_\mathcal{T}} \cdot {\varphi }$ denote the metric on $V$ defined by

  $$\begin{aligned} ({d_\mathcal{T}} \cdot {\varphi })(x,y) := {d_\mathcal{T}}(\varphi (x),\varphi (y)) \quad (x,y \in V). \end{aligned}$$

• Let $\mathcal{E}_{\varphi , \mathcal{T}}$ be the set of inclusion-maximal segment $\omega \subseteq \mathcal{T}$ not meeting the image of $\varphi$, vertices, and root $r$ (if exists).

• For $\omega \in \mathcal{E}_{\varphi , \mathcal{T}}$, let $|\omega |$ denote the length of $\omega$, and

• let $X_{\omega }$ denote the set of nodes $x \in V$ such that $\varphi (x)$ belongs to the connected component of $\mathcal{T} {\setminus } \omega$ not containing $r$.

• For a set function $h$ on $V$, define $h *(\varphi , \mathcal{T})$ by

  $$\begin{aligned} h *(\varphi , \mathcal{T}) := \sum \limits _{\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}} |\omega | h(X_{\omega }). \end{aligned}$$

One can easily see that

$$\begin{aligned} \{X_\omega \mid \omega \in \mathcal{E}_{\varphi , \mathcal{T}}\} \;\hbox {is laminar, and}\; \displaystyle {d_\mathcal{T}} \cdot {\varphi } = \sum \limits _{\omega \in \mathcal{E}_{\varphi , \mathcal{T}}} |\omega | \delta _{X_{\omega }}. \end{aligned}$$

(3.7)

Therefore a tree metric is a nonnegative sum of cut metrics for a laminar family.

Recall the tree representation of a laminar family (see [29, Section 2.2], [43, Section 13.4], and [44]); the converse of (3.7) is also true:

$$\begin{aligned}&\hbox {For any nonnegative set function}\; \pi \; \hbox {on}\; V \;\hbox {having a laminar support}, \nonumber \\&\hbox {there exist a metric-tree}\; \mathcal{T}\; \hbox {with root}\; r\; \hbox {and a map}\; \varphi : V \rightarrow \mathcal{T}\; \nonumber \\&\hbox {such that}\; \{X_\omega \mid \omega \in \mathcal{E}_{\varphi , \mathcal{T}}\} = \mathcal{D}^+ \pi \; \hbox {and}\; |\omega | = \pi (X_{\omega })\; \hbox {for}\; \omega \in \mathcal{E}_{\varphi , \mathcal{T}}. \end{aligned}$$

(3.8)

In this case, we say that $(\varphi , \mathcal{T})$ realizes $\pi$.

4 Combinatorial min–max theorem

The goal of this section is to prove the min–max relation (1.2) in Theorem 1.1. Throughout this section, $G = (V,E)$ is an undirected graph with terminal set $S \subseteq V, \mu$ is a terminal weight on $S$, and $a$ is an edge-cost. Since $\mathop {\mathrm{val}}(2\mu ;G,2a) = 2 \mathop {\mathrm{val}}(\mu ; G,a), \overline{\mathop {\mathrm{val}}}(2\mu ;G, 2a) = 2 \overline{\mathop {\mathrm{val}}}(\mu ; G,a)$, it suffices to consider the case where

$$\begin{aligned} \hbox {both}\; \mu \; \hbox {and}\; a\; \hbox {are even-valued, and}\; \mu \; \hbox {is realized by}\; ({\varGamma }, \{p_s\}_{s \in S}; 1). \end{aligned}$$

(4.1)

Also we may assume the following nonredundancy:

$$\begin{aligned} \hbox {For each}\; p \in V(\varGamma )\; \hbox {of degree one, there is}\,s \in S\; \hbox {with}\; p= p_s. \end{aligned}$$

(4.2)

Under the assumptions (4.1) and (4.2), we are going to show:

$$\begin{aligned} \mathop {\mathrm{val}}(\mu ;G,a) = \overline{\mathop {\mathrm{val}}}(\mu ;G,a) = \min _{\rho } \max _{F} (d_{\varGamma } \cdot \rho - a) (E {\setminus } F). \end{aligned}$$

(4.3)

In Sect. 4.2, we introduce a special dual of (2.2), which is a continuous relaxation of the RHS of (1.2). In Sect. 4.3, we show that the optimal value of this special dual is always attained by a discrete solution, which implies that the optimal value of (2.2) is equal to the RHS of (1.2). Finally, in Sect. 4.4, we prove that (2.2) has an integral optimal solution, which establishes the formula (1.2).

4.1 Feasible triple $(\rho , \varphi , \mathcal{T})$

In this section, we introduce a special dual problem of (2.2). Consider a triple $(\rho ,\varphi ,\mathcal{T})$ of a metric-tree $\mathcal{T}$ with root $r$, maps $\rho : V \rightarrow \bar{\varGamma }$ and $\varphi : V \rightarrow \mathcal{T}$. We view $(\rho (x),\varphi (x))$ as a node-potential that is a point in the Cartesian product $\bar{\varGamma } \times \mathcal{T}$ of two metric-trees.

A triple $(\rho ,\varphi , \mathcal{T})$ is said to be feasible (to $G$) if it satisfies

$$\begin{aligned}&\hbox {(1)}\quad \rho (s) = p_s\; \hbox {and}\; \varphi (s) = r\; \hbox {for}\; s \in S, \hbox {and}\nonumber \\&\hbox {(2)}\quad (d_\mathcal{T} \cdot {\varphi })(e) \le | d_{\bar{\varGamma }} \cdot {\rho } - a|(e)\; \hbox {for}\, e \in E. \end{aligned}$$

(4.4)

A feasible triple $(\rho ,\varphi ,\mathcal{T})$ is said to be rational if the length of each segment in $\mathcal{E}_{\rho , \bar{\varGamma }}$ and in $\mathcal{E}_{\varphi , \mathcal{T}}$ is rational. For a feasible triple $(\rho ,\varphi ,\mathcal{T})$, define the objective function $\tau$ by

$$\begin{aligned} \tau (\rho ,\varphi ,\mathcal{T}) := (d_{\bar{\varGamma }} \cdot {\rho } - a)^+ (E) - h[d_{\bar{\varGamma }} \cdot {\rho } - a] *(\varphi , \mathcal{T}). \end{aligned}$$

(4.5)

Consider the optimization problem of minimizing $\tau$:

$$\begin{aligned} \text{ Min. } \tau (\rho , \varphi , \mathcal{T}) \ \text{ s.t. }\, (\rho , \varphi , \mathcal{T}): \,\hbox {feasible triple.} \end{aligned}$$

(4.6)

It turns out soon that this is an alternative expression of the LP-dual to (2.2). In the sequel, we will often use the following simplified notation:

$$\begin{aligned} d^{\rho }&:= d_{{\bar{\varGamma }}} \cdot \rho ,\nonumber \\ d^{\varphi }&:= d_{\mathcal{T}} \cdot \varphi , \nonumber \\ \mathcal{D}^{\pm }_{\rho }&:= \mathcal{D}^{\pm }(d_{\bar{\varGamma }} \cdot {\rho } - a), \nonumber \\ h_{\rho }&:= h[d_{\bar{\varGamma }} \cdot \rho - a]. \end{aligned}$$

(4.7)

Recall (3.1) for the definition of $h$. In particular,

$$\begin{aligned} h_{\rho }(X) = \left\{ \begin{array}{ll} 1 &{} \mathrm{if}\ | \delta X {\setminus } \mathcal{D}^-_\rho |\,\text{ is } \text{ odd }, \\ 0 &{} \mathrm{if}\ | \delta X {\setminus } \mathcal{D}^-_\rho |\,\text{ is } \text{ even }, \end{array}\right. \quad (X \subseteq V {\setminus } S). \end{aligned}$$

(4.8)

The problem (4.6) is rewritten as

$$\begin{aligned} \text{ Min. }&(d^{\rho } - a)^+(E) - h_{\rho } *(\varphi , \mathcal{T}) \nonumber \\ \text{ s.t. }&\mathcal{T}: \text{ metric-tree } \text{ with } \text{ root }\; r, \nonumber \\&\varphi : V \rightarrow \mathcal{T}, \varphi (s) = r \ (s \in S), \nonumber \\&\rho : V \rightarrow {\bar{\varGamma }}, \rho (s) = p_s \ (s \in S), \nonumber \\&d^{\varphi }(e) \le |d^{\rho } - a|(e) \ (e \in E). \end{aligned}$$

(4.9)

4.2 Duality

The goal of this subsection is to establish the duality and the (dual) stability of LP (2.2):

Lemma 4.1

The following values are equal:

• (1) $\overline{\mathop {\mathrm{val}}}(\mu ;G,a)$.

• (2) $\min \tau (\rho ,\varphi ,\mathcal{T})$, where the minimum is taken over all rational feasible triples $(\rho ,\varphi ,\mathcal{T})$.

• (3) $\min \max (d - a)(E {\setminus } F)$, where the maximum is taken over all inner-odd-joins $F$, and the minimum is taken over all metrics $d$ on $V$ satisfying $d(s,t) \ge \mu (s,t)$ for $s,t \in S$.

• (4) $\min \max (d^{\rho }- a)(E {\setminus } F)$, where the maximum is taken over all inner-odd-joins $F$, and the minimum is taken over all maps $\rho : V \rightarrow \bar{\varGamma }$ with $\rho (s) = p_s$ for $s \in S$.

• (5) The optimal value of the following problem:

  $$\begin{aligned} \text{ Min. }&(d - a)^+(E) - \sum \limits _{X} \pi (X) h[d - a](X) \nonumber \\ \text{ s.t. }&\sum \limits _{X} \pi (X) \delta _X(e) \le |d-a|(e) \quad (e \in E), \nonumber \\&d(s,t) \ge \mu (s,t) \quad (s,t \in S), \\&d: \text{ metric } \text{ on }\; V,\nonumber \\&\pi : 2^{V {\setminus } S} \rightarrow \mathbf{R}_+. \nonumber \end{aligned}$$

  (4.10)

Lemma 4.2

Let $(\rho ,\varphi , \mathcal{T})$ be a nonoptimal feasible triple. For every $\epsilon > 0$, there exists a rational feasible triple $(\rho ',\varphi ',\mathcal{T}')$ such that $\tau (\rho ',\varphi ',\mathcal{T}') < \tau (\rho ,\varphi , \mathcal{T}), \Vert d^{\rho '} - d^{\rho }\Vert \le \epsilon$, and $\Vert (d^{\varphi '} - d^{\varphi })^+\Vert \le \epsilon$.

4.2.1 Proof of Lemma 4.1

(1) $\equiv$ (3). Dualize (2.2) with fixed $\xi \in Q$. Then we get

$$\begin{aligned} \overline{\mathop {\mathrm{val}}}(\mu ; G,a) = \max _{\xi \in Q} \min _l \{(l - a)(E) - (l - a) \cdot \xi \}, \end{aligned}$$

(4.11)

where the minimum is taken over all $l: E \rightarrow \mathbf{R}_+$ satisfying $l(P) \ge \mu (s_P,t_P)$ for $P \in {\varPi }$. By the minimax theorem we obtain

$$\begin{aligned} \max _{\xi \in Q} \min _l \{(l - a)(E) - (l - a) \cdot \xi \}&= \min _l \max _{\xi \in Q} \{(l - a)(E) - (l - a) \cdot \xi \} \\&= \min _l \max _F (l - a)(E {\setminus } F). \end{aligned}$$

Note that the first equality can also be directly obtained by the LP-duality with the help of the explicit description (3.4) of $Q$.

Let $g: \mathbf{R}^E_+ \rightarrow \mathbf{R}$ be defined by

$$\begin{aligned} g(l):= \max _F (l - a)(E {\setminus } F) \quad (l \in \mathbf{R}^E_+), \end{aligned}$$

(4.12)

where the maximum is taken over all inner-odd-joins $F$. Here $g$ is monotone nondecreasing. Indeed, for $l \le l'$, take an inner-odd-join $F^*$ with $g(l) = (l-a)(E {\setminus } F^*)$. Then $(l-a)(E {\setminus } F^*) \le (l'-a)(E {\setminus } F^*) \le g(l')$. Therefore we can replace $l$ by the shortest path metric $d_{G,l}$ on $G$ with respect to $l$. From this we obtain (1) $\equiv$ (3); obviously the minimum of $g$ is attained by a rational solution.

(3) $\equiv$ (4). (4) $\ge$ (3) is obvious. Since $g$ is monotone nondecreasing, (3) $\ge$ (4) follows from the following claim; the proof is given for completeness.

Claim 4.3

[17, 19] For any metric $d$ on $V$ with $d(s,t) \ge \mu (s,t)$ for $s,t \in S$, there exists a map $\rho : V \rightarrow \bar{\varGamma }$ such that $\rho (s) = p_s\;(s \in S)$ and $d^{\rho } (x,y) \le d(x,y)$ for $x,y \in V$.

Proof

Suppose $V = \{x_1,x_2,\ldots ,x_n\}$ and $S = \{x_1,x_2,\ldots ,x_k\}$. Define $\rho : V \rightarrow \bar{\varGamma }$ recursively by

$$\begin{aligned} \rho (x_i) := \left\{ \begin{array}{l@{\quad }l} p_{x_i} &{} \mathrm{if}\ i \le k, \\ \text{ an } \text{ arbitrary } \text{ point } \text{ in }\; \mathop {\bigcap }\nolimits _{j < i} B(\rho (x_j), d(x_j,x_i)) &{} \mathrm{if}\ i > k, \end{array}\right. \quad (1 \le i \le n). \end{aligned}$$

We show by induction that $\bigcap _{j < i} B(\rho (x_j), d(x_j,x_i))$ is nonempty, i.e., $\rho$ is well-defined. If this is true, then $\rho (x_i) \in B(\rho (x_j), d(x_j,x_i))$ implies $d^\rho (x_i,x_j) \le d(x_i,x_j)$.

Recall that any collection of subtrees has the Helly property. So it suffices to show the pairwise nonempty intersection. Here two balls $B(p,r)$ and $B(p',r')$ intersect if and only if $d_{\bar{\varGamma }}(p,p') \le r + r'$. Therefore $B(\rho (x_j), d(x_i,x_j)) \cap B(\rho (x_{j'}), d(x_i,x_{j'})) \ne \emptyset$ follows from $d(x_i,x_j) + d(x_i,x_{j'}) \ge d(x_j, x_{j'}) \ge d^{\rho }(x_j,x_{j'})$, where the last inequality follows from the induction. $\square$

In the proof, if $d$ is rational, then we can choose $\rho$ so that the length of each segment in $\mathcal{E}_{\rho , \bar{\varGamma }}$ is rational.

(3) $\equiv$ (5). This follows from Lemma 3.3.

(5) $\equiv$ (2). For a feasible solution $(d,\pi )$ in (4.10), let $\tau (d,\pi )$ denote the objective value. For a feasible triple $(\rho ,\varphi ,\mathcal{T})$, let $\pi ^{\varphi ,\mathcal{T}}: 2^{V {\setminus } S} \rightarrow \mathbf{R}_+$ be defined by

$$\begin{aligned} \pi ^{\varphi ,\mathcal{T}}(X) = \left\{ \begin{array}{l@{\quad }l} |\omega | &{} \mathrm{if}\ X = X_{\omega }\, \text{ for }\; \omega \in \mathcal{E}_{\varphi , \mathcal{T}}, \\ 0 &{} \mathrm{otherwise,} \end{array}\right. \quad (X \subseteq V {\setminus } S). \end{aligned}$$

(4.13)

By (3.7) and (4.4) (2), $(d^{\rho }, \pi ^{{\varphi ,\mathcal{T}}})$ is feasible to (4.10) with $\tau (d^{\rho },\pi ^{{\varphi ,\mathcal{T}}}) = \tau (\rho ,\varphi ,\mathcal{T})$. Conversely, by (4) $\equiv$ (5) we can take an optimal solution $(d,\pi )$ in (4.10) such that $d = d^{\rho }$ for a map $\rho : V \rightarrow \bar{\varGamma }$ with $\rho (s) = p_s$ for $s \in S$. By the uncrossing process in the previous section, we can make $\pi$ laminar, with keeping $(d^{\rho }, \pi )$ feasible (and optimal). There are a metric-tree $\mathcal{T}$ with root $r$ and a map $\varphi : V \rightarrow \mathcal{T}$ such that $(\varphi , \mathcal{T})$ realizes $\pi$. Then we have $d^{\varphi }(e) = \sum \nolimits _{X} \pi (X) \delta _{X}(e) \le |d^{\rho } - a|(e)$ for $e \in E$. Also $\varphi (S) = \{r\}$ by $\mathcal{D}^+ \pi \subseteq 2^{V {\setminus } S}$. This means that $(\rho , \varphi , \mathcal{T})$ is a feasible triple with $\tau (\rho , \varphi , \mathcal{T}) = \tau (d, \pi )$. We can assume that both $d$ and $\pi$ are rational-valued. Consequently $(\rho , \varphi , \mathcal{T})$ can be taken to be rational. The proof of Lemma 4.1 is complete. $\square$

4.2.2 Proof of Lemma 4.2

Suppose that $(\rho ,\varphi ,\mathcal{T})$ is a nonoptimal feasible triple. We can assume that $h_\rho (X_{\omega }) = 1$ for every $\omega \in \mathcal{E}_{\varphi , \mathcal{T}}$. Otherwise, contract each $\omega \in \mathcal{E}_{\varphi , \mathcal{T}}$ with $h_\rho (X_{\omega }) = 0$ to obtain a feasible triple $(\rho , \hat{\varphi },\hat{\mathcal{{T}}})$ with $\tau (\rho , \hat{\varphi }, \hat{\mathcal{{T}}}) = \tau (\rho , \varphi , \mathcal{T}), d^{\hat{\varphi }} \le d^{\varphi }$, and $h_{\rho }(X_{\omega }) =1$ for $\omega \in \mathcal{E}_{\hat{\varphi }, \hat{\mathcal{{T}}}}$. Applying the statement (of Lemma 4.2) to $(\rho , \hat{\varphi }, \hat{\mathcal{{T}}})$, we obtain the statement for $(\rho , \varphi , \mathcal{T})$.

Our goal is to show the following claim:

Claim 4.4

For every $\tilde{\epsilon }> 0$, there exists a rational feasible solution $(\tilde{d}, \tilde{\pi })$ in (4.10) such that

• (1) $\tau (\tilde{d},\tilde{\pi }) < \tau (\rho ,\varphi ,\mathcal{T})$,

• (2) $\Vert \tilde{d} - d^{\rho } \Vert \le \tilde{\epsilon }$,

• (3) $\Vert \tilde{\pi }- \pi ^{\varphi , \mathcal{T}} \Vert \le \tilde{\epsilon }$, and

• (4) $\tilde{d} = d^{\tilde{\rho }}$ for a map $\tilde{\rho }: V \rightarrow V(\bar{\varGamma })$ with $\tilde{\rho }(s) = p_s\;(s \in S)$.

Recall that $\tau (d,\pi )$ is the objective value of (4.10), and $\pi ^{\varphi , \mathcal{T}}$ is defined in (4.13). Suppose that this claim is true. Take a sufficiently small $\tilde{\epsilon }> 0$, and take $(\tilde{d},\tilde{\pi })$ with properties (1–4) in this claim. By (2), $\mathcal{D}^{\sigma }_{\rho } \subseteq \mathcal{D}^{\sigma }(\tilde{d} - a )$ holds for $\sigma \in \{+,-\}$. By this fact together with $|d^{\rho } -a|(e) \ge d^{\varphi }(e) \ge |\omega | > 0\;(\omega \in \mathcal{E}_{\varphi , \mathcal{T}}, e\in \delta X_{\omega }), d^{\rho } -a$ and $\tilde{d} - a$ have the same sign pattern on $\delta X_{\omega }$. This means $h[\tilde{d} - a](X_{\omega }) = h_{\rho } (X_{\omega }) = 1\;(\omega \in \mathcal{E}_{\varphi , \mathcal{T}})$. Therefore we can assume $\mathcal{D}^+ \pi ^{\varphi , \mathcal{T}} \subseteq \mathcal{D}^+ \tilde{\pi }\subseteq \mathcal{D}^+ h[\tilde{d}-a].$ Take a sufficiently small $\tilde{\epsilon }>0$. Applying Lemma 3.6 to $(\pi , \pi ') := (\pi ^{\varphi , \mathcal{T}}, \tilde{\pi })$ and $w := \tilde{d}-a$, we obtain laminar $\tilde{\pi }'$ such that $(\tilde{d}, \tilde{\pi }')$ is (rational) feasible in (4.10), $\tau (\tilde{d},\tilde{\pi }') \le \tau (d', \pi ')$, and $\Vert \tilde{\pi }' - \pi ^{\varphi , \mathcal{T}} \Vert \le C \tilde{\epsilon }$, where $C$ is a constant independent of $\tilde{\epsilon }$. Take $(\tilde{\varphi },\tilde{\mathcal{T}})$ realizing $\tilde{\pi }'$. Then $\tau (\tilde{\rho }, \tilde{\varphi },\tilde{\mathcal{T}}) < \tau (\rho ,\varphi ,\mathcal{T}), \Vert d^{\tilde{\rho }} - d^{\rho }\Vert \le \tilde{\epsilon }$, and $\Vert d^{\tilde{\varphi }} - d^{\varphi } \Vert \le 2 |V| C \tilde{\epsilon }$. Since $\tilde{\epsilon }$ can be taken to be arbitrary small, $(\tilde{\rho }, \tilde{\varphi },\tilde{\mathcal{T}})$ is a required rational feasible triple in Lemma 4.2.

We show Claim 4.4. Compare $\tau (\rho ,\varphi ,\mathcal{T})$ with $g(d^{\rho })$ [defined by (4.12)]. By (the proof of) Lemma 4.1, $g(d^{\rho }) \le \tau (\rho ,\varphi ,\mathcal{T})$ holds. Suppose that $g(d^{\rho }) < \tau (\rho ,\varphi ,\mathcal{T})$. This means that $\pi ^{\varphi ,\mathcal{T}}$ is feasible but nonoptimal to (4.10) with $d = d^{\rho }$ fixed. By convexity, there is a feasible $\tilde{\pi }$ in an arbitrary open neighborhood of $\pi$ with $\tau (d^{\rho },\tilde{\pi }) < \tau (\rho ,\varphi ,\mathcal{T})$.

Suppose $g(d^{\rho }) = \tau (\rho , \varphi , \mathcal{T})$. This means that $d^{\rho }$ is nonoptimal to the following convex optimization:

$$\begin{aligned} \text{ Min. } \quad g(d) \quad \text{ s.t. }\quad d: \text{ metric } \text{ on }\; V\; \text{ with }\; d(s,t) \ge \mu (s,t)\; \text{ for }\; s,t \in S. \end{aligned}$$

Take a sufficiently small $\epsilon ' > 0$. By convexity, there exists a rational metric $d'$ on $V$ with $d(s,t) \ge \mu (s,t)$ for $s,t \in S$ such that $g(d') < g(d^{\rho })$ and $\Vert d' - d^{\rho } \Vert \le \epsilon '$. According to Claim 4.3, take a map $\rho ':V \rightarrow \bar{\varGamma }$ such that $\rho '(s) = p_s, d^{\rho '} \le d'$, and the length of each segment in $\mathcal{E}_{\rho ', \bar{\varGamma }}$ is rational. Then

$$\begin{aligned} \rho '(x) \in B(\rho (x), \epsilon ') \quad (x \in V). \end{aligned}$$

(4.14)

Indeed, by assumption (4.2), there exists $s \in S$ with $d_{\bar{\varGamma }}(\rho '(x),\rho (x)) + d_{\bar{\varGamma }}(p_s,\rho (x)) = d_{\bar{\varGamma }}(p_s,\rho '(x))$. Thus we have

$$\begin{aligned} d_{\bar{\varGamma }}(\rho '(x),\rho (x))&= d^{\rho '}(s,x) - d^{\rho }(s,x)\\&= (d'(s,x) - d^{\rho }(s,x)) + (d^{\rho '}(s,x) - d'(s,x)) \le \epsilon ', \end{aligned}$$

where the last inequality follows from $\Vert d' - d^{\rho } \Vert \le \epsilon '$ and $d^{\rho '} \le d'$. Moreover, since $\epsilon '$ is small,

$$\begin{aligned} B(\rho (x), \epsilon ') \cap B(\rho (y), \epsilon ') = \emptyset \quad (x,y \in V: \rho (x) \ne \rho (y)). \end{aligned}$$

(4.15)

For $\alpha \in [0,1]$, define $\rho _\alpha : V \rightarrow \bar{\varGamma }$ by $\rho _{\alpha }(x) :=$ the (unique) point $p$ in $[\rho (x), \rho '(x)] \subseteq B(\rho (x), \epsilon ')$ with $d_{\bar{\varGamma }}(\rho (x),p) = (1 - \alpha ) d_{\bar{\varGamma }}(\rho (x), \rho '(x))$ and $d_{\bar{\varGamma }}(p, \rho '(x)) = \alpha d_{\bar{\varGamma }}(\rho (x), \rho '(x))$. Then, by (4.15), we can take a simple path in $\bar{\varGamma }$ containing $[\rho (x),\rho '(x)]$ and $[\rho (y),\rho '(y)]$ for $x,y \in V$. From this we obtain

$$\begin{aligned} d^{\rho _{\alpha }} = (1- \alpha ) d^{\rho } + \alpha d^{\rho '}. \end{aligned}$$

(4.16)

Take a rational optimal solution $\pi '$ of (4.10) with $d = d^{\rho '}$ fixed. Then $\tau (d^{\rho '}, \pi ') = g(d^{\rho '}) < \tau (\rho ,\varphi ,\mathcal{T})$. For $\alpha \in [0,1]$, define $\pi _{\alpha }$ by

$$\begin{aligned} \pi _{\alpha } := (1- \alpha ) \pi ^{\varphi , \mathcal{T}} + \alpha \pi '. \end{aligned}$$

We are going to verify that for small rational $\alpha > 0, (d^{\rho _{\alpha }}, \pi _{\alpha })$ is a required rational solution. By $\rho _{\alpha }(x) \in B(\rho (x), \epsilon ')$, we have $\Vert d^{\rho _{\alpha }} - d^{\rho } \Vert \le 2 \epsilon '$. Therefore we have

$$\begin{aligned} \mathcal{D}^\sigma _{\rho } \subseteq \mathcal{D}^\sigma _{\rho _{\alpha }} = \mathcal{D}^\sigma _{\rho '} \quad (\sigma \in \{-,+\}, \alpha > 0). \end{aligned}$$

(4.17)

Then $(d^{\rho _{\alpha }}, \pi _{\alpha })$ is feasible to (4.10) since

$$\begin{aligned} \sum \limits _{X} \pi _\alpha \delta _X(e) \le (1 -\alpha ) |d^{\rho } - a|(e) + \alpha |d^{\rho '} -a|(e) = |d^{\rho _{\alpha }} - a|(e) \quad (e \in E), \end{aligned}$$

where the last equality follows from (4.16) and (4.17). Therefore $(d^{\rho _\alpha }, \pi _{\alpha })$ satisfies (2), (3) and (4) of Claim 4.4 for small $\alpha > 0$. Finally, we verify that $\tau$ is linear on $\alpha$:

$$\begin{aligned} \tau (d^{\rho _\alpha }, \pi _{\alpha }) = (1 - \alpha ) \tau (\rho , \varphi , \mathcal{T}) + \alpha \tau (d^{\rho '}, \pi '). \end{aligned}$$

(4.18)

This implies (1) in Claim 4.4 since $\tau (d^{\rho '},\pi ') < \tau (\rho ,\varphi ,\mathcal{T})$. We show (4.18). By (4.17) we have $(d^{\rho _{\alpha }} - a)^+(E) = (1- \alpha ) (d^{\rho }-a)^+(E) + \alpha (d^{\rho '}-a)^+ (E)$. Moreover, by (4.17) (with the same argument after Claim 4.4), $h_{\rho _{\alpha }} = h_{\rho '}$ for $\alpha > 0$, and $h_{\rho _{\alpha }}(X_{\omega }) = h_{\rho }(X_{\omega })$ for $\omega \in \mathcal{E}_{\varphi , \mathcal{T}}$. Thus we have

$$\begin{aligned} \sum h_{\rho _{\alpha }}(X) \pi _{\alpha } (X) = (1-\alpha ) \sum h_{\rho } (X) \pi ^{\varphi , \mathcal{T}} (X) + \alpha \sum h_{\rho '} (X) \pi ' (X). \end{aligned}$$

This implies (4.18). $\square$

4.3 Dual integrality

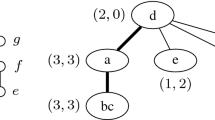
A feasible triple $(\rho , \varphi , \mathcal{T})$ is said be bipartite if $\mathcal{T} = \bar{T}$ for some graph-theoretical tree $T, \varphi (V) \subseteq V(T), \rho (V) \subseteq V(\varGamma )$, and $d^{\rho } + d^{\varphi }$ is even-valued. Consider the Cartesian product graph ${\varGamma } \times T$ of two trees $\varGamma$ and $T$, which is also a bipartite graph. From the last condition, the image of $(\rho ,\varphi )$ belongs to the color class containing $(p_s,r)$; see Fig. 1. The main result in this section is that the minimum of $\tau$ is attained by a bipartite triple. For $r \in \mathbf{R}$, let $\lceil r \rceil ^\mathrm{even}$ denote the smallest even integer not less than $r$.

Fig. 1

Product of two trees

Theorem 4.5

(Dual integrality) For every rational feasible triple $(\rho ,\varphi ,\mathcal{T})$, there exists a bipartite feasible triple $(\rho ^*,\varphi ^*,\mathcal{T}^*)$ such that

• (1) $\tau (\rho ^*, \varphi ^*, \mathcal{T}^*) \le \tau (\rho ,\varphi ,\mathcal{T})$, and

• (2) $(d^{\rho ^*} + d^{\varphi ^*})(x,y) \le \lceil (d^{\rho } + d^{\varphi })(x,y) \rceil ^\mathrm{even}$ for $x, y \in V$.

In particular, the minimum of $\tau$ is attained by a bipartite feasible triple.

Since the image of $\rho$ belongs to $V(\varGamma )$, we have the following.

Corollary 4.6

$\overline{\mathop {\mathrm{val}}}(\mu ;G,a) = \min \max (d^\rho - a) (E {\setminus } F),$ where the maximum is taken over all inner-odd-joins $F$ and the minimum is taken over all maps $\rho : V \rightarrow V(\varGamma )$ with $\rho (s) = p_s$ for $s \in S$.

Assuming Theorem 4.10 (and Lemma 4.2), we obtain the dual stability:

Lemma 4.7

(Dual stability) If a bipartite feasible triple $(\rho ,\varphi ,\mathcal{T})$ is not optimal, then there exists a bipartite feasible triple $(\rho ', \varphi ', \mathcal{T}')$ such that $\tau (\rho ', \varphi ',\mathcal{T}') < \tau (\rho , \varphi ,\mathcal{T})$, and $({d}^{\rho '} + {d}^{\varphi '})(x,y) \le ({d}^{\rho } + {d}^{\varphi })(x,y) + 2$ for $x,y \in V$.

Proof

By Theorem 4.10, $(\rho ,\varphi , \mathcal{T})$ is not optimal to (4.6). By Lemma 4.2, there is a rational feasible triple $(\tilde{\rho },\tilde{\varphi }, \tilde{\mathcal{T}})$ with $\tau (\tilde{\rho },\tilde{\varphi }, \tilde{\mathcal{T}}) < \tau (\rho ,\varphi ,\mathcal{T})$ and $(d^{\tilde{\rho }} + d^{\tilde{\varphi }})(x,y) \le (d^{\rho } + d^{\varphi })(x,y) + 2\;(x,y \in V)$. By Theorem 4.10, there is a bipartite feasible triple $(\rho ',\varphi ',\mathcal{T}')$ with $\tau (\rho ',\varphi ',\mathcal{T}') \le \tau (\tilde{\rho },\tilde{\varphi }, \tilde{\mathcal{T}}) (< \tau (\rho ,\varphi ,\mathcal{T}))$ and $(d^{\rho '} + d^{\varphi '})(x, y) \le \lceil (d^{\tilde{\rho }} + d^{\tilde{\varphi }})(x,y)\rceil ^\mathrm{even} \le (d^{\rho } + d^{\varphi })(x,y) + 2\;(x,y \in V)$. $\square$

The remainder of this subsection is devoted to the proof of Theorem 4.5, which is the most technical part of the paper. Readers may skip the rest and proceed to Sect. 4.4 in the first reading.

0: Notation. Let $(\rho ,\varphi ,\mathcal{T})$ be a (nonbipartite) feasible triple. We may assume that

$$\begin{aligned} h_{\rho } (X_\omega ) = 1 \quad (\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}). \end{aligned}$$

(4.19)

Otherwise, by contracting segment $\omega$ with $h_{\rho }(X_{\omega }) = 0$, we obtain a new $(\tilde{\varphi }, \tilde{\mathcal{T}})$ with $d^{\tilde{\varphi }} \le d^{\varphi }$. Then $(\rho ,\tilde{\varphi }, \tilde{\mathcal{T}})$ is feasible, and $\tau (\rho , \tilde{\varphi },\tilde{\mathcal{T}}) = \tau (\rho ,\varphi ,\mathcal{T})$. Therefore it suffices to prove Theorem 4.5 for $(\rho , \tilde{\varphi }, \tilde{\mathcal{T}})$.

By applying repeated local changes to $(\rho ,\varphi ,\mathcal{T})$, we try to construct a bipartite feasible triple $(\rho ^*,\varphi ^*,\mathcal{T}^*)$ satisfying conditions (1) and (2). We need some notation to describe such local changes. For notational simplicity, we often denote $d_\mathcal{T}, d_{\bar{\varGamma }}$ by $d$, if they are distinguished in the context. Let $\{R, B\}$ be the color classes of (bipartite graph) $\varGamma$. Since $\mu$ is even-valued, we may assume $\{p_s\}_{s \in S} \subseteq B$. By rationality of $(\rho ,\varphi ,\mathcal{T})$, the length of each segment in $\mathcal{E}_{\rho , \bar{\varGamma }}$ and in $\mathcal{E}_{\varphi ,\mathcal{T}}$ is a multiple of $\epsilon := 1/M$ for a positive integer $M$. An $\epsilon$-point is a point $q$ in $\mathcal{T}$ such that $d_\mathcal{T}(q,p)$ is a multiple of $\epsilon$ for some (every) vertex $p$ in $\mathcal{T}$; the image of $\varphi$ belongs to the set of $\epsilon$-points. Similarly we can consider $\epsilon$-points in $\bar{\varGamma }$. So we can regard $\mathcal{T}$ (and $\bar{\varGamma }$) as a (graph-theoretical) tree on the set of $\epsilon$-points with uniform edge-length $\epsilon$. For an $\epsilon$-point $p$ in $\bar{\varGamma } {\setminus } V(\varGamma )$, there is a unique edge $uv$ in $\varGamma$ with $p \in [u,v]$ and $(u,v) \in R \times B$. Let $p^{\rightarrow B, \epsilon }$ denote the adjacent $\epsilon$-point $p'$ close to $B$, the unique point $p'$ satisfying $d(p,v) = d(p',v) + \epsilon$. Similarly, let $p^{\rightarrow R, \epsilon }$ denote the unique point $p'$ with $d(p,u) = d(p',u) + \epsilon$.

Recall the partial order $\preceq$ (Sect. 3.4). For $q \in \mathcal{T}$, let $X_{q}, X_{q, \preceq }$, and $X_{q, \prec }$ denote the sets of nodes $x \in V$ with $q = \varphi (x), q \preceq \varphi (x)$, and $q \prec \varphi (x)$, respectively. For an $\epsilon$-point $q \in \mathcal{T}$, let $\mathcal{C} = \mathcal{C}_q$ be the set of connected components of $\mathcal{T} {\setminus } B^{\circ }(q,\epsilon )$. Let $C_0$ denote the (unique) component in $\mathcal{C}$ containing $r$; it exists exactly when $q \ne r$. By (4.19) and Lemma 3.4 (1) we have:

$$\begin{aligned}&h_{\rho } (X_{q, \preceq }) = 1, \end{aligned}$$

(4.20)

$$\begin{aligned}&h_{\rho } (X_{q, \prec }) \equiv |\mathcal{C} {\setminus } \{C_{0}\} | \mod 2 \quad (q \in \mathcal{T} {\setminus } \{r\}). \end{aligned}$$

(4.21)

1: Critical points. Consider an $\epsilon$-point $q \in \mathcal{T}$ with the following properties:

$$\begin{aligned}&\hbox {(i)}\quad \rho (X_{q, \prec }) \subseteq V({\varGamma }).\nonumber \\&\hbox {(ii)}\quad \hbox {For each}\; \omega \in \mathcal{E}_{\varphi , \mathcal{T}}\, \hbox {belonging to a component in}\; \mathcal{C} {\setminus } \{C_0\},\; \hbox {the length}\; |\omega |\nonumber \\&\hbox {is an integer.}\nonumber \\&\hbox {(iii)}\, \hbox {For}\, x,y \in X_{q, \prec }, (d^{\rho } + d^{\varphi })(x,y)\, \hbox {is an even integer if}\, \varphi (x)\, \hbox {and}\, \varphi (y)\nonumber \\&\hbox {belong to the same component in}\; \mathcal{C} {\setminus } \{C_0\}. \end{aligned}$$

(4.22)

This means that the restriction of $(\rho ,\varphi ,\mathcal{T})$ to (the preimage of) each component in $\mathcal{C} {\setminus } \{C_0\}$ is bipartite. Therefore we can draw a grid on $C \times \bar{\varGamma }$ (as in Fig. 2) so that its vertices are points having even distance-sum $d_{\bar{\varGamma }} + d_\mathcal{T}$ from some (every) image of $(\rho ,\varphi )$ in $C \times \bar{\varGamma }$. We try to extend these partial grids to the whole grid; the subsequent argument is based on this intuition. A critical point is a minimal $\epsilon$-point having the property (4.22). We will make local changes on $(\rho ,\varphi , \mathcal{T})$ at critical points, and move critical points toward $r$.

Fig. 2

Drawing grids in $C \times \bar{\varGamma }$ for (B) $C \in \mathcal{C}^B \cup \mathcal{I}^B$ and (R) $C \in \mathcal{C}^R \cup \mathcal{I}^R$

Let $q \in \mathcal{T}$ be a critical point. Fix $b \in B$. For a component $C \in \mathcal{C} {\setminus } \{C_0\}$, take a node $x$ with $\varphi (x) \in C$ [it exists by (4.19)]. By condition (4.22), we see that $d(q, \varphi (x)) - \lfloor d(q, \varphi (x)) \rfloor$ and the parity of $d(b, \rho (x)) + \lfloor d(q, \varphi (x)) \rfloor$ are determined independent of the choice of $x$ and $b$. We denote them by ${\varDelta }_C$ and $D_C$, respectively. Partition $\mathcal{C} {\setminus } \{C_0\}$ according to ${\varDelta }_{C}, D_{C}$ as:

$$\begin{aligned} \mathcal{C}^B&:= \{C \mid {\varDelta }_{C} \ne 0,\ D_{C}=\text{ even } \},\ \mathcal{C}^R := \{C \mid {\varDelta }_{C} \ne 0,\ D_{C}=\text{ odd } \}, \\ \mathcal{I}^B&:= \{C \mid {\varDelta }_{C} = 0,\ D_{C}=\text{ even } \},\ \mathcal{I}^R := \{C \mid {\varDelta }_{C} = 0,\ D_{C}=\text{ odd } \}. \end{aligned}$$

Figure 2 illustrates a portion of $C \times \bar{\varGamma }$ for $C \in \mathcal{C} {\setminus } \{C_0\}$.

Let $X^B$ be the set of nodes $x \in X_{q, \preceq }$ such that $d(b, \rho (x)) + d(q, \varphi (x))$ is even. $X^B$ consists of nodes $x \in X_{q}$ with $\rho (x) \in B$ and nodes $x \in X_{q, \prec }$ with $\varphi (x) \in C \in \mathcal{I}^B$. Similarly, let $X^R$ be the set of nodes $x \in X_{q, \preceq }$ such that $d(b, \rho (x)) + d(q, \varphi (x))$ is odd. For $C \in \mathcal{C}$ let $q_C$ denote the (unique) point in $C$ meeting $B(q,\epsilon )$.

2: Local changes at  $q \ne r$. Take a critical point $q$. We first consider the case $q \ne r$. Suppose that $X^B \ne \emptyset$ and $h_{\rho } (X^B) = 0$. This implies $h_{\rho } (X_{q, \preceq } {\setminus } X^B) = 1$ by Lemma 3.4 (1) and (4.20). We construct modification $(\varphi ',\mathcal{T}')$ of $(\varphi ,\mathcal{T})$ as follows. First let $\varphi '(x) := \varphi (x)$ for $x \in V {\setminus } X_q$. Next delete open ball $B^\circ (q,\epsilon )$ from $\mathcal{T}$. Let $\mathcal{C}$ be the set of the resulting connected components. As above, partition $\mathcal{C}$ into $\{C_0\} \cup \mathcal{C}^B \cup \mathcal{C}^R \cup \mathcal{I}^B \cup \mathcal{I}^R$. For each $C \in \mathcal{I}^B$, join $q_C$ and $q_{C_0}$ by a segment of length $\epsilon$. Add a new point $\bar{q}$, and join it with $q_{C_0}$ by a segment of length $\epsilon$. For each $C \in \mathcal{C} {\setminus } \mathcal{I}^B$, join $\bar{q}$ and $q_{C}$ by a segment of length $\epsilon$. Now we obtain a new tree $\mathcal{T}'$ and obtain a map $\varphi ':V {\setminus } X_{q} \rightarrow \mathcal{T}'$. We extend $\varphi '$ to $V \rightarrow \mathcal{T}'$ by defining $\varphi '(x):= q_{C_0}$ for $x \in X^B \cap X_q$ and $\varphi '(x):= \bar{q}$ for $x \in X_q {\setminus } X^B$. See the middle of Fig. 3.

Fig. 3

Tree modification I

Claim 4.8

$(\rho , \varphi ',\mathcal{T}')$ is feasible, and $\tau (\rho ,\varphi ',\mathcal{T}') = \tau (\rho ,\varphi ,\mathcal{T})$.

Proof

To see the feasibility (4.4) (2), take an edge $e = xy \in E$. It suffices to consider the case where $x \in X^B$ and $y \in X_{q, \preceq } {\setminus } X^B$; for the other cases we have $d^{\varphi '}(e) \le d^{\varphi }(e)$, and thus (4.4) (2) is preserved. Then $d^{\varphi '}(e) = d^{\varphi }(e) + \epsilon$. So it suffices to show $d^{\varphi }(e) < |d^{\rho } - a|(e)$. This follows from the fact that $a(e)$ is even and $(d^{\rho } + d^{\varphi })(e)$ is not even. The latter part of Claim 4.8 follows from: $h_{\rho } *(\varphi ',\mathcal{T}') - h_{\rho } *(\varphi ,\mathcal{T}) = \epsilon \{h_{\rho } (X_{q, \preceq } {\setminus } X^B) - h_{\rho } (X_{q, \preceq }) \} = 0,$ where we use Lemma 3.4 (1) with $h_{\rho }(X^B) = 0$ and $h_{\rho }(X_{q, \preceq }) = 1$ (4.20). $\square$

Let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho ,\varphi ',\mathcal{T}')$. Then $X^B$ becomes empty at $q$. Suppose that $X^B \ne \emptyset$ and $h_{\rho } (X^B) = 1$. This implies $h_{\rho } (X_{p,\preceq } {\setminus } X^B) = 0$. Therefore we can apply the above-described process by changing the roles of $X^B$ and $X_{p,\preceq } {\setminus } X^B$. See the right of Fig. 3. Then we get a feasible triple $(\rho ,\varphi ',\mathcal{T}')$. Let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho ,\varphi ',\mathcal{T}')$. Suppose $X^R \ne \emptyset$. Then apply the above-described procedure by changing roles of $B$ and $R$. We remark that (4.19) is preserved.

So consider the case of $X^B \cup X^R = \emptyset$, which implies $\mathcal{I}^B \cup \mathcal{I}^R = \emptyset$. Here we construct two modifications $(\rho ',\varphi ',\mathcal{T}')$ and $(\rho '',\varphi '',\mathcal{T}'')$ as follows. First let $(\rho ',\varphi ')(x):= (\rho , \varphi )(x)$ for $x \in V {\setminus } X_q$. Next delete open ball $B^{\circ }(q,\epsilon )$ from $\mathcal{T}$. Let $\mathcal{C} = \{C_0\} \cup \mathcal{C}^B \cup \mathcal{C}^R$ be the set of resulting connected components. For each $C \in \mathcal{C}^R$, join $q_C$ and $q_{C_0}$ by a segment of length $2 \epsilon$. For each $C \in \mathcal{C}^B$, identify (glue) $q_C$ and $q_{C_0}$. For each $x \in X_{q}$, let $\varphi '(x) := q_{C_0}$ and let $\rho '(x) := (\rho (x))^{\rightarrow B, \epsilon }$ (well-defined by $X^B \cup X^R = \emptyset$). Let $(\rho ', \varphi ', \mathcal{T}')$ be the resulting triple. See Fig. 4 for the construction of $\mathcal{T}'$. Namely $\mathcal{T}'$ is also obtained from $\mathcal{T}$ by contracting by $\epsilon$ each segment connecting $q$ and $C \in \{C_0\} \cup \mathcal{C}^B$ and extending by $\epsilon$ each segment connecting $q$ and $C \in \mathcal{C}^R$. The second triple $(\rho '', \varphi '', \mathcal{T}'')$ is obtained by changing roles of $B$ and $R$.

Fig. 4

Tree modification II

Claim 4.9

• (1) Both $(\rho ',\varphi ',\mathcal{T}')$ and $(\rho '',\varphi '',\mathcal{T}'')$ are feasible.

• (2) $\mathcal{D}^{\sigma }_{\rho '} \subseteq \mathcal{D}^{\sigma }_{\rho }$ and $\mathcal{D}^{\sigma }_{\rho ''} \subseteq \mathcal{D}^{\sigma }_{\rho }$ for $\sigma \in \{-,+\}$.

• (3) Either $\tau (\rho ',\varphi ',\mathcal{T}') \le \tau (\rho , \varphi ,\mathcal{T})$ or $\tau (\rho '',\varphi '',\mathcal{T}'') \le \tau (\rho , \varphi ,\mathcal{T})$ holds.

Let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho ',\varphi ',\mathcal{T}')$ if $\tau (\rho ',\varphi ',\mathcal{T}') \le \tau (\rho ,\varphi ,\mathcal{T})$, and let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho '',\varphi '',\mathcal{T}'')$ otherwise. Repeat this process. Then critical points move toward $r$. After finitely many steps, $r$ becomes critical; go to paragraph 3 after the proof of Claim 4.9.

Proof

(1). It suffices to show the feasibility of $(\rho ',\varphi ',\mathcal{T}')$. Take an edge $e = xy \in E$ with $(\rho ,\varphi )(x) \ne (\rho ,\varphi )(y)$. We verify condition ($*$) $d^{\varphi '}(e) \le |d^{\rho '}(e) - a(e)|$ for the cases (i) $\varphi (x) = q \prec \varphi (y) \in C \in \mathcal{C}^R$, and (ii) $\varphi (x) \in C \in \mathcal{C}^R, \varphi (y) \in C' \in \mathcal{C}^R$, and $C \ne C'$. For the other cases, $d^{\varphi '}(e) < d^{\varphi }(e)$, or $d^{\varphi '}(e) = d^{\varphi }(e)$ and $d^{\rho '}(e) = d^{\rho }(e)$; the condition ($*$) is easily verified.

Case (i): $\varphi (x) = q \prec \varphi (y) \in C \in \mathcal{C}^R$. In this case, $d^{\varphi '}(e) = d^{\varphi }(e) + \epsilon$. We are going to show that ($*1$)$|d^{\rho '} - a|(e) = |d^{\rho } - a|(e) + \epsilon$ or ($*2$) $|d^{\rho } - a|(e) - d^{\varphi }(e) \ge 2\epsilon$, which implies the feasibility ($*$). Take $uv \in E(\varGamma )$ with $\rho (x) \in (u,v)$. We may assume $d^{\rho }(e) = d(\rho (x),u) + d(u,\rho (y))$ (since $\rho (y) \in V(\varGamma )$). By the tree structure, we have $u \in B \Leftrightarrow d^{\rho '}(e) = d^{\rho }(e) - \epsilon$, and $u \in R \Leftrightarrow d^{\rho '}(e) = d^{\rho }(e) + \epsilon$. If $u \in B$ and $d^{\rho }(e) < a(e)$ then ($*1$) holds. Also, if $u \in R$ and $d^{\rho }(e) > a(e)$ then ($*1$) holds. So suppose that $u \in B$ and $d^{\rho }(e) > a(e)$. Let $t := d^{\varphi }(e) - \lfloor d(\varphi (y),q) \rfloor$. Then we obtain

$$\begin{aligned} |d^{\rho } - a|(e) - d^{\varphi }(e) = d(u,\rho (y)) + d(\rho (x),u) - a(e) - \lfloor d(\varphi (y),q) \rfloor - t. \end{aligned}$$

By $\rho (y) \in C \in \mathcal{C}^R, u \in B$, and $a(e) \in 2\mathbf{Z}$, integer $N := d(u,\rho (y)) - \lfloor d(q, \varphi (y)) \rfloor - a(e)$ is odd. Furthermore, both $d(\rho (x),u)$ and $t$ belong to $[\epsilon , 1- \epsilon ]$. Hence we have

$$\begin{aligned} N - 1 + 2\epsilon \le |d^{\rho } - a|(e) - d^{\varphi }(e) \le N + 1- 2 \epsilon . \end{aligned}$$

Here $N \le -1$ is impossible; otherwise $|d^{\rho } - a|(e) - d^{\varphi }(e) < 0$, contradicting the feasibility of $(\rho ,\varphi ,\mathcal{T})$. Thus $N \ge 1$, implying ($*2$). The analysis for the case of $u \in R$ and $d^{\rho }(e) < a(e)$ is similar.

Case (ii): $\varphi (x) \in C \in \mathcal{C}^R, \varphi (y) \in C' \in \mathcal{C}^R$, and $C \ne C'$. In this case, $d^{\rho '}(e) = d^{\rho }(e)$ and $d^{\varphi '}(e) = d^{\varphi }(e) + 2 \epsilon$. Here $d^{\varphi }(e) = d(\varphi (x),q) + d(\varphi (y),q)$. Let $t:= d(\varphi (x),q) - \lfloor d(\varphi (x), q) \rfloor$ and $t':=d(\varphi (y),q) - \lfloor d(\varphi (y), q) \rfloor$. Then we have

$$\begin{aligned} | d^{\rho } - a|(e) - d^{\varphi }(e) = |d^{\rho } - a|(e) - \lfloor d(\varphi (x), q) \rfloor - \lfloor d(\varphi (y), q) \rfloor - t - t'. \end{aligned}$$

The integer $N := |d^{\rho } - a|(e) - \lfloor d(\varphi (x), q) \rfloor - \lfloor d(\varphi (y), q) \rfloor$ is even since $C,C' \in \mathcal{C}^R$ and $|d^{\rho } - a|(e) \equiv d(b,\rho (x)) + d(b,\rho (y)) \mod 2$. By $t,t' \in [\epsilon , 1- \epsilon ]$, we have

$$\begin{aligned} N - 2 + 2 \epsilon \le | d^{\rho } - a|(e) - d^{\varphi }(e) \le N - 2\epsilon . \end{aligned}$$

From this, $N \ge 2$ is necessary, and we have $| d^{\rho } - a|(e) - d^{\varphi }(e) \ge 2 \epsilon$, implying ($*$).

(2). Take an edge $e = xy \in E$. We show that ($**$) neither $(d^{\rho '} -a)(e) < 0 \le (d^{\rho } -a)(e)$ nor $(d^{\rho '} -a)(e) > 0 \ge (d^{\rho } -a)(e)$ occurs. We may consider the case $\rho (x) = q$. Suppose $\rho (y) \ne q$. Then $|d^{\rho } - a|(e) \ge d^{\varphi }(e) \ge \epsilon$, and $d^{\rho '}(e) - d^{\rho }(e) \in \{\epsilon , - \epsilon \}$, implying ($**$). So suppose $\varphi (x) = \varphi (y) = q$. Then $d^{\varphi '}(e) = d^{\varphi }(e) = 0$, and $d^{\rho '}(e) - d^{\rho }(e) = \{2\epsilon , 0, - 2\epsilon \}$. We may consider the case where $\rho (x) \in (u,p)$ and $\rho (y) \in (u',p')$ for different edges $e = up, e' = u'p' \in E(\varGamma )$ (otherwise $d^{\rho '}(e) - d^{\rho }(e) = 0$). We can assume that $d^{\rho }(x,y) = d(\rho (x),p) + d(p,p') + d(p', \rho (y))$. If $p$ and $p'$ belong to different color classes, then $\rho (x)$ and $\rho (y)$ move toward the same direction in the path from $\rho (x)$ to $\rho (y)$, and hence we have $d^{\rho '}(e) = d^{\rho }(e)$ implying ($**$). Suppose that $p$ and $p'$ belong to the same color class. Then $N := d(p,p')$ is even. By $d(\rho (x),p), d(p', \rho (y)) \in [\epsilon , 1 - \epsilon ]$ we have

$$\begin{aligned} N - a(e) + 2\epsilon \le (d^{\rho }- a) (e) \le N - a(e) + 2 - 2\epsilon . \end{aligned}$$

Since $a(e)$ is even, we have $|d^{\rho }- a| (e) \ge 2 \epsilon$ implying ($**$).

(3). We first compare $(d^{\rho '} -a)^+(E)$ with $(d^{\rho } -a)^+(E)$. For a node $x \in V$ with $\rho (x) \not \in V(\varGamma )$, define disjoint subsets $\delta ^B x, \delta ^R x$ of $\delta x$ as follows. Take edge $uv \in E(\varGamma )$ with $\rho (x) \in [u,v]$. Suppose $u \in B$ and $v \in R$. Let $\delta ^B x$ (resp. $\delta ^R x$) be the set of edges $e= xy \in \delta x$ such that $\rho (y)$ belongs to the connected component of $\bar{\varGamma } {\setminus } \{\rho (x) \}$ containing $u$ (resp. $v$). Then we have

$$\begin{aligned}&(d^{\rho '} - a)^+(E) - (d^{\rho }-a)^+(E) = (d^{\rho '} - d^{\rho })(E {\setminus } \mathcal{D}^-_{\rho }) \nonumber \\&\quad = \epsilon \sum \limits _{x \in X_{q}} \left( |\delta ^R x {\setminus } \mathcal{D}^-_{\rho } | - |\delta ^B x {\setminus } \mathcal{D}^-_{\rho }|\right) \nonumber \\&\quad = (d^{\rho } - a)^+(E) - (d^{\rho ''}-a)^+(E). \end{aligned}$$

(4.23)

Here we use (2) for the first equality. To see the second equality, consider an edge $e \in E {\setminus } \mathcal{D}^-_{\rho }$ joining $X_q$; the other edges do not contribute. Further we may assume $d^\rho (e) > 0$; otherwise $d^{\rho }(e) = d^{\varphi }(e) = 0$ (by $a(e) \ge 0$) and $e$ does not contribute. Suppose $e= xy$ and $x \in X_q$. Then $e \in \delta ^R x \cup \delta ^B x$. By the case-by-case analysis, we see

$$\begin{aligned} d^{\rho '}(e) - d^{\rho }(e) = \left\{ \begin{array}{l@{\quad }l} - \epsilon &{} \mathrm{if}\ e \in \delta ^B x,\ y \not \in X_q, \\ + \epsilon &{} \mathrm{if}\ e \in \delta ^R x,\ y \not \in X_q, \\ - 2 \epsilon &{} \mathrm{if}\ e \in \delta ^B x \cap \delta ^B y,\ y \in X_q \\ + 2 \epsilon &{} \mathrm{if}\ e \in \delta ^R x \cap \delta ^R y,\ y \in X_q \\ 0 &{} \mathrm{otherwise}.\end{array}\right. \end{aligned}$$

(4.24)

By a simple counting argument, we see the second equality. The third equality is obtained by changing the roles of $R$ and $B$.

Next we compare $h_{\rho '} *(\varphi ',\mathcal{T}')$ with $h_{\rho } *(\varphi ,\mathcal{T})$. Here $\mathcal{T}'$ is obtained from $\mathcal{T}$ by contracting and extending segments in $\mathcal{E}_{\varphi , \mathcal{T}}$; so we can naturally regard $\mathcal{E}_{\varphi ', \mathcal{T}'}$ as $\mathcal{E}_{\varphi ', \mathcal{T}'} \subseteq \mathcal{E}_{\varphi , \mathcal{T}}$. Moreover it holds that

$$\begin{aligned} h_{\rho '} (X_{\omega }) = h_{\rho }(X_{\omega }) = 1 \quad (\omega \in \mathcal{E}_{\varphi ', \mathcal{T}'}). \end{aligned}$$

(4.25)

Indeed, for $\omega \in \mathcal{E}_{\varphi ', \mathcal{T}'}$, we have $|d^{\rho '}-a|(e) \ge d^{\varphi '}(e) > 0\;(e \in \delta X_{\omega })$, and by (2) $d^{\rho '}-a$ and $d^{\rho } - a$ must have the same sign pattern on $\delta X_{\omega }$. This implies (4.25).

$\mathcal{T}'$ is obtained from $\mathcal{T}$ by decreasing the length of $\omega$ by $\epsilon$ if $\omega$ connects $q$ and a component in $\{C_0\} \cup \mathcal{C}^B$ and by increasing the length of $\omega$ by $\epsilon$ if $\omega$ connects $q$ and a component in $\mathcal{C}^R$. By this fact together with (4.25), we have

$$\begin{aligned} h_{\rho '} *(\varphi ',\mathcal{T}') - h_{\rho } *(\varphi ,\mathcal{T}) = \epsilon |\mathcal{C}^R| - \epsilon |\mathcal{C}^B| - \epsilon . \end{aligned}$$

(4.26)

Similarly we have

$$\begin{aligned} h_{\rho ''} *(\varphi '',\mathcal{T}'') - h_{\rho } *(\varphi ,\mathcal{T}) = \epsilon |\mathcal{C}^B| - \epsilon |\mathcal{C}^R| - \epsilon . \end{aligned}$$

(4.27)

Let ${\varDelta }' := \{\tau (\rho ', \varphi ', \mathcal{T}') - \tau (\rho ,\varphi , \mathcal{T})\}/\epsilon$ and ${\varDelta }'' := \{\tau (\rho '', \varphi '', \mathcal{T}'') - \tau (\rho ,\varphi , \mathcal{T})\}/\epsilon$. By (4.23), (4.26), and (4.27), we have

$$\begin{aligned} {\varDelta }'' = - {\varDelta }' + 2. \end{aligned}$$

Therefore it suffices to show that ${\varDelta }'$ is an even integer, which implies (3) either ${\varDelta }' \le 0$ or ${\varDelta }'' \le 0$. By (4.23) and (4.26), we have

$$\begin{aligned} {\varDelta }'&\equiv \sum \limits _{x \in X_q} \left( |\delta ^R x {\setminus } \mathcal{D}^-_{\rho }| + |\delta ^B x {\setminus } \mathcal{D}^-_{\rho } |\right) + |\mathcal{C}^B| + |\mathcal{C}^R| + 1 \\&\equiv \sum \limits _{x \in X_q} |\delta x {\setminus } \mathcal{D}^-_{\rho } | + h_{\rho } (X_{q, \prec }) + 1 \\&\equiv \sum \limits _{x \in X_{q}} h_{\rho } (x) + h_{\rho }(X_{q, \prec }) + 1 \equiv h_{\rho } (X_{q,\preceq }) + 1 \equiv 0 \quad \mod 2. \end{aligned}$$

In the second equality, we use the observation that for $e = xy \in E {\setminus } \mathcal{D}^-_{\rho }, x \in X_{q}$ and $e \not \in \delta ^B x \cup \delta ^Rx$ imply $d^{\rho }(e) = d^{\varphi }(e) = 0, y \in X_{q}$ and $e \not \in \delta ^B y \cup \delta ^R y$. Also we use (4.20), (4.21), and Lemma 3.4 (1). $\square$

3: Local changes at $r$. Suppose that $r$ is the unique critical point. Let $q:= r$. The argument is essentially the same (or simpler). Suppose $X_{q, \preceq } {\setminus } (X^B \cup X^R) \ne \emptyset$. As above, we construct $(\rho ', \varphi ',\mathcal{T}')$ and $(\rho '', \varphi '',\mathcal{T}'')$ in the following way. Define $\rho ': V \rightarrow \bar{\varGamma }$ by $\rho '(x) := (\rho (x))^{\rightarrow B,\epsilon }$ for $x \in X_q {\setminus } (X^B \cup X^R)$, and $\rho '(x) := \rho (x)$ for $x \in X^B \cup X^R$. Also define $\varphi '(x) := \varphi (x)$ for $x \in V {\setminus } X_q$. Next delete open ball $B^{\circ }(q, \epsilon )$ from $\mathcal{T}$. Let $\mathcal{C} = \mathcal{C}^B \cup \mathcal{C}^R \cup \mathcal{I}^B \cup \mathcal{I}^R$ be the set of the resulting connected component in $\mathcal{T}$. Add a new root $r$. For all $C \in \mathcal{I}^B \cup \mathcal{I}^R$, join $q_C$ and $r$ by a segment of length $\epsilon$. For each $C \in \mathcal{C}^B$, join $q_C$ and $r$ by a segment of length $2\epsilon$. For each $C \in \mathcal{C}^R$, identify (glue) $q_C$ and $r$. Define $\varphi '(x) = r$ for $x \in X_q$. Then we obtain a triple $(\rho ', \varphi ', \mathcal{T}')$. The second triple $(\rho '', \varphi '', \mathcal{T}'')$ is obtained by changing the roles of $B$ and $R$. By a similar analysis in Claim 4.9, both $(\rho ', \varphi ', \mathcal{T}')$ and $(\rho '', \varphi '', \mathcal{T}'')$ are feasible, and $\tau (\rho ',\varphi ',\mathcal{T}') - \tau (\rho ,\varphi ,\mathcal{T}) = - \tau (\rho '',\varphi '',\mathcal{T}') + \tau (\rho ,\varphi ,\mathcal{T})$ (in (4.23) and (4.24), replace $X_q$ by $X_q {\setminus } (X^B \cup X^R)$ and in (4.26) and (4.27), delete $-\epsilon$ in RHS since $C_0$ does not arise). Let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho ',\varphi ',\mathcal{T}')$ if $\tau (\rho ',\varphi ',\mathcal{T}') \le \tau (\rho ,\varphi ,\mathcal{T})$ and let $(\rho ,\varphi ,\mathcal{T}) \leftarrow (\rho '',\varphi '',\mathcal{T}'')$ otherwise. Increase $\epsilon$ to its multiple until $X^B \cup X^R$ increases. Repeat it until $X_{r, \preceq } = X^B \cup X^R$. Also these changes keep (2) in Claim 4.9.

If $X^R = \emptyset$, then the current $(\rho , \varphi , \mathcal{T})$ is bipartite, as required. So suppose $X^R \ne \emptyset$. Delete open ball $B^{\circ } (r, \epsilon )$ from $\mathcal{T}$. Then $\mathcal{C} = \mathcal{I}^R \cup \mathcal{I}^B$. Consider a segment of length $1$ with vertices $r,q$; $r$ is a new root. For each $C \in \mathcal{C}^B$, join $q_C$ and $r$ by a segment of length $\epsilon$. For each $C \in \mathcal{C}^R$, join $q_C$ and $q$ by a segment of length $\epsilon$. For $x \in X_q$, define $\varphi '(x):= r$ if $x \in X^B$, and $\varphi '(x):= q$ if $q \in X^B$. The resulting $(\rho ,\varphi ',\mathcal{T}')$ is feasible. Indeed, if $e$ joins $X^B$ and $X^R$, then $d^{\varphi }(e)$ and $|d^{\rho }(e) - a(e)|$ have different parity, and this implies $d^{\varphi }(e) + 1 \le |d^{\rho }(e) - a(e)|$. From this we see the feasibility. Now $(\rho ,\varphi ',\mathcal{T}')$ is bipartite, and $\tau (\rho , \varphi ',\mathcal{T}') = \tau (\rho , \varphi , \mathcal{T}) - h_{\rho }(X^B) \le \tau (\rho , \varphi ,\mathcal{T})$. Hence (1) of Theorem 4.5 is proved.

4: Stability. Finally we verify that the resulting $(\rho ^*, \varphi ^*, \mathcal{T}^*)$ satisfies the condition (2) in Theorem 4.5. It suffices to verify that for each change $(\rho , \varphi ,\mathcal{T}) \leftarrow (\rho ',\varphi ',\mathcal{T}')$ above, $(d^{\rho }+ d^{\varphi })(x,y) \le L$ implies $(d^{\rho '} + d^{\varphi '})(x,y) \le L$ for an even integer $L$. This has already been done. Add an edge $e$ joining $x$ and $y$ with even cost $a(e) = L$. Then $(\rho , \varphi ,\mathcal{T})$ is feasible to the new graph, and then so does $(\rho ', \varphi ',\mathcal{T}')$ with property (2) in Claim 4.9. In any change, we have $(d^{\rho '} + d^{\varphi '})(x,y) \le a(e) = L$. Thus the proof of Theorem 4.5 is complete. $\square$

4.4 Primal integrality

Here we prove the existence of an integral optimal solution in (2.2):

Theorem 4.10

(Primal integrality) Suppose that $\mu$ is a tree metric. Then there exists an integral optimal solution in (2.2). In particular, $\mathop {\mathrm{val}}(\mu ;G,a) = \overline{\mathop {\mathrm{val}}}(\mu ;G,a)$.

Together with Corollary 4.6, this establishes the min–max formula (1.2). The proof of Theorem 4.10 is based on an inductive approach by edge-deletion, along the line described in Sect. 2.2. Take an edge $e \in E$, consider $G - e$. Then we have

$$\begin{aligned} \overline{\mathop {\mathrm{val}}}(\mu ; G - e,a) \le \overline{\mathop {\mathrm{val}}}(\mu ; G,a). \end{aligned}$$

(4.28)

To see this, take any optimal solution $(\xi ,f)$ in (2.2) for $G - e$. Extend $\xi$ to $\bar{\xi }: E \rightarrow \mathbf{R}_+$ by defining $\xi (e) := 1$. The resulting $(\bar{\xi },f)$ is feasible to (2.2) for $G$. In particular, if (0) holds with equality and there exists an integral optimal solution in (2.2) for $G-e$, then there also exists an integral optimal solution in (2.2) for $G$.

An edge $e \in E$ is called deletable if $\overline{\mathop {\mathrm{val}}}(\mu ; G - e,a) = \overline{\mathop {\mathrm{val}}}(\mu ; G,a)$. Our goal is to prove the following criterion of deletable edges.

Proposition 4.11

(Edge-deletion property) Let $(\xi ,f)$ be an optimal solution in (2.2). For an edge $e \in E$, if $\xi (e) > 0$, then $e$ is deletable.

As in Sect. 2.2, we first prove Theorem 4.10 assuming Proposition 4.11 and then prove Proposition 4.11.

4.4.1 Proof of Theorem 4.10

We use the induction on the number of edges. Take any optimal solution $(\xi ,f)$ in (2.2). Suppose $\xi = 0$. Then $\overline{\mathop {\mathrm{val}}} (\mu ;G,a) = \overline{\mathop {\mathrm{val}}} (\mu ; G,0) - a(E)$. Moreover $G$ is necessarily inner Eulerian. By the laminar locking theorem (Lemma 3.1), we can take an edge-disjoint set $\mathcal{P}$ of $S$-paths with $\sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) = \overline{\mathop {\mathrm{val}}} (\mu ; G,0)$. Then $\mathcal{P}$ attains the maximum since $\sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(P) \le \mathop {\mathrm{val}}(\mu ;G,a) \le \overline{\mathop {\mathrm{val}}}(\mu ;G,a) = \overline{\mathop {\mathrm{val}}} (\mu ; G,0) - a(E) \le \sum \nolimits _{P \in \mathcal{P}} \mu (s_P,t_P) - a(P)$.

Suppose that there is an edge $e \in E$ with $\xi (e) > 0$. By Proposition 4.11, $e$ is deletable. By induction together with the construction above, there exists an integral optimal solution. $\square$

4.4.2 Proof of Proposition 4.11

We need two lemmas below, the first is about the parity and the second is the complementary slackness condition. In the following, we often compare parameters of $G-e$ with that of $G$. Hence we denote $\tau ^{G-e}$ and $h^{G-e}$ by $\tau '$ and $h'$, respectively. We note:

$$\begin{aligned} \begin{array}{ll} (1)&{}\quad h'_{\rho }(X) \ne h_{\rho }(X)\quad \hbox {if and only if}\;e \in \delta X {\setminus } \mathcal{D}^{-}_{\rho }.\\ (2)&{}\quad \displaystyle h'_{\rho } *(\varphi , \mathcal{T}) = h_{\rho } *(\varphi , \mathcal{T}) + \sum \limits _{\omega \in \mathcal{E}_{\varphi , \mathcal{T}}: e \in \delta X_{\omega }} |\omega | (h'_{\rho }(X_{\omega }) - h_{\rho }(X_{\omega })).\\ \end{array} \end{aligned}$$

(4.29)

This follows from the definition of $h_{\rho }$; see (4.8).

Lemma 4.12

If a feasible triple $(\rho ,\varphi ,\mathcal{T})$ is bipartite, then $\tau (\rho , \varphi ,\mathcal{T})$ is an even integer.

Proof

We use the induction on the number of edges; if $E = \emptyset$ then the statement is obvious. Take an edge $e = xy \in E$. $(\rho ,\varphi ,\mathcal{T})$ is feasible to $G-e$. If $e \in \mathcal{D}^-_{\rho }$ then $\tau '(\rho ,\varphi ,\mathcal{T}) = \tau (\rho ,\varphi ,\mathcal{T})$ by (4.29). Suppose $e \not \in \mathcal{D}^-_{\rho }$. By (4.29) (1), the second term of RHS in (4.29) (2) is equal to $d^{\varphi }(e)$ modulo $2$; recall (3.7) in Sect. 3.4. Also $({d}^{\rho } - a)^+(E) - ({d}^{\rho } - a)^+(E {\setminus } e) = ({d}^{\rho } - a)^+(e) \equiv {d}^{\rho }(e) \mod 2$. Since ${d}^{\rho }(e) \equiv {d}^{\varphi }(e) \mod 2$ by bipartiteness, we have $\tau '(\rho ,\varphi ,\mathcal{T}) \equiv \tau (\rho ,\varphi ,\mathcal{T}) \mod 2$, as required. $\square$

Lemma 4.13

Let $(\xi ,f)$ be a feasible solution in (2.2) and $(\rho ,\varphi ,\mathcal{T})$ a feasible triple. Then $(\xi ,f)$ and $(\rho ,\varphi ,\mathcal{T})$ are both optimal if and only if the following conditions hold:

• (a) For each $e \in E$ with $d^{\rho }(e) > 0$ we have $\xi (e) + \sum \nolimits _{P \in {\varPi }, e \in P} f(P) = 1$.

• (b) For each $e \in E$ with $d^{\varphi }(e) < |d^{\rho } - a|(e)$ we have

  $$\begin{aligned} \xi (e) = \left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm{if}\ e \in \mathcal{D}^-_{\rho }, \\ 0 &{} \mathrm{otherwise}. \end{array}\right. \end{aligned}$$

• (c) For each $\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}$, we have

  $$\begin{aligned} \xi (\delta X_{\omega } {\setminus } \mathcal{D}^-_{\rho }) + (1 - \xi ) (\delta X_{\omega } \cap \mathcal{D}^-_{\rho }) = h_{\rho }(X_{\omega }). \end{aligned}$$

• (d) For each $P \in {\varPi }$ with $f(P) > 0$ we have $d^{\rho }(P) = \mu (s_P,t_P)$.

Proof

By direct calculations, we obtain

$$\begin{aligned}&(d^{\rho } -a)^+ (E) - h_{\rho } *(\varphi ,\mathcal{T}) - \sum \limits _{P \in {\varPi }}\mu (s_P,t_P)f(P) + a(E) - \sum \limits _{e \in E}a(e) \xi (e)\nonumber \\&\quad = \sum \limits _{e \in E} d^{\rho }(e) (1 - \xi (e) - f(e)) + \sum \limits _{P \in {\varPi }} f(P) \left( d^{\rho }(P) - \mu (s_P,t_P)\right) \nonumber \\&\qquad + \sum \limits _{e \in E {\setminus } \mathcal{D}^-_{\rho } } \xi (e) (|d^{\rho }- a| - d^{\varphi })(e) + \sum \limits _{e \in \mathcal{D}^-_{\rho }} (1 - \xi (e)) (|d^{\rho }- a| - d^{\varphi })(e) \nonumber \\&\qquad + \sum \limits _{\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}} |\omega | \left( \xi (\delta X_{\omega } {\setminus } \mathcal{D}^-_{\rho }) + (1 - \xi )(\delta X_{\omega } \cap \mathcal{D}^-_{\rho }) - h_{\rho }(X_{\omega })\right) , \end{aligned}$$

(4.30)

where $f(e) := \sum \nolimits _{P \in {\varPi }, e \in P} f(P)$. To see this, use the relations:

$$\begin{aligned} \sum \limits _{P \in {\varPi }} f(P) d^{\rho }(P)&= \sum \limits _{e \in E} f(e) d^{\rho }(e),\sum \limits _{e \in E {\setminus } \mathcal{D}^-_{\rho }} \xi (e) d^{\varphi }(e) + \sum \limits _{e \in \mathcal{D}^-_{\rho }} (1 - \xi (e)) d^{\varphi }(e) \nonumber \\ =&\sum \limits _{\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}} |\omega | \left( \xi (\delta X_{\omega } {\setminus } \mathcal{D}^-_{\rho })\right. \left. + (1 - \xi )(\delta X_{\omega } \cap \mathcal{D}^-_{\rho })\right) , \end{aligned}$$

and

$$\begin{aligned}&(d^{\rho } - a)^+ (E) + a(E) - \sum \limits _{e \in E} a(e) \xi (e) \\&\quad = \sum \limits _{e \in E} d^{\rho }(e) (1 - \xi (e)) + \sum \limits _{e \in E {\setminus } \mathcal{D}^-_{\rho }} \xi (e) (d^{\rho }- a)(e) + \sum \limits _{e \in \mathcal{D}^-_{\rho }} (1 - \xi (e))(a - d^{\rho })(e). \end{aligned}$$

By feasibility, all terms in RHS of (4.30) are nonnegative; see also (3.4). Therefore $(\rho ,\varphi ,\mathcal{T})$ and $(\xi ,f)$ are both optimal if and only if all the terms are zero, which is equivalent to the case where (a), (b), (c), and (d) hold. $\square$

Proof of Proposition 4.11

We are ready to prove Proposition 4.11. Take an optimal solution $(\xi ,f)$ in (2.2) and take a bipartite optimal triple $(\rho ,\varphi ,\mathcal{T})$. Let $e = xy \in E$ be an edge with $\xi (e) > 0$. Here we can assume

$$\begin{aligned} d^{\rho }(e) = d^{\varphi }(e) = 0 = a(e). \end{aligned}$$

(4.31)

Indeed, replace $e$ by a series of two edges $xz$ and $zy$, and define $a(xz) := 0$ and $a(zy) := a(e)$.

Then the problem (2.2) does not change; from any feasible solution $(\xi ,f)$ in the original instance we get a feasible solution in the new one with the same objective value by setting $\xi (xz) = \xi (zy) := \xi (e)$, and the converse is also possible by contracting edge $xz$. In particular $e$ is deletable in the original graph if and only if $xz$ is deletable in the new graph. Also we can extend $(\rho , \varphi )$ by defining $(\rho ,\varphi )(z) := (\rho ,\varphi )(x)$, which is optimal to the new instance (since it is feasible and has the same objective value).

Suppose indirectly that $e$ is not deletable. Then $(\rho ,\varphi , \mathcal{T})$ is obviously feasible to $G-e$. Moreover $\tau '(\rho ,\varphi ,\mathcal{T}) = \tau (\rho ,\varphi ,\mathcal{T})$. Indeed, by $d^{\rho }(e) = a(e) =0$, we have $(d^{\rho }-a)^+(E {\setminus } e) = (d^{\rho }-a)^+(E)$. Also $d^{\varphi }(e) = 0$ implies $e \not \in \delta X_{\omega }$ for $\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}$, which in turn implies $h_{\rho }(X_{\omega }) = h'_{\rho }(X_{\omega })$ by (4.29) (1). Thus $h'_{\rho } *(\varphi ,\mathcal{T}) = h_{\rho } *(\varphi ,\mathcal{T})$.

Therefore $(\rho ,\varphi ,\mathcal{T})$ is feasible and not optimal to $G-e$. According to Lemmas 4.12 and 4.7, we can take a bipartite feasible triple $(\rho ', \varphi ', \mathcal{T}')$ for $G-e$ such that

• $\tau '(\rho ', \varphi ', \mathcal{T}') + 2 \le \tau '(\rho ,\varphi ,\mathcal{T}) = \tau (\rho ,\varphi ,\mathcal{T}) = \overline{\mathop {\mathrm{val}}}(\mu ,G,a)$ and,

• $(d^{\rho '} + d^{\varphi '})(u,v) \le (d^{\rho } + d^{\varphi })(u,v) + 2 \quad (u,v \in V)$.

In particular,

$$\begin{aligned} d^{\rho '}(e) + d^{\varphi '}(e) \le d^{\rho }(e) + d^{\varphi }(e) + 2 = 2. \end{aligned}$$

So there are four cases $(d^{\rho '}(e), d^{\varphi '}(e)) = (0,0), (2,0), (1,1), (0,2)$. The first case is impossible. Otherwise $(\rho ',\varphi ',\mathcal{T}')$ is also feasible to $G$ with $\tau (\rho ',\varphi ',\mathcal{T}') = \tau '(\rho ',\varphi ',\mathcal{T}') < \overline{\mathop {\mathrm{val}}}(\mu ;G,a) \le \tau (\rho ',\varphi ',\mathcal{T}')$; a contradiction. As in Section 2.2, we are going to show that $(\rho ', \varphi ', \mathcal{T}')$ or a small modification $(\rho ', \tilde{\varphi }', \tilde{\mathcal{T}}')$ is also optimal to $G$ [see claim $(\clubsuit )$], apply the complementary slackness (Lemma 4.13) to $(\xi ,f)$ and $(\rho ', \varphi ', \mathcal{T}')$ (or $(\rho ', \tilde{\varphi }', \tilde{\mathcal{T}}')$), and derive a contradiction. For simplicity, we denote $h_{\rho '}, h'_{\rho '}$, and $\mathcal{D}^-_{\rho '}$ by $h, h'$, and $\mathcal{D}^{-},$ respectively.

Case 1

$(d^{\rho '}(e), d^{\varphi '}(e)) = (2,0)$. In this case, triple $(\rho ', \varphi ', \mathcal{T}')$ is also feasible to $G$(by $0 = d^{\varphi '}(e) \le |d^{\rho '} - a|(e) = 2$). Hence

$$\begin{aligned} \tau '(\rho ',\varphi ',\mathcal{T}') + 2 \le \overline{\mathop {\mathrm{val}}}(\mu ;G,a) \le \tau (\rho ',\varphi ',\mathcal{T}'). \end{aligned}$$

(4.32)

Moreover $(d^{\rho '}-a)^+(E) = (d^{\rho '}-a)^+ (E {\setminus } e) + 2$, and $h *(\varphi ', \mathcal{T}') = h' *(\varphi ', \mathcal{T}')$ by (4.29) (2) and $e \not \in \delta X_{\omega }$ for $\omega \in \mathcal{E}_{\varphi ',\mathcal{T}'}$ (otherwise $d^{\varphi '}(e) > 0$). Thus we have

$$\begin{aligned} \tau (\rho ',\varphi ',\mathcal{T}') = \tau '(\rho ',\varphi ',\mathcal{T}') + 2. \end{aligned}$$

(4.33)

By (4.32) and (4.33), $(\rho ',\varphi ',\mathcal{T}')$ is also optimal to $G$. In particular $(\rho ', \varphi ', \mathcal{T}')$ satisfies the optimality criterion (Lemma 4.13) with $(\xi ,f)$. By (b) in Lemma 4.13, $0 = d^{\varphi '}(e) < |d^{\rho '}-a|(e) =2$ implies $\xi (e) = 0$, which contradicts $\xi (e) > 0$.

Case 2

$(d^{\rho '}(e), d^{\varphi '}(e)) = (1,1)$. Also in this case, triple $(\rho ', \varphi ', \mathcal{T}')$ is feasible to $G$. Hence (4.32) holds. Obviously $(d^{\rho '}-a)^+(E) = (d^{\rho '} -a)^+(E {\setminus } e) + 1$. There is unique $\omega \in \mathcal{E}_{\varphi ', \mathcal{T}'}$ with $|\omega | = 1$ and $e \in \delta X_{\omega }$. By (4.29), $h *(\varphi ', \mathcal{T}') = h' *(\varphi ',\mathcal{T}') - h' (X_{\omega }) + h (X_{\omega })$. Hence we have

$$\begin{aligned} \tau (\rho ', \varphi ',\mathcal{T}') = \tau '(\rho ', \varphi ',\mathcal{T}') + 1 + h' (X_{\omega }) - h (X_{\omega }). \end{aligned}$$

(4.34)

By (4.32) and (4.34), $h'(X_{\omega }) = 1$ and $h(X_{\omega }) = 0$, and $(\rho ', \varphi ',\mathcal{T}')$ is also optimal to $G$. By $|\omega | > 0, h(X_{\omega }) = 0$, and (c) in Lemma 4.13, we have $\xi (\delta X_{\omega } {\setminus } \mathcal{D}^-) + (1 - \xi )(\delta X_{\omega } \cap \mathcal{D}^-) = 0$, implying

$$\begin{aligned} \xi (e') = \left\{ \begin{array}{l@{\quad }l} 0 &{} \mathrm{if}\ e' \in \delta X_{\omega } {\setminus } \mathcal{D}^-,\\ 1 &{} \mathrm{if}\ e' \in \delta X_{\omega } \cap \mathcal{D}^-. \end{array}\right. \end{aligned}$$

Thus $\xi (e) = 0$ since $e \in \delta X_{\omega } {\setminus } \mathcal{D}^-$. Again this contradicts $\xi (e) > 0$.

Case 3

$(d^{\rho '}(e), d^{\varphi '}(e)) = (0, 2)$. In this case, $(\rho ',\varphi ',\mathcal{T}')$ is not feasible to $G$. We modify $(\varphi ',\mathcal{T}')$ as follows. Let $q := \varphi '(x)$ and $q' := \varphi '(y)$. Let $\bar{q} \in \mathcal{T}'$ be the unique point with $d_{\mathcal{T}'}(\bar{q},q) = d_{\mathcal{T}'}(q',\bar{q}) = 1$. We may assume $\bar{q} \prec q$. Also we may assume that $\bar{q}$ is a vertex of $\mathcal{T}'$; attach a unit segment to $\bar{q}$ if necessary. Then segments $\omega := (\bar{q},q)$ and $\omega ' := (\bar{q},q')$ belong to $\mathcal{E}_{\mathcal{T}',{\varphi }'}$. Delete open segment $(\bar{q}, q)$ from $\mathcal{T}'$, and identify $q$ and $q'$. Let $(\tilde{\mathcal{T}}', \tilde{\varphi }')$ be the resulting metric-tree with a map. Then $(\rho ',\tilde{\varphi }', \tilde{\mathcal{T}}')$ is bipartite feasible to $G$, since $d^{\tilde{\varphi }'}(e) = 0$ and $d^{\tilde{\varphi }'}(e') - d^{\varphi '}(e') \in \{-2,0\}\;(e' \in E)$. Hence we have

$$\begin{aligned} \tau '(\rho ',\varphi ',\mathcal{T}') + 2 \le \overline{\mathop {\mathrm{val}}}(\mu ;G,a) \le \tau (\rho ',\tilde{\varphi }',\tilde{\mathcal{T}}'). \end{aligned}$$

(4.35)

Obviously $(d^{\rho '}-a)^+(E) = (d^{\rho '}-a)^+(E {\setminus } e)$ (by $d^{\rho '}(e) = 0 = a(e)$). Next we estimate $h' *(\varphi ',\mathcal{T}')$ and $h *(\tilde{\varphi }', \tilde{\mathcal{T}}')$. We first consider the case $\bar{q} \prec q'$. Let $X := X_{\omega }$ and $Y := X_{\omega '}$. Then $h *(\tilde{\varphi }', \tilde{\mathcal{T}}') = h' *(\varphi ', \mathcal{T}') - h'(X) - h'(Y) + h(X \cup Y)$ by construction. Hence we have

$$\begin{aligned} \tau (\rho ', \tilde{\varphi }',\tilde{\mathcal{T}}') = \tau '(\rho ',\varphi ',\mathcal{T}') + h'(X) + h'(Y) - h(X \cup Y). \end{aligned}$$

(4.36)

By (4.35), $h'(X) = h'(Y) = 1, h(X \cup Y) = 0$, and $(\rho ',\tilde{\varphi }', \tilde{\mathcal{T}}')$ is optimal to $G$. Consider edge $e' \in \delta X {\setminus } \{e\}$. If $e'$ joins $X$ and $Y$, then $d^{\tilde{\varphi }'}(e') < d^{\varphi '}(e') \le |d^{\rho '} - a|(e')$, and (b) in Lemma 4.13 is applicable. Otherwise $e' \in \delta (X \cup Y)$, and (c) in Lemma 4.13 is applicable with $h(X \cup Y) = 0$. Hence we have

$$\begin{aligned} \xi (e') = \left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm{if}\ e' \in \mathcal{D}^-, \\ 0 &{} \mathrm{otherwise}, \end{array}\right. \quad (e' \in \delta X {\setminus } \{e\}). \end{aligned}$$

(4.37)

Decompose $\xi$ into a convex combination of the incidence vectors of inner-odd-joins $F_1,F_2,\ldots ,F_k$. By (4.37), $F_i \cap (\delta X {\setminus } \{e\}) = \delta X \cap \mathcal{D}^-$ for $i=1,2,\ldots ,k$. By $h' (X) = 1$ and $e \in \delta X {\setminus } \mathcal{D}^-$, we have $h(X) = 0$ ((4.29) (1)), implying that $|\delta X {\setminus } \mathcal{D}^-|$ is even. Hence, for every $i=1,2,\ldots ,k$, we have

$$\begin{aligned} |\delta X| = |\delta X \cap \mathcal{D}^-| + |\delta X {\setminus } \mathcal{D}^-|\equiv |F_i \cap (\delta X {\setminus } \{e\})| \mod 2. \end{aligned}$$

Here $|\delta X| \equiv |F \cap \delta X| \mod 2$ must hold for every inner-odd-join $F$ and every $X \subseteq V {\setminus } S$. Hence $e \not \in F_i$ for $i=1,2,\ldots ,k$, which implies $\xi (e) = 0$; a contradiction to the initial assumption. The argument for the case $q' \prec \bar{q}$ is essentially the same; replace $X \cup Y$ by $Y {\setminus } X$ in the argument above. Then the proof of Proposition 4.11 is complete. $\square$

5 Polynomial solvability and NP-hardness

In this section, we prove the polynomial time solvability of $\mu$-CEDP for a tree metric $\mu$, and the NP-hardness of $\mu$-EDP when $\mu$ is not a truncated tree metric.

5.1 Polynomial time solvability

Our approach is based on the polynomial equivalence between separation and optimization [13] as in [28], We are given an instance $(G=(V,E),S,a,\mu )$ of $\mu$-CEDP. Suppose that $\mu$ is a tree metric. Although the linear programming problem (2.2) has an exponential number of variables and inequalities, the multiflow-variable $f$ has a compact edge-node formulation, and the separation of the inner-odd-join polytope $Q$ can be done in polynomial time by Padberg–Rao’s algorithm for minimum odd cuts [36]; see [29, Section 12.4] (and Exercise 8). Consequently the separation of $(f,\xi )$ can be done in polynomial time. Thus, by the ellipsoid method [13], we can evaluate $\overline{\mathop {\mathrm{val}}}(\mu ;G,a)$ in polynomial time. Consequently, for an edge $e \in E$, we can determine whether $e$ is deletable or not. If $e$ is deletable, then delete it. Repeat it at most $|E|$ times until all edges are not deletable. By Proposition 4.11, the resulting graph $G$ is inner Eulerian. By any algorithm for the laminar locking theorem, e.g., [21], we can find an edge-disjoint set of $S$-paths attaining $\mathop {\mathrm{val}}(\mu ; G,0)$ in polynomial time. This is our desired solution for $\mu$-CEDP.

A generalization to the capacitated setting is straightforward. Now we are also given an integer-valued edge-capacity $c: E \rightarrow \mathbf{Z}_+$. The problem is to maximize $\sum \nolimits _{P \in {\varPi }} f(P) (\mu (s_P,t_P) - a(P))$ over $f: {\varPi } \rightarrow \mathbf{Z}_+$ satisfying the capacity constraint $\sum \nolimits _{P \in {\varPi }, e \in P} f(P) \le c(e)$ for $e \in E$. Let $\mathop {\mathrm{val}}(\mu ;G,c,a)$ denote the maximum value. The LP-relaxation is constructed as follows. Let $Q^c$ be the convex hull of all integer-valued functions $\xi : E \rightarrow \mathbf{Z}_+$ such that $0 \le \xi (e) \le c(e)$ for $e \in E$ and $\xi (\delta x) \equiv c(\delta x) \mod 2$ for $x \in V {\setminus } S$. In (2.2), replace $\xi (e) + \sum \nolimits _{P \in {\varPi }, e \in P}f(P) \le 1$ by $\xi (e) + \sum \nolimits _{P \in {\varPi }, e \in P} f(P) \le c(e)$, and replace $\xi \in Q$ by $\xi \in Q^c$. The resulting LP also has an integer optimal solution if $\mu$ is a tree metric. Since $Q^c$ is a parity-constraint capacitated $b$-matching polytope, the separation for $Q^c$ can also be done in polynomial time, as above. Thus we can evaluate $\mathop {\mathrm{val}}(\mu ;G,c,a)$ in polynomial time. Consequently, for each edge $e \in E$, we can determine the maximum deletion $\alpha ^c(e) := \max \{\alpha \in [0,c(e)] \cap \mathbf{Z}\mid \mathop {\mathrm{val}}(\mu ;G,c - \alpha 1_e,a) = \mathop {\mathrm{val}}(\mu ;G,c,a)\}$ in polynomial time by the bisection method, where $1_e$ is the incidence vector of $e$. The rest is the same as above.

5.2 NP-hardness

The goal of this subsection is to prove the NP-hardness of $\mu$-EDP when $\mu$ is not a truncated tree metric (Theorem 1.3). We will prove two auxiliary results. The first one is a 4-point characterization of truncated tree metrics.

Theorem 5.1

A weight $\mu$ is a truncated tree metric if and only if for all sets of four distinct elements $s,t,u,v\in S$, at least one of the following inequalities holds:

$$\begin{aligned} \mu (s,t)&= 0,\end{aligned}$$

(5.1)

$$\begin{aligned} \mu (u,v)&= 0,\end{aligned}$$

(5.2)

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,v)+\mu (t,u), \end{aligned}$$

(5.3)

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,u)+\mu (t,v). \end{aligned}$$

(5.4)

Note that here we do not require the triangle inequality to hold. Therefore, if $\mu$ is not a truncated tree metric, then there are four elements $s,t,u,v$ such that all inequalities (5.1)–(5.4) do not hold. From this violating quadruple $(s,t,u,v)$, we will reduce some NP-hard problem to $\mu |_{\{s,t,u,v\}}$-EDP. For the reduction, we use the following version of the integer 2-commodity flow feasibility problem for which one of the commodities is unit:

Problem 5.2

The $(1,*)$-edge-disjoint paths problem takes the input of an undirected graph $G=(V,E)$, nodes $r,q\in V$, and disjoint sets $R,Q \subseteq V$ such that $\{r\},\{q\},R,Q$ are disjoint and $|R|=|Q|$. The goal is to determine paths $P_0,P_1,\ldots ,P_{|R|}$ such that they are pairwise edge-disjoint, and $P_0$ connects $r$ with $q$, and $P_i$ connects a node in $R$ with a node in $Q$, for $i=1,\ldots , |R|$, or establish that there is no such a family of paths.

Even, Itai and Shamir [10] actually proved that a directed version of $(1,*)$-edge-disjoint paths problem is NP-hard. Their reduction works for our undirected version with small change.

Theorem 5.3

(Essentially [10]) The $(1,*)$-edge-disjoint paths problem is NP-hard.

We first prove Theorem 1.3 assuming Theorems 5.1 and 5.3 in Sect. 5.2.1, and then prove Theorems 5.1 and 5.3 in Sects. 5.2.2 and 5.2.1, respectively.

5.2.1 Proof of Theorem 1.3

Suppose that $\mu$ is not a truncated tree metric. Then Theorem 5.1 implies that there are four distinct elements $s,t,u,v$ such that each of the following inequalities holds:

$$\begin{aligned} \mu (s,t)&> 0, \end{aligned}$$

(5.5)

$$\begin{aligned} \mu (u,v)&> 0, \end{aligned}$$

(5.6)

$$\begin{aligned} \mu (s,t) + \mu (u,v)&> \mu (s,v) + \mu (t,u), \end{aligned}$$

(5.7)

$$\begin{aligned} \mu (s,t) + \mu (u,v)&> \mu (s,u) + \mu (t,v). \end{aligned}$$

(5.8)

Then either both of

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&> \mu (s,u)+\mu (s,v)+\mu (u,v),\end{aligned}$$

(5.9)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&> \mu (t,u)+\mu (t,v)+\mu (u,v), \end{aligned}$$

(5.10)

or both of

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&> \mu (s,t)+\mu (s,v)+\mu (t,v),\end{aligned}$$

(5.11)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&> \mu (s,t)+\mu (s,u)+\mu (t,u) \end{aligned}$$

(5.12)

hold. Indeed, assume that at most one of (5.9)–(5.10), and at most one of (5.11)–(5.12) holds. By symmetry, we may assume that (5.9) and (5.11) do not hold. Summing them implies that

$$\begin{aligned} 3\mu (s,t)+3\mu (u,v)\le \mu (s,u)+2\mu (s,v)+\mu (t,v). \end{aligned}$$

On the other hand, (5.5)–(5.8) imply that

$$\begin{aligned} 3\mu (s,t)+3\mu (u,v)&> 2\mu (s,v)+2\mu (t,u)+\mu (s,u)+\mu (t,v)\\&\ge \mu (s,u)+2\mu (s,v)+\mu (t,v). \end{aligned}$$

This is a contradiction. So, by symmetry, we may assume that each of the inequalities (5.9)–(5.10) hold.

Now consider an instance of the $(1,*)$-edge-disjoint paths problem, that is an undirected graph $G=(V,E)$, nodes $r,q\in V$, and disjoint sets $R,Q\subseteq V$, such that $\{r\},\{q\},R,Q$ are disjoint and $|R|=|Q|$. Define $G':=(V',E')$ by adding $4$ new nodes to $G$, namely $s,t,u,v$, and add new edges $ur$ and $vq$, and $sx$ for all $x\in R, ty$ for all $y\in Q$. A solution to the $\mu |_{S'}$-EDP with $G',S':=\{s,t,u,v\}$ defines a set of paths so that each path has both its endpoints in $S'$. If this set of paths contains exactly $1$ path from $u$ to $v$, and $|R|$ paths from $R$ to $Q$, then the weight is equal to $|R|\mu (s,t)+\mu (u,v)$. We claim that this routing—i.e. having 1 path from $u$ to $v$, and $|R|$ paths from $s$ to $t$—is the only way to achieve a weight of at least $|R|\mu (s,t)+\mu (u,v)$. This follows from the following claim.

Claim 5.4

Consider the perfect graph $K_{S'}$ with node set $S':=\{s,t,u,v\}$, and edge weights given by $\mu$, and node-capacity $b(s) = b(t) = |R|$ and $b(u) = b(v) =1$. Then $\xi (st)=|R|$ and $\xi (uv)=1$ and $\xi (e)=0$ for other edge $e$ gives the unique maximum integral $b$-matching in $K_{S'}$.

Proof

Recall that an integral $b$-matching is a vector $\xi :E(K_{S'})\rightarrow \mathbf{Z}_+$ such that $\xi \cdot \delta _{\{w\}} \le b(w)$ for all $w \in S'$. Let $\xi$ be a maximum weight integral $b$-matching with respect to weight $\mu |_{s,t,u,v}$. First suppose that $\xi (su) \ge 1$ and $\xi (tv)\ge 1$. Then, by (5.8), decreasing $\xi$ on $su$ and $tv$ by one, and increasing $x$ on $st$ and $uv$ by one will increase the weight of $\xi$. This is a contradiction. This implies that $\xi (su)=0$ or $\xi (tv)=0$. By symmetry we may assume $\xi (su) = 0$. Similarly we have (i) $\xi (sv) = 0$ or (ii) $\xi (ut) = 0$.

Case (i): $\xi (sv)=0$. Now suppose that $\xi (tu) \ge 1$ and $\xi (tv)\ge 1$. Then decrease $\xi$ on $tu$ and $tv$ by one, increase $\xi$ on $st$ by two, and increase $\xi$ on $uv$ by one. This, by (5.10), implies that the weight of $\xi$ increases, a contradiction. Thus we get that $\xi (tu)=0$ or $\xi (tv)=0$. Say, by symmetry, $\xi (tu)=0$. To sum up, we now have $\xi (su)=\xi (sv)=x(tu)=0$. If $\xi (tv)\ge 1$, then decrease $\xi$ on $tv$ by one, and increase $\xi$ on $st$ and $uv$ by one. The weight of $\xi$ increases by (5.7), and this is a contradiction. Hence $\xi (su)=\xi (sv)=\xi (tu)=\xi (tv)=0$. By (5.5) and (5.6), and by the assumption that $\xi$ has maximum weight, we get that $\xi (st)=|R|$ and $\xi (uv)=1$.

Case (ii): $\xi (ut) = 0$. Since $b(v) = 1$, at most one of $\xi (sv)$ and $\xi (tv)$ is positive. By the same argument, we get $\xi (sv) = \xi (tv) = 0$, and hence $\xi (st) = |R|$ and $\xi (uv) = 1$, as required. This completes the proof. $\square$

Thus we conclude that there is a polynomial reduction from the $(1,*)$-edge-disjoint paths problem to $\mu$-EDP, implying that $\mu$-EDP is NP-hard, proving Theorem 1.3.

5.2.2 Characterization of truncated tree metrics: Proof of Theorem 5.1

Here we prove Theorem 5.1. We start with a well-known $4$-point characterization of tree metrics; see [44].

Theorem 5.5

A weight $\mu$ is a tree metric if and only if it satisfies the triangle inequality, and for all sets of four distinct elements $s,t,u,v\in S$, at least one of the following inequalities holds:

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,v)+\mu (t,u),\end{aligned}$$

(5.13)

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,u)+\mu (t,v). \end{aligned}$$

(5.14)

Hirai [15] considered the distance among subtrees in a tree, and derived a similar 4-point characterization for it. A weight $\mu$ is called a subtree distance if there are a metric-tree $\mathcal{T}$ and a family $\{R_s\}_{s \in S}$ of its subtrees (connected subsets) indexed by $S$ such that

$$\begin{aligned} \mu (s,t) = d_\mathcal{T} (R_s,R_t) \quad (s,t \in S). \end{aligned}$$

In this case we say that $(\mathcal{T}, \{R_s\}_{s \in S})$ realizes $\mu$ or is a realization of $\mu$. A truncated tree metric is exactly a subtree distance so that each subtree is a ball around some point. Hirai provided the following characterization of subtree distances.

Theorem 5.6

[15] A weight $\mu$ is a subtree distance if and only if for all sets of four distinct elements $s,t,u,v\in S$, at least one of the following inequalities holds:

$$\begin{aligned} \mu (s,t)&= 0,\end{aligned}$$

(5.15)

$$\begin{aligned} \mu (u,v)&= 0,\end{aligned}$$

(5.16)

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,v)+\mu (t,u),\end{aligned}$$

(5.17)

$$\begin{aligned} \mu (s,t)+\mu (u,v)&\le \mu (s,u)+\mu (t,v),\end{aligned}$$

(5.18)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&\le \mu (s,u)+\mu (s,v)+\mu (u,v),\end{aligned}$$

(5.19)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&\le \mu (t,u)+\mu (t,v)+\mu (u,v),\end{aligned}$$

(5.20)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&\le \mu (s,t)+\mu (s,v)+\mu (t,v),\end{aligned}$$

(5.21)

$$\begin{aligned} 2\mu (s,t)+2\mu (u,v)&\le \mu (s,t)+\mu (s,u)+\mu (t,u). \end{aligned}$$

(5.22)

Note that if a weight function satisfies (5.1)–(5.4), it will clearly also satisfy (5.15)–(5.22).

We are ready to prove Theorem 5.1. First we prove the “only if” part. Consider a realization $(\mathcal{T},\{R_s\}_{s \in S})$ of the truncated tree metric as a subtree distance. Now each subtree $R_s$ is a ball $B(p_s,r_s)$ with center $p_s$ and radius $r_s$. Let $\bar{\mu }(s,t) := d_\mathcal{T}(p_s,p_t)$ for $s,t \in S$. Then $\bar{\mu }$ is a tree metric. Take any quadruple $s,t,u,v \in S$. We may assume that $\mu (s,t)>0$ and $\mu (u,v)>0$, for otherwise (5.1) or (5.2) holds. That implies $\mu (s,t)= \bar{\mu } (s,t)-r_s -r_t$ and $\mu (u,v)= \bar{\mu } (u,v) -r_u- r_v$. By Lemma 5.5, at least one of (5.13) and (5.14) holds for $\bar{\mu }$. Say, $\bar{\mu }(s, t)+ \bar{\mu }(u,v) \le \bar{\mu }(s,u) + \bar{\mu }(t,v)$, for example. Then $\mu (s,t)+\mu (u,v)= \bar{\mu }(s,t) + \bar{\mu }(u,v) -r_s-r_t-r_u-r_v \le \bar{\mu }(s,u) + \bar{\mu }(t,v) - r_s - r_t- r_u -r_v \le \mu (s,u)+\mu (t,v)$. This implies (5.4).

Second, using Lemma 5.6, we prove the “if” part. By Lemma 5.6, if $\mu$ satisfies at least one of (5.1)–(5.4) for every $s,t,u,v\in S$, then it must be a subtree distance. Now suppose that $\mu$ is realized by $(\mathcal{T},\{R_s \}_{s \in S})$. Moreover we may assume that every leaf $p \in \mathcal{T}$ of the tree appears as a single-node subtree $R_{s}=\{p\}$ (for some $s \in S$)—otherwise we could chop off part of $\mathcal T$, and retain a realization of $\mu$. Then we claim that every subtree $R_s$ actually is a ball, which will prove the Lemma. For a fixed $s\in S$, if the diameter of $R_s$ is zero, then we are done. Otherwise consider the median of $R_s$, that is a point $x \in R_s$ such that there are two distinct points $x_1,x_2$ in $R_s$ at maximum distance from $x$. Let $r:=d_\mathcal{T} (x,x_1)=d_\mathcal{T} (x,x_2) =\max _{x'\in R_s}d_\mathcal{T} (x,x')$. We can take leaves $y_1,y_2$ of $\mathcal T$ such that $d_\mathcal{T}(y_1,y_2) = d_\mathcal{T}(y_1,R_s) + d_\mathcal{T}(x_1,x_2) + d_\mathcal{T}(R_t,y_2)$. We claim that $R_s= B(x,r)$. If by contradiction this were not true, then there would be a leaf $y_3$ such that $d_\mathcal{T} (R_s,y_3)>d_\mathcal{T} (B(x,r), y_3)$. Clearly $y_3\ne y_1,y_2$. By our assumption, there must be $s_1,s_2,s_3$ such that $R_{s_1}=\{y_1\}, R_{s_2}=\{y_2\}, R_{s_3}=\{y_3\}$. Clearly, $s, s_1,s_2,s_3$ are four distinct elements of $S$. We claim that for $s = s, t = s_3,u= s_2,v = s_1$, none of the inequalities (5.1)–(5.4) holds: To check this, note that $y_1\ne y_2$, which proves that (5.2) does not hold. From $d_\mathcal{T} (R_s,y_3)>d_\mathcal{T} (B(x,r), y_3)$ we get that $y_3\notin R_s$, which proves that (5.1) does not hold. We also see that $\mu (s,t)+\mu (u,v) =d_\mathcal{T} (y_1,y_2)+d_\mathcal{T} (R_s,y_3)=d_\mathcal{T} (y_1,x)+d_\mathcal{T} (x,y_2)+d_\mathcal{T} (R_s,y_3) > d_\mathcal{T} (y_1,x)+d_\mathcal{T} (x,y_2)+d_\mathcal{T} (x,y_3)-r \ge d_\mathcal{T} (y_1,y_3)+d_\mathcal{T} (x,y_2)-r =d_\mathcal{T} (y_1,y_3)+d_\mathcal{T} (R_s,y_2)=\mu (s,u)+\mu (t,v)$, that is, (5.4) does not hold. A similar computation shows that (5.3) does not hold either. The contradiction proves that $R_s$ is a ball for all $s\in S$, completing the proof of the Lemma. Based on the algorithm from Hirai [15], and the above proof, we get the following.

Corollary 5.7

There is a polynomial time algorithm to decide whether a given weight $\mu$ is a truncated tree metric, and if so, also provide a realization $(\mathcal{T}, \{B(p_s,r_s)\}_{s\in S})$.

5.2.3 Hardness of $(1,*)$-edge-disjoint paths problems: Proof of Theorem 5.3

The proof of Theorem 5.3 is a slight modification of [10]. Consider an instance of $3$-SAT with variables $x_1,\ldots ,x_n$, and clauses $c_1,\ldots ,c_m$. Each clause $c_j$ has three literals like $x_i$ or $\overline{x_i}$.

Now we construct an instance of the $(1,*)$-edge-disjoint paths problem. We introduce nodes $r,q$. For all $i=1,\ldots ,n$, we introduce nodes $s_i,t_i$. For all $i=1, \ldots ,n$ and $j=1,\ldots ,m$, we introduce nodes $p^i_{2j-1}, p^i_{2j}, q^i_{2j-1}, q^i_{2j}$. We introduce edges to create paths $s_i,p^i_1,p^i_2, \ldots ,p^i_{2m},t_i$, and edges to create paths $s_i,q^i_1,q^i_2, \ldots ,q^i_{2m},t_i$. We add edges $rs_1, t_is_{i+1}, t_nq$. For all $j=1,\cdots ,m$, we add nodes $a^j, b_j$, and for $k=1,2,3$, we add nodes $b^{j,k},a^{j,k},a_{j,k},b_{j,k}$ and edges $a^jb^{j,k}, b^{j,k}a^{j,k}, b_{j,k}a_{j,k}, a_{j,k}b_j$. For a literal $c_j=x_{u_1}\vee x_{u_2}\vee x_{u_3}$, and for $k=1,2,3$, we add edges $a^{j,k}p^{u_k}_{2j-1}$ and $b_{j,k}p^{u_k}_{2j}$. If instead of $x_{u_k}$, we have $\overline{x_{u_k}}$ in literal $c_j$, then, instead, we add edges $a^{j,k}q^{u_k}_{2j-1}$ and $b_{j,k}q^{u_k}_{2j}$. Let $G=(V,E)$ denote the graph constructed this way. Let $R'$ be the set of all nodes $a^j,a^{j,k},a_{j,k}$, and let $Q'$ be the set of all nodes $b_j,b^{j,k},b_{j,k}$. Let $R$ and $Q$ be sets introducing a copy of a node in $R'$ and $Q'$, respectively, and connect each of the nodes in $R'$ and $Q'$ with its copy.

The purpose of the construction is the following claim: the 3-SAT formula is satisfiable if and only if there is a set of edge-disjoint paths such that one of the paths goes from $r$ to $q$, and the remaining paths are connecting a node in $R$ with a node in $Q$. For the if part, consider a satisfying assignment. Then we use a path from $s$ to $t$ traversing all nodes $s_i,t_i$ in this order, using the paths $q^i_{l}$ if $x_i$ was “true”, and using the paths $p^i_{l}$ if $x_i$ was “false”. For each $j$, clause $c_j$ has a true literal $x_{u_k} =$ “true” or $\overline{x_{u_k}} =$ “true”. Use path $a^{j,k},p^{u_k}_{2j-1},p^{u_k}_{2j},b_{j,k}$ if $x_{u_k} =$ “true”, and use path $a^{j,k},q^{u_k}_{2j-1},q^{u_k}_{2j},b_{j,k}$ if $\overline{x_{u_k}} =$“true”. So we get a path connecting $a^{j,k}$ and $b_{j,k}$. Furthermore $a^j$ is matched to $b^{j,k}$ and $b_j$ is matched $a_{j,k}$ by one edge. Also for $k' \in \{1,2,3\} {\setminus } k, b^{j,k'}$ is matched to $a^{j,k'}$, and $b_{j,k'}$ is matched to $a_{j,k'}$. Finally add a perfect matching between $R,Q$ and $R',Q'$. We get a solution of the instance of the $(1,*)$-edge-disjoint paths problem. Conversely, suppose there is a solution to the $(1,*)$-edge-disjoint paths problem. This contains one path $P_0$ from $r$ to $q$, and a set of paths connecting each node in $R$ with a node in $Q$. This path must go via the paths $p^i_{l}$ or the paths $q^i_{l}$, for otherwise one of the terminals in $R$ or $Q$ would be cut off. We set $x_i =$ “true” if $P_0$ use $q^i_l$, and $x_i =$ “false” if $P_0$ use $q^i_l$. We show that this assignment is satisfiable. It is also straightforward that for each $j$, the copies of nodes $a^j, b_j, b^{j,k},a^{j,k},a_{j,k},b_{j,k} (k=1,2,3)$ are paired with each other, except for one of the nodes $a^{j,k}$, and one of the nodes $b_{j,k}$. In particular the unpaired node $a^{j,k}$ is necessarily incident to $p_{2j}^{u_k}$ or $q_{2j}^{u_k}$ not used by $P_0$. This means that clause $c_j$ has a true literal in this assignment for each $j$.

6 Concluding remarks

Here we discuss several related issues and raise open problems.

6.1 Node-disjoint $S$-paths

Mader [35] extended the formula (1.1) to openly node-disjoint $S$-paths packing, where $S$-paths are said to be openly node-disjoint if each pair of the $S$-paths has no common node other than the end nodes; observe that edge-disjoint $S$-paths packing problem on $\varGamma$ is reduced to openly node-disjoint $S$-paths packing problem on the line-graph of $\varGamma$. One may naturally ask a node-disjoint generalization of our results. Node-disjoint problems have a quite different nature from edge-disjoint problems. Indeed, an LP-based approach to Mader’s node-disjoint $S$-paths theorem is not known. Also there are algebraic generalizations to group-labeled graphs [8, 37]; see also a recent work [46] for a relation to matroid matching.

In [26, Section 6], Karzanov announced a min-cost generalization of Mader’s node-disjoint $S$-paths theorem. This can be seen as a conjecture since his proof has not been completed (personal communication with A. Karzanov, 2009).

Pap [39] announced a proof of a min–max theorem and the polynomial solvability of node-disjoint $S$-paths packing with truncated tree metric weights. His approach is quite different from that presented in this paper, and their relation is not clear. We do not know whether his approach can be extended to a min-cost version and whether it has a polyhedral interpretation.

6.2 Combinatorial polynomial time algorithm

Our algorithm crucially depends on the ellipsoid method. Karzanov’s algorithm [24] for min-cost edge-disjoint $S$-paths is complicated, though it is combinatorial. So it is desirable to find a combinatorial polynomial time algorithm of a concise description. Such algorithms for disjoint $S$-paths packing are (i) (a reduction to) Lovasz’s linear matroid matching [32, 43], (ii) Chudnovsky–Cunningham–Geelen’s algorithm for non-zero $A$-paths [7], and (iii) Pap’s algorithm for non-returning $A$-paths [38]. They solve node-disjoint problems [on group-labeled graphs for (ii) and (iii)]. A natural approach is to modify or extend (i–iii) to our setting. Here we suggest an alternative approach. As mentioned in the introduction, our formula includes a discrete minimax relation for inner-odd-joins $F$ and tree locations $\rho$:

$$\begin{aligned} \max _F \min _\rho \left( \frac{1}{2} d_{\varGamma } \cdot {\rho } - a\right) (E {\setminus } F) = \min _\rho \max _F \left( \frac{1}{2} d_{\varGamma } \cdot {\rho } - a\right) (E {\setminus } F). \end{aligned}$$

(6.1)

Here the LHS coincides with $\mathop {\mathrm{val}}(\mu ;G,a)$ by (2.1). So our problem also reduces to finding a saddle point in (6.1). Once a saddle point $(F,\rho )$ is found, an optimal $S$-paths packing is obtained by solving an easy multiflow problem on an inner Eulerian graph $G-F$, according to Lemma 3.1. Such a game-theoretic consideration may bring a new algorithm to this problem.

6.3 Integrality gap of the LP-relaxation

The LP-relaxation (2.2) is applicable to $\mu$-EDP/CEDP for any weight $\mu$. Many existing approximation algorithms for $\mu$-EDP use the natural LP-relaxation [4, 14, 47], which is known to have $\Omega (\sqrt{|V|})$-integrality gap [12]. Our LP-relaxation (2.2) is stronger than the natural LP. So it would be interesting to estimate the integrality gap of (2.2) and its dependency on $\mu$, and to design approximation algorithms based on it. For example, consider the integer 2-commodity flow maximization $\mu _{\mathrm{2com}}$-EDP; see Introduction for definition of $\mu _{\mathrm{2com}}$. By Rothschild–Winston theorem [41], for every inner Eulerian graph, the natural multiflow relaxation has an integral optimal solution with the value equal to the minimum 2-commodity cut. Thus the inequality (generally strict) holds:

$$\begin{aligned} \mathop {\mathrm{val}}(\mu _{\mathrm{2com}}; G,0)&= \max _F \mathop {\mathrm{val}}(\mu _{\mathrm{2com}}; G-F,0) = \max _F \min _X |\delta ^{G-F} X| \\&\le \max _{\xi \in Q} \min _X (1 - \xi )(\delta ^G X) \le \min _X \max _{F} |\delta ^{G-F} X|, \end{aligned}$$

where $F$ denotes an inner-odd-join and $X$ denotes a vertex subset with $s,s' \in X \not \ni t,t'$ or $s,t' \in X \not \ni t,s'$. Based on it, can we design a better approximation algorithm than the trivial $2$-approximation algorithm?

6.4 Relation to Karzanov’s approach

In [24], Karzanov established a min–max relation for $\mu$-CEDP with $\mu = p 1\;(p > 0)$; see also [26]. His min–max formula takes a form different from our min–max formula (1.2) or Theorem 4.5. Here we discuss their relationship. We need some notions to explain Karzanov’s min–max formula. An inner fragment $\phi$ is a pair $(X_{\phi }, U_{\phi })$ of $X_{\phi } \subseteq V {\setminus } S$ and $U_{\phi } \subseteq \delta X_{\phi }$ with $|U_{\phi }|$ odd. Let $\mathcal{F}_{0}$ denote the set of all inner fragments. The characteristic function $\chi _{\phi }$ of an inner fragment $\phi$ is a function on $E$ defined by

$$\begin{aligned} \chi _{\phi }(e) = \left\{ \begin{array}{l@{\quad }l} 1 &{} \mathrm{if}\ e \in U_{\phi }, \\ -1 &{} \mathrm{if}\ e \in \delta X_{\phi } {\setminus } U_{\phi }, \\ 0 &{} \mathrm{otherwise}, \end{array}\right. \quad (e \in E). \end{aligned}$$

Given $\beta :\mathcal{F}^0 \rightarrow \mathbf{R}_+$ and $\gamma : E \rightarrow \mathbf{R}_+$, define the function $l^{\beta , \gamma }$ on $E$ by

$$\begin{aligned} l^{\beta , \gamma } := a + \gamma + \sum \limits _{\phi \in \mathcal{F}^0} \beta (\phi ) \chi _{\phi }. \end{aligned}$$

We say that $(\beta ,\gamma )$ is $p$-admissible if $l^{\beta ,\gamma } \ge 0$ and $l^{\beta ,\gamma }(P) \ge p$ for all $P \in {\varPi }$.

Theorem 6.1

[24] For any $p \ge 0$, we have

$$\begin{aligned} \mathop {\mathrm{val}}(p1; G,a) = \min \gamma (E) + \sum \limits _{\phi \in \mathcal{F}^0} \beta _{\phi }(|U_{\phi }| -1), \end{aligned}$$

(6.2)

where the minimum is taken over all $p$-admissible pairs $(\beta , \gamma )$.

In fact, the minimization problem in RHS of (6.2) is the LP-dual of the LP obtained from (2.2) by substituting (3.4) to it and eliminating variable $\xi$. Then Theorem 6.1 follows from Theorem 4.10. Instead of detailed calculations, we explain how to obtain $(\beta , \gamma )$ from our $(\rho ,\varphi ,\mathcal{T})$, and answer affirmatively Karzanov’s question [26, Section 6, (2)]: does there exist a half-integral optimal $p$-admissible pair $(\beta , \gamma )$ when $p$ and $a$ are both integral?

Suppose that $p$ is even and $a$ is even-valued. We show the existence of an integral optimal $p$-admissible pair $(\beta ,\gamma )$. For each $s \in S$, consider a path $P_s$ with length $p/2$ and ends $q_s,p_s$. Next identify $q_s$ over all $s \in S$. The resulting tree (a subdivision of a star) is denoted by $\varGamma$. Then $({\varGamma },\{p_s\}_{s \in S}; 1)$ realizes $p1$. By Theorem 4.5, we can take an optimal bipartite feasible triple $(\rho ,\varphi ,\mathcal{T})$; see also Sect. 4.1 for notation. Contract segment $\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}$ with $h_{\rho }(X_{\omega }) = 0$. Then $(\rho ,\varphi ,\mathcal{T})$ is an optimal (not necessarily bipartite) feasible triple such that $d^{\rho }, d^{\varphi }$, and $|\omega |$ are integral, and $h_{\rho }(X_{\omega }) = 1$ for each $\omega \in \mathcal{E}_{\varphi ,\mathcal{T}}$.

Define $(\beta , \gamma )$ by

$$\begin{aligned} \beta (\phi )&:= \left\{ \begin{array}{l@{\quad }l} |\omega | &{} \mathrm{if}\ \exists \omega \in \mathcal{E}_{\varphi ,\mathcal{T}}:X_{\phi } = X_{\omega },\ U_{\phi } = \delta X_{\omega } {\setminus } \mathcal{D}^-_{\rho }, \\ 0 &{} \mathrm{otherwise}, \end{array}\right. \quad (\phi \in \mathcal{F}^0), \\ \gamma (e)&:= \left\{ \begin{array}{l@{\quad }l} (d^{\rho } - a - d^{\varphi })(e) &{} \mathrm{if}\ e \not \in \mathcal{D}^-_{\rho }, \\ 0 &{} \mathrm{if}\ e \in \mathcal{D}^-_{\rho }, \end{array}\right. \quad (e \in E). \end{aligned}$$

Then $l^{\beta , \gamma }$ is given by

$$\begin{aligned} l^{\beta , \gamma }(e) = \left\{ \begin{array}{l@{\quad }l} d^{\rho }(e) &{} \mathrm{if}\ e \not \in \mathcal{D}^-_{\rho }, \\ (a - d^{\varphi })(e) &{} \mathrm{if}\ e \in \mathcal{D}^-_{\rho }, \end{array}\right. \quad (e \in E), \end{aligned}$$

where we use $d^{\varphi }(e) = -\sum \nolimits _{\phi } \beta (\phi ) \chi _{\phi }(e)$ if $e \in \mathcal{D}^-_{\rho }$ and $d^{\varphi }(e) = \sum \nolimits _{\phi } \beta (\phi ) \chi _{\phi }(e)$ if $e \not \in \mathcal{D}^-_{\rho }$. In particular $l^{\beta , \gamma }(e) \ge d^{\rho }(e) \ge 0$ (by $|d^{\rho }-a|(e) \ge d^{\varphi }(e)$). Hence $l^{\beta ,\gamma }(P) \ge d^{\rho }(P) = p$ for $P \in {\varPi }$, implying that $(\beta ,\gamma )$ is admissible. Moreover,

$$\begin{aligned} \gamma (E) + \sum \limits _{\phi \in \mathcal{F}^0} \beta _{\phi } (|U_{\phi }| - 1)&= (d^\rho -a)^+(E) - d^{\varphi }(E {\setminus } \mathcal{D}^-_{\rho }) \\&\quad + \sum \limits _{\omega \in \mathcal{E}_{\varphi , \mathcal{T}}} |\omega | \{\delta _{X_{\omega }}(E {\setminus } \mathcal{D}^-_{\rho }) - h_{\rho } (X_{\omega })\}\\&= (d^\rho -a)^+(E) - h_{\rho } *(\varphi ,\mathcal{T}) = \tau (\rho ,\varphi ,\mathcal{T}). \end{aligned}$$

Thus $(\beta , \gamma )$ is optimal, and also integral by construction.