Effect of unsteady flow dynamics on the impact of monodisperse and bidisperse granular flow

Abstract

Protective barriers provide crucial resistance against the impact of granular flows. However, the adoption of characterized flow depth and velocity values in impact force estimation remains unclear and requires further investigation, especially with consideration of unsteady flow dynamics. Previous practices suggest that the bulk flow velocity with the assumption of uniform distribution should be used in impact force estimation, while we observe the lower part of the flow consistently exhibits lower velocities than the upper part, because granular shear behavior is enhanced within the boundary layer, which strongly affects the flow velocity. As a result, using a bulk velocity in debris impact force estimation may result in that a larger dynamic pressure coefficient must be used in hydrodynamic model. We made a quantitative assessment. For rapid granular flows, the use of a bulk velocity to calculate the dynamic force component could result in underestimation of approximately 10–30%. Therefore, based on the numerical results, it is suggested that the average velocity of the upper 50% of the flow body can be adopted in impact force estimation. If the front flow depth is used to calculate the dynamic impact force component, the results may be approximately 50% lower than the true value, which indicates that the dynamic force on a barrier is likely not controlled by the granular flow front and that a maximum flow depth may be more appropriate if a hydrodynamic model is adopted. In addition, it seems that the strategy we proposed can be used for both of monodisperse and bidisperse granular flow when boulder impact is excluded.

Introduction

Granular flow is a kind of geologic process that involves the high-speed, massive, flow-like motion of an assembly of granular particles (Hungr et al. 2014), and sometimes can be catastrophic resulting in extensive damage to villages, buildings, bridges, roads, and other engineering facilities because of their extremely high destruction power (e.g., rapid moving velocity and large run-out distance) and unpredictability, especially within mountain areas (Huang et al. 2019; Wang et al. 2019). Accordingly, engineering designs developed to counter possible granular flow disasters are of great importance (Ho et al. 2021; Huang and Zhang 2020a; Kwan 2012).

Impact force estimation is a crucial but challenging task in barrier structure design (Ahmadipur and Qiu 2018; Albaba et al. 2018; Faug 2021; Huang and Zhang 2020a; Kwan 2012; Ng et al. 2018, 2021). Great effort has been made to develop sophisticated models to describe the debris impact force of granular flows; such models primarily incorporate energy and momentum approaches. In an energy approach, an analysis of the energy consumption of the debris–barrier interaction process is used to derive the run-up height against a barrier with the assumption of energy conservation; therefore, the impact force is obtained via the adaptation of a hydrostatic pressure distribution. However, as discussed by Faug (2021), energy approaches are only effective when the flow exhibits a lower Froude number (1–2). Currently, there are two main types of momentum approaches that have been developed. The first momentum approach assumes that the impact pressure is proportional to the square of the flow velocity and can be calculated based on momentum conservation, yielding the famous formula $\alpha \rho {{\overline{u} }_{f}}^{2}$, where $\alpha$ is the pressure coefficient, $\rho$ is the flow density, and ${\overline{u} }_{f}$ is the flow velocity. The main advantage of the velocity-square method is its simplicity because its feeding parameters are all easy to obtain; however, such a method significantly simplifies the impact process and, therefore, $\alpha$ is scattered but generally non-linearly related to the Froude number (Cui et al. 2015; Hübl et al. 2009; Ng et al. 2016). With a focus on the debris–barrier interaction process, Koo et al. (2016) extended the velocity-square method to emphasize the effect of velocity attenuation on the impact force. Jiang and Towhata (2013) conducted a detailed analysis of the components of the impact force of dry granular flows and emphasized that the dynamic component, which is generated by the direct impact of particles on a barrier, is dominant, accounting for more than 60% of the peak total force. Their model was further extended to include the calculation of the action point of the impact force (Jiang et al. 2020). The second momentum approach is based on the observation that the impact process exhibits a discontinuity in the flow velocity and depth, called a momentum jump, which is highly chaotic and difficult to describe; however, mass and momentum conservation can be established across this jump (Albaba et al. 2018; Faug 2021; Li et al. 2020; Pudasaini et al. 2007; Pudasaini and Kroner 2008). Accordingly, the run-up height and total force on a barrier can be deduced (Eqs. (1) and (2)). For a boulder-enriched granular flow, the impulse impact force is important; valuable contributions to the subject have been made by Ng et al. (2021), Song et al. (2018), and Goodwin and Choi (2021).

$$\begin{array}{c}{\left(\frac{{h}_{r}}{{h}_{f}}\right)}^{3}-\frac{1}{\beta }{\left(\frac{{h}_{r}}{{h}_{f}}\right)}^{2}-(1+\frac{2{{N}_{Fr}}^{2}}{\kappa })\left(\frac{{h}_{r}}{{h}_{f}}\right)+\frac{1}{\beta }=0,\end{array}$$

(1)

$$\begin{array}{c}{F}_{n}={C}_{x}{\rho }_{s}{\phi }_{f}{\overline{u} }_{f}^{2}{h}_{f}+\frac{1}{2}{\mathrm{\rm K}}_{x}{\rho }_{s}{\phi }_{f}g{h}_{f}^{2}cos\theta ,\end{array}$$

(2)

where ${F}_{n}$ is total impact force on barrier per unit width; ${h}_{r}$ is jump height. Equation (1) is obtained using granular jump approach for snow avalanches (Jóhannesson et al. 2009) and is further developed for dry granular flow impact problem by Albaba et al. (2018), who deduced the impact force on rigid barrier as formulated by Eq. (2) with the assumption that the run-up height is equal to the jump height. Here, ${\rho }_{s}$ is particle density; flow depth (${h}_{f}$), flow velocity (${\overline{u} }_{f}$), and solid volume fraction (${\phi }_{f}$), respectively, characterize the bulk behavior of granular flow. $\beta$ is the density ratio of the retarding material between the jump and barrier to the incoming flow behind the jump. $\kappa$ is the longitudinal pressure coefficient. ${C}_{x}$ is dynamic force coefficient and can be formulated by ($1+\frac{1}{\beta {h}_{r}/{h}_{f}-1}+\frac{1}{2{{N}_{Fr}}^{2}}$), which accounts for the influence of Froude number on impact force. ${\rm K}_{x}$ is the static force coefficient.

However, there are few studies focusing on the effect of unsteady flow dynamics on the impact effect, which has several important implications for protective system design. When granular flow moves on an inclined surface, because of the gravity attraction and complex deformation, its macroscopic properties including flow velocity, flow depth, and bulk density are time-dependent and also space-dependent. The Froude number (${N}_{Fr}$) has been used to account for flow dynamics (Albaba et al. 2018; Jóhannesson et al. 2009), as formulated in Eq. (1) for run-up height (${h}_{r}$) prediction and Eq. (2) for impact force (${F}_{n}$) estimation, in which the characterized flow depth and velocity are important considerations but it is challenged to determine such parameters and researchers have not reach a general agreement yet. And detailed researches are needed.

Scheidl et al. (2013) adopted the maximum flow velocity and flow depth to examine the applicability of hydraulic model in prediction debris-flow impact load. Jiang and Towhata (2013) measured the flow velocity and depth corresponding to the critical time defined as peak stage of impact force to assess the impact load model. Ng et al. (2016) indicated that the calculation of Froude number has adopted the frontal velocity and flow depth before impact, but the definition of flow front is still obscure.

Ng et al. (2019) firstly gave a detailed and rational discussion concerning the Froude characterization of a granular flow and suggested that the Froude number of the frontmost 5% of a flow dominates the dynamic behavior, including the pileup height and the impact pressure. However, the effectiveness of these conclusions is largely affected by the limitations of the granular jump model (Eq. (2)) proposed by Albaba et al. (2018). The shape of the dead zone in Albaba et al. (2018) model is assumed to be rectangular; the effectiveness of the granular jump model is dependent on Froude number of the considered flow (Faug 2021) and if the dead zone shape has not remained rectangular, which means that portion of flowing material would climb along the free surface of dead zone and directly impact on barrier, the predicted impact force of rapid granular flow is considerably lower than the true value (Zhang et al. 2020). And thus, Ng et al. (2019) suggested the characterization criteria may be not appropriate if the granular impact dynamics would not obey the assumptions of the granular jump model, and for such a reason, further investigation are needed.

To address this issue, we conducted a series of numerical simulations considering monodisperse and bidisperse granular flows under the condition of an open channel with different slope angles ($\theta$) and with lateral periodic boundaries based on 3D discrete element method (DEM). The unsteady flow dynamics and its effect on impact force estimation are analyzed and discussed in detail.

Methodology

Granular flow simulation program

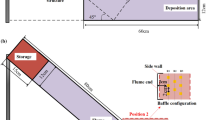
The configuration of the numerical model is shown in Fig. 1. The flume is 4 m long, and the periodic boundaries are introduced 15 cm on the left and on the right of the main flow axis. The periodic boundary condition (PBC) is introduced to remove the effect of the sidewalls. The PBC means that any particles leaving the domain in that direction will instantly re-enter it from the opposite side. And thus, the simulation can be regarded as virtually 2D because the flows can be thought to extend laterally with no limits and no sidewall effects. Gravity is initially perpendicular to the flume base (i.e., negative direction of the z-axis). A total of 40 kg of granular material, represented by spherical particles with a certain particle size, is generated within a virtual box. All of the particles are deposited freely driven by gravity until forming a rectangular deposition shape with dimension of $0.4 \times 0.3 \times 0.23 \mathrm{m}$. After all of the particles completely settling down, a rectangular gate is instantaneously removed and meanwhile the direction of gravity is instantaneously redirected to simulate flume inclination, and thus, the granular flow is formed through a dam-break manner. The flume distal end is open, and the particles are deleted once passing through the flume distal end for saving computation time. And thus, the flows do not come to a complete stop, which means that the run-out and deposition process have not been considered in this paper though they are quite important sometimes.

Fig. 1

Numerical model configuration. a Plain view and b side view

This paper mainly considers the effects of particle-size characteristics and flow conditions. The simulation program is listed in Tables 1 ~2, and total 60 simulation cases are conducted. The simulations were completed based on the previously calibrated chute flow model using commercial software EDEM (DEM solutions 2020) with the parameters presented in Table 4, which were selected based on the properties of quartz sand and calibrated using a small model test. The DEM contact model is presented in the Appendix, and detailed calibration process could be accessed in Supplementary Material S1. As we intend to change the particle size to investigate the particle-size effect on flow dynamics, a sensitive analysis of the parameters based on a rotating drum test (Fig. 2a) is conducted, according to which the granular material is considered to correspond to natural soil with a dynamic repose angle of approximately 38° (Fig. 2b).

Table 1 DEM simulation program

Table 2 Particle size distribution of bidisperse granular flows

Table 3 Characteristic values for computing dynamic impact force on barrier

Table 4 DEM input parameters

Fig. 2

Calibration of DEM input parameter. a Rotating drum; b sensitive analysis results of 8 mm particles. ${\mu }_{rs}$ denotes particle rolling friction coefficient. ${\alpha }_{\mu }$ is dynamic repose angle

Monitoring of flow characteristics

To better understand the flow dynamics, several virtual monitoring sections (similar to Euler coordinates fixed on specific positions of the flume) were set along the flow direction, as shown in Fig. 1. All of the flow features (e.g., flow velocity, depth) can be described at different position and time. The term “flow depth” we used here mainly refers to the distance between the flow free surface and the flume base. Thus, the flow depth can be calculated using the particle position in the z-direction (Albaba et al. 2018), which is formulated as

$$\begin{array}{c}{h}_{f}=\frac{2}{{N}_{p}}\sum\limits_{i=1}^{{N}_{p}}{Z}_{i}\end{array}$$

(3)

where ${N}_{p}$ is the number of particles encompassed within the monitor section and ${Z}_{i}$ is the coordinate of particle i in the z-direction.

The volume fraction and bulk flow velocity can be calculated as follows:

$$\begin{array}{c}{\phi }_{f}=\frac{\sum_{i=1}^{{N}_{p}}{m}_{i}}{{\rho }_{s}{h}_{f}w\Delta l},\end{array}$$

(4)

$$\begin{array}{c}{\overline{u} }_{f}=\frac{\sum_{i=1}^{{N}_{p}}{u}_{i}}{{N}_{p}},\end{array}$$

(5)

where ${m}_{i}$ and ${u}_{i}$ are the particle mass and moving velocity, respectively, $w$ is sampling width, and $\Delta l$ is the length of the monitor section.

Notably, Eq. (3) is only suitable for monodisperse particle flow because when considering multiple particle sizes, the centroid cannot be simplified as the middle point along the flow depth. We give another method. The inset of Fig. 3 gives the idea of the proposed method. The monitoring section is transversely divided into multiple subsections with a certain thickness determined by the maximum particle size encompassed within the flow body. In our analysis, the thickness of the subsection is 20 mm (maximum particle diameter is 16 mm) and the flow depth is formulated as

Fig. 3

Verification of the proposed flow depth estimation method. The flow depth is normalized by initial deposition height ${h}_{0}$, and the time is also normalized using $t/\sqrt{l/g}$, where t is absolute time with the initial point being set as the moment of material releasing. The slope angle is 35°

$${h}_{f}=\frac{1}{k-2}\left(\sum\limits_{i=0}^{k}{h}_{i}-\mathrm{max}\left({h}_{i}, i=0, 1, 2\cdots k\right)-\mathrm{min}\left({h}_{i}, i=0, 1, 2\cdots k\right)\right) (k>2)$$

(6)

where k + 1 is the total number of sub-sections and k should be larger than 2. ${h}_{i}$ denotes the height of the flow slice computed based on the maximum height in the z-direction and the radius of the particles within the subsections. The flow depth is determined by averaging the ${h}_{i}$ values of the sub-sections after removing the maximum and minimum value to avoid the abnormal values.

We present examples to verify our method in Fig. 3. The flow depth of the particle flow of PSD3 was measured from the flow images obtained from the DEM simulations and normalized using the initial deposition height ${h}_{0}$. We observe that, for a monodispersed particle flow (M3), Eq. (6) provides a nearly identical value to that obtained using Eq. (3). For a bidisperse granular flow (PSD3), the measured peak value of ${h}_{f}/{h}_{0}$ is approximately 0.465 (blues stars), Eq. (3) gives a value of 0.432 (lower by 7% compared with the measured value), and Eq. (6) gives a value of 0.461 (an error of approximately 0.8%). In addition, the evolution trend of ${h}_{f}/{h}_{0}$ for PSD3 is reasonably captured by Eq. (6). As a consequence, Eq. (6) is suitable for both monodisperse and bidisperse granular flows.

Numerical simulation results and interpretation

Granular flow dynamics of monodisperse

Granular flow dynamics has been extensively investigated (Bryant et al. 2015; Cagnoli 2021; Cagnoli and Piersanti 2015; Cagnoli and Romano 2010, 2012a, 2012b; Choi and Goodwin 2021). The results we present in this section would offer a verification, and most importantly we intend to use the results to discuss the impact dynamics based on the flow properties of a granular flow.

We use the proposed method to calculate the flow depth and longitudinal flow velocity of a monodispersed granular flow with θ = 25° when passing through S2, and the results are presented in Fig. 4. We here have used non-dimensional values, and for the actual value, please refer to the Supplementary Material S2 (also for figures plotted using actual values).

Fig. 4

Particle size effect on a flow depth and b longitudinal flow velocity monitored at S2 under the conditions with slope angle of 25°. The particle velocity is normalized by $\sqrt{lg}$. Here, l is the length of initial granular deposition (0.4 m) (Fig. 1a) and keeps constant among all simulations. c The Froude number of granular flows. ${L}_{s}$ is the position of monitor section. ${L}_{0}$ denotes the length of flume. The Froude number is calculated based on the strategy suggested by Ng et al. (2019) using ${N}_{Fr}={\overline{u} }_{f}/\sqrt{g{h}_{f}\mathrm{cos}\theta }$. The distinction between Front, Main Body, and Rear is made according to the Savage number shown in Supplementary Material S3

Considering the discrete nature of the front, which prevents the calculation of flow depth and velocity based on the continuum concept, we only address the continuous flow body and later the influence of such an assumption will be discussed.

The continuous flow body is defined as the section with depth exceeding 2 $\delta$ ($\delta$ is the particle diameter). The flow depth is normalized by the initial deposition height ${h}_{0}$, and the particle velocity is normalized by $\sqrt{lg}$. Here, l is the length of initial granular deposition (0.4 m). In Fig. 4, L* is the relative stage of flow that passing the fixed measuring sections. Two ways to describe the flow process: one is time-dependent and another is position-dependent giving the information of flow stage. The latter strategy has been introduced by Goodwin and Choi (2020) and Ng et al. (2019). As shown in Fig. 1, the virtual monitoring section (S2) is fixed on the flume and the granular flow keeps passing the monitoring section with a time-varied velocity. To compute L*, we first obtain the time-varied velocity (${u}_{f}^{t}$) passing the measuring section, then conduct integration of the flow velocity and thus L* can be calculated by ${\int }_{{t}_{0}}^{{t}_{i}}{u}_{f}^{t}dt/{\int }_{{t}_{0}}^{{t}_{1}}{u}_{f}^{t}dt$ (here, ${t}_{0}$ is the time when flow front reaches monitoring section, ${t}_{1}$ is time when flow tail passes monitoring section, and ${t}_{i}$ is the given time point). And thus, the flow front and rear correspond to L* = 0 and L* = 1, respectively.

The flow is highly unsteady with a maximum height at approximately L* = 0.3–0.4 and a maximum flow velocity at L* = 0. As a result, considering unsteady dynamics, it is important to identify the dominant flow body that controls the flow dynamics, especially the impact behavior.

The results indicate that the particle size exerts a larger influence on the flow depth and longitudinal flow velocity. When the particle size is increased from 7 to 16 mm, the maximum flow depth increases by approximately 18% (Fig. 4a). The velocity of flow front and tail shows larger sensitive to particle size, and the maximum flow velocity being reduced by approximately 8.33% when particle size increases from 7 to 16 mm (Fig. 4b). And Fig. 4 also seems to show that the flow front of finer particle flows is faster, whereas their tail is slower, than those of the coarse particle flows. Importantly, the flow front is much faster (difference up to 0.1) than the tail (difference less than 0.05). Figure 4c gives the Froude number of granular flows with 7 mm particles surging downslope under different slope condition. Though increasing slope angle results in larger flow depth, Froude number still undergoes an ascending tendency, which indicates the augmented flow velocity controls the flow dynamics under steeper slope condition.

The bulk flow velocity is often adopted to compute the impact force and run-up height (Albaba et al. 2018; Kwan 2012; Ng et al. 2019, 2016), but typically lacks a detailed investigation of the granular flow velocity structure along the flow depth, which might be very important. Figure 5 shows the velocity distribution along the flow depth at the position where the flow depth reaches its maximum value. Four cases are presented including 7- and 16-mm particle flows under θ = 25° and 45°, respectively. The time scale is normalized by $\sqrt{l/g}$, and each time point depicted in Fig. 5 corresponds to the moment when the flow depth reaches its maximum value, which is computed based on the monitoring section defined in Fig. 1.

Fig. 5

Velocity distribution along flow depth at the position where the flow depth reaches its maximum value. a $\delta$ = 7 mm, $\theta$ = 25°; b $\delta$ = 7 mm, $\theta$ = 45°; c $\delta$ = 16 mm, $\theta$ = 25°; d $\delta$ = 16 mm, $\theta$ = 45°

The results indicate the formation of a highly sheared boundary layer, which is consistent with previous studies that tested for both saturated (Sanvitale and Bowman 2017) and dry granular flows (Zhou and Sun 2013). As shown in Fig. 5, the power-law fitting does not perform well when approaching the bottom, which indicates that the base friction is not sufficiently large to form an ideal parabolic flow profile. Cagnoli (2021) argued that granular debris flowing on a smooth base would slide as a whole with the mobility independent of the stress level. Such conclusion is obtained by using a base static friction coefficient and rolling friction coefficient of 0.45 and 0.035, respectively (0.364 and 0.01 were used in our simulations). And further, Cagnoli (2021) conduct simulation cases with a rougher base (the static friction coefficient is 0.9 and the rolling friction coefficient is 0.07). And the results indicate that the flow structure has been changed, and thus, the flow mobility is largely dependent on stress level. And the difference is mainly due to the boundary shear effect. As a result, the granular flow considered in this study behaves somewhat resemble an en mass flow (unified flow along flow depth) because of the small vertical gradient of velocity above a thin basal layer where most of the deformation of the flow is concentrated. The lower part of the flow consistently exhibits a lower velocity than the upper part; it is thus questionable whether or not the use of a bulk velocity in impact force estimation is reasonable. Furthermore, the computed velocity data points scatter around the trend lines, which means that the highly fluctuating particle velocities resulting in the impact force on the barrier may also be largely unsteady. Other flow properties are presented in Supplementary Material S3 (Figs. S3.1 and S3.2).

Impact dynamics of monodisperse granular flows

In this study, we set a barrier at S2 (Fig. 1) and conducted 6 simulation cases under θ = 45° to consider the impact dynamics of rapid granular flow. As shown by Fig. 6, we give the development process of the granular flow with 10 mm particle under 45° slope and free flow condition when passing S2 where the barrier will be installed. It is observed that the granular mass is actually still deforming and, in terms of shape, it occurs in an intermediate stage between the initial rectangular shape and the mature shape of travel of the flow proper.

Fig. 6

The morphology of granular flow passing S2 where the barrier will be installed. The figure is plotted based on free flow case of 10 mm particle under 45° slope

Our researches are based on the more widely accepted model (Eq. 7) (Huang and Zhang 2020b; Kwan 2012), which mainly calculates the dynamic impact force. And thus, our study divided the impact force on the barrier into two parts: (1) a static component exerted by the dead zone behind the barrier including the transmitted force because of the impact of subsequent flow on dead zone, the transmitted force generated by the weight of flow climbing on dead zone and the force due to self-weight of dead zone and (2) a dynamic component exerted by the direct impact on the barrier by the subsequent flow climbing along the dead zone. The impact force decomposition is achieved by tracking the particle kinetic energy (${E}_{k}$) and labeling the dead particles as those with ${E}_{k}$ < 10⁻⁵ J and moving particles as those with ${E}_{k}$ > 10⁻⁵ J.

Figure 7a presents the analysis of the dynamic and static force components on the barrier exerted by granular flow with particle size of 7 mm. As shown by Fig. 7a, the impact force is normalized by the total weight of the granular material. At critical point 1 defined as the peak of the average total impact force (purple line in Fig. 7a), the dynamic component accounts for nearly 90% of total force, which indicates its overall dominance. The peak impact force is thus not determined by the discrete particles in the flow front although with larger moving velocities; it is reasonable to define the continuous flow body as the section with depths exceeding 2 $\delta$, as presented previously.

Fig. 7

a Analysis of dynamic and static component of force on barrier exerted by granular flow with particle size of 7 mm under slope angle of 45°. The total impact force (${F}_{n}^{\mathrm{total}}$) is normalized by the total weight of the granular material, and both of the dynamic and static component are normalized using ${F}_{n}^{\mathrm{total}}$; b force fluctuation analysis of total impact force and the components

Only a small portion of particles (blue) have settled at critical point 1, whereas at critical point 2, which characterizes the moment that the dynamic component equals the static component, the dead zone expands and the impact process nears the end of the residual stage of the total impact force. The impact force data are highly discrete, especially the dynamic component, owing to the unsteady nature of granular flow. Faug et al. (2009) explained that impact force fluctuations should be attributed to the breaking and reconstitution of force chains formed between the particles and barrier. However, we interpret the impact force fluctuations to result from particle velocity fluctuations because the former is largely controlled by velocity. For a more quantitative assessment, we calculated the impact force fluctuation as the difference between the measured values and average values obtained by the smoothed data. Figure 7b shows the force fluctuation analysis of the total impact force and the components, which demonstrates the dominance of the dynamic component fluctuations, whereas the static component fluctuations are only important during the residual stage.

Figures 8 respectively presents the prediction results of the dynamic impact force components (${F}_{d}$) exerted by monodisperse granular flows on the barrier. The widely accepted hydrodynamic model is adopted (Eq. (7)) (Huang and Zhang 2020b; Kwan 2012) to compute ${F}_{d}$.

Fig. 8

Prediction of impact force of monodisperse granular flows. a 7 mm; b 8 mm; c 10 mm; d 12.5 mm; e 14 mm; f 16 mm. Slope angle is 45°

$$\begin{array}{c}{F}_{d}=\alpha {\rho }_{s}{\phi }_{f}{\overline{u} }_{f}^{2}{A}_{c}\end{array}$$

(7)

here, $\alpha$ denotes an empirical coefficient; ${A}_{c}$ is the nominal contact area between flow and barrier. $\alpha$ is usually obtained by matching the computed ${\rho }_{s}{\phi }_{f}{\overline{u} }_{f}^{2}{A}_{c}$ values with the measured values from experimental or field tests.

The value of $\alpha$ varies substantially owing to different testing conditions and impact force measurement techniques (Ahmadipur and Qiu 2018; Albaba et al. 2018; Jiang et al. 2020; Jiang and Towhata 2013; Ng et al. 2018), and is physically meaningless. And recently studies related the impact pressure coefficients to Froude characteristics of flows but still adopted a regression analysis (Huang and Zhang 2020b). Because a widely accepted ${N}_{Fr}$ characterizing approach for granular impact problems has not been reached yet (Ng et al. 2019), the determination of impact pressure coefficients according to the Froude number of flows would inevitably introduce extract uncertainty and make the impact load prediction more mysterious. As a result, we want to exclude the influence of empirical coefficient and reveal the most relevant flow part for controlling the granular impact dynamics. Out of such a purpose, we thus set $\alpha$ to 1 in this study to discuss the reasonability of the feeding parameters of the hydrodynamic model.

The red lines in Fig. 8 represent the average values of measured impact force. The impact force is found to be underestimated by approximately 10–30% during the peak stage when using time-dependent parameters (i.e., flow depth, depth-averaged velocity, solid volume fraction) to calculate the impact force (blue lines). This indicates that the use of a bulk velocity in impact force estimation is not appropriate because of the shear of the boundary layer at the bottom (Fig. 5) and lower part of the flow consistently exhibit lower velocities than the upper part. We thus adopt the average velocity of the upper 50% of the flow body in the impact force calculation (green lines) and obtain better agreement.

In order to capture the peak force, we feed Eq. (7) with different combinations of ${\phi }_{f}$, ${h}_{f}$, and ${\overline{u} }_{f}$, as summarized in Table 3. ${\phi }_{f}$ is respectively adopted as 0.5 and 0.55, because most of the tested flows exhibit a peak solid volume fraction between 0.5 and 0.55 (Supplementary Material S2). The maximum modified velocity denotes the maximum average velocity of the upper 50% of the flow body, and the flow front depth is selected according to the suggestions of Ng et al. (2019). The maximum flow depth is adopted as the peak value monitored by S2. The results are shown in Fig. 8. The orange dashed lines, which are computed using ${\phi }_{f}$ of 0.5, maximum modified velocity and flow front depth, yield the worst prediction with an underestimation of approximately 50%. When the maximum flow depth and maximum modified velocity are adopted, like cyan dashed lines (${\phi }_{f}$ = 0.5,) and magenta dashed lines (${\phi }_{f}$ = 0.55), the results indicate it is more appropriate for calculating the dynamic impact force component because the peak force is captured and the predicted values are also on the safer side when the impulse force is excluded.

Effect of material inhomogeneity on flow and impact

The particle-size segregation effect is another important aspect of granular dynamics. To focus on fundamental insights into this effect, this study only considers bidisperse granular flows mixing 8 mm and 16 mm particles with different mass percentages (Table 4). Figure 9 compares the average moving velocity of the particles with different diameters within the bidisperse granular flows, showing that the moving velocity of the larger particles appears to be larger than that of the smaller particles. In addition, the inset shows that within bidisperse granular flows, the larger particle moving positions are generally higher than those of the smaller particles as a result of the particle-size segregation effect. The results obtained at the S3 monitoring section of the flow cases with θ = 35° are shown, and Fig. 10 summarizes the maximum bulk velocity of the granular flow. It is observed that the particle-size segregation does not always enhance the flow velocity. Combined with the results shown in Figs. 9 and 10, we conclude that the larger particles may dominate the flow velocity but depend on the particle-size distribution. If the fine content is small, the segregation effect is not sufficient to enhance the flow velocity. Conversely, if the coarser content is small, the velocities of the larger particles are enhanced but not sufficiently to dominate the overall flow behavior. This conclusion is consistent with the observation that the flow velocities of PSD2, PSD3, and PSD4 are slightly higher than that of the monodisperse granular flow in the later stage (Fig. 10). Other flow properties are presented in Supplementary Material S3 (Figs. S3.3 ~ S3.5).

Fig. 9

Comparison of average moving velocity of particles with different diameter within bidisperse granular flows. The results obtained at S3 monitor section of flow cases under 35° are shown

Fig. 10

Summary of maximum bulk velocity of bidisperse granular flow under slope angle of 35°

The velocity structure of bidisperse granular flows (Fig. S3.3 in Supplementary Material S3) indicates that the boundary shear is also significant for bidisperse granular flows, as shown in Fig. S3.3. Therefore, it is necessary to discuss whether the conclusion drawn for monodisperse granular flow could be affected by the material inhomogeneity. Following the same procedure, we obtained Fig. 11. It can be seen that the previous conclusion is fundamentally consistent: because the dynamic impact force of a granular flow is controlled by the upper 50% of the flow body, the maximum flow depth combined with the maximum flow velocity can provide a correct estimation of the dynamic force component. However, it should note that the predictions of the impulse force in Figs. 8 and 11 are only included for reference and need to be further verified because the sampling rate could affect the capture of the impulse force; however, this is beyond the scope of the present paper. In addition, our result could be used as a reference for the debris impact force because the impact force data are smoothed by the removal of the impulse force.

Fig. 11

Prediction of impact force of bidisperse granular flows. a PSD1; b PSD2; c PSD3; d PSD4; e PSD5; f PSD6. Slope angle is 45°

Discussion

Engineering design of barrier structure considering the unsteady nature of granular flow is complex and still needs further investigation, though some preliminary results have been presented.

In the presented work, we only consider dry granular flow and it is the main limitation of our current work, because the impact dynamics is strongly dependent on flow types. For dry granular flow, our research and that of Ng et al. (2019) have both only addressed limited flow conditions as our flow material volume and flume configuration are fixed. Although the whole process of results analysis has used dimensionless quantities and the non-dimensionalization allows presenting the dynamics of granular flow impact transcending different physical systems, researches aiming at different flow condition and model configuration should be encouraged in future for obtaining a more general design strategy. For example, if we continuously input material into the flume, the Froude characteristics of granular flow would be fundamentally changed and thus the currently suggested strategy needs to be further verified.

For saturated granular flow, because of the influence of interstitial fluid, the flow velocity is enhanced and the impact mechanism is much different compared with dry granular flow (Ng et al. 2016). We also note that dry granular flow and two-phase debris share similar flow velocity structures as those observed in debris flow experiments (Sanvitale and Bowman 2017). Thouret et al. (2020) indicated that the bulk velocity of debris flow is approximately 0.7–0.9 times that of the surface flow velocity. This reflects the importance of evaluating the applicability of using the bulk velocity in impact force estimation.

We thus suggest that the average velocity of the upper 50% of the flow body should be used in impact force estimation, which is not unique as Jiang and Towhata (2013) adopted the surface velocity to calculate the dry granular flow impact force. However, as mentioned, our conclusions are limited to dry and rapid granular flows and the effectiveness of the suggestions for other flow types should be further investigated. And we must emphasize that our conclusions are not contradictory with that reported by Ng et al. (2019), because we have addressed different flow cases and it may be better to combine our research conclusions in engineering design. But for more scientific design strategy, further experimental tests and numerical simulations are still needed to extend the findings and engineering design strategy.

Another important issue is the scale effect because small flume simulations are adopted in this study. Cagnoli (2021) showed that the stress level governs the mobility of granular flows when flow dynamics is affected by clast agitation and collisions whereas the mobility of granular flow sliding en mass is not affected by the stress level. The dependence of the granular flow impact dynamics on the stress level is also not fully understood and should be emphasized in the future, for which centrifuge modeling can be effective (Ng et al. 2016; Song et al. 2018). In addition, whether the fluctuations of the particle moving velocities are also needed further investigation as well as the quantitative relation between the force fluctuations and velocity fluctuations. Recently, Goodwin and Choi (2021) have made an analysis of the impact force of dry granular flows transcending different flume configuration but with geometric similarity, but the fluctuations of force and particle velocity have not been quantitatively analyzed. As a result, our conclusions are considerably more relevant to natural granular flows that share similar velocity characteristics, as the impact force of dry granular flow is largely controlled by the particle moving velocities.

Conclusion

The nature of granular flow dynamics is complex and uncertain, which creates challenges with respect to the performance of models used for impact force estimation. We completed a series of numerical simulations to study the unsteady behavior and resulting effect on the impact force to determine a reasonable criterion for improving the effectiveness of the impact load model.

Granular shear behavior is enhanced within the boundary layer resulting in the lower part of the flow consistently exhibits lower velocities than the upper part, and after a quantitative assessment, we indicate that for rapid granular flows, the use of a bulk velocity to calculate the dynamic force component could result in underestimation of approximately 10–30%. Further, the computed velocity data points scatter around the trend lines of velocity distribution, which implies that the non-stationary impact force is qualitatively attributed to the highly fluctuating particle velocities.

Based on numerical results, it is thus suggested that the average velocity of the upper 50% of the flow body may be more appropriate in debris impact force estimation using hydrodynamic model. And when considering unsteady flow dynamics, if the front flow depth is used as the characteristic value in calculating the dynamic impact force component, the results will be approximately 50% lower than the true value. This indicates that the dynamic force on the barrier may be not controlled by the granular flow front, but the maximum flow depth is proved to be more appropriate to be used in estimation of dynamic force component if a hydrodynamic model is adopted.

When bidisperse granular flows with coarse grains are considered, the effect of particle-size segregation on the flow velocity is largely dependent on the particle percentage and, if the flow properties are not significantly changed, a similar strategy as that developed for monodisperse granular flow can be adopted for the impact of a bidisperse granular flow with coarse grains when boulder impact is excluded.

Appendix. DEM contact model and input parameters

The DEM is a promising tool because it directly deals with each individual particle (Bi et al. 2018; Cagnoli and Piersanti 2015; Goodwin and Choi 2021; Ng et al. 2019; Wang et al. 2019). In this study, a non-linear contact model, named Hertz-Mindlin (no slip) model, is adopted to calculate the particle contact force including both the normal and tangential component. And a mature software EDEM is used to run simulations (DEM solutions 2020).

The normal force (${F}_{n}$) between two contact objects is given as

$$\begin{array}{c}{F}_{n}={E}^{*}\sqrt{{R}^{*}}{\lambda }_{n}^\frac{3}{2}\end{array}$$

(8)

where ${E}^{*}$, ${R}^{*}$, and ${\lambda }_{n}$ are respectively the equivalent Young’s modulus, equivalent radius, and normal contact overlap. ${E}^{*}$ and ${R}^{*}$ are formulated as follows:

$$\begin{array}{c}\frac{1}{{E}^{*}}=\frac{\left(1-{\nu }_{i}^{2}\right)}{{E}_{i}}+\frac{\left(1-{\nu }_{j}^{2}\right)}{{E}_{j}}\end{array}$$

(9)

$$\begin{array}{c}\frac{1}{{R}^{*}}=\frac{1}{{R}_{i}}+\frac{1}{{R}_{j}}\end{array}$$

(10)

where subscripts i and j, respectively, represent two contact objects (e.g., particle–particle or particle–wall), and $E$, $\nu$, and $R$ are the Young’s modulus, Poisson’s ratio, and radius, respectively.

The tangential force (${F}_{t}$) is calculated as

$$\begin{array}{c}{F}_{t}=-{S}_{t}{\lambda }_{t}\end{array}$$

(11)

where ${S}_{t}$ is the tangential stiffness, ${\lambda }_{t}$ denotes the tangential overlap, and ${S}_{t}$ is a function of the equivalent shear modulus (${G}^{*}$):

$$\begin{array}{c}{S}_{t}=8{G}^{*}\sqrt{{R}^{*}{\lambda }_{n}}\end{array}$$

(12)

$$\begin{array}{c}\frac{1}{{G}^{*}}=\frac{\left(1-{\nu }_{i}^{2}\right)}{{G}_{i}}+\frac{\left(1-{\nu }_{j}^{2}\right)}{{G}_{j}}\end{array}$$

(13)

A damping component is respectively applied to the normal and tangential directions:

$$\begin{array}{c}{F}_{n}^{d}=-\sqrt{\frac{10}{3}} \cdot \gamma \cdot \sqrt{{S}_{n}{m}^{*}}{v}_{n}^{\underset{rel}{\to }}\end{array}$$

(14)

$$\begin{array}{c}{F}_{t}^{d}=-\sqrt{\frac{10}{3}} \cdot \gamma \cdot \sqrt{{S}_{t}{m}^{*}}{v}_{t}^{\underset{rel}{\to }}\end{array}$$

(15)

where ${m}^{*}$ is the equivalent mass given in Eq. (16), $\gamma$ and ${S}_{n}$ are given in Eqs. (17) and (18), respectively, and ${v}_{n}^{\mathrm{rel}}$ and ${v}_{t}^{\mathrm{rel}}$ are the normal and tangential components of the relative velocity, respectively.

$$\begin{array}{c}{m}^{*}={\left(\frac{1}{{m}_{i}}+\frac{1}{{m}_{j}}\right)}^{-1}\end{array}$$

(16)

$$\begin{array}{c}\gamma =\frac{-\mathit{ln}\;e}{\sqrt{{ln}^{2}e+{\pi }^{2}}}\end{array}$$

(17)

$$\begin{array}{c}{S}_{n}=2\cdot {E}^{*}\sqrt{{R}^{*}{\delta }_{n}}\end{array}$$

(18)

where ${m}_{i}$ and ${m}_{j}$ are the mass of the interacting elements and e is the restitution coefficient.

The magnitude of ${F}_{t}$ is limited by ${\mu }_{s}{F}_{n}$, where ${\mu }_{s}$ is the Coulomb’s friction coefficient of the particles. A torque is also applied to the contact surfaces to account for the effect of rolling friction:

$$\begin{array}{c}{M}_{r}={-\mu }_{r}{F}_{n}{d}_{i}{\widehat{\omega }}_{i}\end{array}$$

(19)

where ${\mu }_{r}$ is the coefficient of rolling friction, ${d}_{i}$ is the distance between the contact point and center of mass, and ${\widehat{\omega }}_{i}$ is the unit angular velocity vector of particle i at the contact point.

Detailed calibration process could be accessed in Supplementary Material S1. And DEM input parameters are presented in Table 4.