Abstract
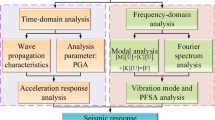
Time-frequency joint analysis was used to investigate the seismic response of rock slopes containing weak structural planes. Four three-dimensional finite element models containing infinite element boundaries were modelled: homogeneous slope, anti-dip slope, bedding slope, and block slope models. The material of the models was elastic material. The influence of the structural planes on the seismic responses of the slopes was systematically analyzed. The results of time-frequency joint analysis show that the structural planes impact the propagation characteristics of the waves and the dynamic amplification effect of the slopes. The wave propagation characteristics and peak ground acceleration distribution of the block slope model are more complex than those of the other models. The influence of structural planes on the amplification effect of the slopes is discussed. Additionally, according to frequency-domain analysis, structural planes have a small impact on the natural frequencies and the peak Fourier spectrum amplitude distribution of the slope but have a significant influence on its dynamic deformation characteristics. The natural frequencies of slopes can be obtained by using modal analysis and Fourier spectrum analysis. The relationships between the natural frequencies of the slopes and their dynamic deformation characteristics were analyzed; in particular, the impacts of low-order and high-order natural frequency on the deformation of the surficial slope were investigated. The applicability of the energy spectrum in the evaluation of the dynamic deformation characteristics of slopes was discussed. The effects of structural planes on the seismic failure mode of the slopes are identified according to the analyses of the dynamic responses of the slopes.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
Introduction
The terrain in Southwest China is complex, and its topography is mainly characterized by mountains (Yu et al. 2014; Tang et al. 2015; Chen et al. 2020; Du et al. 2020). Frequent earthquakes resulting in different scales of landslides often occur in Southwest China (Wei et al. 2014; Zhang et al. 2017). In populated mountainous areas, landslides and rockfalls are considerable natural threats to the daily lives of the locals, and they also represent a relevant risk to structures and infrastructures (Gischig et al. 2015). Engineering experiments have demonstrated that the dynamic stability of rock slopes has been an important topic in geotechnical engineering (Fan et al. 2016).
Multitudes of joints, which constitute weak structural surfaces, are widely distributed throughout rock slopes (Li et al. 2019b; Cecconi et al. 2019; Yong et al. 2018; Sun et al. 2019). Weak structural planes greatly impact the dynamic failure mode of rock slopes (Liu et al. 2008; Liu et al. 2018a, b; Song et al. 2018a, b; Liu et al. 2020b). The failure modes of rock slopes caused by structural planes mainly include landslides, collapses, and creep (Wang 2010; Lin et al. 2016; Liu et al. 2019). The main failure modes of bedding slopes include slip-shear failure, slip-tensile failure, slip-bending failure, and bend-tensile failure, as shown in Fig. 1a (Wang 2010). The typical failure modes of anti-dip slopes are mainly divided into bending toppling deformation, block toppling deformation, and block bending deformation, as shown in Fig. 1b (Goodman 1976). Structural plane distributions are highly complex due to the uncertainties in their geometrical and mechanical parameters (Fan et al. 2016; Song et al. 2018a, b), which makes the seismic failure mode of slopes very complicated. In addition, structural planes have a significant effect on the seismic response of slopes (Li et al. 2019b; He et al. 2020; Liu et al. 2020a, b; Song et al. 2020a, b). In essence, the seismic response of rock slopes is the disturbance effect of waves propagating in the rock mass (Bettess and Zienkiewicz 1977), and the presence of numerous structural planes results in the obvious anisotropy of the rock mass. Wave propagation through the structural planes will cause obvious wave refraction and reflection effects, leading to significant changes in the propagation characteristics of the waves and causing an energy decomposition effect of the wave field (Lenti and Martino 2012; Kumar and Kaur 2014), which further impacts the dynamic amplification effects of slopes (Fan et al. 2016; Li et al. 2018; Song et al. 2019; Song et al. 2020a, b). However, due to the existence of discontinuities in rock slopes, the seismic wave propagation characteristics in rock masses and their impacts on the dynamic response of slopes are more complex (Kumar and Kaur 2014; Zhang et al. 2017; Liu et al. 2018a, b; Zhang et al. 2020). In particular, the seismic failure mechanism of slopes with different structural planes should be systematically analyzed.
Many scholars have adopted the acceleration response to investigate the seismic response of rock slopes in the time domain (Zhang et al. 2017; Li et al. 2018; Zhang et al. 2020). Time-domain analysis has become one of the most direct and effective methods used to evaluate the dynamic stability of slopes (Fan et al. 2016; Li et al 2019a). However, seismic waves have many complex frequency components, and if a rock mass is characterized by nonuniformity, nonlinearity, and anisotropy, it is difficult to fully reveal the influence of the frequency components on the wave vibration characteristics in the time domain. Some scholars have used Fourier spectrum analysis to investigate the seismic response characteristics of slopes in the frequency domain (He et al. 2016; Fan et al. 2017; Song et al. 2019; He et al. 2020), and the results show that frequency-domain analysis cannot be neglected. To fully consider the characteristics of seismic waves, some scholars used the Hilbert-Huang transform (HHT) method to investigate the seismic response of slopes in the time-frequency domain (Yang et al. 2015; Fan et al. 2016; Song et al. 2020a, b). However, at present, the study of the seismic response of slopes attaches great importance to a single domain but ignores the time-frequency joint analysis, limiting the elucidation of the seismic response characteristics of rock slopes. Given the abovementioned analysis and the complexity of the seismic response of rock slopes, it is urgent to establish a time-frequency joint analysis method that can reveal the seismic response characteristics and failure mechanisms of rock slopes from all perspectives.
In this work, the seismic responses of rock slopes with discontinuities were investigated by using finite element numerical simulation based on the time-frequency joint analysis method. The time-frequency joint analysis method fully considers the mutual verification and expansion of the analysis results of the time, frequency, and time-frequency domains. FEM dynamic analyses are conducted on four models, including a homogeneous slope, a bedding slope, an anti-dip slope, and a block slope. According to the dynamic acceleration response, modal analysis, Fourier spectrum, and seismic Hilbert energy spectrum of the slopes, their seismic response is systematically investigated and compared. The effects of the frequency components of waves on the dynamic response of slopes were analyzed. The dynamic response characteristics of slopes are analyzed using an energy-based method, and the applicability of the energy spectrum in the evaluation of the dynamic response of slopes is discussed. The influence of topographic and geological factors on the seismic response characteristics of the slopes is explored. The impacts of structural planes on the dynamic responses and failure mechanisms of the slopes are clarified. The failure modes of the slopes with different types of structural planes are identified. The time-frequency joint analysis can further deepen the understanding of the seismic response of rock slopes and provide theoretical support and a methodology for research on the dynamic responses of rock slopes.
Three-dimensional FEM dynamic analyses
Case study
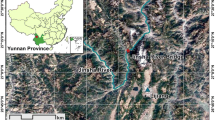
The geographical location of the study area and Jinsha River Bridge is shown in Fig. 2. The study area is a deep valley landform, and several faults cross the Jinsha River obliquely. The bridge site is located in a high mountain valley area with tectonic denudation. In particular, the metamorphism of the slope is more intense than the surrounding area, and basalt schist, slate schist, and phyllite joints and fractures are developed, resulting in generally fragmented rock masses. The overburden and rock mass slope at the front of the bank slope are generally unstable, as shown in Fig. 3. The bridge site is located in a seismic belt, the Zhongdian-Dali seismically controlled tectonic belt, which has a high seismic activity intensity, and frequency. Since seismic recording began in the study area, many earthquakes have occurred there. The average gradient of the slope is approximately 40°, and the slope surface contains 0–5 m of slope colluvial rubble soil and breccia soil. The slope contains three weak-bedding-related structural planes and many toppling structural planes. The lithology of the slope is mainly composed of moderately weathered foliated basalt, moderately weathered sand-bearing slate, and a fault fracture zone (Fig. 4). The slope surface is strongly wind-blown-sand-bearing slate, and the anchoring and piers of the Jinsha River bridge are located in the moderately weathered sand-bearing slate. In the middle of the slope surface, the platform is approximately horizontal. The geological profile of the slope is shown in Fig. 4. The physico-mechanical parameters of the rock mass and the structural planes are obtained by combining a field test and laboratory tests, as shown in Table 1.
Three-dimensional finite element numerical models
ABAQUS/Explicit was used as the solver for the three-dimensional (3D) FEM dynamic analysis of the slope (Che et al. 2016; Song et al. 2020a, b). Considering the slope properties, the 3D finite element model is established, and the model scale is the same as the slope. The geological generalization model of the slope is shown in Fig. 5a. In finite element dynamic analyses, the optimization of the model boundary conditions and the model subdivision size are of great significance for the accurate simulation of wave propagation in discontinuous media. Discontinuities such as faults, joints, and fractures are treated as special joint elements in the continuum numerical method. To simulate rock mass fractures, Goodman and Boyle (1987) proposed the finite element joint element, which is a linear element with four nodes but without thickness. The accuracy and efficiency of calculation should be taken into consideration when conducting grid division. Kuhlemeyer and Lysmer (1973) proposed that the size of the grid unit should not exceed 1/8–1/10 of the shortest wavelength in the model, the grids of structural planes should be set as single-layer grids, and the grids of the rock mass should be set as quadrilateral grids. Since it is difficult to use a quadrilateral grid with the considerable gradient of the topography and landform of the slope, these irregular areas are discretized with triangular grids, and the mesh division is shown in Fig. 5b. The influence of different physical properties of rock mass media on wave propagation is considered during dynamic analysis. The connection mode between the rock mass and structural surface is set as a nonsurface contact connection mode using the tie connection method without setting the viscous damping. Tie connections are used to connect two surfaces, which makes the physical properties of the surfaces the same (Che et al. 2016; Song et al. 2020a, b).
To investigate the effects of structural surfaces on the seismic responses of slopes, four finite element models are established: model 1 (homogeneous slope), model 2 (anti-dip slope), model 3 (bedding slope), and model 4 (block slope with discontinuities). The model size is 1283 × 605 × 559 m3. The rock mass in the slate area is modelled by a quadrilateral grid, and the quadrilateral is a square grid with 5 m, which is less than 1/8–1/10 of the shortest wavelength. An infinite element boundary is set at the edge of the models to simulate the semi-infinite ground conditions. Moreover, the material of the models is regarded as elastic material, and the material parameters are listed in Table 1. To avoid the adverse effect of gravity on the rock mass, the geostress balance calculation is carried out before the FEM dynamic calculation. A horizontal artificial synthetic (AS) wave (0.074 g) is applied at the bottom of each of the four models. The dominant frequency of the AS wave is 4.5–5.5 Hz, with a duration of 40 s, as shown in Fig. 6.
Seismic response of slopes based on time-domain analysis
Wave propagation characteristics through the slopes
To clarify the wave propagation characteristics through the slopes, the wave propagation process in the models is shown in Fig. 7. Figure 7 a–c show that in homogeneous and anti-dip slopes, when waves propagate from the bottom slope to the platform area, the wave propagation characteristics show an obvious acceleration amplification effect with the elevation along the slope surface. However, an obvious acceleration phase shift and local weakening effect between the structural planes can be identified in Fig. 7b, c. This phenomenon suggests that the elevation and structural planes have a magnification effect on the slope dynamic response. Figure 7d shows that the wave propagation characteristics in the block slope are different from those in the other slopes. The acceleration is first amplified toward the slope crest along the bedding structural planes during the process of wave propagation. Local acceleration amplification and weakening are observed between the structural planes. This is due to the refraction and reflection effects of waves between structural planes, resulting in superposition and cancellation of waves. The block slope is cut into blocks by bedding and anti-dip structural planes, resulting in complex wave propagation characteristics in model 4. The seismic wave propagation path was not only through bedding structural planes but also along the slope surface. The wave propagation characteristics of model 4 are more complicated than those of models 1–3.
Dynamic acceleration response
To clarify the seismic acceleration response of the slopes, taking three points of the slopes as examples, their acceleration time histories are shown in Fig. 8. The MPGA of some typical points are shown in Fig. 9. In Fig. 9, the monitoring points (A–E) and (F–I) are located on the slope surface and inside the slope, respectively. The MPGA is the peak ground acceleration (PGA) amplification coefficient, which is the ratio of the PGA of a point to that of the slope toe and represents the amplification of the earthquake response at a point in the slope. Figure 9a shows that the MPGA of the four models increases gradually with elevation inside the slopes. Figure 9b shows that the MPGA of model 1 has a tendency to increase with the elevation at the slope surface; however, the MPGA of models 2–4 increases with elevation below the platform and then decreases gradually. This is because the effect of elevation on homogeneous slope amplification is dominant, while the influence of the slope surface micro-geomorphology is more prominent in slopes with discontinuities. Figure 9 shows that the MPGA of models 2–4 increases nonlinearly, but that of model 1 has a linear increase overall. This is because the complex combination of structural planes results in the wave superposition or weakening effect and further leads to the increase in or dissipation of wave energy and the change in amplification effect. Therefore, elevation has a great magnification effect on the dynamic response of slopes, but the impacts of elevation are different among the models because the structural planes greatly change the amplification effect of the waves in the rock mass.
In addition, the PGA distribution of the models is shown in Fig. 10. The PGAmax is mainly distributed at the slope surface, suggesting that the magnification effect is mainly concentrated in that area. Figure 10a shows that the PGAmax is the largest at the slope crest, indicating that the slope crest will slide or collapse during earthquakes. Figure 10b shows that the PGAmax of the anti-dip slope is mainly distributed in the slope surface above the platform and is amplified intermittently along the toppling structural planes, which indicates that the area above the platform will produce overturning failure during earthquakes. Figure 10c shows that the PGAmax of the bedding slope is mainly distributed in the platform area, suggesting that the seismic stability of the area near the platform is the lowest and that the topmost structural plane is the potential slip surface. Thus, shear sliding failure of the surficial slope will occur during earthquakes. The PGA distribution of the block slope is more complex (Fig. 10d), and the PGAmax is distributed in the surficial slope, which suggests that the surficial slope will experience sliding failure during earthquakes. Comparing the PGA distributions of the models, the amplification effects of the structural planes on the slopes vary and are closely related to the strike and distribution characteristics of the structural planes in the slopes. According to Figs. 9 and 10, the MPGAmax of models 1–4 are approximately 1.27, 1.33, 1.39, and 1.45, respectively. The magnitudes of the amplification effects of the models follow the order of model 4 > model 3 > model 2 > model 1.
Frequency-domain analysis of the dynamic response characteristics of slopes
Modal analysis of the slopes
Modal analysis is mainly used to identify the modal parameters of a system, providing a basis for the analysis of the vibration characteristics of a structural system (Ma et al. 2015). The modal analysis of the models was performed by using ABAQUS/Frequency (Song et al. 2019). The first three vibration modes of the slopes are shown in Figs. 11, 12, 13, and 14. The first eight natural frequencies are listed in Table 2, and the modes of the vibration characteristics are shown in Table 3. Table 2 shows that the natural frequency basically linearly increases with the order. The natural frequencies of the models are similar, but subtle differences can be observed. The presence of different types of structural planes changes the stiffness of a slope, thus changing the natural frequency of the slope to a certain extent but not obviously changing the corresponding mode. Table 3 and Figs. 11, 12, 13, and 14 show that shear deformation, torsional deformation, and bending deformation are the main deformation modes of the slopes. The first three deformation modes of the homogeneous slope mainly include torsion and bending (Fig. 11). The first-order mode shows that the slope mainly presents overall torsional and bending deformation (Fig. 11a), of which the deformation at the slope crest is the largest, indicating that the dynamic failure deformation of the slope crest will occur first. The second- and third-order modes show that the local deformation is mainly manifested in the top of the slope area (Fig. 11b, c). According to the modal analysis, the deformation is greatest at the slope crest, and the top slope is prone to instability. Figure 12 shows that the deformation modes of the anti-dip slope mainly include shear, torsion, and bending. The first mode indicates that the shear and torsional deformation mainly occurs at the slope crest. The second and third modes show that the local deformation is mainly manifested in the slope crest and platform area. Figure 13 shows that the first three deformation modes of the bedding slope mainly include shear, torsion, and bending. The first mode indicates that shear and bending deformation occurs along the entire surface of the slope. The second- and third-order deformation modes show that the local deformation is mainly manifested in the platform area. The surficial slope above the topmost structural plane, especially the platform area, is the main deformation area. The surficial slope and the topmost structural plane were the potential slip mass and surface, respectively. Figure 14 shows that the natural vibration modes of the block slopes with discontinuities mainly include shear, torsional, and bending deformation. The first mode shows the shear and torsional deformation on the whole, suggesting that earthquakes mainly trigger the shear deformation of the slope surface. The second- and third-order modes mainly cause the local deformation of the surficial slope.
Given the abovementioned analysis, according to the analysis of the natural modes of the models, structural planes have a small impact on their natural frequency, but natural frequencies have a significant effect on the dynamic deformation characteristics of slopes. The high-frequency component of seismic waves (> 22 Hz) mainly causes the local deformation of the surficial slope. The low-frequency component of seismic waves (12–15 Hz) mainly causes the overall deformation of the surficial slope. In addition, the structural planes have a significant influence on the dynamic deformation of a slope, and the seismic deformation mechanism of a slope can be inferred by modal analysis. The high-frequency component of waves mainly caused the local deformation to first occur at the surficial slope. When the local deformation accumulates to a certain value, the low-frequency component induces the sliding failure of the slope.
Dynamic response of the slopes using Fourier spectrum analysis
To further study the influence of structural planes on the seismic response of slopes, taking point E as an example, FFT was applied to the acceleration-time history of the models to obtain their corresponding Fourier spectra (Fig. 15). The first three natural frequencies of the models are basically similar, which are 12–15, 22–24, and 27–29 Hz, respectively. To investigate the relationship between the natural frequency and the seismic response of the slopes, taking models 2–4 as examples, the distribution characteristics of the peak Fourier spectrum amplitude (PFSA) of the first-order natural frequency are shown in Fig. 16. Figure 16 shows that the PFSA of the surficial slope is significantly larger than that of the internal slope. Comparing the PFSAs of models 1–4, it can be found that the PFSA distributions of the models are similar, indicating that structural planes have little effect on the PFSA distribution but have a great impact on their PFSA values. To further clarify the natural frequencies on the PFSAs of the slopes, taking model 4 as an example, their PFSAs during the first three natural frequencies are shown in Figs. 16d and 17. The PFSA during f1 is mainly concentrated in the surficial slope, while the maximum PFSA during f2 and f3 is mainly concentrated in a localized area of the surficial slope. This indicates that f1 mainly influences the surficial slope dynamic response and that f2 and f3 mainly affect the local deformation of the slope. That is, the low-frequency band of seismic waves has a controlling effect on the integrity of the slope deformation, and the high-frequency band mainly has an influence on the local deformation of the slopes. In addition, the PFSA of the models is shown in Fig. 18. The PFSA of models 2–4 increases nonlinearly with elevation, but that of model 1 increases linearly overall. This suggests an obvious elevation amplification effect, and structural planes also have a great impact on the amplification effect of slopes. By comparing the PFSA results of the models, their amplification effects follow the order of model 4 > model 3 > model 2 > model 1, which is consistent with the result of the time-domain analysis.
Energy-based dynamic response analysis of the slopes in the time-frequency domain
The HHT method focuses on the concept of the intrinsic mode function (IMF) with the help of empirical mode decomposition (EMD) (Huang et al. 1998). The EMD method is an adaptive data processing or data mining method that can decompose the signal into several IMFs. All the instantaneous frequencies, Hilbert spectra and their marginal spectra of the original signal are obtained by using HHT to transform all the IMFs. The Hilbert spectrum can be obtained by HHT for different IMFs, and then, the Hilbert spectrum can be integrated to obtain the corresponding marginal spectrum. Then, the Hilbert spectrum amplitudes of all the IMFs can be squared to obtain the corresponding energy spectrum, and the seismic Hilbert total energy spectrum of the original seismic signal can be obtained by summing up the energy spectra of all the IMFs.
Taking point A (slope toe) and point C (platform) as examples, the seismic response characteristics of slopes can be identified by using the seismic Hilbert energy spectrum (Fig. 19). The peak Hilbert energy spectrum amplitudes (PHESAs) of points C and A increase to a certain extent, and their energy spectrum characteristics are similar in homogeneous slopes. In models 2–4, when the seismic energy propagates from point A to point C, the spectral amplitude of point C increases substantially and the frequency components near the PHESA become more abundant, as the amplitude of the frequencies increases as well. In addition, Fig. 19 shows that the Hilbert energy spectra at points A and C of the homogeneous slope are characterized by a single peak value. However, in models 2–4, when the seismic wave energy propagates from points A to C, the energy spectrum changes from a single peak value to multiple peak values. This change occurs because the structural surfaces in models 2–4 influence the seismic energy propagation characteristics in the slopes. Figure 19 shows that the PHESAs of the models appear near 17 s and 15 Hz, suggesting that the structural plane has little influence on the position of the PHESA but has a great influence on the spectral characteristics. Therefore, structural planes mainly impact the peak value of the seismic Hilbert energy spectrum and enrich the frequency component near the peak value.
In addition, taking points A–E (at the slope surface) and points F–I (inside the slope) as examples, the change in PHESA is shown in Fig. 20 at these points. The PHESA of model 1 increases linearly with elevation, while that of the other models shows a nonlinear increasing trend because the structural surfaces influence the seismic wave energy transmission and cause the elevation amplification effect to exhibit an obvious nonlinear change. Combined with frequency-domain analysis, the position of the PHESA is similar to that of the first-order natural frequency of slopes in the frequency axis, which indicates that the seismic energy is mainly concentrated in the first-order natural frequency band. The seismic Hilbert energy spectrum can better reflect the overall deformation characteristics of a slope; that is, the seismic Hilbert energy spectrum is suitable for the analysis of the overall dynamic response of a slope.
Influence of structural planes on the dynamic failure mode of a slope
According to the dynamic response characteristics using time-frequency joint analysis, the dynamic failure modes of the models can be inferred (Fig. 21). Figure 21a shows that a homogeneous slope crest area will slide along a certain curved surface during earthquakes. The magnification effect of the surficial slope in the bedding slope is significantly larger than that of the internal slope (Fig. 21b). The dynamic magnification effect of the platform area is the largest, indicating that dynamic damage first occurs near the platform, the damaged area gradually extends to the entire surficial slope with continuous earthquake excitation, and the surficial slope will be damaged along the topmost plane. Figure 21c shows that the surficial slope of the anti-dip slope will exhibit overturning and sliding failure along the sliding surface during earthquakes due to the maximum magnification effect occurring in the surficial slope. Moreover, the failure mode of the block slope is the most complex (Fig. 21d). As the slope is divided into blocks by bedding and topping planes, cracks will appear in the structural planes of the surficial slope during earthquakes. As the seismic force increases, blocks will gradually form. Finally, the surficial slope will overturn and slide in the form of blocks. The failure phenomena of the block slope in the shaking table tests are shown in Fig. 22. The sliding failure of the surficial slope is in the form of a block, which is consistent with the analysis results of model 4. Therefore, structural surfaces have an important impact on the dynamic failure mode of rock slopes.
Seismic failure of model 4 in the shaking table test: a dynamic failure phenomenon of the slope; b dynamic failure mode of the slope (Song et al. 2018a)
Conclusion
The dynamic response characteristics of four models with elastic material were investigated using time-frequency joint analysis. Some conclusions were drawn:
-
Structural planes influence the seismic response and wave propagation characteristics of slopes. The PGA, PFSA, and PHESA of the homogeneous slope increase linearly during an earthquake, while the other models show a strong nonlinear increasing trend. In the time domain, the characteristics of the wave propagation in the slopes are affected by structural planes, which is mainly manifested as the local amplification and reduction effects caused by multiple wave refractions and reflections and then influences the distribution characteristics of the PGA. In the frequency domain, the inherent characteristics of the rock slopes are closely related to the distribution of the structural planes. Structural planes only slightly impact the natural frequency of slopes but clearly influence their vibration modes. In the time-frequency domain, the inclusion of structural planes mainly changes the energy spectrum from exhibiting a single peak to multiple peaks and enriches the frequency component near the peak.
-
According to the analyses of PGA, PFSA, and PHESA, the order of the dynamic amplification effects of the models is as follows: model 4 > model 3 > model 2 > model 1. The slopes have obvious elevation and slope surface amplification effects. Compared with that of the homogeneous slope, the surface micro-topography magnification effect of the slope containing structural planes is more obvious. The PGAmax appears in the platform area with great slope variation in the jointed slopes, and the PGAmax of the homogeneous slope appears at the slope crest.
-
The seismic response of slopes from the perspective of the frequency and time-frequency domains can clearly reveal the interaction mechanism between waves and rock masses. According to the Fourier spectrum and modal analysis, the natural frequency of a slope is closely related to its dynamic response. Structural planes have little impact on the PFSA distribution of a slope but have a great effect on its value. The low-order natural frequency of a slope mainly has a controlling effect on the whole deformation of the surficial slope, and the high-order natural frequency primarily causes local deformation of the surficial slope. The seismic Hilbert energy is mainly concentrated in the first-order natural frequency band, and the Hilbert energy spectrum may be suitable for evaluating the overall dynamic deformation characteristics of slopes.
Nonetheless, this paper only considers the analysis of the elastic domain, without considering the plastic deformation of the slope subject to earthquake excitation. Therefore, to further verify the applicability of the time-frequency joint analysis method, it is necessary to further simulate the dynamic failure process of a slope by using the discrete element method.
References
Bettess P, Zienkiewicz OC (1977) Diffraction and refraction of surface waves using finite and infinite elements. Int J Numer Methods Eng 11(8):1271–1290
Cecconi M, Cencetti C, Melelli L, Pane V, Vecchietti A (2019) Non-dimensional analysis for rock slope plane failure in seismic (pseudostatic) conditions. Bull Eng Geol Environ 78(3):1955–1969
Che A, Yang H, Wang B, Ge X (2016) Wave propagations through jointed rock masses and their effects on the stability of slopes. Eng Geol 201:45–56
Chen Z, Song DQ, Hu C, Ke YT (2020) The September 16, 2017, Linjiabang landslide in Wanyuan County, China: preliminary investigation and emergency mitigation. Landslides 17(1):191–204
Du H, Song D, Chen Z, Shu H, Guo Z (2020) Prediction model oriented for landslide displacement with step-like curve by applying ensemble empirical mode decomposition and the PSO-ELM method. J Clean Prod 270:122248
Fan G, Zhang J, Wu J, Yan K (2016) Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table. Rock Mech Rock Eng 49(8):3243–3256
Fan G, Zhang LM, Zhang JJ, Yang CW (2017) Time-frequency analysis of instantaneous seismic safety of bedding rock slopes. Soil Dyn Earthq Eng 94:92–101
Gischig VS, Eberhardt E, Moore JR, Hungr O (2015) On the seismic response of deep-seated rock slope instabilities-insights from numerical modeling. Eng Geol 193:1–18
Goodman RE (1976) Toppling of rock slopes. In Proc Speciality Conference on Rock Engineering for Foundation and Slopes 201–234
Goodman RE, Boyle W (1987) Non-linear analysis for calculating the support of a rock block with dilatant joint faces. Comput Geotech 3(1):62
He GH, Wang EZ, Liu XL (2016) Modified governing equation and numerical simulation of seepage flow in a single fracture with three-dimensional roughness. Arab J Geosci 9:81
He J, Qi S, Wang Y, Saroglou C (2020) Seismic response of the Lengzhuguan slope caused by topographic and geological effects. Eng Geol 265:105431
Huang NE, Shen Z, Long SR et al (1998) The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc A Math Phys Eng Sci 454:903–995
Kuhlemeyer RL, Lysmer J (1973) Finite element method accuracy for wave propagation problems. J Soil Mech Foundations Div 99(5):421–427
Kumar R, Kaur M (2014) Reflection and refraction of plane waves at the interface of an elastic solid and microstretch thermoelastic solid with microtemperatures. Arch Appl Mech 84(4):571–590
Lenti L, Martino S (2012) The interaction of seismic waves with step-like slopes and its influence on landslide movements. Eng Geol 126:19–36
Li HH, Lin CH, Zu W et al (2018) Dynamic response of a dip slope with multi-slip planes revealed by shaking table tests. Landslides 15(9):1731–1743
Li HB, Liu YQ, Liu LB, Liu B, Xia X (2019a) Numerical evaluation of topographic effects on seismic response of single-faced rock slopes. Bull Eng Geol Environ 78(3):1873–1891
Li LQ, Ju NP, Zhang S, Deng XX (2019b) Shaking table test to assess seismic response differences between steep bedding and toppling rock slopes. Bull Eng Geol Environ 78(1):519–531
Lin P, Liu XL, Hu SY, Li PJ (2016) Large deformation analysis of a high steep slope relating to the Laxiwa Reservoir, China. Rock Mech Rock Eng 49:2253–2276
Liu XL, Wang SJ, Wang EZ, Fan YY (2008) Representation method of fractured rock mass and its hydraulic properties study. Chin J Rock Mech Eng 27(9):1814–1821
Liu X, Han G, Wang E, Wang S, Nawnit K (2018a) Multiscale hierarchical analysis of rock mass and prediction of its mechanical and hydraulic properties. J Rock Mech Geotech Eng 10:694–702
Liu X, Liu Y, He C, Li X (2018b) Dynamic stability analysis of the bedding rock slope considering the vibration deterioration effect of the structural plane. Bull Eng Geol Environ 77(1):87–103
Liu C, Liu XL, Peng XC, Wang EZ, Wang SJ (2019) Application of 3D-DDA integrated with unmanned aerial vehicle–laser scanner (UAV-LS) photogrammetry for stability analysis of a blocky rock mass slope. Landslides 16(9):1645–1661
Liu GW, Song DQ, Chen Z, Yang JW (2020a) Dynamic response characteristics and failure mechanisms of coal slopes with weak intercalated layers under blasting loads. Adv Civ Eng:5412795
Liu X, Ma J, Tang H, Zhang S, Huang L, Zhang J (2020) A novel dynamic impact pressure model of debris flows and its application on reliability analysis of the rock mass surrounding tunnels. Eng Geol 273:105694
Ma GC, Sawada K, Yashima A, Saito H (2015) Experimental study of the applicability of the remotely positioned laser Doppler vibrometer to rock-block stability assessment. Rock Mech Rock Eng 48(2):787–802
Song D, Che A, Chen Z, Ge X (2018a) Seismic stability of a rock slope with discontinuities under rapid water drawdown and earthquakes in large-scale shaking table tests. Eng Geol 245:153–168
Song D, Che A, Zhu R, Ge X (2018b) Dynamic response characteristics of a rock slope with discontinuous joints under the combined action of earthquakes and rapid water drawdown. Landslides 15(6):1109–1125
Song D, Che A, Zhu R, Ge X (2019) Natural frequency characteristics of rock masses containing a complex geological structure and their effects on the dynamic stability of slopes. Rock Mech Rock Eng 52(11):4457–4473
Song D, Chen Z, Hu C, Ke Y, Nie W (2020a) Numerical study on seismic response of a rock slope with discontinuities based on the time-frequency joint analysis method. Soil Dyn Earthq Eng 133:106112
Song D, Chen Z, Ke Y, Nie W (2020b) Seismic response analysis of a bedding rock slope based on the time-frequency joint analysis method: a case study from the middle reach of the Jinsha River, China. Eng Geol 274:105731
Sun H, Liu XL, Zhu JB (2019) Correlational fractal characterization of stress and acoustic emission during coal and rock failure under multilevel dynamic loadings. Int J Rock Mech Min Sci 117:1–10
Tang HM, Liu X, Hu XL, Griffiths DV (2015) Evaluation of landslide mechanisms characterized by high-speed mass ejection and long-run-out based on events following the Wenchuan earthquake. Eng Geol 194:12–24
Wang Q (2010) Study on the deformation characteristics and failure mechanism of bedding rock slope under earthquake, PhD thesis, Jinlin University, Changchun, China
Wei X, Chen N, Cheng Q, He N, Deng M, Tanoli J (2014) Long-term activity of earthquake-induced landslides: a case study from Qionghai Lake Basin, Southwest of China. J Mt Sci 11(3):607–624
Yang C, Zhang J, Bi J (2015) Application of Hilbert-Huang transform to the analysis of the landslides triggered by the Wenchuan earthquake. J Mt Sci 12(3):711–720
Yong R, Ye J, Li B, Du SG (2018) Determining the maximum sampling interval in rock joint roughness measurements using Fourier series. Int J Rock Mech Min Sci 101:78–88
Yu Y, Wang EZ, Zhong JW, Liu XL, Li PH, Shi M, Zhang ZG (2014) Stability analysis of abutment slopes based on long-term monitoring and numerical simulation. Eng Geol 183:159–169
Zhang ZL, Wang T, Wu SR, Tang HM, Liang CY (2017) Seismic performance of loess-mudstone slope by centrifuge tests. Bull Eng Geol Environ 76(2):671–679
Zhang CL, Jiang GL, Su LJ, Lei D, Liu WM, Wang ZM (2020) Large-scale shaking table model test on seismic performance of bridge-pile-foundation slope with anti-sliding piles: a case study. Bull Eng Geol Environ 79(3):1429–1447
Funding
This work was supported by the National Postdoctoral Program for Innovative Talent of China (BX20200191), the National Key R&D Program of China (Grant No. 2018YFC1504801), the National Natural Science Foundation of China (Grant Nos. 51479094, 41772246), and the Shuimu Tsinghua Scholar Program (2019SM058).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Song, D., Liu, X., Huang, J. et al. Characteristics of wave propagation through rock mass slopes with weak structural planes and their impacts on the seismic response characteristics of slopes: a case study in the middle reaches of Jinsha River. Bull Eng Geol Environ 80, 1317–1334 (2021). https://doi.org/10.1007/s10064-020-02008-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10064-020-02008-1