Introduction

Water and mud inrush is a common geological disaster that occurs when building tunnels in karst regions (Bu et al. 2017; Li et al. 2017c; Wang et al. 2019). The development of karst is a complex process (Sauro et al. 2013; Yan et al. 2008; Zarei and Raeisi 2010; Lu et al. 2013). The variable sizes and forms of karst are influenced by many factors, such as topography, geomorphology, geological structure, and lithology. With the promotion of the “Silk Road Economic Belt and the Twenty-First Century Maritime Silk Road” initiative (the “Belt and Road” initiative), many new infrastructure and transportation projects have been initiated. Because of this, an increasing number of tunnels will be built in karst regions, and water and mud inrush disasters will occur more frequently (Li et al. 2014; Li et al. 2015a; Zhao et al. 2013; Ling et al. 2015). Water and mud inrush can increase the risks of construction and significantly increase the difficulty of construction (Kong 2011; Li et al. 2012; Meng et al. 2012; Wang et al. 2016; Zhou et al. 2015; Li et al. 2017b, d). It can also cause significant casualties and economic losses, and can produce negative social impacts (Song et al. 2012; Wang et al. 2004; Zarei et al. 2012; Zhang et al. 2011). Therefore, it is necessary to study the mechanism by which water and mud inrush occurs in order to prevent its occurrence (Hwang and Lu 2007; Hong et al. 2010; Cui et al. 2015).

The resistant body is the rock mass between the karst cave and the tunnel, which can prevent the water and mud from entering the tunnel. Whether or not a disaster occurs depends on the thickness of the resistant body. There are three methods for determining the safe thickness of the resistant body in karst tunnels: qualitative analysis, semi-quantitative analysis, and quantitative analysis (Li et al. 2015).

Qualitative analysis mainly uses empirical analysis, engineering analogies, and expert assessments to analyze the influencing factors and empirical values of the safe thickness. Empirical analysis results can provide information for use in the quantitative analysis. Taking the Yuanliangshan tunnel as an example, Liu et al. (2006) divided karst water burst into several types. He also analyzed the relationship between the safe thickness and tunnel inflow as well as the relationship between the safe thickness and the maximum displacement that occurred during the different types of water inrush. The safe thickness was set as 2.5–3 m. Gan et al. (2007) concluded that to determine the safe thickness, it is necessary to consider the following factors: the depth of the blasting disturbance, the thickness of the loosened surrounding rock, the extension of water-bearing fractures under high water pressure, and the ground stress state and its value. Finally, the safe thickness was set as 5–6 m for a concrete engineering project. Semi-quantitative analysis simplifies the geologic model into a corresponding theory model, and then, it calculates the safe thickness using the theoretical formula. The accepted theories are the elastic beam theory, the elastic plate theory (Song et al. 2006), and the catastrophe theory (Li 2009). Li et al. (2010) concluded that the resistant body (the safe thickness) is composed of the loosened rock zone, the safe thickness zone, and the fractured zone. From this, they produced a semi-analytical expression. Guo (2011) generalized the tunnel and karst system into four mechanical models based on the different location relationships of the karst cave and tunnel. From this, he determined the theoretical formula for the thickness of the resistant body of the different mechanical models. Quantitative analysis establishes a physical–mechanical model or a mathematical model to calculate the safe thickness, but this requires additional parameters, which are difficult to obtain. Therefore, numerical simulation, orthogonal testing, and regression analysis are the methods most commonly used (Cao 2010; Song 2012).

From the previous discussion, when calculating the safe thickness, it is necessary to establish a mechanical model and to determine the force acting on the resistant body. When the karst cave is filled with water, the force exerted on resistant body is due to the high water pressure. When the karst cave is filled with mud or clay, the force is the thrust of the filling mud or clay. Most studies focus on the former condition, and it is easy to obtain the value of the high water pressure. However, few studies have been conducted on the latter condition. Mud inrush often occurs when the resistant body fails due to overloading. Existing research theories and numerical models are complex, and they cannot be successfully applied to this condition. Therefore, a new method is needed that is convenient for engineering applications, where filling medium inrush can occur in a tunnel under construction.

At present, the slice method has been widely applied to the analysis of slope and dam stability. The original Sweden arc method (Fellenius 1936) underwent constant improvement after it was initially proposed. Many scholars had developed new methods for the analysis of slope stability, such as the Bishop method (Bishop 1955), the Morgenstern–Price method (Morgenstern and Price 1965), the Spencer method (Spencer 1967), the Janbu method (Janbu 1973), the Sarma method (Sarma 1979), and the imbalance thrust force method. In addition, new assumptions concerning the sliding surface were presented, rather than using the arc sliding surface, e.g., the arbitrary sliding surface and the double broken line sliding surface. In addition, numerous methods have been conducted to determine the critical failure surface (Florkiewicz and Kubzdel 2009; Cheng et al. 2008; Hu et al. 2014; Kahatadeniya et al. 2009; Li et al. 2009). The horizontal slice method has also been used in slope engineering (Ghanbari et al. 2013). New methods have been developed to predict the critical factors controlling the safety of homogeneous finite slopes (Erzin and Cetin 2014). However, applications of the slice method to tunnel engineering remain rare. Gao et al. (2009) used the slice method for tunnel face stability analysis, and he obtained the analytical expression for the limiting support pressure at the excavation face. Furthermore, until now, there have been few reports concerning the use of the slice method to analyze the stability of a filling medium in a filled-type karst cave setting in karst tunnels. Lin et al. (2016) proposed a simplified computational model to analyze the filling’s stability based on the simplified Bishop method. Li et al. (2017a) analyzed the integral sliding stability of the filling media in karst caves based on the simplified Bishop method. Therefore, using the slice method to analyze the stability of the filling medium can be applied in engineering, as it is easy to use.

In this paper, the slice method is applied to determine the stability of the filling medium in a filled-type karst cave ahead of a tunnel face. A slice-based method calculation model is put forward. For the intact resistant body and the fractured resistant body, theoretical formulas for the minimum safe thickness are deduced from the tension strength and the shear strength criteria of the rocks, respectively. In addition, several factors that influence the minimum safe thickness are analyzed. This study provides references to keep the tunnel face stable and the construction site safe when the tunnel passes through a filled-type hazard-causing structure.

The minimum safe thickness of a filled-type karst cave

Calculation model

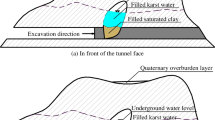
Filled-type karst caves are encountered frequently in the process of constructing tunnels in karst areas. If the situation is not properly taken into consideration and planned for, the filling medium can become unstable and filling medium inrush to the tunnel face can occur. Karst caves can easily form at the junction of soluble rocks and non-soluble rocks, e.g., the junction of limestone and shale. When the non-soluble rock is under the soluble rock, a karst cave develops along the non-soluble rock’s structural plane. If the karst cave is filled with clay or other filling medium, it can cause mud inrush into the tunnel when excavation occurs. There are too many complex factors that influence the stability of filled-type karst caves. Thus, it is necessary to simplify the calculation model to a filled-type karst cave above the structural plane ahead of the tunnel face. The simplified calculation model is established as shown in Fig. 1.

Fig. 1
figure 1

Sketch of a filled-type karst cave ahead of the tunnel face

Full size image

Several assumptions were made when establishing the calculation model.

  1. (1)

    The karst cave developed between non-soluble rock and soluble rock, and the non-soluble rock is below the soluble rock. The sliding surface is simplified as a straight line, and the forces on the sliding surface satisfy the static force equilibrium and moment equilibrium.

  2. (2)

    On the sliding surface, shear failure obeys the Mohr–Coulomb criterion and the shear strength is due to cohesion and friction.

  3. (3)

    The filling medium is an ideal rigid-plastic material, and it experiences no displacement or deformation during the loading process.

Our simplified model of a filled-type karst cave before inrush is based on the slice method and is shown in Fig. 2(a). Line AB is the potential sliding surface. The filling medium above the horizontal line AC is simplified as loads acting on the slices. The rectangle BCDE represents the resistant body between the tunnel face and the karst cave. n is the total number of slices. i is the number of an individual slice, and i = 1, 2,……,n.

Fig. 2
figure 2

Force model of the slice method (a) Diagram illustrating the division of the sliding soil (b) Force analysis of an arbitrary slice (not considering pore water pressure) (c) Force analysis of an arbitrary slice (considering pore water pressure)

Full size image

The most dangerous sliding surface

The slices are in a limit equilibrium state on the potential sliding surface (AB). Therefore, the normal stress (σn) and the shear stress (τ) at the bottom of the slice meet the Mohr–Coulomb strength criterion. Thus, the following expression can be obtained:

$$ {T}_i={N}_i\tan \varphi +{cl}_{\mathrm{i}}, $$
(1)

where Ni and Ti are the normal force and the tangential force at the sliding surface of the ith slice, respectively. c and φ are the cohesion and the internal friction angle of the filling medium, respectively. li is the contact length of the ith slice of the sliding surface.

An arbitrary slice is analyzed and is shown in Fig. 2(b). The expression XLi = XRi is true when it is assumed that the tangential forces at the two sides of the slice are equal in magnitude, but opposite in direction. Equation (2) is the static force equilibrium equation in the vertical direction.

$$ {N}_i\cos \theta +{T}_i\sin \theta -{P}_i-{W}_{\mathrm{i}}= 0, $$
(2)

where XLi and XRi are the tangential forces acting on the left and right sides of the ith slice, respectively. ELi and ERi are the normal forces acting on the left and right sides of the ith slice, respectively. Wi and Pi are the weight and the load acting on the top of the ith slice, respectively. θ is the dip angle of the ith slice’s bottom surface.

The normal force can be solved using the following equation:

$$ {N}_i=\frac{P_i+{W}_{\mathrm{i}}-{cl}_i\sin \theta }{\cos \theta +\sin \theta \tan \varphi }. $$
(3)

The weight of the slice is expressed by the following expression:

$$ {W}_{\mathrm{i}}=\frac{\gamma {hl}_i\left(n-i+1\right)\cos \theta }{n}, $$
(4)

where h is the height of the tunnel face, and γ is the unit weight of the filling medium.

Equation (5) is the static force equilibrium equation in the horizontal direction.

$$ {N}_i\sin \theta \hbox{-} {T}_i\cos \theta +{E}_{Ri}-{E}_{Li}=0 $$
(5)
$$ {E}_{Ri}={E}_{L\left(i+1\right)} $$
(6)

The force (T0), which is the resistant body applied to the first slice, is the normal force acting on the left side of the first slice (EL1). It can be calculated using Eq. (7).

$$ {T}_0={E}_{L1}=\sum \limits_{i=1}^n\left[{N}_i\sin \theta -\left({N}_i\tan \varphi +{cl}_i\right)\cos \theta \right] $$
(7)

In actual engineering, the filling clay may be under the karst water in the karst cave. Therefore, Fig. 2(c) shows the force analysis of an arbitrary slice when the pore water pressure is taken into consideration. Equations (1)–(7) transform as follows in Eqs. (8)–(14):

$$ {T}_i=\left({N}_i-{U}_{bi}\right)\tan {\varphi}^{\prime }+{c}^{\prime }{l}_{\mathrm{i}}=\left({N}_i-{u}_{bi}{l}_i\right)\tan {\varphi}^{\prime }+{c}^{\prime }{l}_i, $$
(8)
$$ {N}_i\cos \theta +{T}_i\sin \theta -\left({P}_i+{U}_{ti}\right)-{W}_{\mathrm{i}}=0\kern0.5em {U}_{ti}={u}_{ti}l\cos \theta, $$
(9)
$$ {N}_i=\frac{P_i+{u}_{ti}{l}_i\cos \theta +{W}_{\mathrm{i}}+\left({u}_{bi}{l}_i\tan {\varphi}^{\prime }-{c}^{\prime }{l}_i\right)\sin \theta }{\cos \theta +\sin \theta \tan {\varphi}^{\prime }}, $$
(10)
$$ {W}_{\mathrm{i}}=\frac{\gamma_{sat}{hl}_i\left(n+1-i\right)\cos \theta }{n}, $$
(11)
$$ {N}_i\sin \theta \hbox{-} {T}_i\cos \theta +{E}_{Ri}-{E}_{Li}=0, $$
(12)
$$ {E}_{Ri}={E}_{L\left(i+1\right)},\kern1em \mathrm{and} $$
(13)
$$ {T}_0={E}_{L1}=\sum \limits_{i=1}^n\left[{N}_i\sin \theta -\left({N}_i\tan {\varphi}^{\prime }-{u}_{bi}{l}_i\tan {\varphi}^{\prime }+{c}^{\prime }{l}_i\right)\cos \theta \right], $$
(14)

where Uti, uti, Ubi, ubi are the pore water pressure, acting on the top and bottom of the ith slice, respectively. c′ and φ′ are the effective cohesion and effective internal friction angle of the filling medium, respectively. γsat is the saturated unit weight of the filling medium.

In order to determine the most dangerous sliding surface, a hypothetical angle of the sliding surface (θ) is initially given. The force (T0) should be calculated in this situation. Then, we change the hypothetical angle and calculate the new value of the force (T0). We repeat this process until the force (T0) reaches its maximum value. The angle θ corresponding to the maximum value is the angle of the surface along which the filling medium would most likely slide, i.e., the most dangerous sliding surface.

The minimum safe thickness for filling medium inrush

When calculating the minimum safe thickness, the intact resistant body and the fractured resistant body are discussed separately. The diagrams of this calculation are shown in Fig. 3.

  1. (1)

    Intact resistant body

Fig. 3
figure 3

Diagram of the resistant body (a) Intact resistant body (b) Fractured resistant body

Full size image

To simplify the calculation model, the resistant body is treated as a homogeneous continuous isotropic elastic body, and its deformation is assumed to follow the small deformation theory. Therefore, the model is simplified as a statically indeterminate beam with two fixed ends. This model is shown in Fig. 3(a).

Assume that the force that the filling medium exerts on the resistant body is a uniform load (q) defined by Eq. (15).

$$ q=\frac{T_0}{h} $$
(15)

The maximum bending moment occurs at the two ends, and it can be calculated using Eq. (16):

$$ {M}_{\mathrm{max}}=\frac{1}{12}{qh}^2, $$
(16)

where Mmax is the maximum bending moment in the beam.

The maximum tensile stress also occurs at the two ends under a uniform load. It can be calculated using Eq. (17):

$$ {\sigma}_{\mathrm{max}}=\frac{My_{\mathrm{max}}}{I_z}=\frac{qh^2}{2{y}^2}, $$
(17)

where Iz is the moment of inertia of the resistant body. ymax is half of the thickness of the resistant body.

Once the maximum tensile stress on the resistant body exceeds the tensile strength [σt], the resistant body will fail and the filling medium inrush will occur. Therefore, when the maximum tensile stress equals the tensile strength, the system reaches its critical state, and thus the y is the minimum safe thickness for resisting filling medium inrush, as is shown by Eq. (18). Here a safety factor is introduced to provide a higher degree of safety assurance and improve the stability of the tunnel face, which is shown by Eq. (19).

$$ {\sigma}_{\mathrm{max}}=\frac{qh^2}{2{y}^2}=\left[{\sigma}_t\right]\kern1em \mathrm{and} $$
(18)
$$ {S}_t= Fh\sqrt{\frac{q}{2\left[{\sigma}_t\right]}}, $$
(19)

where St is the minimum safe thickness, [σt] is the tensile strength of the rock mass, and F is the safety factor.

The calculation should be compared to the minimum thickness required for the resistant body to meet or exceed the shear-resistant strength. The maximum shear force of the resistant body under a uniform load can be calculated using Eqs. (20)–(21).

$$ {\mathrm{Q}}_{\mathrm{max}}=\frac{1}{2} qh\kern1em \mathrm{and} $$
(20)
$$ {\tau}_{\mathrm{max}}=\frac{3{Q}_{\mathrm{max}}}{2y}=\frac{3 qh}{4y}\le \left[\tau \right], $$
(21)

where Qmax, τmax, and [τ] are the maximum shear force, the maximum shear stress, and the shear strength of the rock, respectively.

Accordingly, the minimum safe thickness should be calculated based on the shear-resistant strength using Eq. (14).

$$ {S}_t=F\frac{3 qh}{4\left[\tau \right]} $$
(22)

Therefore, St should be the maximum value between Eqs. (19) and (22).

  1. (2)

    Fractured resistant body

A case often encountered in engineering is when the resistant body has structural planes on the tunnel face, e.g., joints and fissures, caused by weathering, blasting vibrations, and other factors. The existing structural plane would result in a decrease in the integrity of the surrounding rock. If we take into consideration a resistant body with a horizontal crack in the tunnel face and neglect the force between the two sections of the rock above and below the crack, then the model can be simplified as two cantilever beams subjected to uniformly distributed loads as shown in Fig. 3(b).

The maximum bending moment occurs at the end of the beams. Its value can be calculated using Eq. (23).

$$ {M}_{\mathrm{max}}=\frac{1}{2}{qh_0}^2, $$
(23)

where h0 is the effective height of the resistant body, h0 = max[h1, h2], and h1 + h2 = h. h1 and h2 are the heights of the two sections of rock above and below the crack, respectively. The other parameters have been previously described.

Similarly, the maximum tensile stress also occurs at the fixed ends. The value can be calculated using Eq. (24).

$$ {\sigma}_{\mathrm{max}}=\frac{My_{\mathrm{max}}}{I_z}=\frac{3{qh_0}^2}{y^2}\le \left[{\sigma}_t\right] $$
(24)

The minimum safe thickness for this situation can be obtained using Eq. (25).

$$ {S}_t={Fh}_0\sqrt{\frac{3q}{\left[{\sigma}_t\right]}} $$
(25)

The result should be compared to the minimum thickness required for the resistant body to meet or exceed the shear-resistant strength. The maximum shear force within resistant body under a uniform load occurs at the end of the beam, and it can be calculated using Eqs. (26) and (27).

$$ {\mathrm{Q}}_{\mathrm{max}}={qh}_0 $$
(26)
$$ {\tau}_{\mathrm{max}}=\frac{3{Q}_{\mathrm{max}}}{2y}=\frac{3{qh}_0}{2y}\le \left[\tau \right] $$
(27)

Thus, the minimum safe thickness should agree with the shear-resistant strength as described in Eq. (28).

$$ {S}_t=F\frac{3{qh}_0}{2\left[\tau \right]} $$
(28)

The parameters in Eqs. (23)–(28) have been previously described. St is the maximum value between Eqs. (25) and (28).

Case study and discussion

A karst cave filled with clay along the structural plane was encountered in the process of constructing a tunnel, as shown in Fig. 1. The dip angle (θ0) of the structural plane is 30°. The height (h) of the tunnel face is 10 m. The parameters describing the filling clay are as follows: the unit weight (γ1) is 19 kN/m3; the saturated weight (γsat) is 20.1 kN/m3; the cohesion (c) is 14.4 kPa; the effective cohesion (c′) is 11.4 kPa; the internal friction angle (φ) is 20°; and the effective internal friction angle (φ′) is 17.5°. The tunnel face is composed of limestone. Its tensile strength ([σt]) is 5 MPa, and its shear strength ([τ]) is 10 MPa. The load on the slices (pi) is 0.35 MPa; and when taking the pore water pressure into consideration, the load on the slices (pi = 0.25 MPa, ui = 0.1 MPa) is 0.35 MPa. The safety factor is F = 1.3.

The most dangerous sliding surface

The force (T0) is the first slice acting on the resistant body. The force (T0) can be obtained from the different values of the sliding surface angle using the method presented in section "The most dangerous sliding surface". Figure 4 illustrates the relationship between the sliding surface angle and the force (T0). In scenario 1, the filling medium is natural soil and the pore water presure is not taken into consideration. In scenario 2, the filling medium is saturated clay and the pore water presure is taken into consideration.

Fig. 4
figure 4

Plots of (a) the sliding surface angle θ vs. the force T0 and (b) the sliding surface angle θ vs. the change in the force △T0

Full size image

As can be seen from Fig. 4(a), as the sliding surface angle increases, the force (T0) initially increases and then decreases. The force (T0) has a maximum value during the change process of the sliding surface angle. In scenario 1, the maximum value is 2.00 × 103 kN, and the sliding surface angle is 55° when responding to the maximum value and the given parameters. That is to say, the corresponding surface is the most dangerous sliding surface. In addition, the force (T0) cooresponding to the differernt values of the sliding surface angle are perfectly symmetric about the most dangerous sliding surface angle when the angle ranges from 30° to 80°. In scenario 2, the maximum value is 2.99 × 103 kN, and the most dangerous sliding surface is approximately 53.75°. The force (T0) is perfectly symmetric about the most dangerous sliding surface angle when the angle ranges from 30° to 77.5°. In addition, when the filling medium is saturated clay, the force (T0) is much larger than when the pore water pressure is not taken into consideration, i.e., when the filling medium is natural soil. That is to say, it needs a larger supporting force to keep the filling medium stable. Mud inrush occurs more easily when the karst cave is filled with saturated clay.

As can be seen from Fig. 4(b), when the sliding surface angle is significantly different than the angle of the most dangerous sliding surface, the force (T0) increases or decreases significantly as the angle increases. When the sliding surface angle approaches the angle of the the most dangerous sliding surface, the force (T0) increases or decreases slowly as the angle increases. When the filling medium is saturated clay, the change force (△T0) is much larger than when the pore water pressure is not taken into consideration, i.e., when the filling medium is natural soil.

It should be noted that the filling medium can also slide along the interface between the soil and the rock mass when the shear strength parameters (cohesion and interal friction angle) of the interface are different. For example, if the shear strength parameters of the interface are c0=10 kPa and φ0=13°, the force (T0) calculated is 2.18 × 103 kN, which is larger than the maximum value in scenario 1. That is to say, the interface between the filling soil and the rock mass is the most dangerous sliding surface, and the sliding surface angle is 30°. Therefore, the most dangerous sliding surface can be the interface between the soil and the rock mass, or inside the filling medium mass. Thus, when determining the most dangerous sliding surface, the force (T0) should be calculated according to the parameters of both of the conditions. Then the two values can be compared and the maximum one should be chosen as the correct value.

Influence of the shear strength parameters on the force (T0) and the sliding surface angle (θ)

To investigate the influence of the shear strength parameters on the force and the most dangerous sliding surface angle, the angle (θ) and the force (T0) are calculated for different cohesion values and internal friction angles. We use scenario 1 as an example. The shear parameters and calculation results are shown in Table 1. The cohesion values are 8.4 kPa, 10.4 kPa, 12.4 kPa, 14.4 kPa, 16.4 kPa, 18.4 kPa, and 20.4 kPa. The internal friction angle values are 11°, 14°, 17°, 20°, 23°, 26°, and 29°. The relationships betweent the force and the two parameters are shown in Figs. 5 and 6.

Table 1 The most dangerous sliding surface angle θ and the force T0 under different shear strength parameters
Full size table
Fig. 5
figure 5

Plot of the internal friction angle φ vs. the force T0 and the most dangerous sliding surface angle θ

Full size image
Fig. 6
figure 6

Plots of (a) the cohesion c vs. the force T0 and (b) the cohesion c vs. the most dangerous sliding surface angle θ

Full size image

As shown in Fig. 5, the internal friction angle has a significant influence on the force (T0) and the most dangerous sliding surface. The force (T0) decreases nearly linearly as the internal friction angle increases, but the decrease in the force diminishes slightly. The most dangerous sliding surface angle increases as the internal friction angle increases. The relationship between these two parameters is linear. If the internal friction angle increases by 3°, the most dangerous sliding surface angle increases by 1.5°. The relationship of the most dangerous sliding surface angle and internal friction angle is θ = 45 °  + φ/2.

As shown in Fig. 6(a), the force (T0) decreases linearly with increasing cohesion. For example, when the internal friction angle is 11°, if the cohesion increases by 2 kPa, the force (T0) decreases by approximately 33 kN; and when the internal friction angle is 20°, if the cohesion increases by 2 kPa, the force (T0) decreases by approximately 28 kN. Thus, it can be seen that for various internal friction angles, there is a linear relationship between cohesion (c) and force (T0). However, the larger the internal friction angle, the smaller the incremental change in force (T0) is when the cohesion increases by 2 kPa. As shown in Fig. 6(b), curves formed by the two parameters are horizontal lines for all of the various internal friction angles. When the internal friction is constant, the most dangerous sliding surface angle remains constant as cohesion increases. That is to say, the cohesion of the filling medium has no effect on the most dangerous sliding surface angle.

In conclusion, the larger the shear strength parameters, the smaller the force (T0) acting on the resistant body, and the harder it is for inrush to occur. In addition, the internal friction angle has a significant influence on the most dangerous sliding surface angle, while the cohesion has not effect on it.

The minimum safe thickness and its influencing factors

In scenario 1, when the resistant body is intact, the minimum safe thickness is St = 1.84 m, and it agrees with the value of the shear strength, St ≥ 0.20 m. For a fractured resistant body, h1 = 7 m, h2 = 3 m, and an effective height of h0 = 7 m. The minimum safe thickness is St = 3.16 m, and it also agrees with the value of the shear strength, St ≥ 0.27 m.

Similarly, in scenario 2, when the resistant body is intact, the minimum safe thickness is St = 2.25 m. When the resistant body has a crack, h1 = 7 m, h2 = 3 m, and the effective height is h0 = 7 m. The minimum safe thickness is St = 3.85 m. In scenario 2 (with pore water taken into consideration), the minimum safe thickness calculated for both the intact and fractured resistant body scenarios agree with the value shear strength.

As seen from the calculation results, the minimum safe thickness calculated based on the tension strength is much larger than that calculated based on the shear strength. Thus, resistant body failure is controlled by the tension strength when filling medium inrush occurs. That is to say, tensile stress exceeding the tension strength results in failure. It can also be seen that the value of the minimum safe thickness of a fractured resistant body is much larger than that of an intact resistant body. This indicates that the inrush of a filling medium occurs more easily in a fractured rock mass than in an intact rock mass. In addition, when taking pore water pressure into consideration, the minimum safe thickness increases. Filling medium inrush occurs more easily when the filling medium is under karst water.

  1. (1)

    The influence of the shear strength parameters on the minimum safe thickness

The relationships between the strength parameters and the minimum safe thickness are as illustrated in Fig. 7.

Fig. 7
figure 7

Plots of the shear strength parameters vs. the minimum safe thickness (a) Plot of the internal friction angle vs. the minimum safe thickness (b) Plot of cohesion vs. the minimum safe thickness

Full size image

As seen in Fig. 7(a), the minimum safe thickness decreases nearly linearly as the internal friction angle of filling medium increases. The reduction also decreases as the internal friction angle increases. For example, when the cohesion is 14.4 kPa, the reductions are 0.119 m, 0.114 m, 0.110 m, 0.106 m, 0.102 m, and 0.099 m, respectively, when the internal friction increases from 11° to 29° in 3° increments. When the cohesion varies, the decreasing trend is slightly different.

It can be concluded from Fig. 7(b) that the minimum safe thickness decreases as cohesion increases. The decrease in the minimum safe thickness is gradual as the cohesion increases, and the trend is nearly linear. The cohesion increases by 2 kPa, while the safe thickness decreases by approximately 0.013 m.

In summary, the minimum safe thickness decreases as the shear strength parameters increase. When the shear strength parameters increase, the self-stable ability of the filling medium increases, which leads to a decrease in the force acting on the resistant body. Therefore, the minimum safe thickness decreases.

  1. (2)

    The influence of the load and the tensile strength of the rock mass on the minimum safe thickness

We use an intact resistant body as an example. The other parameters are the same as previously mentioned. The load values are 0.05 MPa, 0.15 MPa, 0.25 MPa, 0.35 MPa, 0.45 MPa, 0.55 MPa, and 0.65 MPa, and the tensile strengths values are 3.5 MPa, 4.0 MPa, 4.5 MPa, 5.0 MPa, 5.5 MPa, 6.0 MPa, and 6.5 MPa, respectively. The calculation results of the minimum safe thickness are shown in Table 2. The relationships between the minimum safe thickness, load, and tensile strength are shown in Fig. 8.

Table 2 The minimum safe thickness under different loads and rock tensile strength
Full size table
Fig. 8
figure 8

Plots of (a) the minimum safe thickness vs. the load and (b) the minimum safe thickness vs. the tensile stength

Full size image

As can be seen from Fig. 8(a), as the load increases, the minimum safe thickness increases, and the extent of the increase decreases gradually. In other words, when the load applied to the slice increases, the force (T0) also increases; therefore, a larger minimum safe thickness is needed to maintain the filling medium’s stability. Whereas when the tensile strength of the tunnel rock increases, the resistant body does not easily fail; therefore, the minimum safe thickness is smaller, as shown in Fig. 8(b).

In conclusion, the minimum safe thickness increases with increasing load and decreases with increasing tensile strength.

  1. (3)

    The influence of the effective height of the fractured resistant body on the minimum safe thickness

For a fractured resistant body, different crack locations correspond to different effective heights of the rock face since the effective height is determined from the crack’s location. This results in a change in the minimum safe thickness. The relationships between the location, the effective height, and the minimum safe thickness are shown in Fig. 9. h1 is the vertical distance from the crack to the tunnel floor.

Fig. 9
figure 9

Plot of the crack location vs. the effective height and the minimum safe thickness

Full size image

As can be seen from Fig. 9, as the crack’s location rises, both the effective height and the minimum safe thickness initially decrease and then they increase. The minimum safe thickness increases linearly with increasing effective height, as shown by Eq. (25). When h1 is 5 m, the effective height and the minimum safe thickness are both minimized. That is to say, when the crack occurs in the middle of the tunnel face, the system of tunnel, inrush-prevent layer, and filling medium is more stable than when the crack occurs in a different location. When the crack in the resistant body is close to the vault or the floor (h1 = 0 m or h1 = 10 m), the cantilever beam of the model is the longest. The tension stress reaches its maximum value at the end of the beam under the same load, and the resistant body needs to be thicker to remain stable, i.e., a larger minimum safe thickness is required to prevent filling medium inrush and maintain stability.

In conclusion, when the crack is in the middle of the resistant body, the minimum safe thickness is minimized. The minimum safe thickness increases linearly as the effective height of the resistant body increases.

Engineering application

We use the “+526” karst cave water and mud inrush case of the Yunwushan tunnel in Yichang–Wanzhou railway as an example. The 21 m long karst cave is located between DK245 + 526 and DK245 + 547. It was developed along a fault, which extends from DK245 + 504.8 to DK245 + 633.8. The karst cave is filled with mud, sand, and karst water. The volume of mud and sand is about 250 m3. The karst water pressure is 0.8 MPa. The tunnel is 9.8 m high and 7 m wide. The tensile strength of the tunnel face is 5 MPa. Assuming that the effective cohesion (c′) is 11.4 kPa, the effective internal friction angle (φ′) is 17.5°, and the saturated weight (γ′) is 20.1 kN/m3, then the minimum safe thickness calculated by the proposed method is 3.74 m. The result obtained by Guo (2011) is 3.69 m. The minimum safe thicknesses obtained by the two methods are very close, which verifies that the proposed method is effective and reasonable. When there is a crack in the resistant body, the minimum safe thickness is approximately 9.26 m, which is considered to be the most dangerous condition. Therefore, the minimum safe thickness is between 3.74 m and 9.26 m. The energesis and depressurization technology was used to reveal the dimensions of the karst cave during the construction. The tunnel face can be divided into four zones: zone I is less than 2.5 m, zone II is 2.5–4 m, zone III is 4.5–9 m, and zone IV is greater than 9 m. Both zones I and II are revealed by the survey. The reserved thickness is larger than 4.5 m (zones III and IV), which verifies the validity of the proposed method.

Discussion

A new slice-based method was applied to determine the stability of the filling medium in filled-type karst hazard-causing structures. From the tension strength and shear strength criteria of the rocks, the theoretical formulas for the minimum safe thickness of filling medium inrush were deduced using the strength of materials theory. By using elastic mechanics theory to analyze the force of the resistant body, the accuracy of the calculation was improved. According to the elastic mechanics theory, when the span of the beam is twice as long as its depth, using elastic mechanics theory can provide a 6.7% correction for the bending stress compared to strength of materials theory. When the span of the beam is four times as long as its depth, using elastic mechanics theory can provide a 1.7% correction for the bending stress compare to strength of materials theory. However, the calculation process and function are relatively complex, and it is not easy for technicians to master. In addition, the accuracy of the proposed method meets the accuracy required for engineering projects; therefore, the proposed method can be effective and useful in engineering.

When the karst cave is only filled with water and the water pressure is known, the force acting on resistant body can be figured out directly, and it is equal to the water pressure times the area of tunnel face. Then, the minimum safe thickness can also be figured out according to formulas (19) and (22), or (25) and (28).

The study mainly focuses on the condition that the karst cave is smaller in the transverse width direction of the tunnel face. With the increase of the karst cave along tunnel face width direction, the error will increase when resistant body is simplified as an elastic beam with fixed ends. When the width of the karst cave exceeds the outline of the tunnel face in its transverse direction, the minimum safe thickness of the resistant body should be studied by using elastic plate theory (Guo et al. 2017; Shi et al. 2016).

In addition, the assumed fixed beam is subjected to vertical in situ stress. When the buried depth is shallow, the vertical in situ stress is small, while when the buried depth is large, the vertical in situ stress affects greatly. In general, the minimum safe thickness of water and mud inrush in tunnel increases linearly with the increase of buried depth (Shi et al. 2016).

During the theoretical derivation, we considered a planar problem, and the sliding surface of the filling medium slides along a straight line. Therefore, further research is required to determine the minimum safe thickness when the filling medium slides along a real three-dimensional sliding surface.

Conclusions

  1. (1)

    A new slice-based method is proposed to determine the minimum safe thickness of a filled-type karst cave. A computational slice model of the filling medium in a filled-type karst hazard-causing structure is put forward. The force expression of the slice acting on the resistant body is calculated, and the most dangerous sliding surface is identified.

  2. (2)

    The force acting on the resistant body has a maximum value. The sliding surface that corresponds to this maximum value is the most dangerous sliding surface. The filling medium may also slide along the interface between the filling medium and the rock mass when the shear strength parameters of the interface have small values.

  3. (3)

    The cohesion of the filling medium has no effect on the sliding surface angle, while the angle of the sliding surface increases by 1.5° when the internal friction angle increases by 3°. The force decreases nearly linearly as the cohesion increases, and it decreases nonlinearly as the internal friction angle increases.

  4. (4)

    A model is put forward for an intact resistant body with a statically indeterminate beam with two ends fixed under uniform loads. A model is put forward for a fractured resistant body with a cantilever beam under uniform loads. In addition, the theoretical formulas to calculate the minimum safe thickness are deduced for each model. Our study provides a theoretical basis for the calculation of the stability of the rock mass ahead of the tunnel face.

  5. (5)

    The minimum safety thickness decreases nearly linearly as the shear strength parameters increase. As the load acting on the slices increases, the minimum safe thickness increases nonlinearly. As the tensile strength of the resistant body increases, the minimum safe thickness decreases nonlinearly.

  6. (6)

    For a fractured resistant body, the minimum safe thickness increases linearly as the effective height of the resistant body increases. When the crack is close to the vault or the floor, a larger minimum safe thickness is required to prevent filling medium inrush into the tunnel.