Stability analysis of rock slopes against sliding or flexural-toppling failure

Abstract

Toppling is a mode of failure that may occur in a wide range of layered rock strata in rock slopes. According to the results of physical model tests and field investigations of anti-inclined rock slopes, most real instabilities are of the sliding or flexural-toppling type. Failure often initiates at the slope toe, and the failure surface is usually multi-planar rather than planar. These properties should determined by searching rather than based on assumption. Taking these problems into account, in this paper we propose a theoretical model for rock slopes with a potential for sliding or flexural-toppling failure on the basis of two physical model tests. An innovative approach for the stability analysis of such slopes based on the limit equilibrium theory is then proposed. Subsequently, a comparative analysis is carried out using the discrete element method and the Aydan et al. method with the aim to verify the validity and accuracy of the proposed approach. Finally, the possible difference between angles of the basal calculation plane and the failure surface of the sliding zone and superimposed toppling zone with respect to the plane normal to the discontinuities is presented.

Introduction

Toppling is a typical failure mode of rock slopes that is often encountered in various geotechnical engineering construction projects (Alejano et al. 2010; Goodman and Bray 1976; Liu 2013; Lu 2010; Zuo et al. 2005). However, the toppling failure of rock slopes was not recognized and studied until the 1960s. Toppling failure of rock slopes is associated with rock masses having a dominant discontinuity set (usually bedding or foliation) with strike nearly parallel to the slope face and inward dip (Sagaseta et al. 2001). This failure can be classified into two principal types, namely, flexural-toppling and block-toppling (Goodman and Bray 1976). In this paper, we focus on the former. As shown in Fig. 1, if a rock mass is composed of a set of parallel discontinuities that dip steeply against the face slope, i.e., an anti-inclined rock slope, the rock mass will act in the same manner as a set of rock columns that are placed on top of each other. If the maximum tensile stress in each rock column exceeds its tensile strength, then the rock slope will fail and topple. Such instability is categorized as flexural-toppling failure (Amini et al. 2012). Stability analyses of rock slopes against flexural-toppling failure have been performed. Based on the assumption that the failure surface is perpendicular to the discontinuities, Aydan and Kawamoto (1987, 1992) proposed a method for the stability analysis of rock slopes against flexural-toppling using the limit equilibrium theory. However, based on the results of their centrifuge physical modeling study, Adhikary et al. (1997) reported that the failure surface is not perpendicular to the discontinuities; instead, the basal failure surface observed in the centrifuge models emanated from the toe of the slope and was oriented at an angle of 12–20° upward from the normal to the discontinuities. Zuo et al. (2005) proposed a superimposed cantilever beam model for the stability analysis of rock slopes against flexural-toppling failure on the basis of physical model tests, which led to the establishment of a formula for the critical fracture height for a single rock column. Using the limit equilibrium approach proposed by Aydan and Kawamoto (1992), Lu (2010) analyzed the influence of the discontinuity cohesion and rock column weight on the stability of rock slopes against flexural-toppling failure. Chen and Huang (2004) conducted research on the instability criterion for flexural-toppling failure by generalizing an arbitrary rock column as a beam model bearing a composite force. For rock slopes with geo-structural defects existing in in situ rock columns, Majdi and Amini (2011) proposed a new approach for stability analysis against flexural-toppling failure based on solid and fracture mechanics. These solutions represent useful advances in the techniques for evaluating flexural-toppling mechanisms. However, the mechanisms of initiation, propagation, and coalescence of the fracture surface remain unclear due to the complexity of flexural-toppling failure. The following problems remain in current studies:

• (1) The failure surface is assumed rather than determined by searching. Aydan and Kawamoto (1992) assume that the failure surface is perpendicular to the discontinuities, and Adhikary et al. (1997) consider that the angle between the failure surface and the plane normal to the discontinuities is approximately 10°. However, a method for determining the failure surface has not been established.

• (2) It is assumed that flexural-toppling starts from the rock column above the slope crest, which is inconsistent with actual findings. If failure of the rock columns in the lower section does not occur first, flexural-toppling of the upper rock columns would not occur due to a lack of space to deform and fail.

• (3) For rock columns located near the toe, flexural-toppling may occur less readily because the corresponding slenderness ratios (defined as the ratio of the height of rock column above the failure surface to block thickness; Liu et al. 2009) are relatively small, whereas shear failure occurs more easily. Hence, sliding or flexural-toppling failure rather than pure flexural-toppling failure may occur. Based on numerical simulations and site investigations, previous studies have shown that shear-sliding failure rather than flexural-toppling failure occurs within rock columns near the slope toe (Cai 2013; Lu 2010; Yue et al. 2008). However, only qualitative descriptions of the phenomenon were presented in these studies, and the quantitative analysis method has not been established. In this case, using the existing approaches for pure flexural-toppling failures to evaluate the slope stability may be overly optimistic.

Fig. 1

Flexural-toppling failure in rock slopes

To address these problems, we present a new mathematical model for evaluating the stability of slopes in layered rock masses potentially subject to sliding or flexural-toppling failure.

Failure mechanism of rock slopes against sliding or flexural-toppling failure

An anti-inclined rock slope with a potential for sliding or flexural-toppling failure facing Jingzhu Road was selected for analysis, and two physical model tests were designed and conducted to investigate the failure mechanisms of anti-inclined rock slopes. For these two models, the angles of the discontinuities with respect to the horizontal direction were 78° and 65°, respectively, whereas the other parameters were exactly identical. The prototype slope involves three different lithologies (i.e., middle-thick layered muddy limestone, middle-thick layer limestone, and thick layered limestone), which were simulated by model materials I, II, and III, respectively, as shown in Fig. 2.

Physical model tests are effective tools to evaluate slope stability (Aydan and Kawamoto 1987, 1992; Lin et al. 2015; Ng et al. 2016, 2017). When using a physical model to study the deformation and failure mechanisms of a prototype slope, the three requirements of scale, loading, and material properties must be satisfied (Lin et al. 2015; Zheng et al. 2017). The scale requirement can be met if the model and the prototype are geometrically similar. The type of loading in the model must be similar to that of the prototype, and the magnitude of the loading must be proportional. The model material must have stress-strain properties similar to those of the prototype material. In addition, the materials used in the physical test should satisfy the following principles: (1) the mechanical properties must be stable during the simulation process; (2) the mechanical properties should vary considerably as the material mixture ratios are modified; (3) the raw material must be readily available, be inexpensive, have a short solidification time, and easily allow for model construction. Based on similarity assumptions and several similar materials commonly used in previous studies (Adhikary et al. 1997; Aydan and Kawamoto 1992), we chose quartz sand, gypsum, and cement as the similar materials in this study. The mixture ratios and properties of model materials I, II, and III are given in Table 1. The most important approximations used in this study are as follows (the subscripts p and m denote the prototype and model, respectively.):

• Geometric ratio: ${C}_l=\frac{l_p}{l_m}=80$

• Weight ratio: ${C}_{\gamma}=\frac{\gamma_p}{\gamma_m}=1.8$

• Stress ratio: ${C}_{\sigma}=\frac{\sigma_p}{\sigma_m}={C}_{\gamma}{C}_l=144$

• Ratio between the elasticity moduli: ${C}_E=\frac{E_p}{E_m}={C}_{\sigma}=144$

• Cohesion ratio: ${C}_c=\frac{c_p}{c_m}={C}_{\sigma}=144$

• Ratio between the compressive strengths: ${C}_R=\frac{R_p}{R_m}={C}_{\sigma}=144$

• Ratio between the tensile strengths: ${C}_T=\frac{T_p}{T_m}={C}_{\sigma}=144$

• Strain ratio: ${C}_{\varepsilon}=\frac{\varepsilon_p}{\varepsilon_m}=1.0$

• Ratio between the internal friction angles: ${C}_f=\frac{f_p}{f_m}=1.0$

• Poisson’s ratio: ${C}_{\mu}=\frac{\mu_p}{\mu_m}=1.0$

Table 1 Mixture ratios of properties and three model materials

The model slopes were formed by a succession of small blocks, as shown in Fig. 3. The block sizes of materials I, II, and III were 200 × 50 × 20 mm, 200 × 50 × 20 mm, and 200 × 50 × 40 mm, respectively. To reflect the characteristics of rock columns, the end of each block was bonded using binder (i.e., gypsum slurry), whereas the side face was not bonded. In particular, the binder strength was designed to be slightly greater than that of the small blocks, thereby avoiding the occurrence of failure along block ends.

Fig. 2

Geometry of model slope, and excavation stages and measuring point arrangement in the physical model tests (length unit: millimeters). I, II, III Model materials used to simulate middle-thick layered muddy limestone, middle-thick layered limestone, and thick layered limestone, respectively

Four excavation stages were carried out in the physical model tests, and 15 measuring points were installed on the model slopes, as shown in Fig. 2. For these two models, the measured displacements at the measuring points near the slope surface are shown in Tables 2 and 3, respectively. For the model slope with a discontinuity angle of 78°, the displacement first increased and then decreased from the toe to the crest of slope. Moreover, the displacement direction appeared to be closer perpendicular to the discontinuities with increasing distance from the measuring point to the toe, indicating that toppling deformation of rock columns was more apparent in the crest than in the toe. The displacement at all measuring points except measuring point 13 decreased when the discontinuity angle was reduced to 65° due to the occurrence of large toppling deformation for the slope with a high discontinuity angle. In the case of toppling failure, we noted that interlayer slip must occur before the occurrence of large flexural deformations. This precondition for the anti-inclined rock slopes to undergo flexural-toppling failure has been proposed (Goodman 1989), which can be expressed as:

$$ \left({90}^0-{\beta}_c\right)+{\varphi}_j<\eta $$

(1)

where β _c and η are the angles of the cut slope and the discontinuities with respect to the horizontal direction, respectively, and φ _j is internal friction angle of the discontinuities.

Table 2 The measured displacements of the model slope with a discontinuity angle of 78°

Table 3 The measured displacements of the model slope with a discontinuity angle of 65°

Thus, the larger the discontinuity angle, the more prone the flexural-toppling deformation is to occur in the anti-inclined rock slopes. In the case of the model slope with a discontinuity angle of 65°, overall, the displacement gradually increased with the increase of the distance from the measuring point to the toe. The displacement direction at all measuring points was approximately perpendicular to the discontinuities, except that at measuring points 1 and 13, which indicated that the difference between the toppling deformation of rock columns in the crest and toe tended to be small. It should be noted that failure of the model slopes did not occur when excavations were completed according to the design. Then, the excavation angle of the slope was gradually increased until the slope failure occurred, while the height of the slope remained unchanged.

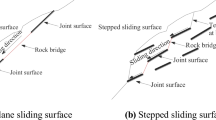
Photographs of the model slopes when completing excavations are shown in Fig. 3. For both of these model slopes, shear-sliding or flexural-toppling failure had occurred, and the failure surfaces were multi-planar. B and E denote the starting point and end point, respectively, and b1, b2, b3, b4, and b5 denote the turning points of the failure surfaces. Rock columns located between the slope toe (point B) and the first turning point (point b1) were in close contact, and no gaps could be observed between adjacent rock columns. Moreover, the failure surface between points B and b1 was approximately planar. For the failure zone located above the first turning point, b1, however, gaps appeared between adjacent rock columns, although this phenomenon in model 2 was not as apparent as that in model 1. The corresponding failure surface presented a stepped type, indicating that the failure surface of flexural-toppling was multi-planar rather than planar. Similar results have also been observed in the physical model tests (Aydan and Kawamoto 1992) and in practice (Majdi and Amini 2011; Cai 2013), as shown in Fig. 4.

Fig. 3

Post-failure photographs of model slopes. B, E Starting point and end point, respectively, b1, b2, b3, b4, b5 Turning points of the failure surfaces

Fig. 4

Flexural-toppling failures observed in laboratory and practice. a Post-failure photograph of the model slope (Aydan and Kawamoto 1992), b flexural-toppling failure in Galandrood mine slope (Majdi and Amini 2011), c flexural-toppling failure in Zhongliang reservoir bank slope (Cai 2013)

Based on the results of physical model tests and observations in practice, it was found that the upper and lower rock columns present different failure modes, with the first turning point (point b1) as the boundary. The lower rock columns can act as superimposed cantilever beams, and the inter-column forces, especially in the direction perpendicular to the discontinuities, play a key role in the instability of rock columns. However, the upper rock columns exhibit typical characteristics of the cantilever beam, and the inter-column forces are approximately equal to 0. Moreover, shear-sliding failure rather than flexural-toppling failure may occur within the rock columns near the slope toe because the corresponding slenderness ratios are relatively small. Note that both internal and external conditions must be met for flexural-toppling failure to occur; i.e., the maximum tensile stress in each rock column must reach its tensile strength, and sufficient space must exist for rock columns to deform and fail. If sufficient deformation or failure does not occur within the lower rock columns, the upper columns are unlikely to undergo flexural-toppling failure. To obtain reliable results, the stability of each rock column should therefore be analyzed individually from the toe to the crest, which is clearly contrary to previous methods (Aydan and Kawamoto 1992; Adhikary et al. 1997; Amini et al. 2012). For anti-inclined rock slopes, the process of sliding or flexural-toppling failure can be interpreted as follows.

As shown in Fig. 5a, the combined force resulting from the self-weight and inter-column forces induces the flexural-toppling failure of rock columns, which are located below the first turning point (point b1), resulting in the formation of the superimposed toppling zone. Moreover, if shear-sliding failure of rock columns near the toe does occur, this section is then further divided into two zones, i.e., the sliding zone and the superimposed toppling zone (Fig. 5b). The occurrence of failure of the lower rock columns would provide sufficient space for deformation and failure of the upper rock columns. Then, one or more stages of flexural-toppling failure of the upper rock columns, which are located above the first turning point b1, would occur under the self-weight. This failure zone is defined as the cantilevered toppling zone, above which is the stable zone. Therefore, three boundaries should be determined, namely, boundary 1, between the sliding zone and the superimposed toppling zone; boundary 2, between the superimposed toppling zone and the cantilevered toppling zone, and boundary 3, between the cantilevered toppling zone and the stable zone.

Fig. 5

Partition schematic of the proposed approach. a Failure model of anti-inclined rock slopes due to flexural-toppling, b failure model of anti-inclined rock slopes due to a combination of sliding and flexural-toppling

Analysis of sliding or flexural-toppling failure

Basic assumptions and mechanical model

Although the real behavior of a rock slope with a potential for sliding or flexural-toppling failure is quite complicated, it is possible to propose a theoretical model to achieve an accurate solution by simplifying the problem. In previous studies (Adhikary et al. 1997; Amini et al. 2012; Goodman and Bray 1976), the following assumptions were made to simplify the analysis:

• (1) The limit friction equilibrium condition is satisfied along the interface of adjacent rock columns.

• (2) The total side force is assumed to be acting at a point χh _i , where h _i is the height of the corresponding rock column above the failure surface, i is the number of the rock column, and χ ∈ (0, 1) is a parameter defining the inter-column force distribution relationship common to all columns.

• (3) All rock columns in a rock mass with the potential for failure have a similar factor of safety equal to that of the whole slope against failure.

In addition to these three assumptions, we have made another two assumptions to simplify the problem:

• (4) The sliding or flexural-toppling failure is divided into three zones from the toe to the crest, i.e., the sliding zone, the superimposed toppling zone, and the cantilevered toppling zone. The failure emanates from the toe of the slope.

• (5) The failure surface is multi-planar. In particular, the failure surface below the boundary between the superimposed toppling zone and the cantilevered toppling zone is planar, while it is step-type above.

A typical geometric model for the sliding or flexural-toppling failure of a rock slope is presented in Fig. 6. To determine the failure surface, an auxiliary plane named the basal calculation plane is introduced. The following auxiliary parameters are defined to simplify the analyses that follow:

$$ \left\{\begin{array}{l}{\beta}_{\mathrm{g}\mathrm{r}}={\beta}_{\mathrm{g}}-\beta \\ {}{\beta}_{\mathrm{c}\mathrm{r}}={\beta}_{\mathrm{c}}-\beta \\ {}{\theta}_{\mathrm{r}}=\theta -\beta \end{array}\right. $$

(2)

where β _gr , β _cr , and θ _r are the angles of the natural ground, the cut slope, and the basal calculation plane with respect to the plane normal to the discontinuities, respectively; β _g , β, and θ are the angles of the natural ground, the plane normal to the discontinuities, and the basal calculation plane with respect to the horizontal direction, respectively, and β = 90^o − η.

Fig. 6

Geometric model for sliding or flexural-toppling failure of an anti-inclined rock slope

The height of the rock column located at the crest, h _m , above the basal calculation plane can be expressed as:

$$ {h}_m=\frac{H}{ \sin {\beta}_{\mathrm{c}}} \cos {\beta}_{\mathrm{c}\mathrm{r}}\left( \tan {\beta}_{\mathrm{c}\mathrm{r}}- \tan {\theta}_{\mathrm{r}}\right) $$

(3)

where H is height of the cut slope.

The rock columns are numbered from the toe to the crest. As shown in Fig. 6, rock columns 1 and m are, respectively, a triangle and a pentagon on the cross-section perpendicular to the slope strike, whereas the others are quadrilaterals. The serial number of the rock column located at the crest is expressed as:

$$ m=\operatorname{int}\left[\frac{h_m \cos {\beta}_{\mathrm{cr}} \cos {\theta}_{\mathrm{r}}-0.5 t \sin \left({\beta}_{\mathrm{cr}}-{\theta}_{\mathrm{r}}\right)}{t \sin \left({\beta}_{\mathrm{cr}}-{\theta}_{\mathrm{r}}\right)}\right]+1 $$

(4)

where t is thickness of the rock columns, and int is the integer part function.

The height of rock column i above the basal calculation plane can be expressed as:

$$ {h}_i=\left\{\begin{array}{l}{h}_m-\left( m- i\right)\left( \tan {\beta}_{\mathrm{cr}}\hbox{-} \tan {\theta}_{\mathrm{r}}\right) t\\ {}{h}_m-\left( i- m\right)\left( \tan {\theta}_{\mathrm{r}}\hbox{-} \tan {\beta}_{\mathrm{gr}}\right) t\end{array}\right.\kern0.24em \begin{array}{l} i< m\hfill \\ {} i\ge m\hfill \end{array} $$

(5)

The weight of rock column i with unit width above the basal calculation plane is expressed as:

$$ {w}_i=\gamma {h}_i t $$

(6)

where γ is unit weight of the rock columns.

A stability analysis of the rock column is performed individually from the toe to the crest. For rock column 1, shear-sliding or flexural-toppling failure may occur. First, the normal external forces needed for rock column 1 to induce shear-sliding failure and flexural-toppling failure are calculated, respectively. Rock column 1 can be classified under the following two categories:

• 1. Rock column 1 has the potential for shear-sliding failure. The normal external force P ₁ (Fig. 7a) that must be exerted by rock column 2 can be computed as:

  $$ {P}_1=\frac{ \cos \theta \left(\frac{ \tan \varphi}{F_s}- \tan \theta \right){w}_1+\frac{ct}{F_s \cos {\theta}_r}}{ \cos {\theta}_r\left(1+\frac{ \tan \varphi}{F_s} \tan {\theta}_r\right)+ \tan {\varphi}_j \cos {\theta}_r\left( \tan {\theta}_r-\frac{ \tan \varphi}{F_s}\right)} $$

  (7)

• b. Rock column 1 has the potential for flexural-toppling failure. The normal external force T ₁ (Fig. 7b) that must be exerted by rock column 2 can be computed as:

  $$ {T}_1=\frac{\left(\frac{\sigma_t}{F_s}+\frac{w_1 \cos \beta}{t}\right)\frac{2 I}{t}-\frac{h_1}{2}{w}_1 \sin \beta}{\chi {h}_1-\frac{t}{2} \tan {\varphi}_j} $$

  (8)

  where c, φ, and σ _t are cohesion, internal friction angle, and tensile strength of the intact rock column, respectively; F _s is the safety factor; I is inertia of the rock column cross section with the form $I=\frac{1}{12}{t}^3$.

Fig. 7

Mechanical models of rock column 1, which is located at slope toe. 1, 2, 3 The cut slope, basal calculation plane, and plane normal to the discontinuities, respectively. a Analysis for shear-sliding failure, b analysis for flexural-toppling failure

The relative magnitudes of P ₁ and T ₁ determine the potential failure mode of rock column 1, which can be evaluated as follows:

• (1) If P ₁ < T ₁, then rock column 1 has the potential for shear-sliding failure.

• (2) If P ₁ > T ₁, then rock column 1 has the potential for flexural-toppling failure.

• (3) If P ₁ = T ₁, then rock column 1 has the same potential for shear failure and flexural-toppling failure. For the sake of brevity, however, the rock column is considered to have the potential for shear failure in this work.

The ease for a rock column to experience toppling failure is determined by the slenderness ratio (Liu et al. 2009): the smaller the slenderness ratio, the more difficult for flexural-toppling failure to occur. As shown in Fig. 6, the height of rock column 1 is the smallest, predicting a smallest slenderness ratio. Thus, if rock column 1 has the potential for flexural-toppling failure, then by inference, so do the others. In this case, the sliding zone would not exist, and the failure rock columns can be divided into two zones, namely, the superimposed toppling zone and the cantilevered toppling zone, as shown in Fig. 5a. Otherwise, if rock column 1 has the potential for shear-sliding failure, then the failure rock columns should be divided into three zones, namely, the sliding zone, the superimposed toppling zone, and the cantilevered toppling zone, as shown in Fig. 5b. In this case, further calculations (Eqs. 9, 10, 11) are needed to determine the potential failure mode of the other rock columns, e.g., rock columns 2 and 3.

For rock columns i and below to develop shear-sliding failure, the normal external force P _i (Fig. 8a) that must be exerted by rock column i + 1 can be computed as follows:

$$ {P}_i=\frac{ \cos \theta \left(\frac{ \tan \varphi}{F_s}- \tan \theta \right)\sum_{j=1}^i{w}_j+\frac{ i ct}{F_s \cos {\theta}_r}}{ \cos {\theta}_r\left(1+\frac{ \tan \varphi}{F_s} \tan {\theta}_r\right)+ \tan {\varphi}_j \cos {\theta}_r\left( \tan {\theta}_r-\frac{ \tan \varphi}{F_s}\right)} $$

(9)

Fig. 8

Mechanical models of rock column i and below, which are located in the sliding zone. a Analysis for shear-sliding failure, b analysis for flexural-toppling failure

For rock column i to develop flexural-toppling failure, the normal external force T _i (Fig. 8b) that must be exerted by rock column i + 1 can be computed as follows:

$$ \begin{array}{l}{T}_i=\frac{1}{\chi {h}_i-\frac{t}{2} \tan {\varphi}_j}\cdot \left[{P}_{i-1}\left(\chi {h}_{i-1}+\frac{t}{2} \tan {\varphi}_j\right)\right.+\\ {}\kern7.5em \left.\left(\frac{\sigma_t}{F_s}+\frac{w_i \cos \beta}{t}\right)\frac{2 I}{t}-\frac{h_i}{2}{w}_i \sin \beta \right]\end{array} $$

(10)

If the values of ${P}_{n_{st}}$, ${T}_{n_{st}}$, ${P}_{n_{st}+1}$, and ${T}_{n_{st}+1}$ calculated from Eqs. 9 and 10 satisfy Eq. 11, rock column n _st can be considered to be the boundary between the sliding zone and the superimposed toppling zone. In this case, rock column n _st lies in the sliding zone.

$$ \left\{\begin{array}{l}{P}_{n_{st}}\le {T}_{n_{st}}\\ {}{P}_{n_{st}+1}>{T}_{n_{st}+1}\end{array}\right. $$

(11)

Fig. 9 shows the mechanical model of the rock columns in the superimposed toppling zone. For a rock column to undergo flexural-toppling failure, the normal external force that must be exerted by its overlying rock column can be computed as follows:

$$ \begin{array}{l}{T}_i=\frac{1}{\chi {h}_i-\frac{t}{2} \tan {\varphi}_j}\cdot \left[{T}_{i-1}\left(\chi {h}_{i-1}+\frac{t}{2} \tan {\varphi}_j\right)\right.+\\ {}\kern7.5em \left.\left(\frac{\sigma_t}{F_s}+\frac{w_i \cos \beta}{t}\right)\frac{2 I}{t}-\frac{h_i}{2}{w}_i \sin \beta \right]\end{array} $$

(12)

Fig. 9

Mechanical model of rock column i for flexural-toppling failure, which is located in the superimposed toppling zone (i > n _st )

If the values of ${T}_{n_{tt}-1}$ and ${T}_{n_{tt}}$ calculated from Eq. 12 satisfy Eq. 13, rock column n _tt can be considered as the boundary between the superimposed toppling zone and the cantilevered toppling zone. In this case, rock column n _tt lies in the superimposed toppling zone.

$$ \left\{\begin{array}{l}{T}_{n_{tt}-1}>0\\ {}{T}_{n_{tt}}\le 0\end{array}\right. $$

(13)

When flexural-toppling failure occurs, a rock column located within the cantilevered toppling zone separates from its overlying rock column. Thus, the inter-column forces can be considered to be 0. In this case, the cantilever beam model can be adopted to describe the stability of the cantilevered toppling zone. The critical height of the cantilever inclined beam under self-weight (Fig. 10) can be obtained by applying the usual formula of strength of materials as (see detailed derivation process in Appendix II):

$$ {h}_{cr}=\frac{t \cos \beta +\sqrt{t^2{ \cos}^2\beta +12 t \sin {\beta \sigma}_t/\gamma}}{6 \sin \beta} $$

(14)

Fig. 10

Evaluation of critical instability length of rock column i, which is located in the cantilevered toppling zone (i > n _tt )

If the height of rock column n _tt  + 1 (the first rock column located within the cantilevered toppling zone) is greater than the critical fracture height (${h}_{n_{tt}+1}>{h}_{cr}$), rock column n _tt  + 1 has the potential for flexural-toppling failure. Note that multi-stage bending with tensile failure of rock column n _tt  + 1 may occur, as shown in Fig. 11. Assuming that the bending height of each stage is equal to the critical fracture height, the number of total bending stages, can be computed as follows:

$$ {BN}_{n_{tt}+1}=\operatorname{int}\left(\frac{h_{n_{tt}+1}}{h_{cr}}\right) $$

(15)

Fig. 11

Evaluation of rock columns located within the cantilevered toppling zone

Thus, the fracture height of rock column n _tt  + 1 is expressed as

$$ {H}_{n_{tt}+1}={BN}_{n_{tt}+1}{h}_{cr}=\operatorname{int}\left(\frac{h_{n_{tt}+1}}{h_{cr}}\right){h}_{cr} $$

(16)

The stability analysis method for the rock columns located above rock column n _tt  + 1 is the same. If the cantilever height of rock column n _sz is smaller than the critical fracture height (${h}_{n_{sz}}<{h}_{cr}$), then rock column n _sz is stable. In this case, rock column n _sz can be considered to be the boundary between the cantilevered toppling zone and the stable zone. The failure surface of the cantilevered toppling zone is depicted in Fig. 11.

Stability criterion for anti-inclined rock slopes

Under limit equilibrium conditions, F _s = 1, the normal external forces needed for failure to occur can be computed for all rock columns using the above relations. First, the boundary between the sliding zone and the superimposed toppling zone (rock column n _st ) can be determined by Eqs. 9, 10, and 11. Then, the boundary between the superimposed toppling zone and the cantilevered toppling zone (rock column n _tt ) can also be determined by Eqs. 12 and 13. The lack of a solution for Eq. 13 implies that the cantilevered toppling zone does not exist. In this case, an external force is required to induce slope failure. However, the external force does not exist in a real slope. Thus, the sign of F ₀, expressed as Eq. 17, can be used to evaluate the stability of a rock slope against sliding or flexural-toppling failure:

$$ {F}_0= \min \left[ \min \left({T}_i,{P}_i\right)\right]\kern2.2em 1\le i\le {n}_{total} $$

(17)

where min is the minimum function; n _total is the total number of rock columns located above the basal calculation plane.

Then, the stability of a rock slope against sliding or flexural-toppling failure can be evaluated as follows:

• (1) If F ₀ < 0, then the slope is unstable.

• (2) If F ₀ > 0, then the slope is stable.

• (3) If F ₀ = 0, then the slope is in the limit equilibrium condition.

Provided that the failure surface has been determined, the factor of safety for an anti-inclined rock slope F _s can be computed by trial and error, assuming F ₀ = 0. Thus, the key challenge in the stability analysis of an anti-inclined rock slope is the determination of the failure surface, which is discussed in the following section.

Search method for determining the failure surface

As noted above, before determining the failure surface, one must determine the failure surface angle of the sliding zone and superimposed toppling zone, θ _f , and the key rock column n _tt . Note that the factor of safety for anti-inclined rock slopes, F _s , can be expressed as:

$$ {F}_s={F}_s\left( H,{\theta}_r,{\beta}_c,{\beta}_g,\gamma, c,\varphi, {\sigma}_t,{\varphi}_j, t\right) $$

(18)

For a specific anti-inclined rock slope, all parameters except θ _r have been given. To minimize F _s , this parameter therefore needs to be varied. The most realistic F _s is the smallest one calculated, and the corresponding value of θ _r is defined as the angle of the failure surface of the sliding zone and superimposed toppling zone with respect to the plane normal to the discontinuities, namely, θ _f . Thesolution process for the value of θ _f is given in Fig. 12. The search direction is from the cut slope to the plane normal to the discontinuities [failure surface of the Aydan et al. method (Aydan and Kawamoto 1992)], which are used as the upper and lower bounds for searching. The detailed solution process is conducted as follows.

Fig. 12

Search process for the failure surface of anti-inclined rock slopes against sliding or flexural-toppling failure

The value of the angle of the basal calculation plane with respect to the plane normal to the discontinuities must be varied following Eq. 18 to achieve the corresponding factor of safety, expressed as Eq. 19:

$$ {\theta}_{r j}={\theta}_{r1}- j\Delta {\theta}_r\kern2.2em 1\le j\le {n}_{\theta} $$

(19)

$$ {F}_s= \min \left[{F}_s\left({\theta}_{rj}\right)\right]\kern2.2em 1\le j\le {n}_{\theta} $$

(20)

where θ _rj is the angle of the basal calculation plane with respect to the plane normal to the discontinuities, corresponding to calculation step j for determining the failure surface; Δθ _r is the iterative step for θ _r ; j is the number of calculation steps of θ _r for determining the failure surface; n _θ is the number of iterations for θ _r .

The most realistic value of F _s , expressed as Eq. 18, can be determined through the above search calculation. Meanwhile, the key rock columns n _st and n _tt can also be determined. Then, failure surface of the cantilevered toppling zone can be obtained by Eqs. 14, 15, and 16, as is the boundary (rock column n _sz ) between the cantilevered toppling zone and the stable zone.

The above approach requires a great amount of calculation, which is time-consuming and error-prone if the calculations are carried out manually. Note that the variables for each rock column’s potential for failure used for the stability analysis of anti-inclined rock slopes are expressed by the geo-mechanical parameters of the slope and the serial numbers of the rock columns and therefore have uniform expressions. Thus, based on the solution proposed in this paper, a computer program [e.g. an Excel sheet (Microsoft Corp., Redmond, WA) or Matlab (MathWorks Inc., Natick, MA) solution] can be developed to simplify the above calculations, enabling fast evaluation of the stability for anti-inclined rock slopes against sliding or flexural-toppling failure.

Verification analysis

To verify the results of the proposed approach, we selected and analyzed an anti-inclined slate slope, located in southern Anhu, China, using the mathematical model. The results obtained by the approach proposed in the preceding sections were compared to those of a discrete element simulation and the Aydan et al. method (Aydan and Kawamoto 1992). We also conducted a comparative analysis of block-toppling failure with the transfer coefficient method (Liu et al. 2009) to make the approach more reliable.

The most important parameter in a toppling failure is the point where the total side forces act. The following assumptions in terms of the determination of the point of action of the total side forces have been suggested in the past:

• (1) If pure block-toppling occurs, then χ = 1.0 (Goodman and Bray 1976).

• (2) If pure shear-sliding failure occurs, then χ = 0.5 (Aydan et al. 1989; Amini et al. 2012).

• (3) If pure flexural-toppling occurs, then χ = 0.5 ∼ 1.0 (Aydan and Kawamoto 1992; Adhikary et al. 1997).

To determine the value of this parameter for the example, we performed a back-analysis using the discrete element code UDEC (Itasca 2004) based on the parameters given in Tables 4 and 5. Alternatively, a user-defined FISH function (i.e., c_result) was written to obtain the magnitude and location of the normal force of contacts between adjacent blocks, based on which the point where total side forces act could be determined. The results of the numerical simulation indicated that this value (χ) was approximately equal to 0.5 for the example (see detailed processes and results in Appendix III). Thus, χ was assumed to be equal to 0.5 in this example analysis.

Table 4 Calculation parameters of rock mass

Table 5 Calculation parameters of joints

An analysis of slope sliding stability was also performed before using the approach proposed in this paper. As shown in Fig. 13, a Bishop’s factor of safety of 1.77 was obtained using SLIDE (Rocscience 2004), indicating that overall sliding failure of this slope would not occur. However, the factor of safety obtained by the proposed approach is 0.49, with a combination failure mode of sliding and flexural-toppling. Thus, for anti-inclined rock slopes, it is inappropriate to simply select overall a sliding failure model when conducting stability evaluation.

Fig. 13

SLIDE model for overall sliding failure of the example

The failure surface and zoning map, involving 47 failure rock columns, is shown in Fig. 14. According to the calculated results, rock columns 1 to 6, 7 to 32, 33 to 47, and beyond belong to the sliding zone, the superimposed toppling zone, the cantilevered toppling zone, and the stable zone, respectively. In this case, θ _f = 0°, indicating that the failure surface of the sliding zone and superimposed toppling zone are perpendicular to the discontinuities.

Fig. 14

Failure surface and zoning map of the example obtained by the proposed approach

Comparative analysis with the discrete element method

To improve understanding of the failure mechanisms of anti-inclined rock slopes and verify the validity and accuracy of the proposed approach, we carried out a numerical simulation using the discrete element code UDEC (Itasca 2004), which has been widely applied in previous rock slope stability studies of toppling (Alejano et al. 2006, 2010; Cai 2013; Zheng et al. 2015). Its application to toppling failures has also been validated (Barla et al. 1995). UDEC is ideally suited to study potential modes of failure directly related to the presence of discontinuous features; shear and tensile failure of blocks (intact rock column) in UDEC can also be simulated and are of particular interest in this analysis.

In the numerical simulation, the model bottom was fixed and the lateral boundaries were subjected to roller conditions (Fig. 15), which are widely used boundary conditions in two-dimensional plane strain analyses (Hou et al. 2014). To better identify the underlying processes and mechanisms contributing towards sliding or flexural-toppling failure of the slope, we arranged a total of 90 displacement monitoring points on the surface of the cut slope and the natural ground, which were numbered from the toe to the crest with a spacing of 1 m. In particular, monitoring points 1 and 50 were located at the toe and crest, respectively. To improve the computational efficiency, the excavation was simulated by eliminating elements associated with one instantaneous stage.

Fig. 15

Geometry sizes and boundary conditions for the UDEC model

In this study, the strain-softening model that reflects a lower shear strength and null tensile strength as expected after failure was adopted. In addition, the joint constitutive model of area contact elastic/plastic with Coulomb slip failure was used to describe the discontinuities. The properties of rock masses and discontinuities are given in Tables 4 and 5.

Inspection of Fig. 16 confirms that the accumulative nature of damage results in the gradual deformation of the slope, eventually leading to sliding and flexural-toppling failure. As the lower rock columns near the toe yielded and deformed, tension-shear failure of the upper rock columns occurred as well. Of key interest in terms of better understanding the failure process of anti-inclined rock slopes, the failure surface did not initiate and begin to accumulate from the crest, but instead one emanated from the toe and developed upward gradually. This process slowly manifested itself in the form of small ranges of plastic zones (between rock columns 1 to 18 over 15,000 time steps; Fig. 16a), which gradually increased until they began to occur in the crest rock column (e.g., after an addition 2 million time steps; Fig. 16d). This process is in agreement with the observations in centrifuge tests by Adhikary et al. (1997), reinforcing the assumption that the failure surface of anti-inclined rock slopes emanates from the toe. The evolution of bending and shear stresses in the lower sections of the slope led to the initiation and propagation of failure through the upper rock columns. Increasing plastic zones of shear failure appeared with the evolution of failure because the shear strength parameter would be lower than expected after failure due to flexural-toppling. Further inspection of Fig. 16d suggests that the failure surface is approximately multi-planar, indicating that the fifth assumption in section Basic assumptions and mechanical model is reasonable. Moreover, the simulated failure surface agreed well with that determined by the proposed approach.

Fig. 16

Evolution of intact rock damage as a function of timesteps. At yield Rock column failures due to shear, Tensile failure rock column failures due to tension

The results from these models, which show the displacements of the slope associated with the progressive development of the plastic zones, are shown in Fig. 17. The deformation on the slope manifested in the form of small slope displacements (between 0.06 and 4.07 mm in the horizontal direction over 15,000 time steps; Fig. 17a), which gradually increased until they began to occur in scale of meters (e.g., after an addition 2 million time steps; Fig. 17d). The magnitude of the displacement first increased and then decreased from the toe to the crest. The maximum horizontal displacement did not occur at the crest, but instead it located below, predicting an apparent difference due to general rock slopes. For example, it was at monitoring point 32 (below the crest), rather than at monitoring point 50 (at the crest), that the horizontal displacement was the largest over 2,000,000 time steps when catastrophic failure would occur. Moreover, with the maximum horizontal displacement point as the boundary, the lower slope displacements were approximately continuous, whereas those above appeared to be discontinuous. In particular, gaps could be observed between the upper rock columns (Fig. 18), which were consistent with observations in the physical model tests (Figs. 3, 4a). These results reinforce the assumption that the toppling rock columns can be divided into two subzones, i.e., the superimposed toppling zone and the cantilevered toppling zone. Moreover, shear failure rather than tensile failure of rock columns 1 to 6 primarily occurred when the failure was initiated (Fig. 16a). Thus, the hypothesis that shear-sliding failure of the rock columns near the toe may occur is reasonable. The simulated ranges of the failure zones were highly consistent with those obtained by the analytical method proposed in this paper, as shown in Table 6.

Fig. 17

Displacements at measuring points located on the cut slope and the natural ground as a function of timesteps. Note that maximum horizontal displacement (xdis) points and crest position (measuring point 50) are marked by vertical dashed lines. ydis Maximum vertical displacement points

Fig. 18

Gaps between adjacent rock columns in the cantilevered toppling zone

Table 6 Results comparison of the proposed approach and discrete element method

Comparative analysis with the Aydan et al. method

To facilitate the comparison, the authors also compiled a corresponding calculation program for the Aydan et al. method (Aydan and Kawamoto 1992), which produced the F _s value of 0.67 for the above example. According to the results of the Aydan et al. method, a total of 75 rock columns had the potential for flexural-toppling failure (Fig. 19). Note that the corresponding failure surface was a plane through the toe. Compared to the results of the proposed approach, the failure zone established by the Aydan et al. method was much larger, extending a greater distance behind the crest. However,results obtained from physical model tests (Aydan and Kawamoto 1992; Zuo et al. 2005) and field investigations (Cai 2013; Majdi and Amini 2011) have shown that the failure surface is usually multi-planar and that the failure distance behind the crest of the slope is unlikely to extend significantly. It can therefore be inferred that the results obtained by the proposed approach align well with those observed in physical model tests and field investigations.

Fig. 19

Failure surface obtained by the Aydan et al. (Aydan and Kawamoto 1992) method

The relationship between the factor of safety, F _s , and the thickness of the rock column, t, calculated by the proposed approach and the Aydan et al. method, respectively, are shown in Fig. 20. F _s increases with the thickness t. Note that the results of these two methods do not different greatly when the thickness t is small; however, the difference increases with increasing thickness t, and the value of F _s calculated by the Aydan et al. method tends to be larger. The reason for this phenomenon may be as follows.

Fig. 20

Influence of rock column thickness on the safety factor obtained by different methods

When the value of the thickness, t, is small, the slenderness ratios for rock columns located near the toe are small, leading to a low resistance against flexural-toppling failure. Therefore, the range of the sliding zone is relatively small or even equal to 0; thus, the values of F _s calculated using these two methods are almost identical. However, when t is sufficiently large, the rock columns located near the toe have the potential for shear failure rather than flexural-toppling failure due to the significant improvement of the resistance against flexural-toppling failure. Hence, the Aydan et al. method may overestimate the value of F _s because it does not consider the shear failure for the rock columns located near the toe.

Further inspection of Fig. 21 suggests that the factor of safety, F _s , increases sharply with the thickness t when t > 3m, indicating that a slight increase in t will lead to a sharp increase in F _s , which is clearly unrealistic. In contrast, the F _s − t curve obtained by the proposed approach is relatively smooth, which appears to be more reasonable.

Fig. 21

Influence of θ _r and H on the safety factor F _s . a t = 1 m, b t = 2 m, c t = 4 m, d t = 6 m, e t = 8 m

Comparative analysis of block-toppling failure with the transfer coefficient method

A block-toppling study is equal to a flexural toppling study in considering null tensile strength and pre-defining the separation or failure surface. For comparative purposes, three cases of block-toppling described by Liu et al. (2008) were also analyzed using the solution developed above with ad-hoc codes. The input parameters and results are given in Tables 7 and 8, respectively, which are compared with those obtained using the transfer coefficient method proposed by Liu et al. (2009).

Table 7 Basic examples of comparison: parameters

Table 8 Basic examples of comparison: results

It can be seen in Table 8 that for the failure modes and ranges of total failure zones of these three cases, the results agree well with those obtained using the transfer coefficient method. However, for the ranges of subzones (i.e., siding zone and toppling zone), there are large discrepancies between the methods, especially for the case of the River Sil viaduct. The discrepancies occur as a result of the different approaches used to determine the location of the transition point for failure modes of rock columns (sliding or toppling). As discussed above, the proposed approach determines the location of the transition point by comparing the relative magnitudes of shearing resistance and bending resistance of rock columns (i.e., P _i and T _i ), whereas the transfer coefficient method calculates the location through the limiting frictional equilibrium condition at the bases of the blocks (rock columns). In other words, the transfer coefficient method assumes that sliding—rather than toppling in the lower section (rock columns 1 to i)—will occur once the shear force at the base of rock columns i is larger than or equal to the shear strength along the base. However, toppling failure may be more likely to occur in this section, which is not considered in the transfer coefficient method. When the slenderness ratio is small (G-B1b, slenderness ratio of rock column 3 is 1.16), the results obtained using the proposed approach agree well with those obtained using the transfer coefficient method. However, when the slenderness ratio is large (River Sil viaduct, slenderness ratio of rock column 9 is 7.08), large discrepancies between these two methods occur. In this case, the range of the sliding zone determined using the transfer coefficient method would be larger than the actual one. Thus, the proposed approach appears to be the more reasonable and accurate of the two methods.

The possible difference between angles θ _r and θ _f

The most critical issue with the limit equilibrium analysis of toppling failures is how to assign the inclination of the total failure surface above which rock columns are subjected to overturning. Previous research on the flexural-toppling of rock slopes has generally specified the angle between the failure surface and the plane normal to the discontinuities rather than establishing it by searching (e.g., the angle is equal to 0°); however, this may not always be the case. It is therefore prudent to explore the influence of the angle θ _r on the calculated value of F _s . The mechanical properties of intact rock columns and discontinuities are the same as those given in Tables 4 and 5, whereas the value of t varies from 1 to 8 m and H varies from 20 to 40 m. For a given slope, the angle θ _r must be varied to minimize F _s . The most realistic θ _f is equal to the value of θ _r corresponding to the smallest F _s calculated.

For different values of rock column thickness, the relationship between the calculated values of F _s , θ _r , and H is shown in Fig. 21, where the horizontal plane and the curved surface denote F _s  = 1 and F _s (θ _r ), respectively. The value of θ _r corresponding to the minimum factor of safety is 0° when t ≤ 4 m (Fig. 21a–c), indicating that the failure surface of the sliding zone and superimposed toppling zone are perpendicular to the discontinuities. Hence, θ _f = 0°. In some cases (e.g., H = 20 m, Fig. 21d, e), however, the value of θ _r corresponding to the smallest F _s is approximately 10° rather than 0° when t > 4m. This result indicates that the value of θ _f may vary for different slopes; therefore, it is unreasonable to specify the failure surface, and the assumption of zero θ _f may overestimate the safety factor of the slope. The innovative approach proposed in this paper can help resolve this problem.

Conclusions

For anti-inclined rock slopes in layered rock masses, failure may occur due to sliding, flexural-toppling, or a combination of the two modes. The total failure surface is usually multi-planar, which should be determined by searching rather than by assumption. Additionally, to better reflect practical situations, a stability analysis of anti-inclined rock slopes should be performed from the toe to the crest when using the limit equilibrium theory. As a means of solving these problems, an innovative approach is proposed in this paper, according to which the failure mode of anti-inclined rock slopes involves two types: pure flexural-toppling and a combination of sliding and flexural-toppling. A search method for determining the failure surface of slopes in layered rock masses potentially subjected to sliding or flexural-toppling failure is also presented. Comparative analysis of this innovative approach, the discrete element method, the Aydan et al. method, and the transfer coefficient method has been performed for case studies to verify the solution’s validity and accuracy. The results reveal that the proposed approach can be used for the stability analysis of slopes in layered rock masses potentially susceptible to sliding or flexural-toppling failure. Traditional models may overestimate the safety factor due to neglecting the shear failure of rock columns located near the toe and assuming the inclination of the total failure surface.

Appendices

Appendix I:

Derivation of the limit equilibrium equation when rock column i (located in the sliding zone and i ≥ 1) has the potential for shear-sliding failure.

In this case, the limit friction equilibrium condition is assumed to be satisfied along the interface of adjacent rock columns, which is generally adopted in the toppling failure analysis in previous studies (Sagaseta et al. 2001; Liu et al. 2008, 2009). Thus,

$$ {Q}_i={P}_i \tan {\varphi}_j $$

(A.1)

where Q _i is inter-column shear force acting at the common boundary of rock columns i and i + 1.

Forces parallel to potential failure surface:

$$ \sum_{j=1}^i{S}_j=\sum_{j=1}^i{w}_j \sin \theta +{P}_i \cos {\theta}_r+{Q}_i \sin {\theta}_r $$

(A.2)

Forces perpendicular to potential failure surface:

$$ \sum_{j=1}^i{N}_j=\sum_{j=1}^i{w}_j \cos \theta -{P}_i \sin {\theta}_r+{Q}_i \cos {\theta}_r $$

(A.3)

If rock columns i and below have shear-sliding potential, then:

$$ \sum_{j=1}^i{S}_j=\sum_{j=1}^i{N}_j\frac{ \tan \varphi}{F_s}+\frac{ i ct}{F_s \cos {\theta}_r} $$

(A.4)

Inserting Eqs. (A.1–A.3) into Eq. (A.4), then

$$ {P}_i=\frac{ \cos \theta \left(\frac{ \tan \varphi}{F_s}- \tan \theta \right)\sum_{j=1}^i{w}_j+\frac{ i ct}{F_s \cos {\theta}_r}}{ \cos {\theta}_r\left(1+\frac{ \tan \varphi}{F_s} \tan {\theta}_r\right)+ \tan {\varphi}_j \cos {\theta}_r\left( \tan {\theta}_r-\frac{ \tan \varphi}{F_s}\right)} $$

(A.5)

Derivation of the limit equilibrium equation when rock column i (located in the sliding zone and i ≥ 1) has the potential for flexural-toppling failure.

In this case, the limit friction equilibrium condition is also assumed to be satisfied along the interface of adjacent rock columns, which is generally adopted in flexural-toppling failure analysis in previous studies (Adhikary et al. 1997; Amini et al. 2012; Aydan and Kawamoto 1992). Thus,

$$ \left\{\begin{array}{l}{Q}_i={T}_i \tan {\varphi}_j\\ {}{Q}_{i-1}={P}_{i-1} \tan {\varphi}_j,\left( note:{P}_0=0\right)\end{array}\right. $$

(A.6)

Moments about the base midpoint:

$$ {M}_i={w}_i \sin \beta \frac{h_i}{2}+{T}_i\chi {h}_i-{Q}_i\frac{t}{2}-{P}_{i-1}\chi {h}_i-{Q}_{i-1}\frac{t}{2} $$

(A.7)

Maximum tensile stress at the base:

$$ {\sigma}_{i, \max }=\frac{M_i}{I}\frac{t}{2}-\frac{w_i \cos \beta +{Q}_i-{Q}_{i-1}}{t}\cong \frac{M_i}{I}\frac{t}{2}-\frac{w_i \cos \beta}{t} $$

(A.8)

If rock column i has flexural-toppling failure, then:

$$ {\sigma}_{i, \max }=\frac{\sigma_t}{F_s} $$

(A.9)

Inserting Eqs. (A.6 to A.8) into Eq. (A.9):

$$ \begin{array}{l}{T}_i=\frac{1}{\chi {h}_i-\frac{t}{2} \tan {\varphi}_j}\left[{P}_{i-1}\left(\chi {h}_{i-1}+\frac{t}{2} \tan {\varphi}_j\right)\right.+\\ {}\kern7.5em \left.\left(\frac{\sigma_t}{F_s}+\frac{w_i \cos \beta}{t}\right)\frac{2 I}{t}-\frac{h_i}{2}{w}_i \sin \beta \right]\end{array} $$

(A.10)

Appendix II

Derivation of the critical height of the cantilever inclined beam under self-weight (located in the cantilevered toppling zone).

In this case, the inter-column forces between rock columns are assumed to be 0.

Weight of the rock column with critical height (see Fig. 10):

$$ w=\gamma {h}_{cr} t $$

(A.11)

Moments about the base midpoint:

$$ M= w \sin \beta \frac{h_{cr}}{2} $$

(A.12)

Maximum tensile stress at the base:

$$ {\sigma}_{\max }=\frac{M}{I}\frac{t}{2}-\frac{w \cos \beta}{t} $$

(A.13)

If the rock column has flexural-toppling failure, then:

$$ {\sigma}_{\max }={\sigma}_t $$

(A.14)

Inserting Eqs. (A.11 to A.13) into Eq. (A.14):

$$ {h}_{cr}=\frac{t \cos \beta +\sqrt{t^2{ \cos}^2\beta +12 t \sin {\beta \sigma}_t/\gamma}}{6 \sin \beta} $$

(A.15)

Appendix III

The user-defined FISH function to obtain the magnitude and location of normal force of contacts between adjacent blocks (please see UDEC 4.0 Help for what the following variable names denote).

def c_result.

b1 = 39,130.

b2 = 39,339.

n = 1.

ic = contact_head.

loop while ic # 0.

if c_b1(ic) = b1.

if c_b2(ic) = b2.

xtable(100,n) = c_y(ic).

ytable(100,n) = c_nforce(ic).

n = n + 1.

endif.

endif.

if c_b1(ic) = b2.

if c_b2(ic) = b1.

xtable(100,n) = c_y(ic).

ytable(100,n) = c_nforce(ic).

n = n + 1.

endif.

endif.

ic = c_next(ic).

endloop.

end

c_result.

set log on.

set logfile cb.log.

pr Table 100.

set log off.

Based on the above user-defined FISH function, the point where total side force acts between rock columns 7 and 8, 16 and 17, and 20 and 21 has been determined, as shown in Table 9. Taking the total side force between columns 7 and 8 as an example, the calculation process is illustrated as follows.

Location of total side force:

$$ {Y}_{7,8}=\frac{\sum {\left(\mathrm{Y}\hbox{-} \mathrm{c}\right)}_i\times {\left(\mathrm{N}\hbox{-} \mathrm{f}\right)}_i}{\sum {\left(\mathrm{N}\hbox{-} \mathrm{f}\right)}_i}=\frac{55.2\times 120+54.4\times 117.4+53.5\times 131.2+52.6\times 121.7}{55.2+54.4+53.5+52.6}=53.9 $$

(A.16)

Then, χ can be determined

$$ \chi =\frac{53.9-52.6}{55.2-52.6}=0.5 $$

(A.17)

Table 9 Magnitude and location of normal force of contacts between adjacent rock columns (blocks) above the failure surface