Introduction

Study of fluid flow through fractured porous rocks is important for managing environmental and energy problems (e.g. Neuman 2005; Kolditz and Clauser 1998). Approaches to modeling fluid flow through fractured porous rocks are roughly classified into two kinds: discrete fracture models in which fractures are represented explicitly by their geometric parameters (e.g. Baca et al. 1984; Hyman et al. 2015); and equivalent fracture (single, dual, or multiple continuum) models in which the hydraulic properties of fractured porous rocks are averaged for grid blocks (Berkowitz et al. 1988; Warren and Root 1963; Pruess and Narasimhan 1985). Although discrete fracture models can accurately describe flow through fractured porous rocks, meshing of complex fracture networks and the solving of a large linear system of equations limit their application in field-scale simulations. Therefore, equivalent fracture models have been widely used due to their more convenient computation; furthermore, multiscale models are also developed for fractured porous rocks (e.g. Zhang et al. 2013; Shah et al. 2016) in order to reduce computational effort, in which the coarse-scale basis functions are based on fine-scale solutions.

One key problem in using equivalent fracture models is calculating the equivalent permeability, also termed as fracture upscaling, which represents the flow properties of the bulk fractured porous rock (Sanchez-Vila et al. 2006). Two kinds of upscaling methods are often used: analytical methods and flow-based methods (e.g. Sævik et al. 2013; Elfeel and Geiger 2012). As an analytical method, the Oda upscaling method (Oda 1985) is widely applied due to its computational efficiency; however, the flow velocity in a fracture used in the Oda upscaling method is based on the assumption that the fracture has an infinite length, as suggested by Snow (1969), which is not capable of reflecting the change of equivalent permeability properly, resulting from the variation of fracture size and position. By contrast, flow-based methods simulate flow for the grid blocks containing fractures based on the discrete fracture model first and then use the flow information for computing the equivalent permeability (Long et al. 1982).

For the flow-based upscaling methods, Koudina et al. (1998) investigated equivalent permeability for three-dimensional (3D) discrete fracture networks. Bogdanov et al. (2003) accounted for rock matrix permeability as well, by using the finite volume method for solving flow in discrete fracture models, since the permeability of the rock matrix may also have an effect on fluid flow (e.g. Nelson 2001; Kaufmann et al. 2010). Karimi-Fard et al. (2006) introduced an upscaling procedure for generalized dual-continuum models. Based on this upscaling approach, Tatomir et al. (2011) developed a workflow for modeling flow in fractured porous rocks with “multiple interacting continua” models. More recently, Fumagalli et al. (2016) extended the procedure proposed by Karimi-Fard et al. (2006) by using an embedded discrete fracture model (e.g. Li and Lee 2008) for speeding up the upscaling process. Lang et al. (2014) calculated equivalent permeability for fractured porous rocks by applying a pressure-flux volume averaging method.

Inspired by the flow-based method developed by Long et al. (1982) and Durlofsky (1991), which uses flow rates on block boundaries during upscaling, a multiple boundary upscaling concept has been developed (Chen et al. 2015) for two-dimensional (2D) fractured porous rocks. In this study, the novel multiple boundary method was chosen for 3D models and was applied to stochastically generated fracture networks, which has as a general application for studying flow in fractured porous rocks. This paper covers two aspects: the first one is presenting the multiple boundary upscaling equation for 3D models; the second one is introducing an upscaling procedure for fractured porous rocks which mainly includes accurate meshing of the intersecting fractures and modeling flow in discrete fractures and rock matrix. Furthermore, the multiple boundary method was compared with the Oda upscaling method, which is frequently used in industrial software and the volume averaging method and is a typical flow-based upscaling method, for assessing its accuracy. Considering that the geometry of fractures in natural rocks shows statistical and fractal distributions to some extent (Bonnet et al. 2001; Molz et al. 2004), the equivalent permeability is related to such statistical properties of fractures (De Dreuzy et al. 2001) or to the scale of measurement (Clauser 1992). Here, the frequency distribution of equivalent permeability within a discrete fracture network was analyzed for exploring the correlation between equivalent permeability and the geometry of a discrete fracture network at the field scale.

To this end, the 3D multiple boundary method and its computational framework are presented for fracture networks and the criteria for comparing the equivalent and the discrete fracture models are introduced. As part of this study, the upscaled results were compared with the analytical solution for a set of rotated fractures and were compared for tortuous fractures. The equivalent fracture models (single continuum) or equivalent porous media based on different upscaling methods were compared for two different fracture networks, a well-connected fracture network and a poorly connected one.

Upscaling methods

Multiple boundary method

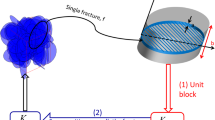
The scale of fracture properties, e.g. fracture aperture, is usually far below the scale of a grid block used in numerical models. Here the former is classified as “fracture scale” and the latter as “block scale”. Assuming a cubic block with identical faces of area A, instead of the specific discharge, the flow rate Q can be used in the block scale for Darcy’s law:

$$ \left[\begin{array}{c}{Q}_{\mathrm{x}}\\ {}{Q}_{\mathrm{y}}\\ {}{Q}_{\mathrm{z}}\end{array}\right]=-A\frac{g}{\upsilon}\mathbf{kJ}=-A\frac{g}{\upsilon}\left[\begin{array}{c}{k}_{\mathrm{x}\mathrm{x}}\kern0.5em {k}_{\mathrm{x}\mathrm{y}}\kern0.5em {k}_{\mathrm{x}\mathrm{z}}\\ {}{k}_{\mathrm{y}\mathrm{x}}\kern0.5em {k}_{\mathrm{y}\mathrm{y}}\kern0.5em {k}_{\mathrm{y}\mathrm{z}}\\ {}\begin{array}{ccc}{k}_{\mathrm{z}\mathrm{x}}& {k}_{\mathrm{z}\mathrm{y}}& {k}_{\mathrm{z}\mathrm{z}}\end{array}\end{array}\right]\left[\begin{array}{c}{J}_{\mathrm{x}}\\ {}{J}_{\mathrm{y}}\\ {}{J}_{\mathrm{z}}\end{array}\right] $$
(1)

where Qx, Qy, and Qz are the flow rates in the x-, y-, and z-directions, respectively, k is the equivalent permeability tensor, J is the hydraulic gradient, g is gravity, υ is the kinematic viscosity.

After solving a steady-state flow problem in the fracture scale with linear boundary conditions along the x-axis (Fig. 1a), the flow rate out of the block boundaries comprises a fracture flow rate and matrix flow rate, Q(f) and Q(m), respectively:

$$ \overline{Q_{\mathrm{x}}}={\overline{Q_{\mathrm{x}}}}^{\left(\mathrm{f}\right)}+{\overline{Q_{\mathrm{x}}}}^{\left(\mathrm{m}\right)} $$
(2)
$$ \overline{Q_{\mathrm{y}}}={\overline{Q_{\mathrm{y}}}}^{\left(\mathrm{f}\right)}+{\overline{Q_{\mathrm{y}}}}^{\left(\mathrm{m}\right)} $$
(3)
$$ \overline{Q_{\mathrm{z}}}={\overline{Q_{\mathrm{z}}}}^{\left(\mathrm{f}\right)}+{\overline{Q_{\mathrm{z}}}}^{\left(\mathrm{m}\right)} $$
(4)

where \( \overline{Q_{\mathrm{x}}} \), \( {\overline{Q_{\mathrm{x}}}}^{\left(\mathrm{f}\right)} \), and \( {\overline{Q_{\mathrm{x}}}}^{\left(\mathrm{m}\right)} \) are total flow rate, fracture flow rate and matrix flow rate in the x-direction, respectively. Similarly, the same notation is used for the flow rates in the y- and z-directions.

Fig. 1
figure 1

a The fracture with an azimuth α relative to the x-axis, the rock matrix cube, and the linear hydraulic head boundary conditions; b Comparisons of the equivalent permeability components between the analytical results and three upscaling methods

Full size image

For the matrix flow rate, the flow rate on the right boundary which is perpendicular to the x-direction was considered. For the fracture flow rate, a multiple boundary expression was extended from 2D (Chen et al. 2015) to 3D models:

$$ {\overline{Q_{\mathrm{x}}}}^{\left(\mathrm{f}\right)}=\sum \limits_{r=1}^{N_{\mathrm{r}}}{Q_{\mathrm{x}r}}^{\left(\mathrm{f}\right)}+\sum \limits_{u=1}^{N_{\mathrm{u}}}{Q_{\mathrm{x}u}}^{\left(\mathrm{f}\right)}+\sum \limits_{l=1}^{N_{\mathrm{l}}}{Q_{\mathrm{x}l}}^{\left(\mathrm{f}\right)}+\sum \limits_{f=1}^{N_{\mathrm{f}}}{Q_{\mathrm{x}f}}^{\left(\mathrm{f}\right)}+\sum \limits_{b=1}^{N_{\mathrm{b}}}{Q_{\mathrm{x}b}}^{\left(\mathrm{f}\right)} $$
(5)
$$ {\overline{Q_{\mathrm{y}}}}^{\left(\mathrm{f}\right)}=\sum \limits_{r=1}^{N_{\mathrm{r}}}{Q_{\mathrm{y}r}}^{\left(\mathrm{f}\right)}+\sum \limits_{u=1}^{N_{\mathrm{u}}}{Q_{\mathrm{y}u}}^{\left(\mathrm{f}\right)}+\sum \limits_{l=1}^{N_{\mathrm{l}}}{Q_{\mathrm{y}l}}^{\left(\mathrm{f}\right)}+\sum \limits_{f=1}^{N_{\mathrm{f}}}{Q_{\mathrm{y}f}}^{\left(\mathrm{f}\right)}+\sum \limits_{b=1}^{N_{\mathrm{b}}}{Q_{\mathrm{y}b}}^{\left(\mathrm{f}\right)} $$
(6)
$$ {\overline{Q_{\mathrm{z}}}}^{\left(\mathrm{f}\right)}=\sum \limits_{r=1}^{N_{\mathrm{r}}}{Q_{\mathrm{z}r}}^{\left(\mathrm{f}\right)}+\sum \limits_{u=1}^{N_{\mathrm{u}}}{Q_{\mathrm{z}u}}^{\left(\mathrm{f}\right)}+\sum \limits_{l=1}^{N_{\mathrm{l}}}{Q_{\mathrm{z}l}}^{\left(\mathrm{f}\right)}+\sum \limits_{f=1}^{N_{\mathrm{f}}}{Q_{\mathrm{z}f}}^{\left(\mathrm{f}\right)}+\sum \limits_{b=1}^{N_{\mathrm{b}}}{Q_{\mathrm{z}b}}^{\left(\mathrm{f}\right)} $$
(7)

where Qxr(f), Qxu(f), Qxl(f), Qxf(f), and Qxb(f) are the flow rates of the r-th, u-th, l-th, f-th, and b-th fracture element in the x-direction on the right, upper, lower, front, and rear boundaries, respectively (Fig. 1a). Nr Nu, Nl, Nf, and Nb are the total number of the fracture elements on the right, upper, lower, front, and rear boundaries, respectively. Similar expressions are used for the fracture flow rates in the y-direction, \( {\overline{Q_{\mathrm{y}}}}^{\left(\mathrm{f}\right)} \), and in the z-direction, \( {\overline{Q_{\mathrm{z}}}}^{\left(\mathrm{f}\right)} \).

Substituting \( \overline{Q_{\mathrm{x}}} \), \( \overline{Q_{\mathrm{y}}} \), and \( \overline{Q_{\mathrm{z}}} \) for Qx, Qy, and Qz in Eq. (1), three equations can be constructed. By changing the direction of the linear boundary condition to the y- and z-axes, nine components of an equivalent permeability tensor can be computed by solving three steady-state flow problems in the fracture scale:

$$ \left[\begin{array}{c}{k}_{\mathrm{x}\mathrm{x}}\kern0.5em {k}_{\mathrm{x}\mathrm{y}}\kern0.5em {k}_{\mathrm{x}\mathrm{z}}\\ {}\begin{array}{ccc}{k}_{\mathrm{y}\mathrm{x}}& {k}_{\mathrm{y}\mathrm{y}}& {k}_{\mathrm{y}\mathrm{z}}\end{array}\\ {}\begin{array}{ccc}{k}_{\mathrm{z}\mathrm{x}}& {k}_{\mathrm{z}\mathrm{y}}& {k}_{\mathrm{z}\mathrm{z}}\end{array}\end{array}\right]=-\frac{\upsilon }{A\cdotp g}\left[\begin{array}{c}\begin{array}{ccc}\frac{{\overline{Q_{\mathrm{x}}}}^{(1)}\ }{\ {J_{\mathrm{x}}}^{(1)}}& \frac{{\overline{Q_{\mathrm{x}}}}^{(2)}\ }{\ {J_{\mathrm{y}}}^{(2)}}& \frac{{\overline{Q_{\mathrm{x}}}}^{(3)}\ }{\ {J_{\mathrm{z}}}^{(3)}}\end{array}\\ {}\begin{array}{ccc}\frac{{\overline{Q_{\mathrm{y}}}}^{(1)}\ }{\kern0.5em {J_{\mathrm{x}}}^{(1)}}& \frac{{\overline{Q_{\mathrm{y}}}}^{(2)}\ }{\ {J_{\mathrm{y}}}^{(2)}}& \frac{{\overline{Q_{\mathrm{y}}}}^{(3)}\ }{\kern0.5em {J_{\mathrm{z}}}^{(3)}}\end{array}\\ {}\begin{array}{ccc}\frac{{\overline{Q_{\mathrm{z}}}}^{(1)}\ }{\kern0.5em {J_{\mathrm{x}}}^{(1)}}& \frac{{\overline{Q_{\mathrm{z}}}}^{(2)}\ }{\ {J_{\mathrm{y}}}^{(2)}}& \frac{{\overline{Q_{\mathrm{z}}}}^{(3)}\ }{\kern0.5em {J_{\mathrm{z}}}^{(3)}}\end{array}\end{array}\right] $$
(8)

where the numbers 1, 2, and 3 denote the flow problems. Considering the fractures in a cubic block may have multiple length scales and random orientations, the equivalent permeability tensor computed by the multiple boundary method could be asymmetric (e.g. Chen et al. 2016). In that case, the off-diagonal components can be averaged to obtain a symmetric permeability tensor.

Details on the mathematical formulation of the Oda upscaling method and the volume averaging method can be found in Oda (1985) and Lang et al. (2014), respectively. The equivalent permeability by using the Oda upscaling method was calculated using FracMan (Dershowitz et al. 1998).

Procedures for upscaling fracture networks

The procedures for flow-based upscaling, i.e. the multiple boundary method and the volume averaging method, mainly contains six steps (Fig. 2). In the first step, the fracture networks were created by using FracMan (Dershowitz et al. 1998). The fractures were exported as a set of polygon surfaces. The planar fracture surface is assumed here, as most fractures in rocks could be considered as planar except veins or the junction of fractures (e.g. Adler et al. 2012). In addition, the scale of roughness is very small compared to the scale of fracture length in this study, which could be neglected. In the next step, after defining the grid size of the equivalent fracture model, the fractures were clipped by the grid elements’ boundaries.

Fig. 2
figure 2

Workflow for upscaling fracture networks

Full size image

Then the meshes of fracture surfaces were created for each grid element. This can be done by using academic or commercial meshing software, e.g. HyperMesh (Altair 2016), Ansys (ANSYS 2016) and Maya (Autodesk 2016), which create an integrated and connected mesh for a fracture network. To account for the rock matrix, the volume of the grid element is meshed using TetGen (Si 2015) for creating a tetrahedral volume mesh, based on the 2D triangular mesh of the fracture and the grid element boundary surfaces generated in the previous step.

After creating the mesh, the object-oriented finite element code OpenGeoSys (Kolditz et al. 2012; Watanabe et al. 2012) was applied for simulating flow in each grid element. For OpenGeoSys, the governing equation for flow is solved by using its weak form. The standard Galerkin method is applied for the spatial discretization of the weak form equation. The variable in the equation, i.e. hydraulic head, is approximated in the Taylor-Hood finite element space. The flux or Darcy velocity for each finite element is reconstructed based on the hydraulic head according to Darcy’s law. As the model is 3D, it needs to do three simulations with different hydraulic gradient directions for each grid element for determining the equivalent permeability tensor. For each flow simulation, the flow information is calculated, i.e. the flow rate for the multiple boundary method and the averaged hydraulic gradient and velocity for the volume averaging method. Finally, this flow information is used for computing the equivalent permeability of each grid element from Darcy’s law.

Comparison of the upscaling methods for fracture networks

For evaluating the performance of the upscaling methods, the frequency distribution of the equivalent permeability was analyzed for a discrete fracture network. Furthermore, their equivalent permeabilities were used for solving a flow problem and the results were compared with those based on the discrete fracture models.

As the fracture geometry, e.g. fracture size and fracture orientation, may be randomly distributed in a fractured porous rock medium, their equivalent permeability tensor will be full, indicating that the main axes of the equivalent permeability ellipse are not aligned with the axes of the model. Accordingly, six components of the equivalent permeability tensor, i.e. kxx, kyy, kzz, kxy, kxz, and kyz, were analyzed for the different upscaling methods.

Both the percentage differences in hydraulic head (eH) and a component of flow rate (eq) will be compared. They can be computed by:

$$ {e}_{\mathrm{H}}=\frac{1}{N}{\sum}_{n=1}^N\frac{\left|{H_{\mathrm{EFM}}}^n-{H_{\mathrm{DFM}}}^n\right|}{{H_{\mathrm{DFM}}}^n}\times 100 $$
(9)
$$ {e}_{\mathrm{q}}=\frac{q_{\mathrm{EFM}}-{q}_{\mathrm{DFM}}}{q_{\mathrm{DFM}}}\times 100 $$
(10)

where HEFMn is the hydraulic head of the n-th grid element of the equivalent fracture model, HDFMn is the averaged hydraulic head within the n-th grid element domain of the discrete fracture model, N is the number of grid elements for the equivalent fracture model, qEFM and qDFM are the flow rate components of the equivalent fracture model and the discrete fracture model, respectively.

Test cases

This section first considers a set of rotated fractures and compares the upscaled results with analytical solutions; next, the equivalent permeabilities of tortuous fractures were calculated with different upscaling methods. Lastly, the upscaling procedure was applied to two fracture networks: the first one is well connected and contains ‘infinitely’ long fractures in the model domain which are truncated by the model’s boundaries. The second one, with multiple-scale fracture sizes, which are generated stochastically, is poorly connected compared to the first one.

Rotation of a single fracture

Consider a fracture parallel to the y-axis in a rock matrix cube of dimensions 0.1 m. The center of the fracture coincides with the cube’s centroid. The fracture subtends an angle α with the x-axis (Fig. 1a) and is infinite which means it passes through the cube and intersects with the cube’s boundaries. The aperture of the fracture is assumed to be 3 × 10−3 m and the fracture permeability is 7.5 × 10−7 m2 according to the cubic law (Witherspoon et al. 1980). The permeability of the rock matrix is assumed to be 1 × 10−12 m2.

The three upscaling methods are now used to compute the equivalent permeability of the fractured porous rock with different fracture azimuths α. It should be noted that different kinds of boundary conditions may influence the results for flow-based upscaling methods. The linear boundary conditions are used here as they mimic the real flow condition for grid blocks in a flow field (e.g. Lang et al. 2014). Nevertheless, it would be interesting to investigate the influence of boundary conditions on the upscaling results, e.g. “open” and “closed” boundary conditions (Fumagalli et al. 2017). For flow along the x-axis, the hydraulic heads applied on the left boundary and the right boundary are 10 and 0 m, respectively. Hydraulic heads on the other lateral boundaries decrease linearly from the left to the right. The discrete fracture model is meshed using Gmsh (Geuzaine and Remacle 2009) in which the fracture element is represented by triangles and the rock matrix by tetrahedrons. The flow problems for the discrete fracture model are solved using the open source thermal-hydraulic-mechanical-chemical simulator OpenGeoSys (OGS; Kolditz et al. 2012) that is based on the finite element method (Watanabe et al. 2012).

Furthermore, the analytical equivalent permeability can be computed by using the coordinate transformation of equivalent permeability tensor components (Lough et al. 1998). When α = 0°, the equivalent permeability computed by the Oda upscaling method and the multiple boundary method is identical; therefore, kxx, kyy, and kzz were taken as 2.25 × 10−8 m2, 2.25 × 10−8 m2, and 0 × 10−8 m2, respectively, for the initial permeability tensor computed by the Oda upscaling method. When α changes, the components of the equivalent permeability tensors will vary correspondingly. The analytical results are plotted in Fig. 1b.

The computed equivalent permeability tensors are symmetric. As the fracture is parallel to the y-axis, kxy and kyz are zero for all values of α; kxx, kxz, kzz, and kyy are compared between the various upscaled results and the analytical results (Fig. 1b). It can be seen that the upscaled results follow the analytical solution very well with varying azimuth. The equivalent permeability computed by the multiple boundary method fits the analytical solutions for kxx, kxz, and kzz best. For kyy, there is a slight increase when using the upscaling methods compared to the analytical solution. This is physically reasonable since, when the fracture rotates, the length of the intersection between the fracture and the xz-plane also varies. It is smallest for α = 0° and α = 90°. Thus, the increased intersection length in the xz-plane results in a larger kyy. This effect is not expressed in the analytical solution since it is formulated by fracture azimuth.

Tortuous fractures

Compared to the Oda upscaling method and the volume averaging method, of which both use volume-averaged velocity, the multiple boundary method uses flow rates across the boundaries of volume grid elements, which is physically intuitive and mimics the laboratory experiments to some extent (e.g. Tidwell and Wilson 1997). To exemplify this point, the equivalent permeability of a synthetic tortuous fracture of simple geometry (Fig. 3a) was calculated by using the multiple boundary method and the volume averaging method. The tortuous fracture is represented by a combination of two connected fractures sharing the same edge. The tortuosity, defined here as the flow path length divided by the straight length, is in the range of 1.0–1.82. The other properties of fractures and rock matrix are the same as those in section ‘Rotation of a single fracture’.

Fig. 3
figure 3

a The fractured porous rock containing fractures with different tortuosity: blue for 1.0, green for 1.35, and orange for 1.82; b Variation of the equivalent permeability components with tortuosity

Full size image

Figure 3b shows that kxz is not zero when using the multiple boundary method, whereas it remains zero when using the volume averaging method. When using the multiple boundary method, e.g. when applying the linear boundary condition along the x-axis, fluid in the fracture will flow out of the right boundary, and the flow rate can be decomposed into its x- and z- components considering the fracture orientation. Flow rate in the opposite direction to the z-axis will result in a negative kxz. When using the volume averaging method, since the tortuous fracture is geometrically symmetric with respect to the yz-plane, a positive flow rate in the z-direction will be on the left part of the fracture and a negative one on the right part. So, the influence of the tortuosity on kxz will be hidden; therefore, the multiple boundary method more clearly reflects the changes of the equivalent permeability with fracture tortuosity than the volume averaging method.

A well-connected fracture network

The dimension of the fractured porous rock model is 500 m × 500 m × 150 m (Fig. 4a). The fracture network contains three sets of fractures of constant orientations. For set 1, the fracture azimuth and dip are 240° and 90°, respectively; for set 2, they are 300° and 90°, respectively; and for set 3, they are 180° and 10°, respectively. In total, there are 33 fractures in this model. The aperture of the fractures is 1.2 × 10−3 m and the permeability of the fractures is 1.2 × 10−7 m2, according to the cubic law for fluid flow in a deformable rock fracture (Witherspoon et al. 1980); rock matrix permeability is 1.0 × 10−15 m2.

Fig. 4
figure 4

a The well-connected fracture network. The green fractures denote set 1, the orange fractures denote set 2, and the gray fractures denote set 3; b The poorly connected fracture network. The green fractures denote set E, the gray fractures denote set W, and the two orange ones are deterministic (shades in green and gray are due to light entrance angles)

Full size image

Based on this fracture model, three equivalent fracture models are created using the Oda upscaling method, the volume averaging method, and the multiple boundary method. The dimension of each volume grid element is 50 m × 50 m ×50 m. Therefore, there is a total of 300 grid elements for the equivalent fracture model. The frequency distributions of equivalent permeability are presented in Fig. 5. To reduce the influence of potentially erroneous data, the third maximum and minimum values of each permeability component were used as the upper and lower limits, respectively, and the range was divided into ten evenly distributed spans. Figure 5 shows that the shapes of the distributions and the range of the equivalent permeability are similar among the three upscaling methods. For the diagonal terms, they appear normal or log-normal distributions. It is more obvious for kxx and kyy than for kzz, which tends to be gently distributed. This is mainly due to the vertical fractures of set 1 and set 2, which constitute a large proportion of the fracture network; thus, the heterogeneity of equivalent permeability mainly occurs on the horizontal plane. The multiple boundary method yields a slightly higher value for kxx and kyy than the other two methods. kxy tends to be evenly distributed for the multiple boundary method, while it tends to a normal or log-normal distribution for the Oda upscaling method or the volume averaging method. kxz and kyz tend to vanish due to the vertical fractures in set 1 and set 2. In summary, these comparisons among the frequency distributions of equivalent permeability indicate that for the well-connected fracture network the multiple boundary method yields results comparable with the other methods.

Fig. 5
figure 5

Frequency distribution of the equivalent permeability based on the different upscaling methods for the well-connected fracture network (see Fig. 4a)

Full size image

In the next step, the equivalent permeabilities of the different upscaling methods were used to solve a flow problem to further compare the performance of the different upscaling methods. The flow problem was also solved for the discrete fracture model with the fracture network shown in Fig. 4a. Figure 6 shows the comparison of the solutions for hydraulic head and flow velocity in the x-direction for all four models. Linear boundary conditions with a hydraulic gradient of 1 were applied in the x-direction. The equivalent fracture models were solved by using the hydrothermal simulator SHEMAT-Suite (Clauser 2003; Rath et al. 2006).

Fig. 6
figure 6

Hydraulic head H and velocity in the x-direction vx for the well-connected fracture network. a and e are hydraulic head and velocity in the x-direction in the discrete fracture model, respectively; b–d and f–h are the same quantities in the equivalent fracture models based on the different upscaling methods, respectively

Full size image

For the discrete fracture model, the hydraulic head varies continuously and the velocity in the x-direction is high within fractures, which act as main fluid pathways. For the equivalent fracture models, both the hydraulic head and the velocity in the x-direction vary relatively continuously, which reflects the good connectivity of the fracture network. It should be noted that vx has a considerably smaller value in the equivalent fracture models compared to the discrete fracture model. This is due to averaging the permeability from discrete fractures with small aperture to equivalent grid elements of large dimension.

Comparing the errors of hydraulic head and flow rate in the x-direction, eH and \( {e}_{{\mathrm{q}}_{\mathrm{x}}} \), with increasing rock matrix permeability (Fig. 7), it is shown that eH is in the range of 15–20%, and the difference between the three upscaling methods is about 5%. For \( {e}_{{\mathrm{q}}_{\mathrm{x}}} \), its absolute value is less than 20%, and the multiple boundary method has a significantly lower error, less than 5%. This may be due to the slightly higher diagonal components of its equivalent permeability tensor (Fig. 7) compared to the other methods.

Fig. 7
figure 7

Error of the equivalent fracture models for the well-connected fracture network regarding a hydraulic head and b Darcy flow rate

Full size image

Based on the resulting frequency distribution of the equivalent permeability and the errors of the equivalent fracture models, it is shown that the results based on the Oda upscaling method and those on the volume-averaging upscaling method are similar (Figs. 5 and 7). This is partially because both methods used a volume-averaged velocity during the upscaling process, and thus could be termed as volume-averaging-based upscaling methods. Furthermore, as the dimensions of the fractures are usually larger than that of the volume grid element in this study, the assumption of fractures with infinite length for the Oda upscaling method is valid. The similarities also indicate the accuracy of the flow-based upscaling procedures, including meshing of grid elements and flow simulations.

A poorly connected fracture network

A synthetic fracture network was created, based on the real fracture geometry data of Soultz-sous-Forêts in western France (Massart et al. 2010; Sausse et al. 2010). This fracture network contains two deterministic fractures and two sets of stochastic fractures. The parameters for generating the two stochastic fracture sets are presented in Table 1. To decrease the complexity in meshing and computation of the fracture network, the minimum size (i.e. equivalent radius) of the fractures was 50 m. Figure 4b shows that both, the fracture size and fracture orientation are random, and the fracture network is poorly connected due to the sparsely distributed fractures with multiple-scale fracture sizes. Apart from the geometry of the fractures, the aperture or permeability of the fractures, the permeability of the rock matrix, and the dimension of the model are the same as that in the previous, well-connected model.

Table 1 Parameters for generating stochastic fracture sets
Full size table

The corresponding equivalent fracture models are constructed from the fracture model by using the three upscaling methods. Again, the dimension of the volume grid element for the equivalent fracture model is 50 m × 50 m × 50 m. It should be noted that the difficulty of meshing the grid elements containing fractures increases, due to the complexity of the fracture geometry. Furthermore, unlike the previous well-connected fracture network in which each set of fractures is parallel to an axis (Fig. 4a), this poorly connected fracture network is generated stochastically regarding orientation (Fig. 4b), which means the fractures may not be parallel to any axis of the model when they completely pass through the grid elements. In these cases, the multiple boundary method overestimates the equivalent permeability by a factor of two, at maximum, as discussed in the following. Therefore, the equivalent permeability was multiplied by a correction factor of 0.7 for the multiple boundary method.

It should be noted that the overestimation of equivalent permeability is not a general result for the multiple boundary method. In the procedures of the multiple boundary method, the permeability is computed from the flow rates in Eq. (8). In one model where a fracture completely cuts through the rock matrix cube and is parallel to the y-axis (Fig. 8a), when applying the linear boundary conditions in the x-direction, the outflow is orthogonal to the right boundary of the rock matrix cube (Fig. 8c). Only the flow rate on the right boundary will be used in Eqs. (5–7); however, in the other model where the fracture is not parallel to the y-axis and the fracture length is infinite (Fig. 8b), the outflow will not be orthogonal to the right boundary, and the flow rates on the right and the rear boundaries will be used (Fig. 8d). This will increase the computed flow rate (Eqs. 5–7) and accordingly increase the equivalent permeability. It should be noted that in 2D discrete fracture models, the fracture could be simply described as a one-dimensional (1D) line and the rock matrix as a 2D continuous plane. The intersection between a fracture and a rock matrix boundary will be a point; hence, the problem of the outflow from a fracture across different boundaries does not exist. Accordingly, the possibility of overestimating the equivalent permeability exists only in 3D models when the fracture completely cuts through the rock matrix cube and is not parallel to any axis simultaneously. As the reason for this is obvious as previously discussed, a factor of 0.6–0.8 may be used for correcting the results in such situations, and the value of the correction factor is related to fracture geometries.

Fig. 8
figure 8

a The infinite and parallel fracture model and c the flow direction on its fracture surface; b the infinite and non-parallel fracture model and d the flow direction on its fracture surface

Full size image

The frequency distributions of the equivalent permeability for all three methods are presented in Fig. 9. It shows that the diagonal components and the off-diagonal components have different distributions: the former tend to follow a power law, the latter a normal or log-normal distribution. Again, the ranges of the permeability components are similar for the three methods. As in the previous well-connected case, the multiple boundary method yields a relatively larger value for the diagonal terms, i.e. kxx, kyy, and kzz, than the other two methods. This may be mainly because during multiple boundary upscaling, the link between the fracture scale and the block scale is the flow rate across the element boundaries. In contrast, during the processes of the Oda upscaling method or the volume averaging upscaling method, the fracture scale and the block scale are linked by the volume-averaged velocity in which some flow information may be merged within the volume grid element, as illustrated in section ‘Tortuous fractures’.

Fig. 9
figure 9

Frequency distribution of the equivalent permeability based on the different upscaling methods for the poorly connected fracture network

Full size image

Again, by applying a linear boundary condition in the y-direction, which is to mimic the real flow direction between the two deterministic fractures at Soultz-sous-Forêts, a flow problem was solved with the equivalent fracture models and the discrete fracture model. In the discrete fracture model, both the hydraulic head and the velocity in the y-direction, are irregularly distributed and are influenced by the geometry of fractures (Fig. 10a,e). For the equivalent fracture models, the distributions of the hydraulic head are similar with those of the discrete fracture model (Fig. 10b–d). The velocity in the y-direction reflects the preferred fluid pathway. Also, as illustrated for the equivalent fracture models, the velocities in the y-direction are lower than for the discrete fracture model. For the multiple boundary method, the velocities in the y-direction are higher than for the other two methods (Fig. 10f–h).

Fig. 10
figure 10

Hydraulic head (H) and velocity in the y-direction (vy) for the poorly connected fracture network. a and e are hydraulic head and velocity in the y-direction in the discrete fracture model, respectively; b–d and f–h are the same quantities in the equivalent fracture models based on the different upscaling methods, respectively

Full size image

By increasing the rock matrix permeability, eH and \( {e}_{{\mathrm{q}}_{\mathrm{y}}} \) were computed for the different equivalent fracture models (Fig. 11). eH is mainly in the range of 50–90% and the absolute value for \( {e}_{{\mathrm{q}}_{\mathrm{y}}} \) is in the range of 0–50%. Both are higher than those in the previous, well-connected model. The flow rates in the y-direction calculated by the multiple boundary method have a smaller error than those by the other two methods. This is also shown clearly in the well-connected fracture networks, where each set of fractures is parallel to an axis; hence, the overestimation of equivalent permeability for the multiple boundary method as discussed previously does not exist for this fracture network. This is mainly because the multiple boundary method uses flow rate information on the boundaries for calculating equivalent permeability as already mentioned. This means, using a method based on flow rate information, i.e. the multiple boundary method, may lead to a higher hydraulic head difference than using volume-averaged velocity-based methods, i.e. the Oda upscaling method or the volume averaging method (Figs. 7 and 11); however, the percentage difference in hydraulic head is not as obvious as that in flow rate between different methods.

Fig. 11
figure 11

Error of the equivalent fracture models for the poorly connected fracture network regarding a hydraulic head and b Darcy flow rate

Full size image

As the phenomenon also exists in heterogeneous porous media, in which the upscaled model statistically has a smaller flow rate than that at the fine scale (e.g. Chen and Durlofsky 2006), the multiple boundary method could be tested for upscaling permeability in heterogeneous porous media. In addition, a further study will apply the multiple boundary method for simulating the transient flow of a pumping test. In this study, the number of the grid blocks is not very large for the equivalent fracture models, so the study concentrates mainly on the accuracy of the upscaling methods. In large equivalent fracture models, more improvement on the calculation speed should be explored for improving the efficiency of the upscaling methods (e.g. Chen et al. 2017).

It is noted that when the rock matrix permeability is 10−14 m2, there is a high hydraulic head error when using the multiple boundary method. This is due to the non-monotonic solutions occurring in this equivalent fracture model, i.e. some hydraulic heads are out of the range of 0– 500 m. The equivalent fracture model is solved by using the mimetic finite difference method; however, when using a full permeability tensor, the monotony of solutions cannot be guaranteed (e.g. Chen et al. 2016). In the case that the rock matrix permeability is 10−14 m2, which is smaller than the fracture permeability by nearly seven orders of magnitude, the equivalent permeability becomes highly anisotropic, so that numerical errors are more likely to occur in such situations.

Furthermore, compared to the Oda upscaling method (Oda 1985) and the volume averaging method (e.g. Lang et al. 2014) which assume symmetric permeability tensors, the equivalent permeability computed by the multiple boundary method is not inherently symmetric for the poorly connected fracture network. The flow equation was solved using asymmetric permeability tensors directly (Fig. 11a,b) with SHEMAT-Suite-mFD (Chen et al. 2016), which handles full permeability tensors based on the mimetic finite difference method. The mimetic finite difference method shares many similarities with the mixed-hybrid finite element method. The weak form of the flow equation includes two kinds of variables: hydraulic head and Darcy velocity. The lowest-order Raviart-Thomas-Nédélec element is used for the approximation spaces (Droniou 2014). So Darcy velocity and hydraulic head can be solved simultaneously in the linear system of equations, which improves the accuracy of Darcy velocity. It shows that using asymmetric permeability reduces the hydraulic head error to a reasonable value as well as the flow rate error, which means that the high errors due to the numerical scheme are removed. As the symmetric permeability tensors are computed from the asymmetric ones by averaging the off-diagonal components, which also indicates that even small changes in off-diagonal components may result in large numerical errors for this highly anisotropic equivalent fracture model. The asymmetric permeability tensors reflect the complexity of fractures’ geometry; however, it does not mean that using asymmetric permeability tensors is always better than using symmetric permeability tensors and keeps the numerics correct, which mainly depends on numerical schemes for solving the flow equation.

It was found that the accuracy of the permeability measured in the field is highly influenced by the flow connectivity (e.g. Pechstein et al. 2016). The numerical upscaling results corroborate this finding. For the well-connected fracture network, the errors of hydraulic head and flow rate are in the range of 10−20% and 0−20%, respectively (Fig. 7); however, for the poorly connected fracture network, the errors of the hydraulic head and of the flow rate are in the range of 50−90% and 0−50%, respectively, regardless of the monotonic error of the numerical scheme for the equivalent fracture model (Fig. 11). This may indicate that the accuracy of upscaling will reduce when the fracture network is less connected. The reason for this may be that when the fractures are well connected, the volume grid element in the equivalent fracture model is more like a representative elementary volume (REV) for a continuous medium. In contrast, the poorly connected fracture network with volume grid elements with few channeled flow pathways does not behave as an REV, which makes it hard to represent the permeability of fractured porous rocks in an equivalent fracture model accurately. Accordingly, further studies about the relationship between the fracture connectivity, the scale of the volume grid element, and the error of upscaling for using equivalent fracture models are suggested.

Although discrete fracture models are accurate when simulating fluid flow in fractured porous rocks, their limitations regarding computational effort make equivalent fracture models more attractive for quantifying uncertainty in fractured aquifers or geothermal reservoirs (e.g. Neuman 2005; Vogt et al. 2012). Constructing equivalent permeability distributions as well as considering fracture network connectivity could help quantifying uncertainty for such models. This study links equivalent permeability distributions to the connectivity of discrete fracture networks, which may be because for the well-connected fracture network, the equivalent permeability of grid blocks is mainly influenced by high permeable fractures. In contrast, for the poorly connected fracture network in which the fluid flow is dominated by few pathways, the equivalent permeability of grid blocks is mainly affected by the rock matrix. Further studies should explore systematically the relationships between equivalent permeability distributions and fracture network geometries at the field scale.

Conclusions

In this study, the 3D multiple boundary method was established and was compared with the Oda upscaling method (Oda 1985) and the volume averaging method (e.g. Lang et al. 2014) for calculating equivalent permeability for fractured porous rocks. Based on the results of test cases and the procedures of upscaling methods, the following conclusions can be drawn.

The multiple boundary method yields an equivalent permeability, which is comparable with results derived by the other two methods, and fits best the analytical solution in the rotated fracture cases. Moreover, the equivalent fracture model based on the multiple boundary method has a higher flow rate than the other two methods, which reduces the upscaling error in flow rate for fractured porous rocks.

Each upscaling method examined in this study has its optimal field of application. As an analytical method, the Oda upscaling method offers an easy and fast way for computing equivalent permeability especially when the number of fractures is too large to be solved with a discrete fracture model. If an efficient discrete fracture model simulator and a meshing tool are available, the flow-based methods can be used, i.e. the volume averaging method or the multiple boundary method. The choice can be made according to the numerical schemes for solving flow equations in a discrete fracture model. For a finite-element-based simulator, both the volume averaging method and the multiple boundary method can be used just as shown in this study. For a finite-volume-based simulator which computes the flow rate on grid boundaries, the multiple boundary method is more convenient, which indicates that the multiple boundary upscaling concept can be easily incorporated into any existing flow-based upscaling procedure.

The results quantitatively illustrate that connectivity of the fracture network influences the accuracy of the equivalent fracture models. The errors for the poorly connected fracture network are higher compared to those for the well-connected fracture network. The diagonal components of the equivalent permeability tensors show different distributions regarding the geometry of fracture networks. They are normal or log-normal like distributions for the well-connected fracture network but exhibit distributions similar to a power-law for the poorly connected fracture network.