Introduction

Injection of cold water after extraction of heat from the reservoir fluid has been in practice over the last few decades. This strategy has been necessary to: (1) maintain the reservoir pressure which gradually declines due to continuous heat extraction (Bodvarsson 1972); (2) enhance the heat recovery and the efficiency of the geothermal reservoir for extracting heat energy (Gingarten 1978); (3) ensure a safe disposal of wastewater (Horne 1982). However, since the injected water is much colder than the reservoir fluid, continuous injection results in cooling near the injection wells. The cold water extracts heat from the hot rock as it moves through the porous media. If the reservoir water fails to extract enough heat from the surrounding media by the time it reaches the production well, the production temperature declines with time and results in loss of energy extraction efficiency (Bodvarsson and Tsang 1982). Hence, it is important to determine the characteristics of movement of the cold temperature front for safe design of a production-injection well scheme and for deciding safe injection rate into the geothermal reservoir.

The movement of the cold temperature front generated due to the cold-water injection into the hot geothermal reservoir environment has been studied by many researchers using analytical and numerical methods, as well as experimental methods. Bodvarsson (1972) derived simple analytical solutions for the movement of the thermal front in rocks with both intergranular flow and fracture flow and discussed practical problems related to the siting of injection wells. Gingarten (1978) showed that the maximum withdrawal rate from an aquifer enhances several times with reinjection. The heat recovery factor, which is the ratio of extracted heat to the totally theoretically recoverable heat in place, is also enhanced by the reinjection process. Bodvarsson and Tsang (1982) developed an analytical model to study the thermal behavior due to cold-water injection into a fractured reservoir with equally spaced horizontal fractures assuming the horizontal conduction to be negligible. They also performed numerical studies to analyze the importance of the assumptions applied in the analytical solution which showed that the assumption of negligible horizontal conductive heat transport gives erroneous temperature distribution at very large amounts of time. Bodvarsson et al. (1982) proposed a two-dimensional (2D) model for vertical-fault-charged geothermal systems. Chen and Reddell (1983) developed an analytical model for thermal injection into a confined aquifer overlain and underlain by rock media; two unsteady-state solutions were derived by them, one for long time periods and another for short time periods. A graphical technique was also proposed to evaluate the aquifer thermal properties, like the longitudinal thermal conductivity and heat capacity of the aquifer, vertical thermal heat conductivity and the heat capacity of caprock. Stefansson’s (1997) review paper, based on the experience gained by reinjection experiments in 44 geothermal fields, addresses practical issues like thermal breakthrough, silica scaling in surface equipment, siting of reinjection wells and energy recovery from the resource.

Shook (2001) used tracer tests to predict the thermal breakthrough of single-phase fluid in porous media. Cheng et al. (2001) examined the problem of heat extraction from hot dry rock systems by circulating water in a fracture by considering several heat transport mechanisms. In that paper, the authors presented the modeling of multi-dimensional heat transport via an integral equation formulation using Green’s function. Stopa and Wojnarowski (2006) developed an analytical model using the method of characteristics, to study the thermal front velocity of cold water injected into the geothermal reservoir. They considered the heat capacity and density of rock and water to be dependent on temperature but neglected the longitudinal heat conduction. Ghassemi and Suresh Kumar (2007) numerically investigated the individual and combined effects of the thermal and chemical processes on fracture aperture and pressure distributions using the dual porosity concept on a single fracture. The study showed that the thermal stress caused by the cooling of the reservoir due to continuous injection of cold water has a profound effect on the fracture aperture and permeability especially near the injection well. With the increase of fluid velocity, the change of the fracture aperture and the permeability enhances, and the effect is felt over a longer distance along the fracture. A small change in the fracture aperture caused by thermal stresses due to cooling results in a change of fluid volume pressure which affects the reservoir efficiency.

Dickinson et al. (2009) outlined the theory of the aquifer thermal energy storage (ATES) system and presented a numerical study using the software package HTSWin, in which they compared their results with operational data collected over 12 months and found a good agreement between them. Li et al. (2010a) performed an experimental study to investigate the effects of temperature and pressure on in situ water saturation due to water injection in a geothermal reservoir. They also investigated the dependence of the productivity of the geothermal reservoir on the mean reservoir pressure. Yang and Yeh (2008), Li et al. (2010b) and Yeh et al. (2012) developed semi-analytical solutions using the Laplace transform to predict the temperature distribution in an ATES system for a confined aquifer bounded by rock media of different geological properties from above and below. They used the numerical routine DINLAP, of the International Mathematics and Statistics Library (IMSL, 2003), to invert their solution, which approximates the Laplace inversion. The routine is based on algorithms proposed by Crump (1976) and modified by de Hoog et al. (1982).

Although a number of numerical and analytical studies have been performed related to this topic, there is a need for a closed-form analytical solution for transient heat transfer in a porous geothermal aquifer due to cold water injection, including all the modes of heat transfer (advection, conduction and heat loss from the geothermal aquifer). The objective of the present paper is to investigate the transient distribution of temperature and the advancement of the thermal front generated by the reinjection of cold water into a confined geothermal aquifer sandwiched between the rocks of different thermo-geological properties. In this study, a general analytical solution for transient temperature distributions is derived, taking into account the heat transfer processes like advection, longitudinal conduction and conductive heat transport to the confining rock media due to a vertical temperature gradient. This is an improvement over the analytical solution of Bodvarsson and Tsang (1982) which neglected longitudinal conductive heat transport. The inclusion of longitudinal conduction has been proven to be very important, as shown later in this paper. Also, in the Bodvarsson and Tsang (1982) study, the same initial temperature throughout the system was considered, whereas it is considered to be different in different layers in the present study. A complete and exact closed-form analytical solution is provided here using the standard Laplace transform and inversion techniques, which is an improvement over semi-analytical solutions like those of Li et al. (2010b) and Yeh et al. (2012) which approximated the Laplace inversion by numerical techniques. The solutions obtained in the present study are useful in designing the injection-production well system and fixing the flow rates in the wells as it is essential for longer life and better productivity of the reservoir. The work can also serve as a reference solution for complex numerical models.

Problem formulation

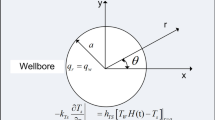
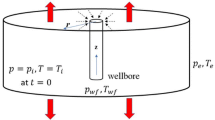
The one-dimensional heat transfer equation for single-phase geothermal fluid flow through an aquifer bounded by rock layers is considered in this study. A schematic representation of the system with an injection well fully penetrating through the porous geothermal aquifer is given in Fig. 1. Cold water is injected continuously at one boundary of the aquifer domain through an injection well. The injection temperature (T in) is assumed constant over time. The geothermal reservoir is initially at a uniform temperature of (T 0). The nomenclature is explained in Table 1 and assumptions that are used in developing the model are as follows

Fig. 1
figure 1

Schematic representation of the confined geothermal aquifer with the injection well

Full size image
Table 1 Nomenclature, with the magnitude of parameters of the rock and fluid used
Full size table
  1. 1.

    The geothermal reservoir here consists of a confined aquifer, homogeneous in nature, which is bounded above and below by rock layers of different thermo-geological properties. All the rock and fluid properties in the geothermal aquifer, namely the specific heat, density and thermal conductivity, are considered to be invariant over space and time. This assumption is valid when the change of temperature in the porous media and geothermal fluid is small (Stopa and Wojnarowski 2006).

  2. 2.

    The underlying and overlying rock layers are impermeable and of different thermo-geological properties. The thicknesses of the rock layers are assumed to be uniform and large but finite. Rock layers are also assumed to be of homogeneous nature.

  3. 3.

    The heat flux from the aquifer to the underlying and overlying rock media is assumed to be one-dimensional (1D) due to the vertical heat gradient between them. Hence, horizontal thermal conduction in the rocks is neglected.

  4. 4.

    The initial temperatures (T 0 for the aquifer, T 01 and T 02 for overlying and underlying rock, respectively) prior to the injection is assumed to be constant over vertical depth in all the three layers. The geothermal gradient is considered to be negligible here.

  5. 5.

    The outer boundaries of the rock layers are assumed to be highly permeable such that large heat transfer allows the temperature there to be constant and equal to the initial rock temperature. Continuity of temperatures is assumed at the interface of the aquifer and rock layers assuming a perfect thermal contact at the interface between them. This is also used as a boundary condition.

  6. 6.

    The temperature of the injection water is assumed to be invariant over the whole injection period. The mixing of temperature makes it uniform over the aquifer depth.

The energy conservation equation is well known from literature (Gringarten 1978; Wangen 1994; Pao et al. 2001). The 1D energy conservation equation for single-phase fluid flow in an aquifer involving heat conduction and convection and the heat transport to the confining rock layers is given by (Stopa and Wojnarowski 2006)

$$ \frac{\partial }{\partial t}\left\{\left(1-\phi \right){\rho}_r{c}_rT\left(x,t\right)+\phi {\rho}_w{c}_wT\left(x,t\right)\right\}+\frac{\partial }{\partial x}\left\{{u}_w{\rho}_w{c}_wT\left(x,t\right)\right\}+{q}_1-{q}_2={\lambda}_e\frac{\partial^2T\left(x,t\right)}{\partial {x}^2} $$
(1)

where Ф is the porosity of the aquifer; ρ r and ρ w are the densities of rock and water, respectively; c r and c w are the specific heats of rock and water, respectively; T is the temperature, u w is the velocity of groundwater; q 1 and q 2 are the heat losses from the aquifer to the overlying and underlying rocks, respectively; t is injection time and x represents the longitudinal direction; λ e is the effective thermal conductivity of the aquifer (Chevalier and Banton 1999) which is the summation of equivalent thermal conductivity of the porous medium (the pure diffusive term) and the thermal dispersion conductivity (the dispersive term). The effective thermal conductivity is thus given by

$$ {\lambda}_{\mathrm{e}}={\lambda}_{\mathrm{a}}+D $$
(2)

where the equivalent thermal conductivity is λ a = (1 – Ф) λ r + Фλ w and thermal dispersion conductivity is D = α 1׀u w(ρ w c w). Here λ r and λ w are the thermal conductivities of the solid and water respectively and α 1 is the thermal dispersivity.

Equation (1) holds well under the assumption of local thermal equilibrium, which states that the temperature of each phase present in a representative elementary volume (REV) equals the average temperature of the REV.

Considering all other parameters to be constant spatially and temporally (assumption 1), Eq. (1) can be written as

$$ C\frac{\partial T\left(x,t\right)}{\partial t}+U\frac{\partial T\left(x,t\right)}{\partial x}+{q}_1-{q}_2=\lambda \frac{\partial^2T\left(x,t\right)}{\partial {x}^2} $$
(3)

where C = (1 – Ф)ρ r c r + Ф ρ w c w is the equivalent volumetric heat capacity of the aquifer and U = ρ w c w u w.

The differential equation describing the transport of heat in the overlying rock (Fig. 1) is given by

$$ {C}_1\frac{\partial {T}_1\left(x,z,t\right)}{\partial t}={\lambda}_1\frac{\partial^2{T}_1\left(x,z,t\right)}{\partial {z}^2} $$
(4)

where C 1 = ρ r1 c r1. Here ρ r1 is the density, c r1 is the specific heat of the overlying rock, λ 1 is the thermal conductivity of the overlying rock and z represents the vertical direction.

For underlying rock it is given by

$$ {C}_2\frac{\partial {T}_2\left(x,z,t\right)}{\partial t}={\lambda}_2\frac{\partial^2{T}_2\left(x,z,t\right)}{\partial {z}^2} $$
(5)

where C 2 = ρ r2 c r2. Here ρ r2 is the density, c r2 is the specific heat and λ 2 is the conductivity of the underlying rock.

The loss term, i.e. the heat flux from the aquifer to the rock at the interface (z = B,0) of the two is modeled by Fourier’s law of heat conduction assuming heat fluxes are proportional to the temperature gradient between the aquifer and the rock and is given by

$$ {q}_{1,2}={\left.-{\lambda}_{1,2}\frac{\partial {T}_{1,2}}{\partial z}\right|}_{z=B,0} $$
(6)

where T 1,2 = T 1,2(x, z, t) is the temperature in the confining rocks and z is the coordinate perpendicular to the axis of the aquifer.

Substituting Eq. (6) into Eq. (3), the full differential equation describing the heat transfer in the porous media is obtained as

$$ C\frac{\partial T\left(x,t\right)}{\partial t}+U\frac{\partial T\left(x,t\right)}{\partial x}{\left.-{\lambda}_1\frac{\partial {T}_1}{\partial z}\right|}_{z=B}+\lambda {\left.{}_2\frac{\partial {T}_2}{\partial z}\right|}_{z=0}=\lambda \frac{\partial^2T\left(x,t\right)}{\partial {x}^2} $$
(7)

The initial and boundary conditions for the heat transfer equation in the aquifer are given by

$$ T\left(x,0\right)={T}_0 $$
(8)
$$ T\left(0,t\right)={T}_{\mathrm{in}} $$
(9)
$$ T\left(\infty, t\right)={T}_0 $$
(10)

The initial and boundary conditions for the equation of heat transfer through the overlying rock (Eq. 4) are given by

$$ {T}_1\left(x,z,0\right)={T}_{01} $$
(11)
$$ {T}_1\left(x,B,t\right)=T\left(x,t\right) $$
(12)
$$ {T}_1\left(x,B+{b}_1,t\right)={T}_{01} $$
(13)

where b 1 is the thickness of the overlying rock.

The initial and boundary conditions for the equation of heat transfer through the underlying rock (Eq. 5) are given by

$$ {T}_2\left(x,z,0\right)={T}_{02} $$
(14)
$$ {T}_2\left(x,0,t\right)=T\left(x,t\right) $$
(15)
$$ {T}_2\left(x,-{b}_2,t\right)={T}_{02} $$
(16)

where b 2 is the thickness of the underlying rock.

The boundary conditions in Eqs. (12) and (15) are responsible for coupling between the aquifer and the confining rocks. Equations (13) and (16) imply that the temperature distribution in the rocks approaches their initial temperature asymptotically.

Analytical solutions

General transient solution

Solution for geothermal aquifer

To solve the second-order differential Eq. (7), Eqs. (4) and (5) are to be solved first in order to determine the loss term. The Laplace transform technique is applied for solving the differential equations since all the thermal and fluid properties are taken to be constant spatially and temporally.

Application of the Laplace transform to Eq. (4), which describes the heat transport in the overlying rock, gives

$$ {C}_1\left\{s\overline{T_1}-{T}_1\left(x,z,0\right)\right\}={\lambda}_1\frac{d^2\overline{T_1}}{d{z}^2} $$
(17)

where \( \overline{T_1}\left(x,z,s\right) \) is the Laplace transform of T 1 (x, z, t) which is defined as

$$ \overline{T_1}\left(x,z,s\right)={\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(- st\right){T}_1\left(x,z,t\right) dt} $$
(18)

where s is a complex number (Kuhfittig Peter 1980)

Substituting the initial condition given by Eq. (11), Eq. (17) becomes

$$ \frac{d^2\overline{T_1}}{d{z}^2}-\frac{C_1s}{\lambda_1}\overline{T_1}+\frac{C_1{T}_{01}}{\lambda_1}=0 $$
(19)

The general solution for Eq. (19) is given by

$$ \overline{T_1}={c}_1^{\prime } \exp \left\{{\left(\frac{C_1s}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}+{c}_2^{\prime } \exp \left\{-{\left(\frac{C_1s}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}+\frac{T_{01}}{s} $$
(20)

Since b 1 is large, the first term of Eq. (20) should vanish in order to satisfy boundary condition in Eq. (13) which requires the solution to be bounded. The particular solution of Eq. (19) is thus derived using the boundary condition in Eqs. (12) and (13)

$$ \overline{T_1}=\left(\overline{T}-\frac{T_{01}}{s}\right) \exp \left\{-{\left(\frac{C_1s}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}+\frac{T_{01}}{s} $$
(21)

Hence, the gradient of \( \overline{T_1} \) at the interface (z = B) of the aquifer and the overlying rock is given by

$$ {\left.\frac{d\overline{T_1}}{ dz}\right|}_{z=B}=-{\left(\frac{C_1s}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\overline{T}-\frac{T_{01}}{s}\right) $$
(22)

Similarly, the gradient of \( \overline{T_2} \) at the interface (z = 0) of the aquifer and the underlying rock is given by

$$ {\left.\frac{d\overline{T_2}}{ dz}\right|}_{z=0}={\left(\frac{C_2s}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\overline{T}-\frac{T_{02}}{s}\right) $$
(23)

Now the Laplace transform is applied on the 1D heat transfer Eq. (7) for the geothermal aquifer. The source terms in the equation are derived multiplying the temperature gradients in Eqs. (22) and (23) by corresponding thermal conductivities (λ 1 and λ 2, respectively). The ordinary differential equation in Laplace domain becomes

$$ \lambda \frac{d^2\overline{T}}{d{x}^2}-U\frac{d\overline{T}}{ dx}-\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\overline{T}+\left(\omega {s}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+C{T}_0\right)=0 $$
(24)
$$ \mathrm{where}\kern6em \alpha ={\left({C}_1{\lambda}_1\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+{\left({C}_2{\lambda}_2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$
(25)
$$ \mathrm{and}\kern6em \omega ={\left({C}_1{\lambda}_1\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{T}_{01}+{\left({C}_2{\lambda}_2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{T}_{02} $$
(26)

The ordinary differential Eq. (24) is derived using Eq. (8) as the initial condition. The general solution of the second-order differential equation given by Eq. (24) is

$$ \overline{T}={c}_1 \exp \left(x{r}_{+}\right)+{c}_2 \exp \left(x{r}_{-}\right)+\frac{\omega +C{T}_0{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)} $$
(27)

where r + and r – are the roots of the auxiliary equation of Eq. (24) which are given by

$$ {r}_{\pm }=\frac{U}{2\lambda}\left[1\pm {\left\{1+\frac{4\lambda }{U^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right] $$
(28)

Now to use Eq. (10) as the boundary condition requires c 1 = 0. Using Eq. (9) as the second boundary condition whose Laplace transform is given by

$$ \overline{T}\left(0,s\right)=\frac{T_{\mathrm{in}}}{s} $$
(29)

the unknown constant c 2 can be determined. Thus, the final solution of the transformed ordinary differential Eq. (24) is obtained as

$$ \overline{T}=\left\{\frac{T_{in}}{s}-\frac{\omega +C{T}_0{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}\right\} \exp \left[\frac{ Ux}{2\lambda}\left\{1-{\left\{1+\frac{4\lambda }{U^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]+\frac{\omega +C{T}_0{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)} $$
(30)

which can also be written as

$$ \begin{array}{l}\overline{T}=\frac{T_0}{s}-\frac{\left({T}_0-{T}_{in}\right)}{s} \exp \left[\frac{ Ux}{2\lambda}\left\{1-{\left\{1+\frac{4+\lambda }{U^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]-\frac{\left(\omega -\alpha {T}_0\right)}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}\\ {}\cdot \exp \left[\frac{ Ux}{2\lambda}\left\{1-{\left\{1+\frac{4\lambda }{U^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]+\frac{\left(\omega -\alpha {T}_0\right)}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}\end{array} $$
(31)

To invert the preceding solution in the Laplace domain, one integral solution (Eq. (32)), given by Gradshteyn and Ryzhik (2007), is invoked, which states

$$ {\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{b^2}{\zeta^2}\right)}\kern0.5em d\zeta =\frac{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{2} \exp \left(-2b\right) $$
(32)

Using the aforementioned result, Eq. (31) is written as

$$ \begin{array}{l}\overline{T}=\frac{T_0}{s}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\frac{\left({T}_0-{T}_{\mathrm{in}}\right)}{s} \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\kern0.6em \frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right) \exp \left\{-\frac{x^2}{4\lambda {\zeta}^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}} d\zeta \\ {}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\frac{\left(\omega -\alpha {T}_0\right)}{C} \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\kern0.6em \frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)\frac{ \exp \left\{-\frac{x^2}{4\lambda {\zeta}^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}{s\left({s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}} d\zeta \\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{C}\frac{1}{s\left({s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}\end{array} $$
(33)

The inverse Laplace transform is applied to Eq. (33) to obtain the transient temperature distribution in the confined aquifer

$$ \begin{array}{l}T={T}_0-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{in}\right) \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\kern0.6em \frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right){L}^{-1}\left[\frac{ \exp \left\{-\frac{x^2}{4\lambda {\zeta}^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}{s}\right]} d\zeta \\ {}-\frac{\left(\omega -\alpha {T}_0\right)}{C} \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{0}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\kern0.6em \frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right){L}^{-1}\left[\frac{ \exp \left\{-\frac{x^2}{4\lambda {\zeta}^2}\left(\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+ Cs\right)\right\}}{s\left({s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}\right]} d\zeta \\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{C}{L}^{-1}\left\{\frac{1}{s\left({s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}+\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$C$}\right.\right)}\right\}\end{array} $$
(34)

The term by term inversion is described in Appendix1. The final solution for the advancement of the cold-water front in an aquifer is thus given by

$$ \begin{array}{l}T={T}_0-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{in}\right) \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\kern0.6em \frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right) erfc\left\{\frac{\alpha {x}^2}{8\lambda {\zeta}^2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}} d\zeta \\ {}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\frac{\left(\omega -\alpha {T}_0\right)}{\alpha } \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)}\cdot \left[ erfc\left\{\frac{\alpha {x}^2}{8\lambda {\zeta}^2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\\ {}\left.- \exp \left\{\frac{\alpha^2{x}^2}{4{\lambda}^2{\zeta}^2C}+\frac{\alpha^2}{C^2}\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)\right\}\cdot erfc\left\{\frac{\alpha {x}^2}{8{\lambda}^2{\zeta}^2\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)\raisebox{1ex}{${}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$}\!\left/ \!\raisebox{-1ex}{$$}\right.}+\frac{\alpha }{C}{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right] d\zeta \\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left\{1- \exp \left(\frac{\alpha^2}{C^2}t\right)\cdot erfc\left(\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right\}\end{array} $$
(35)

where the lower limit of the integration is given by

$$ l=\frac{x}{2}{\left(\frac{C}{\lambda t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} $$
(36)

Equation (35) is the final form of solution describing the time-dependent temperature distribution in the aquifer, which includes the convective and conductive modes of heat transfer as well as the heat transfer to the underlying and overlying rocks. Clearly, the second term of the right-hand side emerges due to the difference in initial temperature of the aquifer and the injection water temperature and has greater contribution to the solution. The third and fourth terms contribute to the solution due to the difference in temperature between the geothermal reservoir and the confining rocks, and the magnitude of the terms is only significant when the injection time t is large, i.e. 1,000 days or more. The final solution given by Eq. (35) can be simplified if an assumption T 01 ≈ T 02 ≈ T 0 is applied which implies that (ω – αT 0 ) ≈ 0. The solution for the time-dependent temperature distribution in the geothermal reservoir in this case becomes

$$ T={T}_0-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{\mathrm{in}}\right) \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right) erfc\left\{\frac{\alpha {x}^2}{8\lambda {\zeta}^2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}} d\zeta $$
(37)

Solution for the overlying and underlying rocks

The solution for heat transfer in the main porous geothermal aquifer will be used now to derive the solutions for transient temperature distribution in the underlying and overlying rocks. The heat transfer equation in the overlying rock (Eq. 4) is considered for this purpose. \( \overline{T} \) is substituted from Eq. (33) in Eq. (21) and the solution is then inverted by the same procedure (described in Appendix 1), which leads to

$$ \begin{array}{l}{T}_1={T}_{01}+\left({T}_0-{T}_{01}\right) erfc\left\{{\left(\frac{C_1}{4{\lambda}_1t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{\mathrm{in}}\right) \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)}\\ {}\cdot erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)}{2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\} d\zeta -\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\frac{\left(\omega -\alpha {T}_0\right)}{C} \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)}\\ {}\cdot \left[ erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)}{2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\left.- \exp \left[\left\{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}\frac{\alpha }{C}+\frac{\alpha^2}{C^2}\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)\right]\cdot erfc\left\{\frac{{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha {x}^2}{4\lambda {\zeta}^2}}{2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right] d\zeta \\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\left\{\frac{{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha {x}^2}{4\lambda {\zeta}^2}}{2{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\left.- \exp \left\{\frac{\alpha }{C}{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha^2}{C^2}t\right\}\cdot erfc\left\{\frac{\alpha {x}^2}{8{\lambda}^2{\zeta}^2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\end{array} $$
(38)

The preceding solution can be simplified as well by applying the assumption T 01 ≈ T 02 ≈ T 0. The simplified solution becomes

$$ {T}_1={T}_{01}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{in}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2\right)}\cdot erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)}{2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\} d\zeta $$
(39)

The solution for the transient temperature distribution for the underlying rock can be determined following a similar procedure and is given by

$$ \begin{array}{l}{T}_2={T}_{02}+\left({T}_0-{T}_{02}\right) erfc\left\{{\left(\frac{C_1}{4{\lambda}_1t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{\mathrm{in}}\right) \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)}\\ {}\cdot erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z}{2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\} d\zeta -\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\frac{\left(\omega -\alpha {T}_0\right)}{C} \exp \left(\frac{ Ux}{2\lambda}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2-\frac{U^2{x}^2}{16{\lambda}^2{\zeta}^2}\right)}\\ {}\left[ erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z}{2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\left.- \exp \left[\left\{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}\frac{\alpha }{C}+\frac{\alpha^2}{C^2}\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)\right]\cdot erfc\left\{\frac{{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z+\frac{\alpha {x}^2}{4\lambda {\zeta}^2}}{2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right] d\zeta \\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\left\{\frac{{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z+\frac{\alpha {x}^2}{4\lambda {\zeta}^2}}{2{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\left.- \exp \left\{\frac{\alpha }{C}{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}z+\frac{\alpha^2}{C^2}t\right\}\cdot erfc\left\{\frac{\alpha {x}^2}{8{\lambda}^2{\zeta}^2{\left(t-\frac{C{x}^2}{4{\lambda}^2{\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\end{array} $$
(40)

Using the assumption T 01 ≈ T 02 ≈ T 0 Eq. (40) can also be simplified as

$$ {T}_2={T}_{02}-\frac{2}{\pi^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\left({T}_0-{T}_{\mathrm{in}}\right){\displaystyle \underset{l}{\overset{\infty }{\int }} \exp \left(-{\zeta}^2\right)}\cdot erfc\left\{\frac{\frac{\alpha {x}^2}{4\lambda {\zeta}^2}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z}{2{\left(t-\frac{C{x}^2}{4\lambda {\zeta}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\} d\zeta $$
(41)

Numerical evaluation of the analytical solution

The analytical solutions for the transient temperature distribution in a geothermal aquifer due to cold-water injection given by Eqs. (35) and (37) and those for the overlying rocks given by Eqs. (38) and (39) are integral solutions. The integrations are solved numerically in MATLAB by applying the Gauss-Kronrod quadrature technique. It is observed that although the upper limit of both the solutions is infinity, the numerically effective range of the integrand extends over a much smaller range. The concerned integral is tested for different upper limits. The upper limit is fixed when the integral value becomes almost invariant for different values of the upper limit. The value of the integral is plotted in Fig. 2 against distance from the injection well for an injection time of 30 days and for three different values of upper limit 10, 100 and 1,000. The figure shows that the value of the integral becomes almost invariant with the upper limit, beyond 10 in this case.

Fig. 2
figure 2

Value of the integral for different upper limits

Full size image

Steady-state solution

The steady state solution can be deduced using of the final value theorem (Churchill 1972).

$$ F=\underset{s\to 0}{ \lim } sf(s) $$
(42)

where F is the steady-state value of a function, the Laplace transform of which is f(s). Application of the preceding theorem shows that the heat transfer in the geothermal reservoir will gradually approach steady state at very large amounts of time, when the temperature of the whole aquifer approaches the injection water temperature.

Transient solution with no conduction (λ = 0 W/m · K)

Solution for geothermal aquifer

Often porous geothermal aquifers are encountered where the conductive heat transfer is negligible compared to the convective mode due to very much less longitudinal thermal conductivity. Mathematically the governing equation for this case reduces to a first-order partial differential equation, the solution of which is of less mathematical rigor.

$$ C\frac{\partial T\left(x,t\right)}{\partial t}+U\frac{\partial T\left(x,t\right)}{\partial x}+{q}_1-{q}_2=0 $$
(43)

The Laplace domain ordinary differential equation for the aforementioned partial differential equation is given by

$$ U\frac{d\overline{T}}{ dx}+\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\overline{T}-\left(C{T}_0+\omega {s}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)=0 $$
(44)

where Eq. (8) is used as the initial condition. Equation (44) is a first-order differential equation with a general solution of the form

$$ \overline{T}=\frac{\left(C{T}_0+\omega {s}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}{\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}+{c}_3 \exp \left\{-\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)x\right\} $$
(45)

To arrive at the particular solution of Eq. (44), Eq. (9) is used as the boundary condition, the Laplace transform of which is given by Eq. (29).

Equation (45) finally becomes

$$ \overline{T}=\left\{\frac{T_{in}}{s}-\frac{\left(C{T}_0+\omega {s}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}{\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}\right\} \exp \left\{-\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\frac{x}{U}\right\}+\frac{\left(C{T}_0+\omega {s}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)}{\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)} $$
(46)

Now the preceding solution is to be inverted to get the distribution of temperature in space and time. Equation (46) is expanded into separate terms for simplifying the inversion.

$$ \overline{T}=\frac{T_0}{s}-\left(\frac{T_0}{s}-\frac{T_{in}}{s}\right) \exp \left\{-\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\frac{x}{U}\right\}-\frac{\left(\omega -\alpha {T}_0\right)}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)} \exp \left\{-\left( Cs+\alpha {s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\frac{x}{U}\right\}+\frac{\left(\omega -\alpha {T}_0\right)}{s\left(\alpha +C{s}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)} $$
(47)

Using the results and procedure described in Appendix 1 (Eqs. 60, 62, 66), Eq. (47) is inverted to obtain the final solution given by

$$ \begin{array}{l}T={T}_0-\left({T}_0-{T}_{in}\right) erfc\left\{\frac{\alpha x}{2U{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}-\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\cdot \left[ erfc\left\{\frac{\alpha x}{2U{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\right.\\ {}\left.- \exp \left\{\frac{\alpha^2x}{ CU}+\frac{\alpha^2}{C^2}\left(t-\frac{ Cx}{U}\right)\right\}\cdot erfc\left\{\frac{\alpha x}{2U{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left\{1- \exp \left(\frac{\alpha^2}{C^2}t\right)\cdot erfc\left(\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right)\right\}\end{array} $$
(48)

The assumption T 01 ≈ T 02 ≈ T 0 leads to a simplified solution as in the previous cases

$$ T={T}_0-\left({T}_0-{T}_{in}\right) erfc\left\{\frac{\alpha x}{2U{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\} $$
(49)

Solution for the overlying and underlying rocks

The temperature distribution in the overlying rock will be derived using the result of Eq. (45). Substituting the result into Eq. (21) and inverting the solution in the Laplace domain, the solution for the overlying rock is obtained as

$$ \begin{array}{l}{T}_1={T}_{01}+\left({T}_0-{T}_{01}\right) erfc\left\{{\left(\frac{C_1}{4{\lambda}_1t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}-\left({T}_0-{T}_{\mathrm{in}}\right)\cdot erfc\left\{\frac{\frac{\alpha x}{U}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\\ {}-\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\frac{\left\{\frac{\alpha x}{U}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}- \exp \left[\left\{\frac{\alpha x}{U}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}\frac{\alpha }{C}+\frac{\alpha^2}{C^2}\left(t-\frac{ Cx}{U}\right)\right]\cdot erfc\left\{\frac{{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha x}{U}}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\left\{{\left(\frac{C_1}{4t{\lambda}_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)\right\}\right.\left.- \exp \left\{\frac{\alpha }{C}{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha^2}{C^2}t\right\}\cdot erfc\left\{{\left(\frac{C_1}{4t{\lambda}_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)+\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\end{array} $$
(50)

Assuming that the initial temperature of the porous aquifer and confining rocks are approximately equal, i.e. T 01 ≈ T 02 ≈ T 0, the preceding solution can be simplified as

$$ \begin{array}{l}{T}_1={T}_{01}-\left({T}_0-{T}_{\mathrm{in}}\right)\cdot erfc\left\{\frac{\frac{\alpha x}{U}+{\left(\frac{C_1}{\lambda_1}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(z-B\right)}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\\ {}\cdot \end{array} $$
(51)

The transient temperature distribution for the underlying rock in this case is given by

$$ \begin{array}{l}{T}_2={T}_{02}+\left({T}_0-{T}_{02}\right) erfc\left\{{\left(\frac{C_2}{4{\lambda}_1t}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}-\left({T}_0-{T}_{in}\right)\cdot erfc\left\{\frac{\frac{\alpha x}{U}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\\ {}-\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\frac{\left\{\frac{\alpha x}{U}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}- \exp \left[\left\{\frac{\alpha x}{U}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}\frac{\alpha }{C}+\frac{\alpha^2}{C^2}\left(t-\frac{ Cx}{U}\right)\right]\cdot erfc\left\{\frac{{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot \left(z-B\right)+\frac{\alpha x}{U}}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}+\frac{\alpha }{C}{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\\ {}+\frac{\left(\omega -\alpha {T}_0\right)}{\alpha}\left[ erfc\left\{{\left(\frac{C_2}{4t{\lambda}_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z\right\}\right.\left.- \exp \left\{\frac{\alpha }{C}{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z+\frac{\alpha^2}{C^2}t\right\}\cdot erfc\left\{{\left(\frac{C_2}{4t{\lambda}_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z+\frac{\alpha }{C}{t}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]\end{array} $$
(52)

which by applying the assumption T 01 ≈ T 02 ≈ T 0 can be simplified to

$$ \begin{array}{l}{T}_2={T}_{02}-\left({T}_0-{T}_{\mathrm{in}}\right)\cdot erfc\left\{\frac{\frac{\alpha x}{U}+{\left(\frac{C_2}{\lambda_2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\cdot z}{2{\left(t-\frac{ Cx}{U}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}\right\}\\ {}\cdot \end{array} $$
(53)

Transient solution with negligible conductivity in the rocks

In certain cases, the rocks confining the porous geothermal aquifer have only a very small thermal conductivity and, therefore, the heat transfer to them is negligible compared to the convective and conductive heat transfer in the longitudinal direction. The resulting governing equation in this case is given by

$$ C\frac{\partial T\left(x,t\right)}{\partial t}+U\frac{\partial T\left(x,t\right)}{\partial x}=\lambda \frac{\partial^2T\left(x,t\right)}{\partial {x}^2} $$
(54)

The application of Laplace transforms to Eq. (54), and using Eq. (8) as the initial condition, yields

$$ \lambda \frac{d^2\overline{T}}{d{x}^2}-U\frac{d\overline{T}}{ dx}- Cs\overline{T}+C{T}_0=0 $$
(55)

The general solution of Eq. (55) is of the form

$$ \overline{T}={c}_4 \exp \left[\frac{ Ux}{2\lambda}\left\{1+{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]+{c}_5 \exp \left[\frac{ Ux}{2\lambda}\left\{1-{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}\right]+\frac{T_0}{s} $$
(56)

The boundary conditions for Eq. (55) are given by Eq. (9) and

$$ T\left({L}_1,t\right)={T}_0 $$
(57)

where L 1 is the distance between the injection and production well. The boundary condition of Eq. (57) is valid until the cold-water front reaches the production well. Application of the boundary conditions leads to the particular solution as follows

$$ \overline{T}= \exp \left(\frac{ Ux}{2\lambda}\right)\left({T}_0-{T}_{in}\right)\left[\frac{ \exp \left\{\frac{ Ux}{2\lambda }{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}}{s\left[ \exp \left\{\frac{ UL}{2\lambda }{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}-1\right]}-\frac{ \exp \left\{\frac{U\left(2L-x\right)}{2\lambda }{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}}{s\left[ \exp \left\{\frac{ UL}{2\lambda }{\left(1+\frac{4 C\lambda}{U^2}s\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\right\}-1\right]}\right]+\frac{T_0}{s} $$
(58)

The aforementioned solution in the Laplace domain is then inverted following the procedure discussed in Appendix 2 to arrive at the final solution as

$$ \begin{array}{l}T={T}_0+ \exp \left(\frac{ Ux}{2\lambda}\right)\left({T}_0-{T}_{\mathrm{in}}\right)\left[\frac{ \exp \left(\frac{ Ux}{2\lambda}\right)- \exp \left\{\frac{U\left(2L-x\right)}{2\lambda}\right\}}{\left\{ \exp \left(\frac{ UL}{\lambda}\right)-1\right\}}+\right.\\ {}\left.{\displaystyle \sum_{n=0}^{\infty}\frac{8 n\pi {\lambda}^2 \sin \left( n\pi \frac{x}{L}\right)}{4{n}^2{\pi}^2{\lambda}^2+{U}^2{L}^2} \exp \left\{-\frac{U^2t}{4 C\lambda}\left(\frac{4{n}^2{\pi}^2{\lambda}^2}{U^2{L}^2}+1\right)\right\}}\right]\end{array} $$
(59)

Equation (59) represents the spatial distribution of temperature at different times for the case of negligible heat transport to the confining rock media.

Results and discussion

The analytical solutions derived in the previous section for the transient temperature distribution in the geothermal reservoir for different cases, will be applied in this section to solve practical problems. All the properties, required for the analysis of the derived solutions, of the aquifer and the underlying and overlying rocks and the properties of the geothermal fluid, are listed in Table 1, where most of the data (ρ r, ρ r1, ρ r2, λ e, λ 1, λ 2 and φ) have been taken from Yeh et al. (2012). The temperature of the injected fluid is assumed to be 293 K (20 °C) and kept constant during the whole injection period. The initial temperature of the aquifer is taken as 353 K (80 °C).

The temperature distribution in the aquifer at different times for the general transient solution described in a previous section “General transient solution” is plotted in Fig. 3 along with temperature distribution curves for the no conduction case described in the section that followed. Figure 3 shows that at a specific injection time, the aquifer temperature has a nonlinear rising trend from the injection water temperature at the injection well and approaching the initial temperature of the aquifer. The aquifer temperature decreases gradually with continuous injection over time as the cold temperature front advances. Hence, for a production well which is situated at a finite distance from the injection point, the temperature of the extracted geothermal fluid remains at the initial reservoir temperature until the thermal front reaches the production well. Afterwards, the production water temperature falls and the reservoir loses its efficiency. The plots also show that the thermal front for the no conduction case always lags behind the general transient case, e.g. in 100 days the thermal front for the general transient case penetrates about 7 m, whereas the same for the no conduction case is only 2.5 m. This difference between the distances penetrated by the thermal front for both the cases increases with injection time. Results also depict that as the confining rock layers serve as storage of heat (in spite of being at lower temperature than the geothermal aquifer), the advancement of the cold-water front considerably reduces, as heat is transferred from the rocks to the geothermal reservoir.

Fig. 3
figure 3

Temperature distribution plots in the geothermal aquifer at different injection time for the general transient solution and no conduction case

Full size image

The transient temperature distributions in the overlying rock for two fixed injection times of 10 and 30 days are presented in Fig. 4a,b, respectively. The figures show that the thermal front is generated in the rocks, the effect of which is mainly concentrated near the injection well. With continuous injection, the 2D thermal front proceeds. From Fig. 4 it can be seen that the thermal front has penetrated about 2.5 and 5.0 m in the vertical direction in 10 and 30 days, respectively, whereas the advancement of it in the horizontal direction is the same as that in the aquifer due to the boundary condition in Eq. (12). The heat loss to the underlying and overlying rocks plays a crucial role in the development of the transient temperature profile in the aquifer. The more the heat loss to the rocks, the slower will be the advancement of the cold-water thermal front in the geothermal aquifer. Figure 5a,b shows the temperature field in the overlying rock for a vertical thermal conductivity of 0.5 W/m · K at the injection times of 10 and 30 days, respectively. Figure 5 shows that the thermal front has penetrated 1.5 and 2.5 m, respectively in the vertical direction. Advancement of the thermal front in the horizontal direction has been more in this case due to lesser heat loss.

Fig. 4
figure 4

Temperature distribution (in K) in the overlying rock for λ 1 = 1.5 W/m · K at a 10 days and b 30 days

Full size image
Fig. 5
figure 5

Temperature distribution (in K) in the overlying rock for λ 1 = 0.5 W/m · K at a 10 days and b 30 days

Full size image

The thermal profile in the overlying rock for the no conduction (λ = 0) case is shown in Fig. 6a,b, respectively, for injection times of 10 and 30 days. Figure 6 shows that the penetration of the thermal front in the vertical direction has been the same as the general transient solution (in Fig. 4a,b) but the horizontal advancement of it is less due to absence of the longitudinal conductive heat flux.

Fig. 6
figure 6

Temperature distribution in the overlying rock for λ = 0 at a 10 days and b 30 days

Full size image

The analysis of the effect of some parameters involved in the heat transfer equation, namely the injection rate Q, the porosity Ф and the thermal conductivity λ of the geothermal aquifer, is important in the transient heat transfer phenomenon in the geothermal reservoir. To determine the effect of the volumetric injection rate, two values of the parameter, 0.3 and 0.6 m3/s, are considered and the results are plotted in Fig. 7 at two fixed times, 100 and 1,000 days. Results show that the advancement of the thermal front is accelerated due to the increase in volumetric injection rate since the injection rate is directly related to the advection velocity of the geothermal fluid, which in turn is related to the convective flux of heat transport and the effect is more pronounced at large amounts of time. As can be seen, the thermal front reaches a distance of 7 and 14 m for Q = 0.3 m3/s and 8 and 23 m for Q = 0.6 m3/s in 100 and 1,000 days, respectively. The aquifer temperature for Q = 0.3 m3/s is also greater than Q = 0.6 m3/s at a specific distance and injection time, e.g. the temperatures of the aquifer at a distance 6 m from the injection well at injection time of 100 days are 318 K (45 °C) and 343 K (70 °C) for Q = 0.6 and 0.3 m3/s, respectively. The phenomenon of decrease in aquifer temperature increases with increasing injection rate and injection time. Hence, the cold-water-injection rate is a very important parameter to consider in maintaining the reservoir efficiency for a longer period of time.

Fig. 7
figure 7

Comparison of temperature distribution in the geothermal aquifer for Q = 0.3 m 3 /s and Q = 0.6 m 3 /s

Full size image

To estimate the influence of the thermal conductivity of the geothermal aquifer on the advancement of the thermal front, the results derived from the general transient solution are compared using two values of the parameter, 2.0 and 1.0 W/m · K. Figure 8 shows the position of the thermal front at two fixed times of 100 and 10,000 days. The cold-water front has reached a distance 6 and 28 m for λ = 1.0 W/m · K, in 100 and 10,000 days, respectively, and 7 and 33 m for λ = 2.0 W/m · K, at the same injection times, which implies that the aquifer with greater thermal conductivity helps in accelerating the thermal front. It is to be noted also that at a specific longitudinal distance and a fixed injection time, the aquifer temperature in the case with λ = 1.0 W/m · K is greater than that with λ = 2.0 W/m · K. The preceding indicates thermal conductivity is an important parameter to consider in the study of transient heat transport.

Fig. 8
figure 8

Comparison of temperature distribution in the geothermal aquifer for λ = 2.0 W/m · K and λ = 1.0 W/m · K

Full size image

The effect of the third parameter porosity of the geothermal aquifer is assessed in the same way using two values of the parameter, Ф = 0.15 and Ф = 0.30, and by plotting the results at two fixed injection times of 10 and 100 days in Fig. 9. The figure shows that the overall aquifer temperature is lower for the aquifer with greater porosity than that with a higher value of it at a fixed injection time, although the effect is less significant due to the low velocity of flow. At injection time of 10 days and a distance of 1.5 m from the injection well, the temperature of the aquifer is 348.5 K (75.5 °C) for Ф = 0.15, whereas it is 347.5 K (75.5 °C) for Ф = 0.30. With the increase of flow velocity, the difference of the temperature increases at a fixed distance and injection time for Ф = 0.15 and Ф = 0.30 (e.g. at a flow velocity of 10-6 m/s, the temperature of the aquifer at the same distance and injection time becomes 339 and 341 K for Ф = 0.15 and Ф = 0.30, respectively).

Fig. 9
figure 9

Comparison of temperature distribution in the geothermal aquifer for Ф = 0.15 and Ф = 0.30

Full size image

The curves of the temperature distribution in the aquifer at different times when the source terms q 1, q 2 are zero are shown in Fig. 10, along with the curves of the general transient solution. Results show that the movement of the cold-water thermal front is much faster for the q 1, q 2 = 0 case where the front reaches 62 m in 1,000 days compared to only 15 m in the general transient solution. The aquifer temperature also decreases much quicker in the q 1, q 2 = 0 case. The results thus demonstrate the effect of the heat transfer to the confining rock layers in slowing down the advancement of the thermal front. The underlying and overlying rocks, having significant value of thermal conductivity, and the temperature difference between the rock layers and the geothermal aquifer not varying so much, can retard the cooling of the reservoir and thus sustain its efficiency for a longer period of time.

Fig. 10
figure 10

The plots of thermal front at different injection times for the case of negligible source terms and for the general transient solution

Full size image

The results for the transient temperature profiles derived by analytical method (Eq. 35) are verified using numerical methods shown in Fig. 11. The existing analytical approaches of Bodvarsson and Tsang (1982), who derived their solution neglecting the longitudinal thermal conductivity, and the analytical solutions by Li et al. (2010b) and Yeh et al. (2012), derived for an aquifer thermal energy storage (ATES) system where hot water is injected into an aquifer at lower temperature, were somewhat different from the present study and hence are not used for comparison. The numerical modeling is performed using the multiphysics software COMSOL, which solves fluid flow and heat transport problems in porous media using the finite element technique. Heat-depleted water is assumed to be injected at one end of the domain at 293 K (20 °C), whereas the temperature of the aquifer at a distance far away from the injection well is considered to be equal to the initial aquifer temperature of 353 K (80 °C). The vertical extent of the domain is considered the same as given in Table 1. The domain for the analysis is discretized using 100000 elements. The time step size used in the simulation is 10 seconds. Figure 11 shows that the thermal fronts at two fixed injection times of 1 day and 30 days match with each other very well. The Nash–Sutcliffe coefficient for the model at injection times of 1 day and 30 days is 0.99 and 0.98, respectively. The numerical model is tested with other spatial discretizations and the results found are almost the same as the present one.

Fig. 11
figure 11

Comparison of temperature distributions in the geothermal aquifer derived by analytical and numerical methods

Full size image

Conclusions

In this study, a general analytical solution for the transient temperature distribution due to the continuous injection of cold water into a porous geothermal reservoir confined by overlying and underlying rock layers is presented using the Laplace transform as the solution technique. In the solution, the heat transfer processes that have been considered are the advection, longitudinal conduction and 1D conduction to the confining rock media due to the vertical temperature gradient between the geothermal aquifer and the rock media. The present solution is better than the previous ones (Bodvarsson and Tsang 1982; Li et al. 2010a, b; Yeh et al. 2012) as it includes all the modes of heat transport and gives a closed-form full analytical solution. Two simple solutions are also developed by considering (1) conductive heat transport, and (2) the heat transfer to the confining rock media, to be negligible. Such solutions are useful in situations where these processes are negligible compared to the other terms in the 1D single-phase heat transfer equation, depending upon the conditions present in the practical situation. The results suggest that the impact of the heat loss to the confining layers is high when the rocks have considerably high thermal conductivity and small temperature difference with the geothermal aquifer. The heat loss slows down the advancement of the thermal front significantly and thus maintains the reservoir efficiency for a longer time. The penetration of thermal front in the case of an aquifer with considerable thermal conductivity, on the other hand, is higher than that with negligible thermal conductivity at a particular injection time. The difference between the distances penetrated by the thermal fronts for both the aquifers increase with the passage of injection time.

Dependence of the heat transfer phenomenon on some parameters, namely the injection rate, the longitudinal conductivity and the porosity of the geothermal aquifer, are studied by varying the parameter and judging the variation in the results. The results demonstrate that the injection rate Q is an important parameter to consider as the movement of the cold-water front is accelerated with increase of Q. Longitudinal heat conductivity λ also has an influence on the temperature profile. Aquifer temperature may be over- or under-estimated depending on lower or higher estimation of λ, respectively. Reservoirs with a small value of thermal conductivity have greater efficiency in retaining its heat reserve for longer time. Porosity, on the other hand, has negligible effects on the temperature distribution when the flow velocity is small (lesser than the order of 10-6 m/s).

The analytical model presented here has been verified using a simple numerical model developed by using COMSOL multiphysics software. The transient temperature profiles that are derived by both methods show excellent agreement with each other.

Although the assumptions applied to derive the solution make the system an idealized one, the present solution provides some insight into the phenomenon of cold-water-front movement in a geothermal reservoir. The results obtained can be effectively used in designing the injection-production well system or to determine the rate of injection to be used. Numerical models developed for complex problems can be validated using the analytical model presented in this study.