Introduction

Tracer transport in fractured rock involves fast, advection-dominated processes in fractures characterized by high permeability and mass transfer between the fractures and the rock matrix in which chemical reactions may occur as well. Modeling tracer transport in fractured rock is relevant to a number of practical applications, including radionuclide transport in geological repositories (Sudicky and Frind 1982), groundwater contamination in fractured aquifers (e.g., Freeze and Cherry 1979), and interpretation of isotopic tracer transport signals for characterizing flow patterns and fracture-matrix interactions (e.g., DePaolo 2006).

With the significant advance of computational technology in recent decades, numerical models have been increasingly employed for modeling tracer transport in fractured rock. However, analytical solutions still play an important role in evaluating transport processes, for several reasons. Firstly, given significant uncertainties in site characterization and parameter variability for a practical application, analytical solutions have often been used for analyzing field-testing results obtained under controlled conditions (Neretnieks 2002), because they involve a small number of parameters and are able to capture key transport processes. Secondly, analytical solutions are generally more useful than numerical models for providing physical insights into solute transport processes (DePaolo 2006), because the relative importance of key parameters (or parameter combinations) and processes can be explicitly identified. Thirdly, analytical solutions are useful for validating numerical models. The focus of this study is on the development of analytical solutions for tracer transport in fractured rock.

A number of analytical solutions for solute transport in fractured rock have been published in the literature. These analytical solutions consider fractured rocks associated with a single, planar fracture or a set of parallel fractures (or other simplified fracture geometries). Neretnieks (1980) reported a solution for one-dimensional transport in a single fracture without considering longitudinal dispersion. Tang et al. (1981) presented both transient and steady-state solutions for a single-fracture system, which were derived using Laplace transformation. Rasmuson and Neretnieks (1981) provided a one-dimensional solution for transport in fractured media consisting of porous blocks separated by fissures (fractures). In their solutions, the porous blocks are represented by spheres that have a finite capacity to store a contaminant. Barker (1982) investigated tracer transport in a system of equally spaced fractures separated by slabs of saturated porous rock. However, his work was based on numerical inversion of the Laplace transformation. Unlike the study by Barker (1982); Sudicky and Frind (1982) developed general analytical solutions for similar systems using analytical inversion of the Laplace transformation. Similar analytical solutions for parallel fracture systems were also reported by Maloszewski and Zuber (1985).

In addition to advection and dispersion in fractures and matrix diffusion processes, all the studies mentioned in the previous consider chemical reactions such as radioactive decay and adsorption (represented by a retardation factor). It is believed that the recent work of DePaolo (2006) probably represents the first effort to develop systematic analytical solutions for tracer transport in fractured rock associated with precipitation-dissolution reactions. DePaolo’s work was particularly focused on describing isotopic tracer transport. Developed relationships between isotopic signals and flow-path properties were demonstrated to be useful for characterizing the corresponding fracture-matrix properties (DePaolo 2006). However, the analytical solutions of DePaolo (2006) are limited to steady-state transport conditions. Transient solutions are required for describing isotopic tracer transport in more general cases.

Practical applications of a variety of analytical solutions for tracer transport in fractured rock to field-scale problems have been widely documented in the literature (e.g., Neretnieks 2002; DePaolo 2006; Maloszewski and Zuber 1985). Water flow in a saturated fractured rock is commonly characterized by one or more dominant flow paths. In these applications, tracer transport through one of the flow paths is approximated by the corresponding analytical solutions. An example of a practical application is that of an enhanced geothermal system (EGS) in which heat is mined using injection and production wells (MIT 2007). An EGS consists of a geothermal reservoir (at sufficient depth for the temperature to be high) that is artificially fractured (Fig. 1). A key parameter for an EGS is the fracture-matrix interfacial area between the injection and production wells, because that area is directly related to heat transfer from the surrounding rock to the working fluid (water) and therefore determines the capacity and longevity of a geothermal power plant. Use of analytical solutions to analyze signals of natural and/or artificial tracers provides a promising and practical way to determine the interfacial area, because tracer transport is considerably affected by area-dependent matrix diffusion and precipitation-dissolution reactions occurring in the rock matrix.

Fig. 1
figure 1

Sketch of an enhanced geothermal system (EGS). A typical distance between injection and production wells is on the order of 1,000 m

Full size image

In this paper, analytical solutions are derived for tracer transport in fractured rock associated with precipitation-dissolution reactions under both steady-state and transient transport conditions. The derivation is based on analytical inversions of the Laplace transformation that are similar to those used by Tang et al. (1981) and Sudicky and Frind (1982). The usefulness of the derived solutions in describing tracer transport is also demonstrated under a number of conditions.

Assumptions and governing equations

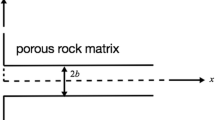
This section considers tracer transport in a single fracture or a set of equally spaced identical fractures. Note that the focus herein is on solutions to tracer transport in fractures, rather than in the rock matrix, although the influence of the rock matrix is explicitly considered. This is simply because tracer concentration data are often obtained from fractures in practical situations (Neretnieks 2002; DePaolo 2006). Figure 2 shows a schematic diagram of a multiple-fracture system, with a single-fracture system being considered a special case with infinite fracture spacing. Water flow rate in each fracture is assumed to be constant and downward. Each fracture has a constant aperture that is much smaller than the fracture spacing. The matrix block is assumed to have homogeneous properties and negligible permeability. Therefore, advection in the rock matrix can be ignored. Because of transverse diffusion and dispersion, it is assumed that there is complete mixing across the width of the fracture at all times. In other words, the solute concentration in the fracture is uniform across the fracture aperture. It is also assumed that molecular diffusion processes within the rock matrix occur only in a direction perpendicular to the fractures. The same assumptions were made in previous studies (e.g., Sudicky and Frind 1982; DePaolo 2006). Furthermore, the longitudinal dispersion and molecular diffusion within a fracture are ignored, because solute transport is dominated by advection in a fracture and the processes of dispersion and diffusion along the flow direction are not important for practical applications (e.g., Neretnieks 2002). Ignoring these processes can significantly simplify the mathematical development of analytical solutions. The dissolution reaction rate is considered to be the same as the precipitation reaction rate within the rock matrix. DePaolo (2006) provides the justification for this assumption within the context of isotopic tracer transport.

Fig. 2
figure 2

Schematic diagram of a fracture-matrix system (modified from Sudicky and Frind 1982). In the figure, v is the groundwater velocity in the fractures (L/T), z and x are the spatial coordinates (L), b is half the fracture aperture (L), and B is half the fracture spacing (L)

Full size image

Applying the above assumptions, the tracer transport process in fractured rock can be described by two coupled equations for transport in the liquid phase (one for the fracture and one for the rock matrix) and a third equation for the solid phase, to take into account precipitation-dissolution reactions. These equations will now be discussed briefly (see DePaolo (2006) for the detailed derivations).

Based on the principle of conservation of mass, tracer transport in fractures is described by (Sudicky and Frind 1982; DePaolo 2006):

$$ \frac{{\partial {c_{\text{f}}}}}{{\partial t}} = - v\frac{{\partial {c_{\text{f}}}}}{{\partial z}} + \frac{{{D_{\text{m}}}{\phi_{\text{m}}}}}{b}{\left\langle {\frac{{\partial {c_{\text{p}}}}}{{\partial x}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} $$
(1)

where t is the time (T), z and x are the spatial coordinates (L) (Fig. 2), c f is the tracer concentration in the fractures (M/L3), v is the groundwater velocity in the fractures (L/T), D m is a matrix-diffusion coefficient defined by the molecular-diffusion coefficient in free water multiplied by tortuosity (L2/T), ϕ m is matrix porosity (dimensionless), c p is the tracer concentration in the matrix pore liquid (M/L3), and b is half the fracture aperture (L). The second term on the right-hand side of Eq. (1) describes the flux crossing two fracture walls.

Within the rock matrix, the pore fluid interacts with the solid phase by dissolution-precipitation, and the pore fluid communicates with the fracture fluid by diffusion. The equations describing these processes are given as (DePaolo 2006):

$$ \frac{{\partial {c_{\text{p}}}}}{{\partial t}} = {D_{\text{m}}}\frac{{{\partial^2}{c_{\text{p}}}}}{{\partial {x^2}}} + {R_{\text{m}}}M\left( {{c_{\text{s}}} - {K_{\text{d}}}{c_{\text{p}}}} \right) $$
(2)
$$ \frac{{\partial {c_{\text{s}}}}}{{\partial t}} = - {R_{\text{m}}}\left( {{c_{\text{s}}} - {K_{\text{d}}}{c_{\text{p}}}} \right) $$
(3)

where c s is the tracer concentration in the solid phase (M/L3), R m is the bulk (dissolution and precipitation) reaction rate (1/T), also called bulk reaction time constant by DePaolo (2006), K d is the dimensionless distribution coefficient for the solid/fluid system, and M is the mass ratio of solid to liquid, given by:

$$ M = \frac{{{\rho_{\text{s}}}\left( {1 - {\phi_{\text{m}}}} \right)}}{{{\rho_{\text{f}}}{\phi_{\text{m}}}}} $$
(4)

In Eq. (4), ρ f and ρ s are fluid and solid density (M/L3) respectively. In Eq. (2), the terms R m Mc s and R m MK d c p correspond to dissolution and precipitation respectively. When these two terms are equal, dissolution and precipitation are in equilibrium.

For isotopic tracer transport processes with typical R m values, DePaolo (2006) demonstrated that the solid-phase concentration c s hardly changes because of low tracer concentration in the liquid phase in natural fractured rocks. Therefore, he assumed c s to be constant when developing steady-state solutions for tracer transport. This study makes the same assumption, so only Eqs. (1) and (2) need to be solved (as a result of assuming c s to be a constant) for modeling tracer transport in the liquid phase.

For convenience, the following variables can be defined:

$$ {C_{\text{p}}} = {c_{\text{p}}} - \frac{{{c_{\text{s}}}}}{{{K_{\text{d}}}}} $$
(5a)
$$ {C_{\text{f}}} = {c_{\text{f}}} - \frac{{{c_{\text{s}}}}}{{{K_{\text{d}}}}} $$
(5b)
$$ \lambda = {R_{\text{m}}}M{K_{\text{d}}} $$
(5c)

C f and C p can be considered as concentration disturbances to equilibrium concentration fields, because they represent differences between tracer concentrations and their equilibrium values. Note that under equilibrium conditions, C f = C = 0. Combining Eqs. (1), (2) and (5a)–(5c) yields:

$$ \frac{{\partial {C_{\text{f}}}}}{{\partial t}} = - v\frac{{\partial {C_{\text{f}}}}}{{\partial z}} + \frac{{{D_{\text{m}}}{\phi_{\text{m}}}}}{b}{\left\langle {\frac{{\partial {C_{\text{p}}}}}{{\partial x}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} $$
(6)
$$ \frac{{\partial {C_{\text{p}}}}}{{\partial t}} = {D_{\text{m}}}\frac{{{\partial^2}{C_{\text{p}}}}}{{\partial {x^2}}} - \lambda {C_{\text{p}}} $$
(7)

It is of interest to note that the transformed Eqs. (6) and (7) are mathematically equivalent to equations describing tracer transport subject to a decay process (with the decay constant λ) occurring in the matrix block only. As will be demonstrated later, this equivalence is important for obtaining analytical solutions based on existing analytical solutions for tracer transport subject to radioactive decay in fractured rock such as those derived by Tang et al. (1981) and Sudicky and Frind (1982).

Assuming the existence of equilibrium at t = 0 and considering a continuous injection case, initial and boundary conditions for Eq. (6) are as follows:

$$ {C_{\text{f}}}(z,0) = 0 $$
(8a)
$$ {C_{\text{f}}}(0,t) = {C_0} $$
(8b)
$$ {C_{\text{f}}}(\infty, t) = 0 $$
(8c)

Similarly, the initial and boundary conditions for Eq. (7) are:

$$ {C_{\text{p}}}(x,z,0) = 0 $$
(9a)
$$ {C_{\text{p}}}(b,z,t) = {C_{\text{f}}}(z,t) $$
(9b)
$$ \frac{{\partial {C_{\text{p}}}}}{{\partial x}}(B,z,t) = 0 $$
(9c)

where B is half the fracture spacing (Fig. 2). The coupling of the matrix to the fracture is expressed by Eq. (9b). Note that Eq. (9c) applies to multiple-fracture systems; for single-fracture systems, it may be replaced by (Tang et al. 1981):

$$ {C_{\text{p}}}(\infty, z,t) = 0 $$
(9d)

Analytical solutions for a single-fracture system

Although a single-fracture system rarely exists in reality, it is a good approximation for many realistic fractured rocks when tracer penetration depth is much smaller than fracture spacing, because in this case, the effects of surrounding fractures can be ignored. Analytical solutions can be obtained with the strategy used by Tang et al. (1981) and Sudicky and Frind (1982) for developing analytical solutions for radioactive tracer transport in fractured rock. Specifically, Laplace transformation can be applied to Eq. (7), with the transformed equation being solved in Laplace space first, followed by the application of Laplace transformation to Eq. (6). The transformed equations are coupled through the term describing mass transfer between fractures and rock matrix and Eq. (9b). Finally, solutions in the Laplace space are inverted.

Applying Laplace transformation to Eq. (7) yields:

$$ p{C_{\text{p}}}\prime = {D_{\text{m}}}\frac{{{d^2}{C_{\text{p}}}\prime }}{{d{x^2}}} - \lambda {C_{\text{p}}}\prime $$
(10)

where \( {C_{\text{p}}}\prime \) is the Laplace transformation of \( {C_{\text{p}}} \) and given by:

$$ {C_{\text{p}}}\prime = \int\limits_0^{\infty } {\exp ( - pt){C_{\text{p}}}(x,z,t)dt} $$
(11)

Considering the boundary conditions Eqs. (9b) and (9d), the solution to the ordinary differential Eq. (10) is obtained as:

$$ {C_{\text{p}}}\prime = {C_{\text{f}}}\prime \exp \left\{ { - E{P^{{1/2}}}(x - b)} \right\} $$
(12)

where

$$ E = {D_{\text{m}}}^{{ - 1/2}} $$
(13)
$$ P = p + \lambda $$
(14)

and \( {C_{\text{f}}}\prime \) is the Laplace transformation of Cf. Based on Eq. (12):

$$ {\left\langle {\frac{{d{C_{\text{p}}}\prime }}{{dx}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} = - E{P^{{1/2}}}{C_{\text{f}}}\prime $$
(15)

Applying the Laplace transformation to Eq. (6) yields:

$$ p{C_{\text{f}}}\prime + v\frac{{d{C_{\text{f}}}\prime }}{{dz}} = \frac{{{\phi_{\text{m}}}{D_{\text{m}}}}}{b}{\left\langle {\frac{{d{C_{\text{p}}}\prime }}{{dx}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} $$
(16)

Substituting Eq. (15) into Eq. (16), the following solution to Eq. (16) is obtained:

$$ {C_{\text{f}}}\prime = \frac{{{C_0}}}{p}\exp ( - \frac{{pz}}{v})\exp \left( { - \frac{{{P^{{1/2}}}z}}{{vF}}} \right) $$
(17)

where

$$ F = \frac{b}{{{\phi_{\text{m}}}{D_{\text{m}}}^{{1/2}}}} $$
(18)

The original tracer concentrationCf can be given in terms of the inverse transform L−1 as:

$$ {C_{\text{f}}} = {L^{{ - 1}}}({C_{\text{f}}}\prime ) = \exp \left( {\frac{{\lambda z}}{v}} \right){L^{{ - 1}}}\left[ {\exp \left( { - \frac{{\lambda z}}{v}} \right){C_{\text{f}}}\prime } \right] $$
(19)

The inverse transform of the term \( \exp \left( { - \frac{{\lambda z}}{v}} \right){C_{\text{f}}}\prime \), Cr(z,t), was already reported by Tang et al. (1981) in their Eqs. (41) and (42). Taking advantage of this, Cf can be directly obtained by multiplying Cr(z,t) by \( \exp \left( {\frac{{\lambda z}}{v}} \right) \) with the following result:

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = 0\quad T < 0 $$
(20a)
$$ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\frac{{{C_{\text{f}}}}}{{{C_0}}} = \frac{1}{2}[\exp \left( { - \frac{{{\lambda^{{1/2}}}z}}{{vF}}} \right){\text{erfc}}\left( {\frac{z}{{2vFT}} - {\lambda^{{1/2}}}T} \right)} \hfill \\ { + \exp \left( {\frac{{{\lambda^{{1/2}}}z}}{{vF}}} \right){\text{erfc}}\left( {\frac{z}{{2vFT}} + {\lambda^{{1/2}}}T} \right)]} \hfill \\ \end{array} \quad T > 0} \hfill \\ \end{array} $$
(20b)

where

$$ T = {\left( {t - \frac{z}{v}} \right)^{{1/2}}} $$
(20c)

The relation between C f and C r can be interpreted in the following way: C r is the concentration at a location z in the fracture for a tracer with decay constant λ. As previously indicated, C f may also be mathematically viewed as a tracer concentration (in the fracture) associated with decay constant λ, while the decay occurs in the matrix only. Consider two tracer particles that initially have the same mass m 0 and are released from the fracture inlet (z = 0). They have exactly the same transport path. The first one is subject to decay in both the fracture and the matrix, and the second one to decay in the rock matrix only. When they reach a given location z within a fracture, the mass for the first particle will become \( {m_0}\exp \left( { - \lambda \left\langle {{\tau_{\text{m}}} + {\tau_{\text{f}}}} \right\rangle } \right) \), where τm and \( {\tau_{\text{f}}} = \frac{z}{v} \) are particle residence times (T) in matrix and fracture respectively; the mass for the second particle is \( {m_0}\exp \left( { - \lambda {\tau_{\text{m}}}} \right) \). The ratio of the corresponding tracer concentrations is the same as the ratio of the particle masses (i.e., \( \exp \left( { - \frac{{\lambda z}}{v}} \right) \)). However, it should be emphasized that although C f can be mathematically viewed to be subject to decay in the rock matrix, it is the dissolution-precipitation reaction, rather than real decay, that occurs in the rock matrix for the problem under consideration.

To study isotopic tracer transport in fractured rock, DePaolo (2006) introduced a parameter, L, for the diffusive reaction length, given by:

$$ L = {\left( {\frac{{{D_{\text{m}}}}}{\lambda }} \right)^{{1/2}}} $$
(21)

This reaction length (L) has the property that diffusion through the pore fluid is faster than reaction at length scales smaller than L, and reaction is faster than diffusion at length scales greater than L (DePaolo 2006). In some practical applications, it is also often useful to relate tracer concentration signals to fracture surface areas, because the surface areas are important parameters for mass and heat transfer between mobile fluid in fractures and the rock matrix. Under steady-state flow conditions, the conservation equation for fluid volume in fractures is as follows:

$$ Q{\tau_{\text{f}}} = Ab $$
(22)

where Q is the fluid flux in a fracture (L3/T), and A is the fracture surface area (L2). In terms of diffusive reaction length and fracture surface area, Eqs. (20a–20c) can be rewritten as:

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = 0\quad T < 0 $$
(23a)
$$ \begin{array}{*{20}{c}} {\frac{{{C_{\text{f}}}}}{{{C_0}}} = \frac{1}{2}[\exp \left( { - \frac{{A{D_{\text{m}}}{\phi_{\text{m}}}}}{{LQ}}} \right){\text{erfc}}\left( {\frac{{AD{{{}_{\text{m}}}^{{1/2}}}{\phi_{\text{m}}}}}{{2QT}} - \frac{{{D_{\text{m}}}^{{1/2}}}}{L}T} \right)} \hfill \\ { + \exp \left( {\frac{{A{D_{\text{m}}}{\phi_{\text{m}}}}}{{LQ}}} \right){\text{erfc}}\left( {\frac{{AD{{{}_{\text{m}}}^{{1/2}}}{\phi_{\text{m}}}}}{{2QT}} + \frac{{{D_{\text{m}}}^{{1/2}}}}{L}T} \right)]} \hfill \\ \end{array} \quad T > 0 $$
(23b)

Using the properties of \( {\text{erfc}}\left( \infty \right) = 0 \) and \( {\text{erfc}}\left( { - \infty } \right) = 2 \), the steady-state solution can be easily obtained by taking the limit \( T \to \infty \):

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = \exp \left( { - \frac{{{\lambda^{{1/2}}}z}}{{vF}}} \right) = \exp \left( { - \frac{{A{D_{\text{m}}}{\phi_{\text{m}}}}}{{LQ}}} \right) $$
(24)

Analytical solutions for a multiple-fracture system

In the previous section, analytical solutions were derived for a single-fracture system, which is a good approximation of many realistic fractured rocks when the tracer transport within a fracture does not significantly interact with tracer transport in surrounding fractures. However, for relatively small fracture spacing and/or long tracer travel times, interactions between adjacent fractures become important. In this case, solutions for multiple-fracture systems are needed for modeling tracer transport in fractured rock. A similar procedure for solving the tracer transport problem in a single fracture system is followed here for a multiple-fracture system. Also note that governing equations are the same for both fracture systems, except for some boundary conditions.

The transformed tracer transport equation for rock matrix is solved first. The general solution to the transformed Eq. (10) is of the form (Sudicky and Frind 1982):

$$ {C_{{\text{p}}}}\prime = {C_{1}}\cosh \left[ { - E{P^{{1/2}}}(B - x)} \right] + {C_{2}}\sinh \left[ { - E{P^{{1/2}}}(B - x)} \right] $$
(25)

where C 1 and C 2 are constants. Based on the boundary condition Eq. (9a), it is found that \( {C_2} = 0 \). Using the boundary condition Eq. (9b), C1 is obtained, and Eq. (25) becomes:

$$ {C_{{\text{p}}}}\prime = {C_{{\text{f}}}}\prime \frac{{\cosh \left[ {E{P^{{1/2}}}(B - x)} \right]}}{{\cosh \left[ {\sigma {P^{{1/2}}}} \right]}} $$
(26)

where again \( {C_{\text{f}}}\prime \) is the Laplace transformation of C f and

$$ \sigma = E(B - b) $$
(27)

The coupling between transformed tracer transport equations for the fractures and the rock matrix is achieved through the concentration gradient term in Eq. (16). In this case, that coupling term is:

$$ {\left\langle {\frac{{d{C_{\text{p}}}\prime }}{{dx}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} = - E{P^{{1/2}}}{C_{\text{f}}}\prime \tanh \left( {\sigma {P^{{1/2}}}} \right) $$
(28)

Then the transformed equation for tracer transport in fractures (Eq. 16) becomes:

$$ p{C_{\text{f}}}\prime + v\frac{{d{C_{\text{f}}}\prime }}{{dz}} = - \frac{{{\phi_{\text{m}}}{D_{\text{m}}}}}{b}E{P^{{1/2}}}\tanh \left( {\sigma {P^{{1/2}}}} \right){C_{\text{f}}}\prime $$
(29)

The solution to Eq. (29), subject to the boundary condition Eq. (8b) is:

$$ {C_{{\text{f}}}}\prime = \frac{{{C_{0}}}}{p}\exp \left[ { - \frac{{pz}}{v}} \right]\exp \left[ { - \omega {P^{{1/2}}}\tanh \left[ {\sigma {P^{{1/2}}}} \right]} \right] $$
(30)

where

$$ \omega = \frac{{{\phi_{\text{m}}}{D_{\text{m}}}^{{1/2}}z}}{{bv}} $$
(31)

The original tracer concentration C f can be determined by the inverse transform of C f′. The inverse transform of \( {C_{\text{f}}}\prime \exp \left( { - \frac{{\lambda z}}{v}} \right) \) has already been derived by Sudicky and Frind (1982). Thus, C f can be easily determined as the inverse transform of Sudicky and Frind (1982) multiplied by \( \exp \left( {\frac{{\lambda z}}{v}} \right) \):

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = 0\quad {T^0} < 0 $$
(32a)
$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = \frac{1}{\pi }\exp \left( {\frac{{2\lambda z}}{v}} \right)\int\limits_0^{\infty } {Id\varepsilon } \quad {T^0} > 0 $$
(32b)

where

$$ I = \frac{\varepsilon }{{{\lambda^2} + {\varepsilon^4}/4}}\exp \left( {{\varepsilon_R}^0} \right)\left\{ {\exp \left( { - \lambda {T^0}} \right)\left[ {\frac{{{\varepsilon^2}}}{2}\sin \left( {{\varepsilon_I}^0} \right) - \lambda \cos \left( {{\varepsilon_I}^0} \right)} \right] + \frac{{{\varepsilon^2}}}{2}\sin \left( {{\Omega^0}} \right) + \lambda \cos \left( {{\Omega^0}} \right)} \right\} $$
(32c)
$$ {\varepsilon _{R}}^{0} = - \frac{{\omega \varepsilon }}{2}\left[ {\frac{{\sinh (\sigma \varepsilon ) - \sin (\sigma \varepsilon )}}{{\cosh (\sigma \varepsilon ) + \cos (\sigma \varepsilon )}}} \right] $$
(32d)
$$ {\varepsilon _{I}}^{0} = \frac{{{\varepsilon ^{2}}{T^{0}}}}{2} - \frac{{\omega \varepsilon }}{2}\left[ {\frac{{\sinh (\sigma \varepsilon ) + \sin (\sigma \varepsilon )}}{{\cosh (\sigma \varepsilon ) + \cos (\sigma \varepsilon )}}} \right] $$
(32e)
$$ {\Omega ^{0}} = - \frac{{\omega \varepsilon }}{2}\left[ {\frac{{\sinh (\sigma \varepsilon ) + \sin (\sigma \varepsilon )}}{{\cosh (\sigma \varepsilon ) + \cos (\sigma \varepsilon )}}} \right] $$
(32f)
$$ {T^0} = t - \frac{z}{v} $$
(32g)

Similarly to the analytical solutions for the single-fracture system as discussed in the previous section, Eqs. (32a–32g) can also be written in terms of diffusive reaction length defined in Eq. (21), fracture surface area A and liquid flux Q. In this case:

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = 0\quad {T^0} < 0 $$
(33a)
$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = \frac{1}{\pi }\exp \left( {\frac{{2A{D_{\text{m}}}^2b}}{{{L^2}Q}}} \right)\int\limits_0^{\infty } {Id\varepsilon } \quad {T^0} > 0 $$
(33b)
$$ \omega = \frac{{{\phi_{\text{m}}}{D^{{1/2}}}A}}{Q} $$
(33c)
$$ {T^0} = t - \frac{{Ab}}{Q} $$
(33d)

It is not straightforward to derive steady-state solutions from Eqs. (32a–32g) or Eqs. (33a–33d), because these transient solutions involve an integration from 0 to ∞. An alternative way to derive steady-state solutions is to directly use governing Eqs. (6) and (7) for tracer transport. While DePaolo (2006) obtained steady-state solutions for a multiple-fracture system in terms of both Laplace transform and Fourier series representation, this paper offers a more straightforward approach for their derivation.

Under steady-state conditions, Eq. (7) becomes:

$$ \frac{{{d^2}{C_{\text{p}}}}}{{d{y^2}}} = \frac{{{C_{\text{p}}}}}{{{L^2}}} $$
(34)

where

$$ y = x - b $$
(35)

The solution to Eq. (34) is of the form:

$$ {C_{\text{p}}} = {C_1}\prime \exp (\frac{y}{L}) + {C_2}\prime \exp ( - \frac{y}{L}) $$
(36)

The constants, C 1′ and C 2′, are obtained by substituting boundary conditions defined in Eqs. (9a) and (9c) into the Eq. (36), which then becomes:

$$ \frac{{{C_{\text{p}}}}}{{{C_{\text{f}}}}} = \frac{{\exp (\frac{y}{L}) + \exp (\frac{{B - b - y}}{L})}}{{1 + \exp (\frac{{B - b}}{L})}} $$
(37)

The (matrix) tracer concentration gradient at the fracture wall can be expressed as:

$$ {\left\langle {\frac{{\partial {C_{\text{p}}}}}{{\partial y}}} \right\rangle_{{{\text{y}} = 0}}} = {\left\langle {\frac{{\partial {C_{\text{p}}}}}{{\partial x}}} \right\rangle_{{{\text{x}} = {\text{b}}}}} = - \frac{{{C_f}}}{L}\left[ {\frac{{\exp (\frac{{B - b}}{L}) - 1}}{{\exp (\frac{{B - b}}{L}) + 1}}} \right] $$
(38)

Substituting the aforementioned equation into the steady-state version of Eq. (6), for tracer transport in fractures, yields:

$$ v\frac{{dC{}_{\text{f}}}}{{dz}} = - \frac{{{D_{\text{m}}}{\phi_{\text{m}}}{C_{\text{f}}}}}{{bL}}\left[ {\frac{{\exp (\frac{{B - b}}{L}) - 1}}{{\exp (\frac{{B - b}}{L}) + 1}}} \right] $$
(39)

The solution to the preceding equation, subject to the boundary condition defined by Eq. (9a), is:

$$ \frac{{{C_{\text{f}}}}}{{{C_0}}} = \exp \left\{ { - \frac{{{D_{\text{m}}}{\phi_{\text{m}}}z}}{{bvL}}\left[ {\frac{{\exp \left( {\frac{{B - b}}{L}} \right) - 1}}{{\exp \left( {\frac{{B - b}}{L}} \right) + 1}}} \right]} \right\} = \exp \left\{ { - \frac{{{\lambda^{{1/2}}}z}}{{Fv}}\left[ {\frac{{\exp \left( {\frac{{B - b}}{L}} \right) - 1}}{{\exp \left( {\frac{{B - b}}{L}} \right) + 1}}} \right]} \right\} $$
(40)

Equation (40) is the same as the steady-state analytical solution derived by DePaolo (2006). As expected, for \( B \to \infty \), Eq. (40) is reduced to Eq. (24), which gives the steady-state solution for a single-fracture system.

Illustrative examples

Analytical solutions for a single-fracture system and a multiple-fracture system are presented in sections Analytical solutions for a single-fracture system and Analytical solutions for a multiple-fracture system. As previously indicated, the focus is on solutions to tracer transport in fractures, because tracer concentration data are often obtained from fractures in practical applications (Neretnieks 2002; DePaolo 2006). Analyses of these tracer data are generally used to understand flow and transport processes in fractured rock and to infer values of important parameters characterizing the relevant processes, including fracture-matrix interaction.

As previously indicated, the current study is mainly motivated by a practical need to characterize a geothermal system in an artificially fractured reservoir using tracers with different transport properties. A key parameter for determining the economic feasibility of a geothermal system is the fracture-matrix interfacial area. In this section, the newly developed analytical solutions are used to demonstrate how sensitive tracer transport processes are to fracture-rock properties. The sensitivity is crucial for successful determination of reservoir properties by analyzing data for natural tracers. Note that parameter values used in this section are typical for a geothermal system in fractured rocks; it may not be the case for other flow and transport systems.

To evaluate analytical solutions for a multiple-fracture system, numerical integration is needed over an interval between 0 and ∞ (Eqs. 32a–32g). As indicated by Sudicky and Frind (1982), although the upper limit of the integration extends to infinity, the numerically significant portion of the integrand extends over a much smaller range. They also suggested using a scanning procedure prior to integration to calculate the numerically significant range. In this study, the range was defined by \( \exp \left( {{\varepsilon_R}^0} \right) \geqslant \exp ( - 20) \). Beyond that range, values for function I (Eqs. 32a–32g) are extremely small and can therefore be ignored. This can be justified based on the fact that for large ε values, Eq. (32c) leads to \( I \to \frac{2}{\varepsilon }\exp (\varepsilon_R^0)[\exp ( - \lambda {T_0})\sin (\varepsilon_1^0) + \sin ({\Omega^0})] \). Thus, the magnitude of function I is largely determined by \( \exp (\varepsilon_R^0) \) for large ε values. Within the numerically significant range, the relatively robust Euler integration algorithm was employed. Typically, about several hundred to a couple of thousand subintervals are needed to get satisfactory and oscillation-free results. In this study, 5,000 subintervals were used for evaluating analytical solutions to tracer transport in a multiple-fracture system.

The parameter values used in the illustrative examples are shown in Table 1. They are within the ranges given in DePaolo (2006) for studying isotopic tracer transport in a number of typical geothermal systems, and are used for the purpose of demonstrating the usefulness of the analytical solutions for a geothermal system.

Table 1 Parameter values used in illustrative examples
Full size table

Figure 3 shows tracer breakthrough curves for multiple-fracture systems with half-fracture spacing B = 2.0 and 0.5 m. The relative concentration in this figure and other figures is defined as \( \frac{{{C_f}}}{{{C_0}}} \). For the purposes of comparison, a breakthrough curve for a single fracture system is also presented. All these breakthrough curves were obtained using the parameter values given in Table 1. For B = 2.0 m, results from the single-fracture system (with infinite fracture spacing) and the multiple-fracture system are essentially identical, indicating that for a relatively large fracture spacing, the impact of surrounding fractures can be ignored, as expected. This also demonstrates the consistency of the analytical solutions obtained for the two systems. For a travel time less than 1 year, all the breakthrough curves remain essentially the same, because tracer penetration depth during this time period is much smaller than the given values for fracture spacing, and therefore the tracer transport process is close to that for the single-fracture case. For a travel time longer than one year, the tracer concentration for B = 0.5 m becomes larger than that for B = 2.0 m, because the interaction between tracer transport from adjacent fractures reduces diffusive transport from the fractures into the rock matrix.

Fig. 3
figure 3

Breakthrough curves for a single-fracture system and a multiple-fracture system with half-fracture spacing B = 2.0 and 0.5 m

Full size image

Figure 4 presents tracer breakthrough curves for a single-fracture system with two different L values (see Eq. 21). The base case corresponds to parameter values given at the beginning of this section; the other curve was obtained by using an L value reduced by half (or a λ value that is 4 times as large as the base-case value). The two curves are very similar at an early time, but become considerably different later. The base case has a smaller λ value, and therefore a higher concentration at late travel times. This example demonstrates how useful it is to view the effects of precipitation-dissolution reactions as a “decay” process with a decay constant λ that is proportional to the bulk reactivity in the matrix (Eq. 5c). The differences between the two curves in Fig. 4 result from the fact that tracer mass loss owing to “decay” is time-dependent and becomes significant only for relatively long travel times.

Fig. 4
figure 4

Breakthrough curves for a single-fracture system with different L values. For the “Decreased L” case, L is reduced by half from the value used in the base case

Full size image

Figure 5 shows breakthrough curves for a single-fracture system with different values for matrix diffusion coefficient D m. The base case and the “Increased D m” case (green dashed line) use the same parameter values (from Table 1) with the exception that the latter has a D m value that is four times as large as the base case. As expected, a large diffusion coefficient gives a relatively low concentration at any given time. This is because a larger matrix diffusion coefficient increases diffusive tracer transfer between a fracture and its surrounding matrix. An increased fracture-matrix surface area would play a similar role. Figure 5 also shows a third breakthrough curve that has the same (increased) D m value as the green dashed line, but with an increased λ value such that its L value is the same as the base case. The difference between the two “Increased D m” cases is similar to the difference between the two curves shown in Fig. 4, as a result of the effects of “decay” processes with different λ values.

Fig. 5
figure 5

Breakthrough curves for a single-fracture system with different D m values. In the “Increased Dm” case, the D m value is four times as large as that in the base case

Full size image

In summary, the illustrative examples show that results are considerably sensitive to rock and tracer properties for the parameter values typical for a geothermal system (DePaolo 2006), indicating that the relevant flow and transport parameters for a geothermal reservoir may be estimated by analyzing tracer signals. It should also be emphasized that the analytical solutions were developed based on several assumptions and approximations, one of which is that change in tracer concentration of the solid phase is not significant. The validity of this approximation for isotopic tracer transport was demonstrated in DePaolo (2006). Most recently, Mukhopadhyay et al. (2010) developed a semi-analytical solution that is not constrained by the constant c s assumption. In that case, they were not able to obtain closed-form solutions, but instead numerically performed the inverse of Laplace transformations. As indicated in Fig. 6, results from their solutions are identical to those obtained from the analytical solutions in this paper for small reaction rates that are typical for natural isotopic tracers, which is consistent with the finding of DePaolo (2006).

Fig. 6
figure 6

Comparisons between simulation results obtained from the current analytical solutions and semi-analytical solutions in Mukhopadhyay et al. (2010). Parameter values from Table 1 and B = 0.5 m are used for all the simulations except R m, which is varied

Full size image

Conclusions

While significant progress has been made in developing analytical solutions for tracer transport in fractured rock under a variety of conditions, analytical solutions for tracer transport associated with precipitation-dissolution reactions are limited in the literature. These reactions are important for a number of applications such as isotopic tracer transport in the subsurface.

This study develops analytical solutions for tracer transport in both a single-fracture and a multiple-fracture system associated with precipitation-dissolution reactions under transient and steady-state transport conditions. These solutions also take into account advective transport in fractures and molecular diffusion in the rock matrix. It has been demonstrated that for studying distributions of disturbed tracer concentration (defined as the difference between the actual concentration and its equilibrium value), the effects of precipitation-dissolution reactions are mathematically equivalent to a “decay” process with a decay constant proportional to the corresponding bulk reaction rate. This important finding significantly simplifies the derivation procedure by taking advantage of the existence of analytical solutions to tracer transport associated with radioactive decay in fractured rock. It is also useful for interpreting tracer breakthrough curves, because the impact of a decay process is relatively easy to analyze. Several illustrative examples (breakthrough curves obtained from analytical solutions) have been presented, which show that the results are considerably sensitive to fracture spacing, matrix-diffusion coefficient (fracture surface area), and bulk reaction rate (or “decay” constant), indicating that the relevant flow and transport parameters may be estimated by analyzing tracer signals.