Introduction

Seawater intrusion is a common problem in coastal aquifers. Density differences between freshwater and seawater together with intense pumping cause seawater to intrude inland along the aquifer bottom. The problem is especially severe in arid and semi-arid zones where alternative water resources are scarce. In such cases, corrective measures are needed to restore groundwater quality and optimally manage the aquifer. However, it is not easy to select the optimal corrective measures to control seawater intrusion because their feasibility and impact depend on the hydraulic and geometric characteristics of the aquifer and on the management structure (Post 2005). Consequently, mitigating seawater intrusion continues to be a challenge.

The most simple and cost-effective measures for seawater intrusion are designed to improve the groundwater balance in an effort to keep heads high. This may be achieved by reducing pumping rates or relocating pumping fields to zones that are less susceptible to intrusion (Sherif 1999). This can also be achieved by artificial recharge, adding water to an aquifer through man-made systems including infiltration basins, canals and recharge ponds (Li et al. 1987; Reichard 1995). One special case is the aquifer storage and recovery (ASR) approach, which consists of injecting freshwater into the aquifer to recover essentially the same water without the need for additional treatment. This approach could be used to set up a hydraulic saltwater intrusion barrier (Misut and Voss 2007). Limiting pumping to the shallowest portions of the aquifer is a good method to redress the hydraulic balance and minimize drawdowns. Although these measures are the most simple, they are not always easy to implement because (1) wells are already drilled and drilling new (shallower) ones is expensive, (2) other water sources or space are not available and (3) implementation of these measures requires a strong management infrastructure.

One attractive solution is to design seawater barriers that prevent seawater from flowing inland, thereby protecting groundwater pumping zones. Different types of barrier designs can be considered. Generally speaking, “positive” indicates a source of fluid to the aquifer. This is true conceptually (heads rise and water resources are increased) and in models and equations (a negative flow often represents an outflow). This terminology is therefore proposed to classify the barriers into four types: low permeability subsurface, positive, negative and mixed.

  • Low permeability subsurface barriers (Fig. 1a) consist of vertical walls (slurry walls, steel or concrete sheet piles) placed inland to block seawater intrusion, (Sugio et al. 1987). This system requires considerable engineering and investment. Moreover, it may be counterproductive if pumping stops or sources of contamination exist (Bolster et al. 2007).

  • Positive hydraulic barriers (Fig. 1b) inject water into the aquifer, which raises the piezometric head, thus preventing saltwater from flowing inland (Bray and Yeh 2008). It is often argued that positive barriers are inefficient because they inject freshwater into the ocean. This is not necessarily the case. Abarca et al. (2006) demonstrated that their efficiency is greater than that belief (i.e., the allowable increase in inland pumping exceeds the recharged flow rate) because they not only increase available resources but also protect inland wells. The main disadvantages of this corrective measure are the need for high-quality water whenever injection is undertaken through wells and the need for space if recharge through basins is necessary. These corrective barriers also require considerable maintenance to control clogging.

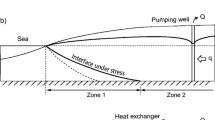
  • Negative hydraulic barriers (Fig. 1c) pump near the shore, thus intercepting inflowing saltwater (Todd 1980). Seawater intrusion is impeded as long as the barrier pumps. In practice, this system is often applied with minimum or no planning. It is common knowledge that inland wells are protected by coastal wells. Inland well owners are prepared to go to great lengths to keep coastal wells pumping. However, these barriers often end up pumping much more freshwater than saltwater, leading to a mixing of freshwater with seawater at the wells and to a reduction in freshwater resources. Nevertheless, negative barriers may be the only possible corrective measures to prevent seawater intrusion in aquifers where the water level cannot be raised. They may also be used to feed desalinization plants.

  • Mixed barriers (Fig. 1d) are injection-pumping systems. Such a system may be used to inject freshwater at shallow depths while pumping saltwater at depth, which makes sense only in thick aquifers and/or in vertically anisotropic systems. Corrective measures may also be used to pump at locations of the aquifer that are well connected to the sea while injecting at locations that are well connected to the land. Therefore, a well-designed mixed barrier is much more sensitive to a good hydraulic characterization than other barrier systems.

Fig. 1
figure 1

Types of barriers to control seawater intrusion: a low permeability subsurface barrier, b positive hydraulic barrier, c negative hydraulic barrier, d mixed barrier (injection-pumping system)

Full size image

Specific methods have been developed for a range of specific problems. In this regard, Van Dam (1999) proposed scavenger wells as a technique to control the position of the interface and prevent upconing when simultaneously pumping freshwater and seawater. Scavenger wells consist of wells near freshwater pumping wells with screens open in the saline groundwater at some depth below the freshwater and seawater interface. This author evaluated the depth of the interface in terms of the pumping rates. Scavenger wells require careful monitoring and are only effective in very thick aquifers.

The study reported here was prompted by seawater intrusion in the Mar del Plata aquifer, Argentina (Bocanegra et al. 2001), where deep pumping is necessary for groundwater supplies because of contaminated sources. Moreover, water levels cannot be raised given the susceptibility of underground urban infrastructures to flooding. This problem occurs in many cities (Vázquez-Suñé et al. 2005). Negative barriers are therefore the only solution to prevent seawater intrusion.

There are few papers on negative barriers. Sherif and Hamza (2001) demonstrated qualitatively that seawater intrusion may be controlled by pumping brackish water from the dispersion zone. These authors used an ideal two-dimensional (2D) leaky aquifer to evaluate the effect of pumping brackish water on the width of the mixing zone. However, the loss of freshwater in the well was considerable.

The present paper addresses the loss of freshwater through mixing at the negative barrier. To minimize this loss, a double pumping barrier system with two extraction wells (Fig. 2) is proposed. One of the wells, the “freshwater well”, is designed to pump freshwater while the other, the “seawater well”, pumps mostly seawater. A vertical cross section (see Fig. 2) suggests little flow between the two wells. In fact, Kacimov et al. (2008) used vertical two-dimensional cross-section simulations to study the possibility of restoring groundwater quality in coastal aquifers by pumping freshwater and seawater from the vicinity of the shoreline. These authors demonstrated that a zone of reduced velocity was created between the pumping strips and that the intrusion was mainly restricted to the area between the sea boundary and the saline groundwater pumping field protecting the freshwater pumping. Unfortunately, the vertical cross section approach is only valid when pumping wells are closely spaced with respect to their distance from the coast. Otherwise, the flow system is complex and fully three dimensional.

Fig. 2
figure 2

Schematic description of a double pumping barrier. Ideally, groundwater flux is low between the two wells

Full size image

The aim of the present work is to elucidate the dynamics of double pumping barriers and to assess to what extent the three dimensionality of the flux compromises the efficiency of the system. Efficiency is assessed here by the pumping rate at the seawater well needed to reach a minimum salinity at the freshwater well. The evolution of seawater intrusion in an ideal system is analyzed in order to identify the optimal location and pumping rates in the system applied, protect freshwater wells and control seawater intrusion. Using this approach the problem is formulated in a dimensionless form and empirical expressions for the controlling variables are obtained.

Dynamics of double pumping barriers

A methodology based on numerical three-dimensional simulations is employed to evaluate the dynamics of double pumping barriers.

Problem description

A homogeneous confined coastal aquifer with constant thickness b is considered. The system consists of lines of fully penetrating freshwater-seawater wells along the coast separated by a distance of 2L c (Fig. 3). Because of the symmetry, only a coastal portion of length L c is simulated (Fig. 3). A constant flow rate (Q p = 648 m 3/d) of freshwater (with salt mass fraction equal to ω = 0 kg/kg) is imposed along the inland boundary. Pressure p is prescribed along the seaside boundary (p = ρ s gz, where ρ s is density of the seawater, g is the magnitude of the gravitational acceleration vector and z is the elevation).

Fig. 3
figure 3

Plan view of the double negative barrier system, vertical cross-sections and model domain. Note that only the AB–A’B’ region needs to be modeled because of symmetry

Full size image

A non-dispersion boundary condition is adopted for transport along the coastal boundary. This implies that salt mass fraction equals either that of seawater (ω s = 0.0386 kg/kg) for inflowing portions of the boundary or that of the resident mass fraction for outflowing portions of the boundary (Voss and Souza 1987; Frind 1982). The remaining boundaries are closed to flow and solute transport.

Flow and transport parameters used for the selected model are as follows: freshwater hydraulic conductivity k = 10.6 m/d, porosity ϕ = 0.25, dimensionless density difference ε = 0.027 (ε is given by \( \varepsilon = \left( {{\rho_{\text{s}}} - {\rho_{\text{f}}}} \right)/\left( {{\rho_{\text{f}}}} \right) \) with ρ f being density of the freshwater), longitudinal dispersivity α L = 10 m, transverse dispersivity α T = 1 m, molecular diffusion coefficient D m = 10−9 m2/s, freshwater viscosity μ = 0.001 kg/ms, aquifer thickness b = 50 m, the width of model domain L c = 500 m and the freshwater well, located at a distance of L f = 300 m from the sea , pumps Q f = 400 m3/d (here and below pumping rates refer to what is pumped from the model domain, which is effectively half of the total pumping rate). Modeling seawater intrusion requires the flow and transport equations to be coupled through water density, giving a set of two coupled non-linear equations. Computer simulations were performed with SUTRA (Voss and Provost 2002).

Modeling methodology and results

The simulations are carried out following a two-step sequence. The first step simulates a typical coastal well salinization. A well pumps freshwater (Q f) at a distance L f from the sea. Salinity of pumped water rises gradually to steady state I. The second step constitutes a double pumping barrier solution to the problem. Using the end of step 1 as the initial condition, a seawater well starts pumping (Q s) at a distance L s from the sea, until steady state II is reached.

The resulting evolution of salinity at the freshwater well (ω f/ω s) is displayed in Fig. 4. At first, the system appears to be effective. Pumping the seawater well causes salinity to fall sharply at the freshwater well. The efficiency of the system remains high for a short period (several years with the parameters adopted here), but the situation is transient. After a relatively short period (3–5 years), salinity at the freshwater well increases again to reach steady state II. Figure 4 shows the two most remarkable features of the double negative barrier: first, an immediate fall in salinity after installation of the seawater well is followed by recovery with the result that the long-term efficiency of the system is poor; second, the long-term behavior is sensitive to the barrier flow rate. These two features are discussed in the following.

Fig. 4
figure 4

Temporal evolution of seawater fraction at the freshwater well for different pumping rates at the seawater well located at 90 m from the coastal boundary. The first steady state represents a typical coastal well salinization. The seawater well starts pumping Qs after this steady state, which causes an immediate drop in salinity but eventually leads to steady-state II

Full size image

The evolution of salinization is displayed in Fig. 5. In stage 1 the freshwater well becomes salinized in the absence of the seawater well. Salinization occurs at the bottom because freshwater floats on top of saltwater (the well is fully penetrating). When the seawater well is activated, groundwater fluxes around the freshwater well drift seawards as does the seawater at the bottom of the freshwater well, which becomes significantly desalinized (Fig. 5, stage 2). However, as shown in Fig. 5, stage 3, the drawdown generated by both wells causes the toe to penetrate further inland along the boundary (i.e. between seawater wells, B–B’, as displayed in Fig. 3). As a result, seawater flows laterally towards the freshwater well along the bottom of the aquifer. It should be noted that this mechanism is a 3D effect, resulting from buoyancy forces, which would not show up in vertically integrated (2D areal) fluxes. At any rate, the higher the pumping rate at the seawater well, the greater the desalinization in stage 2 and the greater the lateral flow from the sea to the freshwater well. The salt mass fraction eventually increases at the freshwater well when the pumping rate at the seawater well intensifies. Therefore, the critical pumping rate at the seawater well (Q c/Q f) is defined as that which yields the lowest salt mass fraction at the freshwater well (ω m/ω s).

Fig. 5
figure 5

Three-dimensional dynamics of the double negative barrier. Concentration maps (same color scale as Fig. 3) and velocity vectors at the top and bottom of the aquifer for two different pumping rates at the seawater well. A fully penetrating well is salinized from the aquifer bottom (stage 1, above). When the seawater well is activated, salinity falls sharply at the freshwater well, especially when the barrier pumping rate is high (stage 2). However, drawdown generated by both wells causes seawater to flow towards the freshwater well at depth (stage 3). Note that the seawater well still draws some freshwater from the top portion of the aquifer at this stage

Full size image

The location of the seawater well considerably affects the critical pumping rate value (Fig. 6). As the distance of the seawater well from the sea decreases (from 150 m to 20 m), both the value of the critical pumping rate and the desalinization level increase. Note that the landward relocation of the seawater well at some distance from the shoreline allows one to reduce the pumping rate at the seawater well despite diminishing desalinization efficiency.

Fig. 6
figure 6

Salt mass fraction at the freshwater well during steady state II versus pumping rate at the seawater well for five distances of the seawater well from the coastal boundary (L s /L c  = 0.3, 0.18, 0.14, 0.08 and 0.04 m). The critical pumping rate at the seawater well (Q c /Q f ) is the one that causes minimum salinity at the freshwater well (ω m /ω s )

Full size image

Sensitivity analysis

A sensitivity analysis is carried out to describe the behavior of the critical pumping rate at the seawater well and the minimum value of the salt mass fraction at the freshwater well. The system is defined in terms of dimensionless numbers.

Dimensionless form of the governing equations

The governing equations are recast in a dimensionless form to obtain the dimensionless numbers that describe the behavior of the system. A Cartesian x,y,z coordinate system is adopted, where the z axis points vertically upwards. The dimensionless coordinates x′, y′ and z′ are defined in terms of the width of model domain L c (see Fig. 3).

$$ x\prime = \frac{x}{{{L_{\text{c}}}}},y\prime = \frac{y}{{{L_{\text{c}}}}},z\prime = \frac{z}{{{L_{\text{c}}}}}, $$
(1)

The dimensionless form of the distances of the freshwater well (L f) and the seawater well (L s) from the sea, and the thickness of the aquifer become

$$ L_{\text{s}}^\prime = \frac{{{L_{\text{s}}}}}{{{L_{\text{c}}}}},L_{\text{f}}^\prime = \frac{{{L_{\text{f}}}}}{{{L_{\text{c}}}}},b\prime = \frac{b}{{{L_{\text{c}}}}} $$
(2)

Darcy’s velocity, density, salt mass fraction and freshwater head are written in a dimensionless form with respect to the constant freshwater flux from inland (q p), the seawater density (ρ s), the seawater salt mass fraction (ω s) and a characteristic equivalent freshwater head, respectively

$$ {{\bf{q}}}\prime = \frac{{{\bf{q}}}}{{{q_{\text{p}}}}},\rho \prime = \frac{\rho }{{{\rho_{\text{s}}}}},\omega \prime = \frac{\omega }{{{\omega_{\text{s}}}}},h\prime = \frac{{h{k_{\text{y}}}}}{{{L_{\text{c}}}{q_{\text{p}}}}} $$
(3)

Note that ω′, the dimensionless salt mass fraction, can be viewed as the proportion of seawater. The flow dimensionless numbers are defined as follows

$$ a = \frac{{{q_{\text{d}}}}}{{\varepsilon {K_{\text{z}}}}},{r_{{\text{k}}1}} = \frac{{{K_{\text{x}}}}}{{{K_{\text{y}}}}},{r_{{\text{k}}2}} = \frac{{{K_{\text{z}}}}}{{{K_{\text{y}}}}} $$
(4)

where ε is given by \( \varepsilon = \left( {{\rho_{\text{s}}} - {\rho_{\text{f}}}} \right)/{\rho_{\text{f}}} \) with ρ f and ρ s the freshwater and seawater densities, respectively.

Here, a is the ratio of the freshwater flux to the characteristic buoyancy flux, and r k1 and r k2 are the hydraulic conductivity anisotropy ratios.

According to these definitions, the dimensionless form of the fluid mass balance equation in steady state (e.g., Bear 1972) including the pumping rates of freshwater and seawater wells reads as

$$ - \rho \prime \left( {{r_{{\text{k}}1}}\frac{{{\partial^2}h\prime }}{{\partial x{\prime^2}}} + \frac{{{\partial^2}h\prime }}{{\partial y{\prime^2}}} + {r_{{\text{k}}2}}\frac{{{\partial^2}h\prime }}{{\partial z{\prime^2}}} + \frac{1}{a}\frac{{\partial \omega \prime }}{{\partial z\prime }}} \right) - {{\bf{q}}}\prime \nabla \prime \rho \prime = \rho {\prime^* }Q_{\text{f}}^\prime \delta \prime \left( {x - {x_{\text{f}}},0} \right)f_{\text{f}}^\prime (z) + \rho {\prime^* }Q_{\text{s}}^\prime \delta \prime \left( {x - {x_{\text{s}}},0} \right)f_s^\prime (z) $$
(5)

where ρ′* is the dimensionless density of the incoming water through the source term, ∇′ expresses the dimensionless form of the del operator, the Dirac’s delta δ′ represents the dimensionless location of the wells and the dimensionless functions \( f_{\text{f}}^\prime (z) \) and \( f_{\text{s}}^\prime (z) \) express the vertical distribution of extraction, assumed to be uniform here. They are zero, except in the portion of the aquifer thickness where the wells are pumping. The dimensionless form of the pumping rates \( Q_{\text{f}}^\prime \) and \( Q_{\text{s}}^\prime \) are defined as the ratio of the pumping rates of the wells to the discharge flowing into the sea

$$ Q_{\text{f}}^\prime = \frac{{{Q_{\text{f}}}}}{{{q_{\text{p}}}{L_{\text{c}}}b}},Q_{\text{s}}^\prime = \frac{{{Q_{\text{s}}}}}{{{q_{\text{p}}}{L_{\text{c}}}b}} $$
(6)

The dimensionless form of the boundary conditions along inland and coastal boundaries becomes

$$ {\left. {\frac{{\partial h\prime }}{{\partial y\prime }}} \right|_{_{y\prime = \frac{{{L_{\text{y}}}}}{{{L_{\text{c}}}}}}}} = - 1\quad {\left. {h\prime } \right|_{{\text{x}}\prime = 0}} = \frac{1}{{a\,{r_{{\text{k}}2}}}}z\prime $$
(7)

As regards the transport equation, Peclet numbers were chosen as dimensionless parameters. They describe the relative importance of advective and diffusive transport mechanisms.

$$ {b_{\text{m}}} = \frac{{{D_{\text{m}}}\phi }}{{{q_{\text{d}}}{L_{\text{c}}}}},{b_{\text{T}}} = \frac{{{\alpha_{\text{T}}}}}{{{L_{\text{c}}}}} $$
(8)

where ϕ is porosity, D m the molecular diffusion coefficient and α T is the transverse dispersivity [L].

The dispersivity anisotropy ratio is also proposed as a dimensionless parameter.

This leads to the dimensionless form of the salt mass conservation in steady state as

$$ \nabla \prime \left( {\rho \prime \omega \prime {{\bf{q}}}\prime } \right) - \nabla \prime \left\{ {\rho \prime \left( {{b_{\text{T}}}{{\bf{D}}}\prime + {b_{\text{m}}}{{\bf{I}}}} \right)\nabla \prime \omega \prime } \right\} = + \rho \prime \omega \prime Q_{\text{f}}^\prime \;\delta \prime \left( {x - {x_{\text{f}}},0} \right)f_{\text{f}}^\prime (z) + \rho \prime \omega \prime Q_{\text{s}}^\prime \;\delta \prime \left( {x - {x_{\text{s}}},0} \right)f_{\text{s}}^\prime (z) $$
(9)

where ω′* is the dimensionless salt mass fraction of the incoming water through source term, I is the identity matrix and D′ is the dimensionless dispersion tensor, defined by

$$ {{\bf{D}}}\prime = \frac{{{D_{i{\text{j}}}}}}{{{\alpha_{\text{T}}}\,{q_{\text{d}}}}} = \left[ {{\delta_{\text{ij}}}\left| {{{\bf{q}}}\prime } \right| + \left( {{r_\alpha } - 1} \right)\frac{{q_{\text{i}}^\prime \,q_{\text{j}}^\prime }}{{\left| {{{\bf{q}}}\prime } \right|}}} \right]\quad, i,j = x,y,z $$
(10)

where r α denotes the ratio between longitudinal and transverse dispersivities (\( {r_\alpha } = {\alpha_{\text{L}}}/{\alpha_{\text{T}}} \)) and q i and q j are the components of the flux.

The transport equation is subject to a zero dimensionless solute flux along all the boundaries except for the coastal boundary where the dimensionless salt mass flux is defined as follows

$$ - \left( {\rho \prime {{\bf{q}}}\prime \omega \prime - \rho \prime {{\bf{D}}}\prime \nabla \prime \omega \prime } \right)\left| {_{{\text{y}}\prime = 0}} \right. \cdot {{\bf{n}}} = \left\{ {\begin{array}{*{20}{c}} {p\prime {{\bf{q}}}\prime \cdot {{\bf{n}}}\quad {\text{if}}\;{{\bf{q}}}\prime {{\bf{n}}} < 0} \\ {\rho \prime {{\bf{q}}}\prime \omega \prime \left| {_{{\text{y}}\prime = 0}} \right. \cdot {{\bf{n}}}\,{\text{if}}\;{{\bf{q}}}\prime {{\bf{n}}} > 0} \\ \end{array} } \right. $$
(11)

where n is the unit vector normal to the boundary and pointing outwards.

Critical pumping rate

Different sets of simulations were carried out by varying independently the distances of the two wells from the sea (L f = 200–400 m and L s = 20–150 m), the pumping rate at the freshwater well (Q f = 100–600 m3/d), the aquifer thickness (b = 9–50 m), the hydraulic conductivity (k x = 10–100 m/d and k z = 1–10 m/d), the longitudinal and transverse dispersivities (αL = 10–50 m and αT = 1–10 m) and the width of the model domain (2L c = 500–1,000 m). For each problem, the pumping rate at the seawater well was modified (382 cases) until the critical pumping rate was found. Table (1) shows the values of the dimensionless numbers used for simulations.

Table 1 Description of the simulations considered in the sensitivity analysis
Full size table

The algorithm of Furnival and Wilson (1974) was used to seek a simple empirical expression for the critical pumping rate from the dimensionless numbers. The algorithm finds the best subset regressions for a regression model with candidate independent variables. The routine eliminates some subsets of candidate variables by obtaining lower bounds on the error sum of squares from fitting larger models.

Basically, the dimensionless parameters defined in the previous section were proposed as independent variables. Some derived dimensionless numbers were also employed. In addition to these, the dimensionless toe penetration for the dispersive Henry problem (Abarca et al. 2007) was also used. Abarca’s correction to the Ghyben-Herzberg toe penetration was modified to read

$$ L_{\text{Ab}}^\prime = \left( {\frac{1}{{{L_{\text{f}}}}} - \frac{1}{{{L_{\text{c}}}}}} \right){L_{\text{GH}}} - \frac{{{F_{\text{LDS}}}}}{{{L_{\text{f}}}}} $$
(12)

where

$$ {F_{\text{LDS}}} = 0.136{\left( {\frac{{\sqrt {{\alpha_{\text{T}}}\,{\alpha_{\text{L}}}} }}{{{a^2}\sqrt {{r_{{\text{k}}2}}} }}} \right)^{0.724}} + 0.69{\left( {\frac{{\sqrt {{\alpha_{\text{T}}}\,{\alpha_{\text{L}}}} }}{{{a^2}\sqrt {{r_{{\text{k}}2}}} }}} \right)^{0.362}} $$
(13)

and L GH is the toe penetration without pumping under the Ghyben-Herzberg approximation

$$ {L_{\text{GH}}} = \frac{{b\,\varepsilon \,{K_{\text{y}}}}}{{2{q_{\text{d}}}\,}} $$
(14)

An empirical expression for the critical pumping rate F c was obtained from the regression model. The equation that best represents the numerical results is (see Fig. 7)

$$ \frac{{{Q_{\text{c}}}}}{{{Q_{\text{f}}}}} \approx {F_{\text{c}}} \approx 1.6\left( {\frac{1}{{{r_{\text{L}}}{{\left( {{r_{{\text{k}}1}}} \right)}^{{2 \mathord{\left/{\vphantom {3}} \right.} }}}}}\,} \right){e^{\left[ {\sqrt \pi \left( {L_{\text{Ab}}^\prime - Q_{\text{f}}^\prime } \right)} \right]}} $$
(15)

where r L is defined as the geometric shape factor of the two wells (r L = L s/L f).

Fig. 7
figure 7

Critical pumping rate in the seawater well obtained from the numerical simulations (Q c/Q f) versus the results from empirical expression, F c (Eq. 15), obtained from the regression model

Full size image

Note that the exponent in Eq. (15) depends on the dispersive case correction to the Ghyben-Herzberg toe approximation (Eq. 12) and on the ratio of the freshwater pumping to the freshwater inflow from inland, i.e. the exponent expresses the seawater invasion distance as evidenced by the reduction in freshwater discharge to the sea because of pumping.

The empirical expression approximates the 3D dynamics of the system satisfactorily. However, it is only aimed at preliminary assessments. The empirical approximation for the critical pumping rate is valid for the range of values of the variables tested here. An exhaustive study is required to fine tune this kind of corrective measure to the individual aquifer.

Equation (15) facilitates the sensitivity analysis (Fig. 8). Perhaps, the most surprising feature is the reduction in critical pumping rate for increasing \( Q_{\text{f}}^\prime \). The reason for this is that the toe along the boundary BB’ (Fig. 3) proceeds inland when \( Q_{\text{f}}^\prime \) increases. Thus an increase in freshwater pumping causes the critical pumping rate to decrease, leading to a reduction in the long term lateral flux of seawater. The effect is more marked when the seawater well is close to the sea (Fig. 8a).

Fig. 8
figure 8

Sensitivity analysis. The critical pumping rate decreases when a distance from the coast increases, b aquifer thickness decreases, c anisotropy increases, or d distance of the freshwater well from the coast increases. Note that the proposed empirical expression, F c Eq. (15), is fairly accurate for the range of values analyzed here

Full size image

When transverse dispersivity is increased with respect to the longitudinal one, the interface retreats seawards and the salt mass fraction at the freshwater well is reduced. However, the efficiency of mixing increases and the mixing zone is broadened. This promotes salinization of the freshwater well when the pumping rate in the seawater well intensifies. Consequently, increasing transverse dispersivity decreases the critical pumping rate.

Buoyancy effects increase in importance with aquifer thickness. Thus, an increase in aquifer thickness would tend to favor lateral fluxes around the seawater well. Intercepting these fluxes requires increasing the pumping rate at the seawater well. Therefore, the thicker the aquifer, the higher the critical pumping rate. This effect is more significant when the seawater well is near the sea (Fig. 8b).

An increase in k x reduces lateral gradients. In fact, it is similar to a reduction in the width of the model domain, which implies a reduction in lateral fluxes. As a result, the critical pumping rate decreases (Fig. 8c). The distance of the two wells from the sea (L f and L s) and the width of the model domain (L c) also affect the critical pumping rate. When the distance of the seawater well from the sea is increased, drawdown caused by the seawater well also increases (pressure along the coastal boundary is prescribed). This would tend to favor the lateral flux towards the pumping well. Thus, the critical pumping rate needs to be reduced to minimize this lateral flux (Fig. 8a). When the distance of the two wells from the sea exceeds that of L c (width of the model domain, see Fig. 3), the flow field becomes increasingly 2D, which reduces the critical pumping rate (Fig. 8d). Figure 8 also illustrates the fit between the numerical and empirical results (Eq. 15), which is fairly good.

Minimum salt mass fraction in the freshwater well

The dimensionless salt mass fraction (ω f/ω s) is the fraction of seawater at the freshwater well. If the seawater well pumped only seawater and if dispersion mechanisms and buoyancy forces were neglected, the seawater fraction at the freshwater well would become the seawater inflow not captured by the seawater well divided by Q f, i.e.,

$$ \frac{{{\omega_{\text{f}}}}}{{{\omega_{\text{s}}}}} = \frac{{\mathop Q\nolimits_{\text{Ts}} - {Q_{\text{s}}}}}{{{Q_{\text{f}}}}} $$
(16)

where Q Ts is the total saltwater flow rate entering from the seaside boundary. Using the method of images for an infinite line of freshwater and seawater wells, the total saltwater flow rate can be approximated as

$$ {Q_{\text{Ts}}} = \int\limits_0^{{L_{\text{b}}}} {\left( {{q_{\text{p}}}b - \frac{{{Q_{\text{f}}}{L_{\text{f}}}}}{\pi }\sum\limits_{i = 1}^n {\frac{1}{{{{\left( {x - 2n{L_{\text{c}}}} \right)}^2} + L_{\text{f}}^2}}} - \frac{{{Q_{\text{s}}}{L_{\text{s}}}}}{\pi }\sum\limits_{i = 1}^n {\frac{1}{{{{\left( {x - 2n{L_{\text{c}}}} \right)}^2} + L_{\text{B}}^2}}} } \right)} dx $$
(17)

where L b is the fraction of the coastal boundary where seawater flows inland (0 ≤ L b ≤ L c).

Unfortunately, this approach neglects the most notable features of seawater intrusion, namely buoyancy and interface mixing. In reality, the seawater well pumps some freshwater. Nevertheless, Eq. (16) was used as an independent variable in the regression model to obtain the empirical expression (G c) for the minimum seawater mass fraction at the freshwater well (ω m/ω s), i.e. the salt mass fraction at the freshwater well when the seawater well is pumping the critical rate. The best regression obtained was (see Fig. 9).

$$ \frac{{{\omega_{\text{m}}}}}{{{\omega_{\text{s}}}}} \approx {G_{\text{c}}} = 0.2\left( {\frac{{{Q_{\text{Ts}}} - {Q_{\text{s}}}}}{{{Q_{\text{f}}}}}} \right) + 0.8\left( {0.175\left( {\frac{{{b_{\text{T}}}}}{{L_{\text{s}}^\prime }}\sqrt {{r_\alpha }} } \right) + \frac{{b\prime }}{{L_{\text{f}}^\prime }} + 0.04\frac{{{r_{\text{L}}}}}{{Q_{\text{f}}^\prime }}} \right) $$
(18)

The fit between numerical and empirical results is not as good as the one for the critical pumping rate but may be used to obtain an idea of the efficiency of desalinization.

Fig. 9
figure 9

Fraction of seawater at the freshwater well from the numerical results versus the empirical expression, G c, Eq. (18), obtained from the regression model

Full size image

Desalinization efficiency (reduction in salinity at the freshwater well between steady state I and steady state II) is displayed versus distance of the seawater well from the sea, and versus aquifer thickness in Figs. 10 and 11, respectively. Decreasing the distance of the seawater well from the sea leads to a reduction in the salt mass fraction at the freshwater well. However, the critical pumping rate at the seawater well shows a marked increase (Fig. 6). For example, the desalinization efficiency increases from 19 to 28% when the seawater well is brought closer to the sea (L s = 40 m), but the critical pumping rate at the seawater well is four times higher when the seawater well is near the freshwater well (Ls = 150 m). Desalinization efficiency is significantly better in the case of a low freshwater pumping rate.

Fig. 10
figure 10

Comparison between numerical and empirical results of seawater fraction at the freshwater well versus the distance of the seawater well from the sea. Reduction in the distance of the seawater well from the sea improves the desalinization efficiency of the barrier, as measured by the percentage (%) reduction in freshwater well salinity with respect to steady-state I. Note, however, the marked increase in the critical pumping rate (see Fig. 8c)

Full size image
Fig. 11
figure 11

Fraction of seawater and desalinization percentage (%) at the freshwater well versus aquifer thickness for \( Q_{\text{f}}^\prime = 0.9 \). The results from the empirical expression provide a satisfactory representation of the numerical results. Note that the double pumping barrier is more efficient for thin aquifers, and that drinking water is obtained from the freshwater well with the double pumping system

Full size image

One critical factor in the efficiency of the double negative barrier is aquifer thickness. A decrease in aquifer thickness leads to a high desalinization efficiency with the double pumping system (Fig. 11). Note that drinking water is pumped from the freshwater well with the double negative barrier when the dimensionless aquifer thickness is 0.018.

A reduction in the aquifer thickness from 50 to 9 m, while increasing the pumping rate at the freshwater well (\( Q_{\text{f}}^\prime = 0.9 \)), gives rise to a seawater fraction of 7% (i.e., some 1,400 mg/L of chloride for a 1,900 mg/L seawater) at the freshwater well in steady state I. Pumping the seawater well causes chloride to fall below 200 mg/L at the freshwater well (<1 % of seawater), i.e. drinking water is obtained from the freshwater well, and the pumping rate at the seawater well is low (Q c/Q f ≈ 1), see Fig. 11.

Partially penetrating wells

As discussed in the preceding, the wells were assumed to be fully penetrating. However, salinity is stratified in coastal aquifers, with freshwater floating on top of seawater. Therefore, one would expect the location and length of the well screen to be a critical factor in a double pumping barrier system. The effect of partially penetrating wells on the efficiency of double pumping barriers is considered.

The simulations with partially penetrating wells were carried out with the same flow and transport parameters as those of aforementioned models, where hydraulic conductivity was assumed to be isotropic. First, the base case was simulated with a fully penetrating freshwater well and a partially penetrating seawater well. The numerical results confirm a decrease in salinity at the freshwater well. This effect would be more evident if both wells were partially penetrating wells. Different sets of simulations were carried out to study the effect of partially penetrating wells. The freshwater well pumps in the top 15 m of the aquifer whereas the seawater well pumps in the bottom 15 m. The numerical results provide evidence that buoyancy allows the freshwater well to pump freshwater, while the seawater well pumps seawater. Hence desalinization efficiency is significantly enhanced with respect to the fully penetrating wells, Fig. 12.

Fig. 12
figure 12

Fraction of seawater in the freshwater well versus pumping rates at the seawater well at distances from the coast of 150 and 90 m (\( L\prime_s = 0.3 \) and 0.18 respectively ). The dashed lines denote the results with fully penetrating wells (FPw) and the solid lines represent the results with partially penetrating wells (PPw). Note that partial penetration significantly improves desalinization efficiency but does not change the critical flow rate

Full size image

It should be noted that the critical pumping rate does not depend on the location of well screen, i.e. whether the wells are fully or partially penetrating. In an anisotropic system, where the vertical hydraulic conductivity is lower than the horizontal hydraulic conductivity, the salinity at the freshwater well must be lower than that in the isotropic system. However, it is very probable that the critical pumping rate occurred at exactly the same discharge given that the critical pumping rate depends on lateral fluxes, i.e. it depends on the horizontal components of the hydraulic conductivity.

Conclusions

A double pumping barrier is proposed as a corrective measure to control seawater intrusion in coastal aquifers where the water level cannot be raised or where artificial recharge or restrictions on pumping are not feasible. The system appears to be effective in the early stages (3–5 years). Pumping the seawater well causes salinity to fall sharply at the freshwater well. However, after a relatively short period, the drawdown generated by both wells causes saltwater to flow around the seawater well along the bottom of the aquifer, contaminating the freshwater well. When the seawater well pumping rate is high, this lateral flow is dominant. However, a low pumping rate at the seawater well would fail to intercept all seawater intrusion. Therefore, there is a critical pumping rate at the seawater well which produces the minimum salt mass fraction at the freshwater well. Paradoxically, a too energetic pumping at the seawater well would considerably increase salinity at the freshwater well.

The location of the seawater well and aquifer thickness significantly affect the efficiency of the system. Efficiency increases as the seawater well is brought closer to the sea but at the expense of a higher pumping rate at the seawater well. A decrease in aquifer thickness leads to a high desalinization at the freshwater well. Therefore, the highest efficiency of a double pumping barrier is reached in thin aquifers.

Empirical expressions were derived for the critical pumping rate and for the corresponding (maximum achievable) desalinization at the freshwater well. These expressions capture the 3D dynamics of the system satisfactorily. However, they should only be used for preliminary assessments. An exhaustive study is required to tailor this type of corrective measure to the individual aquifer. Finally, the efficiency of double-negative barriers is enhanced if the freshwater well is screened only at the top of the aquifer and the seawater well pumps at the bottom of the aquifer. Moreover, the numerical results suggest that the critical pumping rate does not depend on the location of the screen well.

In summary, the double pumping barrier system is not as efficient as it looks from a vertical cross section of the aquifer. Nevertheless, in cases where other options are not viable because of the lack of space or the need to keep water levels low (which is the case of urban aquifers), this corrective measure is a viable alternative. In the case of thin aquifers and/or closely spaced wells, the double pumping barrier is fairly efficient. The system proposed is much more efficient than a simple negative barrier.