1 Introduction

The global estimated volume of methane-hydrate is \(0.82\times 10^{13}\,{\mathrm{m}}^3\)–\(2.10\times 10^{15}\,{\mathrm{m}}^3\); more than 10 times that of conventional gas [2]. This has led to an increasing interest within various scientific and engineering communities, with the hope to harness this energy source in future years. Three methods have been suggested for gas production from methane-hydrate-bearing sediments: depressurization, thermal stimulation, and chemical activation.

To date, methane gas has never been extracted from methane-hydrate-bearing sediments on a commercial scale. A few short-term field trials of gas production have been performed: at the permafrost Mallik gas hydrate site, Canada, in 2007 and 2008 [6]; at the permafrost Ignik Sikumi well, Alaska, in 2012 [28]; at the offshore Eastern Nankai Trough, Japan in 2013 and 2017 [33]; at the coast of India, in 2006 and 2015 [4, 19]; and at the South China Sea, in 2017 [35]. In most of the field trials, geomechanical issues intervened with the production, leading to a recognition that better understanding of the geomechanical behavior of gas hydrate-bearing sediments is needed. It is well recognized that gas hydrate can alter the hosting sediment behavior. For example, laboratory geotechnical triaxial tests of methane-hydrate-bearing sands (both natural and artificial) consistently showed stiffer, stronger and more dilative behavior compared with that of clean sands under the same conditions [11, 21]. In addition, the samples exhibited strength degradation under large axial strains.

Several coupled formulations for the Thermo-Hydro-Mechanical–Chemical (THMC) behavior of gas hydrate-bearing sediments have been developed over the years with the objective of simulating various gas production techniques, their prospective and consequences [8, 16, 18, 20, 22, 27]. One central component of the formulation is the constitutive model relating stress and strain. First models, based on elasto-perfectly plastic laws, modified the Mohr–Coulomb yield criterion to include the contribution of hydrate, and developed a plastic potential function for defining plastic flow [7, 17, 25]. Later developments adopted the critical state soil mechanics approach, which couples volumetric and shearing yielding, for hydrate-bearing sediments [31]. However, further understanding of various phenomena that occur when the gas produced is called for. Specifically, the effect of hydrate dissociation on the existing stresses, the potential of sand migration and particle rearrangement due to high gradient flows, and the effect of hydrate existence and dissociation on stiffness and strength, all of which are strongly related to the micro-mechanical interaction between the hydrate and the sediment.

For better understanding of the hydrate properties, a few numerical discrete element method (DEM) formulations have been proposed for modeling the solid phase of gas hydrate-bearing sediments. These can be broadly divided into three groups: (1) Models in which the hydrate is modeled as solid particles randomly seeded in the pores. This method provides an increase of the strength but without a clear effect on the stiffness and dilatation under small strains [1, 9, 10]. (2) Models in which the hydrate is represented as part of the inter-particle constitutive model, where the force-displacement relation between different sand particles is a function of the hydrate saturation [13, 14, 29]. (3) Models in which the hydrate particles are bonded to sand particles, with a considerable effect on initial stiffness and volumetric dilatancy [15, 34].

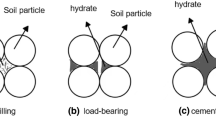
When dealing with hydrate-bearing sediments, three major hydrate morphologies are considered: (1) pore filling, in which the hydrate is found within the pores without any contact with the grains, (2) cementing, in which the hydrate bonds the soil particles, and (3) load bearing, in which the hydrate is sufficiently abundant to become part of the soil skeleton.

The increase of strength as a function of hydrate saturation has been naturally attributed to cementation between the hydrate substance and soil particles; that is, the gas-hydrate “bonds” sand particles. However, according to recent geomechanical investigations, the increase in strength may not necessarily be related to cementation, but rather to kinematic effects in shearing [23]. In this context, the term “cementing” may well be replaced by “grain contact” morphology, to avoid the confusion with true cohesion (or that cementation is the primary contributor to strength increase). Similar conclusions have been drawn by Hyodo et al. [11] based on the deviatoric strength observed in triaxial tests of artificial hydrate samples under diverse confining pressures. In addition, a water layer is commonly observed between quartz grains and gas hydrates in X-ray computed tomographic microscopy studies [3], indicating lack of cementation. To-date, no attempt has been made to represent the “grain contact” morphology without bonding (cementing) the hydrate and soil particles. In this context, this paper presents a non-cohesive DEM formulation aiming to represent methane-hydrate-bearing sands. In the formulation, neither sand–hydrate contacts nor hydrate–hydrate contacts involve bonding. The paper is composed of four main sections. Initially, fundamental analytical relations between the relative position of hydrate and sand particle and the effect on resistance are developed and characterized. Then, artificial DEM soil samples are constructed using the developed model, and the overall stress-strain response of the model is investigated. A parametric study aiming to understand the relation between the distribution of hydrate particles and the global response is performed. Finally, an investigation using Rowe’s stress dilatancy theory is performed to validate that the overall response exhibit the same characteristics as those recognized by the analysis of Pinkert [23, 24] on real hydrate-bearing sands. Lastly, conclusions are drawn.

2 Micromechanical representation through DEM formulation

In view of the recent observations, it is of interest to form a model in which the influence of hydrate on the sediment strength is mostly of frictional nature rather than cohesive. Additionally, experiments have shown that the hydrate significantly influences the stiffness (the initial slope of the stress-strain curve). In the context of DEM models, this means that the hydrate should be positioned such that it would contribute to the stiffness of the skeleton under small displacements. For this aim, hydrate particles need to be positioned near sand contacts, with at least two contacts, such that they become part of the skeleton. The following subsections describe the geometrical approach employed in the current work for positioning hydrate particles. A closed-form solution, for the designated position, is proposed for spherical particles, followed by characterization of the effect of the input parameters on the soil resistance.

2.1 Grain contact morphology by DEM

In this section, a new procedure for particle “seeding” is developed, generating the scenario presented above in which the hydrate affects both stiffness, strength, and dilation without bonding. The procedure identifies proximity of two adjacent soil particles, and positions a non-cohesive hydrate particle in contact with both soil particles, such that it affects the soil skeleton response when relative motion between the soil particles occurs. The approach avoids “gluing” hydrate particles to the soil particles, and thus avoiding the creation of true cohesion. On the other hand, hydrate particles seeded in the proximity of the soil structure are expected to affect the soil skeleton response even to minute deformations.

When considering spheres for the representation of both the soil and the hydrate particles, a closed-form solution can be derived for the hydrate seeding process in a given specimen of sand. Consider two adjacent soil particles, of radii \(R_1\) and \(R_2\), positioned at \(\{X_1,Y_1,Z_1\}\) and \(\{X_2,Y_2,Z_2\}\), respectively, within a Cartesian coordinate system. A hydrate particle, with a radius \(R_{hyd}\), will be in contact with the two nearby soil grains (without any overlap) if its center is positioned at \(\{X_{hyd},Y_{hyd},Z_{hyd}\}\), given by:

$$\begin{aligned} X_{hyd}&= \frac{X_1+X_2}{2} +\frac{\varGamma \varDelta X \varDelta R}{2 N^2 }\nonumber \\&\quad +\frac{D}{2 N^2(\varDelta X^2+\varDelta Y^2)} \Big ( \left( N \varDelta Y^2+\varDelta X^2 \varDelta Z\right) \cos (\theta )\nonumber \\&\quad +\varDelta X \varDelta Y (\varDelta Z-N) \sin (\theta )\Big ) \end{aligned}$$
(1)
$$\begin{aligned} Y_{hyd}&= \frac{Y_1+Y_2}{2} +\frac{\varGamma \varDelta Y \varDelta R}{2 N^2 } \nonumber \\&\quad +\frac{D}{2 N^2(\varDelta X^2+\varDelta Y^2)} \Big ( \left( N \varDelta X^2+\varDelta Y^2 \varDelta Z\right) \sin (\theta )\nonumber \\&\quad +\varDelta X \varDelta Y (\varDelta Z-N) \cos (\theta ) \Big ) \end{aligned}$$
(2)
$$\begin{aligned} Z_{hyd}&=\frac{Z_1+Z_2}{2} +\frac{\varGamma \varDelta Z \varDelta R}{2 N^2 }\nonumber \\&\quad +\frac{D}{2 N^2}\Big ( \varDelta Y \sin (\theta )+\varDelta X \cos (\theta )\Big ) \end{aligned}$$
(3)

where \(\varDelta R = R_1-R_2\), \(\{\varDelta X,\varDelta Y,\varDelta Z\}=\{X_2,Y_2,Z_2\}-\{X_1,Y_1,Z_1\} \), \(N^2=\varDelta X^2+\varDelta Y^2+\varDelta Z^2 \), \(\varGamma \) \(=\) \( R_1+R_2+2R_{hyd}\), \(D^2=(N^2-\varDelta R^2)(\varGamma ^2-N^2)\), and \(\theta \) is the free parameter, representing the radial position in a local cylindrical coordinate system defined by the line between the centers of the two soil particles (see Fig. 1).

Fig. 1
figure 1

Schematic model for positioning the hydrate particle; a within Cartesian system, b radial view

Full size image

The \(\theta \) parameter provides the freedom to locate the hydrate particle at any location along a “ring”, as illustrated in Fig. 1a. While \(\theta \) may be considered a random parameter in the seeding process, it is was chosen such that the hydrate particle will be as close as possible to an additional soil grain, if such exists. Additional particles along the same “ring” are placed such that they are in contact with previous hydrate particles, without any overlap, i.e., \(\varDelta \theta \) for two adjacent hydrate particles is \(2 \sin ^{-1}\left( 2 \varDelta N R_{hyd}/\sqrt{\left( \varGamma ^2-\varDelta N^2\right) \left( \varDelta N^2-\varDelta R^2\right) }\right) \) as seen in Fig. 1b. This seeding process is executed over all pairs of adjacent soil particles which the distance of their centroids (N) is smaller than the sum of the radii (\(\varGamma \)). Figure 2 shows an output of a typical seeding process. In principle, the seeding process is not limited to positioning hydrate particles around sand–sand contacts, but could be extended for further seeding around sand–hydrate and hydrate–hydrate contacts. This additional seeding process will increase the hydrate saturation, but expected to have a secondary (relatively small) effect on the mechanical response, because the additional particles are not part of the soil–hydrate skeleton, unless the strains are significantly large to rearrange the structure of the soil skeleton. Note that this “further seeding” process is not considered in the paper, and all specimens are limited to hydrate particles positioned around sand-sand contacts. It should be noted that the seeding process does not alter the stress within the soil skeleton (i.e. the forces between soil grains), as it is executed after stressing of the “naked” (free of hydrate) skeleton and no overlap between sand and hydrate particles is permitted during the seeding procedure.

Fig. 2
figure 2

A cylindrical sample (hydrate saturation of 25%)

Full size image

2.2 Relation between friction and geometrical configuration at hydrate contacts

A hydrate particle positioned between two soil grains may not necessarily contribute to the resistance and stiffness of the sediment, even in the case two soil grains approach each other (i.e. move towards each other), simply because of the geometrical configuration. Under certain conditions, the hydrate particle may detach (i.e. slip away and escape from the contact) for any load without providing resistance. Figure 3 illustrates the relation between friction and geometrical configuration that defines the limit state of resistance. In order for a hydrate particle to resist the movement of the soil particles, the arctangent of the inter-particle friction coefficient, \(\delta \), needs to be equal to, or higher than, the geometric angle, \(\alpha \), between the normal of the contact and the resultant force (line A and line B in Fig. 3b). In other words, the ratio of the shear and normal forces cannot exceed the inter-particle friction coefficient; the resultant force must lie along the line connecting the two contact points (due to equilibrium).

Fig. 3
figure 3

Schematic model for the friction coefficient calculation

Full size image

The geometric angle, \(\alpha \), is a function of the distance of the sand grains and the radii of the particles. Consequently, if the friction coefficient between the soil particle and the hydrate is known, the radius of the hydrate particle can be established such that it prevents the “escape” of the sphere. Alternatively, for a given geometry the friction angle can be defined to avoid the “escape” condition. The value of this critical angle is:

$$\begin{aligned}&\tan ^{-1} (\delta _{crit}) \equiv \alpha \nonumber \\&\quad = \tan ^{-1}\left( \frac{D \varDelta R}{\varGamma N^2-\varGamma \varDelta R^2}\right) +\tan ^{-1}\left( \frac{D}{\varGamma \varDelta R+N^2}\right) \end{aligned}$$
(4)

Even for a sediment sample with a constant \(R_{hyd}\) value, \(\alpha \) is not unique and has a statistical variation following the distribution of positions and radii of the sand particles. Equation 4 allows for a statistical approach to be implemented to both evaluate and regulate (if required) the inter-particle friction between hydrate and soil particles, such that the contribution of the hydrate to the stiffness of the macro-scale sample could be regulated, without changing the hydrate particle stiffness itself. By analyzing the cumulative distribution function of \(\alpha \) for methane-hydrate grains, it is possible to quantify the relative amount of particles that are expected to participate in the soil skeleton response to loading. This can be performed for any specific value of \(\delta \), as a function of the particle size.

Figure 4a, b represent a typical probability density function and cumulative distribution function, respectively, of the critical friction coefficient for different sizes of hydrate particles, expressed by the parameter k. k is defined as the ratio between hydrate and averaged soil particle size (\(k = R_{hyd}/\overline{R}\)). Figure 4 shows results for dense and loose samples, and as can be seen the \(\alpha \) distributions are very similar. For a given value of \(\delta \), smaller values of k lead to a greater amount of hydrate particles to interact with the soil skeleton. Inversely, for a given k value, a greater value of \(\delta \) leads to a greater amount of interaction. Let us define the cumulative value as a participation factor. That is, if the participation factor is 0 then the hydrate should not contribute to the soil skeleton behavior. On the other hand, if the participation factor is 1.0 then all hydrate particles interact with the soil skeleton, affecting its behavior. Note that for any given participation factor, all hydrate particles are in contact with the soil, and that the participation factor relates to inter-particle forces. It is therefore expected that a hydrate contribution would be more dominant with increasing hydrate participation. It is hypothesized that the overall response can be regulated by defining the participation factor. This hypothesis is evaluated later in the paper.

Fig. 4
figure 4

a Probability density function; b cumulative distribution function of Eq. 4 for DEM samples for different values of k (hydrate particle size)

Full size image

3 Soil samples, hydrate seeding and global stress-strain response

3.1 Sand sample

DEM simulations require significant computational effort, and hence are limited to relatively small soil samples. The representation of hydrate as small particles implies a further restriction on the specimen dimensions—a high number of particles is required to represent a significant volume of hydrate. In view of this limitation, in this study, a rectangular cuboid periodic space was implemented for the boundary conditions. Periodic space, first used in [5], consists of six boundary planes (minimal and maximal coordinates for the three dimensions). When a particle overlaps a boundary plane, it is defined as a “controller” and an imaginary “slave” is created in the opposite boundary plane. Forces and displacements are shared between controllers and slaves. This technique provides the appearance of an infinite sample, allowing the use of smaller samples to represent the stress-strain response of a larger sample. Details of the method are given in [5], and the technique is implemented in \(PFC^{3D}\) [12] which was utilized in the current study.

To investigate the behavior of the proposed model, several soil–hydrate samples were prepared by the suggested seeding process. Initially, a hydrate free sample was generated by randomly seeding 1300 spherical particles with diameters ranging from 0.15 to 0.25 mm, following a uniform distribution, and silica properties.

Firstly, soil particles were randomly seeded within the periodic space without overlaps, with a high porosity. Later, in order to obtain an initial compaction and to provide stability to the sample, strains were equally applied to the specimen, i.e., the vector position of every particle is multiplied by the same deformation gradient tensor applied on the external boundaries position. Numerical experiments included both loose (porosity \(n=0.42\)) and dense (\(n=0.37\)) sand samples. In order to produce dense samples, inter-particle friction coefficient was temporarily reduced. The Herz–Mindlin nonlinear formulation [5] was adopted for the constitutive contact model (force–displacement behavior).

3.2 Methane-hydrate seeding

The mentioned hydrate seeding process initiated after the desired confining pressure (\(\sigma _3\)) was applied over the sand sample. The final, and maximal, hydrate saturation obtained by the seeding process using a single size hydrate particles was about 20%. Recall that additional seeding of the same hydrate particles around hydrate–hydrate contacts and around sand–hydrate contacts was not considered, but could have potentially increased the volumetric hydrate saturation to about 35%, without a major effect on the mechanical response. These values, however, are relatively small compared to the maximal hydrate saturation measured in real samples. This is most likely due to the use of uniform sized hydrate particles and their spherical shape. Since in reality hydrates will not develop in the specific form of spherical particles, one may argue that the achieved DEM hydrate saturation, with a single size hydrate particle positioned in soil particle contacts, underestimates the true hydrate saturation. The evaluation of more complex particle geometry, additional seeding, and non-uniform hydrate particle size are beyond the scope of this paper.

Table 1 presents the properties of the soil and hydrate particles. The elastic parameters of the hydrate material are based on [30].

Table 1 Material properties
Full size table

To examine the proposed model “computerized” triaxial tests were performed. A designated subroutine that regulates the strain to achieve the mixed boundary condition of a triaxial test was considered, in which the vertical axis was controlled with a constant rate and the other boundaries were controlled to generate a constant horizontal stress.

3.3 Global mechanical response

3.3.1 The effect of \(\delta \) and k

With the objective of quantifying the effect of \(\delta \) on the global response, six samples, identical in particle configuration but varying in the inter-particle friction coefficient of hydrate particles, were subjected to triaxial loading. The results of the simulations, in terms of stress-strain curves and volumetric to axial strains, are presented in Fig. 5. For comparison, the results of a “clean sand” sample are presented also in the figure, marked by \(S_h=0\%\). As can be seen, higher values of \(\delta \) increase the initial stiffness, the maximal deviatoric stress, and the dilation. As expected, frictionless hydrate particles (\(\delta =0\)) do not alter by much the response of the soil, resulting in a similar behavior to that of the clean sand. This supports the earlier statement that a participation factor of 0 should not alter the response of the clean sand.

Note that simulation with \(\delta \) greater than 0.75 will result in the same behavior to that of \(\delta = 0.75\), since 0.75 is the friction coefficient of the sand particles.

Fig. 5
figure 5

Influence of the friction coefficient (\(\delta \)) of the hydrate particles (\(\sigma _3 = 1\) MPa, \(n=0.42\), \(S_h=18\%\), \(k=0.2\)); a stress-strain response; b volumetric response

Full size image

An investigation into the effect of hydrate particle size (expressed in parameter k) is exhibited in Fig. 6. Five samples with an identical sand structure, same friction coefficient, similar hydrate saturation (20%), but with different values of k were considered. As can be seen, the stress-strain response becomes stiffer, stronger, and more dilative with decreasing k. This corresponds well to the associated increase of participation factor.

Fig. 6
figure 6

Influence of the grain size (k) of the hydrate particles (\(\sigma _3 = 1\) MPa, \(n=0.42\), \(S_h=18\)–\(22\%\), \(\delta =0.75\)); a stress-strain response; b volumetric response

Full size image

3.3.2 Participation factor and the trade-off between \(\delta \) and k

The trade-off between hydrate size and inter-particle friction coefficient and its effect on the stress-strain response can be analyzed using the concept of participation factor. It was hypothesis earlier that equal participation factors (generated from different combinations of hydrate friction and hydrate particle size) should lead to a similar global response. To evaluate this hypothesis various “computerized” samples of hydrate-bearing sediments were examined, all with the same participation factor but with different combinations of hydrate particles and friction. In specific, three identical sand samples were seeded with different hydrate particles to form 50% participation. The combinations were \(k=0.15,0.20,0.25\) together with \(\delta =0.54,0.63,0.72\). These are shown in Fig. 7. As can be seen, the overall stress-strain response and the dilative response are similar between the cases, especially up to strain of 2%, and relatively to the change that occurs due to modification of only k or \(\delta \) (seen in the earlier figures). This observation supports the hypothesis.

Fig. 7
figure 7

Influence of the grain size ratio (k) and friction coefficient (\(\delta \)) for a participation factor of 0.5; a stress-strain response; b volumetric response; c friction coefficient as function of the grain size ratio and cumulative distribution

Full size image

As already stated, hydrate particles (initially touching two sand particles) with \(\tan (\alpha )\) values higher than the \(\delta \) value will detach when the specimen is compressed. These particles will be defined as “pore filling” particles (as opposed to “participating” particles) and should not affect the small strain behavior. The correctness of this assumption can be verified by investigating the response of the soil sample when deleting the particles with \(\tan (\alpha )>\delta \). If the assumption is correct, the small strain behavior should be similar to that with all particles. Such investigation was performed for 6 samples of 50% participation factor. The 3 new samples are called “50% participation & 0% pore filling” as opposed to the previous 3 samples, which are named “50% participation & 50% pore filling” (presented in Fig. 7). Figure 8 shows the results of the 6 samples. As can be seen, a similar small strain response is observed, both with respect to the initial stiffness and the volumetric response of the samples. This supports the above assumption that only particles with \(\tan (\alpha )<\delta \) contribute to the skeleton under small strains.

Fig. 8
figure 8

Comparison between “50% participation & 50% pore filling” samples and “50% participation & 0% pore filling” samples for different k and \(\delta \) configurations; a stress-strain response; b volumetric response

Full size image

Under large strains, pore filling particles can eventually touch other particles, with a smaller angle \(\alpha \), becoming part of the soil skeleton. This is the reason for the increased deviatoric stress seen in the 50% pore filling particles case under large strains, and it is more profound for large hydrate particles.

Overall, the response of the two cases up to peak strength is quite similar, suggesting that the participation factor may be seen as a parameter related to the effective (or mechanical) hydrate saturation. That is, a new parameter called “mechanical hydrate saturation” may be defined as the ratio of participating particles to the maximum possible hydrate particles in contact with the soil (whether existing or not). This idea of “mechanical hydrate saturation” exists in a somewhat different context of constitutive modeling. Uchida et al. [31], for example, defined such a parameter to express the contribution on the mechanical response separately than the hydrate saturation. Clearly, direct relations between continuum parameters and micro-mechanics formulation are not trivial to establish. Thus, quantifiably linking between the mechanical hydrate saturation of Uchida et al. [31] and that suggested here (as participation factor) requires a separate comprehensive study.

3.3.3 Contribution to strength

Considering that no true cohesion was introduced in the micro scale, it is expected that the global response would also be of noncohesive nature. This means that the additional strength of sediment due to the existence of hydrate should be of frictional nature. A classical Mohr–Coulomb analysis for the peak stress values is shown in Fig. 9. The response was obtained by subjecting the samples presented in Fig. 6 to higher confining stresses before seeding the hydrate (note that the tested samples are not identical due to the random seeding process). As can be seen, the hydrate contribution to strength in this formulation is clearly frictional, increasing the apparent internal friction angle without any intersection with the vertical axis.

Fig. 9
figure 9

Hydrate contribution for the strength for different k values

Full size image

3.3.4 Non-spherical particles

The fundamental investigation presented in the previous section is based on soil samples involving spherical particles. This simplicity of the grain shape, however, results in underestimation of the strength of the soil, even without hydrate. The low value of the friction angle of the macro response (\(\phi = 22^\circ \)) results from the ability of the spheres to develop rotational motion (one rolling over the other). The tendency of rolling is a function of the low value of the coordination number (average quantity of contacts per particle). Increasing the inter-particle friction cannot resolve this instability [32].

One can propose that compaction could overcome this limitation. Indeed, simulations with higher density (\(n=0.37\)) resulted in higher strength (\(\phi = 32^\circ \)), but the dilatation and the stiffness were overestimated to unrealistic values. Nevertheless, it is important to remark that the influence of \(\delta \), k and participation factor on strength, stiffness and volumetric behavior on loose samples are valid to dense samples as well, and this was confirmed by a similar parametric study (not included in the paper).

To extend the investigation to cases which do not involve rotational instability (as in real sand), further analyses were performed with coupling between neighboring sand particles. That is, the major fraction (\(88\%\)) of sand spheres were bonded, essentially converted into new particles with the shape of two coupled particles. The other particles remained spherical particles.

This way looser samples, compared to the perfect spheres grain, could be created (\(n=0.45\)), due to the fact that larger voids can form without losing stability. Those looser samples exhibited a more realistic behavior (compared to real loose samples) for the volumetric compression and for the stress hardening effect. Note that the rules and conditions for hydrate seeding (Eqs. 1–4) are preserved in this case.

In order to reexamine the assumption that the participation factor governs the behavior also for the non-spherical sand model, six DEM samples, based on the same sand skeleton and with the same participation factor (50%), differing by hydrate size (\(k={0.15,0.20,0.25}\)) and “pore filling” particles ratio (50% and 0%) were simulated under triaxial test conditions. The inter-particle friction coefficient was determined for each grain size from the cumulative distribution function for participation factor of 50%. It should be mentioned that hydrate was seeded only around inter-particle contacts, i.e., no hydrate particles were created around sand bonded contacts. Figure 10 shows the results of the simulations. It can be seen that the initial stiffness and dilation are indifferent to the configuration leading to 50% participation. However, the difference on the maximal deviatoric stress is slightly more pronounced than the one obtained for non-bonded sand particles (Fig. 10).

Fig. 10
figure 10

Comparison between “50% participation & 50% pore filling” samples and “50% participation & 0% pore filling” samples for different k and \(\delta \) configurations for coupled sand particles; a stress-strain response; b volumetric response

Full size image

3.3.5 Stress relaxation

The phenomenon of stress relaxation after peak strength has been observed for all the configurations of \(\alpha \), \(\delta \), participation ratio, pore filling ratio, and particle shape. Relaxation is more substantial under large strains and for small hydrate particles. In certain conditions, the developed deviator stress in the hydrate samples was smaller than pure sand samples. This phenomenon can be explained by the micro-scale behavior. The combination of large (sand) and small (hydrate) particles (e.g., the ratio of the sand and hydrate radii ranges between 5 and 8.3 for \(k=0.15\)) results in a system characterized by a ball bearing behavior, i.e., the small hydrate particles allow for more rotational freedom of the soil particles. To quantify the effect of the rolling freedom, an additional simulation was performed with prevention of hydrate rotation (i.e. only translation in space was allowed). Figure 11 shows the results, with the new simulation labeled as “\(\omega =0\)”. Disabling rotational movements for the hydrate particles essentially eliminated the stress relaxation, and the deviatoric stress for a given strain is consistently higher. It is possible that this characterization could be used in future work to regulate the stress relaxation, based on the true ability of the hydrate to rotate (recall that in reality the hydrate is most likely not a spherical particle).

Fig. 11
figure 11

Comparison between rotational velocity restricted and free rotational velocity hydrate particles; a stress-strain response; b volumetric response

Full size image

4 Investigation using Rowe’s stress dilatancy theory

Rowe [26] developed a stress-dilatancy model for granular soils, based on a principle of a minimum energy ratio. The concept was extended for cohesive soils as well, leading to the following constitutive law (for triaxial tests):

$$\begin{aligned} \frac{\sigma _1}{\sigma _3} =\left( \tan ^2\left( \frac{\pi }{4}+\frac{\phi _{cs}}{2}\right) +\frac{2 c}{\sigma _3}\tan \left( \frac{\pi }{4}+\frac{\phi _{cs}}{2}\right) \right) \left( 1-\frac{\dot{\epsilon _v}}{\dot{\epsilon _1}}\right) \end{aligned}$$
(5)

were \(\sigma _1\) and \(\sigma _3\) are the axial and confining stresses respectively; \(\epsilon _1\) and \(\epsilon _v\) are the axial and volumetric strains respectively; c is the cohesion and \(\phi _{cs}\) is the frictional angle of critical state. For non-cohesive soils Eq. 5 leads to a linear proportionality between the stress ratio and the strain incremental ratio. This relation can be visualized as a line from the origin with a slope of \(\tan ^2(\frac{\pi }{4}+\frac{\phi _{cs}}{2})\), independent of the density and confining stress. For cohesive soils the slope of the line should increase by \(\frac{2 c}{\sigma _3}\tan (\frac{\pi }{4}+\frac{\phi _{cs}}{2})\). Pinkert [23] identified that hydrate-bearing sediments have a non-cohesive kinematic behavior in terms of this constitutive law.

For evaluating the kinematic response of the presented DEM formulation, the results of the “50% participation” were examined in terms of Eq. 5, i.e., the values of the ratio \(\sigma _1/\sigma _3\) were plotted as a function of \(1-\dot{\epsilon _v}/\dot{\epsilon _1}\). The results are presented in Fig. 12 for “50% pore filling” (a) and “0% pore filling” (b) for bonded particles and \(\sigma _3=\,1\) MPa. The results infer that the presented model preserves the characteristics noted by Pinkert [23, 24] that the existence of the hydrate affects the kinematic behavior in a non-cohesive manner. This, however, does not constitute a proof of Pinkert’s hypothesis that the mechanical behavior is not characterized by true cohesion for all morphologies, because the current model assumes a frictional behavior in sand–hydrate contacts and ignores any particle bonding.

Fig. 12
figure 12

Stresses ratio as a function of incremental dilation for a “50% participation & 50% pore filling” and b “50% participation & 0% pore filling”

Full size image

5 Conclusions

The need for representative and realistic formulation for studying the response of hydrate-bearing sediments to various stressing and production conditions is a necessity for future successful exploitation of gas-hydrate reservoirs. This paper presented a new discrete element formulation in which the focus was placed on the interaction between the sediment skeleton and the hydrate formation. In specific, the paper relied on recent discoveries that the contribution of the hydrate to the strength of the soil is mostly of frictional, and suggested a micro-mechanical model that captures this essence.

A new technique for seeding hydrate particles in specific places in the pore space was formulated and characterized. It was shown that the hydrate contribution to the skeleton resistance is a function of the geometry and inter-particle friction. In specific, hydrate particles will contribute to the skeleton resistance if the equal angles of the isosceles triangle, formed by the hydrate’s centroid and the two points of hydrate contact with the nearby sand particles, are smaller than the inter-particle friction angle. Considering that the geometry contains significant variability (randomness in the pore scale), it was shown that the response could be characterized statistically. It was found that a participation factor (associated with the value of inter-particle friction and the geometrical distribution of hydrate morphology) governs the stress-strain response, with little dependency of the specific hydrate particle size and the friction angle. This observation was shown to be correct also for a more realistic representation of the hosting sand model (non-spherical sand particles). Finally, it was shown, using Rowe’s stress dilatancy theory, that the model preserves the characteristics noted by Pinkert [23] that the existence of the hydrate affects the kinematic behavior in a non-cohesive manner.

Other complexities could potentially be added to the model by further research. For example the hydrate particles can be replaced by agglomerates of hydrate particles with internal bonding, as considered by [9, 10], and may be bonded to each other to alter the kinematic response under large strains. Rate effect, and other contact aspects between hydrate and sand could be added to the model in future research.