1 Introduction

Powders are agglomerates of particles which interact with one another via dissipative interactions such as surface friction or viscoelastic losses [1]. Surface friction, in addition to the particle size distribution and material composition, has been shown to determine the spatial configurations and the ensuing void structure [2], of static and dynamics powder blends [3–5]. The response of a powder system to external stresses depends upon the system details and its history; for example, the load distribution, or development of shear failure [6, 7]. These factors, in turn, depend upon the packing history of the grains in the powder.

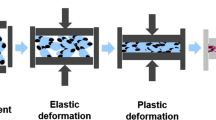
We are interested in understanding the effect of particle size dispersity of pharmaceutical powder blends under uniaxial compaction; in particular, the evolving particle packing characteristics under a compressive strain. To identify the role of size dispersity, we develop four model representations of microcrystalline cellulose, a commonly used pharmaceutical excipient. These model blends are comprised of one, two, four and six components, where the particles in each component have a distinct diameter. We use a particle dynamics simulation technique known as granular dynamics to calculate the trajectories of the model grains. For each model blend, we initiate the particle packing process by allowing the particles to settle under gravity followed by constant strain rate uniaxial compression, applied parallel to the direction of gravity. The gravitational settling process generates a powder bed where the individual grains are loosely packed. The application of uniaxial compaction induces the grains to undergo spatial reorganization. For small strains, we observe the packing fraction of the powder blends to scale linearly with the axial strain, and do not observe any differences in the stress response of the blend with particle size dispersity of the blends. In an earlier study [2], we have shown the evolving pore structure depends upon the ensemble particle size distribution. Our results reported here, along with our earlier study [2], can be used to understand the role of particle dynamics on the development of shear failure, or fracture in compressed granular materials; for example, ocean beds, compacted soil, or medicinal tablets [1, 2, 8].

2 Details of the system

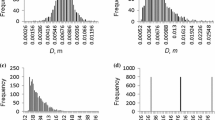
We explore the effect of size dispersity in a 3D assembly of dry non-cohesive powder blends confined between surfaces [9]. Segregation quite often dominates the properties of powder blends with polydispersity in the particle size of the grains. Earlier studies [10] have demonstrated the ability of the smallest grains to fall through the voids between the larger particles due to gravitational sieving, or vibration. We study model powder mixtures which are representative of industrial powder blends [11]. To avoid segregation, the smallest to the largest particle size is much larger than the value required to induce segregation by gravitational sieving alone. The ratio of the largest to the smallest particle diameter must be at least \(1/(\surd {2} - 1) \sim 2.41\) in order for the smaller particles to percolate through. This calculation assumes the larger identical spheres to be centered at the corners of a square whose dimension is equal to the sphere diameter, and the absence of larger interstices. We model the powder blends discussed in [11] by four samples composed of discrete components varying in particle size (\(\upmu \hbox {m}\)): S1 (200), S2 (195, 225), S4 (170, 195, 225, 260) and S6 (150, 170, 195, 225, 260, 295), as indicated by the inset in Fig. 2.

3 Methodology

We used soft spherical particles, which model the mechanical properties of a common pharmaceutical excipient known as microcrystalline cellulose (Young’s modulus of 9.08 GPa [12] and Poisson’s ratio of 0.3 [13]), in 3D granular dynamics simulations with 2D periodic boundary conditions along the x- and y-axes. Our contact model links the normal and tangential interactions through Coulomb’s yield criteria [14, 15] by modeling the presence of both static and kinetic friction. The coefficients associated with the two types of surface friction are equal to one another in our investigations. The particles interact via Hertz–Kuwabara–Kono and linear damped spring force laws along the normal and tangential directions, respectively. For each sample, an assembly of 1,800 particles was constrained along the vertical direction by two bounding surfaces which were generated by randomly fusing together identical spherical particles, to avoid surface induced ordered packing [16]. Further details of the contact model are available in an earlier study [2] by the present authors.

The initial particle positions were spatially homogenized via elastic hard sphere interactions for a given number of cumulative collisions, at a packing fraction of 0.03, such that each sample had the same initial average total energy that encompasses the kinetic energy and the gravitational potential energy [17]. In the numerical experiment, the particles were initially allowed to settle under gravity followed by constant strain uniaxial compression (along the vertical direction) by the top surface at a rate \(\mathop {\gamma _c }\limits ^{\bullet } \). The simulation cell dimensions are determined by the height of the cell (parallel to the direction of gravity and the applied compression), and the dimensions of the bounding surface. The latter are measured from the centers of mass of the surface particles located at its extremities (as shown in Fig. 2 of reference [9]). The simulation cell dimensions remain unchanged throughout the simulation; however during the compaction phase, the height of the top surface reduces at a rate proportional to the compressive strain rate. Simultaneously, the magnitude of the difference in the system particle positions, at the extremities, along the x- and y-directions increases by a small amount so as to allow the particles to rearrange themselves. The latter is allowed on account of the two-dimensional periodic boundary conditions along the x- and y-directions. All quantities presented are dimensionless, and have been calculated by normalizing with a suitable system of units. To obtain a comparison between the effects of gravity and the compressive strain, we use the average particle diameter a (\(\hbox {a} = 200\,\upmu \hbox {m}\)), mass m and the acceleration due to gravity g to develop a system of units. The units of strain rate, time t’ and stress are \(\surd {(2 \hbox {a g})}, \surd {(2 \hbox {a/ g})}\) and \(\hbox {mg/a}^{2}\), respectively. The strain rate has the dimensions of length/ time. The integrating time step has been chosen such that the particles in the four samples undergo quasi-static compression. For S1 with \(\mathop {\gamma _c }\limits ^{\bullet } (=\! 0.016)\), the integrating time step is \(1.5 \times 10^{-5}\) such that at each iterative step, the compressive surface moves by a distance of \(2.4 \times 10^{-7}\) a. The axial strain \(\upvarepsilon \) is given by the ratio of the vertical displacement of the strain-applying surface to the initial height of the sample \(\hbox {h}_{\mathrm{o}},\,\hbox {or}\,\upvarepsilon = \mathop {\gamma _c }\limits ^{\bullet } \hbox {t'/h}_{\mathrm{o}}\). The total compressive strain applied for samples S1, in the units of particle diameter a, is about 1.075–1.857 a. Simulations of all four powder samples with different values of the surface friction support previous findings on the effect of friction on the packing of mono-disperse sphere collections [4]. To minimize the effect of surface friction, we present results for those systems where both the coefficients of static and kinetic friction are set to 0.1.

4 Results and discussions

Gravity settling process produces a loosely packed agglomerate of grains whose interstitial voids, or pore-bodies, are connected via thin channels, or pore-necks [2]. The packing fraction \(\uprho \) and the coordination number Z increases rapidly as the particles quickly dissipate their kinetic energy, and pack to form a static configuration. The coordination number is defined as the number of nearest neighbors. We define the number of nearest neighbors to be those particles that are within the interaction cut-off distance from a reference particle. The gravity settling phase over a fixed time interval, for the different powder samples, produces agglomerates with different values of \(\uprho \). Given the importance of the packing history [6, 7] of an agglomerate to an external load, it becomes critical that the gravitationally settled agglomerates for each of the samples are at the same packing fraction prior to the commencement of the compression phase. Therefore, the duration of the gravity settling phase for each sample is determined by the time taken to achieve a predetermined threshold packing fraction \(\uprho _\mathrm{o}\). Following the gravity settling phase, the compaction phase for each sample lasts until the packing fraction attains a maximum value of \(\uprho = 0.645\). This value of packing fraction is slightly higher than the random close packing limit for monodisperse spheres [18]. We would like to note that we were able to attain all the four cut-off packing fraction values for the single component blend. However, we were unable to generate packings at the following threshold packing fraction \(\uprho _\mathrm{o}\), for the binary, quaternary and six-component blends: S2 (\(\uprho _\mathrm{o} = 0.57\)), S4 (\(\uprho _\mathrm{o} = 0.57\)) and S6 (\(\uprho _\mathrm{o} = 0.56, 0.57\)). We have repeated the gravitational settling phase for these blends using various initial configurations of the grains but were unsuccessful in generating a loose gravitational settled phase at the desired threshold packing fractions. One possible hypothesis for this result is that the threshold packing fractions were set using the random loose packing fraction for monodisperse spheres. We would expect the random loose packing fraction to change with the size dispersity of the blend. Hence, the most probable explanation for our result is that the threshold packing fractions that we were unable to attain for the specific blends are higher than their corresponding loose random packing fractions (after accounting for the standard deviation in the packing trials). For S1, this value of \(\uprho \) corresponds to a compressive strain \(\upvarepsilon \,\sim \, 0.105\), and an average contact deformation \(\updelta \,\sim \,0.01\). The average contact deformation \(\updelta \) is the average overlap distance between two particles that are within the interaction range cut-off distance. The average is computed over all the pairs of particles that are within the interaction range cut-off distance.

We can estimate the relation between the bulk axial strain \(\upvarepsilon \) and the average contact deformation \(\updelta \) by showing \(\upvarepsilon = \mathop {\gamma _c }\limits ^{\bullet } \hbox {t'/h}_{\mathrm{o}}\,\sim \hbox {N}_{\mathrm{c}}^{\mathrm{zz}} \updelta /\hbox {h}_\mathrm{o},\,\hbox {or}\,\upvarepsilon \propto \updelta \,(\hbox {N}_{\mathrm{c}}^{\mathrm{zz}}\) is the number of particle contacts where the contact vector is closely aligned with the direction of compaction and \(\mathop {\gamma _c }\limits ^{\bullet } \) is the strain rate). The initial stages of the compaction phase perturb the particle positions, causing changes in their collective spatial organization, and reduction in the void volume. This process continues until the particles begin to find themselves in spatially frustrated configurations. At this stage, we surmise that the number of contacts that a particle has where the contact vector is closely aligned with the compression direction reaches a constant value. Therefore, for small strains, the average contact deformation varies linearly with the strain once \(\hbox {N}_{\mathrm{c}}^{\mathrm{zz}}\) reaches a constant value. Our computations of the evolution of the average contact deformation with the axial strain, as shown in Fig. 1, are observed to support our hypothesis. Figure 1 demonstrates computations of two additional blends R1 and R2 which have a random grain size distribution. We would like to reiterate that the work will be focusing on blends S1, S2, S4 and S6. The inset in Fig. 1 shows the particle size distribution for the single, binary, quaternary and six-component blends. The ratio \(\hbox {N}_{\mathrm{c}}^{\mathrm{zz}} \hbox {/h}_{\mathrm{o}}\) varies across the different samples due to differences in their random loose packed configurations, and the response to an uniaxial compressive strain. For larger strains, the deformation response for all samples becomes indistinguishable. We would like to note that we have presented data for large axial strains, and have restricted the focus of the current work to small compressive axial strains.

Fig. 1
figure 1

The variation in the average contact deformation \(\updelta \) with the axial strain \(\upvarepsilon \). The numbers in the legend present values of the cut-off packing fraction \(\uprho _\mathrm{o}\). The inset shows the particle size distribution of the single, binary, quaternary and six-component blends

Full size image

The individual particle dynamics provides insight into the microscopic response of the powder blend to compression. The uniaxial compaction process involves moving the upper bounding surface at a constant speed. The gravity settling phase produces a loosely packed powder bed with the packing fraction increasing from the upper two or three particle layers and attaining a constant value in the bulk particle packing. During the early stages of the compaction phase, the strain applying surface comes into contact with the particles in the topmost layer of the agglomerate. The initial impact with the surface disturbs these particles from their positions of mechanical stability, inducing them to move into adjacent neighboring voids. The compaction process continues to induce the collective particle rearrangement, and the accompanying void filling, thereby propagating the material response to the uniaxial loading through the lower layers of the powder packing. The particle reorganization during the compaction phase leads to the simultaneous formation and breakage of multiple interparticle contacts. Figure 2 captures the evolution in the number of interparticle contacts during the uniaxial loading phase. The data corresponding to a given blend is attributed a different color: S1 (black), S2 (red), S4 (green) and S6 (blue). The data corresponding to different threshold packing fractions have been assigned different line styles. We use this format for all the figures in the paper. For the early stages of the compaction phase or small strains (\(\upvarepsilon \le 0.05\)), the perturbation of the top layer particles due to impact with loading-applying surface induces significant changes in the particle positions and the interparticle contacts. This transient phase continues until the particles begin to find themselves in local close-packed or frustrated spatial configurations. The densification of the powder bed is accompanied by the coordination number distribution favoring an increase in the average and minimum number of contacts per particle; however, the maximum coordination number per particle remains unchanged. The evolution of the packing fraction can also elucidate the changes in the collective particle dynamics induced by the compressive strain.

Fig. 2
figure 2

The variation in the average coordination number Z with the axial strain \(\upvarepsilon \). The numbers in the legend present values of the cut-off packing fraction \(\uprho _\mathrm{o}\). The inset shows the particle size distribution of the single, binary, quarternary and six-component blends (color figure online)

Full size image

The available volume used to calculate the packing fraction \(\uprho \) is determined from the positions of the particles at the extremities of simulation cell, along each dimension. This approach was used as the top surface of the gravitationally settled grain assembly is not flat. The dependence of the packing fraction \(\uprho \) on the strain \(\upvarepsilon \), as shown in Fig. 3, can be calculated as follows: \(\uprho = \hbox {total occupied volume/[L}_{\mathrm{x}} \hbox {L}_{\mathrm{y}} (\hbox {h}_{\mathrm{o}}-\mathop {\gamma _c }\limits ^{\bullet } \hbox {t}')]= \uprho _{\mathrm{o}}/(1 - \mathop {\gamma _c }\limits ^{\bullet } \hbox {t'/h}_{\mathrm{o}})=\uprho _{\mathrm{o}}/(1 - \upvarepsilon )=\uprho _{\mathrm{o}} (1 + \upvarepsilon +\upvarepsilon ^{2} + \cdots ) \sim \,\uprho _\mathrm{o} (1 + \upvarepsilon )\) for \(\upvarepsilon \,< 1.\,\, \hbox {L}_\mathrm{x}\) and \(\hbox {L}_{\mathrm{y}}\) are the dimensions of the simulation cell along the x- and y-directions, and \(\uprho _\mathrm{o}\) is the packing fraction prior to the compaction phase (or the cut-off packing fraction, as defined earlier). The packing fraction measurements shown in Fig. 3 commence following the particle rearrangements induced by the initial impact between the strain applying surface and the particle agglomerate. The packing configurations of single, binary and quaternary component powders are such that the strain applying surface remains in contact with the simulation particles for the entire duration of the compaction phase which is supported by the linear increase in the packing fraction with the uniaxial strain. However, for the six-component powder blend, the strain applying surface loses contact with the particles after the onset of compaction phase, for a short duration, before resuming contact. There onwards, the packing fraction grows linearly with the uniaxial strain, but the total strain required to achieve the same packing density for six-component mixture is almost double that of single-component mixture. Our results shows that for strains \(\upvarepsilon \,> 0.05\), the slope of the packing fraction versus strain graph \(\hbox {d}\!\uprho /\hbox {d}\!\upvarepsilon \) is much smaller for the six-component blend than the single, binary and quaternary blends. This observation supports our premise that the compatibility of the six-component blend is higher than the other blends studied in this paper. We would like to note that the binary blend could be loaded with a larger compressive strain to attain the same packing fraction as the quaternary blend. This observation seems to hint that there might be a critical size dispersity profile at which blends response very differently than those whose size distribution is below the critical threshold. We hypothesize that the critical size distribution threshold enables the blend to gradually evolve a void structure with pore volumes whose distribution closely follow the blend particle size distribution under a compressive strain. Such a threshold would also support our observation of the loss in contact between the six-component blend and the strain applying surface, during the compressive phase.

Fig. 3
figure 3

Variation in the packing fraction \(\uprho \) with the axial strain \(\upvarepsilon \). The numbers in the legend present values of the cut-off packing fraction \(\uprho _\mathrm{o}\)

Full size image
Fig. 4
figure 4

Dimensionless axial stress \(\sigma \) as a function of the axial strain \(\upvarepsilon \). The numbers in the legend present values of the cut-off packing fraction \(\uprho _\mathrm{o}\)

Full size image

The differences in the particle size distribution and configurations within the different blends will influence the stress response of the material. This premise is based upon the following hypothesis: rearrangements in the local neighborhood of the particles lead to changes in the contact history, and therefore the load distribution through the powder blend. However, we have found that the macroscopic axial stress response is not sensitive to the size distributions in each sample for small strains (see Fig. 4). We have used the approach details in reference [19] to calculate the macroscopic axial stress. At larger strains, the six-component mixture remains compactible, whereas the maximum strains for four-component and two-component mixtures are relatively unchanged relative to single-component sample. This is due to the range of particle sizes in the six-component mixture, and the suggestion of a critical size dispersity threshold that is important in achieving high compactibility in pharmaceutical powders. We find our measurements for the evolution of the stress with the axial strain to qualitatively agree with earlier studies using modeling techniques and experimental approaches [20–23]. We would like to note that existing studies [24–28] have investigated the role of loading and unloading of polydisperse granular assemblies.

5 Conclusions

We have shown the influence of size dispersity on the particle packings in uniaxially compressed dense powder blends via numerical simulation. We study four blends (S1, S2, S4 and S6), of varying particle size distributions, which are uniaxially compressed at a constant strain rate following gravitational settling. For small strains, we find the packing fraction of the powder blends to scale linearly with the axial strain, and do not observe any differences in the stress response of the blend with particle size dispersity of the samples. At larger strains, the mixtures with widest size distributions remain compactible to higher strains. Our results can be used to obtain insight into the microscopic response of powders to compressive strains, and the development of constitutive models for powdercompaction.