1 Introduction

The impact of particle properties on their packing and the packing structure is a fundamental problem relevant to a large number of industries and has been studied for several decades [1, 2]. A better understanding of particle packing is beneficial for designing and optimizing the industrial processes involved so that the processes and performance of particle materials can be efficiently controlled and improved. For example, in the concrete and ceramic industries, optimizing the particle packing helps enhance the performance of concrete and ceramic materials [3, 4]. In the pharmaceutical industry, the packing structure of particles is related to the flowability which impacts the compaction process, ultimately influencing the quality of the tablet. Similarly, packing impacts processing and product performance in many other industries, as well. Therefore, it is useful to understand how the particle properties such as friction, cohesiveness, shapes, and sizes, etc., influence the packing structure. Such information may help develop predictable models to describe the packing properties of particles.

Packing density, defined as the volume ratio of particles to the total volume occupied by packed particles, being the complement of porosity, is an important macroscopic parameter to describe the particle packing and is also one of the most easily accessible parameters in experiments and simulations. Currently, both experimental and numerical methods are applied to study the particle packing and development of parametric models [5–15]. It has been shown that factors such as the methods to construct the packing [5, 16, 17] and the particle properties can impact the particle packing [13, 18, 19]. Generally speaking, lower supplied energy and higher energy dissipation during the process of packing tend to increase the porosity of packing [2]. Understanding of particle packing requires consideration of the relationship between the microscopic information, including radial distribution function (RDF), force distribution, and contact geometry, and macroscopic parameters, such as porosity. For that purpose, experimental techniques, such as X-ray micro-tomography (XMT) and carbon paper technique, are available to measure RDF or the force distribution of the particle assembly [20, 21], making it possible to bridge the gap between macroscopic parameter(s) and microscopic properties.

With the ongoing rapid development of computer technology, discrete element method (DEM) simulation has been broadly used in many fields, including in particle packing. The packing of both cohesive and non-cohesive particles has been investigated using DEM simulations [12–15, 18, 19, 22, 23]. The validity of DEM simulations has been tested by means of comparison between experimental and simulated results. For example, DEM simulation obtained packing density is 0.633 [15], which is comparable to experimental data about random close packing (RCP) of \(0.6366\pm 0.0005\) [24]. For random loose packing (RLP), simulation results also show that the packing density could range from 0 to 0.64, depending on the initial simulation conditions and parameters such as cohesive force, frictional force and so on [6]. The DEM simulation approach can also provide other useful information including the RDF and force distributions and hence has become more and more popular in studying the particle packing problem.

By combining experiments and DEM simulations, Yu et al. developed a useful parametric model to predict the porosity based on the particle properties [7, 12, 25]. In their model, particle size, density, and Hamaker constant are three critical variables that influence the packing porosity. The prediction of porosity based on this model agrees well with previously published experimental data [25]. However, the recent experimental results of pharmaceutical powders, which are inherently highly cohesive and have irregular shapes, show that this model does not match the porosity measured in the experiments [26] as the predictive value from the model is less than the measured porosity of the powders, which is expected due to the shape and surface roughness. However, according to the experimental data, the porosity of powders after surface modification of the particles (also described in their paper) agrees well with the modeling prediction, suggesting that reduced cohesion due to dry coating based surface modification may help negate other effects such as the particle shapes that lead to very high porosity of uncoated powders and hence the discrepancy with the model [26].

In fact, the effect of particle shapes on the porosity has been studied experimentally [27]. Moreover, the effect of different particle shapes and their impact on packing density has also been examined via computer simulations [28–37]. Typical approaches to construct the packing in these references include mechanical contraction [28], relaxation algorithm [34–36], generalized Lubachevsky-Stillinger approach [30], Monte Carlo technique [37], etc. These methods and results will be further discussed later for the purpose of comparison with DEM results in this paper. Regardless of the simulation/computational method used, perhaps due to its simple geometric form, which can be described using either the sphere assembly method or mathematical equations [28, 34, 35], the spherocylinder particle has been popular in reported work on the investigation of shape effect on packing.

In spite of various non-DEM approaches used in the previous work focusing on the effect of shape on packing, none of those considered the cohesiveness of particles, which is expected to play an important role in the packing, especially in the case of fine particles, where the cohesive force is far larger than the weight of particle; i.e., having large granular Bond numbers [38]. Therefore, one of the major goals of this work is to examine the role of cohesion through computer simulations about packing of spherocylinder particles, in particular when there are relatively strong cohesive forces involved. In addition, although DEM simulations have also been widely used to study the behavior of spherical particles, there have not been many studies that target specific behavior of particles with large aspect ratios along with strong cohesive forces. The lack of information about the effect of various particle shapes and cohesiveness on the packing may inhibit establishing more accurate predictive packing models.

In this paper, the particle packing is studied using DEM simulations. Unlike previous work, where the van der Waals force is used to represent the cohesiveness between particles [11, 12, 22], in this work, the cohesive force is based on the JKR model [39]. The details about the simulation, including initial conditions and particle properties, are described in Sect. 2 and results are presented in Sect. 3, which includes the information about the porosity, RDF, and contact geometry, for various particle sizes, surface energies, and aspect ratios. Based on these results, the packing configurations are analyzed to identify a cage-like structure, which is a kind of microscopic jammed configuration within the particle packing even when the coordination number for one of the particles is very low in the presence of strong cohesive force. This is followed by the conclusions in Sect. 4.

2 Simulation approach

2.1 DEM simulation

In this research, the packing model is created using EDEM (EDEM 2.4, DEM Solutions, Edinburgh, Scotland). The governing equations for individual particles can be written as follows:

$$\begin{aligned}&m_i \frac{d{\vec {v}}_{i}}{dt}=\sum \limits _{j\ne i}^k {\vec {F}}_{ij} +m_i {\vec {g}}\end{aligned}$$
(1)
$$\begin{aligned}&I_i \frac{d{\vec {\omega }}_{i}}{dt}=\sum \limits _{j\ne i}^k {\vec {T}}_{ij}\end{aligned}$$
(2)
$$\begin{aligned}&{\vec {F}}_{ij} ={\vec {F}}_{ij}^n +{\vec {F}}_{ij}^{t}\end{aligned}$$
(3)
$$\begin{aligned}&{\vec {T}}_{ij} ={\vec {R}}_i \times {\vec {F}}_{ij}^t -{\vec {\tau }}_{ij}^{r} \end{aligned}$$
(4)

where \(m_i, {\vec {v}}_i, {\vec {\omega }}_i, {\vec {R}}_i, I_i\) represent the mass, translational velocity, rotational velocity, vector connecting the center of particle \(i\) and the contact point, and the moment of inertia of particle \(i\). \({\vec {F}}_{ij}\) is the contact force induced by particle \(j\) and it can be divided into two parts: normal contact force \({\vec {F}}_{ij}^n\) and tangential contact force \({\vec {F}}_{ij}^t\). \({\vec {T}}_{ij}\) represents the torque induced by particle \(j\) due to tangential contact force and rolling friction force. The total contact force and torque is the summation over \(k\) particles in contact with particle \(i\). The contact model including the cohesive force based on JKR model is used in this work to describe the interaction between particles [39]. Further details about contact model can be found in the references [40, 41]. For incorporating cohesion, two different surface energy values are considered: a low value of \(10\,\text{ mJ }/\text{ m }^{2}\) is used to see how the behavior changes from no cohesion to low cohesion, and a higher value of \(50\,\text{ mJ }/\text{ m }^{2}\) is also used that represents a typical pharmaceutical material.

The equations used to calculate the attractive force based on JKR model are [39]:

$$\begin{aligned}&F_{jkr}=\frac{4E^{*}}{3R^{*}}a^{3}-4\sqrt{\pi \gamma a^{3}E^{*}}\end{aligned}$$
(5)
$$\begin{aligned}&\frac{1}{E^{*}}=\frac{1-v_{i}^{2}}{E_{i}}+\frac{1-v_{j}^{2}}{E_{j}}\end{aligned}$$
(6)
$$\begin{aligned}&\frac{1}{R^{*}}=\frac{1}{R_{i}}+\frac{1}{R_{j}} \end{aligned}$$
(7)

where with \(\upsilon _i, E_{i}, R_{i}\) and \(\upsilon _j, E_{j}, R_{j}\) being the Poisson ratio, Young’s modulus, and radius of every sphere in contact, respectively. \(\gamma \) and \(a\) are surface energy and contact radius.

It is noted that there are several options for handling cohesive particles in DEM simulations. Most popular ones include, van der Waals model and JKR model, which are widely used in the reported work [11, 12, 22, 42–44]. One of the advantages of van der Waals model is that it is easy to implement in the DEM code. However, it cannot account for the effect of contacting particle deformation, which is often due to strong inter-particle forces. Such forces cause deformation of the contacting objects, which form a flattened contact region [39]. JKR model assumes that the attractive force acts only inside the flattened contact region, and hence ignores the attractive force beyond this region [39]. However, it has been used extensively, and has also been validated by experiments. For example, experimental results using the atomic force microscopy (AFM) have shown the JKR model is capable of predicting the adhesion between polybutylene terephthalate and silicone [45].

2.2 Geometry and initial parameters

Initially, five thousand particles are randomly generated in the cylindrical container, called cylinder hereafter, without allowing overlap between them. The volume of the cylinder is changed according to the size of the particles so that the initial porosity for all simulations is constant at 94 %. Once initialized, the particles fall down under gravitational force and settle down at the bottom of the cylinder. To minimize the effect of the wall of the geometry, periodic boundary conditions are used along the horizontal directions (x and y). Particles with three different aspect ratios of 0.0 (sphere), 1.0, and 3.0 are used in this paper. The spherocylinder particles are formed with multi-sphere approach [46–49], which allows the particles to superimpose to form a composite particle with complex shape. One of the advantages of multi-sphere approach is that it leads to the simplicity of contact detection algorithms, thus decreasing the computation challenge as compared with other methods [50, 51]. Four and twelve ideal spherical particles are used to constitute the spherocylinder particles with aspect ratios of 1.0 and 3.0, respectively. The aspect ratio \(\alpha \), here defined as \(\alpha =\frac{L}{d}\), where the L is the overall length of cylinder and d is the diameter of an individual particle, is the same as in other references [34, 35].

The system is regarded to be steady if the porosity does not change during a large number of DEM time steps. After the steady state is achieved, the porosity, RDF, and contacts corresponding to the steady state are obtained according to the simulation results. Figure 1 shows the initial configuration of simulation model used in this paper. The magnified pictures in Fig. 1b, c show the spherocylinder particles with aspect ratio of 1.0 and 3.0, respectively, which are composed through the multi-sphere assembly. The values of the initial parameters and material properties used in this simulation are listed in Table 1.

Fig. 1
figure 1

The schematic representation of the simulation model for packing at different aspect ratios. a Aspect ratio, 0.0 (sphere), b aspect ratio, 1.0, and, c aspect ratio, 3.0

Full size image
Table 1 Initial parameter and material properties used in the simulation
Full size table

3 Results and discussion

3.1 Porosity

Figure 2 shows the porosity as a function of different particle sizes, surface energies, and aspect ratios. For the spherocylinder particles with \(\alpha =1.0\) or \(\alpha =3.0,\) the particle diameter is defined as the diameter of a sphere which has volume equivalent to the corresponding spherocylinders. The porosity decreases with increasing particle size for the case of non-zero surface energy for \(\alpha =0.0,\) as seen in the Fig. 2a. However, when the surface energy is zero, corresponding to non-cohesive particles, the porosity is almost constant, independent of the size of the particles. For the experimental results for coarse particles, where the effect of cohesive force on packing can be ignored compared to gravitational force, it has been reported that there are two reproducible packing states, named RLP and RCP with porosity of 0.40 and 0.36, respectively [1]. Simulation results shown here for the case of no cohesive force are within this range, as expected. With increasing surface energy, the porosity also increases. However, the effect of surface energy on the porosity becomes weaker with increasing particle size because the gravitational force becomes dominating. For example, there is no significant difference between particles having the surface energy of \(10\) and \(50\,\text{ mJ }/\text{ m }^{2}\) for sizes of 500 and \(1{,}000\,\upmu \text{ m }\).

Fig. 2
figure 2

The relationship between porosity and surface energy for different aspect ratios. Surface energy values are \(0, 10\), and \(50 \,\text{ mJ }/\text{ m }^{2}\). a Aspect ratio, 0.0, along with comparison from Yang et al. [12], b aspect ratio, 1.0, and, c aspect ratio, 3.0

Full size image

The porosity values from the present simulations are also compared with previously published results from DEM simulations where the van der Waals force model is used instead of the JKR model [12].

As shown in the Fig. 2a, our results at the surface energy of \(10\,\text{ mJ }/\text{ m }^{2}\) are comparable with the previously published results where van der Waal model was used. While it is unreasonable to expect that two results employing different models would match, it is encouraging that the trends for the porosity as a function of particle size for cohesive particles are comparable. Since the models employed as well as the other material properties involved, such as density, friction coefficient, and so on, are different between two studies, one cannot really compare two sets of results. In principle, it is possible to utilize an equivalent relationship between surface energy, \(\upgamma \), and Hamaker constant, H. According to that relationship, which is \(\gamma =\frac{H}{24\pi D_{0}^{2}}\), as long as the \(D_{0}\) that is the cut-off distance when two particles contact each other has the value that is within the recommended range of 0.165–0.4 nm [52, 53]. However, since the cut-off distance employed is 1.0 nm in the reference [12], such equivalence is not warranted, particularly because the other material parameters in two studies are also different. Nevertheless, it is remarkable that qualitative consistency is observed between current and previous results in terms of the trend between the particle size and porosity for cohesive particles.

Figures 2b, c show the simulation results of the porosity for \(\alpha =1.0\) and \(\alpha =3.0.\) The relationship between porosity and particle size is generally similar to that of aspect ratio of 0.0 (Fig. 2a). Therefore, for all three aspect ratios, when the surface energy is not zero, porosity increases with decreasing particle size, and increases with increasing surface energy. Otherwise, porosity is almost constant regardless of the size of the particles. In addition, it can be seen from Fig. 2b, c that while the porosity becomes significantly higher for finer particles in the presence of cohesive force, i.e., as surface energy goes from 0 to \(10\,\text{ mJ }/\text{ m }^{2}\), the difference in porosity when the surface energy changes from \(10\,\text{ mJ }/\text{ m }^{2}\) to \(50\,\text{ mJ }/\text{ m }^{2}\) for both aspect ratios is not so significant for the fine particles, e.g., size of \(10\,\upmu \text{ m }\), although the values are very different from those at zero surface energy. The reason for this could be the fact that the porosity is already very high (about 0.75 for aspect ratio of 1.0 and 0.82 for aspect ratio of 3.0), and it may be reaching a level where relative differences in the surface energy values become less significant, as long as the surface energy is high enough. This observation is similar to that in bulk measurements like angle of repose, where the outcome becomes less sensitive as powders become very cohesive.

It is clear that the results about porosity trends seen in Fig. 2 have combined effects of both the cohesion, represented via surface energy, and the aspect ratio in addition to the particle size. Also, the surface energy and particle size together determine the influence of cohesion. Thus it is not very easy to assess the main impact of aspect ratio, which can be better highlighted when the results shown in Fig. 2 are reorganized, shown in Fig. 3. From Fig. 3a, it can be seen that when surface energy is zero, the porosity for the aspect ratio of 1.0 is less than that of the aspect ratio 0.0, and the aspect ratio of 3.0 corresponds to the largest porosity among the three of them.

Fig. 3
figure 3

The effect of aspect ratio on porosity for different surface energy values; a surface energy, \(0\, \text{ mJ }/\text{ m }^{2}\), b surface energy, \(10\, \text{ mJ }/\text{ m }^{2}\), c surface energy, \(50\, \text{ mJ }/\text{ m }^{2}\)

Full size image

As mentioned before, different results for packing of particles with varying aspect ratios based on different simulation methods have been published. In the mechanical contraction method, the packing is constructed by means of moving particles to avoid overlap between them as the simulation box is compressed, until it is impossible to separate the overlapping particles if the box is contracted further [28]. The results from that method indicate that porosity first decreases, and then begins to increase after arriving at a minimum value. Qualitatively similar phenomena were obtained using the relaxation algorithm, although the specific value of the aspect ratio corresponding to the minimum porosity was in the range from about 0.35–0.50 as reported in different reports [34–36]. For the simulation of packing using the relaxation algorithm, the packing of particles is performed by means of relaxation of compacted particles with initially unrealistically large overlap between them until the maximum overlap of all the particles in the system is lower than a critical value [34–36]. The previous results based on mechanical contraction and relaxation algorithm have shown that the porosity for aspect ratio of 0.0 is higher than that of the 1.0, but lower than that of the 3.0 [28, 34, 35]. Thus our current results qualitatively agree with previously reported results when there is no cohesion. Note that cohesion has not been accounted for in the relaxation or contraction algorithms.

When the surface energy is \(10\,\text{ mJ }/\text{ m }^{2}\) as is shown in Fig. 3b, the porosity corresponding to the aspect ratio of 1.0 increases faster and eventually becomes larger than the porosity for the aspect ratio of 0.0 for particles sizes less than \(200 \,\upmu \text{ m }\). For the larger particles, the porosity for the aspect ratio of 0.0 is still larger than the porosity for the aspect ratio of 1.0, consistent with the results for the surface energy of \(0.0\,\text{ mJ }/\text{ m }^{2}\). It is reasonable, as previously discussed, that since the gravitational force dominates for the larger particle size, cohesion effects are reduced. When the surface energy increases to \(50\,\text{ mJ }/\text{ m }^{2}\), the porosity for the aspect ratio of 1.0 is larger than the corresponding result for the aspect ratio of 0.0, except for the larger particle size of \(1{,}000 \,\upmu \text{ m }\). Irrespective of the surface energy values, the porosity for aspect ratio of 3.0 is always higher than that of the other two aspect ratios. Thus, higher porosity values in the experimental results for pharmaceutical powders as compared to the prediction of the published model may be explained based on the aspect ratio, since most of those powders have acicular shapes with high aspect ratio. This also indicates that our simulation results, including the effects of aspect ratios, better agree with experimental results of pharmaceutical powders [26], where although higher surface values may offer one reason for the deviation, the effect of the aspect ratio may be most relevant.

3.2 Radial distribution function

In order to better understand how the particle properties impact the packing structure and hence the porosity, the RDF values are computed. RDF, expressed as \(g(r)\), is the probability associated with finding particles at a certain distance of \(r\) of a reference particle. Function \(g(r)\) is given by:

$$\begin{aligned} g(r)=\frac{dN(r)}{4\pi r^{2}\rho dr} \end{aligned}$$
(8)

where the dN(r) is the particle numbers within a spherical shell with the radius of \(r\) and r+dr, and \(\rho \) is the particle number in the unit volume.

Figure 4 shows the results of RDF for different particle sizes when \(\alpha =0.0\) and surface energy \(=50\,\text{ mJ }/\text{ m }^{2}\). It reveals that for the largest particle size, i.e., \(1{,}000 \,\upmu \text{ m }\), there are two peaks in the RDF at the distance of 1.73 and 2.0 d (see inset, note trimmed ranges for x and y axes), agreeing with known two characteristic contacts of spherical particles: edge-sharing in-plane equilateral triangle and the centers of three particles in a line. This represents packing of non-cohesive spherical particles, since the particle size is large enough to negate any influence of cohesion. With decreasing particle size, the first peak at 1.73 d disappears, which indicates more uniform packing for fine particles [12]. Therefore, overall, these results of RDF for spherical particles agree with previously published data [12, 54, 55].

Fig. 4
figure 4

The radial distribution function (RDF) for spherical particles of different particle sizes for the surface energy of \(50\,\text{ mJ }/\text{ m }^{2}\)

Full size image

The RDF is commonly used with spherical particles, but generalizations of the RDF are also used to analyze the packing of non-spherical particles [28, 56]. The results of RDF for different aspect ratios, particle sizes, and surface energies are presented in Fig. 5, where the vertical scale is trimmed to show the details of the distributions. For large particles, e.g., \(1{,}000 \,\upmu \text{ m }\), Fig. 5a–c show that the number of peaks are different corresponding to the different aspect ratios of 0.0, 1.0, and 3.0. For the aspect ratio of 0.0, there are three peaks for all the different surface energy cases. However, for the aspect ratio of 1.0, the first peak at the distance of 1.0 d is followed by a depletion region, while there is another peak at the distance of 1.5 d. Thus, the characteristic of RDF of spherical particles vanishes with increasing aspect ratio. When the aspect ratio increases to 3.0, only the first peak at the distance of 1.0 d still exists, then the RDF decays to a nonstructural value.

Fig. 5
figure 5

The effect of aspect ratio on radial distribution function (RDF) for different surface energy values for the particle size of \(1{,}000\,\upmu \text{ m }\), except for case (d). Here, \(r\) is the distance in the multiple of particle diameter; a surface energy, \(0\,\text{ mJ }/\text{ m }^{2}\), b surface energy, \(10\,\text{ mJ }/\text{ m }^{2}\), c surface energy, \(50\, \text{ mJ }/\text{ m }^{2}\), and d particle size \(10\,\upmu \text{ m }\) and surface energy \(50\,\text{ mJ }/\text{ m }^{2}\)

Full size image

Similar to the effect of surface energy on porosity for various particle sizes, where the surface energy has less influence on the porosity for larger particle size because the gravitational force dominates, the effect of surface energy on RDF is not obvious for large particles, e.g., for \(1{,}000\,\upmu \text{ m }\). The results of RDF based on the method of mechanical contraction qualitatively agree with our simulation results using DEM for different aspect ratios [28]. For example, their results indicate there is only one peak and is not followed by a depletion region for the larger aspect ratio in the plot of RDF, which is actually similar to our results for aspect ratio of 3.0. The variation of number of peaks for different aspect ratios has also been verified by the simulation results using the relaxation algorithm [35].

However, quantitatively, current results only show two possible types of local contact structures for the aspect ratios of 1.0 and 3.0: parallel contact and perpendicular contact as indicated in reference [35], corresponding to the two peaks at 1.0 and 1.5 d in the RDF plot, respectively. As shown by the inset in the Fig. 5a, the parallel contact is two spherocylinders contact with the shortest distance between their centroids and the axes of cylinders are parallel to each other. In contrast, the perpendicular contact is formed by the two spherocylinders with perpendicular axes [35]. For the results based on the relaxation algorithm employing more values of aspect ratios, a peak at 2.0 d appears with the change in aspect ratio and it corresponds to another type of local contact structure [35]. However, performing DEM simulations for many different aspect ratios is outside of the scope of the present paper due to higher computational burden, and in the next sub-section, coordination number analysis is employed for further examining the packing structure.

In order to highlight the effect of surface energy, the RDF functions for fine particles (size \(10\,\upmu \text{ m }\)) and high surface energy (\(50\,\text{ mJ }/\text{ m }^{2}\)) for all three aspect ratios (\(\alpha =0.0,1.0,\) and 3.0) are shown in Fig. 5d. For spherical particles (\(\alpha =0.0\)), results are similar to previous discussion that the second peak at 1.73 d vanishes for fine particles. For aspect ratio of 1.0, the peak at 1.0 d shifts slightly towards a higher value. One possible reason is that the parallel contact structure discussed before for Fig. 5a may have changed as the particle-pair may not get well aligned and result in a small angle shown in the inset in Fig. 5d. When the aspect ratio is 3.0, there are no obvious peaks in the RDF, indicating more uniform packing structure. Therefore, based on the information obtained from RDF, the surface energy has significant effect on the packing structure. As surface energy changes, the packing structure may also correspondingly change.

3.3 Contact geometry

3.3.1 Coordination number

Coordination number distributions provide quantitative description of the contacts between the particle and its neighbors. In the simulation, the specific value of coordination number depends on the definition of critical distance of separation, below which the two particles are regarded as being in contact. Different critical distance values, for example, 1.005 and 1.01 d (d is the particle diameter) have been used to calculate the coordination number in previous work [12, 54]. As expected, the coordination number will increase with increasing critical distance because more neighboring particles that do not direct contact with the specified particle will also be included in the coordination number [12]. Therefore, in the present work, two different values are used but it is understood that the comparison between present works with previous ones is only quantitative.

Information about the contacts can be computed and saved during the simulation using the EDEM software, where the cut-off distance employed by EDEM is 1.0 d. These results are shown in Fig. 6a. As can be seen, these results show little impact of particle size on coordination number for the aspect ratio of 0.0, and do not agree with previously published results [12]. In order to have a better qualitative comparing of the present simulation results with previously published data, the coordination numbers for spherical particles are specifically calculated for the cut-off distance of separation of 1.005 d, shown in Fig. 6b. These results have a better qualitative agreement with previous work, suggesting that the trends observed in our work are reasonable. Comparing Fig. 6a to b, as would be expected, the results with 1.005 d cut-off distance are higher than those exported data from EDEM in Fig. 6a.

Fig. 6
figure 6

The coordination numbers for different surface energy values as a function of particle size. a The aspect ratio 0.0 and coordination number directly computed through EDEM (cut-off distance is 1.0 d), b coordination number computed using the cut-off distance 1.005 d for the aspect ratio is 0.0, c the probability distribution of the coordination number for particle size of \(10\,\upmu \text{ m }\) for various surface energy values, d the probability distribution of the coordination number for particle size of \(1{,}000\,\upmu \text{ m }\) for various surface energy values

Full size image

For the spherocylinder particles, it is not convenient to calculate the coordination numbers at various, specific cut-off distances because the shortest distance between two spherocylinders is dependent on the relative orientation of their axes. Consequently, for the sake of consistency between various aspect ratios, the subsequent results and the discussion of the coordination numbers at non-zero aspect ratios only be concerned with the results directly obtained from the EDEM. According to the Fig. 6a, when the surface energy is zero, the coordination number ranges from 4.37 to 4.64, depending on the size of the particles. These results are comparable to some of the previously reported experimental and simulation results. For example, Mason obtained the coordination number of \(4.76\pm 0.02\) from the experimental results of Scott [57, 58], which is also in good agreement with the simulation result of \(4.79\pm 0.02\) [59]. The slight difference between our simulation results and the experiment is probably due to the larger particle size (\(3{,}175\,\upmu \text{ m }\)) with higher density (steel, \(7.8\,\text{ kg }/\text{ m }^{3}\)) used in the experimental investigation, and because the shaking was done after pouring the particles into the cylindrical container in the experiment, causing the particles to rearrange and pack more densely [57].

For zero aspect ratio particles, as per Fig. 6a, the coordination number decreases when the surface energy is increased to \(10\) and \(50\,\text{ mJ }/\text{ m }^{2}\). The reduction in the coordination number for various surface energy values demonstrates that the surface energy, hence the cohesive force, is an important material property that influences the packing structure, just like what has been observed with the friction coefficient [18].

Within the packing, not every particle has the same coordination number. Therefore, the distributions of coordination numbers, which can provide more detailed information about how the coordination number changes under various conditions, are examined. Figure 6c, d show the results of the distributions of the coordination numbers for particle sizes of \(10\,\upmu \text{ m }\) (very fine, hence cohesive, except when surface energy is zero) and \(1{,}000\,\upmu \text{ m }\) (large, hence mostly non-cohesive). As depicted in Fig. 6c, when the surface energy changes from 0 to \(10\,\text{ mJ }/\text{ m }^{2}\), the coordination number distribution shifts towards the lower value and the width becomes narrower. When the surface energy increases from 10 to \(50\,\text{ mJ }/\text{ m }^{2}\), there is no further variation in the width of distribution and the overall distribution shifts towards the lower value, and hence it is the main reason behind the decreasing coordination number. According to the previous results, the effect of surface energy on the coordination number is different than the effect of the friction coefficient, where only overall distribution shift is observed with increasing friction coefficient [18], but no change in the width. In addition, when the surface energy is \(50\,\text{ mJ }/\text{ m }^{2},\) the minimum value seen in the distribution is one, indicating there are a few particles that only have a single contacting neighbor. Note that although there is very low probability for a particle to have a coordination number of one, it is a finite, non-zero value. This was found to be the case regardless of the cut-off distance of separation, which was changed from 1.0 to 1.01 d (results are not shown for the sake of brevity). Having a coordination number of one in a static packed-bed may be a special case of packing and, to our knowledge, such situations have not been discussed before. The lack of previous references on such structure may also be due to the fact that our observations are for the case of packing of fine, cohesive powders, which have not been previously well-discussed. In order to identify the corresponding structure for this situation, the snapshots showing the particle with only one contact and all its neighbors within the distance less than 2.0 d are shown in Fig. 7. In Fig. 7a, b, two different particles, each having only one contact, are shown, and they were randomly selected from the list of such particles (for reference, their identity numbers during the simulation are 4,230 and 619, respectively). In Fig. 7a, b, the blue color represents the particle with a single contact (central particle) and the red ones represent its neighbors. While it may not be easy to discern from these figures, the blue particle only contacts with one red particle, and an arrow identifies that contacting red particle in each case. One could visualize from these pictures that the neighbors formed a cage-like structure around the central particle, and the central particle is attached to only one of them. This cage structure forms due to the strong cohesive force between the fine particles induced by the higher surface energy, and is an interesting situation previously not identified.

Fig. 7
figure 7

Snapshot of the simulation depicting the cage structure. Central sphere (pointed by an arrow, and blue in on-line version) represents the specified particle having only one contact with a contacting sphere pointed to by an arrow. a Particle identity number is 4,230, b particle identity number is 619

Full size image

It is worth noticing that in the previous simulation results based on the van der Waals model, it is shown that the a single contact appears, although at very low probability, for the particle size of \(5 \,\upmu \text{ m }\), but not for the size of \(10\,\upmu \text{ m }\), and the corresponding cage structure has not been identified in that work [12]. The investigation about the effect of friction coefficient uncovered that the coordination number decreases to two with increasing friction coefficient, indicating the appearance of arching structure within the packing [18]. However, our results show a unique influence of surface energy on the coordination number and packing structure, indicating the appearance of particles with as few as one contact if the cohesive force is dominating compared to the gravitational force, because the cage structure can be supported and created within the packing. Compared to the arching structure, the cage structure should correspond to more sparse packing, leading to higher porosity values.

To further examine the influence of cohesion, or lack thereof, distributions for larger particles are considered. Accordingly, Fig. 6d shows the coordination number distribution for particle size of \(1{,}000\,\upmu \text{ m }\). It can be seen that the change in the coordination number distribution due to increased surface energy is mainly in terms of the shift of distribution towards the lower values. However, the width and shape of the distributions stay approximately the same for various surface energy values. In addition, the differences in the distributions for three different values of surface energy are not prominent compared to the particle size of \(10\,\upmu \text{ m }\). Moreover, the minimum attainable value of the coordination number is two for the particle size of \(1{,}000\,\upmu \text{ m }\) at surface energy of \(50\,\text{ mJ }/\text{ m }^{2}\), indicating that there is no cage structure in the packing of \(1{,}000 \,\upmu \text{ m }\) particles in contrast to \(10\,\upmu \text{ m }\) particles which exhibit the effect of cohesion.

Figure 8a, b show the results of coordination numbers for aspect ratios of 1.0 and 3.0, which are directly obtained from EDEM simulation, thus each contact is true contact between the particles. When the surface energy is zero, the coordination numbers only slightly increase with increasing particle size for both cases. Upon examination of Fig. 8a, b along with the zero aspect ratio case of Fig. 6a, it is seen that the coordination number increases with increasing aspect ratio for all values of the surface energy. This is an important observation and has implications to porosity as will be discussed next.

Fig. 8
figure 8

The coordination numbers for different surface energy values as a function of particle size for non-zero aspect ratios; a aspect ratio, 1.0, b aspect ratio, 3.0

Full size image

When the results for porosity shown in Fig. 3 are examined along with the results for coordination number for different non-zero aspect ratios shown in Figs. 6 and 8, it can be seen that there is no monotonously corresponding relationship between porosity and coordination number, which is indeed the case for monodispersed spherical particles (zero aspect ratio case) shown in [12]. In fact, for spherocylinder particles, as indicated by random contact equation [60, 61], the aspect ratio plays a role in the relationship between porosity and coordination number. However, it is not very clear how the aspect ratio impacts the contact geometry. Considering that the coordination number only provides information about how many neighboring particles exist around the specified particle within a certain distance, it lacks information about how those neighbors are arranged in space, hence information on the spatial packing structure. Next, we analyze the distribution of angles of contact vectors, which can represent the orientation of contacts, so that the effect of aspect ratio on porosity can be understood in more detail.

3.3.2 Distribution of contact vector

Contact vector is defined as the vector connecting the center of the particle and the contact point with its neighbor. Figure 9 shows the schematic diagram depicting the contact vector. The angles \(\uptheta \) and \({\phi }\) define the azimuthal angle and polar angle in the spherical coordinate system, respectively. \(\uptheta \) and \(\phi \) can range from \([0, 90^{\circ }]\) and \([0, 180^{\circ }],\) respectively. However, the overall characteristic of distribution in each case can be obtained within \([0, 90^{\circ }]\) due to symmetry. Therefore, the values of \(\uptheta \) and \(\phi \) are constrained within \([0, 90^{\circ }]\) for simplicity. For each contact vector indicated by a green line with arrow in Fig. 9, the value of \(\uptheta \) and \(\phi \) is calculated and the statistical distribution is given in Fig. 10.

Fig. 9
figure 9

The schematic diagram depicting the angles of the contact vector. The angles of \(\uptheta \) and \(\phi \) are the azimuthal angle and polar angle in the spherical coordinate system, respectively. Arrow with solid line indicates the contact vector between two spherical particles

Full size image
Fig. 10
figure 10

The probability distribution of the contact vector angles. a Surface energy, \(0\,\text{ mJ }/\text{ m }^{2}\), b surface energy, \(10\,\text{ mJ }/\text{ m }^{2}\), c surface energy, \(50\,\text{ mJ }/\text{ m }^{2}\)

Full size image

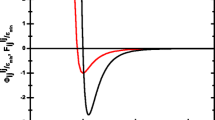
According to Fig. 10a, when surface energy is zero, the distribution of \(\uptheta \) is increasingly wide (solid lines) as aspect ratio increases from 0.0 to 3.0. This is indicated by the height of two peaks; for case of the aspect ratio of 0.0 at about \(48^{\circ }\) and \(90^{\circ }\), decreasing as surface energy increases and the distribution becomes flatter. In contrast, the distribution of \(\phi \), shown in dashed lines, is flat and lacks any obvious peaks for the aspect ratios of 0.0 and 1.0. However, as the aspect ratio increases to 3.0, it develops a small peak at \(90^{\circ }\) at the expense of decreasing values at the lower angles. Therefore, with increasing aspect ratio, the \(\uptheta \) distribution of contact vector widens and the amplitude of the peak at \(90^{\circ }\) decreases, but the \(\phi \) distribution tends to develop a peak at \(90^{\circ }\), which differentiates it from the \(\uptheta \) distribution.

The presence of peaks in the distribution of contact vector indicates that certain orientations are more preferable than others; in other words, the particles pack in a more orderly fashion compared to the case of the distributions without peaks. However, here, we see that while the \(\uptheta \) distribution indicates less order as aspect ratio increases, the \(\phi \) distribution suggests higher order. Therefore, we believe that the opposite trends of \(\uptheta \) and \(\phi \) distributions with respect to the aspect ratios are two competing mechanisms that influence the porosity of packing. With increasing aspect ratio, the distribution of \(\uptheta \) becomes wider, indicating less order in the structure and thus leading to higher porosity. However, the distribution of \(\phi \) begins to develop a peak at \(90^{\circ }\) and it is expected to lead to decreased porosity. Meanwhile, from Fig. 10, the change of \(\phi \) is not as pronounced as compared to the \(\uptheta \) distribution. Therefore, the \(\uptheta \) distribution should have a more significant effect on the porosity, which indicates decreasing porosity as surface energy increases, although the coordination numbers also increase at the same time.

The distributions of \(\uptheta \) and \(\phi \) for the surface energies of \(10\) and \(50\,\text{ mJ }/\text{ m }^{2}\) are also calculated and shown in Fig. 10b, c so that the influence of surface energy on the distributions, and hence on packing as well as porosity, can be revealed. According to the results, the general trends of the distribution are similar for all different surface energy values, although there are characteristic differences (for example, the position of the first peak of the \(\uptheta \) distribution). With increasing aspect ratio, the height of \(\uptheta \) distribution at \(90^{\circ }\) continues to decrease, and the initial peak at \(90^{\circ }\) for the aspect ratio of 0.0 continues to diminish as the aspect ratio and surface energy increase and finally forms a valley instead of a peak. On the other hand, the amplitude of the \(\phi \) distribution at \(90^{\circ }\) keeps increasing and forms a small but obvious peak at all non-zero surface energy values. At the same time, the amplitude of the distribution corresponding to the smaller angles decreases.

The variations seen in the \(\uptheta \) and \(\phi \) distributions for different aspect ratios can be used to explain the results about porosity shown in Fig. 3a–c. For the Fig. 3a, the surface energy is zero and the porosity for aspect ratio of 3.0 is higher than that for aspect ratio of 0.0. However, the coordination number is also higher at higher aspect ratio as compared to lower ones. The reason for this is that the \(\uptheta \) distribution tends to become flat and the packing becomes more disordered for aspect ratio of 3.0, which results in the higher porosity. For the Fig. 3b, c, the interpretation is similar to that of Fig. 3a. In addition, the results shown for RDF in Fig. 5 show that for the fine particles with higher surface energy, parallel contact structure can change slightly and become non-parallel. As shown in the inset in the Fig. 5d, such configuration is likely to result in the distribution of \(\uptheta \) changing accordingly and consequently the peak at \(90^{\circ }\) would vanish. Therefore, the information from both the RDF plots and the distributions of contact vector match each other and explain the apparent contradiction between increased porosity for increased coordination numbers of fine, cohesive particles with non-zero aspect ratios.

In previous work, the \(\uptheta \) distribution has been used to analyze the contact force in the assembly of spherical particles and the anisotropy of force network is illustrated, indicated by the appearance of the peaks in the probability distribution [19, 22]. According to our results in Fig. 10, for the particles with aspect ratio of 0.0, the \(\phi \) distribution is flatter for various surface energies. Therefore, only the \(\uptheta \) distribution influences the contact geometry in this case and it is reasonable to ignore the effect of the \(\phi \) distribution. However, when the aspect ratio is 1.0 or 3.0, the \(\phi \) distribution begins to develop a peak at \(90^{\circ }\) and this tendency is strengthened by the increased surface energy, which is an obvious deviation compared to the aspect ratio of 0.0. Although the increased porosity trends are mostly explained by the \(\uptheta \) distribution, it would be interesting to examine how the \(\phi \) distribution impacts the packing of non-spherical particles with higher cohesive force and aspect ratio, and to what extent it impacts the packing property; and hence would be a topic of future research.

4 Conclusions

The DEM is used to simulate the dynamic process of particle packing for different particle sizes, their surface energies, and aspect ratios. The JKR model and multi-sphere method are employed so that the effect of the surface energy (thus cohesion) and aspect ratio can be revealed. The results are obtained for the porosity, RDF, and finally the coordination number as well as the distribution of the contact vectors to better understand the packing structure.

Regarding the porosity, the simulation results show that particle sizes, surface energy, and aspect ratio all influence it to various degrees. For non-cohesive spherical particles, i.e., when the surface energy is zero and the aspect ratio is zero, the coordination number and porosity almost stay constant regardless of the particle size, indicating the packing is independent of particle size, this generally agrees with some of the previous observations. However, for cohesive, spherical particles, i.e., when surface energy is not zero, the coordination number increases with decreasing porosity. This is in agreement with the previously published results. For the various aspect ratios, porosity corresponding to aspect ratio 0.0 is higher than that at the aspect ratio of 1.0, but less than that at the aspect ratio of 3.0, which is qualitatively in agreement with the results based on the mechanical contraction approach and the relaxation algorithm, validating the presented DEM simulations as a useful method to study the effect of particle shape on packing. Thus in summary, in the presence of surface energy, particles are cohesive, and the porosity increases with decreasing particle size and increasing aspect ratio; all of which are generally expected.

The RDFs for all cases are computed. For the case of spherical particles, the patterns agree well with the previously published results for both non-cohesive and cohesive particles. As the aspect ratio is increased from zero (spheres) for the case of no-cohesion or large sizes, the trends begin to deviate from those of the spherical particles but exhibit trends qualitatively similar to the simulation results based on the relaxation algorithm. However, for the cohesive particles, quantitative examination reveals that two characteristic peaks in the RDF representing parallel and perpendicular contacts for non-spherical particles at 1.0 and 1.5 d, respectively, show deviations, and reveal an interesting pattern that high cohesion leads to contacts where two particles are misaligned instead of being perfectly parallel.

The analysis of the relationship between coordination number and porosity reveals interesting patterns; the most novel outcome is the identification of the existence of single contact for a finite number of particles, attributed to the formation of a cage structure around the particle, when there exist strong cohesive forces as compared to the particle weight, due to higher surface energy and small particle size. This phenomenon has not been reported or discussed previously, and supports the observation that the surface energy tends to influence both the peak position and the width of the distribution because fewer contacts are required to achieve the mechanical equilibrium for the particles with higher surface energy. The results also reveal that in the case of the spherical particles, i.e., aspect ratio of 0.0, the higher porosity corresponds to the smaller coordination number. In contrast, the higher porosity does not always imply smaller coordination numbers for the case of particles having non-zero aspect ratios and high surface energies. In fact, for higher aspect ratios, both coordination number and porosity increase as surface energy increases; hence, the coordination number analysis by itself is not sufficient to corroborate the porosity because of the lack of information regarding the orientation of contact vector for particles with higher aspect ratios. Consequently, the distribution of the angles of contact vector between the particles is analyzed to reveal useful information about the packing structure. Those results indicate that the distributions of \(\uptheta \), the azimuthal angle, \(\phi \), and the polar angle, have different trends with various aspect ratios. However, the \(\uptheta \) distribution, being more dominant between the two, better explains the results of increased porosity in spite of higher coordination numbers for high aspect ratio particles.

In summary, the DEM simulation results presented here shed light on the packing density and structure for fine particles as well as coarse particles with various aspect ratios and surface energies, revealing interesting features not easily discerned via experiments, and shed light on the role of cohesion as well as particle aspect ratios on packing.