Abstract
Caffeic acid (C9H8O4) and its conjugate base C9H7O4 − (anionic form—known as caffeate) were analyzed computationally through the use of quantum chemistry to assess their intrinsic global and local reactivity using the tools of conceptual density functional theory. The anionic form was found to be better at coordinating the silver cation than caffeic acid thus suggesting the use of caffeate as a complexation agent. The complexation capability of caffeate was compared with that of some of the most common ligand agents used to coordinate silver cations. Local reactivity descriptors allowed identification of the preferred sites on caffeate for silver cation coordination thus generating a plausible silver complex. All silver complexes were analyzed thermodynamically considering interaction energies in both gas and aqueous phases; the complexation free energy in aqueous phase was also determined. These results suggest that more attention be paid to the caffeate anion and its derivatives because this work has shed new light on the behavior of this anion in the recovery of silver cations that could be exploited in silver mining processes in a environmentally friendly way.

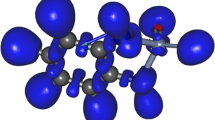
The dual descriptor (DD) presented as lobes of two colors; f(2)(r) > 0 implies a dark-colored lobe, indicating attraction of nucleophilicattack; f(2)(r) < 0 implies a light-coloredlobe, indicating attraction of electrophilic attack. All isosurfaces depicted at 0.001 au
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Caffeic acid [also called hydroxycinnamic acid or trans-3-(3,4-dihydroxyphenyl)propenoic acid (C9H8O4; pKa = 4.4)] presents two functional oxygenated groups: catechol and carboxylic [1] groups (Fig. 1). Caffeic acid is a naturally occurring organic compound, where the caffeate anion (C9H7O4 −) corresponds to the predominant species at pH ≃ 7 (Fig. 2). It is found in all plants [2, 3] because it is a key intermediate in the biosynthesis of lignin—one of the principal sources of biomass [4].
Because of the two functional groups, this acid has two coordination sites in competition (Figs. 1 and 2) [5]. One site corresponds to the catechol group and the other to the carboxylic group. This molecule is known to form metallic complexes easily, but caffeic acid exhibits a different behavior depending on the nature of the metal, which implies a classification for the interacting species (ligand and metal) within the framework of Pearson’s HSAB principle [6]. This molecule and/or its conjugate base would be plausible candidates to replace cyanide in silver or gold recovery operations. In fact, some experiments supported by quantum chemical calculations have demonstrated that Al3+ forms a chelate with the catechol group of caffeic acid [7, 8]. In addition, fluorescence and Raman spectroscopies have suggested that Pb2+ coordinates with the carboxylic acid function [9] along with time-dependent density functional theory (DFT), which has predicted the electronic spectra, with complete assignment of the UV-vis spectrum of the Pb complex [10] and UV-visible and synchronous fluorescence spectroscopic of the complexation of Al3+ [11].
According to the information above, caffeic acid derivatives [12–14] should offer similar possibilities to coordinate other metal cations. However, the tools available from “conceptual DFT” [15, 16] have not been used systematically with this molecule and its derivatives in order to assess possible coordination sites for metal cations at different pH values. Since pH=7 (at which caffeic acid does not exist significantly) is an environmentally friendly condition in which to carry out metal complexation procedures in aqueous solution, the present work examines the interaction between Ag+ and caffeate, with ionic and covalent interactions being measured through the use of V(r), which is the molecular electrostatic potential (MEP) [17, 18], and some local reactivity descriptors given by conceptual DFT, respectively.
Theoretical background
There are three kinds of reactivity descriptors: global reactivity descriptors (GRDs), which do not depend on position vector, r; local reactivity descriptors (LRDs), which do depend on r; and non-local reactivity descriptors, which depend on more than one r. Details of the physical meaning and working equations to obtain the most important GRDs and LRDs are defined in the following sections. Non-local reactivity descriptors will not be explained because they were not used in this work.
Global reactivity descriptors
Conceptual DFT [6, 19] has provided a set of reactivity descriptors based on the fact that, in the canonical ensemble, the energy E is a function of N (the number of electrons) and a functional of υ(r) (the external potential). In consequence, E ≡ E [N, υ(r)].
Chemical potential, molecular hardness and electrophilicity descriptors
Assuming differentiability of E with respect to N and υ(r), a series of response functions emerge: the chemical potential that characterizes the escaping tendency of electrons from the equilibrium system is defined as [19, 20]:
the molecular hardness that measures the resistance to charge transfer, is defined as [19, 21]:
Both μ and η are GRDs that describe reactivity of a molecular system [19] as a whole. A first level of approximation—the three-point finite difference approximation—leads to the following working equations for these quantities: [6, 19]
where I and A are the first vertical ionization potential and the first electronic affinity of the molecule under study, respectively. A second level of approximation based on the use of the Koopmans’ theorem [22] from the closed-shell Hartree-Fock theory [23] (I ≃ −εH and A ≃ −εL) allows one to write μ and η in terms of energies of the lower unoccupied molecular orbital and higher occupied molecular orbital, LUMO (εL ) and HOMO (εH), respectively:
Following Parr et al. [24], the square of the chemical potential of a chemical species divided by twice its molecular hardness defines its electrophilicity descriptor:
which measures the energetic stabilization when the system gains electrons from its surroundings. Lastly, the global softness, S, is defined mathematically as the reciprocal of molecular hardness [19]:
It can be written rigorously as \( S = - {{\left\{ {\frac{{{{\partial }^{2}}\Omega }}{{\partial {{\mu }^{2}}}}} \right\}}_{{u(\mathbf r)}}} = {{\left\{ {\frac{{\partial N}}{{\partial \mu }}} \right\}}_{{\upsilon(\mathbf r)}}} \) because the latter arises from the grand canonical ensemble in a natural way.
Local reactivity descriptors
At a local level, electronic density is the first LRD to be used when electrostatic interactions are predominant between molecules; within the framework of conceptual DFT, it is defined as follows:
But when chemical reactions are governed by interactions that are mainly covalent in nature, a second order LRD called the Fukui function [6, 21–25, 27] is used instead of electronic density. The Fukui function is defined in terms of the derivative of ρ(r) with respect to N; through a Maxwell relation, the same descriptor is interpreted as the variation of μ with respect to υ(r) [28, 29]:
The function f (r) reflects the ability of a molecular site to accept or donate electrons. High values of f (r) are related to a high reactivity at point r [28, 29].
Since the number of electrons N is a discrete variable [30], right and left derivatives of ρ(r) with respect to N have emerged. By applying a finite difference approximation to Eq. (10), two definitions of Fukui functions depending on total electronic densities are obtained:
where ρ N+1(r), ρ N (r) and ρ N−1(r) are the electronic densities at point \( {\mathbf{r}} \) for the system with N +1, N and N −1 electrons, respectively. The first one, f +(r), has been associated to reactivity for a nucleophilic attack so that it measures the intramolecular reactivity at the site r toward a nucleophilic reagent. The second one, f −(r), has been associated to reactivity for an electrophilic attack so that this function measures the intramolecular reactivity at site r toward an electrophilic reagent [31].
The densities of frontier molecular orbitals (FMOs), ρ L (r) (LUMO density) and ρ H (r) (HOMO density), now enter the picture since it has been shown [31, 32] that when the frozen orbital approximation (FOA) is used there is a direct relationship between f +/−(r) and the density of the appropriate FMO, thus avoiding calculations of the system with N + 1 and N − 1 electrons:
On the other hand, the use of Eqs. (13) and (14) instead of Eqs. (11) and (12) allows one to decrease the computational effort without losing the qualitative picture of local reactivity, but this approach should always be checked by comparison of these two pairs of working equations because the first level of approximation based on total electronic densities will always be more accurate that the second level of approximation based on densities of FMOs.
Condensation to atoms is achieved through integration within the kth-atomic domain Ωk [26, 33–36]
\( f_k^{{ + / - }} \) is now an atomic index that is used to characterize the electrophilic/nucleophilic power of atom k.
More recently, Morell et al. [37, 38] found, at a third order, a physical interpretation for a new LRD [39] for chemical reactivity called dual descriptor (DD), f (2)(r) ≡ Δf (r). The notation Δf(r) will not be used in this article; only the f (2)(r) notation for the DD will be used.
This LRD is defined in terms of the derivative of f (r) with respect to N . Through a Maxwell relation, the same descriptor is interpreted as the variation of η with respect to υ(r). The definition of f (2)(r) is shown as indicated by Morell et al. [37, 38]:
According to expressions given by Eqs. (11) and (12), f (2)(r) is written as the difference between nucleophilic and electrophilic Fukui functions [37]:
The use of densities of FMOs provides an easier-to-compute working equation:
The DD allows simultaneous determination of the preferred sites for nucleophilic [f (2)(r) > 0] and electrophilic [f (2)(r) < 0] attacks over the system at point r. The DD can also be condensed through an appropriate integration within the kth-atomic domain Ωk:
When \( f_{k}^{{(2)}} > 0 \), the process is driven by a nucleophilic attack on atom k, and then that atom acts as an electrophilic species; conversely, when \( {{f}^{{(2)}}}({\mathbf{r}}) < 0 \), the process is driven by an electrophilic attack over atom k, and therefore atom k acts as a nucleophilic species.
Particular attention has been paid to the DD, f (2)(r), because it has been demonstrated to be a robust tool with which to predict correctly specific sites of nucleophilic and electrophilic attacks much more efficiently than the Fukui function by itself because the DD distinguishes true nucleophilic and electrophilic sites. Consequently, several works have noted the power of f (2)(r) and all those LRDs based on it [40–44]. The molecular symmetry influences the local reactivity and, as a consequence, the Fukui function conserves the symmetry as shown by Flores-Moreno [45]. Previously, Martínez proposed a simple procedure to take into account FMO degeneration [46] when using the FOA based on Koopmans’ theorem [22], so that f (2)(r) and any other LRD depending on the DD can be properly depicted, thus allowing a local reactivity isosurface adapted to the molecule symmetry to be obtained as demonstrated in a previously published article where the local reactivity on Buckminster fullerenes [47] was established using the degenerate FMO approach mentioned above.
Finally, other LRDs depending on the DD promise to reveal interesting results that imply interactions of the nucleophilic–electrophilic type. One of them is the local hypersoftness, which permits a comparison between the selectivity of different size molecules. The exact equation can be presented as follows [41, 42, 48–50]:
And the corresponding working equation is the following:
Computational methods
All ligands and complexes formed with silver atoms were optimized geometrically without symmetry restrictions according to the Schlegel algorithm [51] at the DFT level of theory. The functionals used in these calculations were Becke-3 for exchange and Lee-Yang-Parr for correlation [52–55]. The 6-31G(d) [56–58] basis set was used. The double-zeta quality LANL2DZ [59, 60] basis was used to describe the silver atom. Frequency calculations were performed at the same level of theory in order to ensure that each optimized structure corresponds to an energy minimum. Both gas and aqueous phases were taken into account. The solvent effect was included by means of the self-consistent reaction field method through the polarizable continuum model (SCRFPCM) [61–64]. 3-D maps of MEP were obtained for both caffeic acid and the caffeate anion. All calculations were carried out using Gaussian 09 [65] code. Koopmans’ theorem was used to obtain μ, η and ω through the use of Eqs. (5) and (6). For condensation of Fukui function, Fukui REV 1.1 software was used [26, 33, 66, 67].
Results and discussion
Global and local reactivity
As can be seen in Table 1, the chemical potential of the caffeate anion is greater than that of caffeic acid. In addition, the molecular hardness of the caffeate anion is smaller than that of caffeic acid. So, in the case of covalent interactions with soft cations like silver or gold, the caffeate anion can be considered a better ligand than caffeic acid. In fact, the electrophilicity values reveal that the caffeate anion needs less energy to gain electrons from its surroundings than caffeic acid.
However, the most important information on site reactivity is given by LRDs. A preliminary analysis already published by Cornard, Lapouge and coworkers [5, 8] of the capabilities of caffeic acid and its conjugate base to coordinate some cations of metallic atoms will be described in terms of MEP and DD in the following paragraphs. These authors revealed that the catechol group is the most favorable functional group to coordinate the aluminum cation. In fact, the only site that coordinates to Al3+ is the catechol group at pH ≃ 6.5; this complexation capability also increases as the pH increases [11]. This experimental and theoretical evidence supports the capability of the catechol group to coordinate the metal cation Al3+.
In order to explain the nature of such interactions, a 3-D map of MEP is depicted in Fig. 3a. According to this picture, the MEP of caffeic acid (left-hand side) indicates that the carboxylic group is slightly more likely to interact with an approaching cation than the catechol group, but this distinction is not detectable easily from the MEP. Besides (see right-hand side), the carboxylate in the caffeate anion is the most reactive functional group. Indeed, according to the MEP, the catechol group cannot overcome the coordination capabilities of either the carboxylic group in caffeic acid or the carboxylate group in the caffeate anion. This apparent contradictory statement would be true if electrostatic interactions were the driving force of the elementary chemical reaction.
a,b Species of the acid–base equilibrium represented by means of two local reactivity descriptors (LRDs) described as 3-D maps. a Molecular electrostatic potential (MEP), ranging from negatives (red) to positive (blue) values; a red zone indicates a dominant effect of electrons (electrically negative), green zones indicate sites where the effects of nuclei and electrons are balanced, and blue zones show sites where the nuclear effect is dominant (electrically positive) so that an interval {V (r)}min ≤ V (r) ≤ {V (r)}max is depicted. b The dual descriptor (DD) exhibits lobes of two colors; f (2)(r) > 0 leads to a dark colored lobe, indicating nucleophilic attack; f (2)(r) < 0 leads to a light colored lobe thus indicating electrophilic attack. All isosurfaces are depicted at 0.001 au
The MEP never fails when electrostatic interactions play the main role in an elementary chemical reaction. In consequence, the only way to understand the actual preference of the catechol group to coordinate Al3+ as reported is based on the predominance of covalent interactions, hence an LRD like DD, that reveals sites of reactivity in the framework of covalent interactions, must be used. After applying DD, the LRDs for caffeic acid and its conjugate base are displayed in Fig. 3b. After releasing the acidic proton from the caffeic acid, the negative phase of the DD has changed its position from the catechol group toward the carboxylate group as shown in Fig. 3b. In consequence, this region of the conjugate base is the only site that could coordinate a species such as Ag+. Note that the negative phase of the DD of caffeic acid is located at the catechol group, thus supporting the experimental and theoretical evidence about Al3+ described above. This is proof that DD may be used as a complementary tool to take into account covalent interactions that MEP cannot detect.
So, the catechol and carboxylic functional groups could be preferred sites to coordinate Ag+. The predominance of caffeic acid, which occurs at pH values < 4.4, indicates an acidic, and thus undesirable, working condition that is not environmentally friendly as proposed in this study. Therefore the most favorable working condition corresponds to pH ≃ 7. At this pH value, the caffeate anion predominates over caffeic acid and, consequently, research to locate the most reactive site should be oriented solely towards the caffeate anion rather than the caffeic acid.
Having demonstrated the capacity of DD by itself to justify interactions that cannot be explained by the use of MEP, attention is now focused on the caffeate anion for reasons described in the preceding paragraph. From Fig. 3, readers should note that the caffeate anion cannot interact with a metallic cation through the catechol group, either by covalent or electrostatic reasons because, as depicted in Fig. 3, the MEP shows that the negative charge concentrates at the carboxylate group. On the other hand, the DD reveals that the carboxylate group shows greater availability for attack also by an electrophilic species, so the carboxylate group should be a suitable site to coordinate a metal cation such as Ag+.
To quantify the qualitative discussion presented above, attention should be paid to the local hypersoftness descriptor s(2)(r) condensed on atoms. Table 2 lists the values of condensed LRDs on the oxygen atoms. A negative value of the local hypersoftness is favorable to coordination of a metallic cation. The more negative the value, the higher the capacity to coordinate a metal cation. As can be observed, caffeic acid is discarded not only for global reactivity reasons and because of unfavorable environmental working conditions, but also for local reactivity reasons because, in spite of negatives values at oxygens 3 and 4 from the catechol group in caffeic acid, more negative values of \( s_{k}^{(2)} \) are exhibited at oxygens 1 and 2 of the carboxylate group from the caffeate anion thus demonstrating that the caffeate anion is a better ligand for Ag+ than caffeic acid.
An attempt to obtain all possible silver complexes was carried out by means of placing the Ag+ at different positions around the caffeate anion to perform geometrical optimizations, but not all optimization computations were able to converge except when the silver cation was positioned over the oxygen atoms of the carboxylate group, thus giving only a couple of optimized structures (cis-like and trans-like with respect to the position of catechol groups). The most stable silver complex was selected and is depicted in Fig. 4.
Since the coordination number of the silver cation is two and there are two oxygen atoms in the carboxylate group of the caffeate anion, the optimized geometry of the respective silver complex acquires a proper conformation that allows it to satisfy this coordination number through a stoichiometry of 2:2 as can be observed in Fig. 4, which gives the following molecular formula: Ag2(C9H7O4)2. This silver complex is a stable compound that will be analyzed thermodynamically in the next section.
Thermodynamic aspects
To quantify the stability of the silver complex obtained, a set of theoretical thermodynamic calculations was performed to compute three types of variations of standard Gibbs’ free energies as follows. The first type of energetic value is defined as the interaction energy, \( {\Delta}\mathrm{G}^{\circ}_{int\, (g)} \), according to the following model of reaction:
where L corresponds to one of the most common monodentate ligands used to form a complex with silver cation, and they are the following five ligands: 1, CN−; 3, S2O3 −2; 4, NH3; 5, Cl− and 6, H2O; meanwhile, q corresponds to the respective net charge. Since ligand 2 (caffeate anion) is a bidentate ligand, a different reaction model was defined according to this characteristic and can be shown as follows:
\( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (g)} \) reveals energetic aspects as a consequence of the intrinsic reactivity observed between silver cation and each type of ligand. This provides a pure idea of the coordination power of every ligand.
The second type of energetic value corresponds to the interaction energy including the solvent effect, \( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (aq)} \), which is calculated as follows by means of this reaction model, for monodentate ligands such as the caffeate anion:
\( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (aq)} \) gives a similar idea of the intrinsic reactivity exhibited between each ligand and silver cation, but including the solvent effect through a continuum model. In this case, a dramatic modification might occur because the solvent effect could alter the local reactivity of a ligand in comparison with the gas phase depending on the ligand’s size and the functional groups exposed by it.
And lastly, the complexating energy, \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)} \), is calculated from the following reaction models:
This reaction model is closer to experimental results because it is nearer the reality according to the exchange of ligands that does occur in aqueous media (exchange between water molecules coordinated with silver cation and the ligand molecules considered in this work). The solvent effect is included too through the model mentioned above, although a more refined model could be obtained, such as putting a finite number of solvent molecules around each component of the reaction; this has not been performed in the present work.
Despite the simplicity of the model, the observed indirect trend between theoretical obtained \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)} \) values and the corresponding experimental values, should be enough to assess the capability of the caffeate anion to coordinate silver cations in aqueous mediaFootnote 1
According to Fig. 5, the intrinsic capacity of caffeate to coordinate silver cation given by \( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (g)} \) surpasses the capabilities of the remaining ligands; however, after adding the solvent effect, this kind of interaction energy \( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (aq)} \) is surpassed only by cyanide. This can be understood in terms of the functional groups of caffeate that interact with solvent. As the solvent surrounds the entire molecule, destabilizing effects emerge with more intensity in the case of ligands presenting a net charge equal to −1 and more electronegative atoms, but the case of caffeate it is noticeable because, after adding the solvent effect, the unfavorable variation of energy is about 315 kcal mol−1. Another reason might be based on the size of caffeate in comparison with the remaining ligands. As the caffeate anion is the biggest ligand selected in this work, it is easier to decrease its local reactivity because, compared with chloride, cyanide or thiosulfate, which posses the same net charge, in the case of caffeate this ligand must scatter the net charge over more atoms, configuring the ligand, and the solvent exerts a stronger destabilizing effect than that exerted over the remaining ligands and metal complexes. As the reader can verify easily, the best second ligand after cyanide is caffeate anion, followed by thiosulfate, ammonia, chloride and water. This trend does not change much when considering the interchange with water ligand molecules as exhibited by \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)} \).
Standard Gibbs’ free energies for the silver cation and ligand of the type: black squares interaction energy without solvent \( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (g)} \), red circles interaction energy with solvent \( \mathrm{\Delta}\mathrm{G}^{\circ}_{int\, (aq)} \), green triangles complexation energy with solvent \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)} \)
Conclusions
The interest in this study lay not with analyzing the coordination capacity of caffeic acid because the main working condition must be at an environmentally friendly pH, essentially around 7 and not in acidic conditions (pH < 4.4 where caffeic acid predominates over caffeate anion). The desirable experimental working condition (pH ≃ 7) allows the caffeate anion to predominate over caffeic acid. It was found that the carboxylate group of the caffeate anion overcomes the catechol group’s capacity to coordinate a metallic cation such as Ag+, being the outstanding coordination capability supported by the MEP and the DD, respectively, thus revealing that electrostatic and covalent interactions complement each other, resulting in a favorable interaction between the silver cation and the caffeate anion through the carboxylate functional group. Since there is a connection between the Fukui function and the average local ionization energy (ALIE) [68], an interest in using ALIE [69–73] has emerged with the aim of verifying, in future investigations, if ALIE would give the same predictions for both caffeic acid and caffeate anion as indicated by DD.
In particular, it has been demonstrated that the intrinsic reactivity of the caffeate anion is better than that of the most common ligands that form silver complexes. Even after adding the solvent effect, and although the caffeate anion is surpassed only by cyanide anion, it was observed that the caffeate anion was the more affected ligand due to the presence of the solvent effect rather than the remaining ligands. Conceptual DFT, mainly through DD (qualitatively) and local hypersoftness (quantitatively), is demonstrated to be a very useful tool in the search for new ligands that can be found in nature to be used as ligands to extract metals of economic interest like silver, thus helping to diminish the negative effects on the environment of using mining chemicals. The results analyzed in this work indicate that there are possibilities to study systematically derivatives of the caffeate anion by using the DD to complement the MEP to facilitate the search for new ligands that would help increase the original coordination capability of the caffeate anion and surpass the capacity of cyanide in order to avoid the use of the latter in some specific mining processes.
Notes
Note that experimental values of \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)} \) may be obtained from any book on quantitative analysis that provides stabilization constants of metal complexes, to give the following relationship:\( \Delta G_{{comp\left( {aq} \right)}}^o[Ag(CN)_2^{ - }] < \Delta G_{{comp(aq)}}^o[Ag({S_2}{O_3})_2^{{ - 3}}] < \Delta G_{{comp(aq)}}^{ + }[Ag(N{H_3})_2^{ + }] < \Delta G_{{comp(aq)}}^o[AgCl_2^{ - }] < \Delta G_{{comp(aq)}}^o[Ag({H_2}O)_2^{ + }] \). These experimental values were not included in this work because there is no interest in showing statistical relationships between energetic values given by theoretical computations and experimental results reported in books; the only interest was to reveal that the qualitative trend found from theoretical calculations can be supported by experimental information. Consequently it is expected experimentally, that \( \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)}[Ag(CN)_2^{ - }] < \Delta G_{{comp(aq)}}^o[A{g_2} {({C_9}{H_7}{O_4})_2}] < \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)}[Ag({S_2}{O_3})_2^{{ - 3}}] < \mathrm{\Delta}\mathrm{G}^{\circ}_{comp\, (aq)}[AgCl_2^{{ -}}] \)
References
Timberlake CF (1959) J Chem Soc 2795-2798
Olsen RA, Brown JC, Bennet JH, Blume D (1982) J Plant Nutr 5:433–445
Iiyama K, Lam TB-L, Stone BA (1994) Plant Physiol 104:315–320
Boerjan W, Ralph J, Baucher M (2003) Annu Rev Plant Biol 54:519–546
Cornard JP, Lapouge C (2007) Chem Phys Chem 8:473–479
Pearson RG (1987) J Chem Educ 64:561–567
Cornard JP, Lapouge C (2004) J Phys Chem A 108:4470–4478
Cornard JP, Lapouge C (2006) J Phys Chem A 110:7159–7166
Boilet L, Cornard JP, Lapouge C (2005) J Phys Chem A 109:1952–1960
Cornard JP, Lapouge C (2007) Chem Phys Lett 438:41–46
Cornard JP, Caudron A, Merlin JC (2006) Polyhedron 25:2215–2222
Nagels L, Van Dongen W, Parmentier F (1982) Phytochemistry 21:743–746
Maas M, Petereit F, Hensel A (2009) Molecules 14:36–45
Xiang M, Su H, Hu J, Yan Y (2011) J Med Plant Res 5:1685–1691
Hohenberg P, Kohn W (1964) Phys Rev B 136:864–871
Kohn W, Sham LJ (1965) Phys Rev A 140:1133–1138
Politzer P, Murray JS (2002) Theor Chem Acc 108:134–142
Murray JS, Politzer P (2011) The electrostatic potential: an overview. Wiley Interdisciplinary Reviews: Computational Molecular Science 1:153–163
Geerlings P, De Proft F, Langenaeker W (2003) Chem Rev 103:1793–1873
Parr RG, Yang W (1989) In: Density-functional theory of atoms and molecules. Oxford University Press, New York, pp 70–86
Parr RG, Yang W (1989) In: Density-functional theory of atoms and molecules. Oxford University Press, New York, pp 95–97
Koopmans TA (1934) Physica 1:104–113
Szabo A, Ostlund NS (1996) Modern quantum chemistry: introduction to advanced electronic structure theory. Dover, New York, pp 108–230
Parr RG, Szentpaly LV, Liu S (1999) J Am Chem Soc 121:1922–1924
Parr RG, Yang W (1989) In: Density-functional theory of atoms and molecules. Oxford University Press, New York, pp 99–102
Contreras RR, Fuentealba P, Galván M, Pérez P (1999) Chem Phys Lett 304:405–413
Senet P (1996) J Chem Phys 105:6471–6489
Parr RG, Yang W (1995) Annu Rev Phys Chem 46:701–728
Ayers P, Parr RG (2000) J Am Chem Soc 122:2010–2018
Ayers PW (2008) J Math Chem 43:285–303
Parr RG, Yang W (1984) J Am Chem Soc 106:4049–4050
Yang W, Parr RG, Pucci R (1984) J Chem Phys 81:2862–2863
Fuentealba P, Pérez P, Contreras R (2000) J Chem Phys 113:2544–2551
Bulat FA, Chamorro E, Fuentealba P, Toro-Labbé A (2004) J Phys Chem A 108:342–349
Tiznado W, Chamorro E, Contreras R, Fuentealba P (2005) J Phys Chem A 109:3220–3224
Fuentealba P, Florez E, Tiznado W (2010) J Chem Theory Comput 6:1470–1478
Morell C, Grand A, Toro-Labbé A (2005) J Phys Chem A 109:205–212
Morell C, Grand A, Toro-Labbé A (2006) Chem Phys Lett 425:342–346
Fuentealba P, Parr RG (1991) J Chem Phys 94:5559–5564
Toro-Labbé A (2007) Theoretical aspects of chemical reactivity, vol 19. Elsevier Science, Amsterdam
Ayers PW, Morell C, De Proft F, Geerlings P (2007) Chem Eur J 13:8240–8247
Morell C, Ayers PW, Grand A, Gutiérrez-Oliva S, Toro-Labbé A (2008) Phys Chem Chem Phys 10:7239–7246
Morell C, Hocquet A, Grand A, Jamart-Grégoire B (2008) THEOCHEM 849:46–51
Cárdenas C, Rabi N, Ayers PW, Morell C, Jaramillo P, Fuentealba P (2009) J Phys Chem A 113:8660–8667
Flores-Moreno R (2010) J Chem Theory Comput 6:48–54
Mart ınez J (2009) Chem Phys Lett 478:310–322
Mart´ınez JI, Moncada JL, Larenas JM (2010) J Mol Model 16:1825–1832
Labet V, Morell C, Cadet J, Eriksson LA, Grand A (2009) J Phys Chem A 113:2524–2533
Labet V, Morell C, Grand A, Cadet J, Cimino P, Barone V (2008) Org Biomol Chem 6:3300–3305
Morell C, Hocquet A, Grand A, Jamart-Grégoire B (2008) J Mol Struct (THEOCHEM) 849:46–51
Schlegel HB (1982) J Comp Chem 3:214–218
Becke AD (1988) Phys Rev A 38:3098–3100
Becke AD (1993) J Chem Phys 98:5648–5652
Becke AD (1993) J Chem Phys 98:1372–1377
Lee CL, Yang W, Parr RG (1988) Phys Rev B 37:785–789
Jensen F (2007) Introduction to computational chemistry, 2nd edn. Wiley, Chichester, pp 192–252
Hariharan PC, Pople JA (1973) Theor Chim Acta 28:213–222
Frisch MJ, Pople JA, Binkley JS (1984) J Chem Phys 80:3265–3269
Jeffrey Hay P, Wadt WR (1985) J Chem Phys 82:270–283
Jeffrey Hay P, Wadt WR (1985) J Chem Phys 82:299–310
Tomasi J, Mennucci B, Cammi R (2005) Chem Rev 105:2999
Barone V, Cossi M, Tomasi J (1997) J Chem Phys 107:3210–3221
Barone V, Cossi M (1998) J Phys Chem A 102:1995–2001
Barone V, Cossi M, Tomasi J (1998) J Comp Chem 19:404–417
Frisch MJ et al (2010) Gaussian 09, Revision B.1, Gaussian, Wallingford, CT
Provided by the author upon request: E Chamorro, “Fukui.Exe, a Visual Basic tool for evaluating global and local reactivity DFT descriptors” REV 1.1, 2011
Chamorro E, Pérez P (2005) J Chem Phys 123:114107–114116
Toro-Labbé A, Jaque P, Murray JS, Politzer P (2005) Chem Phys Lett 407:143–146
Sjoberg P, Brinck T, Murray JS, Politzer P (1990) Can J Chem 68:1440–1443
Murray JS, Politzer P (1996) In: Parkanyi C (ed) Theoretical organic chemistry. Elsevier, Amsterdam
Politzer P, Murray JS (2007) In: Toro-Labbé A (ed) Chemical reactivity, Chap. 8. Amsterdam, Elsevier
Bulat FA, Toro-Labbé A, Brinck T, Murray JS, Politzer P (2010) J Mol Model 16:1679–1671
Politzer P, Murray JS, Bulat FA (2010) J Mol Model 16:1731–1742
Acknowledgments
This work was financed partially by the fund of the Vice-Rectory of Research and Development to promote and support research in the UPV University community. The author wishes to thank the Fondo Vicerrectoría de Investigación y Desarrollo No. 000012A26 from Universidad Pedro de Valdivia for financial support, and FONDECYT grant No. 11100070 (A Project for Research Initiation) for providing computational equipment and software.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Martínez-Araya, J.I. Revisiting caffeate’s capabilities as a complexation agent to silver cation in mining processes by means of the dual descriptor—a conceptual DFT approach. J Mol Model 18, 4299–4307 (2012). https://doi.org/10.1007/s00894-012-1405-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00894-012-1405-4