1 Introduction

Control of underactuated surface vessels is a challenging topic due to its practical significance in ship motion control field. Firstly, the common configuration of surface vessels possesses only two actuators, while three-degree-of-freedom (3-DoF) motion needed to be controlled. The other challenge is that the ship motion is of strong nonlinearity, large inertia and time delay. The difficulties of tracking of underactuated surface vessels have stirred vast interests from control community [1].

Papoulias and Oral proposed several linear controllers by linearizing the ship dynamics, where the stability was lost due to the linearization [2, 3]. Godhavn developed a backstepping control law for tracking of underactuated surface vessel under the assumption that the forward velocity of the surface vessel was always positive [4], where uncertainties or environmental disturbances were not taken into account. In [5], a continuous time-invariant state controller was designed to achieve global exponential position tracking where the yaw angle could not be controlled. Lefeber obtained a global tracking result using cascade approach where the stability analysis depended on the linear time-varying theories [6]. The model of underactuated surface vessels cannot directly be transformed into chained form. Through a coordinate transformation, Pettersen and Nijmeijer [7] transformed the model into a triangular-like form which made it possible to use integrator backstepping and developed a tracking control law. Lefeber et al. [8] divided the tracking error dynamics into a cascade of two linear subsystems which could be stabilized independently of each other where a global solution to the tracking of underactuated ship was obtained. Jiang [9] developed two constructive tracking solutions based on Lyapunov’s method and passivity approach which were shown to be robust to the thruster dynamics. However, no other uncertainties or environmental disturbances were considered. All the works mentioned above [5–9] are under a sufficient condition for persistent excitation (PE) which requires that the reference yaw velocity does not converge to zero. This condition is rather restrictive from a practical perspective because it means that it is impossible to track a straight-line reference trajectory. This condition was first removed in [10]. Then, Do et al. [11] designed a universal controller based on Lyapunov’s direct method and backstepping technique to achieve stabilization and tracking simultaneously. They developed multivariable controllers to stabilize ocean surface ships on a linear course and to reduce the roll and pitch based on Lyapunov’s direct method and backstepping technique where the Lipschitz continuous projection algorithm is used in updating the estimation of the unknown parameters to avoid the parameters’ drift due to the time-varying environmental disturbances [12]. However, from [10–12], it can be found that these controllers were complex and dependent on reference signal. Complex control algorithm is not suitable for practical implementation. Smooth time-varying controllers are constructed by Cao and Tian [13] who introduced a time-varying coordinate transformation and used the cascade-design approach. However, no uncertainties or environmental disturbances were considered. A tracking controller for underactuated nonlinear autonomous ship was constructed in [14] using unscented Kalman filter (UKF) to update the estimation of the uncertain parameters online to avoid the parameters’ drift due to time-varying added mass matrices. Ashrafiuon et al. [15] proposed an asymptotically stable trajectory tracking sliding mode control law using two sliding surfaces for calculation of the two propeller forces. This control law was shown to be exponentially convergent for tracking a position while the angular velocity was only BIBO stable as long as the vessel was in motion. The work in [15] was extended to the case where the vessel could start from any initial condition and follow any desired trajectory at a practical desired orientation in [16] where setpoint control is dealt with as a special case. Li et al. [17] presented a novel backstepping design for 2-DoF path following kinematics and used 4-DoF model in simulations. A way-point tracking controller for underactuated surface vessels was obtained based on the combined model predictive control (MPC) scheme and line-of-sight (LOS) method [18]. Chwa [19] proposed a global tracking control method for underactuated ships with input and velocity constraints using the dynamic surface control (DSC) method, where the control structure is formed in a modular way that cascaded kinematic and dynamic linearizations can be achieved similarly as in the backstepping method. Movahhed et al. [20] used two sliding surfaces to determine the two propeller forces based on Lyapunov direct method and sliding mode scheme, where the parameter update laws were used to estimate uncertainties. Siramdasu and Fahimi [21] proposed a nonlinear model predictive controller (NMPC) for trajectory tracking of underactuated surface vessels, where NMPC is applied to calculate the future control inputs based on the present state variable by optimizing a cost function.

It can be seen from the works mentioned above that it is necessary to develop simple controllers for tracking of underactuated surface vessels with less computational burden from practical viewpoint. In addition, the designed controllers should be robust to the uncertainties and external disturbances. Last but not least, the real trajectory should follow desired signal very well no matter what kind of the trajectory is. In this paper, we design controllers for tracking of underactuated surface vessels by incorporating neural networks and hierarchical sliding mode technique [22]. Neural network is used for approximating nonlinear function in the underactuated system. Two sliding mode surfaces are introduced. The first one which contains two levels is for calculation of yaw moments, while the second one is common sliding mode surface for calculation of surge forces. The stability of the closed-loop system is proved by Lyapunov stability theorem. Various simulations are conducted to validate the performance of the proposed controllers.

2 Preliminaries and problem formulation

2.1 Neural network

In this section, RBF neural network is used as a tool for approximating the nonlinear function in the underactuated system [23]. It belongs to a kind of linearly parameterized neural networks and can be described as:

$$f_{n} (Z) = W^{T} H({\text{Z}})$$
(1)

with the input vector Z ∊ Ω z  ⊂ R n, weight vector W ∊ R l, weight number l, and basis function vector

$$H(Z) = [h_{1} (z),h_{2} (z), \ldots ,h_{l} (z)]^{T} \in R^{l}$$
(2)

Choose RBFs as the Gaussian functions in the following form:

$$h_{i} (z) = \exp \left( { - \frac{{\left\| {z - \mu_{i} } \right\|}}{{2\delta_{i}^{2} }}} \right),\;\quad (i = 1,2, \ldots l)$$
(3)

where μ i  = [μ i1, μ i2, …, μ in ]T is the center of the receptive field and δ i is the width of the Gaussian function. It has proved that function (1) can approximate any continuous function on a compact set Ω z  ⊂ R l to arbitrary accuracy as:

$$f(Z) = W^{*T} H(Z) + \varepsilon ,\quad \;\forall Z \in \Omega_{z}$$
(4)

where W* is the ideal constant weights, and ɛ is the approximation error.

The ideal weight vector W* is defined as the value of W that minimizes |ɛ| for all Z ∊ Ω z  ⊂ R n

$$W^{*} \,\triangleq \,\arg \;\mathop {\hbox{min} }\limits_{{W \in R^{l} }} \left\{ {\mathop {\sup }\limits_{{z \in \varOmega_{z} }} \left| {f(Z) - W^{T} H(Z)} \right|} \right\}$$
(5)

3 Problem formulation

In this section, we consider the ship motion model of three-degree-of-freedom in the horizontal plane with two actuators, i.e., propeller and rudder. The motion model comprises the kinematics model and the dynamics model [24]

$$\begin{gathered} \dot{x} = u\cos \psi - v\sin \psi \hfill \\ \dot{y} = u\sin \psi + v\cos \psi \hfill \\ \dot{\psi } = r \hfill \\ \dot{u} = \frac{{m_{22} }}{{m_{11} }}vr - \frac{{d_{u} }}{{m_{11} }}u - \sum\limits_{i = 2}^{3} {\frac{{d_{ui} }}{{m_{11} }}} \left| u \right|^{i - 1} u + \frac{1}{{m_{11} }}\tau_{1} + \tau_{uw} \hfill \\ \dot{v} = - \frac{{m_{11} }}{{m_{22} }}ur - \frac{{d_{v} }}{{m_{22} }}v - \sum\limits_{i = 2}^{3} {\frac{{d_{vi} }}{{m_{22} }}} \left| v \right|^{i - 1} v + \tau_{vw} \hfill \\ \dot{r} = \frac{{(m_{11} - m_{22} )}}{{m_{33} }}uv - \frac{{d_{r} }}{{m_{33} }}r - \sum\limits_{i = 2}^{3} {\frac{{d_{ri} }}{{m_{11} }}} \left| r \right|^{i - 1} r + \frac{1}{{m_{33} }}\tau_{2} + \tau_{rw} \hfill \\ \end{gathered}$$
(6)

where (x, y) denotes the coordinates of the vessel in earth-fixed frame. ψ is the yaw angle; u and v are the velocity of surge and sway, respectively; r is the yaw rate. The surge force τ 1 and yaw moment τ 2 are control inputs. m jj (j = 1, 2, 3) are the ship inertia; d u , d v , d r , d ui , d vi and d ri (i = 2, 3) are the hydrodynamic damping. τ uw , τ vw and τ rw are the external disturbances. Assumption 1 is employed to solve the problem of uncertainties of the model of ship's motion. The model we employed here is only for simulation rather than design procedure, because it is widely used in different works and it could be a good comparison. For our design, due to the merit of neural network, we do not care for the exact form of the model which means that we do not care for the exact form of f u , f v and f r .

Define

$$f_{u} = \frac{{m_{22} }}{{m_{11} }}vr - \frac{{d_{u} }}{{m_{11} }}u - \sum\limits_{i = 2}^{3} {\frac{{d_{ui} }}{{m_{11} }}} \left| u \right|^{i - 1} u,$$
$$f_{v} = - \frac{{m_{11} }}{{m_{22} }}ur - \frac{{d_{v} }}{{m_{22} }}v - \sum\limits_{i = 2}^{3} {\frac{{d_{vi} }}{{m_{22} }}} \left| v \right|^{i - 1} v,$$
$$f_{r} = \frac{{(m_{11} - m_{22} )}}{{m_{33} }}uv - \frac{{d_{r} }}{{m_{33} }}r - \sum\limits_{i = 2}^{3} {\frac{dri}{{m_{11} }}} \left| r \right|^{i - 1} r.$$

We can rewrite system (6) in the following form:

$$\begin{gathered} \dot{x} = u\cos \psi - v\sin \psi \hfill \\ \dot{y} = u\sin \psi + v\cos \psi \hfill \\ \dot{\psi } = r \hfill \\ \dot{u} = f_{u} + \frac{1}{{m_{11} }}\tau_{1} + \tau_{uw} \hfill \\ \dot{v} = f_{v} + \tau_{vw} \hfill \\ \dot{r} = f_{r} + \frac{1}{{m_{33} }}\tau_{2} + \tau_{rw} \hfill \\ \end{gathered}$$
(7)

Assumption 1

f u , f v and f r are unknown continuous functions.

Assumption 2

The disturbances are bounded, such that |τ uw | ≤ d 1, |τ vw | ≤ d 2, |τ rw | ≤ d 3.

The desired trajectory is generated by a virtual ship that is described by the following models:

$$\begin{gathered} \dot{x}_{d} = u_{d} \cos \psi_{d} - v_{d} \sin \psi_{d} \hfill \\ \dot{y}_{d} = u_{d} \sin \psi_{d} + v_{d} \cos \psi_{d} \hfill \\ \dot{\psi }_{d} = r_{d} \hfill \\ \dot{u}_{d} = f_{ud} + \frac{1}{{m_{11} }}\tau_{1d} \hfill \\ \dot{v}_{d} = f_{vd} \hfill \\ \dot{r}_{d} = f_{rd} + \frac{1}{{m_{33} }}\tau_{2d} \hfill \\ \end{gathered}$$
(8)

where the symbols have similar meaning as in system (6).

Convert the Eq. 7 into a suitable form as follows [25]:

$$\begin{gathered} z_{1} = x\cos \psi + y\sin \psi \hfill \\ z_{2} = - x\sin \psi + y\cos \psi \hfill \\ z_{3} = \psi \hfill \\ \end{gathered}$$
(9)

Transform Eq. 8 into the following form:

$$\begin{gathered} z_{1d} = x_{d} \cos (\psi_{d} ) + y_{d} \sin (\psi_{d} ) \hfill \\ z_{2d} = - x_{d} \sin (\psi_{d} ) + y_{d} \cos (\psi_{d} ) \hfill \\ z_{3d} = \psi_{d} \hfill \\ \end{gathered}$$
(10)

The tracking error can be defined as follows:

$$\begin{gathered} z_{1e} = z_{1} - z_{1d} \hfill \\ z_{2e} = z_{2} - z_{2d} \hfill \\ z_{3e} = z_{3} - z_{3d} \hfill \\ \end{gathered}$$
(11)

The objective of this paper is to design a simple controller which makes the real trajectory track the desired trajectory as closely as possible. From the above transformation, the trajectory tracking problem is transformed to stabilizing system (11). Let z 1d  = z 2d  = z 3d  = 0, the tracking problem can be transformed into the stabilization case.

4 Controller design

We design two controllers: one is surge force, the other one is yaw moment. Firstly, we design the yaw moment controller with a hierarchical sliding mode which contains two first-level sliding mode surfaces. Then, we design the surge force with a common sliding mode. The RBF neural network is employed to approximate the unknown functions f u , f v and f r in the underactuated system.

Step 1 Define the first first-level sliding mode surface of the yaw moment as follows:

$$\sigma_{1} = c_{1} z_{2e} + \dot{z}_{2e}$$
(12)

where c 1 is the positive parameter.

Differentiating Eq. 12, we obtain

$$\begin{gathered} \dot{\sigma }_{1} = c_{1} \dot{z}_{{2e}} + \ddot{z}_{{2e}} \hfill \\ \quad \; = c_{1} \dot{z}_{{2e}} + f_{v} + \tau _{{vw}} - (u + z_{2} r)r - z_{1} \left( {f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} + \tau _{{rw}} } \right) - \ddot{z}_{{2d}} \hfill \\ \end{gathered}$$
(13)

Employing RBF neural network to approximate f v and f r ,

$$\hat{f}_{v} = \hat{W}_{1}^{T} H_{1} (Z)$$
(14)
$$\hat{f}_{r} = \hat{W}_{2}^{T} H_{2} (Z)$$
(15)

where \(\hat{f}_{v}\) and \(\hat{f}_{r}\) are the estimations of f v and f r ; \(\hat{W}_{1}\) and \(\hat{W}_{2}\) are the estimations of \(\hat{W}_{{_{1} }}^{*}\) and \(\hat{W}_{{_{2} }}^{*}\).

Let Eq. 13 equal to zero, then we have

$$\tau_{21eq} = - \frac{{m_{33} }}{{z_{1} }} \left( - c_{1} \dot{z}_{2e} - \hat{f}_{v} + (u + z_{2} r)r + z_{1} \hat{f}_{r} + {\ddot {z}}_{2d} \right)$$
(16)

Define the second first-level sliding mode surface of yaw moment as follows:

$$\sigma_{2} = c_{2} z_{3e} + \dot{z}_{3e}$$
(17)

where c 2 is the positive parameter.

Differentiating Eq. 17, we have

$$\begin{gathered} \dot{\sigma }_{2} = c_{2} \dot{z}_{3e} + {\ddot {z}}_{3e} \\ = c_{2} \dot{z}_{3e} + f_{r} + \tau_{rw} + \frac{1}{{m_{33} }}\tau_{2} - {\ddot {z}}_{3d} \\ \end{gathered}$$
(18)

Let Eq. 18 equal to zero. Therefore, we have

$$\tau_{eq22} = m_{33} ( - c_{2} \dot{z}_{3e} - \hat{f}_{r} + {\ddot {z}}_{3d} )$$
(19)

Define second level sliding mode surface of yaw moment as follows:

$$S_{1} = a\sigma_{1} + b\sigma_{2}$$
(20)

where a and b are the positive controller parameters.

The switched law of yaw moment is

$$\tau_{sw2} = \frac{{ - \eta_{1} \text{sgn} (S_{1} ) - k_{1} S_{1} + a\frac{{z_{1} }}{{m_{33} }}\tau_{eq22} - \frac{b}{{m_{33} }}\tau_{eq21} }}{{\frac{b}{{m_{33} }} - a\frac{{z_{1} }}{{m_{33} }}}}$$
(21)

where η 1 and k 1 are the positive parameters.

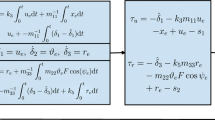
Above all, the control law of yaw moment is

$$\tau_{2} = \tau_{eq21} + \tau_{eq22} + \tau_{sw2}$$
(22)

Step 2 Define the sliding mode surface of surge force as follows:

$$S_{2} = c_{3} z_{1e} + \dot{z}_{1e}$$
(23)

where c 3 is the positive parameter.

Differentiating Eq. 23, we have

$$\begin{gathered} \dot{S}_{2} = c_{3} \dot{z}_{1e} +{\ddot {z}}_{1e} \\ = c_{3} \dot{z}_{1e} + f_{u} + \frac{1}{{m_{11} }}\tau_{1} + \tau_{uw} + (v - z_{1} r)r + z_{2} \left (f_{r} + \frac{1}{{m_{33} }}\tau_{2} + \tau_{rw} \right) - {\ddot {z}}_{1d} \\ \end{gathered}$$
(24)

Employing RBF neural network to approximate f u

$$\hat{f}_{u} = \hat{W}_{3}^{T} H_{3} (Z)$$
(25)

where \(\hat{f}_{u}\) is the estimation of f u ; \(\hat{W}_{3}\) is the estimation of \(\hat{W}_{{_{3} }}^{*}\).

Let Eq. 24 equal to zero. We have

$$\tau_{1eq} = m_{11} \left( - c_{3} \dot{z}_{1e} - \hat{f}_{u} - (v - z_{1} r)r - z_{2} \left(\hat{f}_{r} + \frac{1}{{m_{33} }}\tau_{2} \right) + {\ddot {z}}_{1d} \right)$$
(26)

The switch part of sliding mode for the surge force is

$$\tau_{sw1} = m_{11} ( - \eta_{2} \text{sgn} (S_{2} ) - k_{2} S{}_{2})$$
(27)

where η 2 and k 2 are the positive parameters.

The control law of surge force is designed as:

$$\tau_{1} = \tau_{eq1} + \tau_{sw1}$$
(28)

Step 3 The adaptive laws are

$$\begin{gathered} \dot{\hat{W}}_{1} = \gamma_{1} S_{2} H_{1} (Z) \hfill \\ \dot{\hat{W}}_{2} = a\gamma_{2} S_{1} H_{2} (Z) \hfill \\ \dot{\hat{W}}_{3} = \gamma_{3} (bz_{1} S_{1} - az_{1} S_{1} + z_{2} S_{2} )H_{3} (Z) \hfill \\ \end{gathered}$$
(29)

where γ 1, γ 2 and γ 3 are the positive constants and Z = [u, v, r]T.

5 Stability analysis

Define the following Lyapunov function:

$$V = \sum\limits_{i = 1}^{2} \frac{1}{2} S_{i}^{2} + \sum\limits_{i = 1}^{3} {\frac{1}{{2\gamma_{i} }}} \tilde{W}_{i}^{T} \tilde{W}_{i}$$
(30)

where \(\tilde{W}_{i} = W_{i}^{*} - \hat{W}_{i} \quad(i = 1,2,3)\).

Differentiating Eq. 30, we have

$$\begin{gathered} \dot{V} = S_{1} \dot{S}_{1} + S_{2} \dot{S}_{2} - \sum\limits_{{i = 1}}^{3} {\frac{1}{{\gamma _{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \hfill \\ \quad = S_{1} \left( {a\left( {c_{1} \dot{z}_{{2e}} + f_{v} + \tau _{{vw}} - (u + z_{2} r)r - z_{1} \left( {f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} + \tau _{{rw}} } \right) - \ddot{z}_{{2d}} } \right) + b\left( {c_{2} \dot{z}_{{3e}} + f_{r} + \tau _{{rw}} + \frac{1}{{m_{{33}} }}\tau _{2} - \ddot{z}_{{3d}} } \right)} \right) \hfill \\ \quad \quad + S_{2} \left( {c_{3} \dot{z}_{{1e}} + f_{u} + \frac{1}{{m_{{11}} }}\tau _{1} + \tau _{{uw}} + (v - z_{1} r)r + z_{2} \left( {f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} + \tau _{{rw}} } \right) - \ddot{z}_{{1d}} } \right) - \sum\limits_{{i = 1}}^{3} {\frac{1}{{\gamma _{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \hfill \\ \quad \le S_{1} \left( {a\left( {c_{1} \dot{z}_{{2e}} + f_{v} - (u + z_{2} r)r - z_{1} \left( {f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} } \right) - \ddot{z}_{{2d}} } \right) + b\left( {c_{2} \dot{z}_{{3e}} + f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} - \ddot{z}_{{3d}} } \right)} \right) \hfill \\ \quad \quad + \left| {S_{1} } \right|\left[ {a(d_{2} + \left| {z_{1} } \right|d_{3} ) + bd_{3} } \right] + \left| {S_{2} } \right|(d_{1} + \left| {z_{2} } \right|d_{3} ) + S_{2} \left( {c_{3} \dot{z}_{{1e}} + f_{u} + \frac{1}{{m_{{11}} }}\tau _{1} + \left( {v - z_{1} r} \right)r + z_{2} \left( {f_{r} + \frac{1}{{m_{{33}} }}\tau _{2} } \right) - \ddot{z}_{{1d}} } \right) - \sum\limits_{{i = 1}}^{3} {\frac{1}{{\gamma _{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \hfill \\ \end{gathered}$$
(31)

where \(\tilde{f}_{v} = f_{v} - \hat{f}_{v} ,\;\) \(\tilde{f}_{r} = f_{r} - \hat{f}_{r} ,\) \(\tilde{f}_{u} = f_{u} - \hat{f}_{u}\).

Substituting Eqs. 22 and 28 into Eq. 31, we obtain

$$\begin{gathered} \dot{V} \le - k_{1} S_{1}^{2} - \eta_{1} \left| {S_{1} } \right| + \left| {S_{1} } \right|\left[ {a(d_{2} + \left| {z_{1} } \right|d_{3} ) + bd_{3} } \right] - k_{2} S_{2}^{2} - \eta_{2} \left| {S_{2} } \right| + \left| {S_{2} } \right|(d_{1} + \left| {z_{2} } \right|d_{3} ) \hfill \\ \quad \;\; + S_{2} \tilde{f}_{u} + aS_{1} \tilde{f}_{v} + (bz_{1} S_{1} - az_{1} S_{1} + z_{2} S_{2} )\tilde{f}_{r} - \sum\limits_{i = 1}^{3} {\frac{1}{{\gamma_{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \hfill \\ \end{gathered}$$
(32)

Substituting Eqs. 14, 15 and 25 into Eq. 32, we have

$$\begin{gathered} \dot{V} \le - k_{1} S_{1}^{2} - \eta_{1} \left| {S_{1} } \right| + \left| {S_{1} } \right|(a(d_{2} + \left| {z_{1} } \right|d_{3} ) + bd_{3} ) - k_{2} S_{2}^{2} - \eta_{2} \left| {S_{2} } \right| + \left| {S_{2} } \right|(d_{1} + \left| {z_{2} } \right|d_{3} ) \\ + S_{2} (\tilde{W}_{1}^{T} H_{1} (Z) + \varepsilon_{1} ) + aS_{1} (\tilde{W}_{2}^{T} H_{2} (Z) + \varepsilon_{2} ) + (bS_{1} - aS_{1} + z_{2} S_{2} )(\tilde{W}_{3}^{T} H_{3} (Z) + \varepsilon_{3} ) \\ - \sum\limits_{i = 1}^{3} {\frac{1}{{\gamma_{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \\ \le - k_{1} S_{1}^{2} - \eta_{1} \left| {S_{1} } \right| + \left| {S_{1} } \right|(a(d_{2} + \left| {z_{1} } \right|d_{3} ) + bd_{3} + a\varepsilon_{2} + \left| {b - a} \right|\varepsilon_{3} ) - k_{2} S_{2}^{2} - \eta_{2} \left| {S_{2} } \right| \\ + \left| {S_{2} } \right|(d_{1} + \left| {z_{2} } \right|d_{3} + \varepsilon_{1} + \left| {z_{2} } \right|\varepsilon_{3} ) + S_{2} (\tilde{W}_{1}^{T} H_{1} (Z)) + aS_{1} (\tilde{W}_{2}^{T} H_{2} (Z)) \\ + (bz_{1} S_{1} - az_{1} S_{1} + z_{2} S_{2} )(\tilde{W}_{3}^{T} H_{3} (Z)) - \sum\limits_{i = 1}^{3} {\frac{1}{{\gamma_{i} }}\tilde{W}_{i}^{T} } \dot{\hat{W}}_{i} \\ \end{gathered}$$
(33)

Substituting Eq. 29 into 33, we obtain

$$\begin{gathered} \dot{V} \le - k_{1} S_{1}^{2} - \eta_{1} \left| {S_{1} } \right| + \left| {S_{1} } \right|\left[ {a(d_{2} + \left| {z_{1} } \right|d_{3} ) + bd_{3} + a\varepsilon_{2} + \left| {b - a} \right|\varepsilon_{3} } \right] \\ - k_{2} S_{2}^{2} - \eta_{2} \left| {S_{2} } \right| + \left| {S_{2} } \right|(d_{1} + \left| {z_{2} } \right|d_{3} + \varepsilon_{1} + \left| {z_{2} } \right|\varepsilon_{3} ) \\ \end{gathered}$$
(34)

Let η 1 > a(d 2 + |z 1|d 3) + bd 3 + aɛ 2 + |b − a|ɛ 3, η 2 > d 1 + |z 2|d 3 + ɛ 1 + |z 2|ɛ 3, we have

$$\dot{V} \le - k_{1} S_{1}^{2} - k_{2} S_{2}^{2} \le 0$$
(35)

Above all, we can see that the closed-loop system is stable.

Integrating both sides of Eq. 35,

$$V(t) - V(0) = \int_{0}^{t} { - k_{1} } S_{1}^{2} - k_{2} S_{2}^{2} d\tau$$
(36)

then

$$V(t) = V(0) - \int_{0}^{t} {k_{1} } S_{1}^{2} + k_{2} S_{2}^{2} d\tau \le V(0) < \infty$$
(37)

we can see

$$V(0) = V(t) + \int_{0}^{t} {k_{1} } S_{1}^{2} + k_{2} S_{2}^{2} d\tau \ge \int_{0}^{t} {k_{1} } S_{1}^{2} + k_{2} S_{2}^{2} d\tau$$
(38)

therefore

$$\mathop {\lim }\limits_{t \to \infty } \int_{0}^{t} {k_{1} } S_{1}^{2} + k_{2} S_{2}^{2} d\tau \le V(0) < \infty$$
(39)

According to Barbalat’s lemma, we have

$$\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S_{1} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm and} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S_{2} = 0$$
(40)

Step 1 Substitute Eq. 23 into Eq. 40, we have

$$\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} c_{3} z_{1e} + \dot{z}_{1e} = 0$$
(41)

then, we have

$$\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{1e} = Ce^{{ - c_{3} t}} = 0$$
(42)

where C is constant.

Step 2 From Eq. 40, we have

$$\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} a\sigma_{1} + b\sigma_{2} = 0$$
(43)

There are two scenarios of solution for Eq. 43, the first one is

$$\sigma_{1} = \sigma_{2} = 0$$
(44)

Similar to Step 1, then we can have

$$\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{2e} = C_{1} e^{{ - c_{1} t}} = 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{and}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{3e} = C_{2} e^{{ - c_{2} t}} = 0$$
(45)

where C 1 and C 2 are constants.

The second scenario of solution is

$$a\sigma_{1} = - b\sigma_{2}$$
(46)

However, the σ 1 is related to the ship position, while σ 2 is related to yaw angle. In addition, a and b are positive controller parameters. Therefore, Eq. 46 does not hold in reality when σ 1, σ 2 ≠ 0.

Above all, from Eqs. 42 and 45, we have \(\mathop {\lim }\limits_{t \to \infty } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} z_{1e} ,z_{2e} ,z_{3e} \to 0\). Therefore, the closed-loop system is stable.

6 Simulation results

Three simulations are conducted to validate the proposed control algorithm. The first case is the ship course control. The second case is trajectory tracking with time-varying disturbances. The third case is stabilization of underactuated surface vessels.

6.1 Case 1: Course control

To illustrate the effectiveness of proposed control algorithm, PD controller is conducted as a comparative study. Reference signal starts at 0°, while the tracking signal starts at 20°. Figure 1 shows that the algorithm which combines sliding mode and neural network can converge to desired signal quickly, while the PD algorithm needs almost one cycle.

Fig. 1
figure 1

Course tracking without disturbance

Full size image

The fast convergent speed is only part of reason why we employ sliding mode and neural network. The main reason is to improve robustness of the algorithm, since ship motion is often influenced by wind, wave and current. It is necessary to consider the influence of external disturbances for ship motion control. Keep all the controller parameters the same. Add the time-varying disturbance on the plant. Figure 2 shows that the PD controller almost lose the tracking ability, while the algorithm combining sliding mode and neural network still works well.

Fig. 2
figure 2

Course tracking with disturbance

Full size image

6.2 Case 2: Trajectory tracking

The parameters of ship motion model are [24] m 11 = 120 × 103, m 22 = 177.9 × 103, m 33 = 636 × 105, d u  = 215 × 102, d v  = 147 × 103, d r  = 802 × 104, d u2 = 0.2d u , d u3 = 0.1d u , d v2 = 0.2d v , d v3 = 0.1d v , d r2 = 0.2d r , d r3 = 0.1d r . The controller parameters are c 1 = 0.3, c 2 = 0.3, c 3 = 0.3, a 0 = 0.001, b = 100, k 1 = 100, k 2 = 100, η 1 = 0.001, η 2 = 0.001. The neural network parameters are μ i  = 0.5, δ i  = 5(i = 1, 2, 3).

Remark

The parameters c i (i = 1, 2, 3) are related to the response time to reach the sliding mode surface. The larger the positive value of c i (i = 1, 2, 3), the shorter time is needed. The parameters η i (i = 1, 2) are important which are closely related to the robustness of controllers. However, the larger value of η i (i = 1, 2) would cause chattering problem. Thus, η i (i = 1, 2) should be chosen carefully.

The initial values are x 0 = 5 m, y 0 = 1 m, ψ 0 = 45°; u 0 = v 0 = r 0 = 0, x d0 = 15 m, y d0 = 15 m, ψ d0 = 0, u d0 = v d0 = r d0 = 0. The time-varying external disturbances are τ uw  = 11 × 102 (1 + sin (0.01t))/m 11, τ vw  = 26 × 102 (1 + sin (0.01t))/m 22,  τ rw  = 950 × 102 (1 + sin (0.01t))/m 33. Figure 3 depicts the tracking performance of the proposed controllers. It can be seen from Fig. 3 that tracking trajectory fits the desired trajectory quite well. Figure 4 depicts the velocity of surge and sway, respectively. Figure 5 depicts yaw angle and yaw rate. Figure 6 shows the surge force and yaw moment, respectively. From these figures, we can conclude that the proposed controllers are robustness to the external disturbances.

Fig. 3
figure 3

Tracking performance of the proposed controller

Full size image
Fig. 4
figure 4

Velocity of surge and sway

Full size image
Fig. 5
figure 5

Yaw angle and yaw rate

Full size image
Fig. 6
figure 6

Surge force and yaw moment

Full size image

7 Case 3: Stabilization

The initial parameters are (x s0, y s0, ψ s0, u s0, v s0, r s0) = (3 m, 1.6 m, 45°, 0, 0, 0). Figure 7 depicts the stabilization performance of the proposed controllers. It can be seen from this figure that the ability of stabilization of the proposed controllers is quite well under time-varying disturbances. Figure 8 depicts the velocity of surge and sway. Figure 9 shows the yaw angle and yaw rate. Figure 10 shows the surge force and yaw moment.

Fig. 7
figure 7

Stabilization performance of the proposed controllers

Full size image
Fig. 8
figure 8

Velocity of surge and sway in stabilization case

Full size image
Fig. 9
figure 9

Yaw angle and yaw rate in stabilization case

Full size image
Fig. 10
figure 10

Surge force and yaw moment in stabilization case

Full size image

8 Conclusions

In this paper, we propose adaptive robust controllers for trajectory tracking and stabilization of underactuated surface vessels. Two sliding mode controllers are designed: a common sliding mode controller for the surge force control and a hierarchical controller for the yaw moment control. Neural network is employed to approximate the model uncertainties. Time-varying disturbances are involved to test the performance of the proposed controllers. The closed-loop stability of the system is proved by Lyapunov stability theorem. Simulation results validate the effectiveness of the proposed controllers.

The main motivation of combined neural network and sliding mode is for its robustness. In reality, the disturbance is usually existed. The robustness of the controller algorithm is very important. The proposed algorithm, actually, can be applied into many other applications, such as robot, aircraft, and underwater vehicle, etc.