1 Introduction

The problem of buckling for a circular cylindrical shell has been widely investigated due to its great importance in the design of marine structures. Both the straight and curved pipes are used in an actual pipeline. At the time of operation, the pipeline will be subject to a wide range of loads. Buckling of structural components under various types of loading is a common cause of fatal failure in a structure.

In the followings, the formulas for estimating buckling stress and moment of cylinder under bending and the previous researches are briefly explained.

The maximum bending stress of a cylinder under the critical (buckling) moment M cr can be expressed by Eq. 1:

$$\sigma_{\text{cr}} = \frac{{M_{\text{cr}} }}{{\pi r^{2} t}}$$
(1)

where r is the pipe radius, and t is the wall thickness.

If the critical buckling stress of the cylinder under bending is the same as the buckling stress of the cylinder under uniform compression, the critical stress can be expressed by Eq. 2:

$$\sigma_{\text{cr}} = \frac{E}{{\sqrt {3\left( {1 - \nu^{2} } \right)} }}\left( \frac{t}{r} \right).$$
(2)

Then, the buckling moment can be derived as follows:

$$\begin{aligned} M_{\text{cr1}} \text{ } &= \text{ }\sigma_{\text{cr}} .\pi r^{2} t \hfill \\ &= \text{ }0.605\pi Ert^{2} . \hfill \\ \end{aligned}$$
(3)

Timoshenko and Gere [1] stated that the maximum compressive stress at the critical buckling moment is about 30 % higher than that obtained from Eq. 2:

$$M_{\text{cr2}} \text{ } = \text{ }1.3M_{\text{cr1}} .$$
(4)

The calculation results of previous investigation by authors (Yudo and Yoshikawa [2]) for a straight pipe, whose L/D varies from 5 to 20, and D/t varies from 50 to 200, showed that the critical bending moment in linear calculation is expressed by Eq. 5:

$$\begin{aligned} M_{{{\text{cr}}3}} &= 1.1 \times M_{{{\text{cr}}1}} \hfill \\ &= 0.666\pi Ert^{2} . \hfill \\ \end{aligned}$$
(5)

One of the earliest efforts in nonlinear structural analysis was performed by Brazier [3]. His paper is concerned with the problem of the stability of long cylindrical shells under bending. If a long cylinder is subjected to bending, its cross-section flattens. Consequently, its bending stiffness deteriorates with increasing bending moment as a function of applied curvature, and exhibits a maximum. Brazier performed a somewhat approximate analysis and found that the buckling moment is given by Eq. 6:

$$M_{\hbox{max} } = (2\sqrt 2 /9)\pi Ert^{2} /\sqrt {1 - \nu^{2} } = 0.329\pi Ert^{2} .$$
(6)

If the maximum stress caused by this moment is computed using Eq. 1, it is found that with \(\nu\) = 0.3

$$\sigma_{\hbox{max} } = 0.33Et/r.$$
(7)

Chwalla [4] derived the Eq. 8 as the maximum moment, considering the oval deformation of section by the energy method. He also showed that the maximum stress occurs at another bending curvature and it can be expressed by Eq. 9:

$$M_{\hbox{max} } = M_{k} = 0.378\pi Ert^{2}$$
(8)
$$\sigma_{\hbox{max} } = 0.51Et/r.$$
(9)

Seide and Weingarten [5] solved as a bifurcation buckling problem. Assuming that the pre-buckling behavior can be defined with sufficient accuracy by a linear membrane solution, they found that the critical buckling stress is only 1.5 % higher than Eq. 2 for a cylinder with r/t = 100. For thinner cylinders the difference is even smaller.

Odland [6] calculated the collapse moment of cylinder with R/t = 100 and showed that the collapse moment of cylinder with L/D = 5, 10, and infinity is ab. 70, 60, and 50 % of M cr1, respectively, because of oval deformation of a section.

Ju and Kyriakides [7] also mentioned that the oval deformation reduces the bending rigidity and leads to a limited load instability associated with local collapse.

The initial yield moment of a pipe under bending is shown below:

$$M_{\text{y}} = \sigma_{\text{y}} \pi \cdot r^{2} \cdot t$$
(10)

where σ y is the yield stress.

SUPERB [8] declared that the geometrical imperfections (excluding corrosion) that are normally allowed in pipeline design will not significantly influence the maximum strength, and the buckling moment in plastic region can be calculated as:

$$M_{\text{p}} = \left( {1.05 - 0.003 \cdot \frac{r}{t}} \right) \cdot \sigma_{\text{y}} \cdot D^{2} \cdot t.$$
(11)

If r/t equals to 50, Eq. 11 becomes:

$$M_{\text{p}} = 1.14 \cdot \sigma_{\text{y}} \pi \cdot r^{2} \cdot t.$$
(12)

The ultimate moment in Eq. 11 is only 15 % higher than the initial yielding moment, and this seems to be a considerably conservative value.

Hauch and Bai [9] had obtained a set of equations for calculating the maximum allowable bending moment including proposed safety factors for different targeted safety levels.

As for the curved pipe, Boyle [10] presents using a thin shell theory developed by Reissner, how classical thin shell models of this component can be deduced in making certain simplifying assumptions concerning the mode of deformation. Zhang [11] obtained the expressions for the bending moment and flattening ratio in terms of curvature. Boussaa [12] explained an original treatment for the finite bending of curved pipe with an arbitrary cross-section.

But, a comprehensive study on the buckling strength of pipe under bending has not been found. In this study, the series of calculations of buckling and collapse strength of straight and curved pipe under bending are performed by utilizing nonlinear FE software.

2 Procedures of calculation

2.1 Parameters for calculation

In the calculation of the straight pipe, the ratio between pipe length and diameter (L/D) and the ratio between diameter and thickness (D/t) are taken as the calculation parameters. In this paper as shown in Table 1, L/D varies from 5 to 20, in which the diameter is changed from 1,000 to 4,000 mm, and D/t varies from 50 to 200 where D is the pipe diameter, t is the wall thickness, and L is the pipe length.

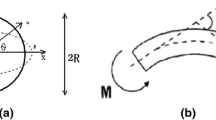
Table 1 Calculation parameter for straight pipe
Full size table

In calculation of the curved pipe, the pipe diameter is originally fixed at 4,000 mm, and the thickness is fixed to 20 mm. L/D varies from 2.5 to 20 by changing the pipe length. R/D varies from 50 to 200 as shown in Table 2 where R is radius of curvature in curved pipe. The geometry for a curved pipe is shown in Fig. 1.

Table 2 Calculation parameter for curved pipe
Full size table
Fig. 1
figure 1

Geometry curved pipe

Full size image

2.2 Model for calculation and calculation program

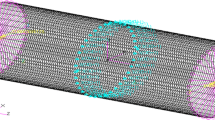
The buckling calculations of pipe under pure bending were performed. The full-length models of straight and curved pipe are used in FEA. Figure 2 shows the finite element model for straight pipe.

Fig. 2
figure 2

Finite element model for straight pipe

Full size image

General-purpose FE software Msc Marc was used for nonlinear buckling analysis in which the cross-sectional oval deformation before buckling is taken into account. The quadrilateral 4-node element (No. 75) was used. The calculating region is divided into 36 elements in a circumferential direction. The element number in length is basically 120 elements and more elements are used to maintain the calculation accuracy in the case of a long cylinder. The mesh convergence study was done in reference [2].

2.3 Boundary condition and loading condition

Cylindrical coordinates shown in Fig. 3 were used. The following boundary conditions are given at the midspan of cylinder, except at four points in Fig. 3.

Fig. 3
figure 3

Midspan of section

Full size image
$$\begin{gathered} U_{\text{R}} \ne 0\text{ }R_{\theta } \text{ } \ne \text{ }0 \hfill \\ U_{\theta } \ne 0\text{ }\theta_{\theta } \text{ } \ne \text{ }0 \hfill \\ U_{\text{Z}} \ne 0\text{ }Z_{\theta } \text{ } \ne \text{ }0 \hfill \\ \end{gathered}$$
(13)

The rigid body elements (RBE) are inserted at both end sections to connect the center of a circle and the points on a circle. The bending moment is loaded at the center of circle at both ends. The RBE prevent the oval deformation of both end sections, and keep the section in plane under rotational deformation by a bending moment.

Figure 4 shows the caption of straight and curved pipe, respectively. The oval deformation of each section at midspan is defined by δ.

Fig. 4
figure 4

Geometry for a straight pipe and b curved pipe

Full size image

2.4 Method to obtain bifurcation moment in nonlinear calculation

To obtain the bifurcation buckling moment and its mode, the eigenvalue calculations are performed at the proper load increment, and the cross-section point of the critical moment between the buckling moment and the applied moment is defined as the bifurcation buckling moment, as the schematics shown in Fig. 5. In this figure, the horizontal axis shows the applied load, and the vertical axis shows the bifurcation buckling eigenvalue.

Fig. 5
figure 5

Schematic diagram for estimation of bifurcation moment

Full size image

The eigenvalue is calculated at each load increment considering the pre-buckling deformation. The bifurcation buckling load is judged as follows. When the value of eigenvalue is larger than the applied load, the buckling does not happen. When the value of eigenvalue is smaller than the applied load, the buckling has already happened. The cross-section point of eigenvalue and applied load is treated as the bifurcation buckling load.

3 Calculation result

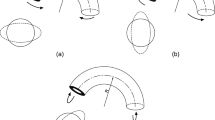
The typical buckling mode, which is obtained from nonlinear calculation, is shown in Fig. 6. The stress at the lower side of the cylinder is compression, and that at the upper side is tension. The oval deformation is larger in the vicinity of midspan than at the span end. Therefore, the region of buckling is limited in the bottom area close to the center.

Fig. 6
figure 6

Buckling modes of pipe (D/t = 200, L/D = 2.5) under pure bending a straight pipe, b curved pipe R/D = 50

Full size image

3.1 Calculation results for straight pipe

Figure 7 shows the relationship between the applied bending moment and the oval deformation at midspan when the pipe behaves elastically. The vertical axis shows the non-dimensional moment (M/M cr1). In a long pipe, such as L/D = 10, 15, and 20, the oval deformation increases a lot with the increasing of the applied load. On the other hand, in a short pipe, such as L/D = 2.5 and 5.0, the oval deformation is smaller by the restriction of the sectional deformation at both ends. The maximum moment of each curves shows the bifurcation buckling moment explained in Fig. 5. Due to the oval deformation before the buckling occurs at midspan, the maximum moments of the long pipes reduced more as compared to the short pipes.

Fig. 7
figure 7

Ovalization at midspan for straight pipe (D/t = 200) by elastic analysis

Full size image

Figure 8 shows the relationship between the applied bending moment and the oval deformation at midspan considering the yielding effect of the material when the yield strength is 621 MPa. In this figure, the elastic calculation results are also plotted with dotted lines. The maximum moments of elasto-plastic calculation is much smaller than that of elastic calculation. Although the oval deformations of the long pipes are larger than those of short pipes, the maximum bending moments of the former are not much lower than those of short pipes because the maximum bending moments are limited by yielding.

Fig. 8
figure 8

Ovalization at midspan for straight pipe (D/t = 200)

Full size image

Figure 9 shows the relationship between the buckling moment and L/D. In this figure, the elastic calculation results are plotted with solid lines, and the elasto-plastic calculation results are plotted with dotted lines. In elastic analysis, the buckling moment will be decreased with the increasing value L/D and become constant when the pipe has an infinite length. From the calculation results, the maximum moment for a long pipe considering oval deformation is shown as follows:

$$M_{\hbox{max} } = 0.52M_{\text{cr1}} = 0.314\pi Ert^{2} .$$
(14)
Fig. 9
figure 9

Relationship between buckling moment and L/D for straight pipe

Full size image

The maximum moment by Eq. 14 is slightly lower than Eq. 6 and much lower than Eq. 8.

In elastic analysis, the buckling strength of shorter pipes is larger than longer pipes, because the effect of boundary condition on the oval deformation at midspan of pipe is larger. In elasto-plastic analysis, the buckling moment is almost constant regardless of the pipe length, because the maximum bending moment is limited by yielding. In the cases of D/t = 200, in which the pipes buckle more elastically than D/t = 50 and 100, the buckling strength of shorter pipes is slightly higher than longer pipes.

For the thick pipe, such as D/t = 50, the difference of the buckling moment between elastic and elasto-plastic analysis is very large. But for a thin pipe, such as D/t = 200, the difference of the buckling moment of them is not so large. This means that the pipes with a large value of D/t buckle elastically and the pipes with a small value of D/t buckle in elasto-plastic region.

Figure 10 shows the relationship between the buckling moment and D/t. The elastic calculation results are plotted with solid lines, and the elasto-plastic calculation results are plotted with dotted lines, same as in Fig. 9.

Fig. 10
figure 10

Relationship between buckling moment and D/t for straight pipe

Full size image

For the pipe with a small D/t or with a large D/t and small L/D, the difference of the buckling moment between in elastic and elasto-plastic analysis is large. On the other hand, for the pipe with large D/t and large L/D, the difference is small. The buckling stress of the former pipe is larger than the latter, and then the former pipe buckles more plastically than the latter. Therefore, the difference of buckling strength of the former pipe in elastic and elasto-plastic analysis is large. To investigate the yielding effect on the buckling strength of pipe in bending, the non-dimensional parameter (β) shown below is considered

$$\beta = (D/t)(\sigma_{\text{y}} /E) \propto \left( {M_{\text{cr1}} /M_{\text{y}} } \right).$$
(15)

This parameter is proportion to the ratio of linear buckling moment and initial yielding moment. The elasto-plastic buckling strength is examined by changing the yield stress and the diameter.

Figure 11 shows the relationship between the buckling moment and L/D. The vertical axis is the maximum moment, which is shown non-dimensionally by dividing it with the initial yielding moment (M y).

Fig. 11
figure 11

Relationship between buckling moment and L/D for straight pipe by elasto-plastic analysis

Full size image

The solid lines are the calculation results for σ y = 621 MPa. Solid lines are the results for (D/t) (σ y/E) equals to 0.15, 0.3, and 0.6, respectively. In this calculation, the diameter of pipe is taken as the calculating parameter. The dotted line with the circle marker shows the results for σ y = 315 MPa and (D/t) (σ y/E) equals to 0.3. The dotted line with a triangle marker is the results for σ y = 1260 MPa and (D/t) (σ y/E) equals to 0.6. The solid and dotted lines with both circle and triangle marker are the pipes with the same value of (D/t) (σ y/E) and the different yield strength. When the value of β = (D/t) (σ y/E) is same, the buckling moment is almost the same. Therefore, the parameter of β is possible to be the parameter which represents the yielding effect on the buckling strength of pipe under bending.

3.2 Calculation result for curved pipe

Figure 12 shows the distribution of oval deformation along the pipe length for a curved pipe with D/t = 200, in which R/D varies from 50 to 200. Maximum oval deformation occurs at midspan and no oval deformation occurs at both ends of pipe because of boundary condition. The oval deformation decreases with increasing R/D. The oval deformation will be uniform all over the pipe without a boundary condition. Therefore, the zero oval deformation range is limited in the vicinity of end support. Considering the axis-symmetrical deformation of cylinder, the nearly zero oval deformation region is assumed to be within the 3π/4β 1 from support end, where β 41  = 3(1−ν 2)/(r 2 t 2) [13].

Fig. 12
figure 12

Distribution oval deformation along the pipe length for curved pipe (L/D = 20, D/t = 200)

Full size image

Figure 13 shows the relationship between the applied bending moment and the oval deformation at midspan when the pipe behaves elastically. Similarly, with a curved pipe in the elastic analysis the buckling moment of pipe will be decreased with increasing oval deformation before buckling. Figure 14 shows the relationship between the applied bending moment and the oval deformation at midspan considering the yielding effect of material when the yield strength is 621 MPa. In this figure, the elastic calculation results are also plotted with dotted lines. The vertical axis shows the non-dimensional moment (M/M cr1). The maximum moments considering yielding effect are smaller than that of elastic calculation.

Fig. 13
figure 13

Ovalization at midspan for curved pipe (L/D = 20, D/t = 200) by elastic analysis

Full size image
Fig. 14
figure 14

Ovalization at midspan for curved pipe (L/D = 20, D/t = 200)

Full size image

Figure 15 shows the relationship between the buckling moment and L/D. In this figure, the elastic calculation results are plotted with solid lines, and the elasto-plastic calculation results are plotted with dotted lines. In elastic analysis, the buckling moment will be decreased with increasing value L/D and become constant when the pipe has infinite length. A pipe with a small value of L/D at the buckling moment is almost the same for each value of R/D. It is supposed that the effect of the curvature of a curved pipe on buckling strength is reduced by the effect of constraint at the supported end. Similarly, in elasto-plastic analysis, the buckling moments of small L/D are almost the same regardless of the value of R/D. Figure 16 shows the difference in the buckling moment between the elastic analysis and the elasto-plastic analysis. The horizontal axis is R/D and the vertical axis is non-dimensional buckling moment. For a small value of R/D and large value of L/D, the differences between them are very small or almost the same. It is because the buckling stress is small and the buckling takes place elastically in these cases. On the other hand, the difference is very large for a small value of L/D.

Fig. 15
figure 15

Relationship between buckling moment and L/D for curved pipe (D/t = 200)

Full size image
Fig. 16
figure 16

Relationship between buckling moment and R/D for curved pipe (D/t = 200)

Full size image

4 Conclusions

In this study, the series calculations of buckling and collapse strength of straight and curved pipe under bending are performed by utilizing nonlinear FE software. The typical buckling modes for straight pipe and curved pipe are obtained by numerical calculations. The followings are clarified by the numerical calculations.

  1. 1.

    The region of buckling is limited at the compressive side in the vicinity of midspan.

  2. 2.

    For the straight pipe, the reduction rate of the buckling moment due to oval deformation of pipe was clarified for various values of L/D and D/t in elastic and elasto-plastic buckling. In a short pipe, the oval deformation before buckling is small due to the restriction of sectional deformation at both ends. Therefore, the reduction of buckling strength due to oval deformation is smaller in shorter pipes than longer pipes.

  3. 3.

    The maximum moment for long pipes, considering oval deformation, is shown as follows:

$$M_{\hbox{max} } = 0.52M_{\text{cr1}} = 0.314\pi Ert^{2}$$
  1. 4.

    The pipes with a small D/t buckle more plastically, and the pipes with a small L/D buckle more plastically because of the restriction of the sectional deformation at both ends.

  2. 5.

    The parameter non-dimensional β is proposed. The parameter of β = (D/t) (σ y/E) is possible to be the parameter which represents the yielding effect on buckling strength of pipe under bending. Using Fig. 12, the yield moment can be predicted without FEA.

  3. 6.

    The buckling moment of curved pipe is smaller than the straight pipe, because the oval deformation is larger than straight pipe. The oval deformation increases when R/D decreases (where R is the curvature of curved pipe) This tendency is remarkable for small L/Ds.