1 Introduction

Shipping water is a dangerous phenomenon for ships. When ships encounter heavy seas, the water level sometimes exceeds the bow height and green water flows down on the deck. This phenomenon is called shipping water. Shipping water causes serious damage to containers, hatch covers, and other structures on the deck and can lead to a ship capsizing in the worst case.

Shipping water has been experimentally studied and various mathematical models have been developed, e.g., those by Tasaki [1], Goda and Miyamoto [2], Mizoguchi [3], Ogawa et al. [4] and Greco et al. [5] The shipping water volume and impact pressure can be estimated by using these mathematical models; however, they cannot predict the three-dimensional behavior of shipping water, and it is difficult to apply the models using various parameters such as ship speed, heading angle, bow shape, and superstructure. Therefore, numerical analysis based on the Navier–Stokes equations is required for wider application.

Recently, some numerical methods have been developed for incompressible flows with a free surface, and these have been applied to the analysis of shipping water. For example, Yamasaki et al. [6] simulated green water on a rectangular solid using the density function method. Nielsen and Mayer [7] calculated green water loads on a moored floating production storage and offloading unit (FPSO) in head seas using the volume of fluid (VOF) method of Hirt and Nichols [8]. Hu and Kashiwagi [9] calculated violent wave-body interactions using the constrained interpolation profile (CIP) method of Yabe et al. [10]. Gómez-Gesteira et al. [11] analyzed green water overtopping with the smoothed particle hydrodynamics (SPH) method, a particle method, in two dimensions. In the SPH method, numerical diffusion does not occur because the Lagrangian description is used and the convection terms are not discretized. Since calculation grids are not used, grid distortion never occurs.

In the authors’ previous paper [12], shipping water was numerically analyzed by the moving particle semi-implicit (MPS) method, [13, 14] which is a particle method for incompressible flow. In that article, shipping water on a stationary deck in head seas was analyzed in three dimensions. The geometry was simplified as a semicircle for the primary assessment of the particle method, and the three-dimensional behavior of shipping water and the surface elevation around the deck were in agreement with the experiment, although the impact pressure on the deck was lower than the experimental value by about 50%. The error was mainly due to the low spatial resolution.

The objectives of the present study were to develop a numerical analysis method based on the MPS method for simulating shipping water on a moving ship with a realistic bow shape, and to verify the calculated fluid behavior and the impact force acting on the deck. The calculated results were compared with the experiment carried out by Tanizawa et al. [15]. In the calculation, the ship was forced to move in order to follow the ship oscillations obtained in the experiments by Tanizawa et al. [15].

2 Moving particle semi-implicit method

2.1 Governing equations

The governing equations are the mass and momentum conservation equations for incompressible flow and are expressed as follows:

$$ \frac{D\rho }{Dt} = 0, $$
(1)
$$ \rho \frac{{D\vec{u}}}{Dt} = - \nabla P + \mu \nabla^{2} \vec{u} + \vec{K}. $$
(2)

The mass conservation equation is represented by density, although velocity divergence is usually used in the finite volume method. Numerical diffusion does not arise because a fully Lagrangian description is employed and the convection terms are not discretized.

2.2 Particle models

In the MPS method, the governing equations are transformed to dynamic equations of the particles using particle models. Gradient and Laplacian operators are represented as the following particle models:

$$ \langle \nabla \phi \rangle_{i} = \frac{Z}{{n^{0} }}\sum\limits_{j \ne i} {\left[ {\frac{{\phi_{j} - \phi_{i} }}{{|\vec{r}_{j} - \vec{r}_{i} |^{2} }}(\vec{r}_{j} - \vec{r}_{i} )w(|\vec{r}_{j} - \vec{r}_{i} |)} \right],} $$
(3)
$$ \langle \nabla^{2} \phi \rangle_{i} = \frac{2Z}{{n^{0} \lambda }}\sum\limits_{j \ne i} {(\phi_{j} - \phi_{i} )w(|\vec{r}_{j} - \vec{r}_{i} |)} $$
(4)

where Z is the number of spatial dimensions, n 0 is a constant of the particle number density, and w() is a weight function. The weight function is expressed as follows:

$$ w(r) = \left\{ {\begin{aligned} {\left( {\frac{{r_{\text{e}} }}{r}} \right)- 1} &\quad {(r < r_{\text{e}} )} \\ 0 &\quad {(r \ge r_{\text{e}} )} \\ \end{aligned} } \right., $$
(5)

where r is the distance between two particles and r e is the radius of the interaction domain.

The particle number density is also calculated with the above weight function as follows:

$$ n_{i} = \sum\limits_{j \ne i} {w(|\vec{r}_{j} - \vec{r}|).} $$
(6)

The particle number density has two meanings: one is the value proportional to the fluid density and the other is the normalization factor of the weighted average. Therefore, the particle number density is required to be constant to satisfy the mass conservation equation, the incompressibility condition expressed as Eq. 1. Parameter n 0 denotes the constant particle number density.

Parameter λ in Eq. 4 is the constant calculated as follows:

$$ \lambda = \frac{{\sum_{j \ne i} {|\vec{r}_{j} - \vec{r}_{i} |^{2} w(|\vec{r}_{j} - \vec{r}_{i} |)} }}{{\sum_{j \ne i} {w(|\vec{r}_{j} - \vec{r}|)} }}. $$
(7)

This parameter adjusts the increase of the variance by the Laplacian model to that of the analytical solution.

These particle interaction models are substituted for the differential operators in the governing equations and then the governing equations are transformed to dynamic equations of the particles. Grids are not necessary at all in this discretization process.

2.3 Algorithm for incompressible flow

A semi-implicit algorithm is employed in the MPS method; the momentum conservation equations, except for the pressure gradient terms, are explicitly solved (at time step k) in the first phase, and then the Poisson equation of pressure is implicitly solved (at time step k + 1) in the second phase. The following Poisson equation of pressure is deduced from the implicit mass conservation equation and the implicit pressure gradient term:

$$ \left\langle {\nabla^{2} P} \right\rangle_{i}^{k + 1} = - \frac{{\rho_{0} }}{{\Updelta t^{2} }}\frac{{n_{i}^{*} - n^{0} }}{{n^{0} }} $$
(8)

where \( n_{i}^{*} \) is the temporal particle number density after the explicit phase. The Laplacian operator on the left hand side of Eq. 8 is discretized with the Laplacian model (Eq. 4). The right hand side of Eq. 8 represents the source term which is expressed as the deviation of the temporal particle number density from the constant value, n 0. Consequently, simultaneous linear equations are obtained from Eq. 8, and these equations are solved using the conjugate gradient (CG) method.

This semi-implicit algorithm is similar to that of the finite volume method for incompressible flow. The difference is in the right hand side of the Poisson equation of pressure: the deviation of the particle number density is used in Eq. 8, whereas the velocity divergence is used in the finite volume method.

2.4 Dirichlet boundary condition

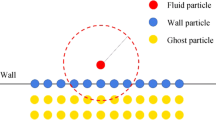
The Dirichlet boundary condition is necessary to solve the Poisson equation of pressure. In the MPS method, zero is given to the free surface particles as the Dirichlet boundary condition. The free surface particles are defined using the particle number density. Particles with a particle number density below βn 0 were identified as being on the free surface: the parameter β was 0.97 in this study.

Only the particle number density is required for this boundary condition: the contours of free surfaces are not necessary. Therefore, fluid fragmentation and coalescence are easily calculated with this simple boundary condition.

2.5 Radius of the interaction domain

The radius of the interaction domain, r e, needs to be determined carefully because it influences the calculation cost, although the calculated results are not sensitive to the radius. The radius determines how far a particle interacts with its neighborhood. If the radius is large, it takes a long time to calculate the particle interactions because each particle has many neighboring particles. After several trials, 2.1l 0 was selected as the radius in this study, where l 0 is the distance between adjacent particles in the initial configuration. The neighboring particles were searched for using the bucket algorithm [16].

3 Analysis of shipping water

3.1 Experiment

An experiment was performed by Tanizawa et al. [15] to verify the numerical analysis. In their study, several running tests were carried out with a ship model of a very large crude carrier (VLCC) in the 50-m-long towing tank of the National Maritime Research Institute. The experimental setup is shown in Fig. 1. The ship model was attached to the carriage with a heave rod and gimbals and was towed in regular head seas. Heave and pitch motions were free, and the other motions were fixed. The shipping water was measured for three typical wavelengths, i.e., λ/L pp values of 0.70, 1.00, and 1.50, where λ is the wavelength and L pp is the ship length between perpendiculars. Fluid behavior on the port side of the deck was recorded with two high-speed cameras located on the starboard deck as illustrated in Fig. 1a. The mirror on the starboard deck was used to reflect the image, and the starboard deck was covered with a waterproof case. The pressure was measured on the port side of the deck with pressure gauges.

Fig. 1
figure 1

Experimental setup: a oblique view, b top and side view

Full size image

3.2 Flume and wave maker

3.2.1 Experiment

In the experiment, regular waves were generated with a flap wave maker located at the end of the flume and propagated to the ship model. The flume dimensions were 50 m in length, 8 m in breadth, and 4.5 m in depth.

3.2.2 Calculation

It is impossible to calculate the above huge domain because of the limit of current computer capabilities. Therefore, in this study, the entire flume was not modeled. Figure 2 shows the calculation domain. The depth was 0.52 m, the breadth was 1.06 m, and the length was dependent on the wavelength. Each length is summarized in Table 1, where Length1 and Length2 are the distances illustrated in Fig. 2a.

Fig. 2
figure 2

Calculation domain: a side view, b rear view (cross section). The starboard side of the calculation domain was eliminated to reduce the calculation cost. Length1 distance between the left wall and the wave trough. Length2 the distance between the right wall and the wave trough

Full size image
Table 1 Length of the calculation domain
Full size table

As shown in Fig. 2b, because the ship model was towed in head seas and the shipping water behavior was symmetric against the centerline of the ship, the starboard side was eliminated to reduce the calculation time and memory requirements. A wall was located on the centerline as a boundary condition. The center wall consisted of fixed particles and viscosity was not calculated between the fluid and the center wall to avoid boundary effects.

The total number of particles was between 1.0 and 1.5 million, as shown in Table 2. The fluid particles were surrounded with four walls: the left, right, center, and bottom walls. The bottom wall of the flume had a slope in the calculation. There was a gap between the ship bottom and the right side wall to avoid collision. The gap size was 0.06 m. All the walls except for the center wall were forced to move with the velocity distribution of linear waves to mitigate boundary effects. The details of the velocity distribution are explained in Sect. 3.4. These moving wall boundaries reduced the large number of outside particles and made it possible to calculate shipping water at high resolution with reduced boundary effects.

Table 2 Number of particles for each wavelength
Full size table

All the walls were composed of three layers of wall particles. The inner single layer that was in contact with fluid particles was composed of wall particles whose pressures were calculated to repel fluid particles. The outer double layers were composed of dummy wall particles that did not have pressures and were used only to calculate the particle number densities.

3.3 Calculation conditions

In this study, the experiment performed by Tanizawa et al. [15] was numerically analyzed in three dimensions. Figure 2 shows the calculation domain. A model of a VLCC was located on linear waves: the principal dimensions of the VLCC are shown in Table 3. The ship model was calculated as a rigid body composed of rigid particles. The ship was forced to move in regular head seas with the translational and rotational velocity components measured in the experiment by Tanizawa et al. [15] Heave and pitch motions were given as obtained by the experiment, while the other motions were zero. The ship speed was 0.724 m/s (a Froude number of 0.134) and was kept constant. The starting time in the calculation was synchronized with the time when the pitching angle became zero in the experiment.

Table 3 Principal dimensions of the model of a very large crude carrier
Full size table

All particles were initially placed in a simple cubic lattice. The initial spacing between adjacent particles, l 0, was 1.0 × 10−2 m. The water density ρ was 1000 kg/m3, the kinematic viscosity υ was 1.004 × 10−6 m2/s, and the acceleration of gravity was 9.8 m/s2. The effects of the surrounding air and the surface tension of water were neglected. Shipping water was calculated in three typical wave conditions: λ/L pp values of 0.7, 1.0, and 1.5. The wave conditions are shown in Table 4.

Table 4 Principal parameters of the incident waves
Full size table

The shipping water caused by the first incident wave was calculated for 1.3 s in simulation time. The calculated impact pressure and shipping water behavior on the bow were compared with the experimental results obtained by Tanizawa et al. [15]. The pressures were compared at locations p1–p5 in Fig. 3. The shipping water behavior was compared with the experiments at location PLANE1 in Fig. 4. A single personal computer (CPU: Pentium 4, 3.6 GHz; main memory: 2 GB) was used for the calculation. The calculation times are shown in Table 5.

Fig. 3
figure 3

Location of pressure gauges on the deck

Full size image
Fig. 4
figure 4

Measurement location of the fluid behavior on the deck: a top view, b side view

Full size image
Table 5 Calculation time
Full size table

3.4 Initial condition and the boundary conditions of the fluid

The following analytical solution of the linear wave was used for the initial fluid velocity distribution, wave profile, and the velocity components of the boundary particles:

$$ \eta = \zeta_{\text{a}} { \sin }(kx - \omega t), $$
(9)
$$ \Upphi = - \frac{{\zeta_{\text{a}} c}}{{{ \sin}{\text{h}}(kh)}}{ \cos}\text{h}[k(z + h)]\cos (kx - \omega t), $$
(10)
$$ u = \frac{\partial \Upphi }{\partial x} = \frac{{\zeta_{\text{a}} ck}}{{{ \sin}\text{h}(kh)}}{ \cos}\text{h}[k(z + h)]{ \sin }(kx - \omega t), $$
(11)
$$ v = \frac{\partial \Upphi }{\partial z} = - \frac{{\zeta_{\text{a}} ck}}{{{ \sin}\text{h}(kh)}}{ \sin}\text{h}[k(z + h)]{ \cos}(kx - \omega t), $$
(12)
$$c = \frac{\omega }{k} = \sqrt {\frac{g}{k}{ \tan }\text{h}(kh)} = \sqrt {\frac{g\lambda }{2\pi }{ \tan}\text{h}\left( {\frac{2\pi h}{\lambda }} \right)} $$
(13)

where η is the wave profile, ζa is the amplitude, Φ is the velocity potential, t is time, c is the phase velocity, k is the wave number (k = 2π/λ), and ω is the angular frequency (ω = 2πf). The x-axis is in the horizontal direction in which the wave propagates and the z-axis is in the vertical direction. Although the above analytical solution is valid for a fluid unbounded in the horizontal direction and of finite and constant depth, these equations were applied in this study. The reason is that it was assumed that the boundary effects such as the reflection waves from the sidewalls and bottom wall were small because all the boundary particles were forced to move at the velocity of the above analytical solution, and only the first incident wave was calculated in this study. The bottom particles were also forced to move at the velocity of the analytical solution. The depth of the towing tank used in the experiment, 4.5 m, was used for the depth parameter z in the analytical solution, although the actual depth was 0.52 m in this calculation domain. Therefore the above analytical solution can be applied to this computational domain. Table 4 shows the principal parameters of the incident waves.

4 Results and discussion

4.1 Fluid behavior of shipping water

Figure 5a shows images of the calculated shipping water for a wave of short wavelength (λ/L pp = 0.7). As shown in the left column, the wave propagated to the right (0.0 s) and the ship model ran to the left in head seas. The pitching and heaving motions were small for this short wave. The wave impinged on the bow (0.3 s), and the fluid was lifted above the bow. After that, the lifted fluid fell onto the deck (0.6 s), and finally flowed onto the deck (0.9 s).

Fig. 5
figure 5figure 5figure 5

Shipping water behavior for wavelength/(ship length between perpendiculars) (λ/L pp) values of a 0.7, b 1.0, c 1.5

Full size image

Figure 5b shows the shipping water behavior for a wave of medium wavelength (λ/L pp = 1.0). The relative ship motion against the wave surface is large. As shown in the left column, the ship goes down into the wave crest with a pitching motion (0.3 s). A large amount of fluid flowed onto the deck (0.6 s). This tendency was in agreement with the experiment.

Figure 5c shows the shipping water behavior for a wave of long wavelength (λ/L pp = 1.5). As shown in the left column, the heaving motion follows the wave elevation and the pitching motion follows the wave slope. Since the impinged wave was not largely deformed by the bow, the green water flowed smoothly. This tendency was in agreement with the experiment.

As shown in Fig. 5, some fluid particles spilled out over the boundaries. The spillage over the sidewalls was due to the waves made by the ship. The spillage over the sidewall reduces the reflection wave from the sidewall, so that spillage was advantageous in this study. The spillage around the ship bottom was due to the narrow gap between the ship bottom and the sidewall; the gap was 0.06 m in the initial state, and changed with the wave motion. Since the gap was necessary to avoid a collision between the ship hull and the boundary particles, spillage from the gap was inevitable. The lost particles that left the calculation domain were not considered in further calculations. Since the lost particles were few (1.1–3.4% of the total fluid particles), as shown in Table 6, and only the first incident was calculated in this study, the reduction in the amount of water was negligible.

Table 6 Number of particles spilling over the boundaries
Full size table

4.2 Green water on the deck

Figure 6 shows enlarged views of the green water on the deck for each wavelength. The left column shows experimental data taken at PLANE1 in Fig. 4. The thick solid curve was drawn on the water surface to emphasize the fluid profile. The center column shows the calculated results for the same area, PLANE1. The right column shows the calculated green water behavior around PLANE1. The quadrangular frame drawn on each figure means the shooting area for which photographs were taken in the experiment. The initial timing between the experiment and the calculation was manually synchronized for comparison. The time intervals of the sequential pictures of the experiment are the same as those of the calculation.

Fig. 6
figure 6figure 6figure 6

Enlarged view of the shipping water on the deck for λ/L pp values of a 0.7, b 1.0, c 1.5

Full size image

Figure 6a shows an enlarged view of green water on the deck for a wave of short wavelength (λ/L pp = 0.7). The calculated free-surface profile and the amount of water were close to the experimental results. However, from 0.45 to 0.50 s, the calculated free-surface profile does not show a thin curved edge, although such an edge is present in the experimental profile. The reason is that the spatial resolution was not adequate to express the thin curved edge. Tanizawa et al. [15] reported that the curved edge in the experiment was due to the backward wave breaker. The heaving and pitching motions of the ship were small at short wavelengths, and the incident wave hit the bow front horizontally. The wave was reflected upward along the bow shape, then broke backward, and finally fell onto the foredeck. The thin curved edge in the experiment was formed in this way. Because the spatial resolution was not adequate to express the backward reflection, the thin curved edge did not occur in the calculation.

Figure 6b shows an enlarged view of green water on the deck for a wave of medium wavelength (λ/L pp = 1.0). The ship went down into the wave crest (0.3 s) and a large volume of fluid flowed onto the deck (0.6 s). This tendency was in agreement with the experiment. The free surface had a gentle slope in both the calculation and the experiment. The amount of the water on the deck was also close to the experimental result.

Figure 6c shows an enlarged view for a wave of long wavelength (λ/L pp = 1.5). Since the wave was not largely deformed by the bow, the green water flowed smoothly on the deck. This tendency was in agreement with the experiment.

4.3 Time history of the impact pressure

Figure 7 shows the time histories of the impact pressure for waves of short, medium, and long wavelengths (λ/L pp = 0.7, 1.0, and 1.5), respectively. The location at which the pressure was compared with the experiment was p2 in Fig. 3. The calculated pressure shown in Fig. 7 was obtained from the average pressure for 25 wall particles around the location of p2; this was done because the time history of the pressure obtained by the particle method shows large numerical oscillations in general. However, the oscillations in the calculated pressure remained and the peak value was higher than the experimental value in all three cases.

Fig. 7
figure 7

Time history of the impact pressure on the deck for a λ/L pp = 0.7, wave encounter period (T e) = 0.828 s; b λ/L pp = 1.0, T e = 1.039 s; c λ/L pp = 1.5, T e = 1.333 s. The measurement location was p2 in Fig. 3. MPS, moving particle semi-implicit method. The vertical and horizontal axes are nondimensionalized with the wave amplitude and the encounter wave period, respectively

Full size image

Pressure oscillations also occurred in the experiment, although the mechanism is different. Tanizawa et al. [15] stated that the experimental oscillations were due to air entrapment. During the impact process, air is trapped in the shipping water and some air bubbles are generated. The water pressure compresses those bubbles, and pressure oscillations occur.

The reason why pressure oscillations occur in the MPS method is that the particles keep moving in the fully Lagrangian description. This is a fundamental drawback of the particle method because the fully Lagrangian description is necessary to analyze large deformations of the free surface. In addition, the pressure oscillations may be enhanced in the present study by the lack of spatial resolution and the experimental noise included in the ship motion. Moreover, air-cushion effects were ignored, which also contribute to the differences in the pressure peaks. Therefore, it is difficult for the MPS method to predict the peak value of the local load. To restrain the pressure oscillations caused by the particle model, higher spatial resolution is necessary in addition to some postprocessing such as time averaging and spatial averaging. Recently, new algorithms have been studied to suppress the numerical pressure oscillations in particle methods [17–19].

4.4 Time integral of the impact pressure

The time integral of the impact pressure is also important for ship design because large structures such as hatch covers have large time constants. Figure 8 shows the time integral of the impact pressure. The location at which the pressure was compared with the experiment was p2 in Fig. 3. This pressure integration was evaluated from the pressure of a single particle without averaging.

Fig. 8
figure 8

Time integration of the impact pressure on the deck for a λ/L pp = 0.7, T e = 0.828 s; b λ/L pp = 1.0, T e = 1.039 s; c λ/L pp = 1.5, T e = 1.333 s. The measurement location was p2 in Fig. 3. The vertical and horizontal axes are nondimensionalized with the wave amplitude and the encounter wave period, respectively

Full size image

Figure 8a shows the result for a wave of short wavelength (λ/L pp = 0.7). Compared to the experiment, the slope of the calculated result was steep. On the other hand, the rise time was in agreement with the experiment. The calculation result was higher than the experiment by 14.7% when the simulation time was 1.30T e (1.08 s). This difference is due to the edge shape of the green water. As mentioned above, the edge had a linear slope in the calculation, whereas it had a thin curve in the experiment.

Figure 8b shows the result for a wave of medium wavelength (λ/L pp = 1.0). The slope was in good agreement with the experiment; however, the calculated result was lower than the experiment by 21.2% when the simulation time was 1.25T e (1.3 s). Tanizawa et al. [15] reported that the highest impact pressure was measured at this wavelength in the experiment, and this tendency was reproduced in the calculation. The rise time was later than the experiment by about 0.04T e.

Figure 8c shows the result for a wave of long wavelength (λ/L pp = 1.5). The slope was in agreement with the experiment. The calculated result was lower than the experiment by 27.2% when the simulation time was 0.97T e (1.3 s), and the rise time was later than the experiment by about 0.15T e. The further forward the measurement locations were, the higher the total impulses obtained. The reason is that the green water flowed smoothly and the static pressure was dominant in the pressure components for long wavelengths. This tendency was in agreement with the experiment.

From these figures, it can be seen that the tendency of the time integral of the impact pressure in terms of changes in λ/L pp agreed with the experiment. The rise time of the impact pressure was delayed in all three cases. This was due to the initial condition of the free-surface profile and the velocity distribution. In the calculation, the analytical solution of the linear wave was given as the initial condition; however, in the experiment, there were reflection waves in the initial state. This difference in the initial condition delayed the rise time. It is still unclear why the rise time was delayed so much for the wave of long wavelength.

4.5 Total impulse

Figure 9 shows the total impulses at locations from p1 to p5 in Fig. 3. These impulses were obtained by the time integration of the pressure on the measuring positions for 1.3 s from the starting time of the calculation. This pressure integration was evaluated from the pressure of a single particle without averaging. Figure 9a shows the result for a wave of short wavelength (λ/L pp = 0.7). The errors were from −25.0 to 153.5% of the experimental values. The highest impulse was measured at the front point, p1, in the calculation, although it was at p4 in the experiment.

Fig. 9
figure 9

Total impulse on the deck for λ/L pp values of a 0.7, b 1.0, c 1.5. The numbers on the horizontal axis are the measurement locations as given in Fig. 3. The vertical axis is nondimensionalized with the wave amplitude

Full size image

Figure 9b shows the result for a wave of medium wavelength (λ/L pp = 1.0), and the errors were from −31.6 to 17.2% of the experimental values. Figure 9c shows the result for a wave of long wavelength (λ/L pp = 1.5), and the errors were from −0.4 to −46.9% of the experimental values.

In this article, the effect of the spatial resolution is not shown. The convergence of the MPS method in two dimensions was investigated by Koshizuka et al. [20]. They calculated the shipping water on a stationary deck at several spatial resolutions and showed that higher spatial resolutions led to larger amounts of shipping water, although they were not able to reach adequate convergence. We need to investigate what constitutes adequate spatial resolution for three-dimensional shipping water analyses.

5 Conclusions

Shipping water was numerically analyzed using the MPS method. The towing tests carried out by Tanizawa et al. [15] were modeled at three typical wavelengths. The ship model was forced to move with the translational and rotational velocity components measured in the experiment, and the calculation domain was made as small as possible to reduce the calculation cost.

The shipping water behavior and the impact pressure on the deck were compared with the experimental results. The main findings were as follows:

  1. 1.

    The calculated shipping water behavior for three typical wavelengths was in agreement with the experiment, although the edge shape was different for the wave of short wavelength due to the inadequate spatial resolution of the calculation.

  2. 2.

    The calculated water volume of the shipping water on the deck was in close agreement with the experiment.

  3. 3.

    The time history of the impact pressure on the deck oscillated in the calculation. This pressure oscillation was due to the full Lagrangian description of the particle method in addition to the inadequate spatial resolution and the experimental noise included in the ship motion.

  4. 4.

    The tendency of the time integral of the impact pressure in terms of changes in λ/L pp agreed with the experiment, although the errors were still large. The error was −46.9% at the negative maximum and 153.5% at the positive maximum.

From these results, it can be seen that the present approach based on the MPS method is able to predict the shipping water behavior and the time integral of the impact pressure on a moving ship, although higher spatial resolution is necessary to estimate the impact force more accurately.