Introduction

Proficiency testing being carried out to assure the quality of test and calibration and demonstrate a laboratory competence is based on certain quantitative criteria of judging the quality of results obtained in the process of interlaboratory comparisons that have been called performance indicators. Among various statistics [1, 2] Z scores and E n numbers are most often used as that kind of indicators and are being expressed in symbols of [1] as follows:

$$ Z = |x - X|/s; $$
(1)
$$ E_n = |x - X|/\big({U_{{\rm lab}}^2 + U_{{\rm ref}}^2 }\big)^{1/2}, $$
(2)

where x and X are the result of participating laboratory and the assigned value respectively (for E n numbers X is usually the result obtained by reference laboratory); s is the estimate or measure of variability (standard deviation as a rule); U lab and U ref are the expanded uncertainty of the result of participating and reference laboratory respectively. The usage of performance indicators is specified [1] as Z≤2 = satisfactory, 2<Z<3 = questionable, Z≥3 = unsatisfactory; and E n ≤1 = satisfactory. The vagueness of these conditions (estimation criteria) for Z scores, as well as measurement uncertainties (if bearing in mind their absence in Z scores, and the way of interpreting E n numbers) influence the quality of estimation results.

Whilst meeting with the recommendations of ISO/IEC Guide 43-1 [1] and currently developing ISO/DIS 13528 [2], a correct choice of proper performance indicator sometimes does also present a problem, which stems from the lack of well-founded criteria and methods of proving the choice. In measurement comparison schemes, for instance, the traditional use of E n numbers for some combinations of measurement uncertainties of participating laboratories may lead to erroneous results, whereas the non-traditional transition to Z scores might in some cases improve the situation. Likely occasions of preferable usage of E n numbers instead of Z scores also cannot be excluded from the practice.

Methodologically, either a performance indicator or (and) its applying is far from being perfect. In this connection the ignoring of measurement uncertainty (as pointed out in [3]), and the lack of certainty in estimation condition (non-optimal estimation) inherent in the usage of Z scores, the way proposed, for example, in [4] and aimed at allowing for the uncertainties for a case of applying in-house reference materials, is noteworthy that actually has led to using the performance indicator similar E n numbers, rather than traditionally Z scores. In [2] the usage of two modernized performance indicators (so-called z′-scores and zeta-scores): \(z^\prime = |x-X|/(s^2+u_x^2)^{1/2}\) and \({\it zeta} = {|{x - X}|} / {({u_x ^2 + u_X ^2 })^{{1{/{{2}}}}} }\), where u x and u X are standard uncertainties of the results of participating laboratory and the assigned value respectively, has yet been also stipulated for improving estimation capability.

As for E n numbers, the consideration of this performance indicator in terms of statistics as being derived from Z scores [2] is not matching the metrological nature of the comparison of calibration laboratories with the reference one. The estimation reliability when using E n numbers depends on both how the absolute error |x−X| is normalized with respect to U lab and U ref, and of the correctness of allowing for these uncertainties. The most reliable normalization E nr =|x−X|/U lab is achievable when U lab≫U ref. Irrespective of the last condition, E nr has been used [5] through 1992 [6]. Expression (2), based on comparing the difference between the results obtained by laboratories and the uncertainty of calculating the difference as the criterion of proper estimating the competence of a laboratory, is incorrect in principle. A formal use of (2) may in some cases distort estimations and decrease their reliability, therefore the declared in [7] convenience of the method based on (2) is not a sufficient substantiation for its practical usage.

For all reasons given above, the present work is focused on the following two purposes: (1) the determination of practical conditions of correct applying Z scores and E n numbers based on the uncertainties of participating laboratories, and (2) the improvement of performance indicators as such; this concerns the expression and estimation criteria for E n numbers, and the optimal estimation criterion for Z scores. For achieving these goals the paper suggests classification approach. It does not discuss problems of designing and interpretation of proficiency tests, of determining the assigned value and its uncertainty, of the standard deviation for proficiency assessment and calculation of performance statistics that have been circumstantially presented in ISO/DIS 13528 [2]. In the author's opinion, the approach and methods proposed in the paper are not in contradiction with these problems, but in complement of one another.

Classification approach and general criterion of applying Z scores and E n numbers

The two performance indicators under consideration are based on different approaches. The difference |x−X| for Z scores belongs to the system of statistical treatment of test or measurement result, whereas for E n numbers it is considered as the estimated measurement error when comparing laboratories, one of which is the reference laboratory. For the best usage, the performance indicators should be considered as being intended for the different hierarchical levels of accuracy in principle. It is possible to tell that unlike Z scores E n numbers is based on the principle of etalon (the less ratio U ref /U lab the more reliable estimation). Thus the reliable use of E n numbers demands the higher level of accuracy classification for a reference laboratory in comparison with other participants, whereas the Z scores normally (X and s are derived from participants' results) is applicable for the laboratories of the same accuracy level. This level represents the range of relative values farther derived and substantiated.

No matter how many laboratories participate in an intercomparison, the final judging for each participant is the result of comparing either directly with reference lab or with some conditional (virtual) reference lab, to which the assigned value together with its uncertainty could be attributed. Clearly, this is the process of classifying the laboratories by means of certain numerical value—the classification factor (as estimation criterion). The same approach is true when classifying measurement capabilities of laboratories, by analogy with the accuracy classification of measuring instruments.

In general view, the classification approach in applying the performance indicators requires collating the uncertainties U a and U b of any two (A and B) from the number of participating laboratories, one of which can specifically be the reference or conditional reference laboratory, for deciding if they belong to the same classification level or not, and on this basis to decide what performance indicator is particularly applicable. In order to do that, the relative influence of U a and U b (for the model of errors) or \(U_a ^2\) and \(U_b ^2\) (for the exclusively statistical model) on the estimation quality may be presented as weights K a =U a /(U a +U b ) and K b =U b /(U a +U b ), or \(K_a = {{U_a ^2 } / {( {U_a ^2 + U_b ^2 } )}}\) and \(K_b = {{U_b ^2 } / {( {U_a ^2 + U_b ^2 } )}}\) respectively, which are analogous to the estimates of probability forming the complete group of independent events (K a +K b =1). Such an analogy gives us the exclusive chance of applying the optimal selection model, borrowed from information theory [8], for classifying components of the group onto informative and redundant ones.

The ratio ρ=min(K a /K b )±1 represents special coefficient, the best value of which is evaluated for the optimal (necessary and sufficient) rational or irrational positive number ϕ o of components (2≥ϕ o ≥1) [9]. For the least certain situation about allowing or ignoring the lesser of two components (50% confidence), ϕ o matches the following equation:

$$ \varphi _o = \exp ( - K_a \ln K_a - K_b \ln K_b ) = 1.5 $$
(3)

Accordingly, the optimum coefficient ρ o of the weightiest component K (equals to either K a or to K b ) as function of ρ is determined and approximately calculated as follows:

$$ \rho _o = \arg \left\{\exp \left[-\left(\frac{K}{K + \rho K}\right)\ln \left( {\frac{K}{{K + \rho K}}} \right)\right.\right.\nonumber\\ \left.\left.\, - \left( {\frac{{\rho K}}{{K + \rho K}}} \right)\ln \left( {\frac{{\rho K}}{{K + \rho K}}} \right) \right] = 1.5 \right\}\nonumber\\ = \arg \left\{ \exp \left[ - \left( {\frac{1}{{1 + \rho }}} \right)\ln \left( {\frac{1}{{1 + \rho }}} \right)\right.\right.\nonumber\\ \left.\left. -\, \left( {\frac{\rho }{{1 + \rho }}} \right)\ln \left( {\frac{\rho }{{1 + \rho }}} \right) \right] = 1.5 \right\} = 1/2\pi $$
(4)

The next expressions (5) and (6) result from the replacement of weights in formulas (3) and (4) by respective ratios of uncertainties.

$$ {\rm For}\,{\rm the}\,{\rm model}\,{\rm of}\,{\rm errors}\,(E_n \,{\rm numbers})\!:\nonumber\\ \quad \rho _o = \min (U_a /U_b )_o^{ \pm 1} = 1/2\pi ,$$
(5)
$$ {\rm For}\,{\rm the}\,{\rm statistical}\,{\rm model}\,(Z\,{\rm scores})\!:\nonumber\\ \quad \rho _{os} = \rho _o^2 = {\rm min}\left( {U_a^2 /U_b^2 } \right)_o^{ \pm 1} = 1/2\pi ,$$
(6)

Expression (5) has been called optimum accuracy coefficient which, being the factor of relative classification, is also of fundamental significance for creating optimal systems of accuracy classification [10]. As the classification factor, the optimum accuracy coefficient is the first and most general criterion of judging, with the aid of which one can realize whether two compared laboratories belong to the same accuracy level (when \(\min ({{U_a } / {U_b }})_{\rm o} ^{ \pm 1} \ge {1 / {2\pi }}\)). If not, the use of E n is the only correct decision. However, in case of laboratories of the same level of accuracy, but of different measurement capabilities, the situation is not so definite to make decision what performance indicator preferably to use; and the nearer \(\min ({{U_a } / {U_b }})_{\rm o} ^{ \pm 1}\) to 1/2π the more it is indefinite. The more circumstantial estimation is achievable by using (5) and (6) expressions jointly; the details are given in the following section.

Peculiarities of applying Z scores and E n numbers

Allowing for expressions (5) and (6), Fig. 1 reflects peculiarities of applying the performance indicators, namely the possibilities and preferences of their usage depending on decreasing accuracy coefficient ρ=min(U a /U b )±1, i.e. the increase of quality of reference laboratory in carrying out intercomparisons.

Fig. 1
figure 1

Schematical illustration of boundaries and areas of possible and best usage of E n numbers and Z scores when comparing two laboratories in the framework of proficiency testing programmes depending on the accuracy coefficient ρ=min(U a /U b )±1

Full size image

In accordance with Fig. 1 there is a variety of possibilities in applying Z scores and E n numbers depending on the accuracy coefficient regarding the laboratories undergoing comparison. Among the possibilities, special attention may be drawn to the following practical situations:

  1. 1.

    If all laboratories participating in the comparison meet the condition U ref/U lab≥1/2π (where U ref is somehow appointed, even from the participants), and their performance estimation determined by E n numbers is unsatisfactory, then a final decision ought to be done using Z scores.

  2. 2.

    A laboratory with the uncertainty less than 1/2π part in the comparison with others ought to be appointed as the reference laboratory. In this case E n numbers should be used only.

  3. 3.

    In case of two or more laboratories, uncertainties of which match the situation (1), for comparing their results it is reasonable to apply the Z scores model, whereas the model of E n numbers—for the others. In this instance any of laboratories that matches the situation (1) might be chosen as the reference laboratory, and the less uncertainty of a laboratory, the more reliable choice will be made.

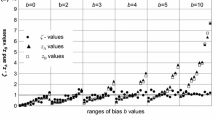
The significant limitation of applying E n numbers in the area of Z scores (within the range 1/2π≤ρ≤1) is the often observed estimation uncertainty due to instability (drift) of the result of testing or calibration during the intercomparison period, even if the instability is within admissible limits of measurement uncertainty. Essential difference in the sensitivity of these two performance indicators to the instability of artifact is clearly demonstrated (Fig. 2) for the case of the same uncertainty (U) of two laboratories undergoing the comparison, and for the above-mentioned maximum permissible instability. In this case, the expressions E n =0.707(Δ+U)/U=0.707(Δ/U+1) and Z=[Δ 2+(U/2)2]1/2 /(U/2)2=(4Δ 2 /U 2+1)1/2, where Δ=|x−X|, were obtained using formulas (2) and (1) and the coverage factor 2 in determining U.

Fig. 2
figure 2

Illustration of the advantage of Z scores regarding the influence of instability of measurand upon the results of intercomparison in the case of the same uncertainty (U) of two laboratories undergoing the comparison: the area of insensitivity of Z scores to the ratio Δ/U, where Δ=|x−X |, for which the decision of satisfactory estimation (Z≤2) is true, is significantly greater than for E n numbers in the respective area (E n ≤1)

Full size image

Optimum estimation criterion for Z scores

The model of Z scores has an affinity with well-known statistics used for detecting the outlying observations [11], where the quality of estimation depends upon the level of confidence chosen without taking into account the systematic character of quality estimation for system-defined measurements [12]. This method, despite relying on practical experience, is the clear-cut example of usage of exclusively statistical estimation towards the quality of estimation information that is a not always correct.

In reality the information obtained with Z scores should be optimum, and the aim of the optimization is to find out the best value (Z o ) of the ratio between |x−X| and s as the optimal estimation criterion. However, until now it has been difficult to solve this problem. The difficulty can be successfully overcome by using the proposed above criterion of optimal classification for the statistical model as follows:

$$ {{|x - X|^2 } / {s^2 }} \le 2\pi \,\,\, {\rm or},\;{\rm approximately},{{|x - X|} / {s_c }} \le 2.5$$
(7)

Applying this principle, the following convenient expression for comparing calibration laboratories through their uncertainties by means of Z scores may be recommended:

$$ Z_o = {{|x - X|} / {[ {({{U_{{\rm lab}} } / {k_{{\rm lab}} }})^2 + ({{U_{{\rm ref}} } / {k_{{\rm ref}} }})^2 } ]}}^{1/2} \le 2.5,$$
(8)

where k lab and k ref = the coverage factors in determining the uncertainties. The left part of this condition is analogous as specified in [2] for zeta-scores, just expressed by using expanded uncertainties.

Thus, obtained condition (8) differs from presently used ones in principle since the new is characterized by the strictly established optimal estimation criterion (classification level = 2.5). However, it should be emphasized that this criterion, excluding vagueness in the interpretation of estimation results, is mostly useful and preferably applicable on the final stage of intercomparison. The presently used criteria may perform another function—the maintenance of the process on intermediate stages, if any, in order to consider participant's result in terms of (2) as giving an “action signal” (when Z score above 3.0 or below −3.0), or a “warning signal” (when Z score above 2.0 or below −2.0). Naturally, in this case being applied together the proposed criterion and the presently used ones do not contradict, but are the complement of one another.

Modernized expressions for E n numbers

The improved expression for E n numbers uses the accuracy coefficient ρ=U ref /U lab as follows [13]:

$$ E_{ni} = E_{nr} = {{|x - X|} / {U_{{\rm lab}} }} \le (1 - \rho );$$
(9)

This condition is based on the comparison of maximal errors by using the modulus of the uncertainties together with the discrepancy of measurement results. The maximum estimation reliability is achievable with such modular approach when compare the uncertainty U lab with the maximal (due to U ref) difference of measurement results, i.e. max|x−(X±U ref)|=|x−X|+U ref. The less reliable but the more optimistic estimation is when in formula (9) the criterion \(\sqrt {1 - \rho ^2 }\) is used instead of (1−ρ).

The graphical illustration of all discussed expressions for E n numbers (Fig. 3) demonstrates that, as distinct from commonly used E n , the improved expressions E ni and E nio ensure toughening of the requirement to the difference |x−X| due to the uncertainty of reference laboratory for achieving satisfactory result of the comparison.

Fig. 3
figure 3

Different expressions of E n numbers as functions of accuracy coefficient ρ=U ref /U lab. Essential difference between E n and E ni (or E nio ) results from the opposite approaches to the estimation: unlike E n , the increasing of accuracy coefficient leads to more strict acceptability condition for E ni and E nio as the compensation to lowering the quality of reference laboratory

Full size image

For achieving the best estimation, the uncertainty U lab in the expression (9) ought to be taken with the optimum level of confidence C o =(1−0.5ρ o )×100%=(1−1/4π)×100%=92%. Because C o and ρ o characterize the absence of redundant estimation information, instead of (9) the following informatively more accurate expressions are preferable:

$$ E_{ng} = E_{nr} = {{|x - X|} /{U_{{\rm lab}} }} \le (k_i /k_o )(1 - \rho );$$
(10)
$$ E_{ngo} - E_{nro} = {{|x - X|} / {U_{\rm lab} }} \le (k_i /k_o )\sqrt{1-p^2},$$
(11)

where k l = the coverage factor in determining the uncertainty U lab (usually k l =2); k o =1.75 is the coverage factor, which matches C o .

Example

Here is the example of determining the suitable model for comparing the seven testing or calibration laboratories, the results and uncertainties of which are presented (in conditional units) in the Table 1. The estimates of assigned value (X) and the variance (s) were calculated as follows: \(X = {{( {\sum_{i = 1}^7 {X_i } } )} / 7} = 5.44\), and \(s = [ {\sum_{i = 1}^7 {(x_i - X)^2 /6} } ]^{1/2} = 0.15\).

Table 1 Data and results for the presented example of seven laboratories
Full size table

The results of Z i calculation (Table 1) show all participants meet the condition (7). However, the uncertainty of Lab #2 is less than 1/2π of the uncertainty of any other participating laboratory; therefore this laboratory can be truly recognized as the reference laboratory regarding the rest of participants. Thus, this is a good case for further reasonable applying the E n numbers instead of Z scores in order to ensure the correct estimation. Calculated by the expressions (10) and (11) E n data (here k l =k 2 =2) demonstrate the non-conformance of the two (#4 and #7) laboratories by E n numbers criterion, as well as the necessity of using just this criterion to prevent erroneous estimation conclusions. Thus, for this case the use of E n numbers, instead of Z scores has enabled to evade a misconception regarding above-mentioned two laboratories. It should be recommended to decrease their best measurement capabilities by means of increasing the respective uncertainties.

Conclusions

  1. 1.

    Applying the performance indicators, the positive decision (in terms of acceptance) tells about the two in principle distinct estimation results, namely: (1) the belonging of compared laboratories to the same accuracy class—in case of Z scores model, and (2) the acceptable measurement error of a laboratory against the reference laboratory—in case of E n numbers.

  2. 2.

    The combined application of improved Z scores model and the optimum conditions for the uncertainties of participating laboratories is proposed that enables recognizing the suitable model (Z scores or E n numbers or even both of them) to use in a proficiency-testing situation. This makes it possible to achieve an optimum estimation when calculating and judging the quality of results in interlaboratory comparisons.

  3. 3.

    Proposed approach gives a chance to all those responsible for the fulfillment of interlaboratory comparisons to carry out the correct treatment of test, measurement and estimation data concerned. In the author's opinion, the current philosophy of development and operation of proficiency testing schemes [1] and methods being used [2] can be materially improved on the basis of the suggested ideas. First of all this concerns the simple and effective procedure for the optimal treatment of intercomparisons data that may be easily developed and unified on the basis of this paper as well. The classificational analysis of participating laboratories regarding their uncertainties represents an integral part of such a procedure.

  4. 4.

    The availability of different (proposed and presently used) philosophies in realizing estimation criterion of Z scores for the different stages of intercomparison process is the major inference drawn from their consideration. Acknowledging the practical significance of currently developing ISO/DIS 1358 [2], this may also pay attention to its improvement.