1 Introduction

Majorana fermions are particles identical to their own antiparticles [1]. Up-to-date stable particles with Majorana properties have not been found. Recent investigations suggest that quasiparticles in a special class of condensed matter could have the properties of Majorana fermions [2]. Among other systems, this kind of Majorana quasiparticles was predicted to exist at the edges of superfluid 3He [3, 4]. Several experimental approaches were suggested to detect Majorana quasiparticles’ edge states in superfluid 3He [5–7]. So far only Grenoble experiments have shown the direct observation of Majorana quasiparticles’ influence on superfluid 3He-B properties [8].

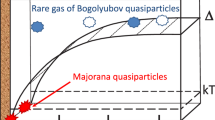
At the critical temperature T c = 0.93 mK (at 0 bar) 3He passes a phase transition to its superfluid state with the formation of Cooper pairs near the Fermi surface [9]. Excited states of the system are separated from the ground superfluid state by an energy gap Δ. At T < 0.4 T c the 3He properties are dominated by the Bogoliubov quasiparticle excitations (i.e., “broken” Cooper pairs). The heat capacity of Bogoliubov quasiparticles has the well-known exponential dependence on the temperature [9]

$$C_{\text{bulk}} \sim Vp_{F}^{2} \left( {\frac{\Delta }{kT}} \right)^{3/2} \exp \left( { - \frac{\Delta }{kT}} \right).$$
(1)

The theory of superfluidity treats quasi-particle and quasi-hole excitations on an equal footing and has all excitations appear as a pair at opposite energies

$$\gamma^{ + } \left( \varepsilon \right) = \gamma \left( { - \varepsilon } \right).$$
(2)

Combined particle-hole, i.e., Majorana, states can occur at \(\varepsilon = 0\) only [10]

$$\gamma^{ + } (0) = \gamma (0).$$
(3)

As shown by G.E. Volovik [11], a stable energy level at \(\varepsilon = 0\) with the finite density of states can exist at edges of the superfluid 3He-B. The dimension of these edge states localization is about the coherence length \(\xi\) of superfluid 3He. The heat capacity in this case has the power-law dependence on temperature (G.E. Voloovik, pers. commun.):

$$C_{\text{maj}} \sim S\xi p_{F}^{2} \left( {\frac{\Delta }{kT}} \right)^{ - 2}.$$
(4)

The computer simulation of this dependence was performed in [7]. It can be seen from Eqs. (1) and (4) that depending on the surface-to-volume ratio the Majorana states can give the significant contribution to the superfluid 3He heat capacity. In our experiments, the ratio \(S\xi /V\) was about 10−4 so the Majorana quasiparticles’ contribution should be about 10 % of the total heat capacity at the limit of the ultra-low temperature of 135 µK. It should be noted that the surface is rough so some coefficient was involved in fitting the experimental data. Indeed, we performed experiments very similar to those in [8] but we extend the temperature range down to 125 µK for increasing the contribution of Majorana quasiparticles’ heat capacity.

2 Results

The experimental cell consisted of a closed copper box with small orifice [8]. The cell was filled by superfluid 3He. The extremely low specific heat of 3He at ultra-low temperatures makes it possible to measure the increase in temperature inside the box after releasing the small amount of energy (down to 1 keV). The temperature inside the cell was monitored by measuring the resonance width of the vibrating wire resonator (VWR) which strongly depends on the temperature [12]:

$$W_{0} = \alpha \exp \left( { - \Delta /kT} \right).$$
(5)

For the heating events, the second VWR (heater wire) was used. This wire was driven by short-time excitation current at the resonance frequency introducing controllable amount of energy into the system. After the heating pulse, the temperature inside the cell suddenly rises, and then goes back to its initial temperature by thermalization via the orifice with some time constant. This time constant is determined as

$$\tau_{box} = RC,$$
(6)

where R is the thermal resistance of the orifice and C is the superfluid 3He heat capacity. So by measuring the time constant of the box, it is possible to extract the data of 3He heat capacity. In Fig. 1, the dependence of the 3He heat capacity normalized to theoretical Bogoliubov quasiparticle heat capacity Eq. (1) on the resonance width of VWR is shown. The up temperature axis is obtained by Eq. (5). Consequently, the dashed line shows the theoretical temperature dependence of the heat capacity with given parameters of the cell. The solid curve represents the theoretical dependence of 3He heat capacity with contribution of Majorana quasiparticles Eq. (4). The geometrical sizes of the cell lead to the ratio \(S\xi /V = 10^{ - 4}\). But it should be taken into account that the surface is rough. The cooper surface of the cell has not been specially prepared or polished and it is difficult to estimate accurately the rugosity of the surface. That is why the rugosity was chosen as fitting parameter. The quite good agreement with experimental data was obtained when rugosity was equal to 10 (Fig. 1).

Fig. 1
figure 1

Temperature dependence of superfluid 3He heat capacity normalized to its theoretical value for only Bogoliubov quasiparticles Eq. (1). Solid line shows the theoretical temperature dependence of the heat capacity for bulk 3He with contribution of Majorana edge states

Full size image

It can be seen that the experimental data deviate from the theoretical curve for bulk 3He when the temperature goes down 150 µK. The temperature dependence of this deviation agrees quite well when taking into account the Majorana quasiparticles’ contribution to the total heat capacity of superfluid 3He.

It is known [13] that the adsorbed layers of superfluid 3He have a huge heat capacity by comparison with bulk 3He. But in our case, the contribution of adsorbed 3He to the total heat capacity is excluded because the surface of the cell was covered by 4He. It was done in the following way. The small amount of 4He was added to the pure 3He in the storage tank. It was found that less than a 7 ppm concentration of 4He is sufficient to cover the whole walls of the cell. If condensation is started slowly at very low temperatures when the experimental cell is cooled down 10 mK then 4He is separated from 3He in the heat exchangers. As a result, the liquid arriving at the experimental cell will be absolutely pure 3He and the cell walls will be covered by adsorbed layers of 3He which have a huge heat capacity [13]. To avoid it, the filling in our experiments was started at high temperatures of about 4 K. In this case during the further cooling process, 4He enters the cell, condenses in the cell, and due to its lower zero point energy covers the cell walls. One can suggest that some islands of adsorbed 3He remained in the cell which could give the additional heat capacity to the bulk 3He. But two experimental facts show that it is not the case. Firstly, the independence of the heat capacity of the magnetic field was observed while the heat capacity of adsorbed 3He is proportional to magnetic field [14]. Secondly, the temperature decay after the typical heating event is well described by the single exponential function. The presence of the adsorbed 3He leads to the two exponential behavior of the decay after heating event [14]. So we can conclude that we had no contribution of adsorbed layers of 3He to the total heat capacity and that we observed the Majorana quasiparticles’ edge states.

2.1 NMR Investigations

Our observation of the Majorana quasiparticles’ states in superfluid 3He open wide possibilities to its investigation by means of nuclear magnetic resonance (NMR). Recently, it was proposed to probe the spin relaxation of injected electrons near the surface of 3He [6]. The Majorana nature of the edge states leads to the anisotropy of the spin susceptibility in the vicinity of the 3He surface so that the relaxation rate of injected electrons should be sensitive to the direction of external magnetic field.

We propose another magnetic resonance probe to detect Majorana states at the edges of superfluid 3He-B. Particularly, at the limit of extremely low temperatures the extremely long-lived NMR induction signals were observed [15]. These signals were also observed by continuous wave NMR method [16]. These states have been described in terms of Bose–Einstein condensation of magnons and in terms of Q-ball in the field theory [17]. The free decay of the Q-ball may exceed half an hour at the limit of ultra-low temperatures [18] due to a very small density of the Bogoliubov quasiparticles. The Q-ball represents the special state of coherent precession of magnetization localized in the magnetic field minimum along the cell axis. Remarkably, with moving the magnetic field minimum, for example, by varying the current value through gradient coil, the location of Q-ball in the cell is changed. Recently, the additional surface relaxation mechanism of Q-ball was observed [19]. It appears when the applied field gradient is such that the field minimum occurs close to the edge of the cell, i.e., when Q-ball is located near the Majorana states in 3He-B. In this case, the lifetime of Q-ball was shortened considerably [19]. In light of our detection of Majorana quasiparticles at the edges of 3He-B, it would be interesting to study this surface relaxation mechanism in more detail, especially its dependence on the direction of external magnetic field. Our experiments are in progress now. Particularly, we have invented the new type of texture magnetic trap for Q-ball which gives a high possibility to manipulate with the Q-ball at a frequency of about 1 MHz [20]. The comprehensive review of NMR methods of superfluid 3He investigations can be found in [21, 22].

3 Conclusion

We have presented the observation of the Majorana quasiparticles at the edges of superfluid 3He. It manifests itself by strong contribution to the superfluid 3He heat capacity at the limit of ultra-low temperatures. In this case, the Bogoliubov quasiparticles’ heat capacity drops down exponentially with temperature while the Majorana quasiparticles’ heat capacity has the power-law dependence on temperature. The prospect of the detection Majorana quasiparticles by means of NMR was discussed.