Mechanically manipulated in-plane electric currents and thermal control in piezoelectric semiconductor films

Abstract

This study explores the new findings of in-plane mechanical forces on electric currents and thermal control in piezoelectric semiconductors. The thermo-electro-elastic theory is considered based on the thermo-piezoelectricity theory and drift–diffusion theory for semiconductors. A two-dimensional nonlinear model for in-plane deformations of piezoelectric semiconductor films is developed, where thermo-elastic, pyroelectric and thermoelectric couplings are involved. The newly developed nonlinear equations are directly solved based on the finite element method, while linearized equations derived from the nonlinear theory and corresponding analytical solutions are also obtained as a reference for validation. Our findings indicate that the in-plane mechanical forces exerted on piezoelectric semiconductors significantly influence both currents and thermal fluxes through piezoelectric coupling. Specifically, the angle of in-plane mechanical force relative to the c-axis significantly impacts the currents, with the potential to suppress, enhance or alter the direction, thereby affecting the temperature field. Based on these findings, an application simulation that focuses on mechanically induced current manipulation and thermal control is introduced and realized.

1 Introduction

During the past few decades, a substantial interest has existed in piezoelectric semiconductors (PSs). Semiconductors based on functional piezoelectric materials have facilitated widespread applications in energy harvesting and biomedicine [1,2,3,4]. Benefiting from the advantages of low-cost, high-energy conversion efficiency, as well as being environmentally friendly, applications of PSs like smart wearable electronics, portable electronic devices and self-powered sensors are generally used in people’s daily life [5,6,7,8]. Studies on new high-performance composite materials and structural design with high efficiency have been analyzed by many researchers [9,10,11,12,13,14]. In PSs, the built-in potential barriers modulated by mechanical loads can effectively manipulate the charge transport behaviors [15,16,17]. Multi-couplings of piezoelectric and semiconductor materials have created a new research field called piezotronics [18,19,20]. Within the realm of piezotronics, the piezoelectric coupling responses in extension, shear, torsion, bending and thickness stretch scenarios have been systematically analyzed [21,22,23,24,25,26,27,28]. Hence, a specific piezoelectric potential barrier in the PSs can be achieved by the target deformations.

Nevertheless, the operating environment of PS devices is invariably subject to temperature variations. Factors including pyroelectric, thermo-elastic and thermoelectric couplings (including Seebeck and Peltier effects) are influenced by temperature change [29,30,31]. Various phenomenological theories based on continuum mechanics have been applied in investigating the thermal problems [32,33,34,35,36,37,38,39,40,41]. These thermally involved couplings and piezoelectric coupling exist simultaneously in the PSs, which results in an extraordinary coupling mechanism for energy conversion between mechanical energy, thermal energy and electric energy. Recently, Qu et al. [42] have claimed that thermal dipoles can take place in PS devices during a variety of mechanical deformations. In addition, the existence of thermal fluxes in a PS plate generated by the thermoelectric effect via the electric currents can be controlled, especially under uniform transverse loadings.

PSs with thermoelectric properties have attracted significant attention in temperature sensors, electronic cooling and thermal control [43,44,45,46]. More specifically, the solid-state PS devices have main advantages in durability, reliability and safety under extreme environments compared to the conventional fluid- or gas-state devices. To extend the above-mentioned work and enhance the safety performance of PS devices, the physical responses of PS devices under the action of in-plane mechanical loads are desirable to be investigated. To effectively generate in-plane mechanical loads, the application of friction on both sides of a plate-type’s surfaces can facilitate the creation of appropriate midplane forces. Furthermore, strategically distributing magnetic materials within the body of PS devices can enable the remote manipulation of these external mechanical forces. This approach not only enhances the precision of force application but also broadens the scope of control in various technological applications.

This paper aims to establish a model framework for in-plane extensional thermo-piezoelectric semiconductor films and explore the new application about current manipulation and thermal control in PS devices. Note that very few models considered the Peltier effect in thermo-piezoelectric semiconductors and disregarded the electric currents formed by the temperature gradient due to the Seebeck effect, leading to incorrect predictions. Hence, we consider the combined thermoelectric effects (i.e., the Peltier and Seebeck effects), pyroelectric effect and thermo-elastic effect on the overall physical field distributions in the current two-dimensional boundary value problems under simultaneous mechanical loads.

In this paper, Sect. 2 briefly derives the two-dimensional governing equations for thermo-piezoelectric semiconductor films considering thermo-couplings. Section 3 demonstrates the numerical analysis of the nonlinear models considering thermal couplings by the finite element (FE) method, along with the interpretation of current manipulation and thermal control. An application simulation of the previous findings about thermal control of periodic structures is introduced in Sect. 4. The final section concludes with some observations and suggestions.

2 Two-dimensional theory for thermo-piezoelectric semiconductors

For a thermo-piezoelectric semiconductor, the time-independent field equations are composed of the stress equation of motion (Newton’s law), the charge equation of electrostatics (Gauss’ law) including doping and mobile charges, the conservation of charge for holes and electrons (continuity equations), and the heat conduction equation [42, 47,48,49,50]:

$$ \begin{gathered} T_{ij,j} + f_{i} = 0, \hfill \\ D_{i,i} = q(p - n + N_{D}^{ + } - N_{A}^{ - } ), \hfill \\ J_{i,i}^{p} = 0, \hfill \\ J_{i,i}^{n} = 0, \hfill \\ q_{i,i} = (J_{i}^{p} + J_{i}^{n} )E_{i} , \hfill \\ \end{gathered} $$

(1)

where T_ij represents the stress tensor; f_i is the body force; D_i denotes the electric displacement; q is the elementary charge; p and n are the concentrations of holes and electrons; N_D⁺ and N_A⁻ are the concentrations of ionized donors and acceptors; $J_{i}^{p}$ and $J_{i}^{n}$ represent the current densities for holes and electrons; q_i denotes the heat flux density; and E_i is the electric field.

Let θ be the small temperature change between the current temperature θ_A and the reference temperature θ_R, with θ = θ_A − θ_R. The constitutive equations can be expressed as [42, 49, 51]

$$\begin{gathered} T_{ij} = c_{ijkl} S_{kl} - e_{kij} E_{k} - \lambda_{ij} \theta , \hfill \\ D_{i} = e_{ijk} S_{jk} + \varepsilon_{ij} E_{j} + p_{i} \theta , \hfill \\ J_{i}^{p} = qp\mu_{ij}^{p} (E_{j} - \alpha_{jk}^{p} \theta_{,k} ) - qD_{ij}^{p} p_{,j} , \hfill \\ J_{i}^{n} = qn\mu_{ij}^{n} (E_{j} - \alpha_{jk}^{n} \theta_{,k} ) + qD_{ij}^{n} n_{,j} , \hfill \\ q_{i} = - k_{ij} \theta_{,j} + (P_{ij}^{p} J_{j}^{p} + P_{ij}^{n} J_{j}^{n} ), \hfill \\ \end{gathered}$$

(2)

where c_ijkl denotes the elastic tensor; S_kl is the strain tensor; e_kij is the piezoelectric tensor; λ_ij is the thermo-elastic tensor; ε_ij is the dielectric tensor; p_i is the pyroelectric tensor; $\mu_{ij}^{p}$ and $\mu_{ij}^{n}$ denote the carrier mobility; $\alpha_{jk}^{p}$ and $\alpha_{jk}^{n}$ represent the Seebeck coefficients; $P_{ij}^{p}$ and $P_{ij}^{n}$ are the Peltier coefficients; $D_{ij}^{p}$ and $D_{ij}^{n}$ represent the carrier diffusion constants; and k_ij represents the thermal conductivity.

The gradient relations read,

$$S_{ij} = (u_{i,j} + u_{j,i} )/2,\quad E_{i} = - \varphi_{,i} ,$$

(3)

where u_i is the mechanical displacement and φ is the potential for electrostatics.

It is noted that, for thermo-piezoelectric semiconductors used in microelectronic devices, the temperature changes are minimal. Thereby, we have the following relations under the small temperature perturbation assumption (i.e., θ << θ_R) [29, 51]:

$$\frac{{P_{11}^{n} }}{{\alpha_{11}^{n} }} = \frac{{P_{11}^{p} }}{{\alpha_{11}^{p} }} = \theta_{{\text{A}}} \simeq \theta_{{\text{R}}} ,{\kern 1pt} \quad \frac{{D_{11}^{n} }}{{\mu_{11}^{n} }} = \frac{{D_{11}^{p} }}{{\mu_{11}^{p} }} = \frac{{k_{{\text{B}}} \theta_{{\text{A}}} }}{q} \simeq \frac{{k_{{\text{B}}} \theta_{{\text{R}}} }}{q},$$

(4)

where k_B = 1.3806 × 10⁻²³ J K⁻¹ is the Boltzmann constant.

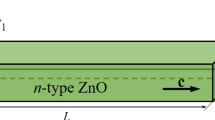
As shown in Fig. 1, for a thermo-piezoelectric semiconductor of crystals in the 6mm point group (e.g., ZnO), the c-axis is parallel to the x₃-direction. The in-plane electromechanical loads are considered in this model, thus, the zero-order field equations describing the extension deformations are needed [49]:

$$\begin{gathered} u_{1} = u(x_{1} ,x_{3} ),\quad u_{3} = v(x_{1} ,x_{3} ),\quad \varphi = \varphi (x_{1} ,x_{3} ),{\kern 1pt} \hfill \\ \theta = \theta (x_{1} ,x_{3} ),\quad p = p(x_{1} ,x_{3} ),\quad n = n(x_{1} ,x_{3} ). \hfill \\ \end{gathered}$$

(5)

Fig. 1

A piezoelectric semiconductor thin film with an in-plane c-axis and coordinate system

Let the thickness of the film be 2h₀. Assume that the semiconductor film is subjected to n-type doping, and ignore the effects of p-type doping (i.e., p = 0). Consider stress relaxation T₂₂ = 0 for plane stress problems. The constitutive equations for the film can be expressed as:

$$\begin{gathered} T_{11} = \overline{c}_{11} S_{11} + \overline{c}_{13} S_{33} - \overline{e}_{31} E_{3} - \overline{\lambda }_{11} \theta , \hfill \\ T_{33} = \overline{c}_{13} S_{11} + \overline{c}_{33} S_{33} - \overline{e}_{33} E_{3} - \overline{\lambda }_{33} \theta , \hfill \\ T_{13} = 2\overline{c}_{44} S_{13} - \overline{e}_{15} E_{1} , \hfill \\ D_{1} = \overline{\varepsilon }_{11} E_{1} + 2\overline{e}_{15} S_{13} , \hfill \\ D_{3} = \overline{\varepsilon }_{33} E_{3} + \overline{e}_{31} S_{11} + \overline{e}_{33} S_{33} + \overline{p}_{3} \theta , \hfill \\ J_{1}^{n} = qn\mu_{11}^{n} (E_{1} - \alpha_{11}^{n} \theta_{,1} ) + qD_{11}^{n} n_{,1} , \hfill \\ J_{3}^{n} = qn\mu_{33}^{n} (E_{3} - \alpha_{33}^{n} \theta_{,3} ) + qD_{33}^{n} n_{,3} , \hfill \\ q_{1} = - k_{11} \theta_{,1} + qP_{11}^{n} (n\mu_{11}^{n} (E_{1} - \alpha_{11}^{n} \theta_{,1} ) + D_{11}^{n} n_{,1} ), \hfill \\ q_{3} = - k_{33} \theta_{,3} + qP_{33}^{n} (n\mu_{33}^{n} (E_{3} - \alpha_{33}^{n} \theta_{,3} ) + D_{33}^{n} n_{,3} ), \hfill \\ \end{gathered}$$

(6)

where

$$\begin{aligned} & \overline{c}_{11} = c_{11} - \frac{{c_{12}^{2} }}{{c_{11} }},\quad \overline{c}_{13} = c_{13} - \frac{{c_{12} c_{13} }}{{c_{11} }},\quad \overline{c}_{33} = c_{33} - \frac{{c_{13}^{2} }}{{c_{11} }},\quad \overline{c}_{44} = c_{44} , \\ & \overline{\lambda }_{11} = \lambda_{11} - \frac{{c_{12} }}{{c_{11} }}\lambda_{11} ,\quad \overline{\lambda }_{33} = \lambda_{33} - \frac{{c_{13} }}{{c_{11} }}\lambda_{11} ,\quad \overline{e}_{15} = e_{15} ,\quad \overline{e}_{31} = e_{31} - \frac{{c_{12} }}{{c_{11} }}e_{31} , \\ & \overline{e}_{33} = e_{33} - \frac{{c_{13} }}{{c_{11} }}e_{31} ,\quad \overline{\varepsilon }_{11} = \varepsilon_{11} ,\quad \overline{\varepsilon }_{33} = \varepsilon_{33} + \frac{{e_{31}^{2} }}{{c_{11} }},\quad \overline{p}_{3} = p_{3} + \frac{{e_{31} }}{{c_{11} }}\lambda_{11} . \\ \end{aligned}$$

(7)

Substituting the field equations in Eq. (5) and constitutive equations in Eq. (6) into Eq. (1), and integrating the equations along the thickness direction (i.e., x₂-direction), we got the 2-D governing equations:

$$\begin{gathered} {\mathcal{N}}_{11,1} + {\mathcal{N}}_{31,3} + {\mathcal{F}}_{1} = 0, \hfill \\ {\mathcal{N}}_{13,1} + {\mathcal{N}}_{33,3} + {\mathcal{F}}_{3} = 0, \hfill \\ {\mathcal{D}}_{1,1} + {\mathcal{D}}_{3,3} + {\mathcal{D}} = 2qh_{0} ( - n + N_{D}^{ + } ), \hfill \\ {\mathcal{J}}_{1,1}^{n} + {\mathcal{J}}_{3,3}^{n} + {\mathcal{J}} = 0, \hfill \\ {\mathcal{Q}}_{{{\kern 1pt} 1,1}} + {\mathcal{Q}}_{{{\kern 1pt} 3,3}} + {\mathcal{Q}} = {\mathcal{J}}_{1}^{n} E_{1} + {\mathcal{J}}_{3}^{n} E_{3} , \hfill \\ \end{gathered}$$

(8)

where the film forces for the extensional motion, the electric displacement resultants, the current resultants and the thermal flux resultants are defined by the following integral along the film thickness:

$$[{\mathcal{N}}_{ij} ,\;{\mathcal{D}}_{i} ,\;{\mathcal{J}}_{i}^{n} ,\;{\mathcal{Q}}_{i} ] = \int_{{ - h_{0} }}^{{h_{0} }} {[T_{ij} ,\;D_{i} ,\;J_{i}^{n} ,\;q_{i} ]\;} dx_{2} ,\quad i,j = 1,3.$$

(9)

In Eq. (8), the contributions from the internal body force loads, the surface electromechanical loads and the surface heat fluxes on the top and bottom of the film are represented by

$$\begin{aligned} & {\mathcal{F}}_{i} = T_{2i} (h_{0} ) - T_{2i} ( - h_{0} ) + \int_{{ - h_{0} }}^{{h_{0} }} {f_{i} } dx_{2} ,\quad {\mathcal{D}} = D_{2} (h_{0} ) - D_{2} ( - h_{0} ), \\ & {\mathcal{J}} = J_{2}^{n} (h_{0} ) - J_{2}^{n} ( - h_{0} ),\quad {\mathcal{Q}} = q_{2} (h_{0} ) - q_{2} ( - h_{0} ). \\ \end{aligned}$$

(10)

We denote n₀ = $N_{D}^{ + }$, a constant for uniform doping and write n = n₀ + ∆n. In addition, the contributions of electrical and thermal surface loads in Eq. (10) are ignored. Substituting Eqs. (3), (6) and (9) into Eq. (8), we obtain five governing equations for u, v, φ, θ and n:

$$\begin{gathered} \overline{c}_{11} u_{,11} + \overline{c}_{13} v_{,31} + \overline{e}_{31} \varphi_{,31} - \overline{\lambda }_{11} \theta_{,1} + \overline{c}_{44} (u_{,33} + v_{,13} ) + \overline{e}_{15} \varphi_{,13} + \frac{{{\mathcal{F}}_{1} }}{{2h_{0} }} = 0, \hfill \\ \overline{c}_{44} (u_{,31} + v_{,11} ) + \overline{e}_{15} \varphi_{,11} + \overline{c}_{13} u_{,13} + \overline{c}_{33} v_{,33} + \overline{e}_{33} \varphi_{,33} - \overline{\lambda }_{33} \theta_{,3} + \frac{{{\mathcal{F}}_{3} }}{{2h_{0} }} = 0, \hfill \\ \overline{e}_{15} (u_{,31} + v_{,11} ) - \overline{\varepsilon }_{11} \varphi_{,11} + \overline{e}_{31} u_{,13} + \overline{e}_{33} v_{,33} - \overline{\varepsilon }_{33} \varphi_{,33} + \overline{p}_{3} \theta_{,3} = q\Delta n, \hfill \\ q[D_{11}^{n} n_{,1} - n\mu_{11}^{n} (\varphi_{,1} + \alpha_{11}^{n} \theta_{,1} )]_{,1} + q[D_{33}^{n} n_{,3} - n\mu_{33}^{n} (\varphi_{,3} + \alpha_{33}^{n} \theta_{,3} )]_{,3} = 0, \hfill \\ - k_{11} \theta_{,11} - k_{33} \theta_{,33} + qP_{11}^{n} [D_{11}^{n} n_{,1} - n\mu_{11}^{n} (\varphi_{,1} + \alpha_{11}^{n} \theta_{,1} )]_{,1} + qP_{33}^{n} [D_{33}^{n} n_{,3} - n\mu_{33}^{n} (\varphi_{,3} + \alpha_{33}^{n} \theta_{,3} )]_{,3} \hfill \\ = - q\varphi_{,1} [D_{11}^{n} n_{,1} - n\mu_{11}^{n} (\varphi_{,1} + \alpha_{11}^{n} \theta_{,1} )] - q\varphi_{,3} [D_{33}^{n} n_{,3} - n\mu_{33}^{n} (\varphi_{,3} + \alpha_{33}^{n} \theta_{,3} )]. \hfill \\ \end{gathered}$$

(11)

The following boundary conditions can be prescribed at the lateral boundaries of the film [42]:

$$\begin{gathered} u = \overline{u}\quad {\text{or}}\quad T_{NN} = \overline{t}_{N} ,\quad v = \overline{v}\quad {\text{or}}\quad T_{NS} = \overline{t}_{S} , \hfill \\ D_{N} = \overline{D}_{N} \quad {\text{or}}\quad \varphi = \overline{\varphi },\quad J_{N} = \overline{J}_{N} \quad {\text{or}}\quad n = \overline{n}, \hfill \\ q_{N} = \overline{q}_{N} \quad {\text{or}}\quad \theta = \overline{\theta }. \hfill \\ \end{gathered}$$

(12)

3 Numerical results and discussion

In this section, we solved the nonlinear governing equations given in Eq. (11). When the thermal couplings are considered, the flow of electric currents gives rise to the Joule heating effect. Concurrently, the Peltier effect induces heat fluxes to converge at the boundaries and flow through the structure, thereby affecting the temperature field. Moreover, temperature change is incorporated into the iterative calculation of both stress and polarization, making the acquisition of an analytical solution challenging. Therefore, we employ COMSOL® Multiphysics for FE analysis to perform numerical results.

In our research, we employed the two-dimensional partial differential equation (PDE) module for conducting nonlinear analysis. Equation (11) was input into this PDE module, and the simulation results were then obtained by processing this equation with the predefined boundary conditions. For our analysis, we opted for a steady-state approach. We utilized the automatic Newton method for solving the nonlinear equations and setting the convergence criterion such that the process terminates when the tolerance level falls below 0.001. This approach ensured that we achieved accurate and reliable results from our simulations.

To validate the accuracy of FE analysis, a comparison between analytical results and FE results is made in Appendix A. Notably, both results are obtained from the linearized governing equations, and to a certain extent, the accuracy can be validated.

Our objective in solving the defined boundary value problem is to investigate the impact of mechanically induced potential on electric currents and thermal fluxes. This holds potential utility for applications involving thermal control in PS devices.

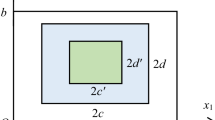
This research focuses on an n-type doped ZnO semiconductor thin film that is subjected to in-plane static extensional deformations. Consider a planar model under in-plane mechanical loads as shown in Fig. 2. Size of the film is a × b, and the size of the mechanical loading area, which is located in the center of the film, is a₀ × b₀. The thickness of the film is 2h₀, and all four edges are fixed mechanically. Geometric parameters in this section are: a = b = 1μm, a₀ = b₀ = 0.2μm and 2h₀ = 20nm. The material parameters employed in the numerical examples are given in Table 1 (under the reference temperature θ_R = 300 K) [42, 49, 51, 52].

Fig. 2

Planar model under in-plane mechanical loads and the loading area

Table 1 Material parameters of n-type ZnO

Based on the requirement of linear constitutive, the deformation of the material is limited at the elastic level. In our methodology, the effective von Mises strain S_eff is used as a reference for strain level analysis [53]:

$$S_{{{\text{eff}}}} = \sqrt {\frac{2}{3}(S_{11}^{2} + S_{33}^{2} + 2S_{13}^{2} )} .$$

(13)

Note that the zero items have been ignored in S_eff. We limit the equivalent von Mises strain S_eff to less than or equal to 0.01% to ensure that the material is in the elastic deformation stage (i.e., S_eff ≤ 0.01%).

Furthermore, because the piezoelectric coefficients are considered constants in our analysis, the strain magnitude is one of the key determinants of the piezoelectric potential of the structure. We have observed that when the piezoelectric potential is close in magnitude to the external voltage, the piezoelectric effect becomes more pronounced. Meanwhile, the doping level influences the currents in the structure. Therefore, in our study, the given external voltage and doping level are the determinants in determining the magnitude of force that can produce a noticeable piezoelectric effect.

3.1 Current manipulation switches

Assuming that the temperature variations at x₃ = 0 and b are zero, and the thermal fluxes vanish at x₁ = 0 and a (i.e., adiabatic). The voltage $\overline{\varphi}$ is applied at x₃ = b with $\overline{\varphi}$ = 0.05V. Ohm contacts are used at x₃ = 0 and b so that no charge accumulations are formed, and x₁ = 0 and a are electrically open. A uniform mechanical load ${\mathcal{F}}_{3}$ is applied at the loading area, with the magnitude t₃ ranges from − 3 × 10⁶ N m⁻² to 3 × 10⁶ N m⁻². That is, for the planar model in Fig. 2, the boundary conditions are:

$$\begin{aligned} & u = 0,\quad v = 0,\quad J_{1} = 0,\quad D_{1} = 0,\quad q_{1} = 0\quad {\text{at}}\quad x_{1} = 0,\;a, \\ & u = 0,\quad v = 0,\quad \varphi = 0,\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{3} = 0, \\ & u = 0,\quad v = 0,\quad \varphi = \overline{\varphi },\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{3} = b, \\ & \left\{ \begin{gathered} {\mathcal{F}}_{1} = 0,\quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} \quad \;\;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{all}}, \hfill \\ {\mathcal{F}}_{3} = t_{3} ,\quad in\quad \frac{{a - a_{0} }}{2} < x_{1} < \frac{{a + a_{0} }}{2}\quad {\text{and}}\quad \frac{{b - b_{0} }}{2} < x_{3} < \frac{{b + b_{0} }}{2}, \hfill \\ {\mathcal{F}}_{3} = 0,\quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{elsewhere}}. \hfill \\ \end{gathered} \right. \\ \end{aligned}$$

(14)

Figures 3 and 4 show the field distributions within the n-type ZnO film induced by uniform mechanical loads t₃ =  ± 2 × 10⁶ N m⁻², respectively. As depicted in Figs. 3a and 4a, observations indicate that the forces applied generate electrostatic potential barriers through the piezoelectric coupling. In Figs. 3c and 4c, the electrons are attracted to regions with high potential, driven by the electric field, and form electric currents in the plane. It can be seen that the current density is indeed symmetrical about both the centerlines x₁ = a/2 and x₃ = b/2.

Fig. 3

Field distributions in the n-type ZnO film induced by a uniform mechanical load t₃ = 2 × 10⁶ N m⁻²: a electrostatic potential, b temperature field, c electric current density and d thermal flux density

Fig. 4

Field distributions in the n-type ZnO film induced by a uniform mechanical load t₃ =  − 2 × 10⁶ N m⁻²: a electrostatic potential, b temperature field, c electric current density and d thermal flux density

Figures 3b and 4b display the distributions of temperature change, which are significantly influenced by the variation in currents. Figures 3d and 4d show the synthesis process of thermal fluxes under the influence of the Peltier effect. It should be noted that the thermal fluxes are the sum of the Peltier effect-induced fluxes and the heat conduction fluxes. Given that the temperature fields are not symmetric about the centerline x₃ = b/2, the thermal density is only symmetric about the centerline x₁ = a/2.

However, given that the defined boundary conditions restrict the temperature change on the boundary in the x₃-direction, the heat fluxes resulting from the Peltier effect are ultimately flowing out of the boundaries, thereby not influencing the temperature field in this instance.

Comparing the temperature fields in Figs. 3b and 4b, it can be seen that the temperature change is more intense when the force points to the positive x₃-direction. In order to explore the reason of this phenomenon, we define the magnitude of the total average current $I_{3}^{{{\text{Tot}}}}$ through the boundaries in the x₃-direction, as

$$I_{3}^{{{\text{Tot}}}} = h_{0} \int_{0}^{a} {\left. {J_{3} } \right|_{{x_{3} = 0}} {\text{d}}x_{1} } + h_{0} \int_{0}^{a} {\left. {J_{3} } \right|_{{x_{3} = b}} {\text{d}}x_{1} } .$$

(15)

As depicted in Fig. 5, the magnitude of the total average current fluctuates in response to changes in mechanical force. When a force is applied pointing to the positive x₃-direction (i.e., the c-axis direction) to the structure, there is an increase in the total current, whereas the application of a force in the opposite direction suppresses the total current. At the max strain level of 0.01% (i.e., $S_{{\text{max \, eff}}}$ = 1 × 10⁻⁴, approximately t₃ =  − 2.2 × 10⁶ N m⁻²), the magnitude of electric current can be reduced by 70.4% in comparison with its counterpart in the absence of an external force. Such a PS device under mechanical loadings provides a design for electronic components that need current switches, such as sensors.

Fig. 5

Magnitude of total average current through the boundary in the x₃-direction and temperature perturbation under different uniform mechanical loads

As previously mentioned, the thermal fluxes resulting from the Peltier effect contribute rarely to the temperature field in this case. When the boundary conditions change, the thermoelectric effect will significantly affect the temperature field of the structure, an instance that will be discussed in Sect. 3.2.

3.2 Influence of Peltier effect on temperature field

To investigate the impact of the Peltier effect on the temperature field of the structure, we interchange the thermal boundary conditions at the boundaries of x₁- and x₃-directions. It is assumed that the temperature changes at x₁ = 0 and a are zero, while x₃ = 0 and b are adiabatic. The other boundary conditions remain the same as in Sect. 3.1. The boundary conditions are changed as

$$\begin{aligned} & u = 0,\quad v = 0,\quad J_{1} = 0,\quad D_{1} = 0,\quad \theta = 0\quad {\text{at}}\quad x_{1} = 0,\;a, \\ & u = 0,\quad v = 0,\quad \varphi = 0,\quad \Delta n = 0,\quad q_{3} = 0\quad {\text{at}}\quad x_{3} = 0, \\ & u = 0,\quad v = 0,\quad \varphi = \overline{\varphi },\quad \Delta n = 0,\quad q_{3} = 0\quad {\text{at}}\quad x_{3} = b, \\ & \left\{ \begin{gathered} {\mathcal{F}}_{1} = 0,\quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} \quad \;\;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\text{all}}, \hfill \\ {\mathcal{F}}_{3} = t_{3} ,\quad in\quad \frac{{a - a_{0} }}{2} < x_{1} < \frac{{a + a_{0} }}{2}\quad {\text{and}}\quad \frac{{b - b_{0} }}{2} < x_{3} < \frac{{b + b_{0} }}{2}, \hfill \\ {\mathcal{F}}_{3} = 0,\quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{elsewhere}}. \hfill \\ \end{gathered} \right. \\ \end{aligned}$$

(16)

Figure 6 presents a comparison of the temperature fields and thermal flux distributions (indicated by the arrow) under identical boundary conditions when the uniform mechanical force t₃ = 2 × 10⁶ N m⁻², both with and without considering the Peltier effect. In a steady state, thermal fluxes are generated by the electric currents due to the Peltier effect in the direction opposite to the currents, until the Peltier effect-induced fluxes reach equilibrium with the heat conduction fluxes caused by the temperature gradient in the x₃-direction. Finally, the heat fluxes flow to the boundaries, which maintain a constant temperature (i.e., x₁ = 0 and a). This results in a significant difference in temperature fields between Fig. 6a and b. Owing to the influence of Joule heat, the distribution of the temperature field is not completely symmetrical in Fig. 6a. This underscores the substantial influence of the Peltier effect on thermo-piezoelectric semiconductors.

Fig. 6

Influence of the Peltier effect on the distribution of temperature field and thermal flux, a with Peltier effect and b without Peltier effect

To further demonstrate the influence of the Peltier effect, Fig. 7a displays the maximum and minimum temperature variation (i.e., θ_max and θ_min) of the structure as the uniform mechanical loads change. When considering Peltier effect, the temperature change reaches a maximum value of 2.71 × 10⁻⁴ K at t₃ = 7 × 10⁵ N m⁻² and a minimum value of − 1.29 × 10⁻⁴ K at t₃ = 0. Figure 7b shows the max temperature range ∆θ of the film under varying mechanical loads (i.e., ∆θ = θ_max − θ_min). The maximum value is achieved at t₃ = 6 × 10⁵ N m⁻², reaching 3.95 × 10⁻⁴ K, while its counterpart is merely 0.86 × 10⁻⁴ K. When taking the Peltier effect into account, the maximum temperature difference due to heat accumulation can escalate to a 4.6-fold increase in comparison with the scenario that neglects the Peltier effect.

Fig. 7

Temperature variation under different uniform mechanical loads, a maximum and minimum temperatures, b influence of Peltier effect on maximum temperature range

Modifications in the thermal boundary predominantly impact the temperature field of the structure, whereas the temperature change induced by the Peltier effect and the Joule heating effect exerts a minimal influence on the electrostatic potential field and current density of the structure. The distributions of electrostatic potential and current density acquired are nearly identical to those in Fig. 3a and c. When we attempt to introduce an external temperature load, the substantial temperature difference influences the potential field of the structure via the Seebeck effect, thereby impacting the magnitude and direction of the structure’s currents. This phenomenon has been extensively studied and discussed by many scholars [54,55,56].

3.3 Thermal control in PS device

In this section, a voltage $\overline{\varphi}$ is applied at x₁ = a, with $\overline{\varphi}$ = 0.05V. The edge boundaries x₃ = 0, b are electrically open. The mechanical loads in both the x₁- and x₃-directions are considered. Thermally, x₃ = 0, b are adiabatic, and x₁ = 0, a maintain a constant temperature. The boundary conditions have the following forms:

$$\begin{aligned} & u = 0,\quad v = 0,\quad \varphi = 0,\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{1} = 0, \\ & u = 0,\quad v = 0,\quad \varphi = \overline{\varphi },\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{1} = a, \\ & u = 0,\quad v = 0,\quad J_{3} = 0,\quad D_{3} = 0,\quad q_{3} = 0\quad {\text{at}}\quad x_{3} = 0,\;b, \\ & \left\{ \begin{gathered} {\mathcal{F}}_{1} = 0,\quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} \quad \;\;{\kern 1pt} {\kern 1pt} {\text{all}}, \hfill \\ {\mathcal{F}}_{3} = t_{3} ,\quad in\quad \frac{{a - a_{0} }}{2} < x_{1} < \frac{{a + a_{0} }}{2}\quad {\text{and}}\quad \frac{{b - b_{0} }}{2} < x_{3} < \frac{{b + b_{0} }}{2}, \hfill \\ {\mathcal{F}}_{3} = 0,\quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} {\kern 1pt} {\text{elsewhere}}. \hfill \\ \end{gathered} \right. \\ & {\text{or}} \\ & \left\{ \begin{gathered} {\mathcal{F}}_{3} = 0,\quad \quad \quad \quad \quad \quad \quad \quad {\kern 1pt} \quad \;\;{\kern 1pt} {\kern 1pt} {\text{all}}, \hfill \\ {\mathcal{F}}_{1} = t_{1} ,\quad in\quad \frac{{a - a_{0} }}{2} < x_{1} < \frac{{a + a_{0} }}{2}\quad {\text{and}}\quad \frac{{b - b_{0} }}{2} < x_{3} < \frac{{b + b_{0} }}{2}, \hfill \\ {\mathcal{F}}_{1} = 0,\quad \quad \quad \quad \quad \quad \quad \quad \;{\kern 1pt} {\text{elsewhere}}. \hfill \\ \end{gathered} \right. \\ \end{aligned}$$

(17)

Figure 8 shows the distributions of electrostatic potential and current density (indicated by the arrow) under different uniform mechanical loads. It can be seen that, under the action of mechanical loads, potential barriers and wells are generated within the film due to the piezoelectric coupling, as mentioned before. Electrons are attracted to areas with higher potential, while simultaneously bypassing areas with lower potential, thereby generating corresponding currents. Mechanical loads in both the x₁- and x₃-directions significantly affect the temperature distribution of the structure. The force directed toward the positive x₃-direction generates a potential barrier at the center part of the film, as shown in Fig. 8a. Thereby, the currents accumulate at the potential barrier and heat up, leading to a temperature rise. Figure 9 depicts the distributions of temperature field and heat flux (also indicated by the arrow) under different mechanical loads. As depicted in Fig. 9a, the magnitude of temperature is increased by 1.4 times compared with the place where the current density is sparse on the line a-a. On the contrary, a force in the opposite direction induces a potential well (see Fig. 8b) and modulates the currents to bypass the loading area, thereby generating a temperature loss. The lowest temperature on the line a-a is only 0.39 times the highest temperature in Fig. 9b. In Fig. 8c and d, the external forces directed to the x₁-direction induce pairs of centrally symmetric electrostatic potential barriers and wells. In the presence of an applied voltage, the potential difference in certain regions becomes more pronounced. Consequently, the currents follow the path of high potential, leading to a more effective heating effect in some regions, as shown in Fig. 9c and d.

Fig. 8

Distributions of electrostatic potential and current density due to uniform mechanical loads: a t₃ = 2 × 10⁶ N m⁻², t₁ = 0, b t₃ =  − 2 × 10⁶ N m⁻², t₁ = 0, c t₁ = 2 × 10⁶ N m⁻², t₃ = 0 and d t₁ =  − 2 × 10⁶ N m⁻², t₃ = 0

Fig. 9

Distributions of temperature field and thermal flux due to uniform mechanical loads: a t₃ = 2 × 10⁶ N m⁻², t₁ = 0, b t₃ =  − 2 × 10⁶ N m⁻², t₁ = 0, c t₁ = 2 × 10⁶ N m⁻², t₃ = 0 and d t₁ =  − 2 × 10⁶ N m⁻², t₃ = 0

It should be noted that the results indicate that the field distributions show the characteristics of linear superposition. The resultant force in any direction can be decomposed into forces pointing to the x₁- and x₃-directions, and the field distributions are linearly superimposed. In addition, when the direction of the current is perpendicular to the poling direction of the material, the intervention of the external force primarily acts on redirecting the local electric current rather than its magnitude, which is obviously different from that in Sect. 3.1. Therefore, this study proposes a potential method for mechanically controlling the temperature of the structure. These findings offer theoretical support for the potential to manipulate electric heating devices through external mechanical loadings, a topic that is discussed in the next section.

4 Application of thermal control to periodic structures

In this section, we develop a model of a micro-electric heating device for periodic structures that utilizes an n-type doped ZnO semiconductor substrate, as presented in Fig. 10. The uniform doping concentration (i.e., n₀) increases from 10²¹ m⁻³ to 10²² m⁻³. It is assumed that the structure is sufficiently long in the x₃-direction, while its length in the x₁-direction is limited. In this context, for two lines in close proximity along the x₃-direction, we find that the temperature and potential distributions are continuous, and the temperature changes are negligible; therefore, we choose to focus on a small segment of the structure. This approach not only ensures the key assumption of small temperature perturbation, but also reduces the computational demands of FE analysis.

Fig. 10

Model of a micro-heating device using n-type doped ZnO-based substrate for periodic structure and the research segment

In Fig. 10, a square part comprising several symmetrically distributed loading areas is chosen as the subject of our research. Size of the chosen segment is a × b and the thickness is 2h₀. All edges are mechanically fixed. Ohm contacts are assumed at x₁ = 0 and a, while x₃ = 0 and b are electrically open. A voltage $\overline{\varphi}$ is applied at x₁ = 0, with $\overline{\varphi}$ = 0.4V. The edge boundaries x₃ = 0, b are thermally adiabatic, and x₁ = 0, a maintain a constant temperature. The dimension of the chosen segment is kept at a microscale to sustain the assumption of small temperature perturbation. In addition, the loading areas are indicated by colored squares. The yellow region and green region are applied with opposite in-plane uniform mechanical loads − t and t in the x₃-direction, respectively. Each loading area is a square with a side length of l and is distanced at b/8. The geometric parameters are as follows: 2h₀ = 50nm, a = 1.5μm, b = 6μm and l = 0.5μm.

The boundary conditions of the research section can be displayed as:

$$\begin{aligned} & u = 0,\quad v = 0,\quad \varphi = \overline{\varphi },\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{1} = 0, \\ & u = 0,\quad v = 0,\quad \varphi = 0,\quad \Delta n = 0,\quad \theta = 0\quad {\text{at}}\quad x_{1} = a, \\ & u = 0,\quad v = 0,\quad J_{3} = 0,\quad D_{3} = 0,\quad q_{3} = 0\quad {\text{at}}\quad x_{3} = 0,\;b, \\ & \left\{ \begin{array}{ll} {\mathcal{F}}_{1} = 0, &\quad {\text{all}}\;\;{\text{segment}}, \\ {\mathcal{F}}_{3} = t, &\quad {\text{in}}\;\;{\text{the}}\;\;{\text{green}}\;\;{\text{region}}, \\ {\mathcal{F}}_{3} = - t, &\quad {\text{in}}\;\;{\text{the}}\;\;{\text{yellow}}\;\;{\text{region}}, \\ {\mathcal{F}}_{3} = 0, &\quad {\text{in}}\;\;{\text{the}}\;\;{\text{white}}\;\;{\text{region}}. \\ \end{array} \right. \\ \end{aligned}$$

(18)

As mentioned in Sect. 3.3, mechanical loads generate electrostatic potential barriers and wells, induce current redirection, and thereby affect the temperature fields. In the initial step of heating, to quickly heat the aimed object, we apply uniform mechanical forces in the negative x₃-direction in the yellow regions to induce potential barriers and opposite forces in the green regions to induce potential wells. Figure 11 shows the field distributions and currents under the action of symmetrical reaction loads t = 3.5 × 10⁶ N m^­2 and an applied voltage $\overline{\varphi}$ = 0.4V. In Figs. 11a and 12a, the arrows denote the current's magnitude and direction, with longer arrows indicating higher current densities. This visualization reveals that electron-generated currents are drawn toward potential barriers, effectively circumventing the wells. This accumulation of current raises the temperature in these areas through the Joule heating effect. The average temperature of the solid square areas can reach up to 47.4% higher than the dotted square areas.

Fig. 11

Field distributions under the action of symmetrical reaction loads t = 3.5 × 10⁶ N m⁻² and the voltage $\overline{\varphi}$ = 0.4 V, a electrostatic potential and current density, which are indicated by the arrows. The length of the arrow represents the magnitude of the current density. b Temperature field

Fig. 12

Field distributions under the action of symmetrical reaction loads t =  − 3.5 × 10⁶ N m⁻² and the voltage $\overline{\varphi}$ = 0.4 V, a electrostatic potential and current density, which are indicated by the arrows. The length of the arrow represents the magnitude of the current density. b Temperature field

Once the targets are heated, we can apply reverse loads (i.e., t =  − 3.5 × 10⁶ N m⁻²) to shift the heating area to the dotted square areas. As depicted in Fig. 12, the field distributions and current density differ from those shown in Fig. 11. By changing the magnitude of the mechanical forces, the temperature of the specified region can be effectively controlled. This strategy of periodic heating provides an easily controlled and uniform distribution of temperature fields, thereby reducing the risk of overheating and allowing for more efficient energy usage. In applications such as electronic devices or precision manufacturing, periodic thermal management can ensure safety and enhance product quality by maintaining optimal temperature conditions. For example, overheating can reduce efficiency in a computer chip, while periodic thermal control is essential for maintaining optimal chip temperatures and performance [57, 58]. Similarly, in 3D printing and semiconductor lithography and deposition, precise temperature control ensures material integrity in 3D printing and the fidelity of microstructures in semiconductor manufacturing, directly impacting product yield and quality. These examples highlight the importance of meticulous thermal management in high-precision technology applications.

5 Conclusion

This paper established a nonlinear model of thermo-piezo-elastic semiconductors that analyzes the response of thermo-electric fields under in-plane mechanical loads. Importantly, the model takes the performance of the thermoelectric effects into account in PSs, factors not considered in many previous studies. We interpret how external excitation affects the currents, and propose the possibility of thermal control by in-plane mechanical force.

According to our study, a few novel phenomena with application potential can be observed from the numerical models:

• 1. When an in-plane mechanical load is applied to a PS film with an in-plane c-axis, it may induce local polarization, significantly influencing the currents and temperature field. The angle between the material’s poling direction and the direction of the current significantly impacts the currents. In addition, when the currents run parallel to the c-axis, at an effective von Mises strain level of 0.01%, the magnitude of electric currents can be reduced by 70.4% compared to a scenario without any external forces.

• 2. This finding holds significant implications for devices that use PS materials as sensors. In addition, the temperature variation at the adiabatic boundary due to the heat fluxes generated by the thermoelectric effects can exhibit a substantial increase, reaching up to 4.6 times the value predicted under the assumption of pure Joule heat conditions. Furthermore, when the currents run perpendicular to the c-axis, external loads can cause temperature increases in regions with a high current density and decreases in regions with a low current density through piezoelectric coupling.

• 3. By applying mechanical loadings to a micro-heating device, it becomes possible to shift the main heating position to the desired locations. This mechanically induced current manipulation offers an effective way to control the temperature field within heating components. Such a method of thermal control is invaluable for safeguarding electronic components against thermal damage.

Appendix A: Validation of FE analysis

In this section, we aim to validate the accuracy of the results obtained from the FE analysis. We first linearize the nonlinear equations in Eq. (11) by removing the temperature as an independent variable. In the absence of an applied voltage on the boundaries, the Joule heating effect and Peltier effect vanish since no current is generated. For small Δn, we assume that the carrier concentration term in the drift current remains unchanged:

$$\theta \simeq 0,\quad J_{i}^{n} = qn\mu_{ij}^{n} (E_{j} - \alpha_{jk}^{n} \theta_{,k} ) + qD_{ij}^{n} n_{,j} \simeq qn_{0} \mu_{ij}^{n} E_{j} + qD_{ij}^{n} \Delta n_{,j} .$$

(A.1)

Equation (11) can be linearized into

$$\begin{gathered} \overline{c}_{11} u_{,11} + \overline{c}_{13} v_{,31} + \overline{e}_{31} \varphi_{,31} + \overline{c}_{44} (u_{,33} + v_{,13} ) + \overline{e}_{15} \varphi_{,13} + \frac{{{\mathcal{F}}_{1} }}{{2h_{0} }} = 0, \hfill \\ \overline{c}_{44} (u_{,31} + v_{,11} ) + \overline{e}_{15} \varphi_{,11} + \overline{c}_{13} u_{,13} + \overline{c}_{33} v_{,33} + \overline{e}_{33} \varphi_{,33} + \frac{{{\mathcal{F}}_{3} }}{{2h_{0} }} = 0, \hfill \\ \overline{e}_{15} (u_{,31} + v_{,11} ) - \overline{\varepsilon }_{11} \varphi_{,11} + \overline{e}_{31} u_{,13} + \overline{e}_{33} v_{,33} - \overline{\varepsilon }_{33} \varphi_{,33} = q( - \Delta n), \hfill \\ - qn_{0} \mu_{11}^{n} \varphi_{,11} + qD_{11}^{n} (\Delta n)_{,11} - qn_{0} \mu_{33}^{n} \varphi_{,33} + qD_{33}^{n} (\Delta n)_{,33} = 0. \hfill \\ \end{gathered}$$

(A.2)

The planar model under in-plane mechanical loads is shown in Fig. 2. The geometric parameters in this section are: 2h₀ = 20nm, a = b = 1μm and a₀ = b₀ = 0.2μm.

The homogeneous boundary conditions, excluding thermal boundaries, are given by

$$\begin{gathered} v = 0,\quad T_{11} = 0,\quad \varphi = 0,\quad \Delta n = 0\quad {\text{at}}\quad x_{1} = 0,\;a, \hfill \\ v = 0,\quad T_{13} = 0,\quad \varphi = 0,\quad \Delta n = 0\quad {\text{at}}\quad x_{3} = 0,\;b, \hfill \\ {\mathcal{F}}_{3} = \left\{ {\begin{array}{*{20}c} {10^{6} {\text{N/m}}^{2} ,\quad {\text{in}}\quad \frac{{a - a_{0} }}{2} < x_{1} < \frac{{a + a_{0} }}{2}\quad {\text{and}}\quad \frac{{b - b_{0} }}{2} < x_{3} < \frac{{b + b_{0} }}{2},} \\ {0,\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad {\text{elsewhere}}{.}\quad \quad \quad \quad \quad \quad \quad \quad \quad } \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(A.3)

Given that only the displacement in the x₃-direction is constrained, the model is limited to applying mechanical force solely in the x₃-direction, implying ${\mathcal{F}}_{1} = 0$. The Navier method is employed to solve the linear equations, and the field functions are expanded as trigonometric series to satisfy the boundary conditions in Eq. (A.3):

$$\begin{gathered} u = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } U_{mn} \cos (\xi_{m} x_{1} )\cos (\xi_{n} x_{3} ), \hfill \\ v = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } V_{mn} \sin (\xi_{m} x_{1} )\sin (\xi_{n} x_{3} ), \hfill \\ \varphi = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } \Psi_{mn} \sin (\xi_{m} x_{1} )\sin (\xi_{n} x_{3} ), \hfill \\ \Delta n = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } N_{mn} \sin (\xi_{m} x_{1} )\sin (\xi_{n} x_{3} ), \hfill \\ {\mathcal{F}}_{3} = \mathop \sum \limits_{m = 0}^{\infty } \mathop \sum \limits_{n = 0}^{\infty } F_{mn}^{(3)} \sin (\xi_{m} x_{1} )\sin (\xi_{n} x_{3} ), \hfill \\ \end{gathered}$$

(A.4)

where U_mn, V_mn, Ψ_mn and N_mn are undetermined constants, and F(3) mn is known from the given mechanical loads:

$$\begin{gathered} F_{mn}^{(3)} = \frac{4}{ab}\int_{0}^{a} {\int_{0}^{b} {{\mathcal{F}}_{3} \sin (\xi_{m} x_{1} )\sin (\xi_{n} x_{3} ){\text{d}}x_{1} {\text{d}}x_{3} } } , \hfill \\ \xi_{m} = \frac{m\pi }{a},\quad {\kern 1pt} \xi_{n} = \frac{n\pi }{b},\quad m,n = 1,\;2,\;3,\; \cdots . \hfill \\ \end{gathered}$$

(A.5)

Substituting Eq. (A.4) into Eq. (A.2) yields a system of linear algebraic equations for the undetermined constants:

$$\begin{gathered} U_{mn} ( - \overline{c}_{11} \xi_{m}^{2} - \overline{c}_{44} \xi_{n}^{2} ) + V_{mn} (\overline{c}_{13} \xi_{m} \xi_{n} + c_{44} \xi_{m} \xi_{n} ) + \Psi_{mn} (\overline{e}_{31} \xi_{m} \xi_{n} + \overline{e}_{15} \xi_{m} \xi_{n} ) = 0, \hfill \\ U_{mn} (\overline{c}_{44} \xi_{m} \xi_{n} + \overline{c}_{13} \xi_{m} \xi_{n} ) + V_{mn} ( - \overline{c}_{44} \xi_{m}^{2} - \overline{c}_{33} \xi_{n}^{2} ) + \Psi_{mn} ( - \overline{e}_{15} \xi_{m}^{2} - \overline{e}_{33} \xi_{n}^{2} ) = - \frac{{F_{mn}^{(3)} }}{{2h_{0} }}, \hfill \\ U_{mn} (\overline{e}_{15} \xi_{m} \xi_{n} + \overline{e}_{31} \xi_{m} \xi_{n} ) + V_{mn} ( - \overline{e}_{15} \xi_{m}^{2} - \overline{e}_{33} \xi_{n}^{2} ) + \Psi_{mn} (\overline{\varepsilon }_{33} \xi_{n}^{2} + \overline{\varepsilon }_{11} \xi_{m}^{2} ) + qN_{mn} = 0, \hfill \\ \Psi_{mn} (qn_{0} \mu_{11}^{n} \xi_{m}^{2} + qn_{0} \mu_{33}^{n} \xi_{n}^{2} ) + N_{mn} ( - qD_{11}^{n} \xi_{m}^{2} - qD_{33}^{n} \xi_{n}^{2} ) = 0. \hfill \\ \end{gathered}$$

(A.6)

Figure 13a displays the distribution of electrostatic potential obtained from the analytical method. Figure 13b provides a comparative analysis of the analytical method with the FE result concerning the perturbation of electron concentration along x₁ = a/2, resulting in identical findings with the analytical result. In an n-type doped semiconductor, where electrons are abundant, carriers tend to accumulate in areas of high electrostatic potential. Therefore, the distributions of electrons and electrostatic potential are in complete agreement. By comparing the numerical results from the FE method with the analytical solutions for the reduced linear case, the accuracy of the FE results is verified.

Fig. 13

Field distributions of an n-type doped ZnO film under mechanical loads, a electrostatic potential obtained from the analytical method and b comparison of perturbation of electron concentration with FE result along x₁ = a/2