Seismic design optimization of engineering structures: a comprehensive review

Abstract

In the last decades, design optimization of structures received significant attention to reconcile economic aspects, after the recent advances in computer technology. Many solution methods have been developed in order to solve different kinds of optimization problems defined for design of structures. Concerning various types of structural loads, earthquake loading is a crucial factor influencing structural design. The procedures for analysis and design of structures to resist seismic excitations are in a progressive state of development, for which numerous optimization problems have been proposed. This article presents an overview of seismic design optimization of structures, focusing on common solution methods, types of optimization problem and goals of optimization. Past and recent developments are reviewed, and current gaps as well as some open concerns deserving more research in future studies are discussed.

1 Introduction

Analysis and design are two main interrelated phases in the definition of a structural system. Structural analysis aims to calculate structural responses under some external effects (loads, temperature changes and support settlments), while structural design aims to find suitable arrangement of members, materials and sections to withstand those structural responses in accordance with requirements of design codes. Analysis and design process for a structure is a cycle requiring many repetitions in order to achieve a desirable design. The process may be tedious as its number of repetitions relies on experience and intuition of an engineer to be familiar with the structure at hand. Variety in configuration of structures makes it impossible for an engineer to simultaneously achieve a well-designed and cost-effective structure irrespective of some design experiences. Therefore, a computer-aided procedure for carrying out this cycle is necessary. This procedure is called optimal structural design in which the cycle is repeated from several to thousands of times to reach an optimal/sub-optimal solution. The process can be very time-consuming, but it can be performed faster by using efficient structural analysis methods. Accordingly, structural optimization can be classified into optimal structural analysis and optimal structural design. In optimal structural analysis, sparse, well-structured and well-conditioned matrices must be generated for reducing the analysis time [1]. Also, efficient methods may be employed for static and/or dynamic analysis of structures to reach this scope [1,2,3,4]. On the other hand, optimal structural design aims to find the best selection of design variables for which a structural quantity (e.g., cost) is optimized subjected to some constraints like the criteria specified by design codes.

Seismic behavior of structures is far from being understood sufficiently. The analysis phase, which leads to the assessment of stresses and deformations due to seismic action, invokes knowledge from several engineering fields, such as geotechnical earthquake engineering, structural earthquake engineering and computational mechanics [5]. Therefore, in order to perform reliable seismic design optimization of a structural system, many conceptual points should be incorporated for rendering a practical design.

There are many studies on structural optimization considering various types of loads such as gravity, wind and seismic load effects. However, only a part of those studies were fully focused on seismic design of structures because many investigations considered the aforementioned loads as generic loads. Although many review papers were published on sizing optimization [6,7,8], shape optimization [9,10,11] and topology optimization [12,13,14,15,16,17] of structures, only one review paper focused on design optimization of structures under seismic loading, published in 2011 [18]. Seismic actions are important in structural design, as they significantly affect the structural demands, like stresses and displacements, for which suitable arrangement of members must be selected according to design codes. Therefore, optimizing the structural design under such a condition can be very beneficial for reducing total costs.

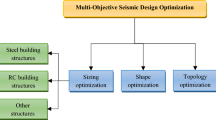
This article reviews sizing, shape and topology optimization of structures subjected to seismic excitations. Preliminaries on structural optimization as well as seismic analysis and design are concisely presented to introduce the research area focusing on seismic design optimization, and to provide some backgrounds for the studies reviewed here. Relevant studies on this topic will be surveyed and discussed. Commonly used solution methods as well as recently developed optimization problems are discussed. These problems can be divided into traditional and performance-based seismic designs requiring various analysis procedures like linear static, linear dynamic, nonlinear static and nonlinear dynamic analyses depending on the problem at hand. Past and present studies are herein surveyed and future research directions are presented. It should be noted that this article focuses on the investigations emphasizing the topic of seismic design optimization. Therefore, the optimization studies which only considered other structural loads and the optimization studies on seismic control of structures are excluded from this article unless they are remarkably related to the topic. The structure of this review article is schematized in Fig. 1 pertaining to Sect. 5, for which the main searched keywords in “Scopus” and “Google Scholar” databases are as follows: structural optimization, seismic design optimization, performance-based seismic design, optimal seismic design, optimal design, dynamic loading, seismic loading and earthquake loading. These searches illustrate that the relevant investigations have been carried out in recent three decades.

Fig. 1

The structure of this review article for categorizing the investigations on seismic design optimization; as for Sect. 5

The remainder of this article is organized as follows: Sect. 2 presents the general formulation of structural design optimization. Section 3 describes the different types of optimization algorithms that may be utilized in seismic design. Section 4 introduces various approaches for seismic design of structures. Single-objective optimization for seismic design is presented in Sect. 5, which is categorized with respect to structural analysis and design optimization. This framework for the multi-objective cases will be published in another paper due to the limitation of paper length of the journal. Section 6 provides a statistical analysis of the previous studies. In Sect. 7, conclusions will be derived based on the observations gathered from previous sections. This section also highlights directions for future research.

2 Statement of structural design optimization problem

According to the type of design variables, optimal design of structures can be categorized into three groups including sizing optimization, shape optimization and topology optimization. Sizing optimization considers finding suitable sizing variables upon reaching optimum value of the predefined objective function. In shape optimization, design variables are often regarded as geometrical properties of the structure such as nodal coordinates. Topology optimization may be interpreted as generalized form of the previous cases, in which material distribution is arranged so that an optimum design is obtained. These three groups will be described in more detail. The general statement of an optimization problem is:

$$\begin{aligned} & {\text{To}}\;{\text{optimize}}: \\ & f_{k} ({\mathbf{x}}) \\ & {\text{where}} \\ & k \ge 1; \\ & {\mathbf{x}} = [x_{1} ,x_{2} , \ldots ,x_{n} ]; \\ & x_{i} \in \Re ;\quad i = 1,2, \ldots ,n \\ & {\text{such}}\;{\text{that}} \\ & g_{j} (\mathbf{x}) \le 0;\quad j = 1,2, \ldots ,m ,\\ \end{aligned}$$

(1)

where x is the vector of design variables of size n and hence ${\mathbf{x}} \in \Re^{n}$. Here, the variables belong to the set of real numbers, and hence the problem is of continuous optimization. On the other hand, design variables of discrete optimization problems are selected from a list of available values or they may even be integer numbers. f is the objective function that should be minimized or maximized depending on the task. k denotes the number of objective functions. The optimization problem is called single-objective when the k is equal to unity, while it is called multi-objective when k is larger than one. One of the common approaches to handle a multi-objective optimization problem is the transformation of the problem into a single-objective case. For this purpose, weighted sum method and weighted global criterion method can be used, by which a single-objective function is defined in terms of all the objective functions existing in the multi-objective optimization problem [19]. However, in order to make a decision on selecting the appropriate method, a comparison of the most common methods has been made in Ref. [20] which can be helpful in finding the most appropriate method for a certain application. g denotes the constraint function and m is the number of constraints. Constraints can be imposed to the problem by either penalty or Lagrange multipliers approach [20].

In sizing optimization, variables often correspond to cross-sectional properties of structural members. Objective function can be structural weight, structural cost or another desired quantity. Due to homogeneity of steel structures, the total structural weight is easily calculated using the weight density. For concrete structures, weight of each member consists of reinforcement and concrete weights, and each one is determined similarly to that of steel structures. Obviously, apart from reinforcement and concrete costs, the formwork cost should be considered when the constructional cost optimization is taken into account. There are many kinds of constraints for optimizing structural design such as stress/strength ratio, drift ratio, other design restrictions, geometrical limitations and practical and fabrication issues.

In shape optimization, geometry is modified in order to reach the optimal value of an objective function like structural weight. In other words, the boundary of the structural domain is modified. Architectural limitations are important here because every shape modification is not permitted due to aesthetics, space and other practical restrictions. Other definitions are similar to those of sizing optimization.

In topology optimization, the members (or elements) can be either eliminated or rearranged so as to optimize the objective function(s), for example, to achieve minimum structural compliance constrained by a maximum material volume ratio. Likewise, constraints can be selected similar to those of sizing optimization and shape optimization. For continuum structures, the simplified isotropic material with penalization (SIMP) is one of the most common topology optimization methods where nearly zero density of an element enforces the element removal [14], whereas unit density of an element compels full contribution of that element.

Ideally speaking, shape optimization is a subset of topology optimization, but their practical implementations follow very different methods [21]. Conversely, sizing and topology optimization are very different, but closely related from practical aspects. In mathematical view, if we look at the stated problem as a differential equation, shape optimization can be seen as a tool for controlling the equation domain, while sizing and topology optimization stand for its parameter control. In structural view, topology, shape and sizing optimizations may be seen as the implementation of optimization at the conceptual design, the preliminary design and the detailed design stages, respectively [22].

3 Optimization algorithms

Based on the problem at hand, an analyst often has to choose the best optimization technique. In fact, some algorithms perform better in certain problems while other algorithms cannot be applied to some optimization problems. Classification of optimization algorithms is not unique in the literature and various classifications are used interchangeably [19]. Generally, optimization algorithms are classified into two groups: deterministic and stochastic ones as shown in Fig. 2. A deterministic algorithm contains rigorous procedure so its path will be repeatable and for the same initial conditions, it gives the same results whenever the procedure (or computer program) is run. A stochastic algorithm contains random procedure so that not only its path may be different, but also with the same initial condition it may give different results whenever the procedure (or computer program) is run. Deterministic algorithms may need gradient information or not. For example, the Newton–Raphson method is a gradient-based algorithm which is usually employed for solving nonlinear equations derived from continuous and unimodal functions, while Nelder–Mead downhill simplex is a non-gradient-based algorithm which is suitable for discontinuous and multimodal functions. Gradient-based optimizers can guarantee the local optimality and are based on robust mathematical proofs. Although majority of stochastic algorithms do not need gradient data, they may also be divided into gradient-based and non-gradient-based forms as there are some mixed algorithms combining both forms (i.e., hybridized gradient-based methods); see Ref. [11]. Metaheuristic and heuristic methods are non-gradient-based optimizers which do not need derivatives of objective function or constraints. There is no unique distinction between metaheuristic and heuristic methods in the literature. Nevertheless, metaheuristic algorithms are in higher level and more general with respect to heuristic algorithms. Ant colony optimization (ACO) [23], simulated annealing (SA) [24], particle swarm optimization (PSO) [25], genetic algorithm (GA) [26], bat algorithm (BA) [27], differential evolution (DE) [28], harmony search (HS) [29], big bang–big crunch (BB-BC) [30], teaching–learning-based optimization (TLBO) [31], colliding bodies optimization (CBO) [32, 33], cuckoo search (CS) [34], charged system search (CSS) [35], adaptive charged system search (ACSS) [36] and the improved grey wolf optimizer (IGWO) [37] are metaheuristic algorithms, among many others [19, 38]. These algorithms randomly explore the search space in order to find the best solution leading to an optimal/sub-optimal value of objective function. Although their problem independency features many multi-disciplinary applications in engineering optimization [7, 36, 39,40,41,42,43], the optimality cannot be guaranteed by them. In spite of some existing applications [11, 44], prior studies have demonstrated that metaheuristic methods are not a suitable choice for topology optimization due to the presence of a large number of variables leading to a huge search space [45]. Alternatively, these are suitable for either sizing or shape optimization. For topology optimization, deterministic gradient-based algorithms like optimality criteria (OC) methods and the method of moving asymptotes (MMA) are two well-known solvers [14, 46], which have also been applied to sizing optimization [47, 48].

Fig. 2

Classification of optimization algorithms

4 Seismic design approaches

The most important parameters describing the behavior of structures subjected to earthquake ground motion are mass, damping and stiffness. Also, stiffness, strength and ductility are the main requirements to be adequately provided for a structure designed for seismic loading. Design of structures against earthquakes is often performed by two main approaches: force-based design and ductility-based design. Force-based design has been presented in traditional design codes [49, 50], while ductility-based design has been proposed in modern design codes [51, 52] particularly for seismic retrofit of existing structures. With these modern design codes, one can also design new structures leading to performance-based seismic design. In performance-based design, the structure is designed for a specific performance level subjected to a specific seismic hazard level. Immediate occupancy (IO), life safety (LS) and collapse prevention (CP) are the main performance levels for structural components. Traditional force-based seismic design relies on force capacity of structural components to resist the earthquake excitations expressed as a set of horizontal actions proportional to weight of the structure. A ductility-based seismic design is significantly less sensitive to unexpected increase in the force demand than its force-based counterpart. The ductility-based approach has been developed due to the great uncertainty associated with estimating seismic demand, and in order to improve the distribution of forces among ductile structural members and avoid the issues of stiffness guiding force distribution. In general, while ductility-based designed structures are lighter and use less material, they need more workmanship [5].

The inclusion of uncertainty is a prevalent conceptual thread throughout all performance-based engineering methods. Uncertainty and variability existing in predicting seismic demand and response suggest that these methods are posed within a risk-based context [53]. A robust conceptual framework has been proposed at the Pacific Earthquake Engineering Research (PEER) center. This framework consists of four fundamental steps: hazard analysis, structural analysis, damage analysis, and loss analysis [54]. The PEER framework equation is often expressed in a convenient form to facilitate design-centric and simplified performance-based engineering analysis and design. The mean annual frequency of a decision variable (DV) being exceeded can be represented as [53, 54]

$$\lambda ({\it\text{DV}}) = \iiint {G({\it\text{DV}}}\left| {{\it\text{DM}}){\text{d}}G({\it\text{DM}}\left| {{\it\text{EDP}})} \right.} \right.{\text{d}}G({\it\text{EDP}}\left| {{\it\text{IM}})} \right.{\text{d}}\lambda ({\it\text{IM}}),$$

(2)

in which $G({\it\text{DV}}\left| {{\it\text{DM}})} \right.$ indicates the probability that the DV exceeds specified values given that a particular damage measure (DM) is achieved; $G({\it\text{DM}}\left| {{\it\text{EDP}})} \right.$ indicates the probability that a DM will be exceeded given a specific engineering demand parameter (EDP); $G({\it\text{EDP}}\left| {\it\text{IM)}} \right.$ is the probability that an EDP will be exceeded given that a specific intensity measure (IM) happens; and $\lambda ({\it\text{IM}})$ is the mean annual frequency of an intensity measure (seismic hazard curve). In the case where the most general form of the PEER framework is intended to be implemented, probability density functions describing all random variables must be defined. Some examples of decision variables are casualties, direct economic loss and indirect economic losses [53]. These variables are the basis for minimizing fatalities, costs and downtime caused by the seismic hazard. Damage measures depend on the type of building component. Common performance levels corresponding to damage of structural components are the IO and CP. Damage to displacement-sensitive nonstructural building components, acceleration-sensitive nonstructural building components, and the structural system has also been characterized with four damage measures: slight, moderate, extensive and complete.

Every structural design method needs its relevant seismic analysis and there are four kinds of seismic analysis: linear static analysis, linear dynamic analysis, nonlinear static analysis and nonlinear dynamic analysis, as depicted in Fig. 3.

Fig. 3

Classification of seismic analyses. *Incremental dynamic analysis (IDA), multiple-stripe analysis (MSA) and cloud analysis (CA) are probabilistic approaches using nonlinear response history analysis

4.1 Linear static procedure

Linear static analysis, also known as equivalent static analysis, is the simplest method for analyzing structures under statically applied lateral loads due to earthquake. The material behaves linearly elastic, while geometric nonlinearities like P-Delta effects can implicitly be accounted for. The P-Delta effect is considered as the second-order analysis in order to capture the stiffness reduction caused by the interaction of axial and lateral loads applied to structural members. Material nonlinearity is implicitly considered by the force reduction factor depending on the lateral load-resisting system. The horizontal loads are laterally applied along the height of the structure and are combined with gravity (vertical) loads.

4.2 Linear dynamic procedure

Response spectrum and response history analyses are two kinds of linear dynamic method. In response spectrum analysis, modal analysis is performed and contribution of each mode is considered in the structural response. In other words, the response of a structure to a representative ground motion spectrum (i.e., design spectrum) is computed by decomposing the structure into a series of single degree of freedom systems whose number is equal to the number of selected modes. This decomposition is manifested as the conversion of the coupled differential equations of motion into decoupled differential equations, thereby the maximum response of each mode is calculated by the solution of each decoupled differential equation in the time domain. Then, the desired response quantities are obtained by combination of the maximum modal responses calculated in the previous step. Square root of the sum of squares (SRSS) or complete quadratic combination (CQC) method [55] is used for the modal combination. The SRSS is a special case of the CQC when the vibration modes are well-separated, interpreted as uncorrelated modes. Indeed, the methods like CQC and SRSS try to take into consideration that the time at which the maximum response occurs for each mode is not necessarily identical to those of other modes. Since response spectrum analysis is based on principle of superposition, it is limited to linear systems.

Response history analysis (also known as time history analysis) is inherently a dynamic method which uses earthquake ground motions for calculating structural response at every time instance. In this method, the response of a structure to a ground motion may be calculated by direct integration methods (step-by-step methods) [2] where series of coupled differential equations of motion are solved like static equations for every time step, in which inertia and damping effects are considered.

4.3 Nonlinear static procedure

Nonlinear static analysis can be carried out with pushover and adaptive pushover analyses. Pushover analysis pushes the structure through incremental lateral forces until structural collapse, reaching ultimate limit states or the target displacement. In pushover analysis, the incremental lateral forces can be represented in terms of either horizontal forces (force-control) or displacements (displacement-control), which are applied to the lateral load-resisting system. For simulating the effects of inertia forces, static forces or displacements are distributed along the height of the structure. These lateral forces are compatible with one or more modal shapes. The analysis is called conventional pushover when a constant lateral load pattern is imposed to the structure. Nevertheless, if an updating procedure is defined for the lateral load pattern so that the load pattern changes due to variations of the mode shapes in the inelastic range, it will be known as adaptive pushover analysis. More information on adaptive pushover can be found in Ref. [56].

4.4 Nonlinear dynamic procedure

Nonlinear dynamic analysis can only be performed by nonlinear response history analysis, which employs earthquake ground motions, while material and geometrical nonlinearities are considered. Under strong ground motion, generally, structures undergo inelastic deformations. Since these deformations are relatively large, geometrical nonlinearity must be considered. A nonlinear system is approximated by a collection of piecewise linear systems wherein the structural properties are constant. This is the most accurate and natural method for seismic analysis of structures. However, it is difficult to interpret the results of this analysis. Thus, it is usually performed along with one of the previously mentioned methods to decrease those uncertainties. Furthermore, selecting and scaling ground motions are two fundamental steps in either linear or nonlinear response history analysis, for which there are various rules but here we briefly explain these rules according to the ASCE 7-16 [49], as follows: A minimum of three suitable ground motions must be chosen for analysis. These ground motions should be selected from events having source mechanisms, magnitudes and fault distance that are consistent with the maximum considered earthquake (MCE). A SRSS spectrum is computed for each pair of horizontal ground motion components. Then, each pair of ground motions shall be scaled in such a way that the average of the SRSS spectra from all horizontal component pairs for a period between 0.2T and 1.5T (where T is the fundamental period of structure) does not fall below the corresponding ordinate of the design response spectrum.

Nonlinear dynamic procedure may use a parametric method called incremental dynamic analysis (IDA) employing probabilistic concepts and several nonlinear response history analyses in order to obtain the robust results. The IDA can be employed to estimate structural capacity under seismic loading. It provides continuous snapshots of the structural response ranging from elasticity to yielding and ultimately to collapse. The IDA consists of analyzing a structural model under one or more ground motion records, each of which is scaled to several levels of intensity. Many response history dynamic analyses are carried out during the IDA and the responses from these analyses are reported versus the intensity level of ground motion record. The attained IDA curves provide suitable demonstration of the structural performance at every level of excitation, which is similar to the load–displacement curve of pushover analysis. More details on the IDA can be found in Ref. [5, 57].

There are also alternative methods to the IDA for considering the record-to-record uncertainty of the structural response, such as multiple-stripe analysis (MSA) and cloud analysis (CA). Nevertheless, in contrast to the IDA, the MSA does not necessarily resort to scaling the same suite of ground motion records to reach the intensity levels, instead it uses various sets of scaled/unscaled records at each intensity level [58]. On the other hand, the CA uses sets of unscaled acceleration records, that is, only a single record corresponds to each intensity level. Indeed, the CA considers an even spread of intensity values within the range of interest, leading to a “cloud” of points. A probabilistic relation between an engineering demand parameter and an intensity measure can be obtained through the linear regression and some statistical assumptions. Further details of the CA can be found in Ref. [59].

4.5 Optimal seismic design

First, the objective function is expressed for defining an optimization problem. Structural weight, initial structural cost and life-cycle cost are the most common types of objective functions [18]. Definition of constraints depends on the seismic design approach, whereby a certain design code is utilized. Stress ratio, drift, torsional irregularity index, strong column-weak beam index, stability index, chord rotation, plastic hinge rotation and so on are the main constraints usually considered in seismic design [60,61,62,63,64,65]. Furthermore, some dimensional constraints may be added into the problem for practical and fabrication reasons. For example, dimensions of a column’s cross section at upper story of a building structure should be equal to or smaller than the column beneath. Apart from structural viewpoint, modern seismic design guidelines consist of stringent drift limitations to ensure sufficient lateral stiffness of the structure for minimizing non‐structural damages [5].

An important task in defining a seismic design optimization problem is the selection of the analysis method and its corresponding constraints. A linear static analysis needs a system of linear equations, as follows:

$${\mathbf{KU}} = {\mathbf{F}},$$

(3)

in which K, U and F are stiffness matrix, displacement and force vectors, respectively. In the case of a nonlinear system of equations, the stiffness matrix is not constant and is a function of the displacement vector. Efficient solvers must be employed for solution of Eq. (3) to reduce the optimization time [1,2,3]. This point will be more important for a linear dynamic analysis wherein the following system of linear equations should be solved:

$${{\mathbf{M}\ddot{\mathbf{U}}}}(t) + {{\mathbf{C}\dot{\mathbf{U}}}}(t) + {\mathbf{KU}}(t) = {\mathbf{F}}(t)$$

(4)

with M, C and K being mass, damping and stiffness matrices, respectively; ${\ddot{\mathbf{U}}}$, ${\dot{\mathbf{U}}}$, ${\mathbf{U}}$ and F denote acceleration, velocity, displacement and force vectors varying with time, respectively. In contrast to the linear case, stiffness matrix varies based on the constitutive law and geometrical nonlinearities existing in nonlinear equations. Hence, it changes upon the variation of structural responses during the analysis. Moreover, when considering the Rayleigh damping, the damping matrix is not constant due to the variations in the stiffness matrix. However, the mass matrix is often assumed to be constant [55].

Response spectrum analysis requires solution of an eigenproblem because natural frequencies (i.e., square root of eigenvalues) and their corresponding mode shapes (i.e., eigenvectors) are necessary for such an analysis. This eigenproblem is stated as:

$${{\mathbf{K}\varvec{\Phi} }} = {{\mathbf{M}\varvec{\Phi} }}\,{{\varvec{\Lambda}}},$$

(5)

where K, M, ${{\varvec{\Phi}}}$ and ${{\varvec{\Lambda}}}$ are stiffness, mass, eigenvector and eigenvalue matrices, respectively. There are also efficient techniques for solving Eqs. (4) and (5) [1, 2, 66].

Obviously, response spectrum method requires significantly lower computational efforts with respect to response history method regardless of whether or not it is nonlinear. Indeed, nonlinear response history analysis needs tremendous computational time when it is utilized for every iteration of an optimization algorithm. Furthermore, convergence failure is much more probable for nonlinear procedures needing suitable automated treatments during optimization.

There are two fundamentally different approaches for evaluating structural response to dynamic loading: deterministic and nondeterministic (probabilistic) [55]. The selection of method depends upon how the loading/structure is defined. In other words, uncertainties can be defined for either structural system properties or loading properties [4, 18]. Accordingly, two kinds of seismic design optimization are considered in the literature. In the deterministic approach, all the objective functions and constraints of an optimization problem are evaluated by deterministic analyses [63, 64, 67], whereas reliability-based and/or stochastic methods are employed to solve the problem in the nondeterministic approach [68,69,70,71,72].

Optimum design in the realm of real-life structures under design code provisions is a complicated optimization procedure due to the existence of numerous highly nonlinear constraints and inherently discrete design variables. Therefore, every investigation uses simplifications to overcome this cumbersomeness. These simplifications rely on either solution methods or selection of objective functions and constraints [40].

5 Optimal seismic design: single-objective cases

Single-objective optimization of structures subjected to static and dynamic loadings is reviewed in this section emphasizing on earthquake effects. These studies are categorized based on optimization type. Because of the extensive literature available on sizing optimization, studies on steel building structures, RC building structures and other structures are discussed in three subsections (see Fig. 1).

5.1 Sizing optimization

5.1.1 Steel building structures

First, we focus on the studies developing the sizing optimization of steel building structures considering both traditional and performance-based seismic design codes.

In this field, Gong et al. [73] formulated the sensitivity of displacements to member size modifications for performance-based design of steel moment frames with inelastic behavior under bending moment. Equivalent static analysis was utilized and a three-story frame was selected as a continuous optimization test case. One of the earlier works on formulation of gradient-based methods in optimal design of nonlinear frame structures was due to Pezeshk [48], who developed an optimization algorithm based on the optimality criteria method to minimize the structural weight with some displacement constraints. Both linear and nonlinear static behaviors of the structure were considered and demonstrated through a design example.

Moghaddam et al. [74] presented a concept of uniformly distributed deformation for finding optimum distribution of structural properties for concentrically braced steel frames against earthquake excitation. According to that concept, member cross-sectional areas were modified to minimize structural weight until a state of uniform deformation was met, leading to a better design than the conventional design.

Salajegheh and Heidari [75] utilized the wavelet transform for decomposing the earthquake records into some approximate signals by which one can perform linear response history analysis faster. The results accuracy depends on the level of decomposition: increasing the number of decompositions yields a higher amount of approximation. Decomposed earthquake accelerogram contains low-frequency and high-frequency parts, and since the low-frequency part is important for dynamic analysis of the structures, only this part is utilized for the analysis [75]. The time integration (e.g., Newmark scheme) for an approximate accelerogram can be accomplished with larger steps based on the decomposition level. Therefore, number of discrete time instances (i.e., the number of points in an earthquake accelerogram) is reduced so that response history analysis performs much faster with respect to the case where the original accelerogram is utilized. Since the computational cost of the analysis decreases, optimal design of structures under response history dynamic loading can be performed swiftly. Thus, this development was added to weight minimization of structures including drift and sometimes also stress constraints. Metaheuristic algorithms were utilized for that purpose. In some cases, a neural network served to increase optimization speed regarding the dynamic analysis: The network was properly trained, thus making the dynamic analysis unnecessary in the optimization process [76,77,78,79,80].

Lagaros et al. [60] evaluated seismic design techniques for optimizing three-dimensional steel frames based on the Eurocodes [81]. Both linear and nonlinear response history analyses were adopted using natural and synthesized ground motion records compatible with the design spectrum. An evolutionary algorithm was adopted to minimize structural weight with stress and stability constraints for the linear analysis as well as inter-story drift for the nonlinear analysis.

Jármai et al. [82] performed optimization of an interior three-story frame structure with inter-story drift constraint as well as stability of columns and beams constraints. Member sections were welded box for columns and rolled I-section for beams. The fabrication cost was found not very effective in the optimum design using particle swarm optimization algorithm, as it was proportional to the weight.

Rojas et al. [83] developed an automated performance-based design methodology for optimizing the structural performance. FEMA-350 [84] and HAZUS procedures were utilized to assess confidence levels associated with restricting the probability of exceedance meeting the target performance levels. The GA solved this optimization problem in which the confidence levels were incorporated into the objective function along with initial construction cost within a collection of optimal design scenarios. Nonlinear response history analysis was employed to design under various levels of hazard. The effects of seismic hazard, initial construction cost, and confidence levels for both structural and nonstructural components were studied.

We note that, in the context of seismic hazard analysis [5], a probability of exceedance of P% in t years is a limit state corresponding to earthquakes with a return period of T_R. Also, the return period is defined as the averaged time between the occurrences of earthquakes with a specified hazard level (that is, a range of earthquake magnitude limited to a lower bound). For example, the design earthquake in international building codes correspond usually either to the probability of exceedance 10% in 50 years (T_R is about 475 years) or to 2% in 50 years (T_R is about 2475 years). The Poisson distribution is utilized for describing these probability percentages such that $P = (1 - e^{{ - \frac{t}{{T_{R} }}}} ) \times 100$.

Gholizadeh and Salajegheh [85] proposed a new meta-model reducing the computational burden of the structural optimization for linear response history analysis. Two stages were performed for this scope. The first one was a meta-model called fuzzy self-organizing radial basis function networks to predict dynamic response of structures. Fundamental natural periods of the structure were selected as the inputs of the neural network. In the second stage, particle swarm optimization was used for finding optimum design. A planar and a space steel frames were examined for weight minimization under stress ratio and drift constraints.

Kaveh et al. [86] carried out performance-based optimal seismic design of frame structures using the ant colony optimization (ACO) algorithm. Since the ACO is inherently a discrete algorithm, it is useful for discrete optimization where cross sections are selected from an available W-Section list. Pushover analysis was utilized to find the structural response for various seismic performance levels. Structural weight was minimized by means of a two-phase design. The first phase includes linearly static analysis under gravity loads and imposes stress constraints. The second phase includes pushover analysis followed by plastic hinge rotation constraint. Two steel frames were optimized by the ACO and the optimized designs were compared to the GA for different performance levels. This optimization problem was also solved with charged system search algorithm [87]. In addition, Gholizadeh [64] presented a new neural network model named as wavelet cascade-forward back-propagation to predict structural responses and a modified firefly algorithm for such optimization problem. The study presented different examples of steel frames ranging from low-rise to high-rise planar cases.

In the recent decade, there has been a growing interest in the progressive collapse of structure under extreme loads like impacts and earthquakes. Liu [88] investigated on progressive collapse seismic design incorporating structural optimization to design a cost-effective steel moment frames with additional resistance to progressive collapse mobilized by sudden removal of critical columns. The progressive collapse potential was evaluated using these three analysis methods: linear static, nonlinear static, and nonlinear dynamic. Weight of a planar nine-story regular steel intermediate moment frame was optimized in accordance with seismic provisions of AISC and UFC progressive collapse requirements. Optimization results of the GA revealed that the traditional seismic design approach for minimizing weight neglects progressive collapse and fails to satisfy the UFC alternate path criteria corresponding to each of those analysis procedures. Linear static analysis provided the most conservative and hence heaviest design against progressive collapse. Unlike the linear static analysis, nonlinear static and dynamic analyses result in more economical designs with acceptable resistance to progressive collapse, while entailing tremendous computational efforts.

Li et al. [89] minimized life-cycle cost of moment frames with a modified modal pushover analysis which was able to capture higher modes effects influencing inelastic seismic demands of structures under design earthquakes implied in the Chinese seismic code. These effects are especially important for high-rise and/or irregular buildings. The life-cycle cost was expressed in terms of the initial material cost and the future expected damage loss, which can be related to seismic performance levels and their consequent failure probability. The damage loss was explicitly expressed through an inter-story drift index based on the fuzzy-decision theory. An adaptive simulated annealing algorithm was implemented to solve the optimization problem with discrete sizing variables. A planar 9-story steel frame was chosen as a design example.

Oskouei et al. [90] evaluated the effects of beam–column connections for minimizing the weight of structural frames using the GA and nonlinear static analysis. Constraints were defined on stresses, target displacement and the number of plastic hinges and their locations. Box and I-shaped standard sections were assigned to beams and columns, respectively. The degrees of connection rigidities were considered in the optimization process. Structural analysis and optimization stages were performed by creating an interface between SAP2000 and MATLAB, respectively. Nine moment frames were studied and optimum connection stiffness was obtained for each one. The optimization results indicated that the nonlinear analysis provides lower weights for short-period frames made of semirigid connections than in the case of linear analysis. Furthermore, in the case of nonlinear analysis with semirigid connections, optimum weight decreased significantly as for increasing the frame periods.

Kaveh and Zakian [61] investigated on optimal design of planar steel frames using linearly elastic response history dynamic analysis. Charged system search and improved harmony search algorithms were selected as metaheuristic optimizers. Both shear and moment frames were considered employing stress and drift constraints. Cross-sectional areas of frame members were taken as discrete variables chosen from an available section database. Performances of optimally designed moment and shear frames were compared. Two groups of constraints were imposed including only drift, and both drift and stress constraints, such that optimum solutions obtained by drift-driven design were compared with those including both constraints. It should be noted that optimum design of structures for response history loading is very time-consuming, and hence it needs efficient methods to accelerate the analysis phase. Thus, Kaveh et al. [91] proposed  the reduced recorded method (RRM) for alleviating the aforementioned challenge. Since in linearly elastic response history analysis of structure we are often looking for minima and/or maxima of structural responses, dynamic analysis can be terminated after reaching those responses. Hence, computational efforts will be reduced significantly. The RRM finds critical time instance of an earthquake accelerogram by means of wavelet decompositions. Substantial time-saving for an optimization process was achieved from the RRM. In another research on efficient analysis, Zakian and Kaveh [66] developed two methods for swift analysis of structures under earthquake loading. The first one utilized graph product rules for efficient response history analysis of cyclically symmetric structures: closed-form solutions were used for computing natural frequencies. The second one was about random vibration of shear frames under seismic excitation in the frequency domain: the canonical forms of structural matrices were presented to perform swift random analysis of the structures through closed-form solutions and symmetry properties of repetitive structural components. Moreover, another achievement in swift analysis of structures under earthquake loading can be found in Ref. [92].

Gholizadeh and Kamyab Moghadas [93] proposed an improved quantum particle swarm optimization metaheuristic algorithm to implement performance-based optimum design through minimizing the structural weight subject to performance constraints on inter-story drift in accordance with FEMA-356 [94] provisions at the IO, LS and CP performance levels. Pushover analysis was conducted to calculate the desired structural responses.

Kaveh et al. [95] utilized response spectrum and equivalent static analyses for optimal seismic design of three-dimensional steel buildings. The process was implemented by creating an interface between SAP2000 and MATLAB with the parallel computing toolbox. The cuckoo search algorithm was used to minimize the weight by exploring the search space defined by the W-sections list of AISC. Strength, displacement and geometric constraints were considered in the optimization. Kaveh et al. [95] obtained similar weights for optimum designs due to both response spectrum and equivalent static analyses, whereas material distribution and seismic performances were different.

Kaveh et al. [96] selected element sections and the connection types as design variables for cost design optimization of steel moment frames when equivalent static loads are applied. Stresses developed in structural members and drift ratios were considered as constraints, according to AISC-LRFD design criteria. Feasibility of column-to-column and beam-to-column dimensions at the joints were also considered as practical restrictions. Local buckling of the sections and column slenderness was checked as well. Three design examples were solved by the enhanced colliding bodies optimization and particle swarm optimization. Reference [65] focused on three-dimensional moment frames with response spectrum analysis. Nine metaheuristic algorithms were utilized for design optimization of steel moment frames with various types of lateral load-resisting systems consisting of ordinary moment frame, intermediate moment frame and special moment frame. In Ref. [97], response spectrum analysis was used for optimal seismic design of three-dimensional steel moment frames utilizing four metaheuristic algorithms. Discrete optimization of moderately irregular frames with in-plane regularity was considered.

Gholizadeh and Fattahi [98] performed performance-based optimum design of steel moment resisting frames to minimize structural cost expressed by the initial construction cost plus the seismic damage cost during operational lifetime of the structure. For estimating the seismic damage cost, Park–Ang damage index was utilized, thereby requiring nonlinear response history analysis during the optimization process. Thus, computational burden of the optimization was huge. To alleviate this burden, neural network was trained to predict structural responses entailed by the dynamic analysis. In addition to the drift limitation as a constraint for immediate occupancy and collapse prevention performance levels, the global damage index was also checked at collapse prevention level to control the damage. A sequential enhanced colliding bodies optimization algorithm solved the optimization problem. An extension of this work to investigate suitability of optimally designed frames by fragility curves resulting from the IDA is documented in [99].

Bybordiani and Kazemzadeh Azad [100] carried out seismic design optimization of steel frames incorporating soil–structure interaction using dynamic analysis. The modeling approach was verified by a reference counterpart in the frequency domain. For response history analysis, some ground motions were chosen and scaled to a target design spectrum using both ordinary scaling and spectral matching techniques. The exponential big bang–big crunch optimization algorithm was applied as a metaheuristic solver. The effects of some factors such as the structural height, soil domain and the scaling technique were studied. It was observed that even though dynamic soil–structure interaction can sometimes decrease the seismic demands, the difference between optimum weights was not remarkable.

Degertekin et al. [101] utilized the school-based optimization algorithm for performance-based optimal seismic design of steel frames in order to minimize the structural weight under inter-story drift and strength constraints. Three benchmark steel frames were used to verify the effectiveness of the algorithm. The optimization results were compared with those of some other optimizers in the literature in terms of optimum solution, convergence speed, and some statistical indices. The proposed algorithm found lighter designs with lower computational efforts than the other optimizers.

Ha et al. [102] utilized pushover analysis to optimize seismic design of steel moment frames. Inelastic analysis of the steel frames was conducted using plastic hinge beam–column elements to localize the plasticity into specified portions of structural members (that is, concentrated plasticity model), thereby reducing computational efforts. An improved differential evolution algorithm was developed as optimizer, and five other metaheuristic algorithms were employed for comparison. Cost optimization was carried out by defining the objective function in terms of columns, beams and panel zone costs. Also, strength, drift and member dimensional constraints were imposed to the optimization problem. Three mid-rise to high-rise steel frames were examined as design examples based on AISC-LRFD.

Although minimizing structural weight for natural frequencies is not directly based on design codes, some researchers work on limiting natural frequencies to make them be far from excitation frequencies of dynamic loading. In earthquake excitation, natural frequencies of a structure should not be close to critical frequency range of the earthquake ground motions so as to avoid the resonance phenomenon in that range. Therefore, this kind of interrelated optimization problem can be solved as well [103]. Design optimization of truss structures with frequency limitations was studied by many researchers. In recent years, only metaheuristic algorithms were used for finding optimum solutions of benchmark trusses and domes [104,105,106]. However, there are a few works on frame optimization including frequency constraints. Seminal investigations on this optimization problem utilized sensitivity analysis and optimality criteria methods for weight optimization of frame structures [107,108,109,110], whereas currently only one paper exists on metaheuristic optimization of these structures under frequency constraints [111].

5.1.2 RC building structures

Continuous sizing optimization of reinforced concrete (RC) structures may be more complicated than that of steel structures. In fact, a RC member includes both steel and concrete materials and this composition cannot be easily expressed in terms of continuous variables. Another challenge is to arrange steel bars within a cross section which must be assigned according to design provisions, even if discrete variables are employed to be assigned to the cross sections drawn from an available list. These challenges forced the researchers to relatively prefer steel structures to simplify the optimization process. Nevertheless, this does not mean that seismic design optimization of RC structures has rarely been investigated. The state of the art for this field is now reviewed.

Ganzerli et al. [112] introduced performance-based criteria for seismic design of RC frames, according to FEMA-273 and 274 provided for retrofitting existing structures. The presented method takes into account the nonlinearity of the structure by means of pushover analysis. The structural cost was minimized under limitations on plastic rotations for beams and columns. Also, upper bounds and lower bounds of concrete and steel reinforcement areas were imposed to design variables. At the end, performance levels of the structure consisting of the IO, LS and CP were assessed by pushover curves.

Chan and Zou [113] presented an optimization technique for performance design of RC buildings based on the elastic and inelastic drifts through response spectrum and pushover analyses, by which the elastic and inelastic drift responses were computed, respectively. The optimization methodology was based on the optimality criteria approach, and the proposed methodology was tested on a ten-story frame. In Ref. [114], pushover analysis was used for performance-based design optimization under inelastic drift constraint. Steel reinforcement ratios were taken as design variables because steel reinforcement cost is higher than concrete material cost. The reinforcements can also be effective to control drift beyond the first yielding and to provide the necessary ductility of RC frames. Moreover, the study was expanded to response history analysis of these frames for finding elastic drifts [67].

Nowadays, external jackets of fiber-reinforced polymer (FRP) composites is a well-known technique for retrofitting of RC structures. In particular, confinement of RC columns with the FRP jackets is very influential in enhancing their strength and ductility. Zou et al. [115] conducted a research on RC frames with FRP-confined columns in order to deploy the minimum amount of the FRP material to improve the seismic performance. Taking the thicknesses of FRP jackets as the design variables, the objective function of the optimization problem was chosen as the material cost of the FRP jackets in terms of their volume. An explicit expression was derived to relate the pushover drift to the FRP thicknesses based on the principle of virtual work and Taylor series approximation. The optimality criteria approach was utilized for finding the optimum solution. Afterward, Zou [116] proposed an optimization technique for the seismic design of base-isolated concrete buildings using response spectrum analysis. Base isolation is an element of passive control of structures against seismic hazards. In order to reach the most cost-effective design for base-isolated structures, simultaneous optimization of base isolation and superstructure is necessary. The total cost of the base-isolated building was minimized under design performance criteria consisting of lateral displacement of the isolation system and inter-story drifts of the superstructure. Member sizes were selected as design variables. These members remain in elastic range during earthquake, while the isolation system can behave nonlinearly and its cost depends on the effective horizontal stiffness of each isolator. As demonstrated by a building example, the technique was able to achieve the optimal balance between the costs of the superstructure and the isolation system, while satisfying all the design performance criteria. In another development for optimal design of base-isolated buildings, Zou et al. [117] added reliability-based approach to the design optimization. This was done because deterministic design optimization cannot provide a satisfactory level of reliability.

Fragiadakis and Papadrakakis [118] performed optimal seismic design of RC frames based on nonlinear response history analysis in both deterministic and probabilistic manners. The reliability-based approach (probabilistic approach) is a more rational approach that can provide consistent design criteria with the performance-based design concept. The probability of exceedance from a limit state was compared with the use of deterministic criteria. Both formulations took the structural response for a number of limit states into account, beginning with serviceability and ending with collapse prevention. The recommended design technique was specifically tailored to the design of RC frame structures. A database of concrete sections was also defined. The concept of multi-database cascade optimization with an evolutionary algorithm was implemented in order to handle the large size of the section databases. The optimized design had to comply with the criteria of the Eurocodes and led to a major reduction of the construction cost, while providing desirable seismic performance.

Liu et al. [119] formulated an optimal seismic design method for RC frames based on time-dependent inter-story drift constraints, to achieve minimum weight design. In order to simplify the time-dependent constrained problem, it was converted into a sequence of unconstrained problems using the integral interior point penalty function method. Consequently, the first two derivatives of the inter-story drift with respect to design variables of Newmark scheme were obtained to form Gradient and Hessian matrices of the integral interior penalty function. Marquardt’s method was utilized to solve those unconstrained problems. The above described approach required lower computational time than the augmented Lagrange multipliers method.

Khatibinia et al. [120] presented a discrete gravitational search algorithm and a meta-model for reliability-based design optimization of RC structures considering soil–structure interaction (SSI) and performance-based design concepts. Estimation of reliability indices was performed with Monte Carlo simulation (MCS). In order to increase the speed of the MCS, a meta-model consisting of a weighted least squares support vector machine and a wavelet kernel function was used to predict the responses of the SSI system.

Kaveh and Zakian [121] presented an optimization formulation for performance-based seismic design of shear walls using pushover analysis. They carried out a discrete optimization in which design variables were selected from a cross-sectional database compatible with the provisions of ACI 318-11 code [122] on sizes, rebar placements and arrangements. The effects of SSI on the optimized shear wall was also assessed. In addition, Kaveh and Zakian [63, 123] proposed an optimization problem for seismic design of RC frames and RC shear wall-frame structures (dual systems). They introduced 16 constraints on stress/strength, drift, practical compatibility of section dimensions, rebar percentage, strong column-to-weak beam ratio, and ratio of shear force distribution for considering the shear wall-frame interaction criterion. These criteria were imposed in accordance with ACI 318-11 and ASCE 7-10 codes. Kaveh and Zakian [63, 123] utilized equivalent static analysis and formulated a detailed cost function in terms of reinforcing steel, concrete and formwork costs. Cross-sectional databases for shear walls, columns and beams were generated in order to perform the discrete cost optimization using charged system search algorithm.

Akin and Saka [124] applied the harmony search algorithm to optimize the structural cost in detailed design of special moment resisting RC frames subjected to earthquakes. The sizes of members, reinforcing bar diameters, reinforcing bar spacing, architectural and other practical requirements in addition to structural requirements were considered to attain constructible designs such that no further modifications were necessary thereafter. For the columns, a predetermined database of cross sections was constructed and sorted in order of resisting capacity. The optimized design had to satisfy the strength, ductility, serviceability and some other constraints. The lateral seismic forces were determined in accordance with ASCE 7-05 and were updated in each iteration because of the changes in structural weight and natural periods. A number of design examples were provided to demonstrate practicability of the optimized designs.

Gharehbaghi and Khatibinia [125] focused on optimum seismic design of RC frames using response history analysis, whereby ten earthquake records were utilized. A hybridized particle swarm optimization algorithm and an intelligent regression model (IRM) were used for the optimization and the response prediction, respectively. This IRM included the subtractive algorithm, k-means clustering approach and wavelet weighted least squares support vector machine in order to reduce the computational cost entailed by the response history analyses during optimization. Nine-story and eighteen-story RC frames were optimized in order to assess the capability of the proposed procedure.

Esfandiari et al. [126] carried out seismic design of RC frames subjected to response history analysis and presented a new algorithm combining multi-criteria decision-making and particle swarm optimization to accelerate convergence rate of the optimization toward the solution. The efficiency of the algorithm was proved by solving weight minimization problems of RC frames considering design code criteria. As an extension of this work [127], seismic design optimization of three-dimensional RC frames was also investigated.

Mergos [128] developed an efficient procedure for performance-based optimal seismic design of RC frames associated with pushover and nonlinear response history analyses. The proposed approach employed a deformation-based procedure for design of reinforcing steel of RC frames that satisfies performance objectives. Accordingly, only the cross-sectional sizes of structural members were taken as independent design variables. The GA was employed to minimize the structural cost under four limit states pertaining to four seismic hazard levels for which deformation of the RC members was limited (e.g., plastic hinge rotation constraint). Moreover, in another study [129], the GA was employed for optimal seismic design of RC frames according to Eurocode 8 and the fib Model Code 2010 (MC2010). It was found that using the MC2010 leads to more cost-effective designs than Eurocode 8 for regions of low-seismicity and almost similar costs for regions of moderate seismicity. For high-seismicity regions, the MC2010 may give higher structural costs. In all cases, the MC2010 provided a better control of structural damage.

Franchin et al. [130] presented a procedure for seismic design of RC frames, in which performance objectives were formulated in terms of maximum accepted mean annual frequency of exceedance, considering multiple limit states. A gradient‐based technique was utilized for solving the optimization problem. Section size and reinforcement ratio of the structural members were selected as design variables. Both equivalent static analysis and response spectrum analysis were employed during the optimization. As a design example, the procedure was applied to a 15‐story planar frame, for which the validation was carried out in terms of drift profiles and mean annual frequency of exceedance, obtained by multiple‐stripe analysis with some records selected to match conditional spectra. The presented procedure is an improvement in the previous work in Ref. [131] which relied on a closed-form solution for the mean annual rate of exceedance of a limit state and an empirical equal-displacement rule.

5.1.3 Other structures

In contrast to the great interest on seismic design optimization of building structures, there are relatively a few studies on non-building structures such as dams, bridges, tunnels, domes, etc. This may be due to two reasons: analysis and design complexities followed by non-building structures, and considerable usage of building structures compared to non-building ones. Of course, in the case of continuum structures, sizing optimization often appears as shape optimization, unless a component of the structure is under consideration.

Sung and Su [132] employed a fuzzy GA for performance-based optimal seismic design of a RC bridge with single-column piers. For minimizing constructional cost, the constraints were defined as structural capacity and reinforcement arrangements for the piers. Violation of the constraints was combined with constructional cost into a penalized objective function. A fuzzy logic control was used in order to embed the penalty function strategy in the genetic search framework.

Taniwaki and Ohkubo [133] optimized transmission tower truss structures under static and seismic loads. Response spectrum analysis was conducted to apply seismic actions on these large-scale trusses. Structural layout, cross-sectional areas and material type were chosen as design variables. Minimizing both material and land costs was selected as the objective function.

Taflanidis [134] developed a probabilistic framework for risk assessment and optimum design of supplemental dampers in multi-span bridge structures supported by abutments and intermediate piers with isolation bearings. The adopted model addressed nonlinear behavior of the dampers and isolators, the dynamic characteristics of the abutments, and the pounding effects between the adjacent spans. Nonlinear dynamic analysis was performed to assess the bridge performance, and a stochastic ground motion was modeled for describing the future near-field ground motions and their seismic hazard consequences for the structure. The proposed probabilistic approach considered various aspects of structural and excitation uncertainties, leading to the seismic risk assessment for the bridge, given by the expected value of the structural response over the undertaken probability models.

Energy dissipation and seismic isolation systems are modern strategies for seismic design and/or retrofit of bridges. For a retrofit design, base isolation devices may be readily utilized in existing bridges as replacement for conventional bearings, enhancing the structural performance. Wang et al. [117] presented discrete cost optimization for designing base isolation of bridges under transient earthquake loads. For that purpose, nonlinear response history analysis was combined along with an optimization method to choose the best base isolators minimizing the cost, while satisfying predetermined design criteria. An improved GA was utilized to find optimal design of a sample highway bridge subjected to multiple dynamic seismic excitations.

Zakian et al. [135] presented a sizing optimization problem for weight minimization of steel pipe rack structures which are skeletal industrial structures subjected to various types of loading such as gravity, seismic, piping and thermal forces. This discrete optimization problem was solved with three metaheuristic algorithms including a modified particle swarm optimization, grey wolf optimizer and the improved grey wolf optimizer. The cross sections of structural members were selected from an available database. Seismic demands were obtained with equivalent static analysis. Stress ratio, drift and dimensional compatibility constraints were imposed for the optimization. The optimized designs were compared to an ordinary design for a real pipe rack in terms of the structural weight and the constraints. Recent investigations on structural optimization demonstrate that the improved grey wolf optimizer outperforms the grey wolf optimizer [135].

5.2 Shape optimization

Shape optimization alters the overall geometry of a structure, which hence occupies more or less space but it may not be desirable in architecture where there is great attention on caring for spaces and estheticism. Therefore, it is somehow impractical for commonly used skeletal structures. However, it is very useful for continuum structures [9, 136, 137].

Seyedpoor et al. [138] introduced an efficient optimization procedure to find optimal shapes of arch dams subject to earthquake loading considering fluid–structure interaction. The optimization was conducted by proposing an efficient combination of stochastic perturbation approximation and particle swarm optimization algorithm. The finite element model defined for the structure was adapted for response history analysis. Concrete volume of the structure was taken as cost function in presence of stress, geometrical and stability constraints.

Akbari et al. [139] presented an efficient methodology for shape optimization of arch dams and developed an algorithm based on Hermite splines to create the arch geometry. Shape sensitivity analysis was carried out in the context of finite element method considering necessary loads including body force, hydrostatic pressure and earthquake forces. The sensitivity analysis was implemented with the concept of mesh design velocity. In order to comply with practical requirements such as constructional stages, many geometrical and response constraints were utilized in the model. The optimization problem was solved with the sequential quadratic programming (SQP) method. The presented strategies were successfully applied to an arch dam built in Iran. Accordingly, an efficient software for shape optimization of concrete arch dams was developed.

Kaveh and Zakian [140] carried out stability-based shape optimization of a gravity dam considering equivalent static seismic and water forces. Cross-sectional area of a gravity dam was considered to be minimized. Charged system search, colliding bodies optimization and enhanced colliding bodies optimization algorithms were selected to optimize the structure. The problem was previously solved with the differential evolution algorithm [141]. Furthermore, Khatibinia and Khosravi [142] implemented a hybrid approach based on an improved gravitational search algorithm and orthogonal crossover to attain optimal shape of concrete gravity dams incorporating the interaction effects of dam–water–foundation rock induced by an earthquake. In order to reduce computational efforts, the weighted least squares support vector machine regression was used as a meta-model for predicting dynamic responses of the dam instead of performing the actual dynamic analysis during the optimization.

Ghabraie et al. [143] used bidirectional evolutionary structural optimization to find the best shape of a passive energy dissipater suiting earthquake risk mitigation. Of course, the evolutionary structural optimization (ESO) method, which has widely been used in topology optimization, uses the gradient information due to the sensitivity analysis required for design updating [17, 45]. Some constraints were stated in order to maintain simplicity and minimize fabrication cost. The optimized shape indicated enhanced energy dissipation capacity and stress distribution. Also, experimental verification was performed to confirm the applicability of the optimized shape, which was resistant to low-cycle fatigue more than before.

As already mentioned for sizing optimization, layout optimization of truss structures for frequency constraints can also be useful to avoid resonance phenomenon. In this regard, Lieu et al. [144] presented an adaptive hybrid evolutionary firefly algorithm for layout and sizing optimization of those structures subject to multiple frequency constraints. There are also more similar works on layout optimization of truss structures [104, 145].

5.3 Topology optimization

Although topology optimization in structural earthquake engineering is not very common due to prescribed architectural design, it can generate new viewpoints for both architectural and structural designs, thus reducing constructional costs while desirable performance is gained. For skeletal structures, member removal or connectivity updating occurs during topology optimization. Meanwhile, layout optimization can be considered as a subset of topology optimization regarding the connectivity updating without changing the number of elements. For continuum structures, material is removed by generating void parts of any shape. Here, first we present a literature survey on the building structures. The few relevant studies on this subject will be surveyed in what follows.

Mijar et al. [146] carried out topology optimization of continua for the concept-based design of structural bracing systems to stiffen tall structures versus sway mechanisms under either wind or seismic forces. Continuum form of structural topology optimization potentially permits to have a helpful design tool for a vast range of structures involved in civil engineering. A variety of continuum topology design formulations including static compliance minimization and eigenvalue optimization were explored, and solution parameters were varied to show practical realizations of some optimized designs. Sequential linear programming was used for solving this topology optimization problem.

Allahdadian and Boroomand [147] carried out layout optimization of structures under seismic loads using earthquake records. The goal was to minimize a displacement norm of the structure, as an indicator representing average strain energy. The MMA algorithm [46] was selected as the optimizer. Since the procedure was very time-consuming, the actual record was replaced by an equivalent record with shorter duration using the frequency domain analysis. For generating the equivalent record, Gaussian wave packet functions were utilized. The computational cost was thus reduced to one-tenth at least. The SIMP approach [14] was selected for topology optimization, which was based on a nodal-based interpolation of design variables and finite element mesh refinement.

Hassanzadeh and Gholizadeh [148] focused on performance-based seismic design optimization of steel concentrically braced frame structures. Their proposed methodology first performs seismic sizing and topology optimization. Then, it employs the IDA to generate fragility curves for the optimized designs resulting from a metaheuristic algorithm called center of mass optimization and to calculate collapse margin ratios. Finally, the frames with two states of fixed and optimized bracing locations were compared in terms of structural weight and seismic collapse capacity. The results demonstrated that the topologically optimal frames have the least structural weight with considerable collapse safety with respect to the case of fixed topology.

Gholizadeh and Ebadijalal [149] conducted topology optimization of structures with bracing systems for which the placement of X-type and diagonal bracing systems was to be optimized. Accordingly, a discrete form of topology optimization was formulated in the context of performance-based seismic design. The center of mass optimization algorithm was presented to solve this problem, which was inspired by the physical concept behind the center of mass. First, the algorithm was verified by two benchmark test cases, and then it was utilized to optimize four multistory steel frames with bracing.

As mentioned before, RC structures are inherently in composite form. Thus, topology optimization of these structures renders impractical results when suitable restrictions are not implemented. In this regard, Zakian and Kaveh [150] obtained vital portions of shear walls and shear wall-frame structures under gravity and equivalent static seismic loads, those which must be preserved (i.e., should not be removed) for supplying structural stiffness and integrity. The effects of shear wall-frame interaction, structural tallness and opening were also investigated in their study. The results highlighted important conceptual outlooks in both architectural and structural aspects. The SIMP method was used for optimizing the compliance. Also, an additional penalty function was defined for enforcing total drift constraint.

Guan et al. [151] presented a principal stress-based evolutionary topology optimization of arch, tied-arch and suspension bridges subjected to both stress and displacement constraints. Two performance indices were introduced for determining the design efficiency. A refined mesh scheme was also suggested to enhance the final topology. In addition, frequency constraints were taken into account to optimize cable-supported bridges.

Hajirasouliha et al. [152] applied a practical optimization method for designing nonlinear truss structures under seismic excitation. To minimize the weight, unnecessary material was gradually moved from strong to weak parts of a structure upon reaching a prevailing state of uniform deformation. Effects of earthquake excitation, target ductility and member buckling on optimum topology were also inspected for various trusses. Optimized weights were much lower than those obtained using linear analysis based on equivalent static loads.

Papavasileiou and Charmpis [153] conducted optimum seismic design of multistory composite buildings having steel columns encased in concrete, steel beams and steel bracings. The goal was to minimize the total material cost of steel and concrete. Member capacity ratios were specified according to the Eurocodes. Seismic behavior was controlled by limiting lateral deflection and fundamental period, which are, respectively, calculated by pushover and eigenvalue analyses. The structure was optimized with a discrete evolutionary algorithm giving cost-effective solutions. The algorithm could activate bracings whenever they are needed. Therefore, the design procedure simultaneously comprised sizing and topology optimization for determining optimum steel sections together with bracings topology.

6 Statistical remarks

Here, a statistical analysis of the surveyed literature is presented. Obviously, the studies on sensitivity analyses without any optimal design are excluded from this analysis. Thus, previously discussed papers on seismic design optimization of structures considering single-objective functions are statistically assessed. Figure 4 shows that sizing optimization is the most popular case (with 79% of the papers) among other optimization types. Also, Fig. 5 indicates that non-gradient-based methods (particularly, metaheuristic algorithms) were applied much more than gradient-based methods in seismic design optimization. Hence, there is a strong need of more studies on applications of gradient-based methods in this field.

Fig. 4

Percentage of optimization types in the past studies focusing on single-objective seismic design optimization

Fig. 5

Percentage of solution methods in the past studies focusing on single-objective seismic design optimization

Tables 1, 2 and 3 briefly summarize the literature survey concentrating on optimization, structure, analysis, objective function and constraint types. Numbers of publications related to single-objective seismic design optimization are categorized in Table 4. Furthermore, we can see that a few studies focused on non-building structures, whereas there are many investigations on optimization of building frames (in particular, for steel frames). Of course, a large number of these publications considered planar frames. The term “3D” in Tables 1, 2 and 3 denotes either the use of three-dimensional model or the use of both two-dimensional and three-dimensional models. Additionally, only a few publications regarding the nonlinear dynamic procedure exist. As seen in Tables 1, 2, 3 and 4, it should be noted that some papers considered more than one type of seismic analysis per one study.

Table 1 Summary of studies on sizing optimization for seismic design of structures: single-objective cases

Table 2 Summary of studies on shape optimization for seismic design of structures: single-objective cases

Table 3 Summary of studies on topology optimization for seismic design of structures: single-objective cases

Table 4 Number of publications in different categories for single-objective seismic design optimization of structures (years 1990–2020)

7 Discussion and concluding remarks

This review article surveyed the progresses in seismic design optimization of structures—a highly nonlinear optimization problem requiring efficient solution methods. It was found that most of the studies have utilized metaheuristic methods for solving the optimization problem due to three main reasons: simplicity, versatility and not needing gradient information. However, this is not true for topology optimization comprising many design variables. Therefore, unlike the size and shape optimization, topology optimization is inevitably solved with gradient-based methods. Nevertheless, there are some hybrid algorithms where a metaheuristic algorithm is upgraded with a gradient-based approach to converge faster within less structural analyses in topology optimization. Moreover, despite the fact that gradient-based methods may sometimes be computationally demanding and have relatively complicated formulations, they can be more effective in guaranteeing the optimality for some problems. Gradient-based methods can solve a problem with fewer number of iterations, but with more efforts per iteration with respect to metaheuristic methods. On the other hand, computational efficiency of metaheuristic methods decreases with increasing the number of design variables. This aspect, when combined with a computationally expensive dynamic analysis, can make the use of these methods inefficient. Hence, development of gradient-based methods for seismic design optimization is still an open concern for future research.

Apparently, previous works have mainly focused on sizing optimization, whereas shape and topology optimization in seismic design received less attention. This fact is more evident for shape optimization. Even though architectural restrictions prohibit either shape or topological changes, the design optimization process can be coupled with both architectural and structural stages to transform a conceptual design into a rational design that can be constructed. However, in contrast to sizing optimization, it is not easy to formulate shape or topology optimization problems covering all structural analysis and design aspects.

The lessons learnt from past earthquakes have revealed the importance of performance objectives in design of structures, what is being followed in performance-based earthquake engineering. Therefore, future studies can address performance-based seismic design more broadly with nonlinear dynamic procedures to capture the real structural behavior, especially due to the increasing advances in computational power. Although many investigations focused on this topic, more studies can further be accomplished even for frame structures. Also, it is useful to establish new optimization problems for seismic design of special structures such as bridges, tall buildings, towers, shell structures, domes, dams and tunnels. Moreover, the past studies mainly considered deterministic analysis of the structures associated with seismic design. Hence, probabilistic analysis of the structures can enrich the state of the art. The IDA is one of the well-known methods in this category. Nevertheless, it needs tremendous computational cost for each objective function evaluation obtained through a seismic analysis during optimization iterations. On the other hand, life-cycle cost optimization is another seismic design discipline which is a vital issue for future research considering the limited amount of relevant literature on this topic.

A delicate issue is the practicability of seismic design optimization. Degree of static indeterminacy and the overstrength are two fundamental requirements for a desirable seismic design. These requirements may be jeopardized when maximum capacities of structural members are exploited through an optimal design. Hence, it will be useful if one imposes conservative tolerance for constraint handling. Another challenge is about practical and fabrication issues which are not considered in many research works. Since implementing all the design and fabrication criteria seldom was covered by any previous study, major investigations in this direction can be very promising. In other words, a design optimization can be equipped with structural detailing. Moreover, fabrication quality control has demonstrated that some differences between the designed and the constructed structure may be introduced. This fact inspires some ideas about the effects of constructional uncertainties.

As outlined in Tables 1, 2, 3 and 4, a number of investigations have concentrated on solving a previously defined optimization problem with another algorithm. Although these kinds of studies are important for testing new optimization algorithms and their abilities, in the sense of developing seismic design optimization, it is worth mentioning that many research topics are reserved for proposing new optimization problems. For example, most studies on steel structures regarded two-dimensional moment resisting frames. Thus, examples of three-dimensional buildings incorporating all structural components like slabs, beams, columns, shear walls, bracings, etc., remain very limited. Of course, every lateral load-resisting system has its own components and obviously a building structure does not contain all of them at the same time. However, it is necessary to widen the variety of building structures in order to obtain the comprehensive results and to enrich the guidelines for optimal seismic design of those structures. Furthermore, in contrast to regular buildings, there is still a research gap needing to be bridged regarding the optimal design of irregular buildings under earthquake excitations.

Heretofore, numerous research topics have been considered in optimal seismic design, but similarly there are many interesting untouched topics deserving attention in this discipline, as already mentioned. Moreover, for briefness, a review of multi-objective cases in optimal seismic design will be published in the near future.