From statistical mechanics to nonlocal theory

Abstract

This paper discusses the relationship between statistical mechanics and nonlocal mechanical theories. Specifically, the relationship among statistical mechanics, nonlocal vector calculus, smoothed particle hydrodynamics (SPH), and peridynamics is established. Furthermore, a general particle dynamics method is proposed to solve the solid mechanics problem based on the nonlocal vector calculus and peridynamic bond constitutive model. The proposed method is a successful nonlocal mechanics theory; the convergence of the nonlocal property is verified by numerical experiments.

1 Introduction

The target of solid physics is to study the macroscopic properties and laws of solids from the micro-level. Two important subjects are quantum mechanics and continuum mechanics, which study the microscopic particles and macroscopic bodies, respectively. Among them, a key process is statistical mechanics, which can give the relationship between the amounts of microscopic particles and the macroscopic bodies. Except for the study of the relationship between them, the multi-scale modeling is also important in the materials and structure analysis, because the mechanical behaviors undergo different stages which focus on different scales. For example, the failure process of an intact body contains the micro-crack nucleation, macro-crack initiation and propagation, and the final failure of materials and structures. In the previous work by Piola et al. [1,2,3,4], the homogenized theory, which is deduced by means of the identification of powers in the discrete microscopic model and the continuous macroscopic model, can be called a nonlocal theory [5, 6]. Nonlocal theory is a theory, which considers the multi-scale effect and some other physical phenomena. In recent years, the nonlocal theory is in frontier research and undergoes a rapid development among various research interests, e.g., physical mechanics [7, 8], sociology [9, 10], artificial intelligence [11, 12], and medical imaging [13,14,15]. Among various works in physical solid, Zhou et al. [16,17,18,19] did pioneering and deep works in the failure of materials and structures by employing the nonlocal theories.

Nonlocal continuum mechanics is an extension of classical continuum theory, and it fully considers the scale and material microstructure influence on macroscopic mechanical properties in the framework of a continuum, so it can effectively explain some phenomena and problems that by classical theory are difficult to explain, such as deformation localization, the crack tip stress singularity, high-frequency wave scattering, and so on. However, in the present nonlocal theories, an important intermediate link, the micromorphic model, is often ignored by the researchers, and a lot of nonlocal models does not include micromorphic models. It is necessary that appropriate micromorphic models should be used in the nonlocal theories to obtain a correct aspect of both the grain-scale mechanisms and macro-mechanisms. As described in Ref. [20]: “Micromorphic models are particularly significant for bridging, in a heuristic way, across spatial scales ranging from that at grain interactions to collective behavior of large numbers of grains.”

The statistical mechanics and nonlocal theory have a tiny connection. Statistical mechanics is one of the most powerful and practical subjects in a large range of theoretical and applied physics. Irving and Kirkwood [21] firstly formulated the conservation laws for continuum mechanics by the principles of statistical mechanics. Although the nonlocal notion did not directly occur in their studies, the nonlocal interaction terms have been developed in their researches. Noll [22, 23] made some progresses in avoiding the use of the $\updelta$ function, and in getting closed-form integral expressions for the stress tensor and the heat flux, etc. Based on these works, Lehoucq [24] directly formulated the peridynamic balance laws from averaging in phase space, and found that nonlocal interaction becomes an intrinsic aspect.

Nonlocal differential operator is an important segment of the nonlocal systemic sphere. Nonlocal theory employs integral–differential equations (IDEs), which always contain a vector two-point function, to describe the nonlocal interaction. The traditional differential operators are local operators which always act on a local point function. Therefore, the nonlocal differentiation operators need to be developed to provide useful tools to better understand nonlocal models and numerical methods involving nonlocality, either on the physical level or for convenience of numerical computation [25]. A lot of scholars have made the effort to develop the nonlocal differential operator. Lehoucq [26] formulated a peridynamic stress tensor derived from nonlocal interactions, and derived the relationship between the peridynamic stress tensor and the corresponding pairwise force density. This peridynamic stress tensor can be considered as a two-point function. Bougleux et al. [14] developed a weighted gradient and divergence operators, which are used to establish a regularization framework on graphs for image and mesh filtering. Gilboa and Osher [15] firstly attempted to extend some known partial differentiation equations (PDEs) and variational techniques to a nonlocal framework, and developed the nonlocal derivative equation which can map the vector point function into a vector two-point function. Gunzburger [27] developed a calculus for nonlocal operators that mimics Gauss’ theorem and Green’s identities of the classical vector calculus, and derived the relationship between the local differential operator and the nonlocal differential operator based on Lemma I and Lemma II in [22, 23]. Du [28] developed a full set of the nonlocal operators, including nonlocal divergence, gradient, curl operators and the derivation of the corresponding adjoint operators systematically. Bergel and Li [29] studied the relation of the state variables which are defined by various nonlocal differential operators in both material and spatial configuration in the context of finite deformation, and applied it to derive new force states and deformation gradients. Tu and Li [30] generalized the notion of the nonlocal derivative of non-ordinary state-based peridynamics by formulating various discrete nonlocal differential operators with respect to different configuration spaces. Yan et al. [31] proposed nonlocal differential operators, and found that the nonlocal differential operator formulation can be derived from the moving least square method. Madenci et al. [13] constructed a nonlocal differential operator by considering the Taylor series expansion of a multi-variable scalar field function in a multi-dimensional space. This nonlocal differential operator can transform the partial derivative of any order into its nonlocal integral representation, and provides a relatively simple solution for the higher derivative. Du [32] extended an earlier analysis [28] on nonlocal gradient operators, and found that one should carefully evaluate the choices of the nonlocal interaction kernels when the corresponding models are adopted. In addition, an intuitive interpretation of their rigorous analysis is that strengthened interactions among close-by materials points tend to promote stability, and the notion of nonlocal gradient may also be related to the use of kernel-based integral approximations to differential operators in methods like smoothed particle hydrodynamic (SPH) and reproducing kernel particle method (RKPM). Ren [33] presented the variation of the general nonlocal operator in continuous and discrete forms, and employed the variation of the nonlocal operator to the nonlocal functional analysis based on the research of the nonlocal operator. Du [25] made a mathematical analysis of the SPH and nonlocal Stokes equation, and found that the SPH model serves as a bridge between the discrete approximation schemes involving a nonlocal integral relaxation and the local continuum models. Zhou et al. [34,35,36] compared the differences and similarities between the nonlocal theories and the kernel-based integral approximations, and proposed a unified theory, smoothed peridynamics, for large deformation and cracking problems.

However, the specific relationship among statistical mechanics, nonlocal differential operators, nonlocal theories, and SPH kernel-based integral approximations has not been fully demonstrated, and the reason for the equivalence between meshless discretization of peridynamics and SPH is not investigated. Therefore, there exists a demand for studying the relationship among these theories to make a deep understanding of the intrinsic connection among them. In this present study, the authors review the statistical mechanics theories and nonlocal theories, and then carry out a thorough investigation of the relationship among statistical mechanics, nonlocal vector calculus, PD and SPH. In addition, based on these investigations, a novel nonlocal theory is proposed for computational mechanics.

The remainder of this paper is organized as follows: the mathematical and physical foundations of the statistical mechanics and nonlocal theories are introduced in Sect. 2, the relationship among statistical mechanics, peridynamics, and SPH is derived in Sect. 3, a novel nonlocal mechanic theory, general particle dynamics (GPD), is proposed in Sect. 4, and the conclusions are drawn in Sect. 5.

2 Mathematical and physical foundation

2.1 Statistical mechanics to continuum mechanics

Whether the matter is atomistically constituted or continuous is a question from early Greeks to present times. Although the regular physical processes, which emerge at the macroscopic level of everyday life from the extremely complex motions of a huge number of particles, can be described by continuous variables, these two descriptions frequently yield the same results. Many scientists used the concept of atom to deduce results about the macroscopic behavior of matter which can be called the discipline of statistical mechanics [37, 38]. In this Section, the equation of continuum mechanics is derived by employing Liouville’s equation in statistical mechanics.

Statistical mechanics stress a probability, while the traditional mechanics theories stress a determinism, which states that everything is determined if the initial conditions are determined. In statistical mechanics theories, the macroscopic state functions (density, velocity, stress, energy density, and heat flux) are interpreted as expected values, and the fundamental equations of continuum thermo-mechanics (continuity equation, equation of motion, and energy equation) are derived by solving the expected values for the physical intensive quantities (mass, momentum densities, and energy density). In a classical statistical system with a set of particles,${\mathbf{x}}_{1}, {\mathbf{x}}_{2}, \dots , {\mathbf{x}}_{n}$, and velocities, ${\mathbf{v}}_{1}, {\mathbf{v}}_{2}, \dots , {\mathbf{v}}_{n}$, in a 6n-dimensional phase space $\mathrm{\mho }$, every possible state of the system has a corresponding point in this phase space, denoted by $\left({\mathbf{x}}_{1}, \dots , {\mathbf{x}}_{n};{\mathbf{v}}_{1}, \dots , {\mathbf{v}}_{n}\right)=({\mathbf{x}}_{i};{\mathbf{v}}_{i})$, and the trajectory of the phase space describes the evolution process of the macro-system.

The probability distribution function ${\mathbb{W}}$ (relative density of representative points in the phase space) of the state in $\mathrm{\mho }$ at time t is denoted by

$${\mathbb{W}}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right) = {\mathbb{W}}\left( {{\mathbf{x}}_{1} ,{ } \ldots ,{ }{\mathbf{x}}_{n} ;{\mathbf{v}}_{1} ,{ } \ldots ,{ }{\mathbf{v}}_{n} ;t} \right)$$

(1)

where ${\mathbb{W}}$ satisfies the normalization condition over the 6n-dimensional space, which implies that the sum of the probabilities of all possible states is 1.

The probability per unit volume, in which the kth molecule is located at ${\mathbf{x}}_{k}$, is denoted by:

$$\mathop \int \limits_{{\mho /{\mathbf{x}}_{k} }}^{{}} {\mathbb{W}}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)d{\mathbf{x}}d{\mathbf{v}} = \int \ldots \int {\mathbb{W}}\left( {{\mathbf{x}}_{1} ,{ } \ldots ,{ }{\mathbf{x}}_{n} ;{\mathbf{v}}_{1} ,{ } \ldots ,{ }{\mathbf{v}}_{n} ;t} \right)d{\mathbf{x}}_{1} \ldots {\text{d}}{\mathbf{x}}_{k - 1} d{\mathbf{x}}_{k + 1} \ldots d{\mathbf{x}}_{n} {\text{d}}{\mathbf{v}}_{1} \ldots {\text{d}}{\mathbf{v}}_{n}$$

(2)

where $d{\mathbf{x}}_{1}\dots \mathrm{d}{\mathbf{x}}_{k-1}d{\mathbf{x}}_{k+1}\dots d{\mathbf{x}}_{n}\mathrm{d}{\mathbf{v}}_{1}\dots \mathrm{d}{\mathbf{v}}_{n}$ means the infinitely small unit volume in the phase space.

For any dynamic intensive quantity, $f\left({\mathbf{x}}_{1}, \dots , {\mathbf{x}}_{n};{\mathbf{v}}_{1}, \dots , {\mathbf{v}}_{n}\right)$ has an expected value given at location ${\mathbf{x}}_{k}$ and time t by:

$${\text{E}}\left[ {f;\left. {{\mathbb{W}}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)} \right|{\mathbf{x}} = {\mathbf{x}}_{k} } \right] = \mathop \int \limits_{{\mho /{\mathbf{x}}_{k} }}^{{}} f\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} } \right){\mathbb{W}}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)d{\mathbf{x}}d{\mathbf{v}}$$

(3)

where $\mathrm{E}\left[f\right]$ denotes the expected value operator of $f$.

By the above equation, the expected value of the quantity can be obtained by employing the probability distribution function ${\mathbb{W}}$ in the phase space.

The potential energy is denoted by U, and the total internal potential energy of the system can be expressed by the sum of potential energy of all particles or all pairs of particles ${U}_{ij}$ as

$$U = U\left( {{\mathbf{x}}_{1} ,{ }{\mathbf{x}}_{2} ,{ }{\mathbf{x}}_{3} ,{ } \ldots ,{ }{\mathbf{x}}_{n} } \right) = \mathop \sum \limits_{i < j} U_{ij} = \frac{1}{2}\mathop \sum \limits_{i \ne j} U_{ij}.$$

(4)

Newton’s third law states that the force exerted by ${\mathbf{x}}_{i}$ on ${\mathbf{x}}_{j}$, denoted by ${\mathbf{f}}_{ij}$, is equal to the force exerted by ${\mathbf{x}}_{j}$ on ${\mathbf{x}}_{i}$, denoted by ${\mathbf{f}}_{ji}$, furthermore we have

$${\mathbf{f}}_{ij} = - \nabla_{{{\mathbf{x}}_{i} }} U_{ij} \left( {r_{ij} } \right) = - U^{\prime}_{ij} \frac{{{\mathbf{x}}_{i} - {\mathbf{x}}_{j} }}{{r_{ij} }} = - {\mathbf{f}}_{ji} = \nabla_{{{\mathbf{x}}_{j} }} U_{ji} \left( {r_{ji} } \right) = U{^{\prime}}_{ji} \frac{{{\mathbf{x}}_{j} - {\mathbf{x}}_{i} }}{{r_{ij} }}$$

(5)

where $r_{ij}$ is the distance between ${\mathbf{x}}_{i}$ and ${\mathbf{x}}_{j}$.

Assuming that the external forces are absent, based on the principle of the conservation of probability (Liouville equation) in phase space, the change rate of ${\mathbb{W}}$ is obtained as:

$$\begin{aligned} \frac{{d\mathbb{W}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right)}}{dt} & = \mathop \sum \limits_{i} \left[ {\frac{{\partial \mathbb{W}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right)}}{{\partial {\mathbf{x}}_{i} }}\frac{{\partial {\mathbf{x}}_{i} }}{\partial t} + \frac{{\partial \mathbb{W}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right)}}{{\partial {\mathbf{v}}_{i} }}\frac{{\partial {\mathbf{v}}_{i} }}{\partial t}} \right] \\ & = \mathop \sum \limits_{i} \left[ {\frac{{\partial \mathbb{W}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right)}}{{\partial {\mathbf{x}}_{i} }}\frac{{\partial {\mathbf{x}}_{i} }}{\partial t} + \frac{{\partial \mathbb{W}\left( {{\mathbf{x}}_{i} ;{\mathbf{v}}_{i} ;t} \right)}}{{\partial {\mathbf{v}}_{i} }}\frac{{{\mathbf{f}}_{i} }}{{m_{i} }}} \right] \\ & = \mathop \sum \limits_{i} \left( { - {\mathbf{v}}_{i} \cdot \nabla_{{{\mathbf{x}}_{i} }} \mathbb{W} + \frac{1}{{m_{i} }}\nabla_{{{\mathbf{x}}_{i} }} U \cdot \nabla_{{{\mathbf{v}}_{i} }} \mathbb{W}} \right) \\ \end{aligned}$$

(6)

where ${m}_{i}$ is the mass of the i-th particle.

When the expected values of physical quantity of mass density $\uprho$ and momentum densities $\uprho \mathbf{v}$ are solved by Eq. (2), it follows immediately:

$${\uprho } = \mathop \int \limits_{{\mho /{\mathbf{x}}_{i} }}^{{}} m_{i} \mathbb{W}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)d{\mathbf{x}}d{\mathbf{v}},$$

(7)

$${\uprho }{\mathbf{v}} = \mathop \int \limits_{{\mho /{\mathbf{x}}_{i} }}^{{}} m_{i} {\mathbf{v}}_{i} \mathbb{W}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)d{\mathbf{x}}d{\mathbf{v}}.$$

(8)

Multiplying Eq. (6) by ${m}_{j}$, we have:

$$\begin{aligned} \mathop \int \limits_{{\mho /{\mathbf{x}}_{j} }}^{{}} m_{j} \frac{{\partial \mathbb{W}\left( {{\mathbf{x}}_{i} ,{\mathbf{v}}_{i} ,t} \right)}}{\partial t} & = \mathop \sum \limits_{i} m_{j} \left( { - {\mathbf{v}}_{i} \cdot \nabla_{{{\mathbf{x}}_{i} }} \mathbb{W} + \frac{1}{{m_{i} }}\nabla_{{{\mathbf{x}}_{i} }} U \cdot \nabla_{{{\mathbf{v}}_{i} }} \mathbb{W}} \right) \\ & = \mathop \sum \limits_{i} m_{j} \left( { - {\mathbf{v}}_{i} \cdot \nabla_{{{\mathbf{x}}_{i} }} \mathbb{W} + \nabla_{{{\mathbf{x}}_{i} }} {\mathbf{v}}_{i} \cdot \nabla_{{{\mathbf{v}}_{i} }} \mathbb{W}} \right). \\ \end{aligned}$$

(9)

Then, substituting Eqs. (7) and (8) into Eq. (9), the continuity equation can be obtained as:

$$\frac{{\partial {\uprho }}}{\partial t} = - \nabla_{{\mathbf{x}}} \cdot \left( {\rho {\mathbf{v}}} \right).$$

(10)

The other fundamental equation of continuum thermo-mechanics can be obtained in a similar way [21,22,23]. Two important Lemmas originating from the above formula which is used in Sect. 2.2 are listed as follows:

Let $f(\mathbf{x},\mathbf{y})$ be a scalar, vector, or tensor function of the two vector variables x and y, which satisfies the essential conditions [21], then the following lemmas are valid:

Lemma 1:

$$\mathop \int \nolimits_{y}^{{}} f\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}} = \nabla_{{\mathbf{x}}} \cdot \mathop \int \nolimits_{{\mathbf{z}}}^{{}} \left\{ {{\mathbf{z}}{ } \cdot \mathop \int \nolimits_{{{\upalpha } = 0}}^{1} f\left( {{\mathbf{x}} + \mu {\mathbf{z}},{\mathbf{x}} + \mu {\varvec{z}} - {\mathbf{z}}} \right){\text{d}}\mu } \right\}{\text{d}}{\mathbf{z}}.$$

(11)

Lemma 2:

As shown in Fig. 1, let $\mathcal{J}$ be any region in space with piece-wise smooth bounding surface $\mathcal{F}$, and let $\mathcal{A}$ be the exterior of $\mathcal{J}$ and ${\mathbf{n}}_{\mathbf{x}}$ be the outward normal unit vector at point $\mathbf{x}$ on $\mathcal{F}$. Then, we have.

$$\mathop \int \nolimits_{{{\mathbf{o}} \in {\mathcal{J}}}}^{{}} \mathop \int \nolimits_{{{\mathbf{w}} \in {\mathcal{A}}}}^{{}} f\left( {{\mathbf{o}},{\mathbf{w}}} \right){\text{d}}{\mathbf{w}}{\text{d}}{\mathbf{o}} = - \frac{1}{2}\mathop \int \nolimits_{{\mathcal{F}}}^{{}} \mathop \int \nolimits_{{\mathbf{z}}}^{{}} \mathop \int \nolimits_{\mu = 0}^{1} f\left( {{\mathbf{x}} + \mu {\mathbf{z}},{\mathbf{x}} + \mu {\varvec{z}} - {\mathbf{z}}} \right)\left( {{\mathbf{z}} \cdot {\mathbf{n}}_{{\mathbf{x}}} } \right){\text{d}}\mu \;d{\varvec{z}}\;d{\mathcal{F}}_{{\mathbf{x}}}.$$

(12)

Fig. 1

The geometric relationship in Lemma 2

2.2 Nonlocal vector calculus

In a classical continuum system, the model can be discretized into many material points, and each material point has a finite volume. Points in ${\mathbb{R}}^{n}$ are denoted by the vectors x, y, or z, and the natural Cartesian basis is denoted by ${\mathbf{e}}_{1}, {\mathbf{e}}_{2},\dots ,{\mathbf{e}}_{n}$. When using a total Lagrangian view, an initial configuration ${\Theta }_{0}$ at $t=0$ is used to illustrate the kinematic relation, and the material coordinate can be denoted by vector $\mathbf{x}=\mathbf{x}({\mathbf{e}}_{1}, {\mathbf{e}}_{2},\dots ,{{\varvec{e}}}_{n})$ which can denote a point. Correspondingly, the current (spatial) coordinate and configuration,$\Theta$, are given by ${\varvec{x}}(\mathbf{x},\mathbf{u},{t}_{1})$ at $t={t}_{1}$ which is used for an updated Lagrangian view. The mapping function between the initial configuration and the current configuration is defined as $\phi :{\Theta }_{0}\to \mathrm{ \Theta or }{\varvec{x}}=\phi (\mathbf{x},t)=\mathbf{x}+\mathbf{u}(t)$, in which u is displacement.

For two open regions ${\Omega }_{1}\subset {\mathbb{R}}^{n}$ and ${\Omega }_{2}\subset {\mathbb{R}}^{n}$ with a common boundary $\partial {\Omega }_{12}$ and a smooth vector-valued function $\mathbf{q}(\mathbf{x})$, the local flux from ${\Omega }_{1}$ to ${\Omega }_{2}$ can be written as:

$$\mathop \int \nolimits_{{\partial {\Omega }_{12} }}^{{}} {\mathbf{q}} \cdot {\mathbf{n}}_{1} d{\text{A}}$$

(13)

where ${\mathbf{n}}_{1}$ denotes the unit normal on $\partial {\Omega }_{12}$ pointing outward from ${\Omega }_{1}$, $d\mathrm{A}$ denotes a surface measure in ${\mathbb{R}}^{n}$, and $\mathbf{q}\cdot {\mathbf{n}}_{1}$ is considered as the local flux density along the common boundary.

A flux operator is served as a proxy for interaction between two domains. In the classical setting of local case, flux is the interaction occurring at the boundary of the domain.

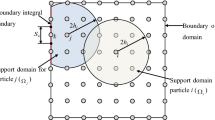
As can be seen, the premise of a contribution to the local flux is that a vector-valued function occurs across their common boundary. However, in nonlocal case, each point external to the domain has a nonlocal flux interaction to the domain, as shown in Fig. 2. The nonlocal flux density at any point $\mathbf{x}\subset {\Omega }_{1}$ to a volume ${\Omega }_{2}$ can be identified as:

$$\mathop \int \nolimits_{{{\Omega }_{2} }}^{{}} {\uppsi }\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}{ }\forall {\Omega }_{2} \subset {\mathbb{R}}^{n}$$

(14)

where $\mathbf{y}$ is another point in ${\Omega }_{2}$, $\uppsi (\mathbf{x},\mathbf{y})$ is a scalar two-point function, which can be viewed as a flux density per unit volume. The nonlocal flux density has unit of a physical intensive quantity per unit volume, in contrast to the local flux density $\mathbf{q}\cdot {\mathbf{n}}_{1}$ which has units of the quantity per unit area.

Fig. 2

The sketch of local and nonlocal flux from ${\Omega }_{1}$ to ${\Omega }_{2}$

With the nonlocal flux density, the nonlocal flux to any domain ${\Omega }_{1}$ considering the contribution of the given domain ${\Omega }_{2}$ can be integrated on ${\Omega }_{2}$, which can be written as:

$$\mathop \int \nolimits_{{{\Omega }_{1} }}^{{}} \mathop \int \nolimits_{{{\Omega }_{2} }}^{{}} {\uppsi }\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} \forall {\Omega }_{1} \subset {\mathbb{R}}^{n} ,\forall {\Omega }_{2} \subset {\mathbb{R}}^{n}.$$

(15)

Before the definition of nonlocal divergence operators, we identify the nonlocal flux density out of a point $\mathbf{x}\in\Omega$ as:

$$\mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} {\uppsi }\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}.$$

(16)

The Gauss theorem defines the relationship between the flux and the divergence of a vector q as:

$$\mathop \int \nolimits_{{\Omega }}^{{}} \nabla \cdot {\mathbf{q}}d{\mathbf{x}} = \mathop \int \nolimits_{{\partial {\Omega }}}^{{}} {\mathbf{q}} \cdot {\mathbf{n}}_{1} d{\text{A}} \forall {\Omega } \subset {\mathbb{R}}^{n}.$$

(17)

Therefore, following the same definition of the local Gauss theorem, the relationship between the nonlocal flux and the nonlocal divergence of a vector two point function can be written as:

$$\mathop \int \nolimits_{{\Omega }}^{{}} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right)d{\mathbf{x}} = \mathop \int \nolimits_{{\Omega }}^{{}} \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} {\uppsi }\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} \forall {\Omega } \subset {\mathbb{R}}^{n} ,$$

(18)

where $\mathcal{D}$ is the nonlocal divergence operator, $\mathcal{G}$ is a vector two-point function, which is related to the quantity q by a constitutive relation. A classical example of the vector two-point function is the pairwise force function [7] used in peridynamics which is employed to describe the interaction force of two material points.

According to the Schwartz kernel theorem [39], the nonlocal flux density per unit volume $\uppsi (\mathbf{x},\mathbf{y})$ is uniquely expressed in terms of the vector $\mathcal{G}(\mathbf{x},\mathbf{y})$ by:

$${\uppsi }\left( {{\mathbf{x}},{\mathbf{y}}} \right) = \frac{1}{2}\mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \left[ {\omega \left( {{\mathbf{x}},{\mathbf{y}},{\mathbf{z}}} \right) \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{z}},{\mathbf{y}}} \right) - \omega \left( {{\mathbf{y}},{\mathbf{x}},{\mathbf{z}}} \right) \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{z}},{\mathbf{x}}} \right)} \right]d{\mathbf{z}} \forall {\mathbf{x}},{\mathbf{y}} \in {\mathbb{R}}^{n}$$

(19)

where $\omega$ is a kernel function, and a simplified assumption of the kernel function $\omega$ can be written as:

$$\omega \left( {{\mathbf{x}},{\mathbf{y}},{\mathbf{z}}} \right) = 2\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right){\updelta }\left( {{\mathbf{x}} - {\mathbf{z}}} \right)$$

(20)

where $\updelta$ is a Dirac delta function, and ${\omega }_{loc}(\mathbf{x},\mathbf{y})$ is often considered as a localized kernel to make a concise and quick computation as:

$$\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right) = 0{\text{ if }}\left| {{\mathbf{y}} - {\mathbf{x}}} \right| \ge \varepsilon$$

(21)

where $\varepsilon$ is a cut-off nonlocal characteristic parameter with many different names in different theories, such as smooth length, influence radius, horizon, etc.

Therefore, combining Eqs. (18)–(20), the nonlocal divergence operator can be written as:

$${\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right) = \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right] \cdot \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}{\text{ for }}{\mathbf{x}} \in {\mathbb{R}}^{n} .$$

(22)

The nonlocal divergence operator of a tensor function can employ Eq. (22) to solve each row of the tensor. The nonlocal divergence operator $\mathcal{D}$ is a point operator that maps two-point functions into point functions defined over ${\mathbb{R}}^{n}$, the scalar point function $u\left(\mathbf{x}\right):{\mathbb{R}}^{n}\to {\mathbb{R}}$ is given, and the adjoint operator of $\mathcal{D}$ can be obtained as [28]:

$${\mathcal{D}}^{*} \left( u \right)\left( {{\mathbf{x}},{\mathbf{y}}} \right) = - \left[ {u\left( {\mathbf{y}} \right) - u\left( {\mathbf{x}} \right)} \right]\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right).$$

(23)

The adjoint operator ${\mathcal{D}}^{*}$ is a two-point operator that maps point functions into two-point functions. Considering the interaction domain ${\Omega }_{\mathrm{\rm I}}$ of $\Omega$, the corresponding point interaction operator $\mathcal{N}\left(\mathcal{G}\right)\left(\mathbf{x}\right): {\Omega }_{\mathrm{\rm I}}\to {\mathbb{R}}$ by its action on $\mathcal{G}$ can be defined as:

$${\mathcal{N}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right): = - \mathop \int \nolimits_{{{\Omega } \cup {\Omega }_{{\text {I}}} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right] \cdot \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}{\text{ for }}{\mathbf{x}} \in {\mathbb{R}}^{n}$$

(24)

where $\mathcal{N}\left(\mathcal{G}\right)\left(\mathbf{x}\right)$ is the flux density at $\mathbf{x}\in {\Omega }_{\mathrm{\rm I}}$ into ${\Omega \cup\Omega }_{\mathrm{\rm I}}$, and $\mathcal{D}\left(\mathcal{G}\right)$ is the flux density at $\mathbf{x}\in {\mathbb{R}}^{n}$ into $\Omega$.

The possible geometry relationship of nonlocal interaction is shown in Fig. 3, and it is found from Fig. 3 that the nonlocal flux does not need the common boundaries between the interaction domains.

Fig. 3

The possible relationship of the nonlocal interaction geometry

Theorem 1 (Nonlocal Gauss theorem)

Let $\Omega \subset {\mathbb{R}}^{n}$,${\Omega }_{\mathrm{\rm I}}\subseteq {\mathbb{R}}^{n}\backslash\Omega$ and $\stackrel{\sim }{\Omega }=\Omega \cup {\Omega }_{\mathrm{\rm I}}$, for any mapping $f\left(\mathbf{x},\mathbf{y}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}$, $\mathcal{D}\left(f\right)\left(\mathbf{x}\right): \stackrel{\sim }{\Omega }\to\Omega$, $\mathcal{N}\left(f\right)\left(\mathbf{x}\right): \stackrel{\sim }{\Omega }\to {\Omega }_{\mathrm{\rm I}}$, we have:

$$\mathop \int \nolimits_{{\Omega }}^{{}} {\mathcal{D}}\left( f \right)d{\mathbf{x}} = \mathop \int \nolimits_{{{\Omega }_{{\text{I}}} }}^{{}} {\mathcal{N}}\left( f \right)d{\mathbf{x}}.$$

(25)

The nonlocal Gauss theorem states that the interaction from $\Omega$ to ${\Omega }_{\mathrm{\rm I}}$ is equal to the interaction from ${\Omega }_{\mathrm{\rm I}}$ to $\Omega$. In the description of flux, the above equation implies that the flux from $\Omega$ to ${\Omega }_{\mathrm{\rm I}}$ is equal to the flux from ${\Omega }_{\mathrm{\rm I}}$ to $\Omega$, whereas by comparing with the local Gauss theorem in which the intensity integral produced in the domain is equal to the flux occurring at the boundary of the domain, the difference between local Gauss theorem and the nonlocal Gauss theorem is that the interaction from the boundary to the domain is transformed from one domain to the other domain, and these two domains have not necessarily common boundaries.

Proof.

For any mapping $f\left(\mathbf{x},\mathbf{y}\right):{\mathbb{R}}^{n}\times {\mathbb{R}}^{n}\to {\mathbb{R}}$, with the symmetry of functional displacement, we have

$$\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} f\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} f\left( {{\mathbf{y}},{\mathbf{x}}} \right)d{\mathbf{y}}d{\mathbf{x}} \forall {\tilde{\Omega }} \subset {\mathbb{R}}^{n}.$$

(26)

If $p\left(\mathbf{x},\mathbf{y}\right)$ is an antisymmetric mapping, then we have

$$p\left( {{\mathbf{x}},{\mathbf{y}}} \right) = - p\left( {{\mathbf{y}},{\mathbf{x}}} \right).$$

(27)

Combining Eqs. (26), (27) yields:

$$\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} p\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} = 0.$$

(28)

With the change of the order of integration in the above equation, the following equation can be obtained:

$$\mathop \int \nolimits_{{\Omega }}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} p\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} = - \mathop \int \nolimits_{{{\Omega }_{{\text{I}}} }}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} p\left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}}.$$

(29)

Considering a vector two-point function $\mathrm{\alpha }\left(\mathbf{x},\mathbf{y}\right):\stackrel{\sim }{\Omega }\times \stackrel{\sim }{\Omega }\to {\mathbb{R}}$, the nonlocal divergence operator maps two-point functions $f(\mathbf{x},\mathbf{y})$ into point functions defined over $\Omega$ by:

$${\mathcal{D}}\left( f \right)\left( {\mathbf{x}} \right) = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {f\left( {{\mathbf{x}},{\mathbf{y}}} \right){\upalpha }\left( {{\mathbf{x}},{\mathbf{y}}} \right) - f\left( {{\mathbf{y}},{\mathbf{x}}} \right){\upalpha }\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right]d{\mathbf{y}}{\text{ for }}{\mathbf{x}} \in {\Omega }.$$

(30)

A similar linear operator $\mathcal{N}\left(f\right)\left(\mathbf{x}\right): \stackrel{\sim }{\Omega }\to {\Omega }_{\mathrm{\rm I}}$ is defined as:

$${\mathcal{N}}\left( f \right)\left( {\mathbf{x}} \right) = - \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {f\left( {{\mathbf{x}},{\mathbf{y}}} \right){\upalpha }\left( {{\mathbf{x}},{\mathbf{y}}} \right) - f\left( {{\mathbf{y}},{\mathbf{x}}} \right){\upalpha }\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right]d{\mathbf{y}}{\text{ for }}{\mathbf{x}} \in {\Omega }_{{\text{I}}} .$$

(31)

Let $p\left(\mathbf{x},\mathbf{y}\right)=f\left(\mathbf{x},\mathbf{y}\right)\mathrm{\alpha }\left(\mathbf{x},\mathbf{y}\right)-f\left(\mathbf{y},\mathbf{x}\right)\mathrm{\alpha }\left(\mathbf{y},\mathbf{x}\right)$ and $\mathrm{\alpha }\left(\mathbf{x},\mathbf{y}\right)={\omega }_{loc}\left(\mathbf{x},\mathbf{y}\right).$ Considering the antisymmetric property of $p\left(\mathbf{x},\mathbf{y}\right)$, we have:

$$\begin{aligned} \mathop \int \nolimits_{{\Omega }}^{{}} {\mathcal{D}}\left( f \right)d{\mathbf{x}} & = \mathop \int \nolimits_{{\Omega }}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {f\left( {{\mathbf{x}},{\mathbf{y}}} \right)\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right) - f\left( {{\mathbf{y}},{\mathbf{x}}} \right)\omega_{loc} \left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right]d{\mathbf{y}}d{\mathbf{x}} \\ & = - \mathop \int \nolimits_{{{\Omega }_{{\text{ I}}} }}^{{}} \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {f\left( {{\mathbf{x}},{\mathbf{y}}} \right)\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right) - f\left( {{\mathbf{y}},{\mathbf{x}}} \right)\omega_{loc} \left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right]d{\mathbf{y}}d{\mathbf{x}} = \mathop \int \nolimits_{{{\Omega }_{{\text{ I}}} }}^{{}} {\mathcal{N}}\left( f \right)d{\mathbf{x}} .\\ \end{aligned}$$

(32)

In the nonlocal theory, the local description is considered as a special case of nonlocal description. Taking the divergence operator as an example, the relationship between the nonlocal differential operator and the traditional differential operator can be written as:

$$\mathop {\lim }\nolimits_{\varepsilon \to 0} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right) = \nabla \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{x}}} \right) \forall {\mathbf{x}} \in {\mathbb{R}}^{n} .$$

(33)

Proof.

First, by using the property of the Dirac delta function $\delta$, the integral expression of the function and its divergence can be written as:

$$f\left( x \right) = \mathop \int \nolimits_{H}^{{}} f\left( y \right)\delta \left( {{\text{x}} - y} \right)dy,$$

(34)

$$\nabla \cdot f\left( x \right) = - \mathop \int \nolimits_{H}^{{}} f\left( y \right) \cdot \nabla \delta \left( {x - y} \right)dy,$$

(35)

and let a compactly supported antisymmetric distribution ${\omega }_{loc}\left(\mathbf{x},\mathbf{y}\right)=-{\nabla }_{\mathbf{y}}\cdot {\omega }_{Gauss}\left(\mathbf{y}-\mathbf{x},\varepsilon \right)$, in which ${\omega }_{Gauss}(\mathbf{y}-\mathbf{x},\varepsilon )$ is a Gauss kernel function. We have

$$\mathop {{\text{lim}}}\nolimits_{\varepsilon \to 0} \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right) = - \nabla_{{\mathbf{y}}} \cdot \omega_{Gauss} \left( {{\mathbf{y}} - {\mathbf{x}},\varepsilon } \right).$$

(36)

From Eqs. (34)–(36), we have

$$\begin{aligned} \nabla \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{x}}} \right) & = \left. {[\nabla_{{\mathbf{x}}} \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)]} \right|_{{{\mathbf{y}} = {\mathbf{x}}}} + \left. {[\nabla_{{\mathbf{y}}} \cdot {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)]} \right|_{{{\mathbf{y}} = {\varvec{x}}}} \\ & = \left. {\left[ {\nabla_{{\mathbf{y}}} \cdot \left( {{\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right)} \right]} \right|_{{{\mathbf{y}} = {\mathbf{x}}}} = \mathop \int \nolimits_{H}^{{}} \nabla_{{\mathbf{y}}} \cdot \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right]\delta \left( {{\mathbf{y}} - {\mathbf{x}}} \right)d{\mathbf{y}} \\ & \approx \mathop {{\text{lim}}}\nolimits_{\varepsilon \to 0} \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \nabla_{{\mathbf{y}}} \cdot \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right]\omega_{Gauss} \left( {{\mathbf{y}} - {\mathbf{x}},\varepsilon } \right)d{\mathbf{y}} \\ & = - \mathop {{\text{lim}}}\nolimits_{\varepsilon \to 0} \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right]\nabla_{{\mathbf{y}}} \omega_{Gauss} \left( {{\mathbf{y}} - {\mathbf{x}},\varepsilon } \right)d{\mathbf{y}} \forall {\mathbf{x}} \in {\mathbb{R}}^{n} \\ & = \mathop {{\text{lim}}}\nolimits_{\varepsilon \to 0} \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right]\omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}} = \mathop {{\text{lim}}}\nolimits_{\varepsilon \to 0} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right). \\ \end{aligned}$$

(37)

Consider Lemma I and Lemma II from statistical mechanics in Eqs. (11) and  (12). When $\varepsilon \to 0$, the relationship between local and nonlocal Gauss’ theorem can be obtained as [27, 28]:

$$\mathop \int \nolimits_{{\Omega }}^{{}} \nabla \cdot {\mathbf{q}}d{\mathbf{x}} = \mathop \int \nolimits_{{\Omega }}^{{}} {\mathcal{D}}\left( f \right)d{\mathbf{x}},$$

(38)

$$\mathop \int \nolimits_{{\partial {\Omega }}}^{{}} {\mathbf{q}} \cdot {\mathbf{n}}_{1} d{\text{A}} = \mathop \int \nolimits_{{{\Omega }_{{\text{I}}} }}^{{}} {\mathcal{N}}\left( f \right)d{\mathbf{x}}.$$

(39)

By the above formulation, we find that the nonlocal vector operators can be considered as a bridge which connects the local theory and nonlocal theory, as shown in Fig. 4. It is worth to note that this bridge is established on the foundation of statistical mechanics by the above two lemmas.

Fig. 4

The bridge between local theory and nonlocal theory: nonlocal vector operators

2.3 Nonlocal theory and peridynamics

As described in the Introduction, the nonlocal theories were already conceived in Piola’s works starting from a clever use of the principle of virtual work. Piola assumed that there always exists an internal force $\mathbf{f}$ acting on each pair of molecules, and when the number of points is equal to n, the internal force can be represented as [1, 2]:

(40)

where $\Delta$ is intended as in the calculus of variations, and ${\mathbf{u}}_{i,j}$ is the relative displacement between the point i and the point j, and ${m}_{i}$ is the mass of point i.

Piola found that in the above formula, one after another lines have a lacking term with respect to the previous line which constitutes an upper triangular matrix-like form, and then he divided the force and rewrited it in such a way that all have exactly n terms and constitute an $n\times n$ matrix-like form:

(41)

All items in Eq. (41) are pair-wised, the pairing term $\frac{1}{2}{m}_{1}{m}_{2}{\mathbf{f}}_{\mathrm{1,2}}\Delta {\mathbf{u}}_{\mathrm{1,2}}+\frac{1}{2}{m}_{2}{m}_{1}{\mathbf{f}}_{\mathrm{2,1}}\Delta {\mathbf{u}}_{\mathrm{2,1}}$ is equivalent to ${m}_{1}{m}_{2}{\mathbf{f}}_{\mathrm{1,2}}\Delta {\mathbf{u}}_{\mathrm{1,2}}$, and so on for the other pairing terms. Each line of Eq. (41) represents the nonlocal interaction between a point and all other points. From such definition and manipulation, the nonlocal internal interaction has been incorporated in the internal force calculation.

In Piola’s work, based on a variational principle and the balance law in the body $\mathcal{B}$, the general equation of mechanics, relative to both motion and equilibrium, of a discrete system of material points can be written as [2]:

$$\mathop \int \nolimits_{{\mathcal{B}}}^{{}} \left\{ {\left[ {{\mathbf{b}}\left( {\mathbf{x}} \right) - {\varvec{a}}\left( {\mathbf{x}} \right)} \right]{\Delta }{\varvec{x}}} \right\}\rho \left( {\mathbf{x}} \right)d{\mathbf{x}} + \mathop \int \nolimits_{{\mathcal{B}}}^{{}} \left[ {\mathop \int \nolimits_{{\mathcal{B}}}^{{}} \frac{1}{2}{\mathbf{f}}\rho \left( {{\mathbf{x^{\prime}}}} \right){\Delta }{\mathbf{u}}d{\mathbf{x^{\prime}}}} \right]\rho \left( {\mathbf{x}} \right)d{\mathbf{x}} + {\Delta }W\left( {\partial {\mathcal{B}}} \right) = 0$$

(42)

where b is the (volume) mass specific externally applied density of force, ${\varvec{a}}$ is the acceleration of a material point x, $\rho$ is the volume mass density, the second integrals express the sum of all terms introduced by the internal active forces, and $\Delta W\left(\partial \mathcal{B}\right)$ denotes the work expended on the virtual displacement by action on the boundary $\partial \mathcal{B}$.

The nonlocal balance law is presented in Eq. (42) in Piola’s work. And the element of attenuating neighborhood hypotheses, action and reaction principle and internal interaction in nonlocal theories all have been conceived in it [1,2,3,4]. However, Piola derived these properties in a classical Newton’s mechanics view and the variational principles. In more recent studies, the nonlocal property is often considered by the long-range force, nonlocal vector operators, and microscopic models in these nonlocal theories rather than the variational principles. For example, the nonlocal theory, peridynamics, collects the microscopic (long-range) forces with a special micro-constitutive relationship to get a macroscopic force by double quadratic integrals.

Considering the isotropic case, the long-range effect between material points is only related to the distance between the other material points, which can be written as [5, 6]:

$$\hat{f}\left( {\mathbf{x}} \right) = \mathop \int \nolimits_{v}^{{}} \omega \left( {\left| {{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right|,h} \right)f\left( {\mathbf{x}} \right)dV_{{{\mathbf{x^{\prime}}}}} ,$$

(43)

where $\widehat{f}\left(\mathbf{x}\right)$ and $f\left(\mathbf{x}\right)$ are, respectively, the estimated field variable and local field variable, $\omega (\left|{\mathbf{x}}^{^{\prime}}-\mathbf{x}\right|,h)$ is the nonlocal kernel function, h is the characteristic length or influence radius which is used to consider the scale effect, and V is the volume.

Peridynamics is a novel nonlocal theory, which was proposed in 2000 [7], and it also considers the long-range force. In a bond-based peridynamic frame, the peridynamic motion equation of a material point obeys

$$\rho \;{\mathbf{\ddot{u}}}\left( {{\mathbf{x}},t} \right) = \mathop \int \nolimits_{H} {\mathbf{f}}\left( {{\mathbf{u}}\left( {{\mathbf{x^{\prime}}},t} \right),{\mathbf{u}}\left( {{\mathbf{x}},t} \right),{\mathbf{x^{\prime}}} - {\mathbf{x}}} \right)dV_{{{\mathbf{x^{\prime}}}}} + {\mathbf{b}}\left( {{\mathbf{x}},t} \right),$$

(44)

$$H = \left\{ {{\mathbf{x}}^{\prime} = {\mathbf{x}} + {\varvec{\xi}},0 < \left| {\varvec{\xi}} \right| \le h} \right\},$$

(45)

where $\rho$ is density, u is the displacement, $\mathbf{x}$ is the material point coordinate, t is time, f is called pairwise force function in peridynamics, H is the interaction set or influence domain of the material point $\mathbf{x}$ in the reference configuration, b is the external body force density, ${\varvec{\xi}}$ is the bond vector, and $h$ is Horizon (influence radius of a material point) in peridynamics.

In a state-based peridynamic frame, the motion equation of a material point obeys

$$\rho_{i} {\mathbf{\ddot{u}}}\left( {{\mathbf{x}},t} \right) = \mathop \int \nolimits_{H} {\mathbf{\underline {T} }}\left( {{\mathbf{x}},t} \right){\varvec{\xi}} - {\mathbf{\underline {T} }}\left( {{\mathbf{x}}^{\prime},t} \right){\varvec{\xi}}^{\prime}dV_{{{\mathbf{x^{\prime}}}}} + {\mathbf{b}}\left( {{\mathbf{x}},t} \right),$$

(46)

where ${\mathbf{T}}$ is the force state. State in peridynamics is a tensor mathematically, for example, the image of a vector ${\varvec{\xi}}\in H$ under the state A is a tensor of order m, which is written as ${\mathbf{A}}\langle {\varvec{\xi}}\rangle$. The shape tensor in peridynamics is defined as:

$${\mathbf{K}} = {\mathbf{\underline {X} }}*{\mathbf{\underline {X} }} = \mathop \int \nolimits_{H} \underline {\omega } \user2{\langle {\varvec{\xi}}\rangle \xi } \otimes {\varvec{\xi}}dV_{\xi }$$

(47)

where $*$ defines the tensor product operator of two states, ${\omega }$ is called the influence function state in peridynamics, and ${\mathbf{X}}$ is the reference position (undeformed) state.

The deformation gradient tensor $\mathbf{F}$ may be approximated as a tensor reduction in the deformation vector state ${\mathbf{Y}}$ and reference position vector state ${\mathbf{X}}$ in [40] with different reference coordinate:

$${\mathbf{F}} = \frac{{d{\varvec{x}}}}{{d{\mathbf{x}}}} = \frac{{d{\mathbf{u}}}}{{d{\mathbf{x}}}} + {\mathbf{I}},$$

(48)

$${\mathbf{F}} \approx \left( {{\mathbf{\underline {Y} }}*{\mathbf{\underline {X} }}} \right){\mathbf{K}}^{ - 1} = \left( {\mathop \int \nolimits_{H} \underline {\omega } {\langle {\varvec{\xi}}\rangle}{\mathbf{\underline {Y} }}{\langle {\varvec{\xi}}\rangle} \otimes {\varvec{\xi}}dV_{\xi } } \right){\mathbf{K}}^{ - 1} = \left( {\mathop \int \nolimits_{H} \underline {\omega } \user2{\langle {\varvec{\xi}}\rangle\underline {x} \langle {\varvec{\xi}}\rangle } \otimes {\varvec{\xi}}dV_{\xi } } \right){\mathbf{K}}^{ - 1},$$

(49)

$${\mathbf{F}} \approx \left( {{\mathbf{\underline {Y} }}*{\mathbf{\underline {X} }}} \right){\mathbf{K}}^{ - 1} = \left( {\mathop \int \nolimits_{H} \underline {\omega } {\langle {\varvec{\xi}}\rangle}{\mathbf{\underline {u} }}{\langle {\varvec{\xi}}\rangle} \otimes {\varvec{\xi}}dV_{\xi } } \right){\mathbf{K}}^{ - 1} + {\mathbf{I}}$$

(50)

where ${\varvec{x}}$ is the spatial coordinate, and $\mathbf{I}$ is the unit matrix.

The relation between peridynamic state and the classical local stress tensor can be directly obtained by mapping the stress tensor into the bond vector via a shape tensor, which is written as:

$${\mathbf{\underline {T} }}\left( {{\mathbf{x}},t} \right){\varvec{\xi}} = \underline {\omega } \langle {\varvec{\xi}}\rangle {\mathbf{S}}_{{\mathbf{x}}} {\mathbf{K}}_{{\mathbf{x}}}^{ - 1} {\varvec{\xi}},$$

(51)

where S is the nominal stress tensor (the first Piola–Kirchhoff stress tensor).

The peridynamic force in a material point can be obtained by Eqs. (51) and (47) as follows:

$$\begin{aligned} {\mathbf{f}}\left( {{\mathbf{x}},{\varvec{\xi}},t} \right) & = \mathop \sum \nolimits_{j \in H} V_{i} V_{j} \left[ {{\mathbf{\underline {T} }}\left( {{\mathbf{x}},t} \right){\varvec{\xi}} - {\mathbf{\underline {T} }}\left( {{\mathbf{x^{\prime}}},t} \right)\user2{\xi^{\prime}}} \right] \\ & = \mathop \sum \nolimits_{j \in H} V_{i} V_{j} \left[ {\underline {\omega } \langle {\varvec{\xi}}\rangle {\mathbf{S}}_{i} {\mathbf{K}}_{i}^{ - 1} {\varvec{\xi}}_{ij} - \underline {\omega } \langle {\varvec{\xi}}\rangle {\mathbf{S}}_{j} {\mathbf{K}}_{j}^{ - 1} {\varvec{\xi}}_{ji} } \right]. \\ \end{aligned}$$

(52)

3 Statistical mechanics and nonlocal mechanical theory

3.1 Statistical mechanics and peridynamics

Silling [7, 40] formulated a nonlocal mechanics model, which is called peridynamics, by amounts of definitions of physical solids and operators. Actually, the peridynamic motion equation can be derived as expectation of momentum density in the phase space by using the well-known Liouville’s equation.

The expectation of momentum density $\mathbf{P}=\uprho \mathbf{v}$ can be solved by substituting the momentum density into Liouville’s equation as follows:

$$\frac{{\partial {\mathbf{P}}^{\alpha } }}{\partial t} + \frac{{\partial {\mathbf{v}}^{\beta } }}{{\partial {\mathbf{x}}^{\beta } }}{\mathbf{P}}^{\alpha } = \frac{{\partial {{\varvec{\upsigma}}}_{k}^{\alpha \beta } }}{{\partial {\mathbf{x}}^{\beta } }} + {\text{E}}\left[ {\mathop \sum \nolimits_{i,j} \left( {{\mathbf{x}}_{j}^{\alpha } - {\mathbf{x}}_{i}^{\alpha } } \right){\mathbf{f}}_{ij} \omega_{i} } \right]$$

(53)

where,$\mathrm{E}\left[f(x)\right]$ is the expectation of$f(x)$, $\omega$ is the Hardy localization function [24] or kernel function,${\omega }_{i}:=\omega ({\mathbf{x}}_{i}-\mathbf{x})$, and ${{\varvec{\upsigma}}}_{k}$ is the kinetic stress tensor which is defined by:

$${{\varvec{\upsigma}}}_{k}^{\alpha \beta } = - {\text{E}}\left[ {\mathop \sum \nolimits_{i} m_{i} \left( {{\mathbf{v}}_{j}^{\alpha } - {\mathbf{v}}^{\alpha } } \right)\left( {{\mathbf{v}}_{j}^{\beta } - {\mathbf{v}}^{\beta } } \right)\omega_{i} } \right].$$

(54)

The kinetic stress tensor ${{\varvec{\upsigma}}}_{k}$ represents stress due to the momentum of the particles relative to the material velocity and corresponds, for example, to pressure in an ideal gas [24]. Utilizing the anti-symmetry of $\left({\mathbf{x}}_{j}^{\alpha }-{\mathbf{x}}_{i}^{\alpha }\right){\mathbf{f}}_{ij}$ and the regularization property of $\omega$, we have the following expression:

$$\begin{aligned} \frac{{d{\mathbf{P}}}}{dt} & = \frac{{\partial {\mathbf{P}}^{\alpha } }}{\partial t} + \frac{{\partial {\mathbf{v}}^{\beta } }}{{\partial {\mathbf{x}}^{\beta } }}{\mathbf{P}}^{\alpha } = \frac{{\partial {{\varvec{\upsigma}}}_{k}^{\alpha \beta } }}{{\partial {\mathbf{x}}^{\beta } }} + E\left[ {\mathop \sum \nolimits_{i,j} \left( {{\mathbf{x}}_{j}^{\alpha } - {\mathbf{x}}_{i}^{\alpha } } \right){\mathbf{f}}_{ij} \omega_{i} } \right] \\ & = \frac{{\partial {{\varvec{\upsigma}}}_{k}^{\alpha \beta } }}{{\partial {\mathbf{x}}^{\beta } }} + \mathop \int \nolimits_{{{\mathbb{R}}^{3} }}^{{}} E\left[ {\mathop \sum \nolimits_{i,j} \left( {{\mathbf{x}}_{j}^{\alpha } - {\mathbf{x}}_{i}^{\alpha } } \right){\mathbf{f}}_{ij} \omega_{i} \omega_{j}^{^{\prime}} } \right]d{\mathbf{x^{\prime}}} \\ & = \frac{{\partial {{\varvec{\upsigma}}}_{k}^{\alpha \beta } }}{{\partial {\mathbf{x}}^{\beta } }} + \frac{1}{2}\mathop \int \nolimits_{{{\mathbb{R}}^{3} }}^{{}} E\left[ {\mathop \sum \nolimits_{i,j} \left( {{\mathbf{x}}_{j}^{\alpha } - {\mathbf{x}}_{i}^{\alpha } } \right){\mathbf{f}}_{ij} \left( {\omega_{i} \omega_{j}^{^{\prime}} - \omega_{i}^{^{\prime}} \omega_{j} } \right)} \right]d{\mathbf{x^{\prime}}} \\ & = \frac{{\partial {{\varvec{\upsigma}}}_{k}^{\alpha \beta } }}{{\partial {\mathbf{x}}^{\beta } }} + \mathop \int \nolimits_{{{\mathbb{R}}^{3} }}^{{}} \left[ {{\mathbf{\underline {T} }}\left( {{\mathbf{x}},t} \right){\varvec{\xi}} - {\mathbf{\underline {T} }}\left( {{\mathbf{x^{\prime}}},t} \right)\user2{\xi^{\prime}}} \right]d{\mathbf{x^{\prime}}}. \\ \end{aligned}$$

(55)

In an Eulerian view of the PD momentum equation, the material derivative on the left side of Eq. (46) is expanded, and yields Eq. (53). The above formulation and expression are natural, strict and concise, they formulate the same form of peridynamic motion equation, which proves that the nonlocal theory has a root from statistical mechanics. Although the ordinary theoretical basis of nonlocal theory can be expressed without statistical mechanics, the application of the specific problem is always indispensable to it, such as the choice of the localization function or kernel and the influence radius. Moreover, the nonlocal interaction is intrinsic in the statistical mechanical formulation.

3.2 Mathematical statistics and SPH

SPH is initially used in astrophysics and fluid hydrodynamics mechanics which is based on a kernel approximation method [41, 42]. If there exists a series of material points of the same mass, the probability of finding a material point in a given unit of volume is considered as the probability density function (PDF). According to mathematical statistics, the kernel approximation of the field function in SPH can be obtained by solving the following expectation [41, 42]:

$$f_{s} \left( x \right) \approx E\left[ {f\left( {x^{\prime}} \right)} \right] \approx \int p\left( {x - x^{\prime},h} \right)f\left( {x^{\prime}} \right)dr^{\prime},$$

(56)

where $E\left[f\left({x}^{^{\prime}}\right)\right]$ is the expectation of $f\left({x}^{^{\prime}}\right)$, h is the influence radius of x, p(x) is the PDF function or a kernel of x, if p(x) is a function which mimics the Dirac delta function property, and then ${f}_{s}\left(x\right)=f(x)$.

Equation (56) is the initial SPH kernel approximation, and it becomes a fluid mechanics theory after the application in hydromechanics. When p(x) in Eq. (56) is unknown, the kernel can be estimated via the sample distribution function as follows [43]:

$$\mathop f\nolimits^{ \wedge }_{n} \left( x \right) {=} \frac{{\mathop \sum \nolimits_{i = 1}^{n} 1_{{ t - h \le x_{i} \le t + h}} }}{n \cdot 2h} {=} \frac{{\mathop \sum \nolimits_{i = 1}^{n} 0.5_{{ t - h \le x_{i} \le t + h}} }}{nh} = \mathop \int \nolimits_{ - \infty }^{ + \infty } \frac{1}{h}K\left( {\frac{x - y}{h}} \right)dF_{n} \left( y \right) {\approx} \frac{1}{nh}\mathop \sum \nolimits_{j = 1}^{n} K\left( {\frac{{x {-} x_{j} }}{h}} \right),$$

(57)

$$K\left( y \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{2}, \left| y \right| \le 1,} \\ {0, \left| y \right| \le 1.} \\ \end{array} } \right.$$

(58)

The kernel approximation method of a derivative with an appropriate kernel ${\omega }_{sph}$ can be written as:

$$\begin{aligned} E\left[ {\nabla \cdot f\left( {x_{i} } \right)} \right] & = \mathop \int \nolimits_{H}^{{}} \left[ {\nabla \cdot f\left( {x_{j} } \right)} \right]\omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \\ & = \mathop \int \nolimits_{H}^{{}} \nabla \cdot \left[ {f\left( {x_{j} } \right)\omega_{sph} \left( {x_{ij} ,h} \right)} \right]dx_{j} - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \\ & = \mathop \int \nolimits_{\partial H}^{{}} \left[ {f\left( {x_{j} } \right)\omega_{sph} \left( {x_{ij} ,h} \right)} \right] \cdot {\mathbf{n}}dx_{j} - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \\ & = 0 - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} = - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j}. \\ \end{aligned}$$

(59)

To compare with the nonlocal vector calculus in Sect. 2.2, we make some manipulations on the kernel approximation of divergence as follows:

$$\begin{aligned} E\left[ {\nabla \cdot f\left( {x_{i} } \right)} \right] & = E\left[ {\nabla \cdot f\left( {x_{i} } \right)} \right] \mp \nabla 1 \\ & = - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \mp \int 1 \cdot \nabla \omega_{sph\;ij} dx_{j} \\ & = - \mathop \int \nolimits_{H}^{{}} f\left( {x_{j} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \mp \mathop \int \nolimits_{H}^{{}} f\left( {x_{i} } \right)\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} \\ & = - \mathop \int \nolimits_{H}^{{}} \left[ {f\left( {x_{j} } \right) \pm f\left( {x_{i} } \right)} \right]\nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)dx_{j} .\\ \end{aligned}$$

(60)

By the above manipulations on the SPH kernel, we find that Eq. (60) has an identical form with the nonlocal divergence operator in Eq. (22) when suitable SPH kernel functions are chosen, such as $-\nabla \cdot {\omega }_{sph}={\omega }_{loc}$. However, no implication arises from this requirement as suitable kernel functions can be chosen which fulfill this requirement. This conditional equivalence of SPH differential approximation and nonlocal differential operators implies that the SPH kernel approximation can be considered as a nonlocal operator, which presents an integral form and delivers local information to nonlocal information the same as the nonlocal vector calculus.

3.3 SPH and PD

By introducing the corrected matrix L in the SPH kernel approximation theory, the corrected kernel approximation of SPH can be written as [44]:

$${\text{E}}\left[ {f\left( {{\varvec{x}}_{i} } \right)} \right] = \mathop \int \nolimits_{H}^{{}} {\mathbf{L}}_{i}^{ - 1} \omega_{sph} \left( {x_{ij} ,h} \right)f\left( {{\varvec{x}}_{j} } \right)d{\varvec{x}}_{j},$$

(61)

$$E\left[ {\nabla \cdot f\left( {{\varvec{x}}_{i} } \right)} \right] = \mathop \int \nolimits_{H}^{{}} {\mathbf{L}}_{i}^{ - 1} \nabla \cdot \omega_{sph} \left( {x_{ij} ,h} \right)f\left( {{\varvec{x}}_{j} } \right)d{\varvec{x}}_{j}$$

(62)

where ${\mathbf{L}}_{i}=\int_{H}\nabla {\omega }_{sph}\left({x}_{ij},h\right)\otimes \left({{\varvec{x}}}_{j}-{{\varvec{x}}}_{i}\right)d{{\varvec{x}}}_{j}$ is the corrected matrix, ${x}_{ij}=\Vert {{\varvec{x}}}_{j}-{{\varvec{x}}}_{i}\Vert$.

The deformation gradient in the corrected SPH differential approximation method can be obtained as follows [33]:

$${\varvec{F}}_{i}^{SPH} = \frac{{d{\varvec{x}}}}{{d{\mathbf{x}}}} = \frac{{d{\varvec{u}}}}{{d{\mathbf{x}}}} + {\mathbf{I}} = \mathop \int \nolimits_{H}^{{}} \left( {{\mathbf{u}}_{j} - {\mathbf{u}}_{i} } \right) \otimes {\mathbf{L}}_{{\varvec{i}}}^{ - 1} \nabla \omega_{sph} \left( {x_{ij} ,h} \right)d{\varvec{x}}_{j} + {\mathbf{I}}.$$

(63)

The peridynamic expression of the deformation gradient can be written as:

$$\begin{aligned} {\varvec{F}}_{i}^{PD} & = \left( {\mathop \int \nolimits_{H} \underline {\omega } {\varvec{\xi}}{\mathbf{\underline {u} }}{\varvec{\xi}} \otimes {\varvec{\xi}}dV_{{\varvec{\xi}}} } \right){\mathbf{K}}^{ - 1} + {\mathbf{I}} = \left[ {\mathop \int \nolimits_{H} \frac{1}{{{\varvec{x}}_{ij} }}\nabla \omega_{sph} \left( {x_{ij} ,h} \right){\mathbf{\underline {u} }}{\varvec{\xi}} \otimes {\varvec{\xi}}d{\varvec{x}}_{j} } \right]{\mathbf{L}}_{{\varvec{i}}}^{ - 1} + {\mathbf{I}} \\ & = \mathop \int \nolimits_{H} {\mathbf{\underline {u} }}{\varvec{\xi}} \otimes \left( {\frac{{{\mathbf{L}}_{{\varvec{i}}}^{ - 1} }}{{{\varvec{x}}_{ij} }}\nabla \omega_{sph} \cdot {\varvec{\xi}}} \right)d{\varvec{x}}_{j} + {\mathbf{I}} \\ & = \mathop \int \nolimits_{H}^{{}} \left( {{\mathbf{u}}_{j} - {\mathbf{u}}_{i} } \right) \otimes {\mathbf{L}}_{{\varvec{i}}}^{ - 1} \nabla \omega_{sph} \left( {x_{ij} ,h} \right)d{\varvec{x}}_{j} + {\mathbf{I}} = {\varvec{F}}_{i}^{SPH} \user2{ }. \\ \end{aligned}$$

(64)

The first line of Eq. (64) considers the equality of the shape tensor K in PD and the correction matrix $\mathbf{L}$ in SPH which has been proved in the literature [44]. This equality is effective in an assumption that $\nabla {\omega }_{sph}/{x}_{ij}={\omega }$. Thus, the peridynamic deformation gradient is equal to the SPH deformation gradient approximation. Therefore, a simultaneous corollary is that the particle force is equivalent as:

$${\mathbf{f}}_{i}^{PD} = {\mathbf{f}}_{i}^{SPH} = \mathop \sum \nolimits_{j = 1}^{N} V_{j} V_{j} \left[ {{\mathbf{S}}_{i} {\mathbf{L}}_{i}^{ - 1} \nabla \omega_{i} \left( {x_{ij} ,h} \right) - {\mathbf{S}}_{j} {\mathbf{L}}_{j}^{ - 1} \nabla \omega_{j} \left( {x_{ji} ,h} \right)} \right]$$

(65)

where the above stress tensor S is the nominal stress tensor which applies here as the stress is expressed in the reference configuration.

Ganzenmüller et al. [44] derived the above process, and Zhou et al. [34,35,36] also discussed these results systematically. However, they did not give a reasonable cause of this equality. Combining the discussion and formulation in the above Section, the authors give two main reasons:

• (i) From the formulation in Sects. 3.1 and 3.2, we find that both SPH and PD can be derived by statistical physics. SPH uses a mathematical statistics formulation to derive the kernel approximation for the field function. PD can also be derived by Liouville’s equation of statistical mechanics, implying that both theories have the same mathematical or physical subject root.

• (ii) Another reason is the invariant form of the physical mechanics in the different model frames. Both the above methods can be regarded as mapping from a local model to a nonlocal model, as discussed in Sects. 2.3 and 3.2. When the same local model is mapped into a nonlocal model with two different methods, it naturally has a similar result.

Therefore, considering the same root and the same mapping function of the two theories, it is a normal result that the discretization of the two theories takes an identical form. The diagram for the relationships among these theories are shown in Fig. 5.

Fig. 5

A diagram for the statistical mechanics and the nonlocal mechanical theories

4 Application: general particle dynamics

Based on the discussion in Sects. 2 and 3, a novel nonlocal mechanical theory, general particle dynamics (GPD), is proposed in this Section. Assume that the rate of the amount of the intensive quantity q in any subdomain $\stackrel{\sim }{\Omega }\subset\Omega$ is denoted by $\mathcal{A}\left(\stackrel{\sim }{\Omega };q\right)$, the rate at which the intensive quantity is produced in the subdomain by sources is denoted by $\mathcal{P}\left(\stackrel{\sim }{\Omega }\right)$, the rate at which the intensive quantity exits the subdomain is denoted by $\mathcal{F}\left(\stackrel{\sim }{\Omega },{\mathbb{R}}^{n}\backslash \stackrel{\sim }{\Omega };q\right)$, and $\Omega \subset {\mathbb{R}}^{n}$ is considered as the solving domain, the balance law can be written as:

$${\mathcal{A}}\left( {{\tilde{\Omega }};q} \right) = {\mathcal{P}}\left( {{\tilde{\Omega }}} \right) - {\mathcal{F}}\left( {{\tilde{\Omega }},{\mathbb{R}}^{n} \backslash {\tilde{\Omega }};q} \right) \forall {\tilde{\Omega }} \subset {\Omega }.$$

(66)

A more usual balance laws considering the influence of the finite set ${\Omega }_{\mathrm{\rm I}}\subseteq {\mathbb{R}}^{n}\backslash \stackrel{\sim }{\Omega }$ can be written as:

$${\mathcal{A}}\left( {{\tilde{\Omega }};q} \right) = {\mathcal{P}}\left( {{\tilde{\Omega }}} \right) - {\mathcal{F}}\left( {{\tilde{\Omega }},{\Omega }_{{\text{I}}} ;q} \right) \forall {\tilde{\Omega }} \subset {\Omega }.$$

(67)

According to the classical definition of the rate, $\mathcal{A}$ and $\mathcal{P}$ can be defined as

$${\mathcal{A}}\left( {{\tilde{\Omega }};q} \right) = \frac{d}{dt}\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} q\left( {{\mathbf{x}},t} \right)d{\mathbf{x}},$$

(68)

$${\mathcal{P}}\left( {{\tilde{\Omega }}} \right) = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathbf{b}}\left( {{\mathbf{x}},t} \right)d{\mathbf{x}}$$

(69)

where b is the external force density.

$\mathcal{F}\left(\stackrel{\sim }{\Omega },{\Omega }_{\mathrm{\rm I}};q\right)$ can be considered as the flux operator on q. Let $\mathcal{G}\left(\mathbf{x},\mathbf{y}\right)$ be the corresponding nonlocal two-point function of intensive quantity q(x). Vector $\mathbf{q}$ is the corresponding local flux vector of quantity q(x). Combining Eqs. (22) and (24), the local and nonlocal cases of $\mathcal{F}$ in two given regions ${\Omega }_{1},{\Omega }_{2}\subset {\mathbb{R}}^{n}$ can be written as:

$${\mathcal{F}}_{loc} \left( {{\Omega }_{1} ,{\Omega }_{2} ;q} \right) = \mathop \int \nolimits_{{\partial {\Omega }_{12} }}^{{}} {\mathbf{q}} \cdot {\mathbf{n}}_{1} d{\text{A}} = \mathop \int \nolimits_{{\Omega }}^{{}} \nabla \cdot {\mathbf{q}}d{\text{V}},$$

(70)

$$\begin{aligned} {\mathcal{F}}_{nonloc} \left( {{\Omega }_{1} ,{\Omega }_{2} ;q} \right) & = \mathop \int \nolimits_{{{\Omega }_{1} }}^{{}} \mathop \int \nolimits_{{{\Omega }_{2} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right] \cdot \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}} \\ & = \mathop \int \nolimits_{{{\Omega }_{1} }}^{{}} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right)d{\mathbf{x}} = - \mathop \int \nolimits_{{{\Omega }_{2} }}^{{}} \mathop \int \nolimits_{{{\Omega }_{1} \cup {\Omega }_{2} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right] \cdot \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}}d{\mathbf{x}}. \end{aligned}$$

(71)

The local flux operator is only valid in ${\Omega }_{1}\cap {\Omega }_{2}=\varnothing\, {\text{and}}\, \partial {\Omega }_{12}=\varnothing$, and the nonlocal flux operator is valid in the arbitrary regions ${\Omega }_{1},{\Omega }_{2}\subset {\mathbb{R}}^{n}$. Using the above flux expression, the general local and nonlocal balance laws can be written as:

$$\frac{d}{dt}\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} q\left( {{\mathbf{x}},t} \right)d{\mathbf{x}} = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathbf{b}}\left( {{\mathbf{x}},t} \right)d{\mathbf{x}} - \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \nabla \cdot {\mathbf{q}}d{\mathbf{x}},$$

(72)

$$\frac{d}{dt}\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} q\left( {{\mathbf{x}},t} \right)d{\mathbf{x}} = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathbf{b}}\left( {{\mathbf{x}},t} \right)d{\mathbf{x}} + \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right)d{\mathbf{x}}.$$

(73)

4.1 Continuity equation

Based on the general balance law given in Eq. (73), consider the rate of the amount of density $\uprho (\mathbf{x},\mathrm{t})$. Let the quantity $q\left(\mathbf{x},t\right)=\uprho (\mathbf{x},\mathrm{t})$, and $\mathcal{G}\left(\mathbf{x},\mathbf{y}\right)$ be the corresponding nonlocal two-point function of density $\uprho (\mathbf{x},\mathrm{t})$, then the nonlocal continuity equation can be written as:

$$\frac{{d{\uprho }\left( {{\mathbf{x}},t} \right)}}{dt} = {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right).$$

(74)

The traditional continuity equation can be written as:

$$\frac{d\rho }{{dt}} = - \rho \nabla \cdot {\mathbf{v}}$$

(75)

where $\mathbf{v}$ is the velocity vector.

It is apparent that the right side of Eq. (75) is the local flux of the velocity along the subdomain, and the local flux of the velocity is equal to the divergence of velocity. Therefore, the divergence of velocity can be understood as the rate of change of the relative volume, and a nonlocal velocity divergence (the nonlocal flux) is defined as $\mathcal{G}\left(\mathbf{x},\mathbf{y}\right)=\frac{\rho \left(\mathbf{x},t\right)}{2}[\mathbf{v}\left(\mathbf{x}\right)+\mathbf{v}\left(\mathbf{y}\right)]$. We have

$${\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right) = \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \left[ {{\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) + {\mathbf{\mathcal{G}}}\left( {{\mathbf{y}},{\mathbf{x}}} \right)} \right] \cdot \omega_{loc} \left( {{\mathbf{x}},{\mathbf{y}}} \right)d{\mathbf{y}} = \rho \mathop \int \nolimits_{{{\mathbb{R}}^{n} }}^{{}} \omega \left( {{\mathbf{x}},{\mathbf{y}}} \right) \cdot \left[ {{\mathbf{v}}\left( {\mathbf{x}} \right) + {\mathbf{v}}\left( {\mathbf{y}} \right)} \right]d{\mathbf{x}}.$$

(76)

A kernel function $\omega (\mathbf{y}-\mathbf{x},h)$, with a finite influence radius h, is used to replace the localized kernel $\omega \left(\mathbf{x},\mathbf{y}\right)$ in Eq. (76), then we have:

$${\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\text{x}} \right) = \rho \mathop \int \nolimits_{H}^{{}} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right) \cdot \left[ {{\mathbf{v}}\left( {\mathbf{x}} \right) + {\mathbf{v}}\left( {\mathbf{y}} \right)} \right]d{\mathbf{x}}.$$

(77)

Then, combining Eqs. (74) and (77), the continuity equation yields:

$$\frac{d\rho }{{dt}} = \rho \mathop \int \nolimits_{H}^{{}} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right) \cdot \left[ {{\mathbf{v}}\left( {\mathbf{x}} \right) + {\mathbf{v}}\left( {\mathbf{y}} \right)} \right]d{\mathbf{x}}.$$

(78)

The continuity equation can also be derived by a kernel approximation method as follows:

$$\begin{aligned} \frac{{d\rho_{i} }}{dt} & = - \rho \nabla \cdot {\mathbf{v}} = - \rho_{i} \mathop \int \nolimits_{H}^{{}} {\mathbf{v}}\left( {{\mathbf{x}}_{j} } \right) \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} - \nabla \cdot 1 \\ & = - \rho_{i} \mathop \int \nolimits_{H}^{{}} {\mathbf{v}}\left( {{\mathbf{x}}_{j} } \right) \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} - \mathop \int \nolimits_{H}^{{}} 1 \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} \\ & = - \rho_{i} \mathop \int \nolimits_{H}^{{}} {\mathbf{v}}\left( {{\mathbf{x}}_{j} } \right) \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} - \mathop \int \nolimits_{H}^{{}} 1 \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} \\ & = - \rho_{i} \mathop \int \nolimits_{H}^{{}} \left[ {{\mathbf{v}}\left( {{\mathbf{x}}_{j} } \right) + {\mathbf{v}}\left( {{\mathbf{x}}_{i} } \right)} \right] \cdot \nabla \omega_{sph} \left( {{\mathbf{x}}_{ij} ,h} \right)d{\mathbf{x}}_{j} \\ & = \rho \mathop \int \nolimits_{H}^{{}} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right)\left[ {{\mathbf{v}}\left( {\mathbf{x}} \right) + {\mathbf{v}}\left( {\mathbf{y}} \right)} \right]d{\mathbf{x}}. \\ \end{aligned}$$

(79)

4.2 Motion equation

Under Cauchy’s postulate, the intensive variable q is the vector momentum density, and $\mathbf{q}$ is the stress tensor with $\mathbf{q}\cdot \mathbf{n}$ being the stress force density at a point of a surface in the local case. Based on the nonlocal balance law given in Eq. (73), consider the rate of the amount of momentum density and let the quantity be $q\left(\mathbf{x},t\right)=\rho \mathbf{v}(\mathbf{x},\mathrm{t})$. The momentum conservation law can be obtained as:

$$\frac{d}{dt}\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \rho {\mathbf{v}}\left( {{\mathbf{x}},{\text{t}}} \right)d{\mathbf{x}} = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathbf{b}}\left( {{\mathbf{x}},t} \right)d{\mathbf{x}} + \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right)d{\mathbf{x}}.$$

(80)

As described in Sect. 2.2, the vector $\mathcal{G}(\mathbf{x},\mathbf{y})$ is a vector two-point function which is related to an intensive quantity by a material constitutive relation. Following a peridynamic bond constitutive model [7, 28], we have:

$${\mathbf{\mathcal{G}}}\left( {{\mathbf{x}},{\mathbf{y}}} \right) = \frac{1}{2}\left[ {{\mathcal{D}}^{*} \left( {\mathbf{u}} \right)} \right]^{T}.$$

(81)

Substituting Eqs. (22) and (23) into Eq. (81) yields:

$$\begin{aligned} {\mathcal{D}}\left( {\mathbf{\mathcal{G}}} \right)\left( {\mathbf{x}} \right) & = \frac{1}{2}{\mathcal{D}}\left\{ {\left[ {{\mathcal{D}}^{*} \left( {\mathbf{u}} \right)} \right]^{T} } \right\}\left( {\mathbf{x}} \right) = - \frac{1}{2}\mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {\left( {{\mathbf{\mathcal{G}^{\prime}}} - {\mathbf{\mathcal{G}}}} \right) \otimes \omega + \left( {{\mathbf{\mathcal{G}}} - {\mathbf{\mathcal{G}^{\prime}}}} \right) \otimes \omega^{\prime}} \right] \cdot \omega d{\mathbf{x}} \\ & = \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {\omega \left( {{\mathbf{x}},{\mathbf{y}}} \right) \otimes \omega \left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right] \cdot \left( {{\mathbf{u}}^{\prime} - {\mathbf{u}}} \right)d{\mathbf{x}} .\\ \end{aligned}$$

(82)

Substituting Eq. (82) into Eq. (80), we have:

$$\rho \frac{{d{\mathbf{v}}\left( {{\mathbf{x}},{\text{t}}} \right)}}{dt} = {\mathbf{b}}\left( {{\mathbf{x}},t} \right) + \mathop \int \nolimits_{{{\tilde{\Omega }}}}^{{}} \left[ {\omega \left( {{\mathbf{x}},{\mathbf{y}}} \right) \otimes \omega \left( {{\mathbf{x}},{\mathbf{y}}} \right)} \right] \cdot \left( {{\mathbf{u}}^{\prime} - {\mathbf{u}}} \right)d{\mathbf{x}}.$$

(83)

Equation (83) is a generalization of the linearized bond-based peridynamic theory[7, 28], which maps the displacement u into the bond by the nonlocal integral operator. Refer to the previous research [34], and a kernel function, $\omega (\mathbf{y}-\mathbf{x},h)$ with a characteristic length h, is used to replace the localized kernel $\omega (\mathbf{x},\mathbf{y})$ in Eq. (83). Another form can be written as:

$$\rho \frac{{d{\mathbf{v}}}}{dt} = {\mathbf{b}}\left( {{\mathbf{x}},t} \right) + \mathop \int \nolimits_{H} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right) \cdot {\mathbf{f}}d{\mathbf{x}}$$

(84)

where $\mathbf{f}$ is the nonlocal long-range force determined by the constitutive relationship.

Therefore, considering a finite nonlocal influence radius H, the governing equation of GPD can be written as:

$$\left\{ {\begin{array}{*{20}l} {\frac{d\rho }{{dt}} = - \rho \mathop \int \nolimits_{H}^{{}} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right) \cdot \left[ {{\mathbf{v}}\left( {\mathbf{y}} \right) + {\mathbf{v}}\left( {\mathbf{x}} \right)} \right]d{\mathbf{x}}} \hfill \\ {\rho \frac{{d{\mathbf{v}}}}{dt} = b\left( {{\mathbf{x}},t} \right) + \mathop \int \nolimits_{H} \omega \left( {{\mathbf{y}} - {\mathbf{x}},h} \right) \cdot {\mathbf{f}}d{\mathbf{x}}} .\hfill \\ \end{array} } \right.$$

(85)

4.3 Convergence of the nonlocal limit

As discussed in Sect. 2, the nonlocal limit converges to the local theory when the nonlocal characteristic length tends to zero. In this Section, an elastic plate stress problem is employed to verify the proposed method. The nonlocal long-range force f is determined by a micro-elastic constitutive relationship in literature [34]. The nonlocal convergence of the proposed theory is validated by comparing with the local finite element method (FEM) solutions.

A two-dimensional isotropic plate with a central circular hole is subjected to a tensile load along its upper edges, and the other end is fully clamped. The geometry of the model is shown in Fig. 6, in which $\mathrm{a}=0.05\mathrm{ m}$, $\mathrm{r}=5\mathrm{ mm}$. Because of the dynamic mechanical property of GPD, the adapted dynamic relaxation algorithm [45] is used to get a fast convergence result in this static numerical test. The other parameters and material properties are listed in Table 1. The loading force is 5000 N, and the time step is set as 1 s.

Fig. 6

Geometry of the 2-D plate

Table 1 The detailed parameters of the model

Figure 7 shows the displacement with different nonlocal influence radii obtained by the proposed method. It is found from Fig. 7 that the obtained results are more consistent with the local results when the nonlocal characteristic length is smaller and smaller, implying the correct convergence property of the proposed nonlocal theory, as analyzed in Sect. 2.

Fig. 7

The displacement in the plate with different nonlocal influence radii

Remark 1

In a theory which considers the nonlocal property appropriately, the horizon can be set as a different characteristic length to obtain a special scale result. In addition, the horizon must be chosen carefully, because the horizon is a microscopic parameter which depends on the microstructure-informed continuum models accounting properly for the deformation mechanisms identifiable at the micro-scale [20]. And in the present model, we theoretically consider the equivalence between the local models and the nonlocal models when the characteristic length tends to zero, as shown in Eq. (33). Therefore, in the present theory, the local solution is a special case which is incorporated in the nonlocal solutions. When the horizon tends to zero, the nonlocal solution converges to a local solution.

5 Conclusions

This paper carries out a thorough investigation on the relationship among statistical mechanics, nonlocal vector calculus, PD and SPH. The conclusions are drawn as follows:

• (i) It is proved that the SPH theory can be considered as a nonlocal theory, and the SPH kernel-based approximation method, which formulates a conditional equivalence with the nonlocal vector calculus with an appropriate kernel, can be classified as a nonlocal vector operator which maps the local information to the nonlocal domain. The literature [32] said “…the notion of nonlocal gradient may also be related to the use of kernel-based integral approximations to differential operators in methods like SPH…”, this paper shows the correctness of the above statement.

• (ii) Nonlocal theory, such as peridynamics, can be derived by the classical statistical mechanics. The peridynamic motion equation can be derived as expectation of momentum density in phase space using the well-known Liouville’s equation easily. This implies that nonlocal theory can be considered as an application branch of statistical mechanics in continuum mechanics.

• (iii) The reason for the similar discretization between PD and SPH is obtained. PD and SPH have the same root of statistical physics, and they can both be formulated by the subject of statistical theories. Furthermore, they are both nonlocal theories which are obtained by mapping the traditional one-point function into a nonlocal two-point function. Since then, the equivalence of the discretization equation between PD and SPH naturally occurs based on the invariant form of physical mechanics in the different model frames and isogenous properties of statistical physics.

• (iv) Nonlocal vector calculus establishes a bridge which can connect the local theory and nonlocal theory. Since PD and SPH are both nonlocal theories, the PD and SPH can both be derived by nonlocal vector calculus from classical local theory.

• (v) A novel General Particle Dynamic method is proposed based on these theories. GPD is a successful nonlocal mechanics theory; the convergence of the nonlocal GPD is verified by numerical experiments.