1 Introduction

Over the past years, microfluidic systems propagated giantly and also employed vastly for micromachining technology, bioengineering, and biomedical applications [1, 2]. Microfluidics is a science that deals with the behavior of fluids in microsized systems [3]. In these systems, the fluids move into microsized channels, and different chemical or biological operations are carried out on them [3]. Particle tracing and trapping [4,5,6,7], drag reduction in microchannels [8,9,10,11], and behavior of bubbles [12,13,14] and droplets [15,16,17,18,19] in microfluidic devices are some of the hottest topics in this field. Microfluidic droplet-based systems are among the most important tools in many chemical and biological devices such as polymerase chain reaction (PCR) and cell separation [20,21,22,23,24,25]. They have been used even in logic systems [26, 27]. Of the advantages of these systems, the low size of the required sample, the possibility of producing a large number of droplets with the same size, the high surface area-to-volume ratio (which increases the reaction rate), and the ability to independently control each droplet can be noted [28,29,30,31]. Many researchers investigated the droplet manipulation process in microfluidic devices under different conditions. Xu et al. [32] examined different regimes of droplet formation in a T-shaped microfluidic device. They concluded that the continuous phase capillary number is one of the most important parameters for detecting the mechanism of the droplet formation process. De Menech et al. [33] numerically investigated the passive formation of droplets inside a microfluidic T-junction. In their work, they recognized three droplet formation regimes named squeezing, dropping, and jetting, by which some important aspects of the dynamics of droplet formation can be developed. For instance, they reported the variation of the dimensionless droplet volume inside the microchannel at different flow rates by considering a specified capillary number for various viscosity ratios (λ). Liu and Zhang [34] presented a phase-field simulation to assess the two-phase dynamics as well as a lattice Boltzmann method for the hydrodynamics of the droplet formation. In their 2D numerical study, to the best of the authors’ knowledge, one of the first studies was done to investigate the effect of the contact angle on the droplet formation. Moreover, they considered the effect of the viscosity ratio at a given flow rate on the droplet formation process. Christopher et al. [35] performed an experimental work in which the formation of droplets was evaluated in terms of the variation of different parameters, including the capillary number, the flow rate, ratios of the inlet widths, and the viscosity ratio. In addition, they proposed a prediction so as to ensure the outcomes they attained. Jullien et al. [36] did experimental research about the droplet breakup process at small capillary numbers in a T-junction. Sivasami et al. [37] investigated the mechanism of the droplet formation in a T-shaped microfluidic channel numerically. Nekouei et al. [38] used the numerical volume of the fluid method to simulate the impacts of viscosity ratio on droplet size in a microfluidic T-junction. They also presented an analytical model for anticipating the droplet size for different viscosity ratios. Zeng et al. [39] did a study about the pressure fluctuations in the droplet formation process in a microfluidic T-junction. They presented a mathematical model for predicting these fluctuations and compared the results with experimental outcomes. They reported that the amplitude of these fluctuations has a relationship with the geometrical parameters of the device. Bashir et al. [40] performed a series of numerical simulations on the process of droplet formation in a T-shaped microfluidic geometry using a two-phase level set method. Soh et al. [41] examined the velocity fields during the process of droplet formation in a T-shaped microfluidic channel numerically. Gu et al. [42] studied the non-Newtonian microdroplets formation in a T-junction with different input angles. Nooranidoost et al. [43] examined the effects of viscoelasticity on the droplet generation process in a microfluidic flow-focusing device. They found that the viscoelasticity delays the transition from squeezing to dripping regime. In an other research, Chiarello et al. [44] investigated the process of droplet formation driven by a shear-thinning fluid in a T-shaped microfluidic device. Liang et al. [45] considered a ferrofluid droplet generation process under the effect of an external magnetic field in a microfluidic T-junction. They performed a parametric study on the process and showed that the time of droplet formation decreases with the increase in the ferrofluid flow rate. They also found that the droplet formation time drops in the presence of a magnetic field. Sahore et al. [46] studied the droplet formation process in the thermoplastic microfluidic devices under the impact of external magnetic and electric fields. The devices including T-junction and K-channels were made by a hot-embossing procedure. They showed that these devices can be used for biochemical analysis. Moreover, the manipulation of the droplet generation process can be easily done in them by changing the electric and magnetic fields. Chen et al. [47] produced an on-demand microfluidic droplet generator which is triggered by an electric field. They used this flow-focusing device under different voltage ramps. They observed that smaller droplet volumes can be obtained in higher voltage ramps. Nhu et al. [48] introduced a microfluidic flow-focusing device for droplet generation. They also investigated the effect of applying an external electric field on the process. They showed that the flow rates of the fluids and the magnitude of the electric field are the most important parameters in the droplet breakup process. Li et al. [49] studied the process of high-viscosity droplets formation under the influence of an external electric field in a flow-focusing microfluidic device. They used the level set method and investigated the process numerically. Two of the most important parameters in the process of droplet formation are the size of the formed droplet and the time required for its formation [50,51,52,53,54,55,56,57].

From the above literature review, it can be concluded that despite the importance and application of non-Newtonian fluids in biological and chemical microfluidic systems, the behavior of such fluids in these systems has been rarely examined, especially under the effects of applying an external electric field. The investigations have been mainly focused on the Newtonian fluids, and two of the most important parameters in the process of droplet formation are the size of the formed droplet and the time required for its formation [50,51,52,53,54,55,56,57]. Therefore, in the present study, the effect of different factors on the process of non-Newtonian droplet formation in a T-junction will be investigated using the level set method. As a typical example of the non-Newtonian fluids, a shear-thinning fluid will be considered as it can be assumed as a model for a variety of non-Newtonian biological fluids such as saliva, blood, and mucus. The rate of the change in droplet size and its formation time for different concentrations of the aqueous solution of CMC is studied under different operating conditions of the system. The creation of an external electric field in the device and examination of its effects on the formation and separation of non-Newtonian droplets in a T-shaped microfluidic geometry will be discussed.

2 General description of the problem

2.1 Geometry description

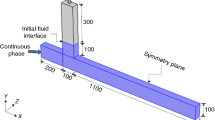
The schematic of the microfluidic T-junction which is used in this study is shown in Fig. 1.

Fig. 1
figure 1

The system geometry considered for the study

Full size image

The problem was solved in an unsteady and two-dimensional mode. Two-phase modeling of the problem was performed using the level set method (LSM). Olive oil was used as the continuous phase, and the aqueous solution of carboxymethyl cellulose (CMC), with different mass concentrations, was used as the droplet phase. This fluid is a non-Newtonian shear-thinning one whose viscosity can be predicted using the Carreau–Yasuda model. With a change in the mass concentration of CMC, its physical properties such as density, surface tension, contact angle, and other parameters related to its viscosity also change. The physical properties of the fluids which are used in this study can be seen in Table 1 [58, 59].

The contact angle is of paramount importance in the droplet formation process as it can change some important features of the generated droplets, including their size and shape. Therefore, it is inevitable to use the consistent numerical method for contact angle modeling. The contact angle in the current work can be simply obtained from the equation of \(\mathrm{cos}{\theta }_{\mathrm{w}}=({\sigma }_{\mathrm{aw}}-{\sigma }_{\mathrm{bw}})/\sigma\) [34]. In this equation, θw represents the contact angle, and σaw and σbw are the surface tensions between the two existing phases and the walls. It is worthwhile to note that the contact angle modeling utilized in this study can be also applied to the dynamic contact angle (DCA) as it is applicable here owing to the low-range capillary numbers [34, 60]. Also, different equations for the contact angle were employed in the numerical modeling to optimize the numerical results and find the most accurate one based on the equations offered theoretically and experimentally in the literature [60,61,62].

2.2 Boundary conditions

The inlet boundary condition is the constant input velocity and that for the outlet is the constant pressure. The wetted wall boundary condition is also considered on the walls. The capillary number, which indicates the ratio of viscous forces to the surface tension, is defined as follows [63]:

$$\mathrm{Ca}=\frac{{\mu }_{c}{U}_{\mathrm{in}}}{\sigma },$$
(1)

where Uin is the continuous fluid velocity, \(\sigma\) is the surface tension between two fluids, and \({\mu }_{\mathrm{c}}\) is the continuous fluid viscosity. The capillary number can be set according to the purposes of the simulation.

The Reynolds number (\(\mathrm{Re}=\frac{\rho {U}_{\mathrm{in}}D}{\mu }\)) of the flow will be less than 1, and the fluid flow can be considered laminar (D is the main channel diameter and μ and ρ are the fluid viscosity and density).

Despite the fact that there still more research is required to fully understand the principles of electro-hydrodynamics when an electric field applies to the system [64], the hydrodynamics boundary condition can be still determined [65]. Some worthwhile theoretical studies have been performed to shed more light on the electro-hydrodynamics, especially for the droplet formation process. In the present study, the zero-charge condition is applied to the walls. Also, a constant electric voltage condition is set for the computational domain in which the droplets are undergone effective changes.

The values of the surface tension between the two fluids and the contact angle of fluids on the wall of PDMS are given in Table 1. The contact angle is varied in this study, and its determination method will be elaborated in the aforementioned Section. The droplet phase enters the T-shaped geometry through the vertical channel. When it enters the horizontal channel in which the continuous phase is moving, the forces applied by the continuous phase fluid create a necking area in the droplet phase flow. Finally, a droplet of the fluid is separated and moves along the horizontal channel. In the following, the relevant equations are discussed.

3 Mathematical formulation

3.1 Level set method

In this study, the LSM was used to follow the boundary between the two phases. This method was first introduced by Osher and Sethian [66]. This method was specifically designed to solve problems where the boundary between two fluids moves during the process, as well as problems in which there is a sharp corner. Classically, in the LSM, a signed distance function is defined, and its basic idea is to consider a continuous scalar function \(\phi\). \(\phi\) = 0 indicates the boundary between the two fluids. \(\phi\) > 0 specifies one side of the boundary, and \(\phi\) < 0 on the other side of the boundary.

At the beginning of the solution, the level set function is defined as the minimum signed distance function to the interface; thus, in the solution domain, \(\left| {\nabla \phi } \right| = 1\). While solving the initialization equation, \(\left| {\nabla \phi } \right| = 1\) is valid at the interface. When the interface goes forward by an external velocity field, the level set function behavior is calculated by the following equation of motion:

$$\frac{\partial \phi }{\partial t}+{\varvec{u}} \cdot \nabla \varnothing =0,$$
(2)

where t is time and u is the velocity field. This equation of motion is solved locally near the interface. If the fluid flow is incompressible, ∇. u = 0, and the equation of motion is defined as follows:

$$\frac{\partial \phi }{\partial t}+\nabla \cdot ({\varvec{u}}\phi )=0.$$
(3)

The above equation is the continuity equation for the level set function.

The level set function is negative in one phase and positive in the other side. In both phases, a step function is used to show the density and viscosity of the fluids [24, 26] 67,68]:

$$H\left(\phi \right)= \left\{\begin{array}{c}0 \phi <0\\ 1 \phi >0\end{array}\right..$$
(4)

The level set function is determined as a signed distance function from the boundary:

$$\left|\phi \left(X\right)\right|=\mathrm{d}\left(X\right)= \mathrm{min}(\left| X-{X}_{I}\right|)\cdot {X}_{I} \epsilon I,$$
(5)

where I is the boundary and X is the distance.

In the numerical simulation, the step function has points of discontinuity, and the value of the function changes suddenly from one value to another. This jump in the numerical simulation using the finite element method causes instability. To overcome this problem, the following function is used instead of the previous one:

$${H}_{\mathrm{sm}}\left(\phi \right)= \left\{\begin{array}{l}0 -\varepsilon <\phi \\ \frac{1}{2}+\frac{\phi }{2\varepsilon } + \frac{1}{2\pi }\mathrm{sin}\left(\frac{\mathit{\pi \phi }}{\varepsilon }\right) -\varepsilon \le \phi \le \varepsilon \\ 1 \phi <\varepsilon \end{array}\right.,$$
(6)

where ε shows half of the interface thickness. Therefore, the new level set function is as follows:

$$\stackrel{\sim }{\varnothing } \left(x\cdot t\right)= {H}_{\mathrm{sm}} \left(\phi \left(x\cdot t\right)\right).$$
(7)

As noted, in a standard LSM, the \(\varnothing\) function is a continuous signed distance function along the interface. Thus, the interface curvature can be calculated with high precision. Although the mass losses in the method mentioned above are small, over the time during the process of solving these small errors grow and become large. To overcome this problem, Olsson and Kriess [69] developed a conservative LSM with high precision and good conservation of mass. In the present study, this method is used to investigate the behavior of the interface between the two fluids. In the level set function using this method, the interface is represented with a value of 0.5. In this method, the continuous phase fluid is denoted by 0 and the droplet phase by 1. In this method, the density and viscosity along the interface are calculated by the following equations:

$$\rho \left(x\cdot t\right)= {\rho }_{\mathrm{c}}+\left({\rho }_{\mathrm{c}}- {\rho }_{\mathrm{d}} \right)\phi ,$$
(8)
$$\mu \left(x\cdot t\right)= {\mu }_{c}+\left({\mu }_{c}- {\mu }_{d} \right)\phi ,$$
(9)

where \({\rho }_{\mathrm{c}}\), \({\rho }_{\mathrm{d}}\), \({\mu }_{\mathrm{c}}\), and \({\mu }_{\mathrm{d}}\) represent densities and viscosities of the continuous and the droplet phases, respectively. In the two-phase flow simulation, the interface normal vector and the boundary curvature are the two values that are needed to model the surface tension. They are calculated by the following equations:

$$\widehat{{\varvec{n}}}= \frac{\nabla \phi }{\left|\nabla \phi \right|},$$
(10)
$$k= \nabla .\frac{\nabla \phi }{\left|\nabla \phi \right|},$$
(11)

where \(\widehat{n}\) is the unit normal vector to the interface and k is the local boundary curvature. In the numerical method, to keep the boundary thickness constant, an artificial compression is added to the equation [70]:

$$\frac{\partial \phi }{\partial {\tau }_{a}}+ \nabla \cdot {\varvec{f}}(\phi )= \varepsilon {\nabla }^{2} \phi$$
(12)

where \({\tau }_{a}\) indicates the artificial time and f is the compressive flux. This artificial compression flux operates in an area where 0 < ∅ < 1, and it is perpendicular to the interface. The artificial compression flux perpendicular to the boundary is defined as follows:

$${\varvec{f}}= \phi \left(1-\phi \right) \widehat{{\varvec{n}}}= \phi \left(1-\phi \right)\frac{\nabla \phi }{\left|\nabla \phi \right|}.$$
(13)

Considering the equivalence of the artificial and the original time, an equation is formed as follows:

$$\frac{\partial \phi }{\partial t}+ \nabla \cdot \left({\varvec{u}}\phi \right)= \varepsilon {\nabla }^{2}\phi - \nabla \cdot f\left(\phi \right).$$
(14)

The Laplacian term of the above equation is an artificial diffusion term that attempts to expand the interface width. The divergence of the flux term acts oppositely. When the interface thickness is ε, these two terms are in equilibrium and keep the interface thickness constant. Equation (14) can also be written as a conservative form. To conserve the level set function, a reinitializing procedure is needed for finite element estimation of the level set equation. Thus, a conservative and reinitialized LSM is used to describe the interface motion. The following equation represents the motion of the reinitialized level set function:

$$\frac{\partial \phi }{\partial t}+ {\varvec{u}} . \left(\nabla \phi \right)= \gamma \nabla \cdot \left[\varepsilon \nabla \phi - \phi \left(1-\phi \right) \frac{\nabla \phi }{\left|\nabla \phi \right|}\right],$$
(15)

where γ and ε are the stabilization parameters of the numerical solution. γ is the initialization parameter, and its value is determined according to the maximum fluid velocity in the system. ε is the interface thickness parameter, and its value is determined based on the mesh size of the system. The above equation is coupled with the Incompressible Navier–Stokes equations and the continuity equation:

$$\rho \frac{\partial {\varvec{u}}}{\partial t}+ \rho \left({\varvec{u}}\cdot \nabla \right){\varvec{u}}= -\nabla p+ \nabla \cdot \mu \left(\nabla {\varvec{u}}+ {\left(\nabla {\varvec{u}}\right)}^{T}\right)+ {{\varvec{F}}}_{\mathrm{st}}+{{\varvec{F}}}_{\mathrm{ef}},$$
(16)
$$\nabla \cdot {\varvec{u}}=0,$$
(17)

where ρ is the density, μ is the dynamic viscosity, and p is the pressure. The force of surface tension (Fst), which operates on the interface between the two fluids, is calculated from the following equation:

$${{\varvec{F}}}_{\mathrm{st}} = \sigma k\widehat{{\varvec{n}}} {\delta }_{\mathrm{sm}},$$
(18)

where σ denotes the surface tension and δsm is a Dirac delta function obtained from the following equation:

$${\delta }_{\mathrm{sm}}\left(\phi \right)= \left\{\begin{array}{l}0 \phi <\varepsilon \\ \frac{1}{2\varepsilon } + \frac{1}{2\varepsilon }\mathrm{cos}\left(\frac{\pi \phi }{\varepsilon }\right) -\varepsilon \le \phi \le \varepsilon \\ 0 \phi <\varepsilon \end{array}\right..$$
(19)

3.2 Non-Newtonian Carreau–Yasuda model

The power law and Carreau–Yasuda are two major models for predicting the behavior of non-Newtonian shear-thinning fluids. Since the power law model is not very precise at very low or very high shear rates, the Carreau–Yasuda model, which has high accuracy at a broad range of shear rates, was chosen to model the non-Newtonian behavior of the droplet phase fluid in this study. The viscosity relation for the shear-thinning fluid in this model is as follows [71]:

$$\mu = {\mu }_{\infty }+\left({\mu }_{0}- {\mu }_{\infty }\right){\left[1+\left(\lambda \dot{\gamma }\right)\right]}^{\frac{(n-1)}{2}},$$
(20)

where μ0 and μ∞ are the viscosities at the zero and infinite shear rates, λ is the relaxation time parameter, γ is the shear rate, and n is a constant.

3.3 Equations of electric power

To take the effects of the electric field applied to the device into account, a term of electric body force must also be added to the Navier–Stokes equations [49]. The electric field distribution is obtained by Poisson’s equation as follows:

$$\nabla \cdot \left(\varepsilon \nabla V\right)= {\rho }_{\mathrm{f}},$$
(21)

where ε is the value of the coefficient of permittivity, V is the electric potential, and \({\rho }_{\mathrm{f}}\) is the density of free charge. The electric field E also relates to the electric potential by the following equation:

$${\varvec{E}}=- \nabla V.$$
(22)

Since the values of the electric permittivity of the two phases are different, ε is changing at the interface between the fluids. Therefore, both the power and the direction of the electric field at the boundary between the two fluids change. The permittivity value at the boundary can be defined using the level set function as follows:

$$\varepsilon ={\varepsilon }_{\mathrm{c}}+\left({\varepsilon }_{\mathrm{d}}-{\varepsilon }_{\mathrm{c}}\right)\phi ,$$
(23)

where εc and εd are the values of the electric permittivity of the continuous phase and the droplet phase, respectively. By changing the permittivity at the interface, a body force enters the interface whose values can be calculated by diverging from the Maxwell stress tensor assuming that the fluid is incompressible:

$${{\varvec{F}}}_{\mathrm{ef}}= \nabla \cdot {{\varvec{T}}}_{\mathrm{MW}}= -\frac{1}{2} \left({\varvec{E}}\boldsymbol{ }\cdot \boldsymbol{ }{\varvec{E}} \right)\nabla \varepsilon + {\rho }_{\mathrm{f}}{\varvec{E}}.$$
(24)

The first term of this equation is due to the electric forces applied by the polarization charges induced by the changes in the permittivity at the interface. The second term is caused by the reaction between the free charges and the electric field. Since both fluids are insulated, the second term of the equation can be ignored.

4 Validation

For validation, the system proposed by Van der Graff et al. [72] was first simulated. In the mentioned study, the process of droplet formation in a microfluidic T-junction was examined by experimental and lattice Boltzmann method (LBM), and the results were compared. In this study, hexanediol diacrylate was used as the droplet phase, and the aqueous solution of 2% polyvinyl alcohol was used as the continuous phase. The wetted wall boundary condition with a contact angle of 135° was applied. One of the most important results presented in this study was the effect of the continuous phase flow rate on the size of the droplets. Considering a constant flow rate of 0.2 ml h−1 for the droplet phase and a change of the continuous phase flow rate from 0.2 to 4 ml h−1, it was observed that as the continuous phase flow rate increases, the droplet diameter decreases. In the present study, the above system was simulated with the same conditions, and the results for the droplet diameter were compared with the results presented by Van der Graff et al. [72] in Fig. 2.

Fig. 2
figure 2

A comparison between the results of the present study and the those obtained by Van der Graff et al. [72] (the changes in the droplet diameter by the continuous phase flow rate)

Full size image

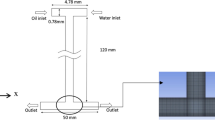
As can be seen, the results are consistent well, and the mean error is about 7% compared to the experimental results. In the next step, the system presented by Li et al. [49] was simulated to verify the accuracy of the applied electric forces. Li et al. [49] studied the effect of an external electric field on the process of high-viscosity droplets’ formation in a flow-focusing microfluidic device. The geometry dimensions used in the study by Li et al. [49] are depicted in Fig. 3.

Fig. 3
figure 3

The system used in the study by Li et al. [49]

Full size image

The inlet flow rate of the droplet phase was considered to be 0.04 ml h−1, and the inlet flow rate of the continuous phase was assumed to be 50 times this value. A voltage difference of 10–660 V was also applied between the two continuous phase inlets. Two different types of silicone oils were selected as the continuous phase and the droplet phase fluids. The density of the continuous phase was 1000 kg m−3, its viscosity was 1 mPa s, and its electric permittivity was 78.5 × 8.854 × 10−12 V−1 m−1. The density of the droplet phase was 1000 kg m−3, its viscosity was 50 mPa s, and its electric permittivity was 2.8 × 8.854 × 10−12 V−1 m−1. Both the fluids were assumed to be insulated, and the wetted wall boundary condition with a contact angle of 145° was applied. One of the most important results presented in this study was the effect of changing the voltage difference on the diameter of the droplets. Since the results have been presented in dimensionless forms, droplets have been scaled by the width of the flow-focusing channel, and the voltage changes were also scaled by the electrical Euler number (Eu = ρcuc2/E02ε0εc). In this study, the above system was simulated with the same conditions mentioned before, and its results were compared with those presented by Li et al. [49] in Fig. 4.

Fig. 4
figure 4

A comparison between the results of the present simulation with those presented by Li et al. [49] (changes in the dimensionless droplet diameter by electrical Euler number)

Full size image

As can be seen in Fig. 4, the simulation results are in line with those presented by Li et al. [49], indicating the high precision of the simulation. In Fig. 5, a qualitative comparison can be seen between the results of the present simulation and those provided by Li et al. [49] for the applied voltages of 480 and 660 V.

Fig. 5
figure 5

a, c The results of the present simulation for the process of droplet formation under the effects of 480 V and 660 V voltage difference, respectively; b, d The results presented by Li et al. [49] for the same voltages

Full size image

5 Investigating mesh independency

In this part of the study, a mesh independency investigation is performed for the T-junction with a droplet phase inlet width and length of 90 and 400 μm, respectively. The continuous phase channel width is 200, and its length is 1500 μm. The solution of 0.60% mass concentration of carboxymethyl cellulose solution (CMC) was used as the droplet phase and olive oil as a continuous phase. The values of the physical properties of these materials are completely given in Table 1. The inlet fluid velocity of the continuous phase was 0.05 m s−1, and that for the droplet phase was 0.0005 m s−1. For the mentioned situation, five different mesh sizes were considered. The number of mesh elements was: 5138, 20,041, 41,141, 52,497, and 70,227. The problem was solved for all the five meshes, and the results of the solution were compared after 0.3 s. It was observed that no droplet was formed at this time when the number of mesh elements was 5138 or 20,041. When the number of elements was increased to 41,141, the droplet diameter became 97.2 μm, and it was not separated from the wall until leaving the main channel. For the case of 52,497 elements, the droplet diameter was 98.96 µm, and for the case of 70,227 elements, it was 98.84 µm. It was observed that for meshes with 52,497 elements and above, the droplet diameter changes very slightly. In general, when using a mesh of more than 52,497 elements, the result will be mesh-independent. In Fig. 6, the effect of changing the number of mesh elements on the droplet formation can be seen.

Fig. 6
figure 6

The effect of changing the number of mesh elements used in the simulation on the droplet formation

Full size image

6 Results and discussion

Figure 7 indicates the effect of the changes in the capillary number on the dimensionless droplet diameter for different CMC concentrations. In this diagram, the droplet phase inlet velocity is assumed to be 0.0005 m s−1, and the continuous phase velocity changes from 0.01 to 0.05 m s−1. (The capillary number changes from 0.03 to 0.17.) In this Figure, all the points are related to the dripping regime, and the droplet is separated at the corner of the T-junction. Therefore, the process of droplet separation is strongly influenced by the shear forces applied by the continuous phase flow on the interface. As can be seen, while the velocity of the droplet phase is constant, changing the continuous phase velocity in the T-junction can affect the size of the droplet. By increasing the inlet velocity of the continuous phase (increasing the capillary number), while the inlet velocity of the droplet phase is assumed to be constant, a decrease in the formed droplet diameter is observed at all the concentrations. As the inlet velocity of the continuous phase increases, the shear forces applied to the interface between the two fluids in the process of the droplet formation increase, the droplet is faster separated, and, consequently, its diameter drops. By changing the continuous phase capillary number from 0.034 to 0.08, while the droplet fluid is a solution of 0.02% CMC with an inlet velocity of 0.0005 m s−1, the droplet diameter can be reduced up to 20%. By increasing the capillary number to 0.17, the decrease reaches 48%. Therefore, by changing the continuous phase velocity, the droplet diameter can be precisely controlled. In Fig. 8, the droplets for the solution of 0.04% CMC at capillary numbers of 0.034 and 0.17 can be seen. It is observed that due to the low contact angle (127.7°), the larger droplet leaves the device before it can be separated from the upper wall of the main channel. However, smaller droplets are separated from the upper wall before leaving the channel and completely dispersed in the continuous phase fluid.

Fig. 7
figure 7

The effects of the change in the capillary number on the dimensionless droplet diameter for different CMC concentrations

Full size image
Fig. 8
figure 8

Droplet formation for 0.04% mass percentage of CMC at a capillary number of a Ca = 0.034, b Ca = 0.17

Full size image

In Fig. 9, the effect of the concentration of the droplet phase on the formed droplet diameter for four different capillary numbers can be seen. Based on this Figure, as the concentration of CMC solution increases, the droplet size decreases slightly. This phenomenon is since with increasing CMC concentration the solution gains more shear-thinning properties and its viscosity drops faster under the influence of continuous phase shear forces; hence, the droplet separates faster and its size declines. In Fig. 10, the droplets formed at the capillary number of 0.17 for the three different CMC concentrations can be seen.

Fig. 9
figure 9

The effect of the change in the CMC concentration on the dimensionless droplet diameter at several different capillary numbers

Full size image
Fig. 10
figure 10

Comparison of the shape of the formed droplet for three different CMC concentrations at a capillary number of 0.17 for CMC concentrations of a 0.02 wt%, b 0.06 wt%, and c 0.1 wt%

Full size image

In the next step, by changing the inlet velocity of the droplet phase between 0.00050 and 0.004 m s−1, the droplet diameter was calculated for several different concentrations of the droplet phase fluid (CMC). The inlet velocity of the continuous phase was considered to be 0.05 m s−1. Figure 11 shows the effect of the change in the inlet velocity of the droplet phase fluid on the droplet diameter. The results indicate that by elevating the velocity of the droplet phase the droplet size also increases. For instance, when the droplet phase was a solution with 0.02% mass concentration of CMC, by increasing the inlet velocity of the droplet phase from 0.0005 to 0.004 m s−1, an increase of approximately 17% is observed in the droplet size. In the dripping regime, the process of the droplet separation occurs at the corner of the T-junction, and shear forces applied by continuous phase fluid cause the droplet phase flow to breakup into the micron-sized droplets. By increasing the velocity of the droplet phase, the inertial force generated by this phase increases, and this force resists the shear forces in the system that are intended to move the interface between the two fluids to the corner of the T-shaped geometry and create a necking and separation area. Thus, an increase in the velocity of this phase can lead to the formation of larger droplets. As the droplet phase velocity increases, more droplet fluid enters the main channel before the processes of necking and separation occur at the corner of the T-shaped geometry; thereby, an increase in the droplet diameter will happen. Figure 12 shows the droplets formed for the mass concentration of 0.02% CMC for two velocity ratios of 0.04 and 0.08.

Fig. 11
figure 11

The effects of changing the droplet phase velocity on the droplet diameter for different CMC concentrations

Full size image
Fig. 12
figure 12

The droplet formed of the mass percentage of 0.02% CMC for the velocity ratio of \({v}_{\mathrm{d}}/{v}_{\mathrm{c}}\) equals to a 0.04 b 0.08

Full size image

In the next Section, similar to the previous step, the inlet velocity of the continuous phase fluid was considered to be 0.05 m s−1. By changing the inlet velocity of the droplet phase from 0.0005 to 0.004 m s−1, the dimensionless time of the first droplet formation was calculated for different CMC concentrations. The results for this Section can be seen in Fig. 13. As it is evident, the changes in the inlet velocity of the droplet phase have a great impact on the time of the first droplet formation. The time of the first droplet formation has a very severe decrease of about 80% by changing the velocity ratio from 0.08 to 0.01. The reason was that as the droplet phase velocity increases, the fluid reaches the main channel faster, and, subsequently, the processes of necking and separation occur in less time.

Fig. 13
figure 13

The effect of changing the droplet phase velocity on the time of the first droplet formation for different CMC concentrations

Full size image

As the interaction of the droplets and the walls is remarkably affected by the size of the droplets, different contact angle values are considered here. By changing the contact angle from 120° to 180°, the droplet diameter was calculated for different concentrations of droplet phase fluid (CMC). The contact angle of 180° indicated a state where the continuous phase fluid completely wetted the wall. The results of this simulation can be seen in Fig. 14. As can be seen, with an increase in the contact angle, a decrease in the droplet size occurs. For example, for a concentration of 0.02% CMC, with an increase in contact angle from 125.7° to 180°, in a state where other parameters were assumed to be the same, a decrease of 4.5% in the droplet size is observed. For smaller contact angles, the droplet phase fluid could spread more on the wall of the main channel. Increasing the contact angle decreases the adhesive force between the droplet phase fluid and the channel wall. This allows the shear forces applied to the interface between the two fluids to create a necking area at the corner of the T-junction faster. In Fig. 15, the effects of changing the contact angle on the droplet formation process (for a solution of 0.02% CMC in the main channel) are observed.

Fig. 14
figure 14

The effect of changing the contact angle on the droplet diameter for different CMC concentrations

Full size image
Fig. 15
figure 15

Formed droplet at different contact angles a 140°, b 155°, and c 180°

Full size image

By changing the contact angle from 120° to 180°, the time of the first droplet formation was also calculated for different concentrations of the droplet phase fluid (CMC). The results can be seen in Fig. 16. As can be seen, as the contact angle increases, the processes of droplet formation and separation took place in a shorter time. For the smaller contact angles, the droplet spreads more on the microchannel wall, and the shear forces applied to the interface between the two fluids require more time to create a necking area. By increasing the contact angle and, subsequently, decreasing the adhesion between the wall and the fluid, the droplet-forming phase separated from the channel wall faster in comparison with the state where the contact angle was low. This makes the formation of the necking area faster and reduces the time of the first droplet formation.

Fig. 16
figure 16

The effect of changing the contact angle on the dimensionless time of the first droplet formation for different CMC concentrations

Full size image

In the following, the effect of changing surface tension between the two fluids on the droplet size is discussed. The inlet velocity of the continuous phase fluid was assumed to be 0.05 m s−1, and the inlet velocity of the droplet phase was 0.0005 m s−1. By changing the amount of surface tension between the two fluids, the droplet diameter was calculated for different concentrations of droplet phase fluid (CMC). To investigate only the effects of changes in the surface tension on the process of droplet formation, other fluid properties were theoretically considered to be constant. As can be seen in Fig. 17, with an increase in the surface tension between the two fluids, the droplet size increases. For instance, when the amount of the surface tension between the two fluids quadruples, the droplet diameter doubles. This phenomenon happens because as the surface tension increases, the force between the droplets phase fluid molecules that attempted to keep the interface between the two fluids as little as possible increases, and this force resists the shear forces applied by the continuous phase fluid and delays the process of necking, resulting in larger-sized droplets. In Fig. 18, the effect of changing the surface tension on the shape of the droplets is plotted.

Fig. 17
figure 17

The effect of changing the surface tension between the two fluids on the formed droplet diameter for different CMC concentrations

Full size image
Fig. 18
figure 18

The formed droplet for different surface tensions a 0.01 N m−1, b 0.02 N m−1, c 0.03 N m−1, and d 0.04 N m−1 for 0.02% mass percentage of CMC

Full size image

In the following, the effect of applying an electric field on the process of droplet formation in a T-junction is investigated. This electric field is made by creating a voltage difference between the inlet and the outlet of the main channel. In Fig. 19, contours of the electric force applied to the interface between the two fluids, during the process of separation in the directions of x and y, are seen. (In this Figure, a voltage difference of 600 V was established between the inlet and the outlet of the main channel.) To investigate the effects of the applied electric field, the inlet phase fluid velocity was assumed to be constant and equal to 0.0005 m s−1 in all the simulations. By changing the voltage difference applied to the system from 0 to 600 V, the effect of creating an electric field in the system on the droplet diameter for different CMC concentrations was investigated. Simulations were performed for three different continuous phase inlet velocities. In Fig. 20a, the results of the change in the voltage difference on the droplet diameter for the continuous phase inlet velocity of 0.01 m s−1 can be seen. As it is evident, as the applied DC voltage increases, the droplet diameter increases. This is because there is an electrical permittivity gradient in the interface of two phases. The interaction between this gradient and the electric field causes some polarization charges to induce on the interface and leads to entering some electrical force on it. The direction of this force is always perpendicular to the interface from the side with lower permittivity to the side with higher permittivity. In the present case, the direction of this force is opposite to the direction of shear forces from the continuous phase and resists the necking process; thus, the droplet diameter will increase. Figure 21 shows the time of the first droplet formation for the continuous phase velocities of 0.01 m s−1, 0.02 m s−1, and 0.05 m s−1, respectively. It is also seen in this Figure that by increasing the voltage difference applied to the system, the time of the first droplet formation also increases. As already explained, this is due to the resistance of the electric forces applied to the interface against the shear forces that sought to create a necking area in the system. Consequently, the droplet separation occurs over a longer period when these forces exist. In fact, it is to be mentioned that inducing the electric forces towards the droplets leads to better control over the droplet formation process. To be more specific, when the electric field applies to the microfluidic T-junction the net force acting on the dispersed fluid to create the droplets becomes weaker as the electric force acts against the shear force; thus, the separation of the droplets from the fluid that enters from the vertical inlet does not hasten and the droplet tends to the right noticeably without tearing.

Fig. 19
figure 19

The electric force on the boundary between the two fluids with uc = 0.01 m s−1 and 0.02 wt% CMC concentration for a y-component, b x-component

Full size image
Fig. 20
figure 20

Droplet diameter as a function of the electric Euler number for continuous phase inlet velocity at a 0.01 m s−1, b 0.02 m s−1, and c 0.05 m s−1

Full size image
Fig. 21
figure 21

The time of the droplet formation as a function of the electric Euler number for continuous phase inlet velocity at a 0.01 m s−1, b 0.02 m s−1, and c 0.05 m s−1

Full size image

7 Conclusions

In this study, the numerical simulation of the process of non-Newtonian shear-thinning droplet formation within a T-junction was performed using the level set method. Olive oil was used as a continuous phase, and a solution of CMC or water-soluble carboxymethyl cellulose, with different mass concentrations, was used as the droplet phase. The viscosity behavior of the droplet phase could be predicted using the Carreau–Yasuda model. One of the most important results presented by other researchers studying the process of droplet formation was the effect of changing the key parameters such as the capillary number or external forces in the system on the droplet diameter and its formation time. In this study, these parameters were also examined, and the results were provided. One of the most significant parameters that affects the process of droplet formation is the capillary number of the continuous phase. Thus, in the beginning, the effect of changing this parameter on the size of the droplet was investigated. It was found that the droplet size was strongly dependent on this parameter such that with an increase in the capillary number a decreasing trend was observed in the droplet size. The reason for this was that one way to increase the capillary number is to increase the continuous phase velocity. This increase in the continuous phase velocity causes the shear forces applied to the interface to increase, which leads to a reduction in the droplet diameter. The other parameter investigated in this study was the effect of changing the concentration of the non-Newtonian droplet phase on the droplet diameter. As the fluid concentration increased, its initial viscosity increased, too. In the studies on the process of Newtonian droplet formation, the drop diameter increases with increasing the droplet fluid phase viscosity. However, when the concentration of shear-thinning fluid and consequently, its initial viscosity increased, an opposite trend was observed and the droplet diameter decreased. The reason for this could be attributed to the non-Newtonian nature of the droplet phase fluid. Increasing the concentration of this fluid increases its shear-thinning properties, and the higher the thinning properties of the fluid, the faster its viscosity decreases as a result of shearing forces applied by continuous phase flow. The decrease in the formed droplet diameter could be justified by this rapid decrease in the viscosity. In the next step, the effects of parameters such as the inlet velocity of the droplet phase, contact angle, and surface tension between the two fluids were examined, and the results were interpreted. Finally, an electric field was created inside the microfluidic device by applying the voltage difference to the inlet and outlet of the system, and the effect of electric forces on the process of droplet formation was investigated. Since the electrical permittivity values of two fluids are different, an electric force is applied to the interface between the two fluids, and as the electrical permittivity of the continuous phase is smaller than that of the droplet phase, the direction of the electric force applied at the interface is from the droplet phase to the continuous one. Moreover, since the direction of the electric forces applied to the interface is opposite to the shear forces applied by the continuous phase fluid, these forces delay the process of separation, resulting in the formation of a larger droplet. In addition, it is compelling to investigate the effects of viscosity ratio towards a better understanding of the influence of dispersed phase viscosity, regardless of its non-Newtonian characteristics, on the size of the generated droplets.

Table 1 Physical properties of CMC aqueous solutions with different mass concentrations [58, 59]
Full size table