An effective procedure for extracting the first few bridge frequencies from a test vehicle

Abstract

This study presents an effective procedure for extracting the first few bridge frequencies using the data collected by a moving test vehicle. Previously, the effectiveness of the vehicle scanning method for bridge frequencies was hampered by factors such as vehicle frequency and road surface roughness. To this end, the contact-point response of the vehicle with the bridge that is free of the vehicle frequency is adopted in the analysis. To enhance the visibility of the first few bridge frequencies for extraction, the variational mode decomposition with band-pass filter (VMD-BPF) is proposed herein. The VMD is neater and more elegant than the empirical mode decomposition (EMD) in that less decompositions are needed, while there exists no mode-coupling problem, and the BPF serves to remove the undesired roughness frequencies. To verify the feasibility of the proposed procedure, both the vehicle and contact-point responses generated either numerically or by the field test are analyzed. It is demonstrated that the VMD-BPF is an effective method for extracting the bridge frequencies using the contact-point response for the scenarios considered.

1 Introduction

The presence of damages in a structure, such as the loss of stiffness, breakage in structural members or joints, and scouring of supports, may result in the drop of natural frequencies of the structure. Frequency-based monitoring methods have been widely used in bridge maintenance and/or rehabilitation, since the frequency is closely related to the health condition of the bridge. Conventionally, vibration sensors are often installed on the bridge to directly monitor the variation of the dynamic properties. Such an approach of health diagnosis of bridges is known as the direct method, which has been widely used in practice. Some reviews on such an approach of measurement for bridges are available in Refs. [1, 2].

The main drawback of the direct approach is that it is designed on a one-system-per-bridge basis, for which the installation and maintenance are generally costly. Besides, for bridges fitted with monitoring systems, the sea-like data generated by the monitoring devices often is not properly utilized. Moreover, the sensors installed on a bridge often deteriorate by years, due to ageing, weathering, etc., and can hardly cover the full life span of the bridge of concern. To overcome the drawbacks of the direct method, the vehicle scanning method (VSM), originally known as the indirect method, for bridge measurement was proposed by Yang and co-workers in 2004 [3]. By this method, an instrumented vehicle is used to extract indirectly the frequencies of the bridge during its passage [4]. At present, the application and research of the VSM are mainly restricted to ordinary bridges with small and medium spans, and only a limited number of studies have been performed on cable-stayed bridges [5] and rails [6]. Based on its mobility, it is anticipated that the VSM has great potential for application to longer bridges, such as cable-stayed bridges, suspension bridges, and even rails. An up-to-date review of the researches globally conducted along the lines of the VSM for bridges is available in Refs. [7, 8].

For any vibration-based structural health monitoring system, the signal processing technique is always crucial. The fast Fourier transform (FFT) [9, 10] is one of the most basic and widely used methods for signal processing. It is an effective implementation of the discrete Fourier transform (DFT) for converting discrete signals from time domain to frequency domain. Since the FFT cannot reveal spectral changes, the short time Fourier transform (STFT) was proposed for detecting the frequency contents as the signal changes over time [11]. The wavelet transform (WT) allows us to grasp the frequencies of the signals with their action period retained. As a convenient and efficient technique for signal processing, the WT has been used in various fields, including earthquake engineering [12, 13], structural vibration control [14, 15], and bridge engineering [16, 17]. The Hilbert–Huang transform (HHT) proposed by Huang et al. [18] is based on two steps, i.e., the decomposition of the signals into a set of intrinsic mode functions (IMFs) by the empirical mode decomposition (EMD) and the use of the Hilbert transform to obtain the instantaneous frequencies for each IMF. Aside from this, the EMD has been widely used as a tool for dealing with various problems [19, 20] and has significant impact on bridge engineering [21,22,23,24]. Techniques based on the EMD, such as the ensemble empirical mode decomposition (EEMD) [25] and complementary ensemble empirical mode decomposition (CEEMD) [26], have also been applied along the lines of the VSM [27, 28]. With regard to bridge health monitoring, choosing an effective method is crucial for both the direct and indirect (VSM) methods, such as using the normalized cumulative power spectral density (NCPSD) to detect structural modifications [29] or using the enhanced “excitation correction” procedure [30].

To enhance the capability of the VSM for bridge frequency retrieval, suitable data processing or filtering techniques are essential. Previously, the EMD-based techniques were adopted [22,23,24]. Due to the lack of rigorous mathematical basis, weak robustness against noise, and the problem of mode mixing in extracting the IMFs by the EMD, the variational mode decomposition (VMD) [31] will be adopted in this study to process the data collected by the passing vehicle. The superiority of the VMD technique in dealing with system identification and fault diagnosis has been previously demonstrated [32, 33]. With this technique, the vibration signal is decomposed into multiple band-limited mode components in frequency domain, where each decomposed mode has its center frequency. In this regard, the recursive formulas used have been demonstrated to be robust in treating the noise due to their close relationship with the Wiener filter [31].

Since road surface roughness can significantly affect the result of bridge frequencies extraction, it is essential that some filtering techniques be adopted to alleviate such an effect. In this study, the band-pass filter (BPF), a popular data processing technique used in bridge engineering [34,35,36], is adopted. By using the BPF in advance to filter out the frequencies beyond the desired range, the VMD technique is then adopted to decompose the vibration data. Such a combined procedure is referred to as the variational mode decomposition with band-pass filter (VMD-BPF).

Previously, the vehicle response recorded by the sensor fitted on the axle of the vehicle has been adopted in analysis, but it is hindered by the vehicle frequency for its overshadowing effect in the spectrum, especially in the presence of road surface roughness [37, 38], as observed in the field test [39, 40]. In fact, the contact-point response of the vehicle with the bridge can be calculated by a backward procedure, which allows the vehicle frequency to be eliminated, along with its overshadowing effect [41]. In this study, the VMD-BPF technique will be tested against both the vehicle and contact-point responses in extracting the bridge frequencies. The combined method can enhance the visibility of bridge frequencies, while extending the feasibility of the VSM, by retaining their respective advantages and avoiding the distress caused by a single method.

The organization of the paper is as follows: In Sect. 2, the analytical response of the passing vehicle and the backward procedure for obtaining the contact point response will be summarized, with the main features highlighted. In Sects. 3 and 4, the VMD and BPF techniques will be briefly introduced. In Sect. 5, the analytical result obtained in Sect. 2 is verified by comparison with the finite element result using the vehicle–bridge interaction (VBI) element [3, 42, 43]. In Sect. 6, the techniques of EMD and VMD will be compared first. Then, a parametric study will be conducted for the effects of vehicle speed and of road surface roughness. In Sect. 7, the applicability of the proposed procedure will be verified in the field test. Finally, conclusions are given in Sect. 8.

2 Analytical formulation of the problem

First, the analytical formulation of the VSM will be presented, followed by the procedure for calculating the contact-point response of the test vehicle.

2.1 Analytical formulation

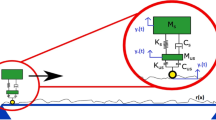
A simple beam subjected to a moving vehicle shown in Fig. 1 is considered [4, 44, 45]. It is realized, however, that the proposed technique is not restricted to such beams. In Fig. 1, the vehicle moving at speed v is modeled as a car body of mass $m_{v}$ resting on a spring of stiffness $k_{v}$. An accelerometer is fitted on the car body for measuring its vertical motion. The beam is of the Bernoulli–Euler type with a span length L, per-unit-length mass m, and stiffness EI. The damping of both the beam and vehicle is ignored in the analytical formulation. Also, repetition of the present formulation with the previous ones is kept to the minimum needed for outlining the concept involved. It is believed that the analytical solution obtained for such a simply supported bridge can be extended to more complicated bridges via the simulation by the finite element method (FEM).

Fig. 1

Simplified model of a lumped sprung mass travelling over a beam

The equation of motion for the vehicle at the static equilibrium position is

$$\begin{aligned} m_{v}\ddot{y}_{v}+k_{v}\left( y_{v}-u_{c} \right) =0, \end{aligned}$$

(1)

where $y_{v} =$ the vehicle’s vertical displacement, $u_{c}=u\vert _{x=vt} =$ vehicle’s contact-point displacement on the beam, and an overdot $=$ time (t) derivative. The equation of motion for the bridge is

$$\begin{aligned} m\ddot{u}+EIu^{''''}=f_{c}\left( t \right) \delta \left( x-vt \right) , \end{aligned}$$

(2)

where $u =$ vertical displacement of the beam, $\delta =$ delta function, a prime $=$ spatial (x) derivative, and $f_{c} =$ contact force between the vehicle and beam, i.e.,

$$\begin{aligned} f_{c}\left( t \right) =k_{v}\left( y_{v}-u_{c} \right) -m_{v}g, \end{aligned}$$

(3)

where g is the gravitational acceleration.

The vertical displacement u of the beam can be represented in terms of the modal shapes $\sin {(n\pi x/L)}$ as [46]:

$$\begin{aligned} u\left( x,t \right) =\sum \limits _n {q_{b,n}\left( t \right) \sin \frac{n\pi x}{L}} , \end{aligned}$$

(4)

where $q_{b,n}$ is the nth modal coordinate of the beam. By substituting Eq. (4) into Eq. (2) and assuming $m_{v}\ll mL$, the contact-point displacement $u_{c}$ (at $x =\textit{vt}$) can be obtained:

$$\begin{aligned} u_{c}\left( t \right) =\sum \limits _n {\frac{{\Delta }_{stn}}{1-S_{n}^{2}}\left( \sin \frac{n\pi vt}{L}-S_{n}\sin \omega _{b,n}t \right) \sin \frac{n\pi vt}{L}} , \end{aligned}$$

(5)

where ${\Delta }_{st,n}$ denotes the nth modal static deflection of the beam due to $m_{v}g$, $S_{n}$ the speed parameter, and $\omega _{b,n}$ is the nth bridge frequency. Namely,

$$\begin{aligned} \Delta _{st,n}=-\frac{2m_{v}gL^{3}}{EIn^{4}\pi ^{4}}, \qquad S_{n}=\frac{n\pi v}{L\omega _{b,n}}, \qquad \omega _{b,n}=\frac{n^{2}\pi ^{2}}{L^{2}}\sqrt{ \frac{EI}{m}}. \end{aligned}$$

(6a-c)

By trigonometric operations, the contact-point displacement (5) can be rearranged and twice differentiated to yield the acceleration response $\ddot{u}_{c}$ of the contact point as

$$\begin{aligned} \ddot{u}_{c}\left( t \right) =\sum \limits _n {\frac{{\Delta }_{st,n}}{2\left( 1-S_{n}^{2} \right) }\left[ {\begin{array}{c} \left( \frac{2n\pi v}{L} \right) ^{2}\mathrm {cos}\frac{2n\pi vt}{L} \\ +S_{n}\left( \omega _{b,n}-\frac{n\pi v}{L} \right) ^{2}\cos {\left( \omega _{b,n}-\frac{n\pi v}{L} \right) t} \\ -{S_{n}\left( \omega _{b,n}+\frac{n\pi v}{L} \right) }^{2}\cos {\left( \omega _{b,n}+\frac{n\pi v}{L} \right) t} \\ \end{array}} \right] } . \end{aligned}$$

(7)

By substituting Eq. (5) into the vehicle equation (1), along with the zero initial conditions for the test vehicle, i.e., $y_{v}\left( 0 \right) =0$ and ${\dot{y}}_{v}\left( 0 \right) =0$, the vehicle response $y_{v}$ can be solved and differentiated twice to yield the acceleration $\ddot{y}_{v}$ as

$$\begin{aligned} \ddot{y}_{v}\left( t \right)= & {} \sum \limits _{n=1}^M \frac{\Delta _{st,n}\omega _{v}^{2}}{2\left( 1-S_{n}^{2} \right) }\left[ \frac{\left( \frac{2n\pi v}{L} \right) ^{2}}{\omega _{v}^{2}-\left( \frac{2n\pi v}{L} \right) ^{2}}\cos \frac{2n\pi vt}{L}-A_{n}\mathrm {cos}\left( \omega _{v}t \right) \nonumber \right. \\&+\frac{\left( \omega _{b,n}-\frac{n\pi v}{L} \right) ^{2}S_{n}}{\omega _{v}^{2}-\left( \omega _{b,n}-\frac{n\pi v}{L} \right) ^{2}}\cos {\left( \omega _{b,n}-\frac{n\pi v}{L} \right) t}\nonumber \\&\left. -\frac{\left( \omega _{b,n}+\frac{n\pi v}{L} \right) ^{2}S_{n}}{\omega _{v}^{2} -\left( \omega _{b,n}+\frac{n\pi v}{L} \right) ^{2}}\cos {\left( \omega _{b,n}+\frac{n\pi v}{L} \right) t} \right] , \end{aligned}$$

(8)

where

$$\begin{aligned} A_{n}= & {} \frac{4\mu _{n}^{4}S_{n}^{2}\left( 1-S_{n}^{2} \right) \left( 2+\mu _{n}^{2}S_{n}^{2}-\mu _{n}^{2} \right) }{\left( 4\mu _{n}^{2}S_{n}^{2}-1 \right) \left[ 1-2\mu _{n}^{2}\left( 1+S_{n}^{2} \right) +\mu _{n}^{4}\left( 1-S_{n}^{2} \right) ^{2} \right] }, \end{aligned}$$

(9a)

$$\begin{aligned} \mu _{n}= & {} {} \frac{\omega _{b,n}}{\omega _{v}}, \end{aligned}$$

(9b)

together with the vehicle frequency $\omega _{v}$ defined as

$$\begin{aligned} \omega _{v}=\sqrt{ \frac{k_{v}}{m_{v}} }. \end{aligned}$$

(10)

As can be seen from Eq. (8), the vehicle response contains the driving frequency $2n\pi v/L$ (referred to as $\omega _{d}$ from here on), the vehicle frequency $\omega _{v}$ and two shifted bridge frequencies, $\omega _{b,n}-n\pi v/L$, $\omega _{b,n}+n\pi v/L$. This offers a clue for extracting the bridge frequencies from a passing vehicle.

2.2 Contact-point response

In extracting the bridge frequencies from the vehicle response, the bridge frequencies $\omega _{b,n}$ may become indistinguishable when the vehicle frequency $\omega _{v}$ has too large a peak in the response spectrum. To overcome such a disturbing effect, it was suggested that the response $\ddot{u}_{c}$ of the vehicle’s contact point with the bridge be used instead [41], since it is free of the vehicle frequency $\omega _{v}$, as revealed by Eq. (7).

The vehicle damping is ignored in computing the contact-point response. In practice, to ensure that enough vibrations are transmitted from the bridge to the test vehicle, i.e., for better transmissibility, it is essential that the test vehicle be designed with as less damping as possible. In the field test, only the dynamic response and parameters of the test vehicle are made available. The contact-point response can be calculated from the recorded vehicle response by a backward procedure. For the single-degree-of-freedom (SDOF) vehicle shown in Fig. 1, the contact-point acceleration of the vehicle with damping ignored can be obtained by rearranging the equation of equilibrium for the vehicle in Eq. (1) and differentiating twice as

$$\begin{aligned} \ddot{u}_{c}\left( t \right) =\ddot{y}_{v}\left( t \right) +\frac{d^{2}\ddot{y}_{v}\left( t \right) }{\omega _{v}^{2}dt^{2}}. \end{aligned}$$

(11)

For the case with the vehicle acceleration $\ddot{y}_{v}$ given in discrete form, as in the field test, the term $d^{2}\ddot{y}_{v}/dt^{2}$ in (11) can be replaced by the central difference formula as

$$\begin{aligned} \frac{d^{2}\ddot{y}_{v}}{dt^{2}}=\frac{{\ddot{y}_{v}\vert }_{i+1}-2{\ddot{y}_{v}\vert }_{i}+{\ddot{y}_{v}\vert }_{i-1}}{{(\Delta t)}^{2}}, \end{aligned}$$

(12)

where i denotes the ith sampling point and $\Delta t$ the sampling interval. Obviously, the vehicle frequency $\omega _{v}$ in the contact-point response has been eliminated by the above back calculation procedure.

3 Brief on variational mode decomposition

The empirical mode decomposition (EMD) [18] is a signal decomposition algorithm capable of analyzing non-stationary and nonlinear data. The original signals can be decomposed into a set of band-limited intrinsic mode functions (IMFs) based on the local characteristic time scales of the data. However, previous applications have revealed that the EMD has some shortcomings, e.g., lacking rigorous mathematical basis, weak robustness against noise, and mode mixing among the IMFs. To cope with these, an alternative technique called the variational mode decomposition (VMD) was proposed, which is theoretically well founded and much more robust to sampling and noise [31].

In this study, the VMD technique will be adopted to decompose the vibration data, either experimentally sensed by the test vehicle or numerically computed in the simulation, into a number of limited bandwidth modes. Each mode updated in frequency domain is compacted around its center frequency $\omega _{k}$, with the bandwidth estimated through the squared $L^{{2}}$-norm. The VMD is essentially a generalization of the classic Wiener filter into multiple, adaptive bands. Such an underlying relationship implies that the VMD has some optimality in dealing with noise. In the following, the procedure of the VMD technique will be outlined.

Theoretically, a signal f(t) can be decomposed into a number of modes,

$$\begin{aligned} f\left( t \right) =\sum \limits _{k=1}^K {u_{k}\left( t \right) } , \end{aligned}$$

(13)

where K is the selected number of modes and $u_{k}\left( t \right)$ the kth narrow-band mode function. Computing for each mode the related signal by the Hilbert transformation, and sifting the mode’s frequency spectrum to “baseband” mixing with an exponential signal, one obtains a new modal function as follows:

$$\begin{aligned} u_{k}=\left( u_{k}\left( t \right) +i{{\mathcal {H}}[u}_{k}\left( t \right) ] \right) e^{-i\omega _{k}t}=\left[ \left( \delta \left( t \right) +\frac{i}{\pi t} \right) *u_{k}\left( t \right) \right] e^{-i\omega _{k}t}, \end{aligned}$$

(14)

where $i=\sqrt{-1}$, $\mathcal {H}[\cdot ] =$ Hilbert transform, $\delta \left( t \right) =$ Dirac function, and * $=$ convolution operator. Then, the constrained variational problem, along with the bandwidth estimated via the squared $L^{{2}}$-norm of the gradient, can be expressed as

$$\begin{aligned} \mathop {\min }\limits _{\left\{ {u_{k} } \right\} ,\left\{ {\omega _{k} } \right\} } \left\{ {\sum \limits _{k=1}^K {\left\| {\left. {\partial _{t} \left[ {\left( {\delta \left( t \right) +\frac{i}{\pi t}} \right) *u_{k} \left( t \right) } \right] e^{-i\omega _{k} t}} \right\| _{2}^{2} } \right. } } \right\} , \end{aligned}$$

(15)

where ${\partial }_{t}$ denotes partial derivative with respect to time t and $\Vert \,\,\Vert _2^2$ the squared $L^{{2}}$-norm. The quadratic penalty term and Lagrangian multiplier are both used here to construct the augmented Lagrangian:

$$\begin{aligned} L\left( \left\{ u_{k} \right\} ,\left\{ \omega _{k} \right\} ,\lambda \right)= & {} \alpha \sum \limits _{k=1}^K {\left\| \partial _{t}\left[ \left( \delta \left( t \right) +\frac{i}{\pi t} \right) {*}u_{k}\left( t \right) \right] e^{-i\omega _{k}t} \right\| _{2}^{2} } \nonumber \\&+\left\| f\left( t \right) -\sum \limits _{k=1}^K {u_{k}\left( t \right) } \right\| _{2}^{2}+ \langle \lambda (t), f(t) - \mathop {\sum }\limits _{k=1}^{K} u_k(t) \rangle , \end{aligned}$$

(16)

where $\alpha$ denotes the penalty number or balancing parameter of the data-fidelity constraint and $\lambda \left( t \right)$ is the Lagrangian multiplier.

To calculate the sub-signals and center frequencies in the Lagrangian of Eq. (16), the alternate direction method of multipliers (ADMM) is adopted herein. The optimization problem in Eq. (16) is solved in frequency domain by the Parseval/Plancherel Fourier isometry. Let K denote the total number of modes (decompositions) desired. Each of the modes (i.e., $k=1:K)$ is sequentially updated at each iteration. For the n-th iteration, the mode ${\hat{u}}_{k}^{n}$ and the corresponding frequency $\omega _{k}^{n}$ are updated using the following formulas:

$$\begin{aligned} {\hat{u}}_{k}^{n}\left( \omega \right)= & {} \frac{{\hat{f}}\left( \omega \right) -\sum \nolimits _{i<k} {{\hat{u}}_{i}^{n}\left( \omega \right) } -\sum \nolimits _{i>k} {{\hat{u}}_{i}^{n-1}\left( \omega \right) } +{\hat{\lambda }}^{n-1}\left( \omega \right) /2}{1+2\alpha \left( \omega -\omega _{k}^{n-1} \right) }, \end{aligned}$$

(17)

$$\begin{aligned} \omega _{k}^{n}\left( \omega \right)= & {} \frac{\int _0^\infty {\omega {\vert {\hat{u}}_{k}^{n}\left( \omega \right) \vert }^{2}} d\omega }{\int _0^\infty {\vert {\hat{u}}_{k}^{n}\left( \omega \right) \vert }^{2} d\omega }. \end{aligned}$$

(18)

In Eq. (17), the first summation $\sum$ goes from 1 to $k-1$ for $1\le k-1$ and the second summation $\sum$ from $k+1$ to K for $k+1\le K$. The Lagrangian multiplier ${\hat{\lambda }}$ in frequency domain is updated using the following formula:

$$\begin{aligned} {{\hat{\lambda }}^{n}\left( \omega \right) ={\hat{\lambda }}}^{n-1}\left( \omega \right) +\tau \left( {\hat{f}}\left( \omega \right) -\sum \limits _{k=1}^K {{\hat{u}}_{k}^{n}\left( \omega \right) } \right) . \end{aligned}$$

(19)

Here $\tau$ is a noise-related parameter. For noise removal, $\tau$ is taken as zero and the step in (19) is skipped. The above iterative procedure is repeated until the following condition is met:

$$\begin{aligned} \sum \limits _{k=1}^K \frac{\left\| {\hat{u}}_{k}^{n}-{\hat{u}}_{k}^{n-1} \right\| _{2}^{2}}{\left\| {\hat{u}}_{k}^{n-1} \right\| _{2}^{2}} <\varepsilon {,} \end{aligned}$$

(20)

where $\varepsilon$ denotes a preset tolerance.

4 Brief on band-pass filter (BPF)

To enhance the visibility of bridge frequencies, the band-pass filter (BPF) is used for the signal recorded by the test vehicle or numerically computed. In the following, the BPF procedure is presented.

A signal f(t) sampled at N discrete times can be expressed as

$$\begin{aligned} f{(}t{)= [}f_{0}{,} f_{1}{,} f_{2},\ldots ,f_{N-1}{],} \end{aligned}$$

(21)

which can be processed by the FFT to yield the frequency response $F{(}\omega {)}$ as

$$\begin{aligned} F\left( \omega \right) =\mathrm {FFT}\left\{ f\left( t \right) \right\} =[F_{0}{,} F_{1}{,} F_{2}{,\ldots ,}F_{M-1}{],} \end{aligned}$$

(22)

with $F_{i}$ denoting the amplitude of the discrete frequency $\omega _{i}$ and M the number of data points in frequency domain. Then, a window function $W{(}\omega {)}$ is selected to retain or eliminate the frequency band by setting a weight of unity for the retained frequency band and zero for the rest. Also, a transitional zone may be added between the retained and eliminated bands such that the weight changes gradually from unity to zero. By multiplying $W{(}\omega {)}$ with Eq. (22), one obtains

$$\begin{aligned} \begin{aligned} F_{W}\left( \omega \right) =F\left( \omega \right) W\left( \omega \right) {.} \end{aligned} \end{aligned}$$

(23)

Performing the inverse FFT to $F_{W}\left( \omega \right)$ yields the filtered response in the time domain as

$$\begin{aligned} f_{W}\left( t \right) =\mathrm {IFFT}\left\{ F_{W}\left( \omega \right) \right\} {.} \end{aligned}$$

(24)

5 Numerical modeling of the problem

The finite element procedure for simulating the problem will be outlined herein. One advantage with the finite element analysis is that the assumptions adopted in theoretical derivations, e.g., the vehicle mass $m_{v}$ is much smaller than the bridge mass mL, i.e., $m_{v}\ll mL$, can be circumvented. However, for comparison of the finite element and analytical results, road roughness is not considered in this section.

Fig. 2

Vehicle–bridge interaction element

5.1 Vehicle–bridge interaction (VBI) element

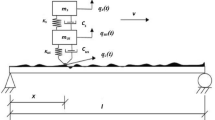
As mentioned in the preceding section, the system is modeled as a sprung mass travelling over a simply supported bridge. In this section, the finite element to be used will be summarized. Figure  2 shows the vehicle–bridge interaction (VBI) element with road surface roughness r(x). The test vehicle is modeled as a sprung mass $m_{v}$ supported by a spring of stiffness $k_{v}$ and a dashpot of damping coefficient $c_{v}$. The coordinate $x_{c}$ denotes the position of the contact point. The matrix equation for the VBI element can be written as [3]:

$$\begin{aligned}&\left[ {\begin{array}{cc} m_{v} &{} 0\\ 0 &{} \left[ m_{b} \right] \\ \end{array} } \right] \left\{ {\begin{array}{c} \ddot{q}_{v}\\ \left\{ \ddot{u}_{b} \right\} \\ \end{array} } \right\} +\left[ {\begin{array}{cc} c_{v} &{} -c_{v}\left\{ N \right\} _{c}^{T}\\ -c_{v}\left\{ N \right\} _{c} &{} \left[ c_{b} \right] +c_{v}\left\{ N \right\} _{c}\left\{ N \right\} _{c}^{T}\\ \end{array} } \right] \left\{ {\begin{array}{c} {\dot{q}}_{v}\\ \left\{ {\dot{u}}_{b} \right\} \\ \end{array} } \right\} \nonumber \\&\qquad +\left[ {\begin{array}{cc} k_{v} &{} -vc_{v}\left\{ N' \right\} _{c}^{T}-k_{v}\left\{ N \right\} _{c}^{T}\\ -k_{v}\left\{ N \right\} _{c} &{} \left[ k_{b} \right] +vc_{v}\left\{ N \right\} _{c}\left\{ N' \right\} _{c}^{T}+k_{v}\left\{ N \right\} _{c}\left\{ N \right\} _{c}^{T}\\ \end{array} } \right] \left\{ {\begin{array}{c} q_{v}\\ \left\{ u_{b} \right\} \\ \end{array} } \right\} \nonumber \\&\quad =\left\{ {\begin{array}{c} c_{v}vr_{c}^{'}+k_{v}r_{c}\\ -{(c}_{v}vr_{c}^{'}+k_{v}r_{c}+m_{v}g)\left\{ N \right\} _{c}\\ \end{array} } \right\} , \end{aligned}$$

(25)

where $q_{v}$ and $\left\{ u_{b} \right\}$ denote the displacement of the vehicle and those of the bridge element, respectively, $\left[ m_{b} \right]$, $\left[ c_{b} \right]$, $\left[ k_{b} \right]$ the mass, damping, and stiffness matrices of the bridge element, $r_{c}$ the road surface roughness at the contact point $x_{c}$, and $\{N \}_{c}$ is the cubic Hermitian function evaluated at the contact point $x_{c}$.

The vehicle displacement $q_{v}$ in Eq. (25) can be condensed to those of the bridge by a condensation procedure [3]. Then, the condensed equation can be assembled with those elements free of the vehicle to form the following equation:

$$\begin{aligned} \left[ M \right] \left\{ \ddot{u} \right\} +\left[ C \right] \left\{ {\dot{u}} \right\} +\left[ K \right] \left\{ u \right\} =\left\{ F \right\} , \end{aligned}$$

(26)

where [M], [C], and [K] denote the mass, damping, and stiffness matrices, $\{u\}$ the displacement vector, and $\{F\}$ the external force vector of the VBI system. The response of the bridge in Eq. (26) can be solved by the Newmark-$\beta$ method (with $\beta =$ 0.25 and $\gamma =$ 0.5 for unconditional stability) [47] via updating of the acting position at each time step, along with the vehicle response calculated by a backward procedure.

5.2 Verification of analytical solution

In this section, the accuracy of the analytical solution and feasibility of using the vehicle and contact-point responses to extract bridge frequencies will be numerically assessed. The following properties are adopted for the simply supported bridge: length $L = 25\hbox { m}$, elastic modulus $E = 2.75 \times 10^{{10}}\hbox { N/m}^{{2}}$, mass per unit length $m = 2000$ kg/m, and moment of inertia $I = 0.10\hbox { m}^{{4}}$, and the following for vehicle: mass $m_{v} = 900\hbox { kg}$, elastic coefficient $k_{v} = 1780\hbox { kN/m}$. The time step ${\Delta }t$ used in the marching scheme is 0.001s. The vehicle and first four bridge frequencies calculated according to Eqs. (10) and (6c) are listed in Table 1.

Table 1 Vehicle and bridge frequencies

For a vehicle speed of $v = 5\hbox { m/s}$ (18 km/h), the accelerations of the test vehicle calculated analytically in Eq. (8) and by the finite element method (FEM) are plotted in Fig. 3. In addition, the accelerations of the contact point calculated analytically in Eq. (7) and from the bridge response by the FEM are shown in Fig. 4, along with the result back-calculated from the car-body response by Eq. (11). Although the contact-point response obtained directly from the bridge is difficult to capture in practice, it serves as a good reference for comparison with the other results. As revealed in Figs. 3 and 4, the responses obtained by FEM all agree well with the analytical solutions. Specifically, the contact-point responses obtained directly from the bridge and by the backward procedure of Eq. (11) from the vehicle response agree well for both the time and frequency responses in Fig. 4a and b, respectively.

Fig. 3

Acceleration response of test vehicle: a acceleration; b spectrum

Comparing Fig. 3b with Fig. 4b, one finds that the bridge frequencies extracted from the contact point response in Fig. 4b are more outstanding than from the vehicle response in Fig. 3b, especially for the higher frequencies $\omega _{{b}_{{,2}}}$, $\omega _{{b}_{{,3}}}$ and $\omega _{{b}_{{,4}}}$, in consistence with the finding of Ref. [41]. In addition, the shifting effect exists in the bridge frequencies $\omega _{b,n}$ extracted from both the test vehicle and the contact point, i.e., they appear in the form of $\omega _{b,n}-n\pi v/L$ and $\omega _{b,n}+n\pi v/L$ as in Eqs. (8) and (7). Particularly, for the higher bridge frequencies detected from the contact-point response in Fig. 4b, the shifts, i.e., $n\pi v/L$, can be clearly observed. Another feature of the contact-point response is that the vehicle frequency was totally eliminated, as can observed by comparing Fig. 3b with 4b. In previous field tests [39, 40], it was reported that the car body frequency can be so high that it overshadows the bridge frequencies for extraction. Since the contact-point response obtained by the backward procedure is quite accurate, as shown in Fig. 4, it can be reliably used in the numerical and experimental studies to follow.

Fig. 4

Acceleration response of contact point: a acceleration; b spectrum

6 Numerical study and validation

First, the EMD will be used to generate results for comparison with those from the VMD. Then, the test vehicle speed will be investigated for its effect on sampling and excitation of the bridge. Since the bridge frequency extraction will be affected by road surface roughness, a shadowing effect, the BPF technique will be employed in advance to filter out the undesired noise to ensure the quality of the VMD results.

6.1 Extraction of bridge frequencies by EMD or VMD

To assess the capability of the VMD and EMD in retrieving bridge frequencies, both the vehicle and contact-point responses obtained in Sect. 5.2 are used here.

Scenario 1: Extraction of bridge frequencies from vehicle response

Firstly, both the EMD and VMD are employed to decompose the vehicle response. The time history acceleration of the test vehicle obtained by the finite element analysis is shown in Fig. 3a. Figure 5a shows the two IMFs and residue decomposed by the EMD, along with the FFT spectra in Fig. 5b. From Fig. 5b, one observes that the EMD technique fails to detect the higher frequencies $\omega _{b,3}$ and $\omega _{b,4}$, as the energies associated with them are generally low. Note that the frequency $\omega _{d}$ appearing in $c_{5}$ and $c_{6}$ denotes the driving frequency of the test vehicle. For comparison, the modes decomposed by the VMD and the associated FFT spectra are plotted in Fig. 6a and b, respectively. From the spectra $u_{{2}}-u_{{5}}$ in Fig. 6b, one observes that all the bridge frequencies listed in Table 1 have been successfully decomposed and detected, together with the driving frequency $\omega _{d}$ as the first mode $u_{{1}}$ in Fig. 6b. In comparison with the EMD, the VMD is an effective and elegant technique for identifying the bridge frequencies, especially of the higher modes.

Fig. 5

Bridge frequencies extracted from the vehicle response by EMD: a modes; b spectra

Fig. 6

Bridge frequencies extracted from the vehicle response by VMD: a modes; b spectra

Scenario 2: Extraction of bridge frequencies from contact-point response

In this scenario, the contact-point acceleration of the test vehicle shown in Fig. 4a is adopted to demonstrate the superiority of the VMD in decoupling the frequency components. Figure 7a shows the ten decomposed IMFs and residue processed by the EMD, along with their FFT spectra in Fig. 7b. Due to the favorable amplification effect brought by the contact-point response for higher frequencies, the EMD can also detect all the bridge frequencies listed in Table 1. However, there does exist the mode-mixing problem in Fig. 7b, in that one frequency may appear in different decompositions, while more than one frequency may appear in a single decomposition.

Fig. 7

Bridge frequencies extracted from the contact-point response by EMD: a modes; b spectra

With the number of modes desired set to four in advance, the modes decomposed by the VMD and the associated spectra are plotted in Fig. 8. Notably, each of the four bridge frequencies can be sequentially andneatly identified from the four spectra in Fig. 8b, meaning that no mode-mixing has occurred with the VMD result. This is another advantage of using the contact point response for extracting the bridge frequencies.

Fig. 8

Bridge frequencies extracted from the contact-point response by VMD: a modes; b spectra

Besides, by comparing Fig. 8b (for contact-point response) with Fig. 6b (for vehicle response), one observes that one more mode is required in the decomposition if the vehicle response is to be used to extract the bridge frequencies. This is likely due to the fact that the driving frequency $\omega _{d}$ has a magnitude larger than those of the high-mode bridge frequencies $\omega _{b,2}$, $\omega _{b,3}$ and $\omega _{b,4}$ in the vehicle response.

From the above comparison based on Fig. 7 (for vehicle response) and Fig. 8 (for contact-point response) for the two techniques EMD and VMD, it is confirmed that the VMD is an effective and elegant tool for retrieval of bridge frequencies, since it allows more bridge frequencies to be neatly identified using less decompositions, while there exists no problem of mode mixing. In addition, the performance of the VMD is enhanced when using the contact-point response, as the vehicle frequency and its overshadowing effect have been totally circumvented.

6.2 Effect of vehicle speed on applicability of VMD

Vehicle speed, a parameter crucial to sampling and excitation of the test bridge, is to be investigated herein. In this connection, three vehicle speeds, i.e., 2, 5, and 10 m/s (7.2, 18, and 36 km/h), are considered to show the applicability of the VMD. Except for the vehicle speed, all the other properties of the vehicle and bridge are identical to those used in Sect. 5.2. The spectra of the vehicle responses for the three speeds processed by the VMD are plotted in Fig. 9. For comparison, the results of the three contact-point responses are plotted in Fig. 10.

Fig. 9

Bridge frequencies extracted from the vehicle response by VMD for three vehicle speeds: a 2 m/s (7.2 km/h); b 5 m/s (18 km/h); c 10 m/s (36 km/h)

Fig. 10

Bridge frequencies extracted from the contact-point response by VMD for three vehicle speeds: a 2 m/s (7.2 km/h);b 5 m/s (18 km/h); c 10 m/s (36 km/h)

As can be observed from Fig. 9 (from left to right), all the four bridge frequencies listed in Table 1 can be identified, and their amplitudes increase as the vehicle speed increases from 2 to 10 m/s (7.2 to 36 km/h), mainly caused by the larger energy brought by higher vehicle speeds. Also, for higher vehicle speeds, the driving frequency $\omega _{d}$ and vehicle frequency $\omega _{v}$ become visible, while the shifting $n\pi v/L$ clearly splits each frequency into two separate ones, i.e., $\omega _{b,n}-n\pi v/L$ and $\omega _{b,n}+n\pi v/L$.

A comparison of Fig. 10 (for contact-point response) with Fig. 9 (for vehicle response) shows that the vehicle response always requires more decompositions, especially for vehicle speeds of 5 and 10 m/s (18 and 36 km/h), due to involvement of the driving frequency $\omega _{d}$ and/or the vehicle frequency $\omega _{v}$. In contrast, all the bridge frequencies can be neatly identified from the contact point response with no extra decomposition.

Although higher speeds for the test vehicle can cause larger excitation on the bridge, too high a vehicle speed is not recommended, to ensure that sufficient data are sampled during each run of measurement in the field test, while keeping the shifting effect to the minimum. From the above analysis, it is concluded that the VMD can be effectively applied to the contact-point response, rather than the vehicle response, to extract bridge frequencies for the range of speeds considered.

6.3 Effect of road surface roughness on VMD-BPF

In the previous sections, the road surface roughness was neglected. Since such an effect can reduce the effectiveness of techniques used in bridge frequency extraction, it will be investigated herein with regard to the performance of the VMD-BPF procedure. Figure 11 shows the road surface roughness constructed by the power spectral density (PSD) function of ISO 8608 with class A [37, 38, 48], along with its displacement PSD in Fig. 12. The smoothed roughness profile shown as the red curve in Fig. 11 is obtained via processing of the ISO roughness profile by the moving average filter (MAF) [49], to roughly account for the fact that the real contact between the wheel and the bridge is a circular surface rather than a point [50]. To simulate the vibration of the test vehicle moving over the bridge with rough surface, the VBI element presented in Eq. (25) will be used, and the properties of the vehicle and bridge are identical to those used in Sect. 5.2.

Fig. 11

Original and smoothed roughness profiles

Fig. 12

Displacement power spectral density

Fig. 13

Acceleration response of test vehicle moving over bridge with rough surface

The acceleration response of the vehicle moving over the bridge with rough surface is plotted in Fig. 13. In order to enhance the feasibility of the VMD, the BPF is applied in advance to filter out frequencies larger than 50 Hz. The results decomposed by the VMD-BPF are plotted in Fig. 14a, along with the FFT spectra in Fig. 14b. As can be seen from the spectra in Fig. 14b, all the bridge frequencies have been clearly identified, except the third frequency $\omega _{b{,3}}$, which is marginally visible in $u_{{3}}$ and $u_{{4}}$ of Fig. 14b, due to the pollution brought by road roughness. From this example, one concludes that the existence of road roughness puts a limit on the number of bridge frequencies that can be identified from the vehicle response by the VMD-BPF

Fig. 14

Bridge frequencies extracted from the vehicle response moving over bridge with rough surface by VMD-BPF: a modes; b spectra

The advantage of contact-point response is that it can totally eliminate the influence of the vehicle frequency, but in the backward procedure of Eq. (11), high-frequency responses of roughness are made more obvious. For this reason, the BPF is adopted to deal with the unnecessary high frequencies.

For comparison, the acceleration of the contact point is plotted in Fig. 15. Correspondingly, the decomposed modes and FFT spectra generated by the VMD-BPF are plotted in Fig. 16a and b, respectively. Previously, it was noted that the bridge frequencies are more prominent in the contact point response, i.e., Fig. 4b, than the vehicle response, i.e., Fig. 3b. For the same reason, one finds that the first four bridge frequencies $\omega _{b,1}$, $\omega _{b,2}$, $\omega _{b,3}$, and $\omega _{b,4}$ can be neatly and sequentially identified from the spectra in Fig. 16b without mode mixing, in comparison with Fig. 14b. The above result also indicates the relative advantage of using the contact point response for extraction of bridge frequencies in the presence of road roughness, partly due to elimination of the vehicle frequencies $\omega _{v}$ and the positive effect of the BPF.

Fig. 15

Acceleration response of contact point for bridge with roughness

Fig. 16

Bridge frequencies extracted from the contact-point response with road surface roughness by VMD-BPF: a modes; b spectra

7 Experimental study and validation of VMD-BPF

In this section, the VMD-BPF technique will be adopted to deal with the experimental data to show its capability in extracting bridge frequencies. Also, the superiority of the contact-point response over the vehicle response will be experimentally verified.

7.1 Description of the test bridge

The Turtle Mountain Bridge located in Chongqing University, Campus B, is tested herein. It is a two-span concrete box girder bridge with a total length of 55.2 m ($=$ 29.2 m $+$ 26 m), as shown in Fig. 17. The bridge deck has a width of 5.2 m and a height of 1.6 m. The dimensions of the bridge are shown in Fig. 18. Due to the lack of structural data, no numerical analysis has been conducted of the bridge. The test results are affected by the noises transmitted from the state highway G75 underneath via the three supports.

Fig. 17

Test bridge

Fig. 18

Dimensions of the bridge: a two-span test bridge; b cross section (in mm)

The bridge frequencies directly measured by vibration sensors mounted on the bridge surface excited by the jumping of a group of people are listed in Table 2 and plotted in Fig. 19, which will be used as the basis of comparison. Particularly, the first two frequencies $\omega _{b,1}$ and $\omega _{b,2}$ were identified to be the flexural (vertical) modes of the bridge, and the third frequency $\omega _{b,3}$ that can be marginally identified relates to the torsional mode. More details on the direct measurement are available in Ref. [40].

Table 2 Vehicle and bridge frequencies identified by direct measurement

Fig. 19

Responses of direct measurement of the bridge: a acceleration; b spectrum

7.2 Description of the test vehicle

In the field test, the bridge frequencies will be extracted using the single-axle test vehicle shown in Fig. 20, of which the details are available in Ref. [40]. The two-wheel trailer is made of steel, weighing about 0.9 t, and has no suspension system. By adjusting the weight of the test vehicle or changing different types of wheels, the desired dynamic properties of the test vehicle can be obtained. According to the study in Ref. [37], a pair of solid rubber tires is adopted to increase the stiffness of the test vehicle such that a higher vehicle frequency $\omega _{v}$ can be obtained. Since the test vehicle cannot move by itself, it will be towed by a 1.5-t passenger car (Mazda CX4) during the test. To ensure that sufficient data can be collected during the test, the tractor is allowed to move very slowly, roughly 0.32 m/s (1.2 km/h). Three vibration sensors (PCB 352C33) are installed each on the left, center, and right sides of the vehicle axle. In the following, only the signal collected by the sensor fitted at the center of the axle will be processed by the VMD. Before the field test was conducted, a flat (ground) road test was conducted for the vehicle to get its frequency in the moving state, for which the result is shown in Fig. 21 and Table 2.

To alleviate the influence of road surface roughness, while increasing the vibration amplitudes of bridges, external excitations have often been introduced in the measurement of bridges. In this section, the way similar to the one used in Sect. 7.1 was adopted during the test, namely by inviting a group of students to jump around (but not too near) the moving test vehicle. Since the total weight of the students is negligible compared with the bridge, it can assist in extracting the dynamic properties of this narrow and stiff bridge.

Fig. 20

Single-axle test vehicle

Fig. 21

Responses of the vehicle moving over flat road: a acceleration; b spectrum

7.3 Results and discussions

The acceleration response recorded by the sensor fitted on the vehicle moving over the centerline of the bridge is shown in Fig. 22. The thick vertical lines around 61 s in the time history of acceleration of the vehicle in Fig. 22 are caused by the small impact between the test vehicle and the tractor during the field test. For the present purposes, only bridge frequencies less than 10 Hz are considered, as these are the ones detected by the direct measurement in Fig. 19. To enhance the identifiability of bridge frequencies, the BPF is first applied to the original signal to filter out unexpected noises prior to processing by the VMD. For the vehicle response, the result of decomposition by the VMD-BPF technique is plotted in Fig. 23, which indicates that the first two frequencies of the bridge can be clearly identified from the first two modes $u_{1}$ and $u_{2}$, but the vehicle frequency appears twice, i.e., in the two modes $u_{3}$ and $u_{4}$.

Fig. 22

Response of test vehicle moving along bridge’s centerline

Fig. 23

Bridge frequencies extracted from the vehicle response by VMD-BPF in field test: a modes; b spectra

The acceleration response of the contact point of the moving vehicle calculated by the backward procedure is plotted in Fig. 24. Correspondingly, the result of decomposition by the VMD-BPF is plotted in Fig. 25a along with the FFT spectra in Fig. 25b. From the first two modes $u_{1}$ and $u_{2}$, the first two bridge frequencies can be clearly identified. The final mode $u_{3}$ is the residue caused by the road roughness and environmental noise that have not been completely filtered out. A comparison of Figs. 25b with  23b indicates that the vehicle frequency has been removed from the contact point response. This verifies the applicability of the backward calculation procedure, Eq. (11), for field measurement.

Fig. 24

Contact-point responses of test vehicle moving along centerline

Fig. 25

Bridge frequencies extracted from the contact-point response by VMD-BPF in field test: a modes; b spectra

It should be noted that the third frequency $\omega _{b,3} (= 6.78$ Hz) that was marginally observed in the direct measurement was not detected using either the vehicle or the contact-point responses. This is mainly due to the overshadowing effect of the roughness frequencies.

The above experimental study indicates that both the vehicle and contact-point responses can be used by the VMD-BPF to exact the first two bridge frequencies. However, the result generated by the contact point response is neater and more elegant than the vehicle response. The advantage is clearer when the stop band to be filtered out is more accurately selected. For instance, the roughness and noise effect in the residue $u_{3}$ can be removed as well, if the stop band is selected for frequencies larger than 7 Hz. In practice, however, it is known that to estimate the most proper stop band for the VMD application involves some sort of experience, as well as operability, before the frequencies of the bridge are made available.

8 Conclusions

The vehicle scanning method for measuring bridge frequencies from a passing vehicle is an attractive method. However, its efficacy may be reduced by factors such as vehicle frequency and road surface roughness. To this end, the variational mode decomposition with band-pass filter (VMD-BPF) is proposed for extraction of bridge frequencies not restricted to the first mode. The performance of such a technique is generally enhanced through use of the contact-point response calculated backward from the vehicle response, due to removal of the vehicle frequency. In this study, both the vehicle and contact-point responses generated by numerical and experimental studies have been analyzed to assess the feasibility of the proposed method.

Based on the numerical and experimental studies, the following conclusions are drawn:

• (1) The VMD is more efficient and elegant than the EMD in detecting the first few frequencies of the bridge from the vehicle response, since less decompositions are needed with basically no mode-mixing phenomenon.

• (2) Basically, the vehicle speed does not affect the performance of the VMD, however, it is recommended not too high in practice for the sake of data sampling and frequency-splitting minimization.

• (3) In the presence of surface roughness, the capability of the VMD-BPF to detect bridge frequencies remains good, especially when using the contact-point response and a proper stop band.

• (4) It was experimentally verified that the VMD-BPF technique is a reliable method for extracting the first few bridge frequencies from both the vehicle and contact-point responses.

• (5) In the numerical and experimental studies, the contact point response has been demonstrated to be better than the vehicle response for use with the VMD-BPF technique to extract bridge frequencies.