Size-dependent electro-static analysis of smart micro-sandwich panels with functionally graded core

Abstract

This paper investigates the electro-static response of smart micro-sandwich panels with functionally graded core, nano-composite facing, and piezoelectric layers. To consider the size-dependent effect, nonlocal theory is adopted to governing equations and boundary conditions. Three-dimensional approach is implemented that takes into account shear effect of thick core and drastic changes of sandwich panel and free from spurious constraints of equivalent plate theories. Closed-form solution is obtained in systematic step-by-step procedure for smart micro-panels to solve the coupled nonlocal differential equations analytically. The obtained results are compared with finite element results for the case of isotropic thick plate and excellent agreement between result is revealed. A detailed parametric study is conducted to bring out the effect of size-dependent parameter, functionally graded material, length-to-thickness ratio, and aspect ratio on the bending behavior of smart micro-sandwich panels.

1 Introduction

Micro-sandwich panels can be considered an important feature of many micro-electro-mechanical systems (MEMS) and devices. They have attracted a great deal of interest in recent years especially in the field of mechanical engineering. These structures consist of two facings and a thick core which provide a high bending modulus at low weight. Smart micro-sandwich panels are particular types of micro-sandwich panels that consist of two embedded piezoelectric layers as sensor and actuator. These smart features respond statically to an applied electric potential in the actuator. Due to electric displacement in the sensor layer, the mentioned features can also be used in sensing micro-mechanical loads, thus these features are of particular interest to designers because of their application as memory, valves, and optical/electrical switches [1].

Bending and vibration behavior of these features have been studied, first in the traditional mechanic literature through using an equivalent single layer (ESL) as well as layer-wise methods used for modeling of layered sandwich structures [2]. The methods of this approach consist of classical plate/beam theory (CPT/CBT), first-order shear deformation theory (FSDT), higher-order shear deformation theory (HSDT), and other non-polynomial displacement field theories. For example, Williams et al. [1] studied the instability of an initially curved micro-beam with clamped boundary conditions. They determined the equilibrium path for an electro-statically actuated micro-beam. Shoghmand and Ahmadian [3] considered a micro-resonator made of functionally graded (FG) material and computed natural frequencies and mode shapes of the system using linear analysis.

In MEMS and NEMS, it is found that size effect parameters play an important role and should not be ignored in small scale devices. The size effect has been experimentally observed in small-scale structures [4]. Three main size-dependent theories exist: nonlocal elasticity theory [5], strain gradient theory [6], and couple stress theory [7]. These theories are adopted in traditional theories such as CPT, FSDT, and HSDT to capture the size effects of micro plates. Sobhy and Radwan [8] considered a four-variable deformation plate theory and studied bending analysis of viscoelastic sandwich microplates with nanocomposite facing and homogeneous core under the effects of a 2D magnetic field. Arefi and Zenkour [9] investigated transient analysis of a sandwich nano-plate with viscoelastic core and piezoelectric face sheets under thermo-electro-mechanical loads by using nonlocal theory as well as two-variable sinusoidal shear deformation plate theory. The free vibration of a bi-directional FG nano-beam was studied by Nejad and Hadi [10]. They considered the size effect of the nano-beam by employing nonlocal theory. Buckling of the mentioned bi-directional FG nano-beam was also studied by Nejad et al. [11]. Li et al. [12] investigated the bending behavior of sandwich plates with FG soft-core and different face sheets. Brischetto et al. [13] studied the free vibration of a sandwich panel with FGM core through 3D exact and generalized 2D methods for cylindrical, spherical, and flat panels. Arefi and Zenkour [14] studied simplified shear and normal deformations using nonlocal theory for bending of functionally graded piezomagnetic sandwich nanobeams in a magneto-thermo-electric environment. They also investigated curved nano-beam considering the size effect via nonlocal theory [15]. Mohammadimehr et al. [16] studied the free vibration of a sandwich panel with higher-order theory as well as modified strain gradient theory. They also investigated the panel in various aspects such as electrical boundary conditions and size effect. The size effect was investigated by Arefi and Zenkour [17] for a microbeam with two integrated piezolayers. In their study, the effect of a visco-Winkler–Pasternak foundation is considered. Farajpour et al. [18] developed a nonlocal continuum model for the nonlinear free vibration of nano-plates under electric and magnetic potentials by using the nonlocal elasticity theory and Hamilton’s principle. They found that the natural frequency of nano-plates can be tuned by adjusting the values of external electric and magnetic potentials. Arefi and Zenkour [19] derived the governing equations of a sandwich nano-plate with nano-core and two piezo-magnetic face-sheets based on the sinusoidal shear deformation plate theory. In an other interesting work, employing trigonometric plate theory, they focused on the bending behavior of a sandwich nanoplate with piezoelectric face-sheets [20]. They also studied bending and vibrational behavior of a sandwich micro-beam integrated with piezo-magnetic face-sheets by using strain gradient and FSDT theories [21]. Zhang et al. [22] compared the Eringen nonlocal plate theory with the Hencky barnet model and nonlocal theory. They analyzed the bending behavior of a simply supported plate under a point load and calibrated the nonlocal small scale coefficient by matching the exact deflections obtained from other theories. Lazar et al. [23] presented three-dimensional nonlocal anisotropic elasticity by incorporating six internal characteristic lengths. They applied their theory to straight dislocations in bcc Fe and showed that the considered theory can predict nonsingular anisotropic stress. It is worth mentioning that for thick sandwich panels, the shear effect of the sandwich layers (especially its core) is very important and this effect should be considered via an appropriate high order theory such as HSDT or elasticity theory [24, 25].

Beside the numerous analytical and numerical studies, exact elasticity solutions have been developed for traditional sandwich panels due to their importance in the optimization and validation of other model-based theories [26]. Pagano [27] implemented a pioneering work that provided closed-form elasticity solutions for bending of cross-ply flat composite laminates. Kardomateas [28] presented a three-dimensional (3D) elasticity solution for sandwich panels with orthotropic layers in special cases. Kardomateas and Phan [29] presented a 3D elasticity solution for sandwich beams/wide plates with orthotropic phases. Venkataraman and Sanker [30] presented an elasticity solution for stresses in a sandwich beam with FG core. Pan and Han [31] presented an exact solution for functionally graded and layered magneto-electro-elastic plates. Kashtalyan and Menshykova [32] presented a three-dimensional elasticity solution for sandwich panels with functionally graded core. A semi-analytical method for vibration analysis of doubly curved FG sandwich panels and shells of revolution was presented by Wang et al. [33]. Kardomateas et al. [34] presented the elasticity solution for curved sandwich beams/panels and validated the solution with structural theories. Following Kardomateas and his coworkers [34], Shaban and Mazaheri [25] presented the two-dimensional elasticity solution for a five layer composite panel with orthotropic layer and piezoelectric layers as sensor and actuator.

In this work, the electro-static governing equations for a smart micro-sandwich panel with a functionally graded core and nano-composite sheets in addition to the sensor and actuator layers are solved analytically by considering the size effect via the nonlocal theory. In this regard, first the elasticity solution is derived for the smart micro-sandwich panel under study. Then, the proposed elasticity solution is examined by comparing the results with finite element simulations. Finally, the proposed elasticity solution is employed to conduct a parametric study of the so-called smart micro-sandwich panel. The presented closed-form solution for these features is of interest for researchers due to its accuracy, simplicity, and low computational cost.

Fig. 1

Schematic presentation of smart micro-sandwich panels with FG core, nanocomposite face sheets and piezoelectric sensor and actuator layers

2 Elasticity solution

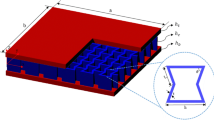
Consider a five-layer sandwich panel as shown in Fig. 1. As shown in this figure, the panel has an FGM thick core and two facing sheets made of nano-composite materials. Also, two piezoelectric layers are attached to the bottom and upper faces of the panel as sensor and actuator, respectively. The panel is exposed to an external sinusoidal pressure load as:

$$\begin{aligned} Q\left( {x_{1} ,x_{2} ,x_{3} } \right) = \,q_{0} \sin \left( {\frac{{\pi x_{1} }}{a}} \right) \, \sin \left( {\frac{{\pi x_{2} }}{b}} \right) . \end{aligned}$$

(1)

An exact solution for the panel based on 3D elasticity theory is proposed in this study. With respect to this, the nonlocal governing equations are derived at the beginning stage of the study. Then, the constitutive equations for the piezoelectric, FGM core, and facing sheets are determined. Thereafter, analytical solutions are obtained for the characteristic equations and the solution procedures are described for each of them. The electro-static analysis is completed by applying suitable continuity and boundary conditions at the final stage.

2.1 Piezoelectric layers

According to Eringen’s nonlocal elasticity theory [5], the size effect parameter is taken into consideration by incorporating a scale parameter $\delta$ into traditional continuum models. In nonlocal elasticity, the small length effects cannot be ignored, and the stress at a reference point depends on the strain at all other points of the continuum [35]. The differential constitutive relation of stress is

$$\begin{aligned} \left( {1 - \delta ^{2} \,\nabla ^{2} } \right) \sigma _{{ij}}^{{nl}} = \sigma _{{ij}}^{l}, \end{aligned}$$

(2)

where $\nabla ^{2}={\partial ^{2}} / {\partial x_{i} \partial x_{i}}, \,i=1,2,3$ is the Laplacian operator. $\sigma _{ij}^{nl}$ and $\sigma _{ij}^{l}$ are the nonlocal and local (macroscopic) stress tensor components, respectively. The constitutive equations of piezoelectric materials for macroscopic stress $\sigma _{ij}^{l}$ in Cartesian coordinates can be presented as [36]:

$$\begin{aligned} \left\{ {\vec {{\sigma }}^{l}} \right\} =\left[ c \right] \left\{ {\vec {{\varepsilon }}} \right\} -\left[ e \right] ^{T}\left\{ {\vec {{\mathbb {E}}}} \right\} . \end{aligned}$$

(3)

In addition to above equation, the constitutive relation between the electric displacement vector in terms of strain and electrical field vectors is as follows [36]:

$$\begin{aligned} \left\{ {\vec {{D}}} \right\} =\left[ e \right] \left\{ {\vec {{\varepsilon }}} \right\} +\left[ \eta \right] \left\{ {\vec {{\mathbb {E}}}} \right\} . \end{aligned}$$

(4)

In Eqs. (3–4), $\left\{ {\vec {{\sigma }}^{l}} \right\} =\left\{ {{\begin{array}{*{20}c} {\sigma _{11}^{l} } &{} {\sigma _{22}^{l} } &{} {\sigma _{33}^{l} } &{} {\tau _{23}^{l} } &{} {\tau _{13}^{l} } &{} {\tau _{12}^{l} } \\ \end{array} }} \right\} ^{T}$, $\left\{ {\vec {{\varepsilon }}} \right\} =\left\{ {{\begin{array}{*{20}c} {\varepsilon _{11} } &{} {\varepsilon _{22} } &{} {\varepsilon _{33} } &{} {\gamma _{23} } &{} {\gamma _{13} } &{} {\gamma _{12} } \\ \end{array} }} \right\} ^{T}$, $\left\{ {\vec {{\mathbb {E}}}} \right\} =\left\{ {{\begin{array}{*{20}c} {{\mathbb {E}}_{1} } &{} {{\mathbb {E}}_{2} } &{} {{\mathbb {E}}_{3} } \\ \end{array} }} \right\} ^{T}$ and $\left\{ {\vec {{D}}} \right\} =\left\{ {{\begin{array}{*{20}c} {D_{1} } &{} {D_{2} } &{} {D_{3} } \\ \end{array} }} \right\} ^{T}$ denote the local stress vector, the strain vector, the electric field vector, and the electrical displacement vector. The according matrixes are as follow:

$$\begin{aligned}&\quad&\quad \left[ c \right] =\left[ {{\begin{array}{*{20}c} {c_{11} } &{}\quad {c_{12} } &{}\quad {c_{13} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {c_{12} } &{}\quad {c_{22} } &{}\quad {c_{23} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {c_{13} } &{}\quad {c_{23} } &{}\quad {c_{33} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {c_{44} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {c_{55} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {c_{66} } \\ \end{array} }} \right] ,\left[ e \right] =\left[ {{\begin{array}{*{20}c} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {e_{5} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {e_{4} } &{}\quad 0 &{}\quad 0 \\ {e_{1} } &{}\quad {e_{2} } &{}\quad {e_{3} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ \end{array} }} \right] , \nonumber \\&\left[ \eta \right] =\left[ {{\begin{array}{*{20}c} {\eta _{1} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\eta _{2} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {\eta _{3} } \\ \end{array} }} \right] . \end{aligned}$$

(5)

[c] is the stiffness matrix that involves material constants as shown in the above relation. $[\eta ]$ is the dielectric constant matrix, and [e] refers to the piezoelectric constants which couple elastic stresses to electrical displacements and vice versa. The components of the elastic strain are given in terms of the three components of the displacement field, $u_{1}$, $u_{2}$, and $u_{3}$, as follows:

$$\begin{aligned} \varepsilon _{ij} =\frac{1}{2}\left( {\frac{\partial u_{i} }{\partial x_{j} }+\frac{\partial u_{j} }{\partial x_{i} }} \right) . \end{aligned}$$

(6)

The three mechanical equilibrium equations in the absence of body forces are:

$$\begin{aligned} \frac{\partial \sigma _{ij}^{nl} }{\partial x_{j} }=0. \end{aligned}$$

(7)

As can be seen in Eq. (7), in nonlocal elasticity theory, the three mechanical equilibrium equations are given in terms of the nonlocal stress components $\sigma _{ij}^{nl}$. So, the constitutive mechanical relation cannot be used directly in the mentioned equilibrium equations. To overcome this problem, the Laplacian operator may be applied to the equations of motions as follows:

$$\begin{aligned} \nabla ^{2}\left\{ {\frac{\partial \sigma _{x}^{nl} }{\partial x_{1} }+\frac{\partial \tau _{xy}^{nl} }{\partial x_{2} }+\frac{\partial \tau _{xz}^{nl} }{\partial x_{3} }} \right\}= & {} \nabla ^{2}\left\{ {\frac{\partial \sigma _{x}^{nl} }{\partial x_{1} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{xy}^{nl} }{\partial x_{2} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{xz}^{nl} }{\partial x_{3} }} \right\} =0, \nonumber \\ \nabla ^{2}\left\{ {\frac{\partial \tau _{xy}^{nl} }{\partial x_{1} }+\frac{\partial \sigma _{y}^{nl} }{\partial x_{2} }+\frac{\partial \tau _{yz}^{nl} }{\partial x_{3} }} \right\}= & {} \nabla ^{2}\left\{ {\frac{\partial \tau _{xy}^{nl} }{\partial x_{1} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \sigma _{y}^{nl} }{\partial x_{2} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{yz}^{nl} }{\partial x_{3} }} \right\} =0, \nonumber \\ \nabla ^{2}\left\{ {\frac{\partial \tau _{xz}^{nl} }{\partial x_{1} }+\frac{\partial \tau _{yz}^{nl} }{\partial x_{2} }+\frac{\partial \sigma _{z}^{nl} }{\partial x_{3} }} \right\}= & {} \nabla ^{2}\left\{ {\frac{\partial \tau _{xz}^{nl} }{\partial x_{1} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{yz}^{nl} }{\partial x_{2} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \sigma _{z}^{nl} }{\partial x_{3} }} \right\} =0. \end{aligned}$$

(8)

The right handside of the above equations can be rewritten as:

$$\begin{aligned} \nabla ^{2}\left\{ {\frac{\partial \sigma _{x}^{nl} }{\partial x_{1} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{xy}^{nl} }{\partial x_{2} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{xz}^{nl} }{\partial x_{3} }} \right\}= & {} \frac{\partial }{\partial x_{1} }\left\{ {\nabla ^{2}\sigma _{x}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\nabla ^{2}\tau _{xy}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\nabla ^{2}\tau _{xz}^{nl} } \right\} , \nonumber \\ \nabla ^{2}\left\{ {\frac{\partial \tau _{xy}^{nl} }{\partial x_{1} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \sigma _{y}^{nl} }{\partial x_{2} }} \right\} +\nabla ^{2}\left\{ {\frac{\partial \tau _{yz}^{nl} }{\partial x_{3} }} \right\}= & {} \frac{\partial }{\partial x_{1} }\left\{ {\nabla ^{2}\tau _{xy}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\nabla ^{2}\sigma _{y}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\nabla ^{2}\tau _{yz}^{nl} } \right\} , \nonumber \\ \nabla ^{2}\left\{ {\frac{\partial \tau _{xz}^{nl} }{\partial x_{1} }+\frac{\partial \tau _{yz}^{nl} }{\partial x_{2} }+\frac{\partial \sigma _{z}^{nl} }{\partial x_{3} }} \right\}= & {} \frac{\partial }{\partial x_{1} }\left\{ {\nabla ^{2}\tau _{xz}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\nabla ^{2}\tau _{yz}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\nabla ^{2}\sigma _{z}^{nl} } \right\} . \end{aligned}$$

(9)

Multiplying Eq. (9) by $\delta ^{2}$ and subtracting Eq. (7) from Eq. (9) leads to

$$\begin{aligned}&\frac{\partial }{\partial x_{1} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \sigma _{x}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{xy}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{xz}^{nl} } \right\} =0, \nonumber \\&\frac{\partial }{\partial x_{1} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{xy}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \sigma _{y}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{yz}^{nl} } \right\} =0, \nonumber \\&\frac{\partial }{\partial x_{1} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{xz}^{nl} } \right\} +\frac{\partial }{\partial x_{2} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \tau _{yz}^{nl} } \right\} +\frac{\partial }{\partial x_{3} }\left\{ {\left( {1-\delta ^{2}\nabla ^{2}} \right) \sigma _{z}^{nl} } \right\} =0, \end{aligned}$$

(10)

which leads to

$$\begin{aligned} \frac{\partial \sigma _{ij}^{l} }{\partial x_{j} }=0, \end{aligned}$$

(11)

where $\sigma _{ij}^{l}$ are the local stress components. More details can be found in Ref. [37]. Furthermore, the three electrostatic charge equations are

$$\begin{aligned} \frac{\partial D_{i} }{\partial x_{i} }=0. \end{aligned}$$

(12)

The electric field-electric potential relations can be proposed as

$$\begin{aligned} E_{i} =-\frac{\partial \psi }{\partial x_{i} }, \end{aligned}$$

(13)

where $\psi$ is the electric potential of the piezo layers.

Equations (12) and (13) are the governing equations of the piezoelectric layer that can be solved analytically. Since the panel is assumed as simply supported, and based on the assumed external load of Eq. (1), we can use the method of variable separation and represent the mechanical and electrical displacement components as:

$$\begin{aligned}&u_{1} \left( {x_{1} ,x_{2} ,x_{3} } \right) \,\, = \,U_{1} \left( {x_{3} } \right) \cos \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\&u_{2} \left( {x_{1} ,x_{2} ,x_{3} } \right) \,\, = \,U_{2} \left( {x_{3} } \right) \sin \left( {p x_{1} } \right) \,\cos \left( {q x_{2} } \right) , \nonumber \\&u_{3} \left( {x_{1} ,x_{2} ,x_{3} } \right) \,\, = \,U_{3} \left( {x_{3} } \right) \sin \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\&\psi \left( {x_{1} ,x_{2} ,x_{3} } \right) \,\,\, = \Psi \left( {x_{3} } \right) \sin \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \end{aligned}$$

(14)

where $p=\frac{n\pi }{a}$, $q=\frac{m\pi }{b}$ and $U_{1} \left( {x_{3} } \right) ,\,U_{2} \left( {x_{3} } \right) ,\,U_{3} \left( {x_{3} } \right) ,\Psi \left( {x_{3} } \right)$ are undetermined functions of the coordinate $x_{3}$. By substitution of Eq. (14) into Eq. (6), the strain components are determined as:

$$\begin{aligned} \varepsilon _{{xx}} \,\,= & {} - \,U_{1} \,p\sin \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\ \varepsilon _{{yy}} \,\,= & {} - \,U_{2} \,q\sin \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\ \varepsilon _{{zz}} \,\,= & {} U^{\prime }_{3} \,p\sin \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\ \gamma _{{yz}} \,\,= & {} \left( {U^{\prime }_{2} + U_{3} \,q} \right) \sin \left( {p x_{1} } \right) \,\cos \left( {q x_{2} } \right) , \nonumber \\ \gamma _{{xz}} \,\,= & {} \left( {U^{\prime }_{1} + U_{3} \,p} \right) \cos \left( {p x_{1} } \right) \sin \left( {q x_{2} } \right) , \nonumber \\ \gamma _{{xy}} \,\,= & {} \left( {U_{1} \,q + U_{2} \,p} \right) \cos \left( {p x_{1} } \right) \,\cos \left( {q x_{2} } \right) , \end{aligned}$$

(15)

The electric field components Eq. (10) are then obtained as follow

$$\begin{aligned} E_{x} \,\,= & {} - \Psi \,p\cos \left( {p x_{1} } \right) \, \sin \left( {q x_{2} } \right) , \nonumber \\ E_{y} \,\,= & {} - \Psi \,q\sin \left( {p x_{1}} \right) \,\cos \left( {q x_{2} } \right) , \nonumber \\ E_{z} \,\,= & {} - \Psi ^{\prime }\,\,\,\sin \left( {p x_{1}} \right) \, \sin \left( {q x_{2} } \right) . \end{aligned}$$

(16)

The stress components and electrical displacements can be determined by using Eqs. (3)–(4). Substituting of the results into the governing equation. (12)–(13), four ordinary differential equations will be obtained as follows:

$$\begin{aligned}&c_{55} {U}''_{1} \left( {x_{3} } \right) +p\left( {c_{13} +c_{55} } \right) {U}'_{3} \left( {x_{3} } \right) +p\left( {e_{1} +e_{5} } \right) {\Psi }'\left( {x_{3} } \right) -\left( {c_{11} p^{2}+c_{66} q^{2}} \right) U_{1} \left( {x_{3} } \right) \nonumber \\&\quad -pq\left( {c_{12} +c_{66} } \right) U_{2} \left( z \right) =0, \nonumber \\&c_{44} {U}''_{2} \left( {x_{3} } \right) +q\left( {c_{23} +c_{44} } \right) {U}'_{3} \left( {x_{3} } \right) +q\left( {e_{2} +e_{4} } \right) {\Psi }'\left( {x_{3} } \right) -pq\left( {c_{12} +c_{66} } \right) U_{1} \left( {x_{3} } \right) \nonumber \\&\quad -\left( {c_{66} p^{2}+c_{22} q^{2}} \right) U_{2} \left( {x_{3} } \right) =0, \nonumber \\&c_{33} {U}''_{3} \left( {x_{3} } \right) +e_{3} {\Psi }''\left( {x_{3} } \right) -p\left( {c_{13} +c_{55} } \right) {U}'_{1} \left( {x_{3} } \right) -q\left( {c_{23} +c_{44} } \right) {U}'_{2} \left( {x_{3} } \right) \nonumber \\&\quad -\left( {c_{55} p^{2}+c_{44} q^{2}} \right) U_{3} \left( {x_{3} } \right) -\left( {e_{5} p^{2}+e_{4} q^{2}} \right) \Psi \left( {x_{3} } \right) =0, \nonumber \\&e_{3} {U}''_{3} \left( {x_{3} } \right) -\eta _{3} {\Psi }''\left( {x_{3} } \right) -p\left( {e_{1} +e_{5} } \right) {U}'_{1} \left( {x_{3} } \right) -q\left( {e_{2} +e_{4} } \right) {U}'_{2} \left( {x_{3} } \right) \nonumber \\&\quad -\left( {e_{5} p^{2}+e_{4} q^{2}} \right) U_{3} \left( {x_{3} } \right) +\left( {\eta _{1} p^{2}+\eta _{2} q^{2}} \right) \Psi \left( {x_{3} } \right) =0. \end{aligned}$$

(17)

which are coupled differential equations. To solve the above equations, we assume that

$$\begin{aligned} U_{i} \left( {x_{3} } \right) =U_{i} e^{s\,x_{3} },\,\,\,\Psi \left( {x_{3} } \right) =\Psi e^{s\,x_{3} }. \end{aligned}$$

(18)

By substituting the above assumed solution into Eq. (17), the following system of homogeneous algebraic equations can be derived:

$$\begin{aligned}&\left[ {{\begin{array}{*{20}c} {-c_{11} p^{2}-c_{66} q^{2}+c_{55} s^{2}} &{} {-pq\left( {c_{12} +c_{66} } \right) } &{} {ps\left( {c_{13} +c_{55} } \right) } &{} {ps\left( {e_{1} +e_{5} } \right) } \\ {-pq\left( {c_{12} +c_{66} } \right) } &{} {-c_{66} p^{2}-c_{22} q^{2}+c_{44} s^{2}} &{} {qs\left( {c_{23} +c_{44} } \right) } &{} {qs\left( {e_{2} +e_{4} } \right) } \\ {-ps\left( {c_{13} +c_{55} } \right) } &{} {-qs\left( {c_{23} +c_{44} } \right) } &{} {-c_{55} p^{2}-c_{44} q^{2}+c_{33} s^{2}} &{} {-e_{5} p^{2}-e_{4} q^{2}+e_{3} s^{2}} \\ {-ps\left( {e_{1} +e_{5} } \right) } &{} {-qs\left( {e_{2} +e_{4} } \right) } &{} {-e_{5} p^{2}-e_{4} q^{2}+e_{3} s^{2}} &{} {\eta _{1} p^{2}+\eta _{2} q^{2}-\eta _{3} s^{2}} \\ \end{array} }} \right] \nonumber \\&\quad \left[ {{\begin{array}{*{20}c} {U_{1} } \\ {U_{2} } \\ {U_{3} } \\ \Psi \\ \end{array} }} \right] =\vec {{0}}. \end{aligned}$$

(19)

The non-trivial solution of Eq. (19) is obtained when the determinant of the coefficients vanishes. This leads to the characteristic equation, which is an eighth-order algebraic equation in terms of s:

$$\begin{aligned} A_{8} s^{8}+A_{6} s^{6}+A_{4} s^{4}+A_{2} s^{2}+A_{0} =0. \end{aligned}$$

(20)

By considering $\lambda =s^{2}$, Eq. (20) can be rewritten in the form of a fourth-order equation as:

$$\begin{aligned} A_{8} \lambda ^{4}+A_{6} \lambda ^{3}+A_{4} \lambda ^{2}+A_{2} \lambda +A_{0} =0. \end{aligned}$$

(21)

For the real positive root of the above equation, $\lambda =\lambda _{\,r}$, two distinct corresponding real roots exist. The corresponding linearly independent solutions are:

$$\begin{aligned} U_{i} \left( {x_{3} } \right)= & {} a_{i1} \cosh \left( {\gamma _{1} x_{3} } \right) +a_{i2} \sinh \left( {\gamma _{1} x_{3} } \right) , \nonumber \\ \Psi \left( {x_{3} } \right)= & {} a_{\psi 1} \cosh \left( {\gamma _{1} x_{3} } \right) +a_{\psi 2} \sinh \left( {\gamma _{1} x_{3} } \right) , \end{aligned}$$

(22)

where $\gamma _{1} =\sqrt{\lambda _{\,r} }$. Of the above eight coefficients, only two are independent and all other six coefficients can be obtained from the two independent ones. The corresponding stresses can be obtained as follows:

$$\begin{aligned} \left\{ {\vec {{\sigma }}} \right\} =\left\{ {{\begin{array}{*{20}c} {\sigma _{11} } \\ {\sigma _{22} } \\ {\sigma _{33} } \\ {\tau _{23} } \\ {\tau _{13} } \\ {\tau _{12} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{11} } &{} {\varsigma _{12} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{21} } &{} {\varsigma _{22} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{31} } &{} {\varsigma _{32} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{41} } &{} {\varsigma _{42} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{51} } &{} {\varsigma _{52} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{61} } &{} {\varsigma _{62} } \\ \end{array} }} \right] } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\cosh \left( {\gamma _{1} x_{3} } \right) } \\ {\sinh \left( {\gamma _{1} x_{3} } \right) } \\ \end{array} }} \right\} , \end{aligned}$$

(23)

where all coefficients $\varsigma _{ij}$ are listed in the Appendix. Meanwhile, let us consider the case of negative discriminant which yields two distinct complex conjugate roots ($\lambda _{2} ,\,\,\lambda _{3} )$. These roots can be represented in the polar form

$$\begin{aligned} \lambda _{2,3} =r\left( {\cos \theta \pm i\sin \theta } \right) . \end{aligned}$$

(24)

Then, one will get four complex roots for s as:

$$\begin{aligned} s_{3,4} =\pm \left( {\gamma _{2} +i\gamma _{3} } \right) ,\,\,\,s_{5,6} =\pm \left( {\gamma _{2} -i\gamma _{3} } \right) , \end{aligned}$$

(25)

where

$$\begin{aligned} \gamma _{2} =\sqrt{r} \cos {\nicefrac {\theta }{2}} ,\,\,\,\,\gamma _{3} =\sqrt{r} \sin {\nicefrac {\theta }{2}}. \end{aligned}$$

(26)

Corresponding to these four roots, the undetermined functions are:

$$\begin{aligned} U_{i} \left( {x_{3} } \right)= & {} a_{i3} e^{\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) +a_{i4} e^{\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3} } \right) +a_{i5} e^{-\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) +a_{i6} e^{-\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3} } \right) , \nonumber \\ \Psi \left( {x_{3} } \right)= & {} a_{\psi 3} e^{\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) +a_{\psi 4} e^{\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3} } \right) +a_{\psi 5} e^{-\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) +a_{\psi 6} e^{-\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3} } \right) .\nonumber \\ \end{aligned}$$

(27)

In these functions, 16 coefficients exist that are $a_{i3} ,\,\,a_{i4} ,\,\,a_{i5} ,\,\,a_{i6} ,\,\,i=1,2,3$, and $a_{\psi 3} ,\,\,a_{\psi 4} ,\,\,a_{\psi 5} ,\,\,a_{\psi 6}$. In this case, from the total number of sixteen coefficients, only four are independent. The corresponding stresses can be obtained in terms of the obtained displacement fields. The stress components arise from the first two coefficients $a_{3i} ,\,\,a_{4i} ,\,\,i=1,2,3,$ as follows:

$$\begin{aligned} \left\{ {\vec {{\sigma }}} \right\} =\left\{ {{\begin{array}{*{20}c} {\sigma _{11} } \\ {\sigma _{22} } \\ {\sigma _{33} } \\ {\tau _{23} } \\ {\tau _{13} } \\ {\tau _{12} } \\ \end{array} }} \right\} =e^{\left( {\gamma _{2} x_{3} } \right) }\left[ {{\begin{array}{*{20}c} {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{11} } &{} {\varsigma _{12} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{21} } &{} {\varsigma _{22} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{31} } &{} {\varsigma _{32} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{41} } &{} {\varsigma _{42} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{51} } &{} {\varsigma _{52} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{61} } &{} {\varsigma _{62} } \\ \end{array} }} \right] } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\cos \left( {\gamma _{3} x_{3} } \right) } \\ {\sin \left( {\gamma _{3} x_{3} } \right) } \\ \end{array} }} \right\} . \end{aligned}$$

(28)

For the stress components of the remaining two other coefficients, namely $a_{5i} ,\,\,a_{6i}$, the relations (28) can again be used by changing $\gamma _{2}$ to $-\gamma _{2}$.

2.2 Nano-composite facing sheets

The facing of micro-sandwich plate is of nano-composite type and made from carbon nanotubes (CNTs) as reinforcement and polymer resin as matrix. The CNTs are dissipated uniformly through the thickness. Here, the extended rule of mixture (ERM) is used for obtaining micro-mechanical properties of the nano-composite. It should be noted that for nano-composites reinforced by CNTs, the rule of mixture (RM) model does not provide an accurate estimation for the mechanical properties of the composite [38]. Instead, ERM is used for nano-composites, which includes efficiency parameters. The effective macroscopic material properties of the facings are calculated following [38]:

$$\begin{aligned} E_{1}= & {} \eta _{1} V_{{\mathrm{CNT}}} E_{1}^{{\mathrm{CNT}}} + V_{m} E_{{\mathrm{MATRIX}}} , \nonumber \\ \frac{{\eta _{2} }}{{E_{k} }}= & {} \frac{{V_{{\mathrm{CNT}}} }}{{E_{k}^{{\mathrm{CNT}}} }} + \frac{{V_{m} }}{{E_{{\mathrm{MATRIX}}}^{{}} }},\,\,k = 2,3 ,\nonumber \\ \nu _{{1k}}= & {} V_{{\mathrm{CNT}}} \,\nu _{{1k}}^{{\mathrm{CNT}}} + V_{m} \nu _{m} ,\,\,k = 2,3 ,\nonumber \\ \frac{{\eta _{3} }}{{G_{{ij}} }}= & {} \frac{{V_{{\mathrm{CNT}}} }}{{G_{{ij}}^{{\mathrm{CNT}}} }} + \frac{{V_{m} }}{{E_{{\mathrm{MATRIX}}}^{{}} }},\,\,ij = 12,23,13 , \end{aligned}$$

(29)

in which $V_{\mathrm{CNT}}$ and $V_{m}$ are the volume fractions of CNTs and matrix, respectively. $\eta _{i}$ is the efficiency parameter for the volume fraction of nanotubes. In these formulas, only two micromechanical parameters, namely $V_{\mathrm{CNT}}$ and $V_{m}$, are used. In addition, Poisson’s ratios are determined according to the compatibility relation $\nu _{ij} =\left( {{E_{i} } / {E_{j} }} \right) \nu _{ji}$. The constitutive equations of the nano-composite facings for stress in Cartesian coordinates are expressed as a relation between the stress and strain vectors:

$$\begin{aligned} \left\{ {\vec {\sigma }^{l} } \right\} = \left[ c \right] \left\{ {\vec {\varepsilon }} \right\} , \end{aligned}$$

(30)

where the matrix [c] can be obtained from the effective properties in Eq. (29) as follows:

$$\begin{aligned}&C_{{11}} = \frac{{1 - \nu _{{23}} \nu _{{32}} }}{{E_{2} E_{3} \Delta }},\,\,\,C_{{22}} = \frac{{1 - \nu _{{13}} \nu _{{31}} }}{{E_{1} E_{3} \Delta }},\,\,\,C_{{33}} = \frac{{1 - \nu _{{12}} \nu _{{21}} }}{{E_{1} E_{2} \Delta }}, \nonumber \\&C_{{12}} = \frac{{\nu _{{21}} + \nu _{{31}} \nu _{{23}} }}{{E_{2} E_{3} \Delta }},\,\,\,C_{{23}} = \frac{{\nu _{{32}} + \nu _{{12}} \nu _{{31}} }}{{E_{1} E_{2} \Delta }},\,\,\,C_{{13}} = \frac{{\nu _{{31}} + \nu _{{21}} \nu _{{32}} }}{{E_{2} E_{3} \Delta }} , \nonumber \\&C_{{44}} = G_{{23}} ,\,\,\,C_{{55}} = G_{{31}} ,\,\,\,C_{{66}} = G_{{12}}, \nonumber \\&\Delta = \frac{{1 - \nu _{{12}} \nu _{{21}} - \nu _{{23}} \nu _{{32}} - \nu _{{31}} \nu _{{13}} - 2\nu _{{21}} \nu _{{32}} \nu _{{13}} }}{{E_{1} E_{2} E_{3} }}. \end{aligned}$$

(31)

The governing equations for the nano-composite layer are the mechanical equilibrium equations introduced in Eq. (8). The displacement field is again assumed to be in the form of Eq. (14). Similar to the previous section, by substituting the assumed displacements into the equilibrium equations (6), the following three ordinary differential equations will be obtained:

$$\begin{aligned}&-\left( {c_{11} p^{2}+c_{66} q^{2}} \right) U_{1} \left( {x_{3} } \right) -\left( {pqc_{12} +pqc_{66} } \right) U_{2} \left( {x_{3} } \right) +c_{55} {U}''_{1} \left( {x_{3} } \right) +pc_{13} {U}'_{3} \left( {x_{3} } \right) +pc_{55} {U}'_{3} \left( {x_{3} } \right) =0, \nonumber \\&-\left( {pqc_{12} +pqc_{66} } \right) U_{1} \left( {x_{3} } \right) -\left( {c_{66} p^{2}+c_{22} q^{2}} \right) U_{2} \left( {x_{3} } \right) +c_{44} U_{2}^{\prime \prime }\left( {x_{3} } \right) +qc_{23} {U}'_{3} \left( {x_{3} } \right) +qc_{44} {U}'_{3} \left( {x_{3} } \right) =0, \nonumber \\&\left( {-c_{55} p^{2}-c_{44} q^{2}} \right) U_{3} \left( {x_{3} } \right) +c_{33} {U}''_{3} \left( {x_{3} } \right) -p\left( {c_{13} +c_{55} } \right) {U}'_{1} \left( {x_{3} } \right) -q\left( {c_{23} +c_{44} } \right) U_{2}^{\prime }\left( {x_{3} } \right) =0. \end{aligned}$$

(32)

By assuming an exponential form of $U_{i} \left( {x_{3} } \right) =U_{i} e^{s\,x_{3} }$, and substituting this into Eq. (32), a system of homogeneous algebraic equations is obtained. The characteristic equation for non-trivial solution is a sixth-order algebraic equation in terms of s and a cubic one in terms of $\lambda =s^{2}$:

$$\begin{aligned} A_{6} s^{6}+A_{4} s^{4}+A_{2} s^{2}+A_{0} =0,\,\,\,\,\,\,\,\,\,\,\,\,\Rightarrow A_{6} \lambda ^{3}+A_{4} \lambda ^{2}+A_{2} \lambda +A_{0} =0. \end{aligned}$$

(33)

Normally, when $A_{6}$ is nonzero, this equation has three roots. However, one of the roots is real, say $\lambda =\lambda _{1}$. If, furthermore, this root is positive, two distinct corresponding real roots exist, say ($\gamma _{1,2} =\pm \sqrt{\lambda _{1} } )$. The corresponding linearly independent solutions are

$$\begin{aligned} U_{i} \left( {x_{3} } \right) =a_{i1} \cosh \left( {\gamma _{1} x_{3} } \right) +a_{i2} \sinh \left( {\gamma _{1} x_{3} } \right) . \end{aligned}$$

(34)

The coefficients $a_{11} ,a_{12} ,a_{21} ,a_{22}$ can be expressed in terms of $a_{31} ,a_{32}$ as discussed in the Appendix. The corresponding stress components are similar to those of Eq. (23), but the associated constants are presented in the Appendix. The procedure for obtaining other roots and their relevant solutions is similar to the previous section and omitted in this section for brevity.

2.3 Functionally graded core

The FGM core is made of ceramic and metal at the bottom and upper faces with Young’s modulus of $E_{c}$ and $E_{m}$, respectively. To derive an exact solution, the Young’s modulus of the FGM core is assumed to vary along the thickness direction according to the power-law variation:

$$\begin{aligned} E\left( {x_{3} } \right) =E_{m} {\hbox {e}}^{\alpha \left( {x_{3} -{z}'_{b} } \right) }, \end{aligned}$$

(35)

where the parameter $\alpha$ is calculated as $\alpha =\left( {1 /{h\,_{c} }} \right) \ln \left( {{E_{c} } /{E_{m} }} \right)$. The constitutive equations for the stress components in the Cartesian coordinates are [39]:

$$\begin{aligned} \left\{ {\vec {{\sigma }}^{l}} \right\} =\left[ c \right] \left\{ {\vec {{\varepsilon }}^{l}} \right\} \end{aligned}$$

(36)

Due to the isotropic nature of the core, its stiffness matrix components can be written in the simple form

$$\begin{aligned}&c_{11} =c_{22} =c_{33} =\lambda +2\mu , \nonumber \\&c_{12} =c_{13} =c_{23} =\lambda , \nonumber \\&c_{44} =c_{55} =c_{66} =\mu , \end{aligned}$$

(37)

where $\mu$ and $\lambda$ are Lamé constants ($\mu =\frac{E\left( {x_{3} } \right) }{2\left( {1+\nu } \right) },\,\,\,\lambda =\frac{\nu E\left( {x_{3} } \right) }{\left( {1+\nu } \right) \left( {1-2\nu } \right) })$. Considering Eq. (7) and substituting into Eq. (8) material constants of the FGM introduced in Eq. (37), the following three ordinary differential equations will be obtained for the FGM core:

$$\begin{aligned}&\left( {1-2\nu } \right) {U}''_{1} \left( {x_{3} } \right) +\left( {1-2\nu } \right) \alpha {U}'_{1} \left( {x_{3} } \right) +pU_{3}^{\prime }\left( {x_{3} } \right) +2\left( {\nu -1} \right) \left( {p^{2}+q^{2}} \right) U_{1} \left( {x_{3} } \right) \nonumber \\&\quad -pqU_{2} \left( {x_{3} } \right) +\left( {1-2\nu } \right) \,\alpha p\,U_{3} \left( z \right) =0, \nonumber \\&\left( {1-2\nu } \right) U_{2}^{\prime \prime }\left( {x_{3} } \right) +\left( {1-2\nu } \right) \alpha U_{2}^{\prime }\left( {x_{3} } \right) +\,\,qU_{3}^{\prime }\left( {x_{3} } \right) +2\left( {\nu -1} \right) \left( {p^{2}+q^{2}} \right) U_{2} \left( {x_{3} } \right) \nonumber \\&\quad -pqU_{1} \left( {x_{3} } \right) +\left( {1-2\nu } \right) \alpha q\,U_{3} \left( {x_{3} } \right) =0, \nonumber \\&2\left( {1-\nu } \right) U_{3}^{\prime \prime }\left( {x_{3} } \right) +2\left( {1-\nu } \right) \alpha U_{3}^{\prime }\left( {x_{3} } \right) -p{U}'_{1} \left( {x_{3} } \right) -qU_{2}^{\prime }\left( {x_{3} } \right) \nonumber \\&\quad -2\nu \alpha \left[ {p\,U_{1} \left( {x_{3} } \right) +qU_{2} \left( {x_{3} } \right) } \right] +\left( {2\nu -1} \right) \,\left( {p^{2}+q^{2}} \right) U_{3} \left( {x_{3} } \right) =0. \end{aligned}$$

(38)

As discussed in detail in the previous sections by assuming the exponential form of the solution, the following system of homogeneous algebraic equations is obtained:

$$\begin{aligned}&\left[ {{\begin{array}{*{20}c} {S-2p^{2}-q^{2}} &{} {-pq} &{} {p\left( {\alpha +s-2\nu \alpha } \right) } \\ {-pq} &{} {S-p^{2}-2q^{2}} &{} {q\left( {\alpha +s-2\nu \alpha } \right) } \\ {-p\left( {s+2\nu \alpha } \right) } &{} {-q\left( {s+2\nu \alpha } \right) } &{} {s^{2}+\alpha s-p^{2}-q^{2}+S} \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {U_{1} } \\ {U_{2} } \\ {U_{3} } \\ \end{array} }} \right] =\vec {{0}} \nonumber \\&S=\left( {1-2\nu } \right) \left( {s^{2}+\alpha s} \right) +2\nu \left( {p^{2}+q^{2}} \right) , \end{aligned}$$

(39)

which leads to a multiplicative sixth-order characteristic equation in terms of s for non-trivial solutions as

$$\begin{aligned} \left( {s^{2}+\alpha s-p^{2}-q^{2}} \right) \left[ {\begin{array}{l} s^{4}+2\alpha \,s^{3}+\left( {\alpha ^{2}-2p^{2}-2q^{2}} \right) s^{2}-2\alpha \left( {p^{2}+q^{2}} \right) \,s \\ \,\,\,\,\,\,\,\,\,\,\,\,+\left( {p^{2}+q^{2}} \right) \left( {\left( {p^{2}+q^{2}} \right) +{\nu \alpha ^{2}} / {\left( {1-\nu } \right) }} \right) \\ \end{array}} \right] =0. \end{aligned}$$

(40)

The first part of the equation is a quadratic form as: $\left( {s^{2}+\alpha s-p^{2}-q^{2}} \right)$, which has two real roots:

$$\begin{aligned} s_{1,2} =-\frac{\alpha }{2}\pm \gamma _{1} ,\,\,\,\gamma _{1} =\sqrt{p^{2}+q^{2}+\frac{\alpha ^{2}}{4}}. \end{aligned}$$

(41)

The second equation is a quadratic equation that by letting $s=x-\frac{\alpha }{2}$ is converted to the simpler

$$\begin{aligned} x^{4}-2P\,x^{2}+\left( {P^{2}+R} \right) =0,\,\,\left\{ {{\begin{array}{*{20}c} {P=p^{2}+q^{2}+\frac{\alpha ^{2}}{4},} \\ {R=\frac{\nu }{1-\nu }\alpha ^{2}\left( {p^{2}+q^{2}} \right) ,} \\ \end{array} }} \right. \end{aligned}$$

(42)

which is a biquadratic equation. For conventional materials, i.e., $0<\nu <1$, the discriminant of the biquadratic equation is negative ($\Delta =-4R<0)$. By setting $X=x^{2}$, we have:

$$\begin{aligned} X=P\pm \sqrt{R} \,i=r\left( {\cos \theta \pm i\sin \theta } \right) ,\,\,\,\,\left\{ {{\begin{array}{*{20}c} {r=\sqrt{P^{2}+R} ,} \\ {\theta =\arctan \left( {\frac{\sqrt{R} }{P}} \right) } \\ \end{array} }} \right. \,\,\,\,\,\, \end{aligned}$$

(43)

Thus, the corresponding roots of the quadratic equation are

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {s_{3,4} =-\frac{\alpha }{2}\pm \left( {\gamma _{2} +i\gamma _{3} } \right) ,} \\ {s_{5,6} =-\frac{\alpha }{2}\pm \left( {\gamma _{2} -i\gamma _{3} } \right) } \\ \end{array} }} \right. \,\,,\,\,\mathrm{where}\left\{ {{\begin{array}{*{20}c} {\gamma _{2} =\sqrt{r} \cos \frac{\theta }{2}} \\ {\gamma _{3} =\sqrt{r} \sin \frac{\theta }{2}} \\ \end{array} }} \right. \,, \end{aligned}$$

(44)

Corresponding to these six roots, the displacement functions are:

$$\begin{aligned} U_{i} \left( {x_{3} } \right) =e^{-\left( \nicefrac {{\alpha x_{3}}}{2} \right) }\left( {\begin{array}{ll} a_{i1} \cosh \left( {\gamma _{1} x_{3} } \right) &{} +a_{i2} \sinh \left( {\gamma _{1} x_{3} }\right) \\ +a_{i3} e^{\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) &{} +a_{i4} e^{\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3} } \right) \\ +a_{i5} e^{-\gamma _{2} x_{3} }\cos \left( {\gamma _{3} x_{3} } \right) &{} +a_{i6} e^{-\gamma _{2} x_{3} }\sin \left( {\gamma _{3} x_{3}} \right) \\ \end{array}} \right) \end{aligned}$$

(45)

Here, of the 18 coefficients, only six are independent: for first two terms, we have:

$$\begin{aligned} \begin{array}{l} a_{u1} =\xi _{11} a_{w1} +\xi _{12} a_{w2} ,\,\,\,\,a_{u2} =\xi _{21} a_{w1} +\xi _{22} a_{w2} ,\,\,\,a_{v1} =\frac{q}{p}a_{u1} ,\,\,\,\,a_{v2} =\frac{q}{p}a_{u2}, \\ \xi _{11} =\xi _{22} =-\frac{pr_{0} }{p^{2}+q^{2}-r_{1} },\,\,\,\,\xi _{12} =\xi _{21} =\frac{p\gamma _{1} }{p^{2}+q^{2}-r_{1} } \\ \end{array} \end{aligned}$$

(46)

For the second two terms, we have

$$\begin{aligned}&a_{u3} =\xi _{33} a_{w3} +\xi _{34} a_{w4} ,\,\,\,\,a_{u4} =\xi _{43} a_{w3} +\xi _{44} a_{w4} \nonumber \\&\xi _{33} =\xi _{44} =\frac{p\left( {r_{0} p^{2}+r_{0} q^{2}-r_{0} r_{1} +r_{2} \gamma _{3} } \right) }{\xi ^{**}} \nonumber \\&\xi _{34} =-\xi _{43} =-\frac{p\left( {-\gamma _{3} p^{2}-\gamma _{3} q^{2}+r_{0} r_{2} +r_{1} \gamma _{3} } \right) }{\xi ^{**}} \nonumber \\&\xi ^{**}=\left( {p^{2}+q^{2}+r_{1} } \right) ^{2}+r_{2}^{2} \end{aligned}$$

(47)

and for the last two terms:

$$\begin{aligned}&a_{u5} =\xi _{55} a_{w5} +\xi _{56} a_{w6} ,\,\,\,\,a_{u6} =\xi _{65} a_{w5} +\xi _{66} a_{w6} \nonumber \\&\xi _{55} =\xi _{66} =\frac{p\left( {r_{0} p^{2}+r_{0} q^{2}-r_{0} r_{1} +r_{2} \gamma _{3} } \right) }{\xi ^{**}} \nonumber \\&\xi _{56} =-\xi _{65} =-\frac{p\left( {-\gamma _{3} p^{2}-\gamma _{3} q^{2}+r_{0} r_{2} +r_{1} \gamma _{3} } \right) }{\xi ^{**}} \nonumber \\&\xi ^{**}=\left( {p^{2}+q^{2}+r_{1} } \right) ^{2}+r_{2}^{2} \end{aligned}$$

(48)

The corresponding stresses of the FGM core can be obtained as follow:

$$\begin{aligned} \begin{aligned} \left\{ {\vec {{\sigma }}} \right\}&=\left\{ {{\begin{array}{*{20}c} {\sigma _{11} } \\ {\sigma _{22} } \\ {\sigma _{33} } \\ {\tau _{23} } \\ {\tau _{13} } \\ {\tau _{12} } \\ \end{array} }} \right\} =\frac{\lambda }{\nu }e^{-\frac{\alpha x_{3} }{2}}\left[ {{\begin{array}{*{20}c} {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{11} } &{} {\varsigma _{12} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{21} } &{} {\varsigma _{22} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{31} } &{} {\varsigma _{32} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{41} } &{} {\varsigma _{42} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{51} } &{} {\varsigma _{52} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {\varsigma _{61} } &{} {\varsigma _{62} } \\ \end{array} }} \right] } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\cosh \left( {\gamma _{1} x_{3} } \right) } \\ {\sinh \left( {\gamma _{1} x_{3} } \right) } \\ \end{array} }} \right\} \\&\quad + \frac{\lambda }{\nu }e^{-\frac{\alpha x_{3} }{2}}\left[ {{\begin{array}{*{20}c} {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{13}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{15}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{14}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{16}^{***} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{23}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{25}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{24}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{26}^{***} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \,\sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{33}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{35}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{34}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{36}^{***} } \\ \end{array} }} \right] } \\ {\sin \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{43}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{45}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{44}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{46}^{***} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \sin \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{53}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{55}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{54}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{56}^{***} } \\ \end{array} }} \right] } \\ {\cos \left( {px_{1} } \right) \cos \left( {qx_{2} } \right) \left[ {{\begin{array}{*{20}c} {e^{\gamma _{2} x_{3} }\varsigma _{63}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{65}^{***} } &{} {e^{\gamma _{2} x_{3} }\varsigma _{64}^{**} +e^{-\gamma _{2} x_{3} }\varsigma _{66}^{***} } \\ \end{array} }} \right] } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\cos \left( {\gamma _{3} x_{3} } \right) } \\ {\sin \left( {\gamma _{3} x_{3} } \right) } \\ \end{array} }} \right\} \\ \end{aligned} \end{aligned}$$

(49)

The coefficients of this equation are presented in detail in Appendix. All the above relations are local stresses. To determining nonlocal stresses from local stresses, the following steps should be followed: if the local stress is in the general form of

$$\begin{aligned} \sigma _{ij}^{l} \left( {x_{1} ,x_{2} ,x_{3} } \right)= & {} {\mathbb {C}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}}\left[ {\mathrm{T}\cosh \left( {\gamma _{1} x_{3} } \right) \gamma _{1} z+{\mathrm{T}}'\sinh \left( {\gamma _{1} x_{3} } \right) } \right] \nonumber \\&+\,{\mathbb {D}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}+\gamma _{2} x_{3} }\left[ {I\cos \left( {\gamma _{3} x_{3} } \right) +{I}'\sin \left( {\gamma _{3} x_{3} } \right) } \right] \nonumber \\&+\,{\mathbb {F}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}-\gamma _{2} x_{3} }\left[ {J\cos \left( {\gamma _{3} x_{3} } \right) +{J}'\sin \left( {\gamma _{3} x_{3} } \right) } \right] \end{aligned}$$

(50)

and the nonlocal form is in the form of:

$$\begin{aligned} \sigma _{ij}^{nl} \left( {x_{1} ,x_{2} ,x_{3} } \right)= & {} {\mathbb {C}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}}\left[ {\chi \cosh \left( {\gamma _{1} x_{3} } \right) \gamma _{1} z+{\chi }'\sinh \left( {\gamma _{1} x_{3} } \right) } \right] \nonumber \\&+\,{\mathbb {D}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}+\gamma _{2} x_{3} }\left[ {\vartheta \cos \left( {\gamma _{3} x_{3} } \right) +{\vartheta }'\sin \left( {\gamma _{3} x_{3} } \right) } \right] \nonumber \\&+\,{\mathbb {F}}\left( {x_{1} ,x_{2} } \right) e^{-\frac{\alpha x_{3} }{2}-\gamma _{2} x_{3} }\left[ {\varpi \cos \left( {\gamma _{3} x_{3} } \right) +{\varpi }'\sin \left( {\gamma _{3} x_{3} } \right) } \right] , \end{aligned}$$

(51)

Then, the relation between local coefficients $\mathrm{T},{\mathrm{T}}'$ and nonlocal coefficients $\chi ,{\chi }'$ are as follow:

$$\begin{aligned}&\mathrm{T}=\left[ {\left( {{\mathbb {W}}-\gamma _{1}^{2}} \right) \delta ^{2}+1} \right] \chi +{\mathbb {V}}{\chi }', \nonumber \\&{\mathrm{T}}'={\mathbb {V}}\chi +\left[ {\left( {{\mathbb {W}}-\gamma _{1}^{2}} \right) \delta ^{2}+1} \right] {\chi }', \nonumber \\&I=\left[ {\left( {{\mathbb {W}}+{\mathbb {N}}} \right) \delta ^{2}+1} \right] \vartheta +{\mathbb {M}}{\vartheta }', \nonumber \\&{I}'=-\,{\mathbb {M}}\vartheta +\left[ {\left( {{\mathbb {W}}+{{\mathbb {N}}}'} \right) \delta ^{2}+1} \right] {\vartheta }', \nonumber \\&J=\left[ {\left( {{\mathbb {W}}+{{\mathbb {N}}}'} \right) \delta ^{2}+1} \right] \varpi -{\mathbb {M}}{\varpi }', \nonumber \\&{J}'=-\,{\mathbb {M}}\varpi +\left[ {\left( {{\mathbb {W}}+{{\mathbb {N}}}'} \right) \delta ^{2}+1} \right] {\varpi }', \nonumber \\&{\mathbb {W}}=-\,\frac{\alpha ^{2}}{4}+p^{2}+q^{2},\,\,\,{\mathbb {M}}=\left( {\alpha \gamma _{3} +2\gamma _{2} \gamma _{3} } \right) \delta ^{2}, \nonumber \\&{\mathbb {N}}=-\alpha \gamma _{2} -\gamma _{2}^{2}+ \gamma _{3}^{2},{\mathbb {V}}=-\,\alpha \delta ^{2}\gamma _{1} \nonumber \\&{{\mathbb {N}}}'=+\,\alpha \gamma _{2} -\gamma _{2}^{2}+\gamma _{3}^{2}. \end{aligned}$$

(52)

2.4 Continuity and boundary conditions

In this section, continuity and boundary conditions in the layer interface and external loadings are presented. The superscripts s, a, t, b, and c used to denote sensor, actuator top facing, bottom facing, and core, respectively. For interfaces between layers, the continuity conditions of in-plane and transverse displacements should be satisfied as follow:

• 1–3: $u_{i}^{s} =u_{i}^{b}$, at $x_{3} =z_{b}$.

• 4–6: $u_{i}^{b} =u_{i}^{c}$, at $x_{3} ={z}'_{b}$.

• 7–9: $u_{i}^{c} =u_{i}^{t}$, at $x_{3} =z_{t}$.

• 10–12: $u_{i}^{t} =u_{i}^{a}$, at $x_{3} ={z}'_{t}$.

Also, continuity of out-of-plate stresses in the interfaces should be satisfied as follow:

• 13–15: $\sigma _{i3}^{s} =\sigma _{i3}^{b}$, at $x_{3} =z_{b}$.

• 16–18: $\sigma _{i3}^{b} =\sigma _{i3}^{c}$, at $x_{3} ={z}'_{b}$.

• 19–21: $\sigma _{i3}^{c} =\sigma _{i3}^{t}$, at $x_{3} =z_{t}$.

• 22–24: $\sigma _{i3}^{t} =\sigma _{i3}^{a}$, at $x_{3} ={z}'_{t}$.

The bottom surface is traction free; therefore, we have

• 25–27: $\sigma _{i3}^{s} =0$, at $x_{3} =z_{s}$.

The top surface is exposed to external transverse loading:

• 23–30: $\sigma _{33}^{s} =Q\left( {x_{1} ,x_{2} ,x_{3} } \right) ,\,\,\,\tau _{13}^{s} =0,\,\,\,\tau _{23}^{s} =0$ at $x_{3} =z_{a}$.

The electrical boundary conditions are as follow:

• 31,32: $\psi ^{a} =V$ at $z=z_{a}$ and $\psi ^{a} =0$ at $x_{3} ={z}'_{t}$.

• 33,34: $\psi ^{s} =0$ and $D_{3}^{s} =0$ at $x_{3} =z_{s}$.

The above 34 conditions should be satisfied to solve the governing equations of the smart micro-sandwich panel completely. It is worth mentioning that in the above conditions, the stresses is nonlocal; but as discussed in Sect. 3.1, the local form of stresses should be considered thus the nonlocal operator $\left( {1-\delta ^{2}\,\nabla ^{2}} \right)$ is applied to the stress component.

Table 1 Mesh convergence of finite element method to analytical result

Fig. 2

Comparison of displacements and stresses obtained by the present method with FE results

3 Result and discussion

3.1 Comparison study

The accuracy of the presented method is examined through examples for isotropic thick plates. As a first example, the accuracy of the method is demonstrated by comparing the maximum transverse deflection of thick core with those of the finite element (FE) solution in Table 1. The results are presented for thick core made of aluminum with $E=$ 70 GPa and $\nu = {0.3}$. The core is square with length 0.1 m, thickness 0.02 m, and $q_{0}= {-1} \, \hbox {Pa}$. FE results are exerted from ABAQUS software and element C3D8R is used which is a cubic three-dimensional element with 8-nodes. According to this table, it is seen that by using a finer mesh with a larger number of smaller elements, the results converge to the analytical solution. The FE results with mesh size equal to or smaller than 2.5 mm have error less than 1 percent compared with the analytical solution. For mesh size equals to 2.5 mm (12,800 elements) through-the-thickness distribution of maximum displacements and stresses are plotted in Fig. 2 for both analytical and FE results. Excellent agreement between results is quite evident. From Fig. 2a, it can be seen that the in-plane displacements u and v have the same order of transverse displacement w (in-plane displacements are equal due to isotropic type of material and only one of them are plotted) and should not be ignored in equivalent plate theory due to its high thickness. The out-of-plane stresses $\sigma _{zz},\tau _{xz}$ in the presented solution satisfied the free-surface boundary conditions in Fig. 2b. As shown in the Fig. 2c, magnitude of in-plane stresses $\sigma _{xx} ,\tau _{xy}$ has generally bigger compare to out-of-plane stress components.

3.2 Numerical results

The current section provides numerical results for sensitivity analysis of geometric and FG properties. The properties of the CNT fibers are listed in Table 2 [40]. It is worth to mentioning that properties of CNTs are transversely isotropic in the 2–3 direction due to the isotropic properties of the graphene sheet [41]. The efficiency parameter for 11% volume fraction of nanotubes is $\eta _{1}= 0.149$ and $\eta _{2}= \eta _{3}= 0.934$ [40]. PZT4 and $\mathrm{Ba}_{2} {\mathrm{NaNb}}_{5} \mathrm{O}_{15}$ are used as sensor and actuator. The elastic stiffness, piezoelectric, and dielectric constants of piezoelectric layers are listed in Table 3 [36]. For FGM core, poly-Si-Ge is considered [42]. The material properties of Ge as metal phase and Si as ceramic phase are $v_{m} =0.26$, $E_{m}= 132$ GPa, and $v_{c} = 0.26$, $E_{c}= 173$ GPa. The geometric dimensions of the smart micro-sandwich panel are as follows unless otherwise declared:

$$\begin{aligned} a=500\,\mu \mathrm{m},\,\,\,\frac{a}{b}=1,\,\,\,\frac{h_{\mathrm{core}} }{h}=0.5,\,\,\,\frac{h_{\mathrm{facing}} }{h}=0.2,\,\,\frac{h_{\mathrm{piezoelectric}} }{h}=0.1,\,\,\,\delta =3\,\mu \mathrm{m} \end{aligned}$$

where h is the total thickness of micro-sandwich panel. The mechanical and electrical loads are as follow: $q=-100\,\mu \mathrm{Pa},\,\,V=0.01\,\mu \mathrm{V}$.

Table 2 Material properties of CNT (TPa) and polymer matrix at room temperature [40]

Table 3 Material properties of piezoelectric layers [36]

Fig. 3

Variation of displacements along x-direction with different metal phase modulus $E_{m}$ for two nonlocal parameters, $a/h={5}$

In Fig. 3a–c, distribution of displacement components across the x-axis for two distinct values of metal phase modulus $E_{m}$ and nonlocal parameters in the top face of actuator layer is plotted. In these figures, the ceramic phase is assumed to be constant. It can be observed that for thick panel $(a/h = {{5}})$ by increasing the metal phase modulus, the absolute value of in-plane displacements ${\bar{U}},\,\,{\bar{V}}$ and transverse deflection ${\bar{W}}$ decreases. From these figures, it can be concluded that generally in-plane displacements cannot be neglected as in two-dimensional shell and plate theories. The existence of nonlocal parameter changes the value of the mentioned parameters. Increasing the nonlocal parameter cause an increase in the displacements. In order to make more clear the bending behavior of the smart micro-sandwich panel, the effect of nonlocal parameter and FG material distribution is studied distinctly in Figs. 4 and 5. In Fig. 4, the variation of mechanical and electrical parameters with respect to the dimensionless thickness of the panel is plotted for four values of nonlocal parameter, namely $\delta = {0, 5, 8, 10} \, \mu \hbox {m}$. According to Fig. 4a–c, it is observed that the absolute value of all displacements ${\bar{U}}$, ${\bar{V}}$and ${\bar{W}}$ has increased when the nonlocal parameter increased. Distribution of $\Psi$ in actuator is linear and does not change due to its very thin thickness and electrical boundary conditions; however, in the sensor the produced electric potential increased by increasing nonlocal parameter. Moreover, it can be observed from Figs. 4e, f that by increasing the nonlocal parameter, the out-of-plane stress components ${\bar{\sigma }}_{zz} ,\,\,\,{\bar{\tau }}_{yz}$ notably increased. The effect of nonlocal parameter at the in-plane stresses ${\bar{\sigma }}_{xx} ,\,\,\,{\bar{\tau }}_{xy}$ is presented in Fig. 4g, h. It is worth mentioning that the distribution of stress components along the thickness has an abrupt change at the interfaces of layers, (i.e., piezo, facing or core layer) due to the drastic change of material properties. The sudden interface slope change for in-plane stresses, ${\bar{\sigma }}_{xx},\,{\bar{\tau }}_{xy}$, is more evident. Furthermore, out-of-plane stresses, ${\bar{\sigma }}_{zz},\,{\bar{\tau }}_{xz}$, satisfy the continuity conditions exerted at the boundary conditions in the free surfaces. The influence of FG material distribution on the bending of smart micro-sandwich panel is studied in Fig. 5 for $\delta = \textit{3} \mu \hbox {m}$ and $a/h= {5}$. The results are provided for three metal phase materials $E_{m} = {120}, {130}$, and 140 GPa with constant $E_{c}=$ 173 GPa. As expected, the panel is stiffer when $E_{m}$ increases; therefore, the overall value of all displacements and stresses reduced. It can be seen in Fig. 5e, f, out-of-plate stresses, ${\bar{\sigma }}_{zz} ,\,\,{\bar{\tau }}_{yz}$, have reduction in general and this reduction is notable. The in-plane stress ${\bar{\sigma }}_{yy}$ has similar manner, but the in-plane shear stress ${\bar{\tau }}_{xy}$ increased by increasing $E_{m}$. Besides, the electrical displacements $D_{xx}$ and $D_{yy}$ are decreased as shown in Fig. 5i, j. Figure 6 represents the effect of length-to-thickness ratio on the through-the-thickness distribution of mechanical and electrical parameters for $a/h = {10, 15}$ and 20. It is obvious that the absolute value of in-plane displacements ${\bar{U}},\,\,{\bar{V}}$ increases when the thickness of the panel becomes smaller and the panel exposed to larger transverse deflection ${\bar{W}}$ in the negative direction of ${{U}}_{3}$. Although the assumed length-to-thickness ratios are equally spaced and have linear increase, the increase in mechanical displacements is nonlinear. The thickness of panel has dominant effect on electric potential produced in sensor layer. As shown in Fig. 6d, a, decrease in thickness made a higher value of $\Psi$ in the sensor layer. In Fig. 7a, b the effect of the aspect ratio a/b on the transverse deflection ${\bar{W}}$ and ${\bar{\tau }}_{xy} ,\,{\bar{\tau }}_{xz} ,\,{\bar{\sigma }}_{zz}$ is plotted. Furthermore, the corresponding roots of characteristic equations are tabulated in Table 4. From Fig. 7, it can be observed that for higher aspect ratio, transverse deflection is increased. The transverse deflection is highly affected by aspect ratio and the maximum deflection occurs in outer surfaces. Indeed in-plane stress decreases by increasing the aspect ratio. On the other hand, the out-of-plane stresses ${\bar{\sigma }}_{zz} ,\,\,\,{\bar{\tau }}_{yz}$ have opposed behavior, i.e., when ${\bar{\sigma }}_{zz}$ decreased, ${\bar{\tau }}_{yz}$ increased. A notable increase in shear stress can be observed at the interface between the FG core and bottom facing as shown in Fig. 7c, d.

Fig. 4

Through the thickness distribution of displacements, stresses, and electrical potential for different values of nonlocal parameter, $a/h=\textit{10}$

Fig. 5

Influences of $E_{m}$ on the variation of the mechanical displacements/stresses and electric displacements, $a/h=\textit{5}$, $\delta = \textit{3}\, \mu \hbox {m}$

Fig. 6

Influences of length-to-thickness ratio on the variation of the mechanical displacements/stresses

Fig. 7

Influences of aspect ratio on the variation of the mechanical displacement/stresses, $a/h= \textit{10}$

Table 4 The roots of the characteristic equation for each layer and different aspect ratio

4 Conclusion

In this study, a precise, systematic, and computationally efficient procedure for determining closed-form solution of smart micro-sandwich panels were presented. The method was developed by combining the nonlocal theory and three-dimensional theory to capture size-dependent effect in micro-structures. The essential concept of characteristic equation and the development of the solution form for both real and complex roots were presented in detail. Through a numerical example, the efficacy and accuracy of the presented method were confirmed. Then, a comprehensive parametric study was conducted to present the influences of the different geometrical and material parameters on the electro-static response of smart micro-sandwich panels with FG core and piezoelectric layers and nano-composite facings. In this regard, the effects of FG material power index, thickness, length, and width on the dimensionless displacements, stresses, and electrical parameters were examined.

Appendices

Appendices

Coefficients for piezoelectric layer

The coefficients $\varsigma _{ij}$ in Eq. (23) for the positive real roots of the characteristic equation of the piezoelectric layers are as following:

$$\begin{aligned} \left\{ {\begin{array}{l} \varsigma _{1i} =a_{\psi i} \gamma _{1} e_{1} -qa_{2\text {i}} c_{12} -pa_{1\text {i}} c_{11} +a_{3\text {i}} \gamma _{1} c_{13} , \\ \varsigma _{2i} =a_{\psi i} \gamma _{1} e_{2} -qa_{2\text {i}} c_{22} -pa_{1\text {i}} c_{12} +a_{3\text {i}} \gamma _{1} c_{23} , \\ \varsigma _{3i} =a_{\psi i} \gamma _{1} e_{3} -qa_{2\text {i}} c_{23} -pa_{1\text {i}} c_{13} +a_{3\text {i}} \gamma _{1} c_{33} , \\ \end{array}} \right. \,\,\,\,\left\{ {\begin{array}{l} \varsigma _{4i} =qa_{\psi i} e_{4} +qa_{3\text {i}} c_{44} +a_{2\text {i}} \gamma _{1} c_{44} , \\ \varsigma _{5i} =pa_{\psi \text {i}} e_{5} +pa_{3\text {i}} c_{55} +a_{1\text {i}} \gamma _{1} c_{55} , \\ \varsigma _{6i} =\left( {pa_{2\text {i}} +qa_{1\text {i}} } \right) c_{66} . \\ \end{array}} \right. \end{aligned}$$

(A.1)

where $\hbox {i} =1,2$. Moreover, these coefficients are in the below form for complex roots of the piezoelectric layer characteristic equation:

$$\begin{aligned} \begin{aligned} \varsigma _{11}&=\left( {-pc_{11} } \right) a_{{13}} +\left( {-qc_{12} } \right) a_{{23}} +\left( {\gamma _{2} c_{13} } \right) a_{{33}} +\left( {\gamma _{3} c_{13} } \right) a_{{34}} +a_{\psi {3}} \gamma _{2} e_{1} +a_{\psi {4}} \gamma _{3} e_{1} , \\ \varsigma _{12}&=\left( {-pc_{11} } \right) a_{{14}} +\left( {-qc_{12} } \right) a_{{24}} +\left( {-\gamma _{3} c_{13} } \right) a_{{33}} +\left( {\gamma _{2} c_{13} } \right) a_{{34}} +a_{\psi {4}} \gamma _{2} e_{1} -a_{\psi {3}} \gamma _{3} e_{1} \\ \varsigma _{21}&=\left( {-pc_{12} } \right) a_{{13}} +\left( {-qc_{22} } \right) a_{{23}} +\left( {\gamma _{2} c_{23} } \right) a_{{33}} +\left( {\gamma _{3} c_{23} } \right) a_{{34}} +a_{\psi {3}} \gamma _{2} e_{2} +a_{\psi {4}} \gamma _{3} e_{2} ,\,\,\, \\ \varsigma _{22}&=\left( {-pc_{12} } \right) a_{{14}} +\left( {-qc_{22} } \right) a_{{24}} +\left( {-\gamma _{3} c_{23} } \right) a_{{33}} +\left( {\gamma _{2} c_{23} } \right) a_{{34}} +a_{\psi {4}} \gamma _{2} e_{2} -a_{\psi {3}} \gamma _{3} e_{2} \\ \varsigma _{31}&=\left( {-pc_{13} } \right) a_{{13}} +\left( {-qc_{23} } \right) a_{{23}} +\left( {\gamma _{2} c_{33} } \right) a_{{33}} +\left( {\gamma _{3} c_{33} } \right) a_{{34}} +a_{\psi {3}} \gamma _{2} e_{3} +a_{\psi {4}} \gamma _{3} e_{3} ,\,\,\, \\ \varsigma _{32}&=\left( {-pc_{13} } \right) a_{{14}} +\left( {-qc_{23} } \right) a_{{24}} +\left( {-\gamma _{3} c_{33} } \right) a_{{33}} +\left( {\gamma _{2} c_{33} } \right) a_{{34}} +a_{\psi {4}} \gamma _{2} e_{3} -a_{\psi {3}} \gamma _{3} e_{3} \\ \varsigma _{41}&=\left( {\gamma _{2} c_{44} } \right) a_{{23}} +\left( {\gamma _{3} c_{44} } \right) a_{{24}} +\left( {qc_{44} } \right) a_{{33}} +qa_{\psi {3}} e_{4} , \\ \varsigma _{42}&=\left( {-\gamma _{3} c_{44} } \right) a_{{23}} +\left( {\gamma _{2} c_{44} } \right) a_{{24}} +\left( {qc_{44} } \right) a_{{34}} +qa_{\psi {4}} e_{4} \\ \varsigma _{51}&=\left( {\gamma _{2} c_{55} } \right) a_{{13}} +\left( {\gamma _{3} c_{55} } \right) a_{{14}} +\left( {pc_{55} } \right) a_{{33}} +pa_{\psi {3}} e_{5} , \\ \varsigma _{52}&=\left( {-\gamma _{3} c_{55} } \right) a_{{13}} +\left( {\gamma _{2} c_{55} } \right) a_{{14}} +\left( {pc_{55} } \right) a_{{34}} +pa_{\psi {4}} e_{5} \\ \varsigma _{61}&=\left( {qc_{66} } \right) a_{{13}} +\left( {pc_{66} } \right) a_{{23}} , \\ \varsigma _{62}&=\left( {qc_{66} } \right) a_{{14}} +\left( {pc_{66} } \right) a_{{24}}. \\ \end{aligned} \end{aligned}$$

(A.2)

Coefficients for facing sheets

The relations between coefficients $a_{ij}$ of Eq. (34) for the facing sheets are presented in the below:

$$\begin{aligned} \begin{aligned} \left[ {{\begin{array}{*{20}c} {a_{11} } \\ {a_{22} } \\ {a_{21} } \\ {a_{22} } \\ \end{array} }} \right]&=\frac{1}{r_{1} r_{2} -r_{0}^{2}}\left[ {{\begin{array}{*{20}c} {-\left( {p{r}'_{{1}} r_{2} -q{r}'_{2} r_{0} } \right) a_{{32}} } \\ {-\left( {p{r}'_{1} r_{2} -q{r}'_{2} r_{0} } \right) a_{{31}} } \\ {\left( {p{r}'_{1} r_{0} -q{r}'_{2} r_{1} } \right) a_{{32}} } \\ {\left( {p{r}'_{1} r_{0} -q{r}'_{2} r_{1} } \right) a_{{31}} } \\ \end{array} }} \right] \\ r_{0}&=-pq\left( {c_{12} +c_{66} } \right) \\ r_{1}&=-c_{11} p^{2}-c_{66} q^{2}+c_{55} \gamma _{1}^{2} \\ r_{2}&=-c_{66} p^{2}-c_{22} q^{2}+c_{44} \gamma _{1}^{2} \\ {r}'_{1}&=\gamma _{1} \left( {c_{13} +c_{55} } \right) \\ {r}'_{2}&=\gamma _{1} \left( {c_{23} +c_{44} } \right) \\ \end{aligned} \end{aligned}$$

(B.1)

In addition to this, the relevant coefficients of the face sheet solution for the real roots are as following:

$$\begin{aligned} \left\{ {\begin{array}{l} \varsigma _{11} =a_{{32}} \gamma _{1} c_{13} -qa_{{21}} c_{12} -pa_{{11}} c_{11} , \\ \varsigma _{12} =a_{{31}} \gamma _{1} c_{13} -qa_{{22}} c_{12} -pa_{{12}} c_{11} , \\ \varsigma _{21} =a_{{32}} \gamma _{1} c_{23} -qa_{{21}} c_{22} -pa_{{11}} c_{12} ,\,\,\, \\ \varsigma _{22} =a_{{31}} \gamma _{1} c_{23} -qa_{{22}} c_{22} -pa_{{12}} c_{12} , \\ \varsigma _{31} =a_{{32}} \gamma _{1} c_{33} -qa_{{21}} c_{23} -pa_{{11}} c_{13} ,\,\,\, \\ \varsigma _{32} =a_{{31}} \gamma _{1} c_{33} -qa_{{22}} c_{23} -pa_{{12}} c_{13} , \\ \end{array}} \right. ,\,\,\left\{ {\begin{array}{l} \varsigma _{41} =\left( {qa_{{31}} +a_{{22}} \gamma _{1} } \right) c_{44} , \\ \varsigma _{42} =\left( {qa_{{32}} +a_{{21}} \gamma _{1} } \right) c_{44} , \\ \varsigma _{51} =\left( {pa_{{31}} +a_{{12}} \gamma _{1} } \right) c_{55} , \\ \varsigma _{52} =\left( {pa_{{32}} +a_{{11}} \gamma _{1} } \right) c_{55} , \\ \varsigma _{61} =\left( {pa_{{21}} +qa_{{11}} } \right) c_{66} , \\ \varsigma _{62} =\left( {pa_{{22}} +qa_{{12}} } \right) c_{66} . \\ \end{array}} \right. \end{aligned}$$

(B.2)

Coefficients for FGM core

For the FGM core, we have six roots for the characteristic equation. For these roots, the stress statements are presented in Eq. (49), that the relevant coefficients are as below for the first two roots:

$$\begin{aligned} \begin{aligned} \varsigma _{11}&=-\left( {1-\nu } \right) pa_{{11}} -\nu qa_{{21}} +\nu a_{{32}} \gamma _{1} -0.5\alpha \nu a_{{31}} , \\ \varsigma _{12}&=-\left( {1-\nu } \right) pa_{{12}} -\nu qa_{{22}} +\nu a_{{31}} \gamma _{1} -0.5\alpha \nu a_{{32}}, \\ \varsigma _{21}&=+\left( {\nu -1} \right) qa_{{21}} -\nu pa_{{11}} +\nu a_{{32}} \gamma _{1} -0.5\alpha \nu a_{{31}} ,\,\, \\ \varsigma _{22}&=+\left( {\nu -1} \right) qa_{{22}} -\nu pa_{{12}} +\nu a_{{31}} \gamma _{1} -0.5\alpha \nu a_{{32}} , \\ \varsigma _{31}&=-\nu pa_{{31}} -\nu qa_{{21}} +\left( {1-\nu } \right) \gamma _{1} a_{{32}} -0.5\left( {1-\nu } \right) \alpha a_{{31}} , \\ \varsigma _{32}&=-\nu pa_{{12}} -\nu qa_{{22}} +\left( {1-\nu } \right) \gamma _{1} a_{{31}} -0.5\left( {1-\nu } \right) \alpha a_{{32}} , \\ \varsigma _{41}&=-\left( {2\nu -1} \right) \left( {-a_{{21}} +2a_{{22}} \gamma _{1} +2qa_{{31}} } \right) , \\ \varsigma _{42}&=-\left( {2\nu -1} \right) \left( {-a_{{22}} +\,2a_{{21}} \gamma _{1} +2qa_{{32}} } \right) , \\ \varsigma _{51}&=-\left( {2\nu -1} \right) \left( {-a_{{11}} +2a_{{12}} \gamma _{1} +2pa_{{31}} } \right) , \\ \varsigma _{52}&=-\left( {2\nu -1} \right) \left( {-a_{{12}} +2a_{{11}} \gamma _{1} +2pa_{{32}} } \right) , \\ \varsigma _{61}&=-2\left( {2\nu -1} \right) \left( {qa_{{11}} +pa_{{21}} } \right) , \\ \varsigma _{62}&=-2\left( {2\nu -1} \right) \left( {qa_{{12}} +pa_{{22}} } \right) . \end{aligned} \end{aligned}$$

(C.1)

and for the third and fourth roots the relevant coefficients are as below:

$$\begin{aligned} \begin{aligned} \varsigma _{13}^{**}&=-p\left( {1-\nu } \right) a_{{13}} -\nu qa_{{23}} +\nu \left( {\gamma _{2} -0.5\alpha } \right) a_{{33}} +\nu \gamma _{3} a_{{34}} , \\ \varsigma _{14}^{**}&=-p\left( {1-\nu } \right) a_{{14}} -\nu qa_{{24}} -\nu \gamma _{3} a_{{33}} +\nu \left( {\gamma _{2} -0.5\alpha } \right) a_{{34}} , \\ \varsigma _{23}^{**}&=-\nu pa_{{13}} -\left( {1-\nu } \right) \,qa_{{23}} +\left( {\gamma _{2} -0.5\alpha } \right) \nu a_{{33}} +\nu \gamma _{3} a_{{34}} ,\,\,\, \\ \varsigma _{24}^{**}&=-\nu pa_{{14}} -\left( {1-\nu } \right) \,qa_{{24}} -\nu \gamma _{3} a_{{33}} +\left( {\gamma _{2} -0.5\alpha } \right) \nu a_{{34}} , \\ \varsigma _{33}^{**}&=\left( {-\nu p} \right) a_{{13}} +\left( {-\nu q} \right) a_{{23}} +\left( {\gamma _{2} -\nu \gamma _{2} -0.5\alpha +0.5\alpha \nu } \right) a_{{33}} +\left( {1-\nu } \right) \gamma _{3} a_{{34}} , \\ \varsigma _{34}^{**}&=\left( {-\nu p} \right) a_{{14}} +\left( {-\nu q} \right) a_{{24}} -\left( {1-\nu } \right) \gamma _{1} a_{{33}} +\left( {\gamma _{2} -\nu \gamma _{2} -0.5\alpha +0.5\alpha \nu } \right) a_{{34}} , \\ \varsigma _{43}^{**}&=\left( {\alpha -2\gamma _{2} } \right) \left( {2\nu -1} \right) a_{{23}} -2\gamma _{3} \left( {2\nu -1} \right) a_{{24}} -2q\left( {2\nu -1} \right) a_{{33}} , \\ \varsigma _{44}^{**}&=2\gamma _{3} \left( {2\nu -1} \right) a_{{23}} +\left( {\alpha -2\gamma _{2} } \right) \left( {2\nu -1} \right) a_{{24}} -2q\left( {2\nu -1} \right) a_{{34}} , \\ \varsigma _{53}^{**}&=\left( {\alpha -2\gamma _{2} } \right) \left( {2\nu -1} \right) a_{{13}} -2\gamma _{3} \left( {2\nu -1} \right) a_{{14}} -2p\left( {2\nu -1} \right) a_{{33}} , \\ \varsigma _{54}^{**}&=2\gamma _{3} \left( {2\nu -1} \right) a_{{13}} +\left( {\alpha -2\gamma _{2} } \right) \left( {2\nu -1} \right) a_{{14}} -2p\left( {2\nu -1} \right) a_{{34}} , \\ \varsigma _{63}^{**}&=-2q\left( {2\nu -1} \right) a_{{13}} -2p\left( {2\nu -1} \right) a_{{23}} , \\ \varsigma _{64}^{**}&=-2q\left( {2\nu -1} \right) a_{{14}} -2p\left( {2\nu -1} \right) a_{{24}} \\ \end{aligned} \end{aligned}$$

(C.2)

finally, the relevant coefficients for the fifth and sixth roots are obtained as:

$$\begin{aligned} \begin{aligned} \varsigma _{15}^{***}&=-p\left( {1-\nu } \right) a_{{15}} -\nu qa_{{25}} -\nu \left( {\gamma _{2} +0.5\alpha } \right) a_{{35}} +\nu \gamma _{3} a_{{36}} , \\ \varsigma _{16}^{***}&=-p\left( {1-\nu } \right) a_{{16}} -\nu qa_{{26}} -\nu \gamma _{3} a_{{35}} -\nu \left( {\gamma _{2} +0.5\alpha } \right) a_{{36}} , \\ \varsigma _{25}^{***}&=-\nu pa_{{15}} -\left( {1-\nu } \right) \,qa_{{25}} -\left( {\gamma _{2} +0.5\alpha } \right) \nu a_{{35}} +\nu \gamma _{3} a_{{36}} ,\,\,\, \\ \varsigma _{26}^{***}&=-\nu pa_{{16}} -\left( {1-\nu } \right) \,qa_{{26}} -\nu \gamma _{3} a_{{35}} -\left( {\gamma _{2} +0.5\alpha } \right) \nu a_{{36}} , \\ \varsigma _{35}^{***}&=-\nu pa_{{15}} -\nu qa_{{25}} -\left( {1-\nu } \right) \left( {\gamma _{2} +0.5\alpha } \right) a_{{35}} +\left( {1-\nu } \right) \gamma _{3} a_{{36}} , \\ \varsigma _{36}^{***}&=-\nu pa_{{16}} -\nu qa_{{26}} -\left( {1-\nu } \right) \gamma _{1} a_{{35}} -\left( {1-\nu } \right) \left( {\gamma _{2} +0.5\alpha } \right) a_{{36}} , \\ \varsigma _{45}^{***}&=2\left( {2\nu -1} \right) \left[ {\left( {0.5\alpha +\gamma _{2} } \right) a_{{25}} -\gamma _{3} a_{{26}} -qa_{{35}} } \right] , \\ \varsigma _{46}^{***}&=2\left( {2\nu -1} \right) \left[ {\gamma _{3} a_{{25}} +\left( {0.5\alpha +\gamma _{2} } \right) a_{{26}} -qa_{{36}} } \right] , \\ \varsigma _{55}^{***}&=2\left( {2\nu -1} \right) \left[ {\left( {0.5\alpha +\gamma _{2} } \right) a_{{15}} -\gamma _{3} a_{{16}} -pa_{{35}} } \right] , \\ \varsigma _{56}^{***}&=2\left( {2\nu -1} \right) \left[ {\gamma _{3} a_{{15}} +\left( {0.5\alpha +\gamma _{2} } \right) a_{{16}} -pa_{{36}} } \right] , \\ \varsigma _{65}^{***}&=-2\left( {2\nu -1} \right) \left[ {qa_{{15}} +pa_{{25}} } \right] , \\ \varsigma _{66}^{***}&=-2\left( {2\nu -1} \right) \left[ {qa_{{16}} +pa_{{26}} } \right] . \\ \end{aligned} \end{aligned}$$

(C.3)