1 Introduction

Recently, lithium ion batteries (LIBs) have been widely used in the portable electronics for their high energy density and high capacity storage [1, 2]. The operation of LIBs involves repeated lithium ions insertion and extraction in active electrodes, which are often accompanied with considerable diffusion-induced stress (DIS). Under the effect of DIS, a volume swelling may be generated, and the electrode will be cracked, which has raised lots of concerns about failure of LIBs [1, 3, 4].

Fig. 1
figure 1

Schematic diagram of lithiation of a Si cylindrical electrode

Full size image

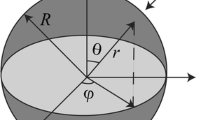
To alleviate the impact of DIS and electrode crack phenomenon, some effective methods have been carried out [5,6,7,8,9]. However, these studies only focus on the DIS analysis and neglect the electrode phase transformation phenomenon. During the lithiation process, it is well-known that the electrode system has multiple phases separated by the moving phase interfaces [10, 11]. The diffusion and phase transformation process make the electrode considered as a core-shell model, just like the Si nanowire electrodes shown in Fig. 1. The core is the crystalline Si phase (c-Si, \(\alpha \) phase) while the shell is the Li–Si phase (\(\beta \) phase). For the phase transformation process, the crack usually initiates at the two-phase interface position. For this, Ovejas et al. [12] investigated galvanostatic discharge at low and moderate rates in an LCO-NMC/graphite cell and evaluated the phase transition by incremental capacity analysis. They observed a relationship between diffusion and phase transformations. Lim et al. [13] carried out operando X-ray absorption spectroscopy (XAS) studies on Ge anodes during the initial cycles to better understand phase transformations during the electrochemical charge and discharge processes. Deshpande et al. [14] investigated the DIS in phase transforming spherical electrodes using a core-shell structural model and studied the influence of the strain energy on the battery durability.

Furthermore, with the phase transformation, the LIBs failure often originates from the electrode cracking, which is due to the great volume expansion of the electrode. So, much efforts have been devoted to study the mechanism of crack propagation. Chen et al. [15] developed an analytical model about the DIS evolution and crack propagation in a spherical particle electrode during phase transformation. Haftbaradaran et al. [16, 17] presented an analytical model analysis of two-phase electrode particles with core-shell structure subject to deintercalation and developed a fracture mechanics study of the phase separating planar electrodes. Chiang et al. [18] proposed the electrochemical shock to study the fracture driven by DIS in electrode materials. Much efforts above are focused on the large plastic deformation induced cracking behavior, but for brittle material, just like Si, when it is in the elastic condition with small deformation, the crack can also originate and propagate, which is called the brittle crack. For a Si electrode, the brittle crack has a significant impact on the mechanical behavior of LIBs [18, 19].

Nevertheless, the above-mentioned researches usually assume that the electrodes are isotropic linear elastic solid particles, while seldom concern the anisotropic properties. Due to the growth mechanism, some particles with cylindrical shape, like nanowires, nanorods and nanotubes, are isotropic in their cross section and anisotropic in the longitudinal direction, which is called the transversely isotropic property [20, 21]. With the insertion of lithium ions, the phase transformation can result in the modulus softening in different directions, which may affect the transversely isotropic properties and have significant influence on the electrode’s mechanical behavior. Therefore, here we want to study the different property ratios (such as Young’s modulus ratio, partial molar volume ratio, and Poisson’s ratio) between the isotropic cross section and the anisotropic axial direction for the Si cylindrical electrodes. And for the sake of evaluating the cylindrical electrodes, we want to shed light on the DIS and brittle crack-induced stress intensity factor (SIF) for cylindrical electrodes with phase transformation by a theoretical analysis.

In this paper, a theoretical model of DIS and SIF in Si cylindrical electrodes with phase transformation is studied by researching the electronic reaction and diffusion process. By the analysis of the model, the theoretical basis for the electrode phase transformation and electrode brittle cracking behavior is provided, and the effect of appropriate transversely isotropic property ratios on electrodes is offered. We believe it will help us understand more about the internal mechanical behavior of the battery electrodes.

2 Theoretical model of DIS and SIF in cylindrical electrodes

2.1 Concentration distribution and stress modeling in the cylindrical electrodes with phase transformation

In the cylindrical coordinate system, the cylindrical body is transversely isotropic about the axial direction, that is, in-plane properties of the body perpendicular to the axial direction are identical. According to the LIB theory, lithium ions usually diffuse into the electrode along the radial direction when charging and extract out when discharging, which results in the generation of the phase transformation [22]. As shown in Fig. 1, the center of the Si particle is assumed to be the \(\upalpha \) phase initially, and it transforms to the \(\upbeta \) phase as a result of diffusion. Furthermore, for the Si electrode, it is prone to brittle fracture, which is the main focus to the mechanical behavior of a Si electrode [19]. So, the linear elasticity model with small deformation is used to study the stress conditions in the \(\upalpha \) and \(\upbeta \) phases. By analogy to the thermal stress, the transversely isotropic stress and strain constitutive relation can be expressed by [20]:

$$\begin{aligned} \left\{ {\begin{array}{lll} \varepsilon _r -\Omega _r C \\ \varepsilon _\theta -\Omega _\theta C \\ \varepsilon _z -\Omega _z C \\ \end{array}} \right\} =\left[ {{\begin{array}{ccc} {\frac{1}{E}}&{} {-\frac{\nu _z }{E}}&{} {-\frac{\nu }{E_z }} \\ {-\frac{\nu _z }{E}}&{} {\frac{1}{E}}&{} {-\frac{\nu }{E_z }} \\ {-\frac{\nu }{E_z }}&{} {-\frac{\nu }{E_z }}&{} {\frac{1}{E_z }} \\ \end{array} }} \right] \left\{ {\begin{array}{l} \sigma _r \\ \sigma _\theta \\ \sigma _z \\ \end{array}} \right\} \end{aligned}$$
(1)

where \(\varepsilon _r\), \(\varepsilon _\theta \), \(\varepsilon _z \) and \(\sigma _r \), \(\sigma _\theta \), \(\sigma _z\) are the strain and stress components along radial, tangential, and axial direction, respectively. E and \(\nu \) are Young’s modulus and Poisson’s ratio in the isotropic plane, \(E_z\) and \(\nu _z\) are Young’s modulus and Poisson’s ratio in the axial direction, \(\Omega \) is the partial molar volume of solute, \(\Omega _r C=\Omega _\theta C\) are in-plane swelling transformation strain. \(\Omega _z C\) is longitudinal swelling transformation strain, and C is the molar concentration of lithium ions.

Since the solute diffusion process is much slower than the elastic deformation, the mechanical equilibrium is established faster than that of diffusion [23]. Then, with the transversely isotropic elastic analysis of the electrode deformation, the equilibrium condition and kinematic relations can be given:

$$\begin{aligned}&\varepsilon _r =\frac{\partial u}{\partial r}, \quad \varepsilon _\theta =\frac{u}{r}, \quad \varepsilon _z =\frac{\partial w}{\partial z}, \end{aligned}$$
(2.1)
$$\begin{aligned}&\frac{\partial \sigma _r }{\partial r}+\frac{\sigma _r -\sigma _\theta }{r}=0, \quad \frac{\partial \sigma _z }{\partial z}=0 \end{aligned}$$
(2.2)

where u and w are the displacement in the radial and axial directions.

Substituting Eq. (2.1) into Eq. (1), the stress equations can be obtained:

$$\begin{aligned} \sigma _r= & {} D_{11} \frac{\partial u}{\partial r}+D_{12} \frac{u}{r}+D_{13} \frac{\partial w}{\partial z}-\gamma _1 C, \nonumber \\ \sigma _\theta= & {} D_{12} \frac{\partial u}{\partial r}+D_{11} \frac{u}{r}+D_{13} \frac{\partial w}{\partial z}-\gamma _1 C, \nonumber \\ \sigma _z= & {} D_{13} \frac{\partial u}{\partial r}+D_{13} \frac{u}{r}+D_{33} \frac{\partial w}{\partial z}-\gamma _2 C \end{aligned}$$
(3)

where the coefficients \(D_{11} \), \(D_{12} \), \(D_{13} \), \(D_{33}\) and moduli \(\gamma _1\), \(\gamma _2\) can be calculated by:

$$\begin{aligned} D_{11}= & {} \frac{E\left( {E_z -\nu _z^2 E} \right) }{M\left( {1+\nu } \right) },D_{12} =\frac{E\left( {\nu E_z +\nu _z^2 E} \right) }{M\left( {1+\nu } \right) },D_{13} =\frac{EE_z \nu _z }{M},D_{33} =\frac{E_z^2 \left( {1-\nu } \right) }{M}, \nonumber \\ \gamma _1= & {} \left( {D_{11} +D_{12} } \right) r+D_{13} z=\frac{EE_z \left( {r+\nu _z z} \right) }{M},M=E_z \left( {1-\nu } \right) -2\nu _z^2 E, \nonumber \\ \gamma _2= & {} 2D_{13} r+D_{33} z=\frac{E_z \left[ {2E\nu _z r+E_z z\left( {1-\nu } \right) } \right] }{M}. \end{aligned}$$
(4)

Substituting Eq. (3) into Eq. (2.2), the equations will become:

$$\begin{aligned} \frac{\partial ^{2}u}{\partial r^{2}}+\frac{\partial u}{r\partial r}-\frac{u}{r^{2}}= & {} \frac{\gamma _1 \partial C}{D_{11} \partial r}, \nonumber \\ \frac{\partial w}{\partial z}= & {} k \end{aligned}$$
(5)

and be solved:

$$\begin{aligned} u= & {} \frac{\gamma _1 }{D_{11} r}\int _0^r {Cr\text {d}r} +Ar+\frac{B}{r}, \nonumber \\ w= & {} \int _0^z {k\text {d}z} =kz \end{aligned}$$
(6)

where k is a constant, A and B are parameters for the electrode particle, and they can be obtained from the boundary conditions for both \(\alpha \) and \(\beta \) phases.

Based on Eq. (3), the stress equations can be expressed:

$$\begin{aligned} \sigma _r= & {} -\,\frac{D_{11} -D_{12} }{D_{11} }\frac{\gamma _1 }{r^{2}}\int _0^r {Cr\text {d}r} +\left( {D_{11} +D_{12} } \right) A-\frac{B}{r^{2}}\left( {D_{11} -D_{12} } \right) +D_{13} k, \nonumber \\ \sigma _\theta= & {} \frac{D_{11} -D_{12} }{D_{11} }\frac{\gamma _1 }{r^{2}}\int _0^r {Cr\text {d}r} +\left( {D_{11} +D_{12} } \right) A+\frac{B}{r^{2}}\left( {D_{11} -D_{12} } \right) +D_{13} k-\frac{D_{11} -D_{12} }{D_{11} }\gamma _1 C, \nonumber \\ \sigma _z= & {} \frac{D_{13} \gamma _1 -D_{11} \gamma _2 }{D_{11} }C+2D_{13} A+D_{33} k. \end{aligned}$$
(7)

Under the plane strain conditions, the axial strain is negligible:

$$\begin{aligned} \varepsilon _z =0. \end{aligned}$$
(8)

It means the parameter k will become zero and it has no effect on stress, so we exclude the discussion of axial stress.

For the \(\alpha \) phase in the region of \(0\le r\le r_1\) (\(r_1\) is the normalized radial location of the moving phase interface), the stress and displacement equations can be obtained:

$$\begin{aligned} \sigma _r= & {} -\,\frac{D_{11}^\alpha -D_{12}^\alpha }{D_{11}^\alpha }\frac{\gamma _1^\alpha }{r^{2}}\int _0^r {Cr\text {d}r} +\left( {D_{11}^\alpha +D_{12}^\alpha } \right) A^{\alpha }-\frac{B^{\alpha }}{r^{2}}\left( {D_{11}^\alpha -D_{12}^\alpha } \right) , \nonumber \\ \sigma _\theta= & {} \frac{D_{11}^\alpha -D_{12}^\alpha }{D_{11}^\alpha }\frac{\gamma _1^\alpha }{r^{2}}\int _0^r {Cr\text {d}r} +\left( {D_{11}^\alpha +D_{12}^\alpha } \right) A^{\alpha }+\frac{B^{\alpha }}{r^{2}}\left( {D_{11}^\alpha -D_{12}^\alpha } \right) -\frac{D_{11}^\alpha -D_{12}^\alpha }{D_{11}^\alpha }\gamma _1^\alpha C, \nonumber \\ u= & {} \frac{\gamma _1^\alpha }{D_{11}^\alpha r}\int _0^r {Cr\text {d}r} +A^{\alpha }r+\frac{B^{\alpha }}{r}, \end{aligned}$$
(9)

and the stress and displacement equations can be obtained for the \(\beta \) phase in the region of \(r_1 \le r\le R\):

$$\begin{aligned} \sigma _r= & {} -\,\frac{D_{11}^\beta -D_{12}^\beta }{D_{11}^\beta }\frac{\gamma _1^\beta }{R^{2}}\int _{r_1 }^r {Cr\text {d}r} +\left( {D_{11}^\beta +D_{12}^\beta } \right) A^{\beta }-\frac{B^{\beta }}{r^{2}}\left( {D_{11}^\beta -D_{12}^\beta } \right) , \nonumber \\ \sigma _\theta= & {} \frac{D_{11}^\beta -D_{12}^\beta }{D_{11}^\beta }\frac{\gamma _1^\beta }{R^{2}}\int _{r_1 }^r {Cr\text {d}r} +\left( {D_{11}^\beta +D_{12}^\beta } \right) A^{\beta }+\frac{B^{\beta }}{r^{2}}\left( {D_{11}^\beta -D_{12}^\beta }, \right) -\frac{D_{11}^\beta -D_{12}^\beta }{D_{11}^\beta }\gamma _1^\beta C, \nonumber \\ u= & {} \frac{\gamma _1^\beta }{D_{11}^\beta R}\int _{r_1 }^r {Cr\text {d}r} +A^{\beta }r+\frac{B^{\beta }}{r} \end{aligned}$$
(10)

where R is the radius of the electrode, and the superscript of \(\alpha \) and \(\beta \) means that these parameters are appropriate for \(\alpha \) or \(\beta \) phase. Then, Young’s modulus E, Poisson’s ratio \(\nu \), and partial molar volume of solute \(\Omega \) will become \(E^{\alpha } E^{\beta }\),\(\nu ^{\alpha } \nu ^{\beta }\), and \(\Omega ^{\alpha } \Omega ^{\beta }\).

Without considering the surface effect, the normal radial stress will be zero at the free surface of the electrode due to the traction-free boundary condition [24]. Since there is no radial displacement at the center of the electrode, and the radial stress and displacement are continuous at the interface, the stress and displacement boundary conditions may be expressed by:

$$\begin{aligned} \left. {\sigma _r } \right| _{r=R} =0 \, \left. u \right| _{r=0} =0~ \left. {\sigma _r } \right| _{r=r_1^\alpha } =\left. {\sigma _r } \right| _{r=r_1^\beta } \, \left. u \right| _{r=r_1^\alpha } =\left. u \right| _{r=r_1^\beta }. \end{aligned}$$
(11)

Using these boundary conditions, the parameters of A and B can be calculated:

$$\begin{aligned} B^{\alpha }= & {} 0, \nonumber \\ B^{\beta }= & {} \frac{\left( {1-\frac{D_{11}^\alpha +D_{12}^\alpha }{D_{11}^\beta +D_{12}^\beta }} \right) \left( {D_{11}^\beta -D_{12}^\beta } \right) \frac{\gamma _1^\beta }{D_{11}^\beta R^{2}}\int _{r_1 }^R {Cr\text {d}r} +2\frac{\gamma _1^\alpha }{r_1^2 }\int _0^{r_1 } {Cr\text {d}r} }{\left( {\frac{D_{11}^\alpha +D_{12}^\alpha }{D_{11}^\beta +D_{12}^\beta }-1} \right) \frac{D_{11}^\beta -D_{12}^\beta }{R^{2}}+\frac{D_{11}^\alpha +D_{12}^\alpha +D_{11}^\beta -D_{12}^\beta }{r_1^2 }}, \nonumber \\ A^{\beta }= & {} \frac{D_{11}^\beta -D_{12}^\beta }{D_{11}^\beta +D_{12}^\beta }\frac{B^{\beta }}{R^{2}}+\frac{D_{11}^\beta -D_{12}^\beta }{D_{11}^\beta +D_{12}^\beta }\frac{\gamma _1^\beta }{D_{11}^\beta R^{2}}\int _{r_1 }^R {Cr\text {d}r},\nonumber \\ A^{\alpha }= & {} A^{\beta }+\frac{B^{\beta }}{r_1^2 }-\frac{\gamma _1^\alpha }{D_{11}^\alpha r_1^2 }\int _0^{r_1} {Cr\text {d}r}. \end{aligned}$$
(12)

Then, the transport of solute is regarded as a concentration-driven diffusion process. The species flux can be written as:

$$\begin{aligned} {J=}-\,MC\nabla \mu \end{aligned}$$
(13)

where M is the mobility of lithium ions, and \(\mu =\mu _0 +RT\ln X-\Omega \sigma _h\) is the chemical potential. Furthermore, \(\mu _0\) is a constant, R is gas constant, T is absolute temperature, X is the molar fraction of a lithium ion, and \(\sigma _h\) is the hydrostatic stress. Then, assuming the temperature is uniform, the species flux can be obtained [25, 26]:

$$\begin{aligned} {J=}-\,D\left( {\nabla C-\frac{\Omega C}{RT}\nabla \sigma _h } \right) \end{aligned}$$
(14)

where \(D=MRT\) is the diffusion coefficient of lithium ions. The conservation of species can be given by:

$$\begin{aligned} \frac{\partial C}{\partial t}+\nabla \cdot J=0. \end{aligned}$$
(15)

Then, substituting Eq. (14) into Eq. (15), the transport of lithium ions can be obtained [27,28,29]:

$$\begin{aligned} \frac{\partial C}{\partial t}= & {} D\left( {\nabla ^{2}C-\frac{\Omega }{RT}\nabla C\nabla \sigma _h -\frac{\Omega C}{RT}\nabla ^{2}\sigma _h } \right) \nonumber \\= & {} D\left[ {\frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r}\frac{\partial C}{\partial r}+\theta \left( {\frac{\partial C}{\partial r}} \right) ^{2}+\theta C\left( {\frac{\partial ^{2}C}{\partial r^{2}}+\frac{1}{r}\frac{\partial C}{\partial r}} \right) } \right] \end{aligned}$$
(16)

where \(\theta =\frac{\Omega }{RT}\frac{2\Omega E}{9\left( {1-\nu } \right) }\), and when \(\theta =0\), it means that the diffusion process doesn’t consider the stress field effect. The stress field has significant influence on the lithium ions diffusion from this. Moreover, for the existence of cracks, they can also affect the diffusion of lithium ions at crack locations, just as the stress field does. Furthermore, from Ref. [30], the crack can help a chloridion to permeate into the concrete. So, just like this, the existence of cracks may also offer an access for the electrolyte infiltration, which will accelerate the diffusion velocity of lithium ions and affect the stress distribution. However, in order to simplify the model, the influence of cracks on lithium ion diffusion is neglected, and it will be further studied to better predict the failure of Li–ion battery in the future.

Then, for simplicity, the diffusion coefficient is considered as a constant, and for the first insertion, the boundary conditions can be obtained:

$$\begin{aligned} {\left. {C{{ (r,t)}}} \right| _{0\le r\le r_1^- } =C_{\mathrm{eq}\alpha } } ~{\left. {C{{(r,t)}}} \right| _{r=r_1^+ } =C_{\mathrm{eq}\beta } } {\left. {~D\frac{\partial C\left( {r,t} \right) }{\partial r}} \right| _{r=0} =0} {\left. {~D\frac{\partial C\left( {r,t} \right) }{\partial r}} \right| _{r=R} =J_b } \end{aligned}$$
(17)

where \(J_b\) is a constant proportional to electric current density, \(C_{\mathrm{eq}\alpha }\) is the equilibrium concentration of \(\alpha \) phase, and its value usually equals zero. \(C_{eq\beta }\) is the equilibrium concentration of the \(\beta \) phase. With this concentration difference between \(\alpha \) phase and \(\beta \) phase, the interface moves from the electrode surface to the center, and the governing equations can be written as:

$$\begin{aligned} \left( {C_{\mathrm{eq}\alpha } -C_{\mathrm{eq}\beta } } \right) \frac{\partial r_1 }{\partial t}=D\frac{\partial C}{\partial r}. \end{aligned}$$
(18)

For the delithiation and the subsequent charging and discharging process, the electrode will be in single-phase condition. Then, the boundary conditions with the galvanostatic charging are:

$$\begin{aligned} {\left. {C{{(r,0)}}} \right| _{0\le r\le R} =C_0 } {\left. {~D\frac{\partial C\left( {r,t} \right) }{\partial r}} \right| _{r=0} =0} {\left. {~D\frac{\partial C\left( {r,t} \right) }{\partial r}} \right| _{r=R} =J_b } \ \end{aligned}$$
(19)

where \(C_0\) is the initial lithium ion concentration in the electrode, and its value usually equals zero, \(J_b >0\) means the charging condition while \(J_b <0\) means the discharging condition.

2.2 SIF of the center and edge cracks in cylindrical electrodes with phase transformation

Recently, the SIF has been widely used to analyze the growth of pre-cracks in the electrode. Here, Si is chosen to be the electrode material. As mentioned above, it is a brittle material and prone to brittle fracture. In view of this, the linear elasticity model with small deformation is used to study the SIF of the brittle center and edge cracks in cylindrical Si electrodes with phase transformation. Then, in order to acquire the SIF resulting from the DIS, weight function w(r) is employed with the r being the spatial coordinate along the crack face. Due to the assumption of the traction-free crack surface, the tensile DIS becomes equal to the pressure imposed on the crack surface. Since the crack plane is normal to the diffusion plane, transient concentration distribution will not be disturbed. Thus, the crack-free concentration files and the resulting DIS field can be used directly on the crack surface. So, the pre-cracks are considered with various sizes of a, and the SIF induced at the tip of the pre-crack can be obtained [31, 32]:

$$\begin{aligned} K_I =\int _0^a {w\left( r \right) \sigma \left( r \right) \text {d}r} \end{aligned}$$
(20)

where \(\sigma \left( r \right) \) is the traction distribution along the crack face, and here it can be expressed by Eqs. (18) and (19). The weight function w(r) is only dependent on the configuration of the crack and the geometry of the electrode, and it is independent on the traction loading. However, a satisfactory reference load for the center and edge crack geometry in the cylindrical electrodes does not exist. For the insertion and extraction of lithium ions, the dimension of diffusion is the main difference between the cylindrical electrode and a planar electrode. Then, by the theory of infinitesimal method, the cylindrical electrode along the radial direction is like the planar electrode along the thickness direction. As a result, an approximate geometry, planar electrode, is used here to obtain the weight function [17], which uses the same method as in Ref. [18]. For the cylindrical electrode, the center crack and the edge crack are considered here, respectively.

For the center crack, the \(K_I\) equation can be written as:

$$\begin{aligned} K_{I,c} =\int _0^a {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} \end{aligned}$$
(21)

where the subscript c means the crack is the center crack, \(w_c (r)\) is the weight function at the tip of a center crack, and it can be given by [17]:

$$\begin{aligned} w_c \left( r \right) =\frac{2}{\sqrt{2R}}\left[ {1+0.297\sqrt{1-\left( {\frac{r}{a}} \right) ^{2}}\left( {1-\cos \frac{\pi a}{2R}} \right) } \right] \frac{\sqrt{\tan \frac{\pi a}{2R}}}{\sqrt{1-\left( {\frac{\cos \frac{\pi a}{2R}}{\cos \frac{\pi r}{2R}}} \right) ^{2}}}. \end{aligned}$$
(22)

Then, for the edge crack, Eq. (20) can be transformed:

$$\begin{aligned} K_{I,e} =\int _{R-a}^R {w_e \left( r \right) \sigma _e \left( r \right) \text {d}r} \end{aligned}$$
(23)

where the subscript e means the crack is the edge crack, \(w_e (r)\) is the weight function at the tip of the edge crack, and it can be given by [17]:

$$\begin{aligned} w_e \left( r \right) =\frac{2}{\sqrt{2a}}\frac{F_e \left( {\frac{R-r}{a},\frac{a}{2R}} \right) }{\left( {1-\frac{a}{2R}} \right) ^{1.5}\sqrt{1-\left( {\frac{R-r}{a}} \right) ^{2}}} \end{aligned}$$
(24)

where

$$\begin{aligned} F_e \left( {\delta ,\eta } \right)= & {} f_1 \left( \eta \right) +f_2 \left( \eta \right) \delta +f_3 \left( \eta \right) \delta ^{2}+f_4 \left( \eta \right) \delta ^{3}, \end{aligned}$$
(25.1)
$$\begin{aligned} f_1 \left( \eta \right)= & {} 0.46\eta +3.06\eta ^{2}+0.84\left( {1-\eta } \right) ^{5}+0.66\eta ^{2}\left( {1-\eta } \right) ^{2}, \end{aligned}$$
(25.2)
$$\begin{aligned} f_2 \left( \eta \right)= & {} -\,3.52\eta ^{2}, \end{aligned}$$
(25.3)
$$\begin{aligned} f_3 \left( \eta \right)= & {} 6.17-28.22\eta +34.54\eta ^{2}-14.39\eta ^{3}-\left( {1-\eta } \right) ^{1.5} \nonumber \\&-\,5.88\left( {1-\eta } \right) ^{5}-2.64\eta ^{2}\left( {1-\eta } \right) ^{2}, \end{aligned}$$
(25.4)
$$\begin{aligned} f_4 \left( \eta \right)= & {} -\,6.63+25.16\eta -31.04\eta ^{2}+14.41\eta ^{3}+2\left( {1-\eta } \right) ^{1.5} \nonumber \\&+\,5.04\left( {1-\eta } \right) ^{5}+1.98\eta ^{2}\left( {1-\eta } \right) ^{2}. \end{aligned}$$
(25.5)

The \(\sigma _c \left( r \right) \) and \(\sigma _e \left( r \right) \) are the traction load along the center crack and edge crack surface, and they will be discussed in detail in Sect. 3.3. Furthermore, as introduced in Tada et al. [32], the weight function given in Eqs. (22) and (24) is singular at integral bounds in Eqs. (21) and (23). Then, for the center crack, the integral in Eq. (21) can be written [20]:

$$\begin{aligned} K_I^c= & {} \int _0^a {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} \nonumber \\= & {} \int _0^{a-\varepsilon } {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} +\int _{a-\varepsilon }^a {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} \end{aligned}$$
(26)

where \(\varepsilon \) is a very small number compared with a. Then, for \(\varepsilon \), the mean value theorem can be used to rewrite the second integral in Eq. (26):

$$\begin{aligned} \int _{a-\varepsilon }^a {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} =\sigma _c \left( r \right) \left| {_{r=a} } \right. \int _{a-\varepsilon }^a {w_c \left( r \right) \text {d}r} =2\sigma _c \left( r \right) \left| {_{r=a} } \right. \sqrt{\frac{2\varepsilon }{\pi }}. \end{aligned}$$
(27)

And similarly, for the edge crack, the integral in Eq. (23) can be written:

$$\begin{aligned} K_I^e= & {} \int _{R-a}^R {w_e \left( r \right) \sigma _e \left( r \right) \text {d}r} \nonumber \\= & {} \int _{R-a+\varepsilon }^R {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} +\int _{R-a}^{R-a+\varepsilon } {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} \nonumber \\= & {} \int _{R-a+\varepsilon }^R {w_c \left( r \right) \sigma _c \left( r \right) \text {d}r} +2\sqrt{\frac{2\varepsilon }{\pi }}\frac{F_e \left( {1,\frac{a}{2R}} \right) }{\left( {1-\frac{a}{2R}} \right) ^{1.5}}\sigma _c \left( r \right) \left| {_{r=R-a} } \right. \end{aligned}$$
(28)

where \(F_e \left( {1,\frac{a}{2R}} \right) \) can be obtained from Eq. (25).

3 Results and discussion

3.1 The lithiation/delithiation process analysis of the cylindrical electrodes with phase transformation

Lithiation proceeds in a core-shell mode with the phase transformation [33]. The moving phase interface is atomically sharp, oriented parallel to the longitudinal axis of the electrode, and the shape of the interface in the cross section is similar with the electrode structure. For crystalline Si nanowire, its phase transformation usually takes place at the first lithium ions insertion process, and for the subsequent charging and discharging process, the amorphous Si will change in single phase [34, 35]. During the two-phase process, the lithium ions diffuse into the inside of the Si particle to form the Li–Si alloy. The interface forms at this moment, and its shape is like a thin walled cylinder and the cross section of it is a circle. As shown in Fig. 1, the blue region is the Li–Si alloy, \(\beta \) phase, while the central part of the model (yellow region) is the c-Si, \(\alpha \) phase. The red line means the moving phase interface. When the lithium ions gather enough, the additional lithium ions can diffuse rapidly in the Li–Si alloy and accumulate more lithium ions at the interface, which sustains further reaction to form more Li–Si alloy and moves the interface toward the center of the Si particle until the lithium ion has reached the center of the electrode [29]. Then, after that, the electrode will continue to be lithiated in single phase. In this moment, the crystalline Si has become the Li–Si, and when the battery is discharging, the Li–Si will become the amorphous Si with the extraction of lithium ions. For the subsequent charging and discharging process, the electrode will be lithiated in single phase.

3.2 Stress analysis of the cylindrical electrodes with phase transformation

Based on the model above, for studying the brittle crack in the Si electrode, we neglect the large plastic deformation influence of Si on the model, and the theoretical model can be used in all cylindrical electrodes with phase transformation. For the purpose of explaining the concentration and stress conditions under the galvanostatic operation, some parameters of Si are used, which are listed in the “Appendix”. Furthermore, the \(\upalpha \) phase transforms into the \(\upbeta \) phase with continuous movement of the interface from the surface to the center of the electrode. Based on this, the plots exhibited the concentration and DIS in cylindrical electrodes at different time conditions in the insertion process, as shown in the Figs. 2, 3, and 4. In addition, the extraction process has also been discussed in this work and is not fully shown in Figs. 2, 3, and 4 to save space.

Figure 2 shows the normalized solute concentration distribution during the first insertion process versus the relative location r / R with different interface positions and dimensionless time under galvanostatic condition. The \(\varphi =\frac{Dt}{R^{2}}\) is the dimensionless time, and \(r_1 =0.9R\) means the moving interface position locates at \(r_1 =0.9R\). When the electrode begins to be lithiated for the first time, it is in the condition of phase transformation, and the solute concentration reduces continuously from the electrode surface to the phase interface location and then becomes a constant zero from the phase interface to the electrode center, as shown in Fig. 2a. Between the two sides of the interface, there exists a large solute concentration jump. Inside the phase interface, the electrode is the c-Si, while outside is the Li–Si phase. With the increment of time, the phase interface moves from the electrode surface to the center, and when it reaches the center \(r_1 =0\), it means the electrode has become Li–Si phase entirely, as shown in Fig. 2b. Afterward, the solute concentration increases with the time increment, which means the ratio of Li–Si is increasing. At the high radial position, the solute concentration reduces sharply while it reduces slowly at the low radial position. Besides, although the time changes, four curves of the lithium ion concentration shown in Fig. 2b are nearly parallel, which means that the concentration of the whole electrode increases near linearly, which is due to the galvanostatic condition.

Figure 3 shows the normalized radial stress during the first insertion process decreasing with the increment of radial position and dimensionless time in the electrode versus different interface positions under galvanostatic condition. It indicates that the radial stress at the electrode surface is zero and keeps constant, which is due to the traction-free boundary conditions. For the condition with the phase transformation, as shown in Fig. 3a, the radial stress keeps constant inside the phase interface and declines to zero when it is outside the interface. What’s more, with the increment of time, more and more lithium ions insert into the electrode, which causes the increase in the stress value. Then, for the condition after the lithium ion has reached the center of the electrode, as shown in Fig. 3b, the radial stress declines continuously versus the normalized radial position. And the radial stress changes slowly at low radial position and changes sharply at high radial position as well.

Fig. 2
figure 2

The normalized lithium ion concentration distribution during the first insertion versus the relative location with different interface positions and dimensionless time under galvanostatic condition. a Means the condition of phase transformation, and b means the condition that the lithium ion has reached the center of the electrode

Full size image
Fig. 3
figure 3

The normalized radial stress during the first insertion process versus relative location with different interface positions and dimensionless time under galvanostatic condition. a Means the condition of phase transformation, and b means the condition that the lithium ion has reached the center of the electrode

Full size image
Fig. 4
figure 4

The normalized tangential stress during the first insertion process versus relative location with different interface positions and dimensionless time under galvanostatic condition. a Means the condition of phase transformation, and b means the condition that the lithium ion has reached the center of the electrode

Full size image

Figure 4 shows the normalized tangential stress during the first insertion process decreasing with the increment of radial position and dimensionless time in the electrode versus different interface positions under galvanostatic condition. For the condition of phase transformation, as shown in Fig. 4a, the tangential stress keeps constant inside the phase interface and declines sharply when it is outside the interface. And at the location of the phase interface, it exists a large tangential stress jump. With the increment of time, the value for the tangential stress inside the phase interface increases little by little, as shown in the enlarged image in Fig. 4a, while the value for the tangential stress outside the phase interface changes sharply. Then, for the condition after the lithium ion has reached the center of the electrode, as shown in Fig. 4b, the tangential stress decreases slowly at first and drops quickly at end, as well as the radial stress does. Furthermore, the tangential stress is tensile at the low radial position and converts to compressive at the high radial position, and it reaches the maximum value at the surface of the electrode.

Fig. 5
figure 5

The normalized tangential stress jump at the different phase interface locations under galvanostatic condition

Full size image
Fig. 6
figure 6

The normalized radial stress versus relative location with different a Young’s modulus ratio \(E_z /E_\alpha \), c partial molar volume ratio \(\Omega _z /\Omega _\alpha \), e Poisson’s ratio \(\nu _z /\nu _\alpha \), and normalized tangential stress versus relative location with different b Young’s modulus ratio \(E_z /E_\alpha \), d partial molar volume ratio \(\Omega _z /\Omega _\alpha \), f Poisson’s ratio \(\nu _z /\nu _\alpha \)

Full size image

From Eqs. (9) and (10), for the tangential stress exists a stress jump and it can be evaluated by:

$$\begin{aligned} \sigma _{int} =\sigma _\theta \left| {_{r_1^- } } \right. -\sigma _\theta \left| {_{r_1^+ } }. \right. \end{aligned}$$
(29)

Then, Fig. 5 shows the normalized tangential stress jump at the different phase interface locations under galvanostatic condition. With the insertion of lithium ions, the phase interface forms. Between the two sides of the interface, the large solute concentration jump results in the large tangential stress jump, as shown in Figs. 2 and 4. In Fig. 5, the stress jump decreases with the phase interface moving from the electrode surface to the center. It reaches the maximum value at the electrode surface and achieves the minimum one at the center. When the interface locates near the surface of the electrode, which means \(r/R >0.7\), the stress jump changes quickly while for \(r/R <0.7\) it changes slowly. With the large stress jump and the phase transformation, the tangential stress plays an important role in cracking the electrodes. It is in good line with Chen et al. [15], and the crack behavior will be detailed discussed later.

Figure 6 shows the normalized radial and tangential stress versus relative location with different property ratios. As is known, a nanostructure-based cylindrical electrode, such as Si nanowire, is usually perceived as a one-dimensional material, and it is isotropic in the cross section while anisotropic in the longitudinal direction [17]. And since we just want to discuss the variation trend of the stress with different property ratios, the Young’s modulus ratio, partial molar volume ratio, and Poisson’s ratio are generously set to vary from 0.5 to 2 for the generous changing of the material properties caused by lithiation process. The moving phase interface position is assumed to be \(r_1 =0.5R\) for this condition. Figure 6a and b means that the stress is under different Young’s modulus ratios \(E_z /E_\alpha \), and Fig. 6c and d means the different partial molar volume ratios \(\Omega _z /\Omega _\alpha \) condition while Fig. 6e and f means the different Poisson’s ratio \(\nu _z /\nu _\alpha \) condition. As shown in Fig. 6a and b, with the increase in Young’s modulus ratio \(E_z /E_\alpha \), the magnitude of normalized radial and tangential stress decreases continuously to a steady value. Moreover, the tangential stress jump decreases with the increase of \(E_z /E_\alpha \). From Fig. 6c and d, with the increase in partial molar volume ratio \(\Omega _z /\Omega _\alpha \), the magnitude of the two stresses increases and the increase magnitude is nearly identical, which has the opposite trend compared with the stress under different Young’s modulus ratio \(E_z /E_\alpha \). Furthermore, the tangential stress jump increases with the increment of \(\Omega _z /\Omega _\alpha \). Then, for Fig. 6e and f, with the increase in Poisson’s ratio \(\nu _z /\nu _\alpha \), the two stresses increase and the increase gap becomes larger. The tangential stress jump also increases with the increment of \(\nu _z /\nu _\alpha \), just like the increase trend in different partial molar volume ratio \(\Omega _z /\Omega _\alpha \) condition, but Poisson’s ratio has a more pronounced effect on stress than the partial molar volume. Because of this, the electrode fracture phenomenon may be alleviated to some degree with the appropriate property ratios.

3.3 SIF analysis of the center crack and edge crack in cylindrical electrodes with phase transformation

In the LIB field, it is recognized that the tensile tangential stress usually leads to the crack propagation and even results in the fracture of the electrode [14, 35]. Furthermore, a crystalline Si electrode is usually lithiated in two-phase transition in the first insertion process while shows single-phase change in the subsequent charging and discharging process when it becomes the amorphous form [34, 35]. In the first insertion process, the tangential stress in the \(\alpha \) phase region is usually tensile and becomes compressive in the \(\beta \) phase region, as shown in Fig. 4, which results in the occurrence of crack propagation in the \(\alpha \) phase region. In this moment, the \(\sigma _c \left( r \right) \) in Eq. (21) can be expressed in Eq. (9) in \(\alpha \) phase. The pre-crack is the center crack, and its length ranges from 0 to \(r_1 \), as shown in Fig. 7a. Then, in the subsequent charging and discharging process, the electrode shows the single-phase change, and the crack propagation is usually induced by the tensile tangential stress, as shown in Fig. 7b. At this moment, \(\sigma _e \left( r \right) \) in Eq. (23) is the stress in single-phase condition. The pre-crack is the edge crack, and with the extraction of Li–ions, the length a will expand from 0 to R.

Fig. 7
figure 7

Schematic diagram of a Si cylindrical electrode with a a center crack in the center of the electrode during the first insertion process, and b an edge crack at the surface of the electrode during the subsequent charging and discharging process

Full size image

With the insertion of lithium ions, the two-phase transition occurs and the SIF changes with the increment of time. Figure 8a shows the normalized SIF of the center crack in two-phase insertion in \(\alpha \) phase versus the crack length ratio and different interface positions. Due to the two-phase transition, the center crack length only ranges from 0 to \(r_1\), which is in line with the tensile tangential stress results in Fig. 4a. For the small center crack, the five SIF curves are nearly coincident, and each one has little change with each other. With the increment of time, the SIF increases gradually, which is due to the smooth increase in tensile tangential stress, as shown in Fig. 4a. For the large center crack, the SIF increases sharply, and it is easy to exceed the critical value of the material fracture toughness which leads to the failure of the electrode. Furthermore, for a given time, the SIF attains its maximum value when the crack length ratio equals the phase interface relative location, and it is the most likely position to lead to the failure of the electrode, which is due to the large concentration jump and tangential stress jump. Then, Fig. 8b shows the normalized SIF of the center crack in single-phase insertion for the condition after the lithium ion has reached the center of the electrode, versus the crack length ratio. For this condition, the lithium ion has reached the center of the electrode, and it continues to insert into the electrode. With the increment of time, the SIF increases rapidly until the dimensionless time reaches 0.2. At that time, the SIF takes the steady value and doesn’t change with time. It is because that the electrode is under galvanostatic operation, and the amount of the lithium ion insertion has its maximum value. The SIF will hold steady when the electrode has been lithiated entirely. For the small center crack, the SIF increases gradually with the increment of crack length ratio and dimensionless time. As the growth of center crack, the SIF gets its maximum value and then decreases away from it. After that, when the crack grows continuously, the SIF returns to its high position and increases sharply until the whole electrode has cracked.

Fig. 8
figure 8

The normalized SIF of the a center crack in two-phase insertion in \(\alpha \) phase, b center crack in single-phase insertion for the condition after the lithium ion has reached the center of the electrode, and c edge crack in single-phase extraction versus the crack length ratio and the dimensionless time

Full size image
Fig. 9
figure 9

The normalized SIF of the center crack in two-phase insertion in \(\alpha \) phase versus the crack length ratio and different property ratios: different a Young’s modulus ratio \(E_z /E_\alpha \), b partial molar volume ratio \(\Omega _z /\Omega _\alpha \), and c Poisson’s ratio \(\nu _z /\nu _\alpha \)

Full size image

With the subsequent charging and discharging process, the single-phase transition occurs. Figure 8c shows the normalized SIF of the edge crack in single-phase extraction in the electrode versus the crack length ratio and the dimensionless time. For this extraction condition, the tangential stress is compressive near the center of the electrode and becomes tensile near the electrode surface. The stress distribution is different from that for the insertion condition. For the small edge crack, the four SIF curves are nearly coincident and increases sharply. It is because the large compressive stress in the region near the electrode center will inhibit the expansion of the crack. So, the small crack grows unstably during deintercalation, and the crack tends to spread more easily for this condition. With the growth of the edge crack, the SIF curves reach the maximum value when the edge crack ratio is nearly 0.3 and then show downtrend and begin to differ from each other. Considering from the time aspect, when the lithium ions begin to extract from the electrode, the stress level and the SIF are relatively high in the electrode. At this moment, at the early stage of lithium ion extraction, the crack and electrode are more unstable, and it is more prone to failure. With the increment of time, the lithium ions continuously extract from the electrode, and the electrode becomes stable gradually. At this moment, the SIF decreases and takes its steady value.

What is more, the property ratios do have some impact on the stress distribution, which is shown in Fig. 6. They may have some influence on the value of SIFs, as well. Based on this, Young’s modulus ratio, partial molar volume ratio, and Poisson’s ratio are set to vary from 0.5 to 2, and the moving phase interface locates at \(r_1 =0.5R\), just like the parameters used in Fig. 6. Figure 9 shows the normalized SIF of the center crack in two-phase insertion in the \(\alpha \) phase versus the crack length ratio and different property ratios. In Fig. 9a, the SIF increases with the crack length ratio. For a small crack, different Young’s modulus ratios have little impact on the SIF. But with the growth of the crack, with the increment of the Young’s modulus ratios, the SIF drops a little, which shows that the electrode becomes more stable. In Fig. 9b and c, for a small crack, different partial molar volume ratios and Poisson’s ratios also have little impact on the SIF, but with the increment of the property ratios, the SIF shows an opposite trend compared with the change trend in Fig. 9a. With the increment of the property ratios shown in Fig. 9b and c, the SIF increases and makes the electrode more prone to failure. This phenomenon is in good line with the results shown in Fig. 6. Furthermore, the different Poisson’s ratios have more influence on the SIF than the different partial molar volume ratios, just like the same trend shown in Fig. 6c–f.

4 Conclusions

This paper provides a theoretical model to study the DIS level and SIF for brittle center and edge cracks in cylindrical electrodes with phase transformation under galvanostatic control. Si is used as the battery anode here, but the theoretical model can be used in all cylindrical electrodes with phase transformation. The concentration distribution, DIS model, and SIF for different cracks in the electrodes are provided. The center and edge cracks are analyzed to investigate the influence of the initial position on crack propagation. With the elastic deformation theory, it is worth noting that there exists a large concentration jump near the phase interface in the first insertion, and it results in a large tangential stress jump (tangential stress discontinuity) at the same location. The tangential stress plays an important role in cracking on the electrodes with the stress jump and phase transformation. It is found that the crack tends to grow more easily when the crack is at the phase interface location for the first insertion. Then, it will grow more easily in the early stage of lithium ions extraction. Furthermore, manufacturing electrodes with appropriate property ratios (the larger modulus ratio \(E_z /E_\alpha \), lower partial molar volume ratio \(\Omega _z /\Omega _\alpha \), and lower Poisson’s ratio \(\nu _z /\nu _\alpha \)), it can be great help to decrease the value of DIS and SIF, and it will alleviate the electrode fracture phenomenon. This work provides a theoretical basis for the electrode phase transformation and electrode cracking when the battery is working, and it will help us understand more about the internal mechanical behavior of the LIBs electrodes.