Statistical distributions of extreme dry spell in Peninsular Malaysia

Abstract

Statistical distributions of annual extreme (AE) series and partial duration (PD) series for dry-spell event are analyzed for a database of daily rainfall records of 50 rain-gauge stations in Peninsular Malaysia, with recording period extending from 1975 to 2004. The three-parameter generalized extreme value (GEV) and generalized Pareto (GP) distributions are considered to model both series. In both cases, the parameters of these two distributions are fitted by means of the L-moments method, which provides a robust estimation of them. The goodness-of-fit (GOF) between empirical data and theoretical distributions are then evaluated by means of the L-moment ratio diagram and several goodness-of-fit tests for each of the 50 stations. It is found that for the majority of stations, the AE and PD series are well fitted by the GEV and GP models, respectively. Based on the models that have been identified, we can reasonably predict the risks associated with extreme dry spells for various return periods.

1 Introduction

The Intergovernmental Panel of Climate Change defines an extreme weather event “as an event that is rare within its statistical reference distribution at a particular place” (IPCC 2001). The amount of extremely high or low precipitation, leading to flood or drought, is an example of a substantial weather risk, about which meteorological service should give the best information to the public. A long period without precipitation causes drought. Drought is defined in four different ways: meteorological, agricultural, hydrological, and socioeconomical (Hales et al. 2003). Meteorological drought is a measure of the departure of the precipitation below normal. Thus, due to climatic differences, what is considered a drought in one location may not be a drought in another location. Agricultural drought refers to a situation when the amount of moisture in the soil no longer meets the needs of a particular crop. Hydrological drought occurs when surface and subsurface water supplies are below normal. Socioeconomical drought refers to the situation when physical water shortage begins to affect people. Thus, prolonged droughts are critical for industrial, agricultural, and domestic water resources and may seriously affect the natural environment.

In this study, an analysis of the distributions of annual extreme (AE) dry spells and a series of long dry spell generated from method of partial duration (PD) has been attempted based on the rainfall amounts recorded at 50 rain-gauge stations in the Peninsular Malaysia for the period from 1975 to 2004. The analyses of both techniques to obtain reliable extreme dry-spell statistics, which may lead to drought situation, are the main objective of this research. Previous distribution studies on spells in the same region are by Yap (1973), Quah and Ooi (1985), and Deni et al. (2008) on occurrence of wet/dry spell series, but published studies has yet to be found for extreme dry spells for this area.

The most common analysis of extreme hydrological events involves the use of AE series. When constructing the AE series, the maximum duration of a dry spell that is the longest number of days without precipitation, for each year in the record is selected; hence, the series obtained would have a length equal to the number of years. Many works that apply the AE series usually involve fitting of a probability model to the data; commonly used distributions are the Gumbel distribution (Gupta and Duckstein 1975; Lana et al. 2003), the generalized extreme value (GEV), and generalized Pareto (GP) distributions (Madsen et al. 1997a, b; Lana et al. 2006a, b). We are going to consider the GEV and GP distributions in this study.

The selection of only one value for each year, as is the case in determining a particular AE series, could sometimes lead to a wrong evaluation of the distribution of extreme dry-spell events. The main drawback is the loss of the information available in annual series of rainfall data for which the data on the dry spell is obtained. It may be possible that other values in a particular annual series, in addition to the maximum value, exceed the maximum dry-spell values in other years. The inclusion of these potential extreme values could improve the estimation of the parameters for the underlying data distribution. An alternative method, known as the PD or Peak over Threshold technique involves the selection of a set of data which consists of dry-spell values that exceed a certain level of threshold value. Literatures on the PD method can be found in works such as by Hershfield (1973), Madsen and Rosbjerg (1997), Madsen et al. (1997a, b), Onoz and Bayazit (2001), and Lang et al. (1999). Examples of applications of PD methods in the area of hydrology can be found in Adamowski (2000), Li et al. (2004), Vicente-Serrano and Begueria-Portugues (2003), and Lana et al. (2006a, b).

The objective of this paper is to compare the return values of extreme dry spells found based on the analysis using AE and PD strategies. In the analysis, the GEV and GP models are fitted to the data found using both sampling strategies. The choice of GEV and GP models to fit the data may seem to be arbitrary; however, these two distributions are the most commonly used for the analysis of extreme dry spells (Lana et al. 2006a, b). Thus, in our analysis, these two models will be fitted to the data obtained using the two strategies. For parameter estimation, the L-moments approach (Hosking and Wallis 1997) is used. In this research, comparison is then made to determine the distribution which is suitable to describe the data for each station using the L-moment ratio diagram and several goodness-of-fit tests. From the best-fitted distribution, the return period values can be generated; thus, the results based on the two strategies can be compared.

The contents of the paper are structured as follows. In Section 2, we describe the data. Section 3 describes the statistical models, the L-moments method of parameter estimation, and the goodness-of-fit procedures. Analysis on the AE and PD series are discussed in Section 4. Finally, a short discussion on the overall findings and conclusion are presented in Section 5.

2 Study area, data, and regional climate

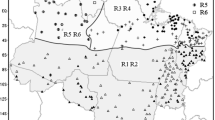
The data consisting of daily rainfall data from 50 rain gauge stations in Peninsular Malaysia from 1975 to 2004 have been obtained from the Drainage and Irrigation Department and Malaysian Meteorological Services. All the 50 stations, numbered from 1 to 50, are located at various places throughout Peninsular Malaysia, as shown in Fig. 1. In the analysis, the stations are divided into four regions based on the geographical coordinates, which are denoted as E1 and E2 for the eastern region and W1 and W2 for the western region. We consider the data from 1975 to 2004 because this is the longest period for which a complete set of data is available for all the stations considered. The problem of unavailability of a large dataset is unavoidable especially in developing countries. This situation is more critical for extreme events analysis, and it is highlighted as one of the key uncertainties in the IPCC 4th Assessment Report (Bernstein et al. 2007). In the report, it is stated that climate data coverage remains limited in some regions with marked scarcity in developing countries, thus making analyzing and monitoring changes in extreme events, including extreme frequency and intensity of precipitation more difficult than for climatic averages as longer data time series of higher spatial and temporal resolutions are required. Despite this, analysis needs to be carried out in order to identify any possible changes in extreme weather events for this region as the impact from extreme events is often severe. Less than 10% missing values are observed throughout the 30-year period, and these missing values in the data series were estimated using the modified spatial interpolation method as suggested by Suhaila et al. (2008). The homogeneity of the data series was checked using the four types of homogeneity tests recommended by Wijngaard et al. (2003), namely, the standard normal homogeneity test, the Buishand range test, the Pettit test, and the Von Neumann ratio test. The results showed that the annual number of dry days for each rain gauge station considered in this study was homogenous. The stationarity of the data series was tested using the KPSS test (Kwiatkowski et al. 1992). It is found that from the 50 stations, only five stations, namely stations 7, 16, 27, 40, and 43, showed significant non-stationarity; thus, these stations would be excluded in further analysis. Hence, this study would be based on 45 stations only.

Fig. 1

Location of stations used in this study

In this study, 1 mm of rainfall amount in a day is considered as the threshold for a wet day; thus, a day with the rainfall amount of less than 1 mm is considered a dry day. A dry spell is, therefore, defined as a period of consecutive days of exactly, say x, dry days immediately preceded and followed by a wet day. The minimum length of a dry spell is taken as 1 day which means a single dry day. Tolika and Maheras (2005) mentioned that the selection of the threshold in order to define a wet/dry day is not fixed; instead, it depends on certain characteristics, the climate, and the needs of each particular study area. Another level which is often selected as the threshold is 0.1 mm corresponding to the resolution of a pluviometer; however, this level is not chosen in this analysis as it is a relatively low level for an area with high humidity such as Peninsular Malaysia.

Peninsular Malaysia experiences a tropical climate due to its location with respect to the equator and the influence of monsoon seasons. It lies in the equatorial zone, situated in the northern latitude between 1° and 6° N and the eastern longitude from 100° and 103° E. Throughout the year, the peninsula experiences wet and humid conditions with daily temperature range from 25.5°C to35°C. The climate of Peninsular Malaysia is influenced by the southwest monsoon, from May to September, and the northeast monsoon which occurs from November until March. The latter monsoon brings about heavier rainfall in the peninsula, with the worst affected areas being the east and south. On the other hand, the driest period for the peninsula usually occurs during the southwest monsoon with the northern part, on average, experiencing relatively long dry spells.

3 Methods

3.1 Probability distributions

In order to describe the behavior of extreme dry spells at a particular location, it is necessary to identify the distribution which best fits the data. Kotz and Nadarajah (2000) indicated that theoretical studies on extreme distribution could be traced back to the work done by Bernoulli in 1709. In terms of the applications of extreme value distributions, according to Nadarajah and Choi (2007), the first application was probably made by Fuller in 1914. Thereafter, several researchers have provided useful applications of extreme value distributions to rainfall data, in particular, long dry spell, obtained from different regions of the world. Examples of applications include Di Giuseppe et al. (2005) for application in Italy, Deni et al. (2008) in Malaysia, Potop and Soukop (2008) in Moldova, and Lana et al. (2003, 2006a, b) in Catalonia.

Two probability distributions associated with modeling extreme events, GEV and GP, are considered in this paper. Let x denote the observed values of the random variable representing the event of interest, F is the cumulative distribution, α is the scale parameter, ε is the location parameter, and κ is the shape parameter. The probability density function for GEV distribution is given by

$$ f\left( x \right) = \frac{1}{\alpha }{\left( {1 - \kappa \frac{{\left( {x - \varepsilon } \right)}}{\alpha }} \right)^{\frac{1}{\kappa } - 1}}\exp \left( { - {{\left( {1 - \kappa \frac{{\left( {x - \varepsilon } \right)}}{\alpha }} \right)}^{\frac{1}{\kappa }}}} \right) $$

(1)

and the quantile function is

$$ Q(F) = \varepsilon + \frac{\alpha }{\kappa }\left( {1 - {{\left( { - \ln (F)} \right)}^\kappa }} \right) $$

(2)

For GP distribution, the probability density function is

$$ f(x) = \frac{1}{\alpha }{\left( {1 - \kappa \frac{{x - \varepsilon }}{\alpha }} \right)^{^{\frac{1}{\kappa } - 1}}} $$

(3)

and the quantile function is

$$ Q(F) = \varepsilon + \frac{\alpha }{\kappa }\left( {1 - {{\left( {1 - F} \right)}^\kappa }} \right) $$

(4)

In order to fit a particular theoretical distribution to the observed distribution of dry spell, parameters are estimated using the L-moments method.

3.2 L-moments

The L-moments method (LMOM), introduced by Hosking in 1990, is widely applied in the field of applied research such as hydrology, meteorology, and civil engineering for estimating parameters of a distribution. It is based on a linear combination of order statistics where the first- until the fourth-order statistics correspond to measures of location, scale, skewness, and kurtosis, respectively. When compared to maximum likelihood methods and method of moments, estimators found based on LMOM are more robust, proven to have smaller mean square error and easier to compute. As described by Vogel and Fennessey (1993), LMOM should be preferred for small sample sizes due to its robust property. The rth LMOM, denoted as λ _r , is defined as

$$ {\lambda_r} = \frac{1}{r}\sum\limits_{k = 0}^{r - 1} {{{\left( { - 1} \right)}^k}} \left( \begin{gathered} r - 1 \hfill \\k \hfill \\\end{gathered} \right)E\left( {{X_{r - k:r}}} \right)\,;\,\,\,\,\,\,\,\,\,\,\,\,r = 1,\,\,2,\,\,.\,\,.\,\,.\,\, $$

(5)

where X _{r − k:r} is the random variable for (r − k)th order statistics. An interesting property of LMOM is the L-skewness, and L-kurtosis can be easily compared with the corresponding empirical values because these theoretical L-moments depend exclusively on just one parameter of the GEV and GP distributions. Thus, the best distribution for each rain gauge will be that leading to the minor discrepancy between empirical and theoretical L-skewness and L-kurtosis. This property can be visualized using the LMOM ratio diagram that can be used for testing the fit of hypothesized distributions to data. Explanation on LMOM ratio diagram can be found in the following section.

Once the distribution of the observed values is determined for each of the AE and PD series, the expected frequencies under the assumed distribution are computed for each station. For both series, the most appropriate distribution for each station is identified using results found based on several goodness-of-fit tests.

3.3 GOF

Two numerical GOF tests considered are relative root mean square error (RRMSE) and probability plot correlation coefficient (PPCC). The first method involves the assessment on the difference between the observed values and the expected values under the assumed distribution while the second method involves measuring the correlation between the ordered values and the associated expected values. The formulas for the tests are

$$ {\hbox{RRMSE}} = \sqrt {{\frac{1}{n}{{\sum\limits_{i = 1}^n {\left( {\frac{{{x_{i:n}} - \hat{Q}\left( {{F_i}} \right)}}{{{x_{i:n}}}}} \right)} }^2}}} \,{,}\,\, $$

(6)

$$ PPCC = \frac{{\sum\limits_{i = 1}^n {\left( {{x_{i:n}} - \bar{x}} \right)\left\{ {\hat{Q}\left( {{F_i}} \right) - \bar{Q}\left( {{F_i}} \right)} \right\}} }}{{\sqrt {{\sum\limits_{i = 1}^n {{{\left( {{x_{i:n}} - \bar{x}} \right)}^2}} }} \sqrt {{\sum\limits_{i = 1}^n {{{\left\{ {\hat{Q}\left( {{F_i}} \right) - \bar{Q}\left( {{F_i}} \right)} \right\}}^2}} }} }} $$

(7)

where x _i:n is the observed values for the ith order statistics of a random sample of size n, $\bar{Q}\left( {{F_i}} \right) = \frac{1}{n}\sum\limits_{i = 1}^n {\hat{Q}\left( {{F_i}} \right)\,\,}$ is the average of the estimated quantile values, $\hat{Q}\left( {{F_i}} \right)$, associated with the ith Gringorton plotting position, F _i . If RRMSE is used to determine the better model in comparing two models, the model that has the smaller value of RRMSE is selected. However, when PPCC test is used, the model with the computed PPCC value closer to 1 is the best. To decide on the best-fitting distribution for a particular series, the distribution which is found to be quoted as the better model by the two tests will be selected.

In addition to the two numerical-based goodness-of-fit tests as described earlier, a graphical test which has been introduced by Hosking and Wallis (1997), known as the L-moment ratio diagram, is also used to enhance the goodness-of-fit test. This method involves plotting of L-kurtosis value, denoted as τ ₄, against the L-skewness value, denoted as τ ₃, both of which are derived from LMOM. As suggested by Hosking (1990), the relationships between τ ₃ and τ ₄ under the assumed distributions are given as follows:

$$ \tau_4^{\rm{GEV}} = 0.10701 + 0.1109{\tau_3} + 0.84838\tau_3^2 - 0.06669\tau_3^3 + 0.00567\tau_3^4 - 0.04208\tau_3^5 + 0.03763\tau_3^6 $$

(8)

$$ \tau_4^{\rm{GP}} = 0.120196{\tau_3} + 0.95924\tau_3^2 - 0.20096\tau_3^3 + 0.04061\tau_3^4 $$

(9)

Using the data, we can compute the sample L-skewness, indicated as t ₃, and the sample L-kurtosis, denoted by t ₄, for all the 45 stations. If we substitute t ₃ in place of τ ₃ in the above equations, we can get the estimated L-kurtosis value under the assumed distribution, $t_4^{\rm{DIST}}$. These computed values are plotted on the L-moment ratio diagram, representing (t ₃,t ₄) and $\left( {{t_3},t_4^{\rm{DIST}}} \right)$. To determine the best fitting distribution for a particular station, the distance between $\left( {{t_3},t_4^{\rm{DIST}}} \right)$ and (t ₃,t ₄) for GEV and GP distributions are compared. The distribution with the smaller absolute distance will be selected as the best-fitting distribution. The additional results based on this graphical test would be combined with the results of the two goodness-of-fit tests to give a more comprehensive decision on the best model.

After determining the best fitted model for a particular AE or PD series, the predicted value for a return period, say T, may be denoted as ${\hat{X}_T}$, can be calculated by substituting the estimated parameters as given by

$$ {\hat{X}_T} = \hat{\varepsilon } + \frac{{\hat{\alpha }}}{{\hat{\kappa }}}\left( {1 - {{\left( { - \ln \left( {1 - 1/T} \right)} \right)}^{\hat{\kappa }}}} \right) $$

(10)

and

$$ {\hat{X}_T} = \hat{\varepsilon } + \frac{{\hat{\alpha }}}{{\hat{\kappa }}}\left( {1 - {{\left( {1/T} \right)}^{\hat{\kappa }}}} \right) $$

(11)

for GEV and GP distributions, respectively. For the PD series, T is replaced with δT where δ is the average number of events per year above a predetermined threshold value.

4 Results

4.1 PD series threshold selection

The decision on the most suitable threshold level to be used as the basis for generating an optimum PD series represents one of the challenges so that the assumptions of the PD model are still satisfied. The particular choice of the threshold value, denoted by S, will affect the arrival time of the extreme events as well as the magnitude of exceedances beyond the selected threshold. This threshold value should be large enough to ensure that the observations are independent without loss of important information. On the other hand, selecting a low threshold value can introduce serial dependence of both occurrence times and magnitudes, thereby violating the assumption of independence. Lang et al. (1999) outlined three tests for threshold selection which they called as Tests 1, 2, and 3, involving statistics which are based on mean frequency of over-threshold events, mean exceedance above threshold and dispersion index, I _t , respectively. They proposed operational guidelines for threshold selection where Test 2 is a linear function of the threshold values, Test 3 falls within the confidence bound [I _t (0.05), I _t (0.95)] and Test 1 more than 2 or 3. Thus, an interval of threshold values that satisfy Tests 2 and 3 can be identified and within this interval of values, we select the threshold value which is the largest value that satisfies Test 1. These guidelines, as proposed by Lang et al. (1999), are used to check whether the proposed threshold level meets the basic assumptions of PD model or not.

On the basis of the three tests using the operational guidelines, the threshold value, S, identified is found to vary according to regions that have been defined. The number of dry days which correspond to percentile values from 90th to 99th for dry days at all stations in a particular region are calculated and data exceeding these percentile values at each station are checked against the guidelines as in the previous paragraph in order to determine S. For all regions, the threshold values where the three tests are satisfied are calculated. The recommended threshold levels for each region is found to be at the 95th percentile value, that is 10 days for E1 and W1 while for E2 and W2, the level is 11 days. To illustrate the application of the three tests, a station from E1 region, Station 1, is selected, and the result of the tests is displayed in Fig. 2. A threshold level of 10 days corresponding to the 95th percentile has been selected based on the three tests. This level leads to an average of more than two spells of dry days per year: μ = 3.6 (Test 1). This threshold level is part of a stable linear function of mean excess versus threshold S (Test 2) and falls within the confidence interval of dispersion index (Test 3). Although the threshold values for almost all of the regions considered are relatively similar, the size of the series for each station differs.

Fig. 2

An example of threshold selection process at Station 1 in region E1 based on Tests 1, 2, and 3. The dotted lines in DI graph refers to the 95% lower and upper limit of dispersion index

4.2 Annual extreme dry-spell length and partial duration series

In assessing the GOF of GEV and GP models for AE and PD series for each rain-gauge station using a graphical method, the empirical and theoretical L-skewness and L-kurtosis are compared for both distributions as illustrated in Fig. 3. It is found that the dispersion of the empirical L-kurtosis for AE series about the theoretical L-kurtosis is higher compared to the PD series. This reflects a greater precision demonstrated by the use of PD series as opposed to the AE series.

Fig. 3

The L-moment ratio diagram showing plots of points representing empirical L-skewness and L-kurtosis for 45 rain-gauge stations and lines representing theoretical L-skewness and L-kurtosis for GEV and GP distributions for a AE series and b PD series

Based on the LMOM ratio diagram test, it is found that for the AE series, the GEV model offers a better fit than GP model for most stations accounting for 67% of all stations as opposed to 33% of all stations. On the other hand, for PD series, 96% of all stations follow the GP distribution. For the AE series, the average absolute distances between the empirical and under theoretical L-kurtosis assuming GEV and GP distribution are 0.050 with standard deviation of 0.035 and 0.102 with standard deviation of 0.061, respectively. For the PD series, the average absolute distances are 0.085 with standard deviation of 0.028 and 0.025 with standard deviation of 0.015 for GEV and GP models, respectively.

The two numerical tests, that is, the RRMSE and PPCC are also calculated according to Eqs. 6 and 7 in Section 3.3. The two tests agree that GEV is a better model for AE series while for PD series, GP is selected as the better model as demonstrated by approximately 78% and 91% of all stations, respectively.

Figure 4 shows the location of rain-gauge stations where either GEV or GP model are found to give a better fit considering AE and PD series. As the selection of the representative distribution has been determined by two goodness-of-fit tests and L-moment ratio diagram, in cases where the two numerical-based tests do not agree on a single distribution, L-moment ratio diagram is referred and used for the final decision. It can be observed that in many parts of the peninsula, there is no clear pattern on the best-fitted distribution associated with any specific location.

Fig. 4

Rain-gauge stations for which either the GEV (solid triangle) or the GP (open circle) models gives better fitting to the a AE and b PD series

4.3 Return periods

Based on the best-fitted models, we can calculate the return values of the periods 5, 10, 25, 30, and 50 years for all stations in the peninsula for the two series. These values are illustrated in Figs. 5, 6, 7, 8, and 9 for all return periods considered. From Figs. 5, 6, 7, 8, and 9, a common pattern of extreme dry spells can be seen for all the return periods, with the northern region being expected to receive a much longer dry spell as compared to the southern region. However, when both series are compared, it is found that the return values based on AE series, on the average, are slightly higher. For all the return periods, the northern region is expected to experience the longest dry spells under both the AE and PD series.

Fig. 5

Dry-spell length in days for return periods of 5 years when considering the a AE and b PD series

Fig. 6

Dry-spell length in days for return periods of 10 years when considering the a AE and b PD series

Fig. 7

Dry-spell length in days for return periods of 25 years when considering the a AE and b PD series

Fig. 8

Dry-spell length in days for return periods of 30 years when considering the a AE and b PD series

Fig. 9

Dry-spell length in days for return periods of 50 years when considering the a AE and b PD series

Based on the best-fitted distribution, the differences in dry-spell lengths between AE and PD relative to AE for various return periods are computed based on regions and summarized in Table 1. The average relative differences are found to be quite large with the return values for the period of 5 years being the largest. The average, minimum, and maximum values of relative differences have positive values implying the return values calculated using the AE series being often higher than the value derived by the PD series. This may be due to the fact that most of the data generated by PD method are not close to the maximum values; that is, the majority of the values are around the threshold level. In this case, the average value from PD series will be much lower compared to AE data, thus resulting in relatively large difference between data derived from both methods which will be reflected when the return values are calculated.

Table 1 Average relative difference (RDave) between dry spell lengths derived from AE and PD series, its standard deviation (RDsd), maximum (RDmax), and minimum (RDmin) values for different return periods (years) at the four subregions (E1, E2, W1, W2) considered

5 Conclusion and discussion

It has been discussed in various literatures that PD has more advantages than AE for estimation of extreme dry-spell length. Despite this, for PD, the selection of appropriate threshold still remains a problem. For example, the choice of the 90th percentile may seem appropriate enough; however, if the data are highly skewed to the left, a large proportion of the data would be selected as extreme values. Thus, the series beyond the threshold may not be representative as extreme events. On the other hand, if the distribution is skewed to the right, the 90th percentile may be a reasonable level of the threshold for some stations; however, the proportion of stations for which this level of threshold is selected may not be large enough. Accordingly, with respect to our data, we found that the appropriate level of threshold is at about the 95th percentile.

There are differences in the characteristics of extreme dry spell according to different regions in the peninsula, particularly between north and south. Although this is not reflected by the differences in the value of thresholds selected for the four regions, calculation of the return values at various return periods showed that the northern part of the peninsula experiences higher number of dry days compared to the southern region. On the other hand, the western part is likely to experience shorter dry spells relative to the other parts of the peninsula. This could be due to the more subtle effect of the Southwest monsoon compared to the Northeast monsoon which affect the eastern part. The middle part of the peninsula is expected to experience higher dry days, which could be due to the higher altitude of the area which is located on the Main Range, known as Banjaran Titwangsa, which runs from the Malaysian–Thai border in the north to the south and spans a distance of 483 km separating the eastern part and western part of the peninsula. With reference to Fig. 10, the average relative difference between AE and PD also show that at shorter dry spells, the differences between values derived from data generated by AE and PD methods are small, but the differences are higher for areas with longer dry spells.

Fig. 10

Differences in dry length in days for return values calculated based on AE and PD data for return periods of a 5 years, b 10 years, c 25 years, d 30 years, and e 50 years

In terms of application, the estimation of extreme dry spell at various return periods could represent a valuable aid for planning and managing the water resources for agricultural use and socioeconomic activity. The decision-making such as construction of a proper drainage system and the management of water resources (reservoirs and ground surface waters) should allow for this prediction in order to be cost-effective. In addition, this information could also facilitate the decision-makers to prioritize resources accordingly.