GoSCAN: Decentralized scalable data clustering

Abstract

Identifying clusters is an important aspect of analyzing large datasets. Clustering algorithms classically require access to the complete dataset. However, as huge amounts of data are increasingly originating from multiple, dispersed sources in distributed systems, alternative solutions are required. Furthermore, data and network dynamicity in a distributed setting demand adaptable clustering solutions that offer accurate clustering models at a reasonable pace. In this paper, we propose GoScan, a fully decentralized density-based clustering algorithm which is capable of clustering dynamic and distributed datasets without requiring central control or message flooding. We identify two major tasks: finding the core data points, and forming the actual clusters, which we execute in parallel employing gossip-based communication. This approach is very efficient, as it offers each peer enough authority to discover the clusters it is interested in. Our algorithm poses no extra burden of overlay formation in the network, while providing high levels of scalability. We also offer several optimizations to the basic clustering algorithm for improving communication overhead and processing costs. Coping with dynamic data is made possible by introducing an age factor, which gradually detects data-set changes and enables clustering updates. In our experimental evaluation, we will show that GoSCAN can discover the clusters efficiently with scalable transmission cost.

1 Introduction

Discovering or identifying groups of similar elements, called data clusters, has always been an important aspect of analyzing large datasets. Clustering algorithms generally require access to the complete dataset, which is one reason why such algorithms have traditionally been carried out in a centralized fashion. However, as data sets are increasingly originating from multiple, dispersed sources, and at the same time are increasing in volume, alternative solutions are needed. In a decentralized clustering algorithm, multiple processes, each running at a different location, collaborate in discovering clusters by exchanging metadata instead of the actual data. In other words, data points belonging to the set that is being analyzed in principle do not, or barely, change location. The dataset as a whole thus remains dispersed. Nevertheless, the processes participating in a decentralized clustering algorithm will gradually discover various clusters and can provide this information to third parties, if so required.

Distributed Data Mining (DDM) explores methods of applying data mining algorithms to decentralized data, utilizing distributed resources of computation and communication. Classically, data mining algorithms attempt to optimize storage and processing costs, whilst additional requirements arise in DDM, such as maintaining scalability, low communication overhead, and privacy. For a survey of DDM refer to [3, 22].

If data are kept in place, then what remains is to distribute the computations. A common approach is to organize the computations in a hierarchical fashion by which local models are computed first, to be sent to a logically higher-level process that aggregates models, possibly returning results to the lower-level processes for further processing [14, 19, 21]. In such approaches, output from the algorithm is much dependent on sound functioning of the highest level process. To maintain scalability, nodes may reduce the size of metadata in the high hierarchy levels. However, this adds a trade-off between the processing load and the output accuracy. In pure unstructured algorithms, where nodes act symmetrically, each node will eventually and individually come to the same final result.

In the approach explored in this paper, all processes are treated the same and each one gradually builds a view of which of its data points belong to which cluster. Processes continuously exchange information on data points as well as information on the clusters found so far. In this case, the robust and efficient dissemination of information across all processes becomes important. Gossiping [5] has been demonstrated to be a simple and effective means to this end, and is also the technique that we have adopted. Moreover, as we will show, gossiping is capable of handling changes in the dataset while cluster discovery is taking place.

Being able to deal with the dynamics of datasets is particularly important when datasets grow in size, and their sources increase and become more dispersed. There are essentially two aspects regarding the dynamics that we need to take into account. First, we must expect that data points are added and removed continuously. As a consequence, a clustering algorithm will need to run continuously as well; there is, in principle, no final answer. Second, and related, is that any information on the currently discovered clusters will most likely always be outdated. Therefore, it is essential that the speed by which clusters are discovered matches the rate at which the underlying dataset changes, or that an indication of the mismatch can be provided.

Existing distributed clustering algorithms either rely on a central site [14], assume a special logical or semantic structure [19, 21], require synchronization or state-aware operation of nodes to some extent [4, 12], or include multiple rounds of message flooding [6, 10], to achieve a global clustering model. Although a majority of algorithms include summarization techniques to reduce communication costs, the employed design principles conflict with scalability requirements in large-scale networks. Moreover, existing algorithms lack efficient solutions for adaptability in dynamic settings, which introduces significant challenges for applying them in large-scale real-world networks. Handling dynamics of data using an adaptive method, without requiring the algorithm to restart, is among the novelties of GoSCAN.

Density-based clustering has proven to be effective for analyzing large amounts of data. Algorithms in this class generally require no previous knowledge of the number of clusters, they can discover clusters with arbitrary shapes, and they inherently allow for discovering outliers [8]. In this paper, we propose GoSCAN: a completely decentralized density-based clustering algorithm. GoSCAN enables each peer to detect which clusters its local (or obtained) data objects belong to. Our solution builds upon DBSCAN [8] employing a continuously changing unstructured peer-to-peer overlay network. We identify two major tasks: finding the core data points, and forming the actual clusters, both for which we use gossiping communication. Gossiping poses no extra burden of overlay formation in the network, while providing high levels of scalability.

We offer several optimizations to the basic clustering algorithm for improving communication overhead and processing costs. An important improvement consists in employing the gossip-based peer selection service Vicinity [29] to let peers find good communication partners.

This paper is organized as follows. First our system model as well as the DBSCAN algorithm are described in Sect. 2. In Sect. 3, the basic decentralized version of GoSCAN is introduced. In the succeeding section we scrutinize the effects of churn and propose adjustments to the basic algorithms. Simulation results are discussed in Sect. 6, followed by related work and conclusions.

2 Basics

In the following subsections, the DBSCAN algorithm is briefly described, followed by the assumptions, notations and basic model of GoScan.

2.1 DBScan

As mentioned, GoSCAN is based on the well-known DBSCAN algorithm [8]. DBSCAN considers data points to be placed in an $m$-dimensional metric space with an associated distance metric $\delta$. Let $x_{}$ denote a data point belonging to the dataset $\mathbf D$. A key concept in DBSCAN is that of a core point, for which we first need to define the $\mathbf \varepsilon$-neighborhood of a data point $x_{}$:

$$\begin{aligned} N_{\varepsilon }(x_{})=\{ x_{}^{\prime } | x_{}^{\prime } \in \mathbf D \wedge \delta (x_{},x_{}^{\prime }) \le \varepsilon \} \end{aligned}$$

(1)

A data point $x_{}$ is a core point if $|N_{\varepsilon }(x_{})| \ge {{ MinPts}}$, where MinPts is a user-defined local-density threshold.

As their name suggests, core points are used to define clusters in the sense that data points should lie “close” to core points. To make this precise, consider a core point $x_{0}$. Each data point $x_{}\in N_{\varepsilon }(x_{0})$ is said to be directly density reachable from $x_{0}$. Likewise, $x_{b}$ is density reachable from $x_{a}$ if there is a chain of data points $x_{a} \equiv x_{1}, x_{2}, \ldots , x_{k} \equiv x_{b}$ such that $x_{i}$ is directly density reachable from $x_{i-1}$ (implying that each $x_{i} (i<k)$ should be a core point). Note that density reachability is an asymmetric relationship. Finally, two data points $x_{a}$ and $x_{b}$ are density connected, if there exists a core point $x_{0}$ such that both $x_{a}$ and $x_{b}$ are density reachable from $x_{0}$. A density-based cluster can now be defined as a maximal set of density-connected points.

To discover the clusters in a dataset, first the $\varepsilon$-neighborhood of each data point is examined, allowing us to identify the core points. Next, the method iterates through each core point and finds all other data points that are density reachable from it, and, consequently, density connected with each other. All such data points belong to the same cluster. The points that do not belong to any cluster are labeled as noise. To clarify, consider a graph whose vertices are formed by core points and an edge indicates that its end points are directly density reachable. In this model, discovering clusters first reduces to finding the connected components. Next, any core point incorporates into its cluster exactly those data points that are in its $\varepsilon$-neighborhood.

2.2 System model

We consider a set $V=\{p_1, p_2, \ldots , p_n\}$ of $n$ networked peers. Each peer $p\in V$ stores and shares a set of data points $D^{int}_p$, denoted as its internal data. We do not assume that internal datasets stay fixed: points may be added to or removed from a set. A data point $x_{}$ is represented as an $m$-dimensional feature vector. $\mathbf D = \bigcup _{p\in V}{D^{int}_p}$ is the set of all data points available in the network. While discovering clusters, $p$ may also store data points from other peers in the network. These data points are referred to as the external data of $p$, denoted as $D^{ext}_p$. The union $D_p$ of internal and external data of peer $p$ constitutes the local data of $p$. That is, $D_p = D^{int}_p \cup D^{ext}_p$. Our algorithm transmits only meta data, including data feature vectors, and the actual data objects are never moved. In the rest of the paper, we ignore this issue and will simply refer to transmission of data objects.

The set of (internal and external) core points at peer $p$ is denoted as $D^{core}_p$, and clearly $D^{core}_p \subseteq D_p$. Like DBSCAN, GoSCAN has two unique parameters, $\varepsilon$ and MinPts, which represent the radius and minimum number of required points for core points, respectively. The result of running GoSCAN is a set of density-based clusters $\mathbf C _{\mathbf{p}} = \{C_{1}^{p}, C_{2}^{p}, \ldots , C_{k_p}^{p}\}$ in each peer $p$, with respect to $\varepsilon$ and MinPts. Each cluster is represented by the set of all its core points, if it has any, or by a single data point, otherwise. DBSCAN is employed as the basic clustering algorithm in each peer.

Generally, each peer should be able to find the correct clusters for its internal data. Nevertheless, the algorithm permits any peer to collect information on any arbitrary cluster. Ideally, the algorithm should be able to adapt itself to changes in the dataset, such that it can produce accurate results on the fly. However, due to latency in distributing changes throughout the system, maximal accuracy cannot be achieved when running GoSCAN under real-world conditions.

3 Decentralized density-based clustering

A density-based clustering algorithm can be separated into two tasks. DETECT identifies the core points in the dataset by exploring the $\varepsilon$-neighborhood of each data point. MERGE merges clusters by looking for core points that are in each other’s $\varepsilon$-neighborhood. DETECT can be executed independently, while MERGE requires the output of DETECT to execute. However, an important observation is that the two tasks can execute repeatedly and continuously in parallel. As DETECT proceeds to identify more core points, MERGE progresses to amend clusters. Note that in a static setting, this approach cannot miscategorize noise points or mistakingly merge different clusters. However, it may take some time for the algorithm to conclude on the actual clusters.

GoSCAN is executed in a completely decentralized manner without requiring central coordination. Because the data is distributed, accomplishing the two tasks requires adequate cooperation of peers and communication among them. Each peer should execute DETECT, continuously attempting to gather sufficient information about the $\varepsilon$-neighborhood of its internal data, and thus identifying its core points. It will advertise this information, upon request, to feed MERGE. Execution of MERGE, however, is performed by peers optionally and selectively, only with respect to clusters they are interested in, i.e., clusters for which they need to know the core points.

We use two gossip-based, cyclic algorithms to accomplish these tasks. In each cycle, each peer $p$ selects another peer $q$ for a three-way information exchange, as shown in Fig. 1. Peer $p$ collects data points that are in $\varepsilon$ range of its internal data. To this end, it sends its internal data $D^{int}_p$ to peer $q$ and expects to receive at most MinPts data points for each of its sent internal data points (which is represented by the trimmed() operation). The operation updateLocalData() is used to store the received data and to decide whether any internal data can be promoted to a core point. Note that only the owner of a data point can decide to promote it to a core point.

Fig. 1

Threads for the core-point detection (task DETECT): a active thread for peer $p$ and b passive thread for selected peer $q$

Recall that the conveyed information in messages is metadata and not the actual data objects. To save bandwidth, a peer may decide to transfer a representative of several close data objects (along with some radius parameter to cover all omitted data), in the active thread of DETECT. In the passive thread however, the amount of transmitted data is bounded and repetitive data objects are sent only once. If plenty of features exist in feature vectors of data objects, messages can grow. This latter concern, which applies to high-dimensional data, can be dealt with by using compression and dimension reduction techniques, which is out of scope of this paper.

The active and passive algorithms executed by an arbitrary peer $p$ on behalf of MERGE, are shown in Fig. 2. Clusters are identified by their constituting core points. However, each cluster can have an estimate representation to reduce transmission costs. For instance, a cluster can be estimated with a minimum bounding hyperrectangle which surrounds its core points, or by a single data point if the cluster has no core. The initiating peer $p$ sends these cluster estimations $\tilde{\mathbf{C}}_p$ to the selected peer $q$, which, in turn, computes overlaps and returns those overlapping clusters to $p$. Peer $p$ also computes any overlaps and returns those to $q$.

Fig. 2

Threads for cluster merging (task MERGE). Note that only cluster estimations, or core points are transferred. a active thread for $p_i$ and b passive thread for selected peer $p_j$

At this stage, both parties have enough information to independently verify which clusters qualify to be merged. In particular, any two core points belonging to different clusters, which are in $\varepsilon$ range from each other, cause those clusters to be merged. Upon successful merging of two clusters, the peer will store all of the core points belonging to the new cluster, executed by the operation mergeClusters(). After merging all received clusters, the peer would again check the local clusters to see if any of them can be locally merged together.

The two algorithms start with a preprocessing operation. In this basic algorithm, these operations have no special function, thus we defer the discussion to Sect. 4. The operation selectPeer() used in Figs. 1 and 2 returns a peer selected uniformly at random (see, e.g. [15]). In Sect. 5, we will introduce another selection operation that can enhance and accelerate both the core detection (DETECT) and the cluster merging (MERGE) tasks.

This basic algorithm will gradually tend to discover the density-based clusters in distributed data. Any peer executing the MERGE task will collect all of the core points belonging to the clusters of its internal data. Also with a minor extension, a peer can gather core points of any cluster: it should first locate a single data point belonging to that cluster, and then look for core points of that cluster.

4 Dynamic dataset

Real-world peer-to-peer systems change continuously. First, nodes join and leave the system, also known as churn. Second, nodes change their data by adding, removing, or changing data points. These dynamics impose changes to our algorithms, not in the least because copies of data points are actually spread throughout the system to allow a node to decide on its clusters. Obviously, at each moment in time, the view that a node has on clusters will, by definition of continuous change in the overall dataset, be outdated. In the following, we discuss how this staleness can be handled.

In order to quantify staleness, each external data point stored by a peer has an associated age. Copies of the same data point may have different ages at different peers. In particular, $age_{p}(x_{})$ denotes the time that peer $p$ believes has passed since $x_{}$ was obtained from its originating owner peer. Time is measured in terms of gossiped cycles. Every time peer $p$ starts a new communication or is contacted by another peer, it increments the ages of all external data points it holds. The age of internal data always remains zero to reflect that it is stored (and up-to-date) at its owner. If a peer $p$ receives a copy $x_{}^{\prime }$ of a data point $x_{}$ it already stores, $age_{p}(x_{})$ is set to $\min \{age_{p}(x_{}),age_{p}(x_{}^{\prime })\}$ (and $x_{}^{\prime }$ is further ignored).

When a data point $x_{}$ is removed (e.g., because its owner leaves the system), the minimal recorded age among all its copies will only increase. At a certain moment, a peer $p$ storing a copy of $x_{}$ will necessarily have to come to the conclusion that $x_{}$ has been removed by its original owner when $age_{p}(x_{})$ passes a threshold MaxAge. At that moment, $p$ will also remove its copy of $x_{}$.

An important observation is that at any time $t$, it is theoretically possible to take a snapshot of the entire dataset and compute a correct set of clusters $\mathbf {C} (t)$. However, using a decentralized algorithm, in order for each peer to correctly assign its internal data points to clusters, it will need to have received sufficient data points from other peers. Propagating data points through gossiping then introduces a natural delay before peers can come to the correct clusters, leading to a global set of clusters $\mathbf {C} (t^{\prime })$, with $t^{\prime } > t$.

Moreover, because propagation speeds are not uniform, if data changes occur concurrently and originate at different sources, only under very specific conditions will it be possible to even attain $\mathbf {C} (t)$. In other words, it may happen that for each time $t$ we may be able to obtain only an approximation $\tilde{\mathbf{C }}(t^{\prime })$ at some later time $t^{\prime }$. Problems are further aggravated if data is removed before having had the chance to be sufficiently propagated. Handling the first case is extremely difficult, if not impossible without introducing a notion of global ordering of updates. The second case can be dealt with by simply treating the removal of internal data the same as with external data: start increasing an internal point’s age until it reaches MaxAge before actually removing it. Note that this procedure can be applied only when a peer wants to remove internal data; it cannot be used for peers crashing or otherwise prematurely leaving the system.

If data points can be removed, then this may affect the status of other data points that had been promoted to core points. To capture this situation, we again associate a (locally computed) core point age with each core point. To this end, let $N_{\varepsilon }^-(x_{},k) \subseteq N_{\varepsilon }(x_{})$ denote the $k$ youngest data points at $\varepsilon$ range of data point $x_{}$. We then define $coreAge_{p}(x_{})$ as the maximum age of the youngest MinPts data points in $N_{\varepsilon }(x)$ local to $p$:

$$\begin{aligned} coreAge_{p}(x_{}) = \max _{x_{}^{\prime } \in N_{\varepsilon }^-(x_{},minPts)}\{age_{p}(x_{}^{\prime })\} \end{aligned}$$

Note that a core point age should be inspected and possibly adjusted at each gossiping cycle. Obviously, the age of a core point may drop if new, younger data points are discovered. It will increase otherwise. Any core point whose age passes a threshold, MaxCoreAge, will be marked as noncore. If the data point demoted from core to noncore is internal, the peer can advertise this new state in later communications to assist other peers in quickly revising their clusters.

To incorporate these new concepts in the basic algorithm, the two preprocessing operations are modified to handle age updates. Also the trimmed() operation of Fig. 1, should now return the youngest MinPts data points for each internal point of the other peer. Moreover, the two operations updateLocalData and mergeClusters should be amended to handle the aging of data points. Operation mergeClusters should now control partitioning of clusters as a result of core point elimination. Figure 3 illustrates these operations. Note that increasing the age and core point age is done both at the initiating and the selected peer. This prohibits propagation of wrong age values through the system.

Fig. 3

Operations used in the DETECT and MERGE algorithms

5 Improvements

In this section we review and improve our algorithm with respect to storage, computational, and communication resources. The reduction of communication may negatively affect the accuracy of the algorithm. In essence, we are trading improvement of convergence speed for lower accuracy, which we consider justified when data changes rapidly. We again discuss optimizations in terms of their benefits for the DETECT and MERGE tasks.

5.1 DETECT

In both the active and passive threads of DETECT, when peer $p$ receives a set $D_q$ of data points from peer $q$, it looks up all local data points within $\varepsilon$ range of any $x_{} \in D_q$. This is, however, not necessary.

Lemma 1

Let $x_{}$ be a core point stored in $q$. Any new data point $x_{}^{\prime }$ added to $D_q$ can affect the core point status of $x_{}$ only if $x_{}^{\prime } \in N_{\varepsilon }^-(x_{},{{ MinPts}})$, that is, $x_{}^{\prime }$ also belongs to the youngest MinPts data points within $\varepsilon$ range of $x_{}$.

Proof

The core point status of $x_{}$ changes only if $coreAge_{q}(x_{})$ exceeds MaxCoreAge. The way $coreAge_{q}(x_{})$ evolves, depends only on data points belonging to $N_{\varepsilon }^-(x_{},\,{{ MinPts}})$. Other data points, although belonging to $N_{\varepsilon }(x_{})$, are older than all points in $N_{\varepsilon }^-(x_{},\,{{ MinPts}})$; Therefore, they have no impact on the core status of $x_{}$.

To elaborate further, note that if $x_{}^{\prime } \in N_{\varepsilon }^-(x_{},{{ MinPts}})$, then $age_{p}(x_{}^{\prime })\le coreAge_{q}(x_{})$. Therefore, $x_{}^{\prime }$ may reduce $coreAge_{q}(x_{})$, causing $x$ to retain its core status longer.

In the original DETECT algorithm, process $p$ constructs a set $D^*_p(x_{}) \subseteq D_p$ of MinPts data items of minimal age and within $\varepsilon$ range of the point $x_{}$, which it has received from $q$. Any data point $x_{}$ only requires ${{ MinPts}}\ - |N_{\varepsilon }(x_{})|$ to be promoted to a core point. However, $D^*_p(x_{})$ can contain more data points, if they are younger than the points already contained in $N_{\varepsilon }^-(x_{},{{ MinPts}})$. Let ${MaxAge }_{\varepsilon }(x_{}) = \max \{age_{q}(x_{}^{\prime }) | x_{}^{\prime } \in N_{\varepsilon }^-(x_{},{{ MinPts}})\}$. If $|D^*_p(x_{})| > {{ MinPts}}\ - |N_{\varepsilon }(x_{})|$ then for each item $x_{}^{\prime } \in D^*_p(x_{})$, a restriction should be set such that $age_{p}(x_{}^{\prime }) < {MaxAge }_{\varepsilon }(x_{})$. According to the lemma above, there is no need to send older data points. To realize this reduction, peer $q$ should send $|N_{\varepsilon }(x_{})|$ and ${MaxAge }_{\varepsilon }(x_{})$ along with its request containing $x_{}$.

5.2 MERGE

If a peer executing MERGE encounters a cluster with many core points in a dense area, it will suffer from a large computation and communication overhead for maintaining and advertising these core points. Here, we describe a solution to this problem, presenting a trade-off between accuracy and efficiency.

The solution enables each peer to independently choose between higher accuracy or more efficiency. Classically, clusters with arbitrary shapes are represented by using all points in the cluster [11]. The cluster, however, can also be approximated as the union of $\varepsilon$-range spheres, one for each core point. As the main cause of inefficiency comes from maintaining a large number of nearby core points, the solution should try to store fewer core points for dense areas. If the sphere $S$ with center $x_{}$ is fully covered by the spheres of nearby core points, then there is no need to keep $x_{}$. However, identifying core points like $x_{}$ is still a complex computational task.

We propose to reduce the number of core points by considering relatively young core points that (approximately) cover the same data points as other (external) core points. Internal data points, and thus also internal core points, cannot be eliminated. More precisely, consider the set $CP^p_k$ of core points of cluster $C^p_k$ of peer $p$. We eliminate a core point $\mathbf{x }_{1} \in CP^p_k$ if there is another core point $\mathbf{x }_{2} \in CP^p_k$ such that:

• 1. $\delta (\mathbf{x }_{1}, \mathbf{x }_{2}) \le \varphi$

• 2. $\forall \mathbf{x }_{a} \in CP^p_k - \{\mathbf{x }_{1}\} \exists \mathbf{x }_{b} \in CP^p_k- \{\mathbf{x }_{1}\}: \delta (\mathbf{x }_{a},\mathbf{x }_{b}) \le \varepsilon$

where $\varphi$ denotes a design-time error-tolerance parameter. We demand that connectivity of a cluster is guaranteed, which is expressed by the second condition. This method of core-point elimination guarantees that the shape of the resulting cluster is close to the original one with no more than $\varphi$ error at each point. To prevent partitioning clusters because of maintaining old core points, an additional requirement can be introduced which ensures that the covering core point is not too old:

$$\begin{aligned} coreAge_{p}(\mathbf{x }_{2}) \le \alpha \cdot {MaxCoreAge }\,\quad \text{ where}\,0 \le \alpha \le 1 \end{aligned}$$

All conditions can be met incrementally as new core points are discovered. If two clusters $C$ and $C^{\prime }$ are to be merged, we can assume that both clusters are already processed in terms of removing core points according to conditions 1 and 2. Thus, after merging clusters, it suffices to check conditions 1 and 2 only for the core points relying in the overlapping region of $C$ and $C^{\prime }$. A range query with radius $\varphi$ should be executed for each of these core points, to determine those which satisfy condition 1 and the extra limitation stated above. Next, the cluster connectivity in the absence of each selected core point should be verified (condition 2). Overall, the operations required to satisfy the conditions incrementally are range and cluster connectivity queries, which are executed (when required) for each core point in the overlapping region.

Several structures exist to facilitate range query processing on dynamic data [2]. For example, if a range tree is constructed for core points of a cluster $C$, updating the tree and executing actual range queries will cost $O(\log ^{m-l}(|CP|)$ and $O(\log ^{m-l}(|CP|)\!+k)$ respectively, where $CP$ is the set of core points in $C$, and $k$ is the number of returned query results.

Consider a graph whose vertices are the core points of a given cluster, and an edge between two core points indicates that they have a maximum distance of $\varepsilon$ from each other. Determining connectivity of the cluster in case of removing a core point reduces to the problem of determining graph connectivity in a fully dynamic graph structure. The connectivity query in the worst case can be answered in $O(|CP|+e)$ using breadth-first search, where $e$ is the number of edges in the graph. However, more efficient solutions exist in the literature such as [13], which guarantees $O(\log ^2(|CP|))$ processing cost for responding to connectivity requests.

Note that, in general, any peer can decide for itself what the value of $\varphi$ should be based on the resources it possesses and the accuracy it desires. Two extreme values for $\varphi$ are $0$ and $\infty$, which result in keeping all core points, or only one of them, respectively.

5.3 Convergence rate

Both DETECT and MERGE tasks can be accelerated if the selectPeer() operation is designed in a clever way. DETECT becomes more effective if peer $p$ gossips with a peer $q$ owning “similar” data, as the two are most likely looking to allocate their data to the same clusters. To this end, we deploy Vicinity [29], a gossip-based protocol for topology construction in overlay networks that tends to link two nodes according to some systemwide user-defined proximity function $\varDelta$. This proximity function essentially defines the target structure. Each peer maintains a dynamic, fixed-length list of neighbors, called its Vicinity view, or just view. In the target structure, each peer’s view is populated with the closest possible other peers based on the defined proximity function. The protocol gradually evolves each view to contain links to other peers so that the target structure is approximated as closely as possible. Evolution is accomplished by exchanging fixed-length subsets of views between peers during gossip. The proximity function is used to select the neighbors to keep.

Here we aim at organizing a topology where the peers whose data points are close to each other, have links to each other. The proximity function $\varDelta$ for peers $p$ and $q$ is defined below:

$$\begin{aligned} \varDelta (p,q) = \left\{ \begin{array}{l@{\quad }l} 0,&\text{ if} \exists x_{p} \in D^{int}_p, x_{q} \in D^{int}_q: \delta (x_{p},x_{q}) \le \varepsilon \\ 1,&\text{ otherwise} \end{array} \right. \end{aligned}$$

To make use of Vicinity, each peer should advertise its internal data when communicating with others. Conveniently, this information is already being exchanged by DETECT.

In the improved version of the algorithm we deploy Vicinity, and selectPeer() is selects some peer from the Vicinity view, rather than a randomly selected one.

6 Performance evaluation

In this section, we evaluate GoSCAN in static and dynamic settings.

6.1 Experimental setting

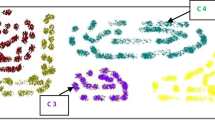
We consider a network of $N$ peers, executing the DETECT and MERGE tasks. The synthetic datasets consist of two-dimensional data points picked by several Gaussian distributions, along with a 5 % random noise. The MinPts parameter of DBSCAN is set to 10 The $\varepsilon$ value for each data set is set to a fraction of the Gaussian distribution variance, such that nonoverlapping distributions with different mean values are assigned to different clusters. Some of the data sets used in the experiments, which contain different numbers of data objects, are depicted in Fig. 4. Overlapping distributions, being assigned to the same cluster, form various cluster shapes.

Fig. 4

Sample data sets with different number of points as used in the experiments

We also use the points data set from the SEQUOIA 2000 benchmark [26]. This dataset contains 62,584 names of landmarks in California, extracted from the US Geological Surveys Geographic Names Information System, together with their location. Regarding the number of data points required in the experiments, a random sample of this dataset is used, which is the same approach taken in [8]

Each peer is assigned internal data points in the beginning of the experiment based on two strategies:

• random data assignment: Each peer is assigned data randomly chosen from the global dataset.

• dense data assignment: If available, data points that are at $\varepsilon$ distance from some internal data of a peer $p$, are assigned to $p$, else a random data point is assigned to $p$. It is ensured that no more than 10 % of the nodes have internal data points within $\varepsilon$-range of a given peer’s data points.

The second assignment strategy abates the average number of peers that have data close to each other. In such a setting, as we will see later, distributed clustering may be more challenging.

In the dynamic setting we use the random data-assignment strategy, which changes cluster core points, yet approximately maintains the overall coverage of clusters. Also, to assess the performance of the algorithm in presence of concept drifts, another data assignment strategy is used, which assigns data randomly from sequentially selected data clusters. This latter strategy is named cluster-aware data assignment, and forces full assignment of data in a cluster before proceeding to the next one.

6.2 Evaluation metrics

Different parameters used in conducting the experiments, along with their default values, are presented in Table 1. Performance is expressed in terms of communication bandwidth (i.e., amount of communicated data) and attained clustering accuracy. The communication cost is measured in terms of average amount of data (in KB) transmitted by each node, per gossip round.

Table 1 Simulation parameters

Clusters are represented by the set of core points they consist of. For instance, a cluster $C_{}$ is represented as $C_{} = \{\mathbf{x }_{1}, \mathbf{x }_{2}, \ldots , \mathbf{x }_{|C|}\}$.

In order to assess the efficiency of GoSCAN in detecting clusters, we compare its outcome to that of (centralized) DBSCAN. Executing DBSCAN centrally on a given data set results in a set of clusters $\{C_{1}, C_{2}, \ldots , C_{k}\}$, which we will be referring to as real clusters. Likewise, at any time while executing GoSCAN  each peer $p$ will have placed its internal data in a set of clusters $\{C_{1}^{p}, C_{2}^{p}, \ldots , C_{k_p}^{p}\}$, which we will call computed clusters of peer $p$.

Finally, for each real cluster $C_{i}$, we define its projection cluster $\hat{C}_{p}^{i}$ on peer $p$ as the computed cluster that shares the most core points with $C_{i}$ among all computed clusters $C_{j}^{p}$ of peer $p$. More than one computed clusters of $p$ could qualify as projections of a given real cluster $C_{i}$, however only one is chosen, typically the one with the least number of core points. For a real cluster $C_{i}$ that has no data points (core or noncore) in common with a peer $p$, we define $\hat{C}_{p}^{i} = \{\}$.

We define two accuracy metrics to assess the performance of GoSCAN. Each metric is defined with respect to a given peer and a given real cluster. To show aggregate results, we first compute the per cluster value by averaging across all peers that host data points of that cluster, and then we average across all real clusters to obtain a global accuracy value.

• Core point accuracy This metric expresses the similarity between a real cluster and its projection on a peer, with respect to the core points discovered by the peer. More specifically, it is defined as the Jaccard similarity coefficient between the set of core points in a real cluster $C_{i}$ and its projection $\hat{C}_{p}^{i}$ on a peer $p$:

  $$\begin{aligned} CorePointAccuracy (C_{i}, p) = \frac{|C_{i} \cap \hat{C}_{p}^{i}|}{|C_{i} \cup \hat{C}_{p}^{i}|} \end{aligned}$$

  (2)

  Edge accuracy Let us assign an imaginary edge between any two core points of the same cluster that are within $\varepsilon$ range from each other. This metric expresses the fraction of edges of a real cluster that have been discovered by peer $p$. If $E({C_{}})$ denotes the set of edges of cluster $C_{}$, the edge accuracy metric with respect to real cluster $C_{i}$ and a peer $p$ that has $k_p$ computed clusters is defined as:

  $$\begin{aligned} EdgeAccuracy (C_{i},p) = \frac{\displaystyle \sum _{1\le j\le k_p} \left| E({C_{i}}) \cap E({C_{j}^{p}}) \right|}{\left|E({C_{i}})\right|} \end{aligned}$$

  (3)

  Note that we consider edges from all computed clusters of peer $p$, not only from the projections of real clusters on $p$.

Core point accuracy favors peers who have correctly discovered the complete cluster, thus it demands completion of both the DETECT as well as the MERGE task. On the other hand, edge accuracy scrutinizes only the discovery of links between nearby core points. Thus, for this metric each peer should complete DETECT and only a rather small part of MERGE; it does not force peers to gather all core points of a cluster. If each peer discovers its own core points and the core points located in $\varepsilon$ region of its internal data, a dedicated application like a crawler can explore this information and build clusters by visiting each peer once. The important point is that in this case the crawler is only responsible of connecting core points, not having to decide which data object are cores (as this is already identified by the peer). So, edge accuracy measures the ability of the algorithm to detect the local structure of clusters in each peer.

6.3 Simulation results

We start by presenting the simulation results for the basic distributed clustering algorithm. We then assess the algorithm improvements, and subsequently analyze the behavior of the algorithm in a dynamic network.

6.3.1 Basic protocol

Figure 5 shows the convergence rate of the basic GoSCAN algorithm, for the synthetic and SEQUOIA data sets. We vary the network size from 128 to 1,024 peers, and use both data assignment strategies. In the basic algorithm peers gossip with random other peers, obtained through the Cyclon layer. With random data assignment, nearly 100 % accuracy is achieved in the first 30 rounds for all network sizes, which shows the scalability of the algorithm. The convergence rate is hardly affected when the network size increases; The set of dense lines on the left hand side of all graphs in Fig. 5 pertain to random data assignment. Under the same data assignment strategy, the algorithm offers good approximations of the final clustering model: in less than 20 rounds the accuracy rises to more than 90 %, which has shown to be adequate in many practical situations.

Fig. 5

Convergence rate of the algorithm versus network size, for random gossip in a static setting. The set of dense lines on the left hand side of all graphs pertain to random DA. a synthetic data (rounds 0–120). b SEQUOIA data (rounds 0–30)

With dense data assignment, the accuracy increases more deliberately compared to random data assignment. This is expected as it takes longer for a peer to locate other peers holding relevant data. Later on, we will show that applying Vicinity can significantly improve the convergence rate of the algorithm when data is assigned densely. The SEQUOIA dataset is rather dense, and this explains the almost similar performance of GoSCAN under both data-assignment strategies for this dataset. When data is dense, many peers hold data objects in $\varepsilon$ region of each other, which facilitates locating target peers to accomplish algorithm tasks.

Figure 5 also shows that, with random data assignment, the algorithm indeed requires less effort to reach high edge accuracy in comparison to reaching high core point accuracy. However, with dense data assignment, when using synthetic data, less distinction can be made between the two accuracy metrics. Nevertheless, it is demonstrated that DETECT and MERGE can be effectively executed in parallel. For both accuracy metrics, the algorithm offers complete accuracy in detecting noise (which is omitted in the figure). As also described before, this is a result of carefully designing the tasks of the algorithm, so that it cannot mistakenly merge inappropriate clusters or noise.

Figure 6 compares the convergence rates of GoSCAN when the number of internal data objects for each peer $(N_{int})$ varies. As observed, changing $N_{int}$ has a minor effect on the algorithm convergence rate. It mainly affects the size of messages and the amount of resource consumption in peers, while having no significant impact on the ability of the algorithm to locate and collect necessary information.

Fig. 6

Convergence rate of the algorithm versus size of internal data, for random gossip in a static setting. The set of dense lines on the left hand side of the two graphs pertain to random DA

6.3.2 Trading clustering error for bandwidth

As mentioned in Sect. 5, peers can reduce the amount of information stored, processed, and exchanged per cluster by tolerating some error in cluster representation. Figure 7 shows the fraction of communication with respect to zero clustering error, for clustering error up to 1. We see a reduction in communication by about 80 % when the clustering error is allowed to be as high as 0.5, after which we do not achieve any further reduction. As the clustering error increases, less and more sparse core points are stored per cluster. Hence, gathering enough information to merge clusters requires more information exchange. However this communication incurs less data, and the improvement in overall data transfer approaches a constant value. Quite remarkable is that tolerating a mere 20 % error in clustering, can save more than 60 % in communication costs.

Fig. 7

Reduction in communication for reaching 90 % accuracy, while varying the clustering error (N = 512)

6.3.3 Targetted gossiping

Let us now consider the effect of deploying the Vicinity protocol. Figures 8 and 9 compare the basic protocol with the improved algorithm for two different network sizes, employing synthetic and SEQUOIA datasets. Two data assignment strategies are applied. As observed, the improved algorithm has minor preference when data is assigned randomly. This is anticipated as the basic algorithm functions suitably with randomly dispersed data. Thus, improving the algorithm has minimum effect on the convergence rate. With the dense data assignment strategy, however, the improved algorithm demonstrates much higher efficiency with synthetic data. This observation confirms the effectiveness of the employed criteria for guiding peers in locating suitable gossip partners. When employing SEQUOIA data, although the difference of accuracy values for different strategies is much less, the prevalence of Vicinity for dense data assignment strategy is still detectable.

Fig. 8

Comparing convergence rate for basic and improved algorithm (synthetic data, rounds 0–70). a n = 512. b n = 1024

Fig. 9

Comparing convergence rate for basic and improved algorithm (SEQUOIA data, rounds 0–30). a n = 512. b n = 1024

The improved algorithm shows minor performance difference when assessing against projection and local accuracies. Both accuracy values quickly approach to 100 %, which clarifies that both algorithm tasks proceed closely when using Vicinity. Detection and connection of core points, along with global cluster formation, are accelerated with the improved algorithm.

6.3.4 Dynamic data

To assess GoSCAN’s behavior in dynamic settings, in each round we replace 1 % of the data points by new ones, chosen by random and cluster-aware assignment policies. It is clear that in this scenario there is no notion of final convergence. Instead, nodes engage in a continuous convergence process, trying to detect and represent clusters as accurately as possible.

Figure 10 shows the evolution of our two evaluation metrics in the dynamic data experiment, for different age threshold (MaxAge) values. The MaxAge values are selected such that extreme cases of algorithm behavior are exposed. The optimal results in the long run, for core point accuracy using random churn, are achieved for an age threshold of 40 rounds. Lower age thresholds (e.g., of 20 rounds, as shown here) lead to significantly suboptimal cluster detection, as data points are removed too soon and peers do not manage to acquire a good representation of the clusters. With higher age thresholds (e.g., of 60 rounds), despite an initially fast cluster detection, accuracy gradually degrades. This is expected, as removed data points are remembered too long, blurring a view on the actual dataset. Note that the edge accuracy scores higher in all configurations. This is expected, as this metric only considers the local structure of core points.

Fig. 10

Comparing convergence rate for different values of MaxAge  computed clusters compared to real clusters of the same round. The selected MaxAge values reveal extreme cases of algorithm behavior. a random churn. b Cluster-aware churn

With cluster-aware data churn, more harsh changes in accuracy is observed. The behavior can be explained considering the fact that existing clusters gradually fade out and new clusters appear. This transition of clusters, quickly out dates the previously data collected by peers, as new data points are eventually located outside the $\varepsilon$ region of collected data. In the random data assignment, in contrast, added data objects are probably located near some existing data point.

Comparing the clusters as perceived by peers to the real clusters corresponding to the data points at a given moment, entails an inherent error due to the expected propagation delay. When data changes dynamically, the clusters perceived by peers at any given moment constitute an approximation of an older version of the dataset. To compensate for this, in Fig. 11 we plot the accuracy metrics again, this time considering the real clusters 10 rounds before the current round. Indeed, this results in higher accuracy values, confirming our reasoning that clusters detected by peers reflect the real state of a few rounds earlier. The argument holds for both data assignment strategies; Nevertheless, cluster-aware data assignment again produces sharper changes in accuracy values.

Fig. 11

Comparing convergence rate for different values of $maxAge$, computed clusters compared to real clusters of 10 rounds before. The selected MaxAge values reveal extreme cases of algorithm behavior. a Random churn. b Cluster-aware churn

We see that even in dynamic settings, peers are able to discover the local structure of the clusters they have data points in. Strictly speaking, the major problem raised when churn is in place, is discovering the overall structure of the cluster and connection between subclusters by all interested peers. In other words, the timely dissemination of core points is the bottleneck of the algorithm.

We also conclude that the age threshold is an important factor with respect to handling dynamism. The overall results show that our algorithm has an acceptable behavior when data churn is in place, and also that our solution more accurately represents a past model of clustering than the current model.

Figure 12 presents aggregate results for the accuracy of GoSCAN with both data assignment strategies, and for data churn rate from 1 to 5 % per round. Each point corresponds to the average accuracy value for the last 50 rounds of each experiment. When compared against current real clusters, accuracy values gradually decrease as higher churn rates are applied. Considering real clusters of 10 rounds ago, however, moderates the decreasing rate of core point accuracy values, while posing a steady value for edge accuracy. This result emphasizes the ability of peers to discover local structure of clusters, albeit being exposed to higher churn rates.

Fig. 12

Average accuracy of the improved algorithm for different data churn ratios, using a random data assignment, b dense data assignment (N = 512, ageTh = 40). Both the Core Points and Edges accuracies are shown with respect to the real cluster in the current round (“offset 0”) and the real clusters 10 rounds earlier (“offset 10”)

6.3.5 Communication overhead

Distributed algorithms are required to maintain low communication overhead in order to be scalable. In this subsection, the average transmission overhead per each peer, in each gossip round, is presented with different configurations. Transmission costs for the static setting, are measured from first round of gossip to the round where core point accuracy reaches 90 %. Figure 13 shows the transmission overhead of the basic algorithm for two data assignment strategies, with SEQUOIA data. Random data assignment increases the data transmission overhead when network size increases. Larger number of peers share more data in the network, while forcing the algorithm to run longer to locate required information. These two conditions pose more overhead when collecting data.

Fig. 13

Average communication cost per node for random gossip in a static setting (SEQUOIA data)

With the dense data assignment, however, a more constant communication overhead is observed. The delicate point which causes this behavior, is the fact that each peer owns several close points which facilitates locating the required data by others. Thus, tasks DETECT and MERGE can converge faster causing less amount of data to be conveyed in the system.

Changing the number of internal data points shared by each peer increases the data in the system, causing the algorithm to transfer larger messages. Figure 14 reveals the effect of changing number of internal data points on the communication load of each peer. As anticipated, an increasing trend is observed in communication overhead as $N_{int}$ gets larger. Compatible with Fig. 13, dense data assignment produces less messages in the system. An interesting observation is that applying Vicinity increases communication overhead in comparison to random gossip. This is first due to more information inserted in the messages to satisfy the protocol requirements, and second due to transmission of data in fewer gossip communication rounds. Recalling previously expressed results, expressing higher convergence rates of Vicinity, a trade-off is detected between rate of algorithm convergence and the communication overhead imposed on peers.

Fig. 14

Average communication cost per node when number of internal data varies

Finally, Fig. 15 assesses communication overhead in a dynamic network, when $maxAge$ varies, for 300 rounds of algorithm execution. Longer existence of data objects in the system increases communication overhead as predicted. However, the increase rate is low, considering that it takes longer for the data collected by peers to be out dated, causing less requests for fresh data in the same amount of time. According to the fact that in random assignment strategy, new data points are located close to previously available points, this strategy makes better use of available data in peers for accomplishing DETECT and MERGE. Therefore, it has less communication overhead, compared to the cluster-aware assignment method.

Fig. 15

Average communication cost per node when $masAge$ varies

7 Related work

Distributed Data Mining (DDM) is a dynamically growing area. Generally, many DDM algorithms are based on algorithms which were originally developed for centralized or parallel data mining. Different proposals have focused on distributed and parallel clustering of data objects. A discussion and comparison of several distributed centroid based partitional clustering algorithms is provided in [28].

References [6, 10] propose parallel K-means clustering, by first distributing data to multiple processors. In each synchronized algorithm round, every processor broadcasts its currently obtained centroids, and updates the centroids based on the information received from all other processors. Note that the two mentioned approaches start by partitioning and distributing data, which is essentially different from GoScan in which data is inherently distributed.

Many existing distributed algorithms in the literature, require a central site to coordinate algorithm execution rounds and/or merge local models into a global clustering result. Requiring global communication rounds, or including multiple rounds of message flooding conflicts the scalability requirement of distributed algorithms. Eisenhardt et al. [7] propose a distributed k-means algorithm to cluster documents in a peer-to-peer network. The algorithm is initiated by one peer, and each round consists of collecting information from all peers in the network, in a recursive manner. Tasoulis et al. [27] propose a distributed algorithm to compute the K-window clustering algorithm in a distributed setting. Their design transfers local models to a central site to be merged into a global model. Merugu et al. [23] build probabilistic models of the data at each local site, and transmit parameters to a central location, for cluster computation.Their algorithm extracts samples from models and fits a global model to these samples.

RACHET [25] is a hierarchical clustering algorithm. Each site executes the clustering algorithm locally, and transmits a set of statistics to a central site. The central site builds a global model based on the local statistics. A method of partition based clustering for clustering distributed high dimensional feature vectors is presented in [18], which uses a central site to build the global model. SDBDC [14] is a distributed density based clustering algorithm which introduces various representations for summarizing local statistics. These statistics are collected from local sites and merged into a global model. In [20] an extension of SDBDC is introduced which better suits high dimensional data.

In [17] local models or prototypes are detected using Expectation Maximization(EM) in a distributed environment, and later merged by computing mutual support among the Gaussian models. Aouad et al. [1] propose a lightweight distributed clustering technique based on merging of independent local sub clusters according to an increasing variance constraint. This algorithm chooses a relatively high number of clusters locally, or employs an approximation technique to find an optimal number of local clusters.

Building clustering algorithms based on existing network overlays, can facilitate execution of the algorithms, while binding the algorithm design to special structures. A hierarchical clustering method based on K-means for P2P networks is suggested in [12]. At the lowest level of the hierarchy a synchronized partitional clustering algorithm is executed. Summary representations are then transferred up the hierarchy and merged to obtain k global clusters. PENS [19] offers a distributed density based clustering based on DBSCAN. This proposal is built upon CAN [24] as the infrastructure, and uses a virtual tree, implicitly defined using the zone splitting mechanism of CAN, to merge partial clusters. Lodi et al. [21] introduce a distributed density based clustering which again uses a semantic overlay as the infrastructure. It utilizes either a gradient-based criterion, to define center-based clusters, or a mean density criterion.

Some solutions considering pure unstructured networks, require state-aware operation of nodes, work in static settings, or are aimed at computing basic functions like average and sum. Datta et al. [4] propose a distributed K-means clustering algorithm for P2P networks, in which nodes communicate with their immediate neighbours. Each node is required to store history of cluster centroids per each K-mean iteration. Eyal et al. [9] provide a generic algorithm for clustering in a static network. They instantiate the algorithm to the K-means clustering method. A generic local algorithm for computing functions of average of data in a distributed system, is proposed by [31]. This method is then used as a feedback loop for the monitoring K-means clustering. Kowalczyk et al. [16] propose a solution for executing EM based on distributedly computing a set of average values. Employing the newscast model, their algorithm proceeds in a series of gossip-based computation rounds.

The major drawback of majority of existing approaches, is lack of efficient solutions for adaptability in dynamic settings, which introduces significant challenges for applying the algorithms in large scale real world networks.

8 Conclusions

In this paper we first identified the necessity of an effective and efficient distributed clustering algorithm. Due to the high transmission, storage and processing costs, it is impractical to collect all data from distributed sources, in a central server, where the data can be analysed by means of clustering. As discussed, dynamic nature of data, demands a continuously running algorithm which can update the clustering model efficiently, and at a reasonable pace. We introduced GoSCAN: a fully decentralized density-based clustering algorithm. GoSCAN consists of two major tasks: identifying core points and cluster formation. Design of gossip-based communication methods, permitted parallel execution of the two tasks, which gradually increased the algorithm accuracy. The algorithm enabled each peer to discover an arbitrary subset of clusters.

GoSCAN allowed each peer to find an individual trade-off between quality of discovered clusters and transmission costs. Also, employing Vicinity, it enabled peers in quickly locating suitable communication partners, which improved convergence rate of the algorithm. Adaptability to dynamics of the dataset was made possible by introducing an age factor per each ordinary and core data object. This parameter assisted in detecting dataset changes, and enabled updating the clustering model. The incremental nature of GoSCAN  avoids re-execution of the algorithm when dataset changes, and promotes the algorithm robustness and scalability. Our experimental evaluation showed that GoSCAN allows effective clustering with efficient transmission costs. In our future work, we plan to develop hierarchical distributed clustering algorithms, which better satisfy specific requirements of distributed systems.