1 Introduction

Rock fracture is common in geotechnical engineering, such as mining and tunneling. On the one hand, we wish to fracture rocks during excavation; on the other hand, we wish to avoid the fracture and failure of geotechnical structures during and after excavation (Ulusay and Hudson 2012). For the latter, rock reinforcement is widely used to avoid the failure of surrounding rocks. Underground excavation and rock support are typical large-scale problems, it is critical to efficiently simulate excavation support.

For the modeling of excavation support, two techniques have been used: continuum-based methods, such as the FEM (finite element method) (Hoek 1998), FDM (finite difference method) (Itasca 2005), BEM (boundary element method) (Shen et al. 2020); discontinuum-based methods, such as the DEM (discrete element method) (Itasca 2014, 2016), DDA (discontinuous deformation analysis) (Huang et al. 2020; Peng et al. 2020; Yu et al. 2020), NMM (numerical manifold method) (Liu et al. 2020a), PD (peridynamics) (Wang et al. 2022), and FDEM (finite-discrete element method) (Deng et al. 2022; Fukuda et al. 2019; Joulin et al. 2020; Knight et al. 2020; Liu et al. 2022; Mahabadi et al. 2012; Munjiza 2004; Xiang et al. 2009; Yan et al. 2022a).

Among them, FDEM combines continuum (FEM) and discontinuum (DEM) to better capture the transition from continua to discontinua for fracture and fragmentation processes of brittle materials (Mahabadi et al. 2012; Munjiza et al. 2011). In FDEM, the deformation and fracture of each element are described by FEM, while the contact interactions between elements are treated by DEM. As a hybrid method, FDEM becomes increasingly popular for geomaterials, such as rocks (An et al. 2017; Barla et al. 2012; Cai et al. 2023; Deng and Liu 2020; Deng et al. 2021; Elmo et al. 2013; Fukuda et al. 2021; Han et al. 2020, 2021; Liang et al. 2021; Lisjak et al. 2017; Sharafisafa et al. 2023; Wang et al. 2020, 2021; Wu et al. 2023; Yao et al. 2020), concretes (Farsi et al. 2019; Wei et al. 2019), masonry (Miglietta et al. 2017; Smoljanović et al. 2018), sands (Chen et al. 2021; Zhou et al. 2020). Moreover, FDEM is also gaining popularity for multi-physics problems due to coupled FDEM solvers, such as the advanced FSIS (fluid–solid interaction solver) (Munjiza et al. 2020).

For the simulation of excavation support based on FDEM, some rock reinforcement models including lining (Deng and Liu 2020; Farsi et al. 2019; Ha et al. 2021; Lisjak et al. 2015; Ma et al. 2022), rockbolt (Batinić et al. 2017; Lisjak et al. 2020; Tatone et al. 2015; Wang et al. 2020; Zivaljic et al. 2013), and grouting (Sun et al. 2019; Yan et al. 2022b) have been reported. However, FDEM-based excavation support simulations are still rare, due to large computational costs. Like other discontinuum-based methods, FDEM is rather computationally expensive (Fukuda et al. 2019). Thus, improving its computational efficiency is essential for large-scale problems.

There are many solutions to improve the computational efficiency. Among them, parallel computing is a preferable solution. It is mainly based on two hardware devices: the CPU (central processing unit) and GPU (graphics processing unit). Parallel FDEM schemes have been reported: the CPU-based methods, such as MPI (message-passing interface) (Lukas et al. 2014; Schiava D’Albano 2014), VPM (virtual parallel machine) (Lei et al. 2014), OpenMP (open multiprocessing) (Xiang et al. 2017; Yan et al. 2014); GPU-based methods, such as OpenCL (open computing language) (Lisjak et al. 2018), and CUDA (compute unified device architecture) (Batinić et al. 2017; Fukuda et al. 2019, 2020; Liu et al. 2019a, 2021; Zhang et al. 2013).

The CPU-based and GPU-based methods have made significant progress: for the former, in cluster computing and multi-core desktop computing, VPM proposed by the Los Alamos FDEM group (Lei et al. 2014) achieves constant CPU efficiency no matter how many processors are used, while also offering greater portability, especially when adapting to new computer architectures that may emerge in the future; the latter also achieves significant speedups in novel desktop hardware architectures.

Although the parallel FDEM schemes show good speedup effects, only a few are parallelized for excavation support. It is essential to further develop parallel FDFM schemes for excavation support covering robust rockbolt and grouting reinforcement models. The existing parallel FDEM schemes focus on parallel implementations on GPUs, which perform well in computational efficiency. However, special hardware and software environments such as parallelization-enabled GPUs and additional compilation tools are required (Yu et al. 2020). Thus, further research on CPU-based FDEM schemes is a good complement to GPU-based FDEM schemes. In the past, the number of CPU cores/threads was usually less than 8/16; now, the maximum number is 128/256. As a CPU-based parallel method, OpenMP has an increasing advantage with the increase in CPU cores and threads.

Therefore, a parallel FDEM scheme for modeling underground excavation and rock reinforcement using OpenMP is implemented. Then, its computational performance is validated in the two advanced CPUs: AMD Ryzen Threadripper PRO 5995WX (64 cores and 128 threads); and 2 × AMD EPYC 7T83 (2 × 64 cores and 2 × 128 threads). Compared to the existing parallel efficiency validation of CPUs with less than 8 cores, the two advanced CPUs include 64 and 128 cores respectively. Hence, the study can better validate the parallel efficiency of FDEM using OpenMP.

2 Implementation of Excavation Support in FDEM

2.1 Fundamentals of FDEM

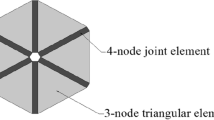
One FDEM simulation can start with an intact domain or a set of discrete bodies (Munjiza 2004). As shown in Fig. 1, each discrete body is discretized into 3-node finite elements, and then fictitious 4-node crack elements are inserted between any neighboring finite elements to capture the transition from continua to discontinua. Any discrete body can achieve motion, elastic deformation, contact interaction, and fracture—once the prescribed failure criteria are met, thus generating new discrete bodies. Once two neighboring 3-node elastic elements are separated, their relationship can only be achieved by DEM (interaction law) instead of FEM (constitutive law) and DEM (interaction law).

Fig. 1
figure 1

Damage and fracture in FDEM (Wang et al. 2021)

Full size image

2.1.1 Governing Equation and Numerical Integration

The governing equation of motion in FDEM

$$ {\mathbf{M}}\ddot{{\mathbf{x}}} + {\mathbf{C}}\dot{{\mathbf{x}}} = {{\mathbf{f}}} = {{\mathbf{f}}}_{{\text{ela}}} + {{\mathbf{f}}}_{{\text{coh}}} + {{\mathbf{f}}}_{{\text{con}}} + {{\mathbf{f}}}_{{\text{ext}}} + {{\mathbf{f}}}_{{\text{oth}}} $$
(1)

where M is the nodal mass matrix; x is the vector of nodal displacements; C is the viscous damping matrix for energy dissipation; f is the vector of nodal forces applied to each node; fela is the vector of elastic forces caused by the deformation of the 3-node finite element; fcoh is the vector of cohesive forces caused by the crack opening and sliding of the fictitious 4-node interface element; fcon is the vector of contact forces induced by the contact interactions; foth is the vector of other equivalent nodal forces caused by the fluid pressure, thermal stress, etc.

An explicit numerical integration scheme—central difference method is adopted to update nodal velocities and coordinates, reflecting the transient evolution of the system

$$ {\dot{\mathbf{x}}}_{t + 0.5\Delta t} = {\dot{\mathbf{x}}}_{t - 0.5\Delta t} + \frac{{{\mathbf{f}}}}{m}\Delta t{;}\,{{\mathbf{x}}}_{t + \Delta t} = {{\mathbf{x}}}_t + {\dot{\mathbf{x}}}_{t + 0.5\Delta t} \Delta t $$
(2)

where m is the equivalent nodal mass; ∆t is the integration time-stepping size.

2.1.2 Transition from Continua to Discontinua

In FDEM, the cohesive crack model is adopted to deal with the transition from continua to discontinua—crack initiation and propagation (Munjiza et al. 1999). As shown in Fig. 1, one crack element may yield or break in the three modes: Mode I; Mode II; and Mixed Mode I–II.

2.1.3 Contact Detection and Interaction

In FDEM, the NBS (no binary search) contact detection algorithm (Munjiza and Andrews 1998) is used to identify potential contact couples. Then, the penalty function method (Munjiza and Andrews 2000) is used to calculate the contact force (Liu et al. 2020b).

More details about FDEM can be found in the three books (Munjiza 2004; Munjiza et al. 2011, 2014) and the two latest chapters (Munjiza et al. 2023a, b) written by Drs. Munjiza, Knight, Rougier, Lei, and Euser.

2.2 Rockbolt Support

The rockbolt is widely used in mining and tunneling to strengthen the surrounding rocks, due to its advantages, such as flexibility, efficiency, versatility, quick installation, and cost-effectiveness. Analytical, numerical, laboratory, and field methods have been implemented to study the interaction between rockbolts and surrounding rocks. Among them, the numerical modeling method has become increasingly popular for rock reinforcement analysis.

For the modeling of rockbolt reinforcement, two methods have been established (Chen et al. 2004; Lisjak et al. 2020; Xu et al. 2022): (i) The structural element approach using virtual springs; (ii) and solid bolt element approach using the explicit bolt mesh. Both methods have their advantages and disadvantages. The former neglects the explicit bolt mesh and is discretized by one-dimensional structural elements, such as bar and beam. Thus, it is easy to implement in complex engineering with intensive joints and rockbolts. However, the former is difficult to capture the interaction between bolt, grout, and rock. Conversely, in the latter, the explicit bolt mesh is generated in the reinforcement zone, and the interaction between rock, bolt, and grout is directly simulated. Thus, the latter can better capture the rockbolt reinforcement in detail, such as load transfer behavior, anchoring mechanism, and failure mechanism. However, the latter usually has larger computational costs, which hinders its application in large-scale problems with intensive bolts. In summary, it is critical to establish an efficient solid bolt model. On the one hand, it can better capture the interaction between bolt, grout, and rock in detail. On the other hand, its computational efficiency promotes its application to excavation support.

As mentioned above, FDEM has the potential to better capture the interaction between bolt, grout, and rock. To date, FDEM-based modelings of rockbolt reinforcement are still rare and focus on the structural element approach (Batinić et al. 2017; Lisjak et al. 2020; Tatone et al. 2015; Wang et al. 2020; Zivaljic et al. 2013). Hence, it is essential to establish an efficient solid bolt model based on FDEM. What’s more, the existing FDEM schemes for rockbolt reinforcement focus on parallel implementations on GPUs, which can be complemented by the further development of CPU-based FDEM schemes. Next, a robust solid bolt model based on FDEM will be described.

The calculation process of the novel solid bolt model based on FDEM is shown in Fig. 2. Before rockbolt activation, the numerical model is established with a mesh generator, then the in-situ stress initialization and core material softening are implemented; during rockbolt activation, the rockbolt elements are automatically marked by vector relations, then the mechanical parameters and constitutive laws of the steel and grout are assigned to the bolt and bolt-rock interface; after rockbolt activation, the interaction between bolt, grout, and rock is calculated.

Fig. 2
figure 2

Calculation process of the novel solid bolt model based on FDEM

Full size image

2.2.1 Automatic Marking of Bolts by Vector Relations

In the 2D simulation, the two boundaries of the rockbolt along the axial direction can be regarded as line segments AB and A′B′. Take AB as an example, when AB intersects with the triangle element 012, it will be marked as a rockbolt element. Taking the positional relationship between the line segments AB and 01 as an example, the two line segments intersect when they satisfy the condition as shown in Fig. 3: AB is distributed on both sides of 01; 01 is distributed on both sides of AB.

Fig. 3
figure 3

Line segment AB intersects line segment 01

Full size image

In geometry, line segment AB intersects line segment 01 when the following vector relationship is satisfied

$$ \begin{gathered} \left( {\overrightarrow {01} \times \overrightarrow {0{\text{A}}} } \right) \cdot \left( {\overrightarrow {01} \times \overrightarrow {0{\text{B}}} } \right) < 0 \hfill \\ \left( {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{A0}}} } \right) \cdot \left( {\overrightarrow {{\text{AB}}} \times \overrightarrow {{\text{A1}}} } \right) < 0 \hfill \\ \end{gathered} $$
(3)

Similarly, one can determine whether there is an intersection between AB and the other two edges 12 or 20. In this way, an automatic search for marking bolt elements by vector relations is achieved. The time spent in marking the bolt elements using this method is negligible. The novel solid bolt model based on FDEM has significant advantages in optimizing the rockbolt design (such as modifying the rockbolt position, spacing, and length) and group bolting.

2.2.2 Interfaces Between Bolt, Grout, and Rock

The positional relationship between the bolt, grout, and rock is shown in Fig. 4. The grout bonds the bolt to the surrounding rock, generating the anchoring force that consists of two components, i.e. cohesion and friction. In FDEM, the action of the grout can be represented using the 4-node crack elements. In this way, only two types of solid units (rock and bolt) remain in Fig. 4, which are represented by triangular elements in FDEM. Only three types of interfacial relationships (rock-rock, bolt-bolt, and rock-bolt) remain, which are represented in FDEM using crack elements.

Fig. 4
figure 4

Schematic diagram of interfaces between bolt, grout, and rock

Full size image

2.2.3 Constitutive Equation of Bolt

The mechanical calculations of bolt elements use the material parameters and constitutive laws of steel. The elastic deformation is directly represented by triangular elements in FDEM; the plastic deformation or rupture judgment is represented by 4-node crack elements. The axial tension constitutive equation for bolt using the classic bilinear elastic strain-hardening model (Fig. 5)

$$ \sigma_{\text{b}} = \left\{ \begin{array}{l} E_{\text{b}} \varepsilon_{\text{b}} { 0} \le \varepsilon_{\text{b}} \le \varepsilon_{\text{y}} \hfill \\ \sigma_{\text{y}} + E_{\text{T}} \left( {\varepsilon_{\text{b}} - \varepsilon_{\text{y}} } \right) \, \varepsilon_{\text{y}} { < }\varepsilon_{\text{b}} \le \varepsilon_{\text{u}} \hfill \\ E_{\text{b}} \varepsilon_{\text{b}} \, - \varepsilon_{\text{y}} \le \varepsilon_{\text{b}} \le 0 \hfill \\ - \sigma_{\text{y}} + E_{\text{T}} \left( {\varepsilon_{\text{b}} + \varepsilon_{\text{y}} } \right) \, - \varepsilon_{\text{u}} \le \varepsilon_{\text{b}} { < } - \varepsilon_{\text{y}} \hfill \\ \end{array} \right. $$
(4)

where σb, σy, and σu are the axial stress, yield strength, and ultimate strength of the bolt, respectively; εb, εy, εu are the axial strain, yield strain, and ultimate strain, respectively; Eb is the elastic modulus of the bolt; ET is the tangent modulus of the bolt at the stage of strain hardening.

Fig. 5
figure 5

Stress–strain curves of the bolt

Full size image

Unlike strain hardening in the axial tension, the bolt is typically brittle in transverse shear. Thus, the transverse shear constitutive equation of the bolt is

$$ \tau_{\text{b}} = \left\{ \begin{array}{ll} G_{\text{b}}&\quad \gamma_{\text{b}} \, - \gamma_{\text{y}} \le \gamma_{\text{b}} \le \gamma_{\text{y}} \hfill \\ 0 &\quad \gamma_{\text{b}} < - \gamma_{\text{u}} {\text{ or }}\gamma_{\text{u}} < \gamma_{\text{b}} \, \hfill \\ \end{array} \right. $$
(5)

where τb, τy, τu are the tangential stress, yield strength, and ultimate strength of the bolt, respectively; Gb is the shear modulus of the bolt; γb, γy, γu are the tangential strain, yield strain, and ultimate strain, respectively. Since γy and γu, τy and τu are highly coincident, they are usually considered equal

$$ \gamma_{\text{y}} \approx \gamma_{\text{u}} {; }\tau_{\text{y}} \approx \tau_{\text{u}} $$
(6)

εy and σy, γy and τy, (εu-εy) and (σu-σy) satisfy the following relations, respectively

$$ \varepsilon_{\text{y}} = \frac{{\sigma_{\text{y}} }}{{E_{\text{b}} }}{;}\quad \gamma_{\text{y}} = \frac{{\tau_{\text{y}} }}{{G_{\text{b}} }}{;}\quad \varepsilon_{\text{u}} - \varepsilon_{\text{y}} = \frac{{\sigma_{\text{u}} - \sigma_{\text{y}} }}{{E_{\text{T}} }} $$
(7)

In this way, after determining the yield point (εy, σy; γy, τy), ultimate point (εu, εy), elastic modulus (Eb), and shear modulus (Gb) of the bolt, the constitutive relationship of the bolt can be determined.

2.2.4 Implementation of Bolt Breakage in FDEM

Bolt breakage sometimes occurs in difficult support conditions, such as high-ground stress and soft rocks (Wang and Liu 2021). However, many numerical codes do not capture the phenomenon of bolt breakage, due to their intrinsic weakness. Thus, it is crucial to directly achieve bolt breakage in FDEM. In the novel solid bolt model based on FDEM, the bolt breakage is achieved by crack elements with the cohesive crack model. Then, the solid bolt model can directly capture the elastic deformation and plastic fracture of the bolt. As shown in Fig. 1, one crack element may yield or break in the three modes: Mode I (tension); Mode II (shear); Mixed Mode I-II (tension-shear).

In Mode I, when the crack opening o of the crack element between two neighboring triangular elements increases the critical crack opening op—corresponding to the normal cohesive stress σb just reaches the yield strength of the bolt σy. Over op, σb monotonically increases from σy to σu with increasing o reaches the maximum crack opening or—a physical discontinuity is formed and then the two triangular elements separate.

In Mode II, when the tangential slip s of the crack element increases the critical slip sp—corresponding to the tangential cohesive stress τ just reaches the shear strength fs of the bolt, Mode II crack initiation and propagation occurs

$$ \tau_{\text{y}} = c + \sigma_{\text{n}} \tan \phi_{\text{i}} $$
(8)

where c is the internal cohesion; σn is the normal stress acting across the crack element; and ϕi is the internal friction angle. Over sp, τ monotonically drops with increasing s, until s reaches the maximum slip sr—corresponding to τ is reduced to a pure friction force

$$ \tau_{\text{r}} = \sigma_{\text{n}} \tan \phi_{\text{r}} $$
(9)

where ϕr is the fracture friction angle.

In Mixed Mode I-II, although o and s are less than or and sr respectively, the fracture still occurs when they simultaneously satisfy the mixed failure law (Lisjak et al. 2013)

$$ \left( {\frac{{o - o_{\text{p}} }}{{o_{\text{r}} - o_{\text{p}} }}} \right)^2 + \left( {\frac{{s - s_{\text{p}} }}{{s_{\text{r}} - s_{\text{p}} }}} \right)^2 \ge 1 $$
(10)

In the axial direction, the peak crack opening op of the bolt is determined by the yield strength σy and the crack penalty parameter pf

$$ o_{\text{p}} = \frac{{2h\sigma_{\text{y}} }}{{p_{\text{f}} }} $$
(11)

In the tangential direction, the peak crack slip sp of the bolt is determined by the shear yield strength τy and the crack penalty parameter pf

$$ s_{\text{p}} = \frac{{2h\tau_{\text{y}} }}{{p_{\text{f}} }} $$
(12)

In the axial direction, the axial yield strength σy, ultimate strength σu, Mode I fracture energy GfI, peak crack opening op, and critical crack opening or satisfy

$$ Gf_{\text{I}} = \int_{o_{\text{p}} }^{o_{\text{r}} } {\sigma \left( o \right)} do $$
(13)

So or is determined by

$$ o_{\text{r}} - o_{\text{p}} = \frac{{2Gf_{\text{I}} }}{{\sigma_{\text{y}} + \sigma_{\text{u}} }} $$
(14)

In the tangential direction, the tangential yield strength τy, ultimate strength τu, Mode II fracture energy GfII, peak crack slide sp, and critical crack slide sr satisfy

$$ Gf_{{\text{II}}} = \int_{s_{\text{p}} }^{s_{\text{r}} } {\left[ {\tau_{\text{b}} \left( s \right) - \tau_{\text{r}} } \right]} ds $$
(15)

So sr is determined by

$$ s_{\text{r}} - s_{\text{p}} = \frac{{\eta \cdot Gf_{{\text{II}}} }}{{\tau_{\text{y}} + \tau_{\text{u}} }} $$
(16)

where η is determined by the lateral softening equation flateral(D), the value is always 6.

In the axial direction, when the bolt is in tension, σb is determined by

$$ \sigma_{\text{b}} = \left\{ {\begin{array}{*{20}l} {E_{\text{b}} \frac{o}{{o_{\text{p}} }}} \hfill & {{0} \le o \le o_{\text{p}} } \hfill \\ {\sigma_{\text{y}} + f_{{\text{axial}}} \left( D \right)\left( {\sigma_{\text{u}} - \sigma_{\text{y}} } \right)} \hfill & {o_{\text{p}} { < }o \le o_{\text{r}} } \hfill \\ \end{array} } \right. $$
(17)

where faxial(D) is an axial softening function that varies from 0 to 1. Unlike the strain-softening feature of rock materials, the steel exhibits a significant strain-hardening feature after reaching its yield strength. Therefore, faxial(D) is not monotonically decreasing, but monotonically increasing, as the normalized crack opening or damage index D increases

$$ f_{{\text{axial}}} \left( D \right) = D $$
(18)

In the transverse direction, the shear stress τb of the bolt

$$ \tau_{\text{b}} = f_{{\text{lateral}}} \left( D \right)\tau_{\text{y}} $$
(19)

where flateral(D) is the lateral softening function that varies from 0 to 1.

2.2.5 Representation of Bolt Row Spacing in a 2D Code

For the 2D code, bolt spacing can be directly reflected, but not bolt row spacing. Since the 2D plane strain assumes a unit depth (1 m) (Lisjak et al. 2020), the bolt row spacing in the 3D effect can be realized by scaling the mechanical parameters in the out-of-plane direction. In the 2D code, if the bolt row spacing sb ≠ 1 m, the mechanical parameters such as the Young’s modulus of the bolt is multiplied by the scaling factor fb (Carranza-Torres 2009)

$$ f_{\text{b}} = \frac{1}{{s_{\text{b}} }} $$
(20)

in this way, the bolt row spacing can be represented in the 2D FDEM code.

2.3 Grouting Reinforcement

The FDEM-based grouting reinforcement simulation has the following assumptions: (i) The slurry can enter into all cracks caused by excavation. According to the principle of crack initiation and propagation in fracture mechanics, the cracks are continuously propagated from the high-stress place to the low-stress place, therefore all the cracks can be connected, and then the slurry can naturally enter into all cracks caused by excavation. (ii) The slurry only flows in the broken crack elements and neither opens new cracks nor penetrates the rock matrix.

As shown in Fig. 6, the implementation of grouting reinforcement in FDEM is accomplished by the two steps: (i) When grouting reinforcement activation, the FDEM solver for excavation support automatically searches and identifies the broken crack elements in the numerical model and marks them as grouting elements. (ii) The grouting elements are rejoined in the calculation of the cohesive stresses in the crack elements; the mechanical parameters of the slurry are assigned to the grouting elements; and the tensile openings and shear slips of the grouting elements are reaccumulated.

Fig. 6
figure 6

Schematic diagram of grouting reinforcement simulation based on FDEM

Full size image

3 OpenMP and Its Implementation in FDEM

3.1 Parallel Computing

Moore’s law proposed in 1965 predicts the development of computers: when the prices remain constant, the number of transistors per integrated circuit chip will double in each technology generation—every 1.5–2 years, resulting in a doubling performance. Dennard scaling proposed in 1974 states that although the density of transistors on a chip doubles, the power consumption per unit area remains the same. The two laws predicted the development trend of integrated circuits for a long time until 2004. Then, the improvement of single-core performance is relatively limited, and multi-core and multi-threading are increasingly popular.

During this period, taking the Intel Core processors as an example, for flagships in the Core 1–13 generations, the CPU base/maximum frequency, and the number of cores/threads over time are shown in Fig. 7. 2010–2023 corresponds to generation 1–13, respectively. With the increase of time or generation, the CPU base frequency fluctuates between 3.0 and 4.2 GHz, the maximum frequency increases approximately linearly from 3.46 to 6.0 GHz, and the number of cores/threads increases gradually from 2/4 to 24/36. In other words, from 2010 to 2023, the CPU base frequency is stable, the maximum frequency increases by 73%, and the number of cores/threads increases by 1100%/800%.

Fig. 7
figure 7

Variation of base/max. frequency and total cores/threads of Intel Core processors in recent years

Full size image

This reflects the development trend of CPUs: single-core performance characterized by base/maximum frequency has increased slightly, while multi-core performance characterized by the number of cores/threads has increased significantly. Therefore, if one program does not implement parallel optimization, it will be possible to use only one core even if there are multiple cores.

3.2 OpenMP

The CPU-based parallel FDEM is mainly based on two parallel tools: MPI and OpenMP. MPI is suitable for cluster computing and supercomputers based on function calls, distributed memory architecture, message-passing communication model, implicit/explicit synchronization, and library implementation; OpenMP is suitable for multi-core processors or multi-socket servers based on compilation directives, shared memory architecture, shared address communication model, implicit synchronization, and compiler implementation.

For cluster computing, its key limiting factor is the maximum connection speed achievable between individual processors over a network, i.e. LAN (local area network) bandwidth. A comparison between LAN and RAM bandwidths shows that transporting data between clustered CPUs is slower than accessing the same data from RAM, but this may change as laser communications evolve (Munjiza et al. 2011). In addition, MPI has explicit control of the memory hierarchy, whereas OpenMP does not. Thus, MPI-based parallel solutions are popular, such as the advanced FDEM schemes VPM and HOSS (Lei et al. 2014; Munjiza et al. 2023a).

MPI and OpenMP have their strengths and weaknesses. OpenMP supports incremental parallelization with minimum additional code, whereas MPI does not. Just like developing MPI-based FDEM schemes, it is also necessary to further develop OpenMP-based FDEM schemes, as well as MPI/OpenMP hybrid schemes. In the next sections, only OpenMP is covered. OpenMP is an application programming interface (API) based on shared memory for writing parallel programs. It supports compiler languages, such as C/C +  + and Fortran. Many programs use OpenMP due to its advantages of portability, scalability, generalizability, and cheapness.

3.2.1 Threads and Fork-Join

In computer programming, a thread is a sequence of instructions that can be executed independently of other parts of a program. It is the smallest and most basic unit of processing that can be scheduled by an operating system. Threads allow for parallel or concurrent execution of tasks, enabling programs to perform multiple operations simultaneously.

OpenMP uses fork-join mode to execute the code, as shown in Fig. 8. The program begins execution with only one main thread in serial mode; after it encounters a parallel statement, it derives multiple branching threads to perform the parallel tasks; after the parallel tasks are completed, the branching threads merge and the control flow is handed over to the main thread again.

Fig. 8
figure 8

Fork-join mode in OpenMP

Full size image

3.2.2 Types of Variables

Variables in OpenMP consist of two types: shared variables, which can be read, written, and accessed by every thread; and private variables, which can be used only within the parallel domain. Shared variables can be read from shared memory, while private variables only can read from their local private memory. The former is slower to read than the latter. Thus, the private variables are preferred to reduce the overhead. For FDEM, the private variables are preferred for large arrays or pointers such as node coordinates.

3.2.3 Loop Scheduling

OpenMP uses the “schedule (type, size)” clause to implement loop scheduling. The “type” consists of four types: static, dynamic, guided, and runtime. The first two are widely used: the “static” has a low overhead and a long wait time, and is suitable for load-balanced cases; the “dynamic” is the opposite. The “size” represents the size of the chunk.

3.2.4 Data Race

Data race refers to variables in the parallel domain that are read or written by multiple threads at the same time, resulting in different computation results from the serial program. To solve the data race problem, data synchronization is achieved in OpenMP through three methods, as shown in Table 1. The “atomic” operation is preferred due to its minimal overhead. However, the “atomic” operation is only applicable to a single statement and must be the most basic operation in the code.

Table 1 Three methods to solve data race in OpenMP
Full size table

3.2.5 Parallel Overhead and Load Balancing

Parallel overhead refers to the computation time consumed by the parallelism itself, while load balancing refers to the degree of difference between the workloads of different threads within the parallel zone. Thus, it is important to ensure that the computation time saved by parallelism is greater than the time consumed by the parallelism overhead. It implies that different parallel strategies should be adopted for different serial programs according to their features. Meanwhile, the structure of serial programs should be optimized to make them suitable for parallel computation. This also indirectly indicates that not all problems are suitable for parallelism. For serial problems with serious dependencies between data or computational processes, they are not suitable for parallelization, improving the hardware is much more cost-effective than parallelizing them.

3.2.6 Parallel Efficiency

Parallel performance is mainly measured by two indicators: speedup ratio and parallel efficiency. From Amdahl’s law, the speedup ratio is

$$ {\text{speedup}} = \frac{{W_{\text{s}} + W_{\text{p}} }}{{W_{\text{s}} + {{W_{\text{p}} } / p}}} = \frac{1}{{\alpha_{{\text{seq}}} + {{\left( {1 - \alpha_{{\text{seq}}} } \right)} / p}}} < \frac{1}{{\alpha_{{\text{seq}}} }} $$
(21)

where Ws and Wp are the serial and parallel parts of the computational problem, respectively; p is the number of processors; and αseq is the proportion of the serial part.

Parallel efficiency refers to the actual speedup ratio to the ideal or linear speedup ratio. The ideal speedup ratio refers to the maximum speedup ratio that can be achieved in parallel assuming αseq = 0, and is related to the number of cores used. The actual speedup ratio is always lower than the ideal speedup ratio.

3.2.7 Data Accuracy and Consistency of Parallel Results

Each byte has 8 bits, and the range and precision of float and double are shown in Table 2. Since computers have limited precision, different computational results may be obtained for sum = x + y + z with different solving: (x + y) + z ≠ x + (y + z). Due to the random order of computation, the results of each parallel computation are not the same, even though there is no data race problem.

Table 2 Range and precision of single and double floating point numbers
Full size table

The problem of data precision is different from the inconsistency of parallel results caused by data race. The former is a false error, each parallel computation result is one of the "correct" results; the serial computation result looks the same every time, but it is only an illusion masked by the fixed order of the solution, which is only one of many "correct" results. The latter is a true computational mistake since the data are not synchronized in time.

3.3 Implementation of OpenMP Parallel Computing in FDEM

3.3.1 Parallel Strategy

To reach the limit of FDEM parallelization, it is necessary to determine which sub-modules (yfd, ycd, yid, ysd, yod as shown in Fig. 9) in FDEM are suitable for parallelization and then develop a parallelization strategy. Theoretically, both the “for” statement and “section” instruction in OpenMP can implement parallelism for FDEM. However, on the one hand, the five modules in FDEM are not completely independent, and on the other hand, the computational workloads of different modules are very different (e.g., yid consumes a longer computation time than the other modules; it is difficult to realize the load balancing among different modules by using the “section” instruction). Thus, it is not suitable to use the “section” instruction between yfd and ycd/yid. What’s more, yfd includes two sub-modules, i.e., 3-node and 4-node elements. Although the “section” instruction can be used, it can only be used with a small number of threads, which is not conducive to the speedup ratio. Thus, it is appropriate to use the “for” statement to achieve parallelism without making major changes to the overall structure of the FDEM serial program. Meanwhile, to improve the speedup ratio, the private variables are preferred for data variables, and the atomic and reductive operations with very low overhead are preferred for data race and data synchronization. Moreover, the AVX 2 or AVX-512, SIMD is used to release the potential of the CPUs.

Fig. 9
figure 9

Flowchart of FDEM simulation

Full size image

3.3.2 Optimization of Program Structures

In terms of data race and data synchronization, variables such as node force are frequently involved in FDEM. Hence, in sub-modules such as yfd, local variable substitutions for shared variables and positional adjustments for data synchronization are used to minimize the parallel overhead. In terms of load balancing, FDEM includes 3-node and 4-node elements, and both are not distinguished in the “for” statement but are only filtered by the “if” statement. It may cause a significant load imbalance problem. Thus, they are separated in the “for” statement. Such a treatment can significantly reduce computation time even for serial program operations. This also implies that the program structure can only be optimized enough for serial conditions to achieve a high speedup ratio for parallel conditions.

4 Computational Efficiency

4.1 Computer Platform and Numerical Model

Two computer platforms for parallel performance validation are used in the simulations. (i) The first, with Windows 10 as the operating system, AMD Ryzen Threadripper PRO 5995WX CPU as the processor, 256 GB RAM, and NVIDIA GeForce RTX 3060 Ti as the graphics card. (ii) The second, with Windows 11 as the operating system, 2 × AMD EPYC 7T83 CPUs as the processor, 256 GB RAM, and no discrete graphics. Detailed parameters of the CPUs are shown in Table 3.

Table 3 Detailed parameters of the CPUs
Full size table

The numerical model for parallel performance validation is the uniaxial compression test. Two groups of tests (33 k elements and 3304 k elements as shown in Fig. 10) are performed on each of the two computer platforms. The parallel effect is validated by measuring the computation time of the simulated 10 k-steps of the test. The two groups of tests were performed by setting 9 and 13 levels on Threadripper and 2 × EPYC CPUs with 1–128 and 1–256 threads, respectively. No matter how many threads are used, the same simulated result including the stress–strain response and fracture pattern is obtained, as shown in Fig. 10. Thus, a detailed analysis of the result is omitted.

Fig. 10
figure 10

Numerical model for parallel performance validation and the simulated result

Full size image

4.2 Computation Time, Speedup Ratio, and Parallel Efficiency

The computation time, speedup ratio, and parallel efficiency of simulating 10 k steps for 33 k elements and 3304 k elements with different threads are shown in Figs. 11 and 12, respectively.

Fig. 11
figure 11

Computation time, speedup ratio, and parallel efficiency for Threadripper

Full size image
Fig. 12
figure 12

Computation time, speedup ratio, and parallel efficiency for 2 × EPYC

Full size image

4.2.1 Computation Time

For the Threadripper (Fig. 11), as the number of threads increases, the computation time decreases nonlinearly for both 33 k elements and 3304 k elements with a decreasing trend and eventually converging. For the former and latter, the longest computation time is 149 s and 32,391 s respectively, and the shortest computation time is 5 s and 834 s, respectively.

For the 2 × EPYC (Fig. 12), as the number of threads increases, the computation time for both 33 k elements and 3304 k elements decreases sharply and then increases slightly. Unlike the single Threadripper, the computation time of dual 2 × EPYC is shortest when the number of threads used = 128, i.e. the number of cores. This is because the 2 × EPYC with two CPUs has high overheads of data exchange between CPUs. Thus, in terms of energy saving, the high-performance single CPU is preferred to the cheap dual CPUs.

4.2.2 Speedup Ratio

For the Threadripper (Fig. 11), as the number of threads increases, the speedup ratio of both 33 k elements and 3304 k elements gradually increases, with the increasing trend gradually slowing down. When the number of threads is 128, their speedup ratios reach their maximum values of 30 and 41, respectively. The speedup ratio of the former is lower, which is consistent with the parallel theory: the increase in granularity contributes to the increase in the speedup ratio.

For the 2 × EPYC (Fig. 12), as the number of threads increases, the speedup ratio of 33 k elements and 3304 k elements increases rapidly and then decreases slowly, with the maximum speedup ratio when the number of used threads = 128. The maximum speedup ratios for the former and the latter are 31 and 43, respectively. The trends in speedup ratios for both are not the same. Unlike the Threadripper, the speedup ratio of the 2 × EPYC shows a decreasing trend. This is because the dual 2 × EPYC includes 2 CPUs, and the high overhead of data communication between different CPUs limits the continuous increase of the speedup ratio.

4.2.3 Parallel Efficiency

For the Threadripper (Fig. 11), as the number of threads increases, the parallel efficiency of both 33 k elements and 3304 k elements gradually decreases, with the downward trend slowing down and eventually converging. After excluding the data with the number of threads = 1 (serial), the decrease in parallel efficiency is manageable. The maximum reduction in parallel efficiency is about 49.0% and 40% for the former and the latter, respectively; their parallel efficiency is always greater than 23% and 32%, respectively.

For the 2 × EPYC (Fig. 12), as the number of threads increases, the parallel efficiency of both 33 k elements and 3304 k elements decreases, with the downward trend slowing down. The speedup ratio is maximized when the number of open threads = 128, so it is sufficient to open only 50% of the total threads. This not only maximizes the speedup ratio but also reduces energy consumption.

4.2.4 Scalability of Speedup Ratio

Good scalability of the speedup ratio means that as the number of threads increases, the speedup ratio continues to increase and the parallel efficiency can remain at a high level. Due to serious data race, many parallel programs have poor scalability and are only suitable for parallelism with less number of threads (up to 8); after using more threads, the actual speedup ratio decreases rather than increases, and the parallel efficiency decreases rapidly.

The simulation results in Figs. 11 and 12 show that: whether 33 k elements or 3304 k elements, when the number of threads used is less than 128, the speedup ratio is always increasing with the increase of the number of threads; although the parallel efficiency shows a decreasing trend, it is always maintained at a high level. This means that the parallel strategy adopted in this study can efficiently deal with the data race problem, and the scalability of the parallel program is good.

4.2.5 Stability of Speedup Ratio

The parallel program in this study has a stable speedup ratio. Some of the parallel programs can maintain high speedup ratios when rock is not fractured; the speedup ratios decrease significantly as the degree of rock fracture increases. For example, the CUDA-based FDEM parallel program (Liu et al. 2019a; Ma et al. 2022) has a speedup ratio of 53–106 before fracture and 20–50 after fracture. FDEM is good at simulating fracture problems, and the most common application is fracture problem simulation. Thus, the FDEM parallel program is useful only if it maintains a high speedup ratio when fracture problems are simulated; on the contrary, it is less useful to maintain a high speedup ratio when non-fracture problems are simulated.

In summary, the OpenMP-based FDEM parallel program can efficiently handle the data race problem, and the parallel program has good scalability, with maximum speedup ratios of 30 (33 k elements) and 41 (3304 k elements) obtained on the Threadripper, and 31 and 43 on the 2 × EPYC.

5 Application in Excavation Support

In the previous section, the high computational efficiency of the OpenMP parallel FDEM is verified. To demonstrate its ability in simulating underground excavation and rock support, a simulation of rockbolt-shotcrete-grouting support is implemented.

5.1 Numerical Model

A tunnel (span S = 11.3 m, height H = 8.8 m) for excavation support is placed at the center of the numerical model, as shown in Fig. 13. The numerical parameters are calibrated from soft rock in a tunnel, as shown in Table 4. The calibration process is based on a common approach (Tatone and Grasselli 2015).The in-situ stress parameters for the tunnel excavation: horizontal stress σH = 18.2 MPa; vertical stress σv = 11.4 MPa.

Fig. 13
figure 13

Geometry and boundary conditions in a numerical model of tunnel excavation

Full size image
Table 4 Numerical parameters of tunnel excavation
Full size table

The rockbolt-shotcrete-grouting support is adopted in the simulation. For the shotcrete lining, a 200 mm thick elastic liner is used. For the mechanical parameters of the lining, Young’s modulus and Poisson’s ratio are 500 MPa and 0.3, respectively. When the softening coefficient αs is reduced to 0.01, the elements of shotcrete lining and rockbolting are activated. When the number of cracks reaches a certain level, the grouting reinforcement is implemented. The arrangement and mechanical parameters of rockbolts and cables (simplified as long rockbolts) are shown in Fig. 14 and Table 5, respectively. The mechanical parameters of rockbolts are obtained from the references (Lisjak et al. 2020; Liu et al. 2019b). Although the solid bolt model can directly reflect the bolt geometry, only the length of the bolt is directly reflected to improve the computational efficiency. This indirectly shows that it is essential to improve computational efficiency through acceleration techniques.

Fig. 14
figure 14

Arrangement of rockbolts and cables

Full size image
Table 5 Mechanical parameters of the rockbolt
Full size table

5.2 Fracture Process of Tunnel Surrounding Rock

The fracture process of the tunnel surrounding rock under rockbolt-shotcrete-grouting support is shown in Fig. 15. With the increase of simulation time, the stress near the tunnel perimeter is redistributed, resulting in stress concentration. When the stress concentration rises to a level, tensile and shear cracks begin to appear around the tunnel; then the cracks continue to develop deeper into the surrounding rock. Because of the significant stress concentration around the tunnel, the crack density is the highest and the fracture is the most significant at this location, and the surrounding rock is cut into some blocks. The combination of the lateral pressure coefficient and tunnel shape leads to more cracks near the tunnel vault. Before grouting, several cracks were distributed around the tunnel perimeter. After the implementation of grouting, the cracks were repaired. With the increase of simulation time, the tunnel surrounding the rock tends to be stabilized and then reaches a new equilibrium. This indicates that the grouting reinforcement has the expected role of repairing the cracks generated before grouting as well as limiting the development of new cracks after grouting.

Fig. 15
figure 15

Fracture process of tunnel surrounding rock under rockbolt-shotcrete-grouting support

Full size image

The variation of the accumulative number of broken elements of the tunnel surrounding rock with time is shown in Fig. 16. Before grouting, the accumulative number of broken elements of surrounding rock gradually increases with the increase of simulation time. After grouting, the accumulative number of broken elements increases slightly and then stabilizes at a lower level. This indicates that grouting not only repairs the cracks generated before grouting but also limits the development of new cracks after grouting.

Fig. 16
figure 16

Accumulative number of broken elements of tunnel surrounding rock with time

Full size image

5.3 Stress Distribution of Tunnel Surrounding Rock

The stress distribution of the tunnel surrounding rock after support stabilization is shown in Fig. 17. The low radial normal stress and high tangential stress in the surrounding rock around the tunnel cause the stress to be converted from a three-directional to a two-directional stress, which leads to intensive cracks in the tunnel periphery. With the increase of the distance from the tunnel, the radial normal stress gradually increases and the tangential stress gradually decreases in the surrounding rock, recovering to the in-situ stress level in the far field. The tensile phenomenon is serious at the locations of the tunnel vault and bottom corner, which is consistent with the crack distribution location in Fig. 15. The rockbolts are significantly stressed and show large tensile stresses. This indicates that the rockbolts work together with the lining and grouting reinforcement.

Fig. 17
figure 17

Stress distribution of tunnel surrounding rock after rock support stabilization

Full size image

5.4 Displacement Distribution of Tunnel Surrounding Rock

The displacement distribution of the tunnel surrounding the rock after support stabilization is shown in Fig. 18. According to the displacement magnitude, the tunnel from inside to outside can be roughly divided into an excavation damage zone and an elastic deformation zone. In the excavation damage zone, crushing and extrusion are severe, and the displacement of surrounding rock is controlled by tensile and shear cracks, resulting in higher radial displacement. With the increase of the distance from the tunnel, the crack density decreases significantly; although the cracks can still nucleate, the higher confining pressure limits the relative displacement of shear cracks along the fracture surface; thus, the further expansion of tensile and shear cracks is effectively prevented, and the radial displacement in the far field is significantly lower than the radial displacement around the tunnel, forming an elastic deformation zone. In the horizontal direction, the displacements on the left and right sides are symmetrical; in the vertical direction, the displacement of the vault is significantly larger than that of the upward arch, and a significant arch shape is presented on the displacement contour.

Fig. 18
figure 18

Displacement distribution of tunnel surrounding rock after support stabilization

Full size image

5.5 Tunnel Deformation Response

The variation of tunnel convergence of the key points around the tunnel with time is shown in Fig. 19b. With the increase of simulation time, the tunnel convergence shows a three-stage development of gentle increase–rapid increase–gentle increase. When the simulation time increases to a certain degree, it tends to converge. Among them, the convergence of the tunnel vault is stabilized at 226.6 mm, the convergence of the left arch shoulder is stabilized at 207.18 mm, and the convergence of the right arch shoulder is stabilized at 211.11 mm.

Fig. 19
figure 19

Tunnel convergence of the key points around the tunnel

Full size image

The ground reaction curve during tunnel excavation under rockbolt-shotcrete-grouting support is shown in Fig. 20. With the increase of tunnel convergence of the key points around the tunnel, the support pressure/in-situ stress decreases gradually from 1.0 and eventually stabilizes.

Fig. 20
figure 20

Ground reaction curve during tunnel excavation under rock support

Full size image

The measured convergence curve of a tunnel is shown in Fig. 19a. A comparison of Fig. 19a, b shows that the simulated and measured results are in agreement. The settlement of the tunnel vault is 223.02 mm and 226.60 mm in the measured and simulated results, respectively, with a relative error of 1.6%; the convergence of the left arch shoulder is 217.86 mm and 207.18 mm in the measured and simulated results, respectively, with a relative error of 4.9%; the convergence of the right arch shoulder is 190.08 mm and 211.11 mm in the measured and simulated results, respectively, with a relative error of 11.1%, as shown in Fig. 21. The trend of the tunnel convergence with time is also consistent with the overall increase in time and eventually stabilized. It is noted that the x-axis in days is real physical time, while the x-axis in ms is virtual time. Although they are not equal, they are directly proportional. It should be noted that although the simulation results are quantitative, they can usually only be used qualitatively, due to the difficulty of exact quantitative comparison between simulated and measured results.

Fig. 21
figure 21

Comparison of the simulated and measured results

Full size image

6 Discussion

The ratio of the number of elements in Fig. 10 is approximately 1/100. Thus, when serial computation is implemented, the ratio of computation time is also about 1/100. However, the ratios are 1/217 (Threadripper) and 1/204 (2 × EPYC), respectively. This may be due to the factors: the number of elements in the former is small, the files of input data and output single-step result are 0.7 MB and 8.6 MB, respectively, and the cache can meet the data reading requirements; the number of elements in the latter is enlarged by 100, which leads to the surge of the files of input data and output single-step result to 81 MB and 1 GB, respectively, thus the cache is far from adequate for data reading, and the data needs to be read from memory and even hard disk; according to the logic of the computer, reading data from the cache is the fastest, and from the hard disk is the slowest; this affects localization and data synchronization in parallel computation and determines the communication overhead between different processors.

As the number of elements increases (from 33 k elements to 3304 k elements), the computation time does not increase linearly, but rather in a non-linear manner with a progressively faster growth rate. This means that when scaling up to million-level elements, in addition to the CPU, it is also necessary to pay attention to the underlying logic of the computer such as data reading and writing. For data reading, it is necessary to make use of the cache as well as prioritize the use of memory with fast reading speed. For data writing, it is necessary to prioritize the use of hard disks with fast speed.

7 Conclusions

An OpenMP-based parallel FDEM scheme for simulating underground excavation and rock reinforcement is implemented. Its computational performance is validated in the two advanced CPUs: AMD Ryzen Threadripper PRO 5995WX (64/128 cores/threads); and 2 × AMD EPYC 7T83 (128/256 cores/threads). Then, its ability in simulating tunnel excavation under rockbolt-shotcrete-grouting support is implemented. Based on the studies above, the following conclusions are drawn:

  1. (i)

    For the maximum speedup ratio obtained on the two computer platforms (Threadripper and 2 × EPYC), the OpenMP-based parallel FDEM scheme obtains maximum speedup ratios of 30 (33 k elements) and 41 (3304 k elements) on the Threadripper, and 31 and 43 on the 2 × EPYC.

  2. (ii)

    For the scalability of the speedup ratio, when the number of threads used is less than 128, the speedup ratio is always increasing with the increase of the number of threads. This means that the parallel strategy can efficiently deal with the data race problem, and its scalability is good.

  3. (iii)

    For the stability of the speedup ratio, unlike some parallel FDEM programs where the speedup ratio decreases significantly after rock fracture, the OpenMP-based parallel FDEM has a stable speedup ratio, regardless of whether the rock is pre- or post-fractured.

  4. (iv)

    The novel solid bolt model based on FDEM can explicitly capture the interaction between bolt, grout, and rock, due to its significant advantages in optimizing the rockbolt design (such as modifying the rockbolt position, spacing, and length) and group bolting, as well as directly simulating bolt breakage.