1 Introduction

Geothermal energy stored in hot dry rocks has long been considered as an energy source alternative to traditional fossil fuels. Heat extraction in geothermal reservoirs is primarily achieved by circulating cold water between injection and production wells through fracture networks, which have been artificially created and/or enhanced by applying various stimulation techniques. As the development of geothermal reservoirs by the transient cooling scheme proceeds, the impedance to flow is decreased. The main mechanisms responsible for such a behavior is the complex interaction among pore fluid pressure, rock mass temperature and mechanical deformation of both fractures and reservoir matrix caused by the fluid injection. The increased pore pressure and transient cooling induce matrix contraction and cause increased fracture apertures. Due to the presence of natural fractures, the thermal stress and pore pressure are often spatially highly variable within the reservoir. The resulting heterogeneous stress field can lead to non-uniform evolution of hydraulic transmissivity and cause flow anisotropy and channeling in the reservoir. To quantitatively characterize the heat extraction process in geothermal reservoirs, a numerical model that can solve coupled thermal-hydro-mechanical (THM) processes is needed.

The numerical methods for simulating such problems can be categorized as continuum and discontinuum models. The conventional continuum models treat a fractured rock as either an equivalent porous medium (Wu 1999) or a superposition of two continua (Pruess and Narasimhan 1985), representing the combined matrix and fracture systems. Because of its simplicity and computational efficiency, these models have been widely used in the analysis of field-scale heat extraction processes. However, they cannot adequately consider the sharp permeability contrast between fractures and matrix, the effect of local stress variation, the connectivity of large fractures and the interaction among multiple discrete fractures. On the other hand, in the discontinuum model, the fractured rock is treated as an assemblage of discrete fractures embedded within the rock matrix. Because the fracture geometries are explicitly represented, such a discontinuum model can well capture many important hydro-mechanical behaviors of fractures such as compression-induced closure and shear-induced dilation as well as resulting permeability variation in complex fracture networks (Lei et al. 2017).

Extensive studies based on discrete fracture networks have been conducted to model the THM behavior of fractured rocks (Ghassemi and Zhou 2011; Salimzadeh et al. 2018), and have shown that transient cooling and fluid overpressure lead to a reduction in effective stress and an increase in fracture transmissivity. The THM coupling can result in faster thermal drawdown comparing to heat extraction simulations with the mechanical effect omitted (Hicks et al. 1996). It has been observed that the poro-elastic effect plays a dominant role in fracture aperture evolution only over short-time scales (~ a few days) whereas the thermo-elastic effect influences the aperture evolution during the entire production phase over long time scales (e.g. a few years) (Ghassemi and Zhou 2011). Moreover, fracture aperture heterogeneity was found to cause flow channelization and extra thermal drawdown (Guo et al. 2016). Such effect is stronger if the aperture correlation length is larger. Other material and operational parameters such as fracture stiffness, thermal expansion coefficient, injection temperature, and injection rate may also introduce additional effects on the fracture aperture evolution (Pandey and Vishal 2017; Wang et al. 2016). Nevertheless, these previous studies were mainly based on thermal drawdown curves, which only represent the bulk behavior of the geothermal system.

A few recent studies have investigated the evolution of fracture transmissivity or aperture in fracture clusters (Vik et al. 2018; Zhao et al. 2015) or discrete fracture networks (Fu et al. 2016; Gan and Elsworth 2016; Han et al. 2019; Koh et al. 2011; Sun et al. 2017; Yao et al. 2018). These studies suggest that the thermal stress tends to have a dominant role in increasing fracture permeability, which is responsible for the enhanced flow channelization and faster thermal drawdown (Fu et al. 2016). The channelized flow and anisotropic heat transfer behavior are found to be controlled by fracture characteristics such as length and orientation (Han et al. 2019; Sun et al. 2017). These previous studies have mostly focused on analyzing the fracture aperture evolution either caused by thermal stresses, whilst the combined effects of thermal and in-situ stresses remain poorly elucidated, especially for complex discrete fracture networks. Such limitations hinder our fundamental understanding of the THM behavior of geothermal reservoirs during thermal extraction.

In this work, we study this issue using high-fidelity numerical modeling of coupled geomechanics, fluid flow and heat transfer in 2D fractured rocks. Here, we approximate the 3D system using a 2D model assuming a plane-strain condition, which is considered to be a reasonable assumption for the deeply buried geological formation here. We specifically focus on investigating how the transient thermal perturbation and in-situ stress mutually interact with each other and how their combined effects affect geothermal reservoir performance. The effect of in-situ stresses was considered in many previous studies on THM modeling (Sun et al. 2017; Yao et al. 2018). We show that in-situ stress loading may induce significant impact on heat transfer in two-dimensional (2D) heterogeneous fracture networks. Ignoring such an effect may exaggerate the enlargement of fracture apertures during the transient cooling process, resulting in biased predictions of the heat transfer behavior and heat production performance of the reservoir, e.g., heat breakthrough and thermal drawdown.

In a recent study, we have shown that anisotropic confining stresses can lead to anomalous heat transport in fracture networks (Sun et al. 2020). However, thermal stress induced by transient cooling due to thermo-poroelastic effects was not included in that study. In this work, we develop a fully coupled THM model to investigate the complex interaction between thermal and in-situ stresses, and elucidate their coupled effects on fracture aperture evolution during the heat extraction process. Our model takes into account compression-induced closure, shear-induced dilation and thermal-induced opening of fracture apertures. The results provide important insights into the dynamic evolutional behavior of the fracture aperture field during transient cooling, which are useful for optimizing thermal extraction strategies for geothermal reservoirs. The remainder of the paper is organized as follows. In Sect. 2, the fully coupled THM numerical model is introduced. Section 3 describes the model setup and simulation procedure with the results further presented in Sect. 4. Finally, in Sect. 5, some discussions and concluding remarks are provided.

2 Numerical Methods

2.1 Discrete Fracture Network Generation

The 2D discrete fracture network (DFN) used in this work is generated with the fracture lengths following a lognormal distribution which has been observed in many outcrops of real fracture systems (Einstein and Baecher 1983; Hudson and Priest 1983). Laboratory experiments (Rives et al. 1992; Wu and Pollard 1995), numerical simulations (Bai et al. 2000; Renshaw and Pollard 1994; Rives et al. 1992; Wu and Pollard 1995) and field observations (Renshaw and Park 1997) have shown that the evolution of fracture spacing is governed by the mechanical interaction between emerging/growing fractures. To consider this important mechanical interaction among fractures, the concept of a stress shadow (or relaxation) zone around pre-existing fractures is implemented in our DFN model to mimic this effect in a statistical framework (Wang et al. 2017).

By integrating the shadow zone model into the random fracture network generation process, the self-organized geometries and topologies of natural joint systems can be more realistically represented. A 2D DFN model can be created by the following steps. (1) Randomly choose a point as the mid-point of a new fracture. If the seed is located within the shadow zone of an existing fracture, remove this seed and regenerate a new one (Fig. 1b). (2) Assign a random length value drawn from the pre-defined length distribution (i.e., lognormal function here) for the new fracture. Assign an orientation value drawn from the pre-defined orientation distribution (i.e., two orthogonal orientations here) for the new fracture. If the fracture intersects with the shadow zone of other pre-existing fractures, it will be truncated (Fig. 1c). If the fracture’s shadow zone overlaps that of an existing orthogonal fracture, it is either truncated (Fig. 1d) or extended (Fig. 1e) so that the new fracture abuts the old one. (3) A new stress shadow zone is also assigned to the most recently generated fracture to constrain the generation of subsequent ones. This procedure is iterated until the fracture network reaches the target intensity. The fracture spacing is not pre-defined, but is controlled by the statistical distribution of fracture mid-points, lengths as well as stress shadow zone parameters. The minimal possible spacing between two fractures is controlled by the half width (we) of the fracture shadow zone (Fig. 1a).

Fig. 1
figure 1

Demonstration of the generic DFN generation model. a A stress shadow zone around a fracture. we is a geometrical parameter that defines the shadow zone width. b If the seed of a new fracture with the same orientation to the pre-existing fracture falls into its shadow zone, the seed is removed and the new fracture will not be generated. c The new fracture, parallel to an existing fracture that enters into its shadow zone, is truncated. d The new fracture, not parallel to an existing fracture that enters into its shadow zone and cross it, is truncated. e The new fracture, not parallel to an existing fracture that enters into its shadow zone but does not cross it, is extended

Full size image

2.2 Thermal–Hydraulic-Mechanical (THM) Coupled Modeling

In this work, the full coupled problem of geomechanical deformation, fluid flow and heat transport in geothermal reservoirs is solved based on the finite element method. The model is implemented in the commercial software, COMSOL Multiphysics. The model domain is discretized using an unstructured mesh with 2D triangular matrix elements and 1-D linear fracture elements (treated as internal interfaces). The governing equations of the THM model are described in detail as follows.

2.2.1 Geomechanical Deformation

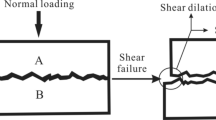
The fractured rock in the geothermal reservoir is modeled as a combination of high-permeability fractures and a low-permeability rock matrix that surround the fractures. Because the magnitude of matrix permeability in hot dry rocks is significantly lower than that of factures, the flow pathways tend to be controlled by fractures. We model the deformability of fractures under normal compression based on a hyperbolic model (Bandis et al. 1983; Barton et al. 1985):

$$ v_{{\text{n}}} = \frac{{\sigma_{{\text{n}}} \nu_{{\text{m}}} }}{{K_{{{\text{n0}}}} \nu_{{\text{m}}} + \sigma_{{\text{n}}} }} $$
(1)

where the vn is the normal closure, Kn0 is the initial normal stiffness, vm is the maximum allowable closure, and σn is the effective normal compressive stress which is equal to the difference between the total normal stress on the fracture and the fluid pressure inside the fracture.

The shear deformation is calculated based on the excess shear stress concept (Rahman et al. 2002; Ucar et al. 2017). The excess shear stress, Δτ, is defined as the difference between the shear stress and shear strength on the fractures:

$$ \Delta \tau = \tau - \sigma_{{\text{n}}} \tan \phi $$
(2)

where τ is the shear stress and ϕ is the friction angle. For a fracture with its shear stress exceeding the yield surface of the Mohr–Coulomb criterion, the shear displacement, us, is approximated by dividing the excess shear stress by the shear stiffness, Ks, such as in linear elastic theory (Rahman et al. 2002; Ucar et al. 2017):

$$ u_{{\text{s}}} = \frac{\Delta \tau }{{K_{{\text{s}}} }} $$
(3)

Ultimately, the dilational displacement vs is related to the shear displacement us via an incremental form as Saeb and Amadei (1992):

$$ \nu_{{\text{s}}} = - u_{{\text{s}}} \tan \phi_{i} $$
(4)

where ϕi is the dilation angle. The fracture aperture b under coupled normal and shear loadings is thus given by Lei et al. (2016):

$$ b = \left\{ {\begin{array}{*{20}l} {b_{0} + w,} \hfill & {\sigma_{{\text{n}}} < 0} \hfill \\ {b_{0} - v_{{\text{n}}} - \nu_{{\text{s}}} ,} \hfill & {\sigma_{{\text{n}}} \ge 0} \hfill \\ \end{array} } \right. $$
(5)

where b0 is the initial aperture, and w is the separation of opposing fracture walls if the fracture is under tension.

The mechanical deformation of rock matrix is modeled based on thermo-poro-elasticity principles (Jaeger et al. 2009). By synthesizing the effect of thermal expansion and pore pressurize, the governing equation for the matrix deformation is written as Zhao et al. (2015):

$$ \sigma_{ij}^{\prime } = \sigma_{ij} - \alpha_{{\text{B}}} p\delta_{ij} = \frac{Ev}{{\left( {1 + v} \right)\left( {1 - 2v} \right)}}\varepsilon_{ki} \delta_{ij} + \frac{E}{1 + v}\varepsilon_{ij} - \frac{E}{{\left( {1 - 2v} \right)}}\alpha_{{\text{T}}} \Delta T\delta_{ij} $$
(6)

where \(\sigma_{ij}^{\prime }\) is the effective stress, εij is the strain, E is the Young’s modulus, ν is the Poisson’s ratio, αB is the Biot’s coefficient, p is the fluid pressure, δij is the Kronecker delta, αT is the thermal expansion coefficient and ΔT is the temperature increment defined as ΔT = T—Tref with T and Tref being the rock and reference temperatures, respectively.

2.2.2 Fluid flow

Single-phase flow of compressible fluids through fractured porous media is governed by the following mass conservation and momentum equations for matrix and fracture elements:

$$ \varepsilon \chi_{{\text{f}}} \frac{\partial p}{{\partial t}} + \nabla \cdot \left( {{\mathbf{u}}_{{\text{m}}} } \right) = 0, $$
(7)
$$ \begin{gathered} {\mathbf{u}}_{{\text{m}}} = - \frac{{\kappa_{{\text{m}}} }}{\mu }\nabla p, \hfill \\ \hfill \\ \end{gathered} $$
(8)

and

$$ b\chi_{{\text{f}}} \frac{\partial p}{{\partial t}} + \nabla_{\tau } \cdot \left( {b{\mathbf{u}}_{f} } \right) = f_{{{\text{up}}}} + f_{{{\text{bottom}}}} , $$
(9)
$$ \begin{gathered} {\mathbf{u}}_{{\text{f}}} = - \frac{{\kappa_{{\text{f}}} }}{\mu }\nabla_{\tau } p, \hfill \\ \hfill \\ \end{gathered} $$
(10)

where u is the velocity vector and κ is the permeability with the subscripts ‘m’ and ‘f’ denoting the matrix and fractures, respectively, ε is the matrix porosity, p is the pressure, t is the time, μ is the fluid dynamic viscosity and χf is the fluid compressibility, \({f}_{i}=-\frac{{\kappa }_{m}}{\mu }\frac{\partial {p}_{i}}{\partial {n}_{i}}\) is the fluid exchange term between fracture and matrix, with subscript ‘i’ representing the up and bottom matrix blocks from two sides of the fracture and ni representing the outward normal direction of the matrix. ∇τ denotes the gradient operator restricted to the fracture’s tangential plane. The fracture permeability κf is calculated using the cubic law based on stress-dependent fracture aperture. The local permeability is assumed to be constant for all matrix elements.

2.2.3 Heat transfer

The energy conservation equations describing the heat transfer process in the fractured rock are given below. In the rock matrix, the energy conservation equation is described as:

$$ \left( {\rho C} \right)_{{{\text{eff}}}} \frac{\partial T}{{\partial t}} + \rho_{{\text{f}}} C_{{\text{f}}} {\mathbf{u}}_{{\text{m}}} \cdot \nabla T + \nabla \cdot \left( { - \lambda_{{{\text{eff}}}} \nabla T} \right) = 0, $$
(11)

where \(\left( {\rho C} \right)_{{{\text{eff}}}} = \varepsilon \rho_{{\text{f}}} C_{{\text{f}}} {\mathbf{ + }}\left( {1 - \varepsilon } \right)\rho_{{\text{s}}} C_{{\text{s}}}\) and \(\lambda_{{{\text{eff}}}} = \varepsilon \lambda_{{\text{f}}} + (1 - \varepsilon )\lambda_{{\text{s}}}\) are the effective heat capacity and the effective thermal conductivity, respectively, obtained through volume averaging, T is the temperature, ρ is the density, C is the specific heat capacity, and λ is the heat conductivity with the subscripts ‘s’ and ‘f’ denoting the rock solid and fluid phases, respectively.

In discrete fractures, the energy conservation equation is given as:

$$ b\rho_{{\text{f}}} C_{{\text{f}}} \frac{\partial T}{{\partial t}} + b\rho_{{\text{f}}} {\mathbf{u}}_{{\text{f}}} C_{{\text{f}}} \nabla_{\tau } T_{{\text{f}}} - \nabla_{\tau } \cdot \left( {b\lambda_{{\text{f}}} \nabla_{\tau } T} \right) = e_{{{\text{up}}}} + e_{{{\text{bottom}}}} , $$
(12)

where eup and ebottom are the energy exchange terms between fractures and matrix. Up and bottom stand for matrix from different sides of the fracture, such that \(e_{i} = \rho_{{\text{f}}} C_{{\text{f}}} T_{i} \cdot f_{i} - \lambda_{{{\text{eff}}}} \frac{{\partial T_{i} }}{{\partial t_{i} }}\) with i meaning up or bottom.

In this study, the relative production temperature is defined as a normalized formulation:

$$ T^{*} = \frac{{T_{{{\text{out}}}} - T_{0} }}{{T_{{{\text{in}}}} - T_{0} }}, $$
(13)

where Tout and Tin are the fluid temperatures at the production and injection wells, respectively; T0 is the initial temperature of the reservoir. To further quantify the timescales of convective and conductive transport processes, we introduce a dimensionless quantity as Sun et al. (2020):

$$ R = \frac{{2\varepsilon_{{\text{m}}} D_{{\text{m}}} }}{{\overline{u}_{{\text{f}}} \overline{d}_{{\text{f}}} }}, $$
(14)

Where \(\varepsilon_{{\text{m}}} = \varepsilon + (1 - \varepsilon )\frac{{\rho_{{\text{s}}} C_{{\text{s}}} }}{{\rho_{{\text{f}}} C_{{\text{f}}} }},\) \(\overline{d}_{{\text{f}}}\) is the mean fracture aperture, \(\overline{u}_{{\text{f}}}\) is the mean fracture velocity and \(D_{{\text{m}}} = \frac{{\lambda_{{\text{s}}} }}{{\rho_{{\text{s}}} C_{{\text{s}}} }},\) is the heat diffusion coefficient in the matrix. Note that the heat transfer in the matrix is dominant by diffusion since the matrix permeability is significantly small. R can be thought as the inverse of a fracture-matrix Péclet number, and it represents a ratio of convection to conduction timescales.

3 Numerical Model Setup

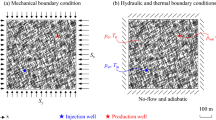
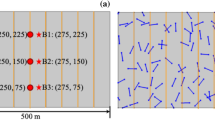
As shown in Fig. 2a, the modeled area has a dimension of 1000 m × 1000 m with 3000 fractures. The DFN consists of two fracture sets with fixed orientations of 30° and 110°. The fracture trace length follows a lognormal distribution with a mean value of 30 m and a variance of 0.6 (Fig. 1b). The stochastically generated fracture network, is well connected and shows a strong geometrical anisotropy. Such a simple DFN is chosen as it preserves the essential geometrical features of the geothermal reservoir, allowing us to focus on investigating the complex THM responses of the fractured geothermal reservoirs in a generic perspective.

Fig. 2
figure 2

a The 2D discrete fracture network used in the coupled THM simulation. b The length distribution of the discrete fracture network. c Schematic showing the stress boundary condition. d Schematic showing the roller boundary condition. e Layout of monitoring points on the 110° fracture set. f Layout of monitoring points on the 30° fracture set

Full size image

We consider the target reservoir at a depth of 3000 m. The overburden stress is Sv = 79.83 MPa assuming the rock density is 2700 kg/m3. We apply horizontal in-situ stresses Sx and Sv, along the x- and y-directions, respectively, and orthogonally to the domain (Fig. 2c). We denote the ratio of the horizontal stresses to the vertical stress as kx = Sx/Sv and ky = Sy/Sv and explore three different scenarios: (1) kx = 0.8, ky = 0.8; (2) kx = 0.8, ky = 1.6; (3) kx = 1.6, ky = 0.8. Another set of simulations with displacement boundary constraints are also performed, where a roller condition is assumed for all model boundaries (Fig. 2d). Such a roller boundary has been adopted by many previous studies without considering in-situ stresses and we will investigate the consequences based on a comparative analysis. A constant initial aperture of 0.4 mm is assigned to all fractures. For the cases applied with stress boundary constraints, an equilibrium state regarding pore pressure, temperature and stress fields is first achieved within the entire reservoir domain before modeling the heat extraction process. Then, the heat production is started at a given time and the flow circulation is established by elevating the hydraulic head at the injection well to create a fixed hydraulic gradient between the injection and production wells (Fig. 2a). During the entire production period, a no-flow condition is imposed for all domain boundaries. The boundary condition for the heat transfer calculation are specified as follows: cold fluid of 20 °C is injected at the injection well when reservoir operations initiates. Three initial temperatures of T0 = 120, 220 and 320 °C are considered. The domain boundaries are assumed to be of adiabatic type. The properties of rock and fluid as well as the initial and boundary condition parameters in the coupled THM simulations are listed in Tables 1 and 2. To track the spatially varying aperture evolution, we set five monitoring points for each fracture set. The locations of the monitoring points are shown in Fig. 2e and f.

Table 1 The rock and fluids properties used in the coupled THM simulation
Full size table
Table 2 The initial and boundary condition parameters used in the coupled THM simulation
Full size table

The coupled THM models were solved using COMSOL Multiphysics V5.4 (COMSOL Multiphysics®, 2018). The model domain was discretized by triangular elements. The mesh size was optimized to ensure calculation accuracy whiling maintaining efficiency. The simulation is implemented by two sequential steps: (1) in-situ stress initialization and (2) heat production. In the first stage, we aim to mimic the in-situ reservoir condition before production. Thus, there is no pressure difference between production and injection wells, i.e., the pressure in both wells equals to the reservoir pressure. The simulation time in this step was set as 2 × 109 s (≈ 63 a) which is long enough to attain an equilibrium state of stress under the combined effect of in-situ stresses, thermal stress induced by initial reservoir temperature and the initial pore pressure of the reservoir. At the time of 2 × 109 s, gradients of pressure (from p0 to pin) and temperature (from T0 to Tin) were established, which indicates the beginning of heat production. The production duration was set to 1011 s for all cases which is enough to extract all heat of the reservoir. Besides, the logarithmic time stepping strategy was adopted to capture the short-time variation of temperature fields. Note that in the text below, the production time refers to the time after the initialization time 2 × 109 s.

4 Results

4.1 Results of Geomechanical Deformation

Figure 3 shows the probability density functions (PDFs) of fracture apertures at selected four production times under different geomechanical boundary conditions. Figure 4 presents the corresponding heterogeneous distributions of fracture apertures for respective cases. The results presented in both figures are for the initial temperature condition of T0 = 220 °C. At the initial stage of heat extraction (i.e., t = 1 a), the Gaussian-like aperture distribution for the case under an isotropic stress loading (Fig. 3a) is similar to that of the roller boundary case (Fig. 3d). This is because the cold front only affects the area around the injection well at early times (Fig. 4) such that the deformation of fractures in the two cases are dominated by compression-induced normal closure. When an anisotropic far-field stress is applied (Fig. 3b and c), the aperture PDFs exhibit a bimodal form with the two peaks corresponding to the two different fracture sets. This is because the two fracture sets at different orientations with respect to the in-situ stress loading tend to accommodate different normal and shear stresses, as expected from the Mohr’s circle stress solution (Jaeger et al. 2009), such that the two fracture sets exhibit different aperture values. In addition, the second peak of the case of kx = 1.6 and ky = 0.8 is slightly shifted towards large aperture values comparing to the case of kx = 0.8 and ky = 1.6. This is caused by the intrinsic geometrical heterogeneity of the fracture pattern, which accommodates more shear displacements and dilations in the former case.

Fig. 3
figure 3

Aperture PDFs for various in-situ stress cases at selected four production times of 1, 5, 10 and 30 years

Full size image
Fig. 4
figure 4

Spatial distribution of fracture apertures for various in-situ stresses at four different production times

Full size image

As the reservoir development proceeds (e.g., t = 5 a and 10 a), the aperture PDFs of cases where anisotropic in-situ stresses are applied (Fig. 3b and c) exhibit a mild change comparing to that at t = 1a. The bimodal form is maintained whereas the apertures of some fractures become larger, due to transient cooling-induced fracture unloading that tends to alleviate normal closure under reduced normal stress and also promote shear dilation under reduced shear resistance (proportional to normal stress via the friction coefficient). The number of large apertures increases gradually with time as the cold front propagates towards the downstream (Fig. 4; rows 2 and 3). For the stress case of kx = 0.8 and ky = 1.6, the aperture increase occurs mainly in fractures of the 110° set, whereas for the case of kx = 1.6 and ky = 0.8, increased fracture apertures mostly happen along fractures of the 30° set. To better understand the process, we derive the components contributing to the aperture variation: the amount of normal closure, vn, shear dilation, vs, as well as the net aperture change, vn + vs. Figure 5 presents the evolution of vn, vs and vn + vs monitored at the probing point 1 on the 110° fracture set when T0 = 220 °C. It can be seen that shear dilation only occurs in the case of anisotropic in-situ stresses with kx = 0.8 and ky = 1.6. Also, the onset of the shearing corresponds to the moment when the normal closure decreases (due to cooling-induced unloading). We interpret the operating mechanism as follows. When the fractured rock is subject to anisotropic in-situ stresses, shear load is imposed along preferentially orientated fractures. Once the thermal front arrives, a thermal stress is generated by the cooling effect, which reduces the effective normal stress acting on the fracture. Consequently, the shear strength is reduced. Once the shear strength is lower than the shear stress, fracture sliding would occur with dilational displacement produced.

Fig. 5
figure 5

Evolution of normal closure (vn), shear displacement (vs) and net aperture change (vn + vs) for sampling point 1 on 30° fracture set under a roller boundary condition, b kx = 0.8, ky = 0.8, c kx = 0.8, ky = 1.6, d kx = 1.6, ky = 0.8

Full size image

If the fractured rock is isotropically stressed, i.e., kx = 0.8 and ky = 0.8, the spread of the aperture distribution is broadened at first but then tapered. The mean value tends to shift towards larger value regimes as the production time increases (Fig. 3a). However, the general unimodal shape of the aperture PDF is kept all the time. In contrast, when the fractured rock is not subject to in-situ stresses (i.e., when roller boundaries are applied), the aperture distribution changed totally with the increased time (Fig. 3d). The mean aperture values increase persistently over time. There is an increase of more than 1.5 times during 30 years of reservoir development. The manner of how the spatial distribution of fracture aperture evolves for the roller boundary case is also different from that of cases subject to stress loadings (Fig. 4). This clearly demonstrates the impact of in-situ stresses on aperture evolution during the heat extraction. If it is neglected, the value of fracture apertures tends to be overestimated. In addition, the overestimation becomes gradually exaggerated as the reservoir development continues.

To further elucidate the in-situ stress effect on fracture aperture, we analyze the aperture evolution of fractures intersecting the monitoring points (Fig. 2e and f) during the entire heat extraction period. Figures 6 and 7 present the results for the 110° and 30° fracture sets, respectively. At very early time (t <  = 0.1 a), the cold front has not yet arrived at the monitoring points within the fracture networks. There is only a small difference in the fracture aperture behavior among these points, indicating that the pressure gradient has a minor effect on the aperture spatial distribution. After that, the curves of aperture evolution exhibit different behaviors depending on the monitoring location and in-situ stress condition. The chronological order of the aperture variation for the stress boundary cases seems to be in accordance to the relative distance between the monitoring point and the injection well along the mean flow direction (Fig. 6; first row; points 1, 3, 5). Moreover, these points all exhibit a similar variation behavior: the aperture first increases and then decreases until it returns to the original value. The magnitude of the variation peak depends on the in-situ stress conditions (Fig. 6; first row). For instance, the aperture variation at point 1 on the 110° fracture set is milder under the stress case of kx = 1.6 and ky = 0.8 in comparison to the other two far-field stress cases, because the 110° set is under higher normal stress (more normal closure) and also more suppressed for shearing (less shear dilation) in the case of kx = 1.6 and ky = 0.8. For monitoring points across the mean flow direction (i.e., points 2 and 4), the aperture variation trend is more complex: a decline in aperture is observed before the variation peak (Fig. 6). Similar phenomena can also be observed in Fig. 7. However, the non-uniform thermal stress distribution due to the complex fracture geometry may lead to different aperture evolution behaviors of the two fracture sets. Such a behavior implies that a fracture may experience a deformation due to the stress perturbation induced by the thermal front remotely, while it could undergo a second influence by the transient cooling upon the arrival of the thermal front at the fracture. On the other hand, if the fractured rock is subject to roller boundaries without in-situ stress loading, all fractures show a similar, simple, behavior of aperture evolution: the aperture increases consistently as the transient cooling operates until reaching and then stabilizing at a maximum value. Because the reservoir temperature at the end of the simulation is 20 °C, which equals to the reference temperature (Tref), the maximum aperture value corresponds the condition of zero thermal stress. Therefore, a higher initial reservoir temperature generates a higher level of thermal expansion under the roller boundary constraint, and corresponds to a lower initial normalized aperture value.

Fig. 6
figure 6

Aperture evolution of the five monitoring points for the 110° fracture set, under different in-situ stresses and reservoir initial temperatures

Full size image
Fig. 7
figure 7

Aperture evolution at the five monitoring points for the 30° fracture set, under different in-situ stresses and reservoir initial temperatures

Full size image

Besides, the aperture evolution behavior depends also on the initial reservoir temperature and the relative configuration between in-situ stress directions and fracture orientation. The former effect can be seen by comparing cases under different initial temperatures but the same reservoir stress condition (i.e., respective cases in different rows in Figs. 6 and 7). When the initial reservoir temperature is increased from 120 to 220 °C, the peak on the aperture evolution curve becomes higher, showing a larger aperture variation. This temperature effect is more profound for the measured 110° fractures under the in-situ stress condition of kx = 0.8 and ky = 1.6. In contrast, for the sampled 30° fractures, larger impacts occur when kx = 1.6 and ky = 0.8. Similar effects of reservoir temperature can also be observed if the initial temperate is further increased to 320 °C.

4.2 Results of Fluid Flow

Figure 8 shows the evolution of normalized flow rate distributions for different in-situ stress cases but the same initial temperature of T0 = 220 °C. To facilitate the comparison, flow rate distributions are normalized against the respective values at 1a. In the cases of the roller boundary, isotropic stress and anisotropic stress with kx = 1.6, ky = 0.8, the flow rates along the mean flow direction seem to be enhanced as the heat extraction proceeds. In contrast, in the case of kx = 0.8, ky = 1.6, flow rate enhancement occurs mainly along fractures of the 110° set. This orientation dependency of flow is related to the shear dilation effect of preferentially oriented fractures under anisotropic in-situ stresses. Figure 9 presents the corresponding velocity PDFs at the four selected times (i.e. 1 a, 5 a, 10 a, and 30 a). At the initial production phase, i.e., when t = 1 a, the isotropic stress loading and roller boundary cases have similar flow rate distributions (Fig. 9a), due to the similar aperture distributions (Fig. 4). As the production time increases, the two flow rate distributions become gradually different (Fig. 9b–d). The velocity distribution of the roller boundary case shifts towards large velocities, although the form of velocity scaling (i.e., the PDF shape) remains unaltered. In contrast, the velocity distributions of the cases with in-situ stress loadings change very slightly over time. In addition, the difference between the two anisotropic far-field stress loadings is small and does not seem to change over time. This demonstrates the dominant role of in-situ stresses in regulating the hydrological behavior of the fractured rock during the entire heat extraction process.

Fig. 8
figure 8

Evolution of flow rate distribution when the reservoir initial temperature is T0 = 220°. Flow rates are normalized by the mean flow rate of the respective 1a case

Full size image
Fig. 9
figure 9

Velocity PDFs for various in-situ stress cases at time a t = 1 a; b t = 5 a; c t = 10 a; d t = 30 a

Full size image

We further elucidate the bulk hydrological response of the fracture network under various conditions of in-situ stress and initial reservoir temperature. This is done by examining the production flow rate evolution are shown in Fig. 10. Normalization is applied with respect to the flow rate at the beginning time of heat production. For a specific condition of initial temperature, the normalized production flow rate varies around 1 for cases where the fractured rock is subject to stress loading. This implies the flow rate does not change much during the heat production. All cases of stressed fracture networks have a similar variation trend of a first increase phase followed by a decline period; the normalized flow rate falls back to 1 at the end. The detailed variation behavior is controlled by the configuration of in-situ stresses. The variation of normalized flow rate is the largest in the stress case of kx = 1.6 and ky = 0.8 while it is the smallest when the far-field stress is rotated by 90°; the flow rate variation of the isotropic stress case is in between the two anisotropic stress cases. It is also observed that an increase in the initial reservoir temperature results in an enhancement of the flow rate variation magnitude, while the general variation trend for different stress cases does not seem to change too much.

Fig. 10
figure 10

Flow rate evolution at the production well for various in-situ stress and reservoir initial temperature cases

Full size image

On the other hand, the roller boundary case behaves very differently. Similar to the evolution of apertures, there is a general increasing trend in flow rate over the entire production period. The rate of flow enhancement increases at first and then decreases. The total flow enhancement depends on the initial reservoir temperature, such that a higher initial temperature leads to a stronger flow enhancement.

4.3 Results of Heat Transfer

4.3.1 Spatial–Temporal Temperature Distribution

Figure 11 displays the spatial distributions of reservoir temperature at times for various in-situ stress cases with an initial temperature of T0 = 220 °C. At early times (e.g., at 1 a or 5 a), the difference in temperature distribution between the isotropic stress and roller boundary cases is small. As reservoir development proceeds (e.g., at 10 a and 30 a), the discrepancy between the distributions become gradually larger (Fig. 11). The thermal front of the roller boundary case appears shaper and its arrival is earlier in comparison to that of the case under isotropic stress loading (i.e., when kx = ky = 0.8). On the contrary, if the fractured rock is loaded with anisotropic in-situ stresses, the thermal breakthrough at the production well is delayed comparing to the isotropic stress and roller boundary cases. However, coning of the thermal front is more apparent when kx = 1.6 and ky = 0.8, where the mean flow direction is in accordance with the preferentially oriented 30° fracture set accommodating shearing and dilation. The blunt thermal front shown in the case of kx = 0.8 and ky = 1.6 is due to the profound closure of fractures in the 30° set and relatively more opening of fractures in the 110° set.

Fig. 11
figure 11

Evolution of normalized temperature distribution for various in-situ stress cases with 0 and 1 corresponding to Tin and T0. The reservoir initial temperature is T0 = 220 °C

Full size image

4.3.2 Heat Extraction Performance

Figure 12 presents the variation of average outlet temperature for various stress cases and different initial reservoir temperature conditions. As the relative temperature T* (defined by Eq. 13) varies from 0 to 1, the temperature of extracted fluids varies from the initial rock temperature to that of injected fluids. If the fractured rock is isotropically stressed with kx = 0.8 and ky = 0.8, the onset time of T* elevation for T0 = 120 °C is delayed by more than five times compared to the roller boundary case, due to compression-induced aperture closures (Fig. 12a). When anisotropic stresses are applied, the thermal breakthrough becomes even later. The onset of T* variation is slightly earlier in the stress case of kx = 1.6 and ky = 0.8, but the difference is much smaller than that between the isotropic and anisotropic stress cases. When the initial temperature is increased, the thermal breakthrough for the roller boundary case becomes strongly delayed, such that onset of T* elevation occurs even later than that of the isotropic stress case, especially when the T0 is increased to 320 °C.

Fig. 12
figure 12

Average temperature curves for various in-situ stress cases and reservoir initial temperature conditions

Full size image

To further elucidate the effect of in-situ stresses, we examine evolutional behavior of the dimensionless number R (Eq. 14), which quantifies the relative timescales of convective and conductive heat transfer processes. The results are shown in Fig. 13. In our recent study, we have shown that for a fixed reservoir operation configuration (e.g., reservoir size, average fracture spacing, initial temperature, distance between injection and production wells) R determines the ultimate heat extraction efficiency (Sun et al. 2020). A similar finding was also reported for heat transfer through single fractures (Martínez et al. 2014). In general, the heat transfer is limited by conduction when R > 1, while by convection when R < 1. Through numerous numerical simulations on a broad range of fracture network connectivity, it was found that, in general, for complex fracture networks, the highest heat extraction efficiency occurs in the vicinity of R = 1 (Sun et al. 2020). Also, for R < 1 the gradient of heat extraction efficiency variation is much higher.

Fig. 13
figure 13

Evolution of R for various in-situ stress and reservoir initial temperature cases

Full size image

The R values of all our simulations are within the range of R < 1.5, implying the heat transfer process of the simulations are within the convection-dominated regime. Note that the R is calculated based on all fractures in the domain so that the value of R will be overestimated. For the main flow channels controlling the heat production performance, R is much smaller. When T0 = 120 °C, the stress boundary cases show a small variation in R over the entire heat extraction process (Fig. 13a). The two anisotropic in-situ cases have a similar R value (~ 1.4), which is about two times higher than that of the isotropic stress case (~ 0.7). In contrast, the roller boundary case exhibits a large R variation but a much lower value. The R value starts to decrease from the initial value of about 0.1 at around 1 a and becomes stabilized again at R = 0.08 after 40 a.

If the initial reservoir temperature is increased, the R values of the stressed fracture networks only show a slightly increased variation magnitude comparing to the results at T0 = 120 °C (Fig. 13b and c). For the roller boundary case, the initial R value is significantly increased, although it will drop to the same level eventually. The initial R value is determined by the temperature level: a higher initial temperature corresponds to a higher initial R value. When T0 = 320 °C, the R of the isotropic in-situ stress case is initially higher than that of the roller boundary case, but the R value drops fast and eventually becomes much lower. This observation suggests that without considering the in-situ stress effect, numerical simulation may unrealistically predict that an initially efficient system tends to become inefficient within a short time of less than 10 years.

5 Discussions and Conclusions

In this study, we have shown how the interplay between thermal and in-situ stresses controls the heat transfer behavior in 2D fractured reservoirs. The in-situ stresses tend to suppress fracture apertures and regulate the fluid flow within fracture networks. The effects of in-situ stress on the transient heat transfer have been demonstrated by the evolution of fracture aperture and velocity statistics. Neglecting the in-situ stress effect, the aperture PDF shifts towards large values as the thermal front propagates from the injection well towards the production well at the downstream. For anisotropic in-situ stresses, an important observation is that the transient cooling may trigger fracture shear dilations. Significant shear dilations occur along the fracture set that is preferentially oriented with respect to the maximum principle stress. Such an important geomechanical effect has not been explored in previous THM modeling studies of fractured geothermal reservoirs (Sun et al. 2017; Yao et al. 2018).

Another important insight from our simulations is that the aperture evolution of a fracture during heat extraction may be controlled by two mechanisms: (1) aperture enlargement due to transient cooling upon the arrival of thermal front at the fracture, which have been discussed extensively in the past (Ghassemi and Zhou 2011; Hicks et al. 1996; Salimzadeh et al. 2018); (2) aperture reduction caused by a stress disturbance transmitted from a stress redistribution process at a remote location experiencing cooling, i.e., before the thermal front propagates to the location of the fracture. The second mechanism is relevant not only to the optimization of heat extraction efficiency as demonstrated in the current paper, but also to the risk management of induced seismicity by fluid injection during the heat production. Our simulations suggest that a stress perturbation caused by cooling may enhance the probability of activating a geological structure, e.g. pre-existing faults, located remotely. This only occurs when the in-situ stress effect is properly modeled in the simulation (Figs. 6 and 7). The remote triggering phenomena of seismicity have been identified in several field observations (Ellsworth 2013; van der Elst et al. 2013). The present study will be further extended to quantitatively investigate how the interaction among thermal, hydraulic and geomechanical processes influences induced seismicity in terms of magnitude and spatial extent in the future.

We have compared the THM behaviors of fractured rocks under stress boundary constraints with that with zero-displacement boundary constraints (i.e., roller boundaries). In previous THM modeling studies of fractured geothermal reservoirs, the roller boundary condition is the most popular numerical boundary type that has been adopted for simulating the geological confinement imposed by surrounding rocks. In contrast, the stress boundary constraints are seldom used (Han et al. 2019). We suggest that the stress boundary constraints may be closer to the actual condition of subsurface geothermal reservoirs. Our results have shown that in a coupled THM model with all external boundaries applied with the roller boundary condition, the fracture apertures increase continuously over the entire production phase. Also, the predicted spatial variation of apertures is very small. These behaviors tend to be unrealistic for real fracture systems at great depth.

Our study highlights the critical importance of incorporating the geomechanical stresses in modeling of heat transfer and geothermal performance. The traditional approaches that ignore the effects of reservoir in-situ stress state may lead to an overestimation of fracture aperture increase and heat extraction. The efficiency of heat extraction declines much earlier and fast when the in-situ stress effect is omitted. The findings in this study have important implications for designing efficient operation scheme for geothermal reservoirs as well as for managing seismic hazards from fluid injections. However, we admit that there are still some limitations. First, this work did not consider shear-induced fracture propagation. This may not affect the general observations and conclusions in this paper, since the connectivity of the natural fracture network is high whereas the stress ratio is low (≤ 2) such that the system is away from the critically-stressed state (Zoback 2007). The effect of new crack formation may become dominant for fracture networks close to the percolation threshold and subject to high stress ratios (Jiang et al. 2019). Furthermore, the current study is based on 2D fracture systems. Efforts are need to extend the THM model to study the potentially important 3D effects.