1 Introduction

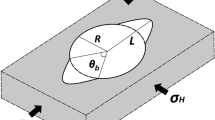
Drilling of a borehole into a rock mass can disturb the in situ stress field and redistribute the stresses around the borehole. According to the Kirsch solution (Kirsch 1898; Jaeger et al. 2009), the maximum stress concentration for a vertical borehole occurs along the minimum horizontal principal stress direction (\(\sigma_{h}\)) and gradually decreases towards the maximum horizontal principal stress direction (\(\sigma_{H}\)). If the horizontal stress magnitudes are high, such that the rock strength is not sufficiently strong to withstand the stress concentration, rock failures will take place around the borehole. The fractures will propagate along the \(\sigma_{h}\) direction and eventually result in symmetrical V-shaped void spaces (Gough and Bell 1982; Zoback et al. 1985; Zheng et al. 1989; Haimson and Song 1995), as shown in Fig. 1.

Fig. 1
figure 1

Borehole breakout

Full size image

This phenomenon was reported by Cox (1970), who observed the elongation in the borehole diameter in Alberta wells using a four-armed dipmeter. Babcock (1978) confirmed this observation and named the phenomenon as ‘borehole breakout’. Since the 1960s, borehole scanning techniques have advanced significantly and been widely implemented in petroleum and mining industries (Zemanek et al. 1969; Nelson et al. 2005; Fowler and Weir 2007; Yaghoubi and Zeinali 2009; Chang et al. 2010; Molaghab et al. 2017). This has enabled more detailed and accurate interpretation of borehole conditions and breakout shapes compared with results obtained from dipmeters or callipers. To date, borehole breakout has been used as a reliable indicator of horizontal stress orientations in sub-vertical boreholes (Stock et al. 1985; Zoback et al. 2003; Lin et al. 2010; Ask et al. 2015; Malinverno et al. 2016).

As illustrated in Fig. 1, borehole breakout generally has two geometries, including depth (\(L\)) and angular span (\(\theta_{b}\)). Many researchers have suggested that both geometries are dependent on horizontal stress magnitudes (Zoback et al. 1985; Haimson and Herrick 1986; Barton et al. 1988; Haimson and Herrick 1989; Haimson et al. 1991; Haimson and Song 1993; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006; Lee et al. 2016; Sahara et al. 2017). In general, under the same \(\sigma_{h}\) and vertical principal stress (\(\sigma_{v}\)), the higher the horizontal stress ratio or \(\sigma_{H}\), the wider and deeper the breakout. Based on the experimental observations, some of these researchers also argued that there exists a unique relationship between the two geometries, regardless of the horizontal stress magnitudes (Haimson et al. 1991; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006; Sahara et al. 2017). This unique relationship states that both geometries increase, such that only one horizontal stress component can be estimated.

To carefully study this hypothesis, a series of breakout experiments has been performed on Gosford sandstone, and detailed studies on the mechanical properties of this rock can be found in Masoumi et al. (2016) and Roshan et al. (2017). In the experiments, the dependence of breakout geometries on stresses is studied. The analytical model developed by Barton et al. (1988) has been widely accepted and used as the basis of the contemporary models for stress estimation from \(\theta_{b}\) and uniaxial compressive strength (UCS) of rock. Therefore, the relationships between \(\theta_{b}\) and horizontal stress ratio are derived and studied according to this model. However, the formation of breakouts and their depth is rather complicated, since the propagation of the breakout involves inelastic deformation and time-dependent behaviour (Mastin 1984; Zoback et al. 1985; Zheng et al. 1989; Schoenball et al. 2014), and its stress dependency has only been studied based on experimental data.

As observed from the uniaxial compression and hollow cylinder tests conducted on pre-drilled rock specimens with various hole sizes (hole radii), it has been reported that the borehole size has significant influence on the breakout initiation stress (Haimson and Herrick 1989; Carter et al. 1991; Van den Hoek et al. 1994; Elkadi and Van Mier 2006; Dresen et al. 2010; Meier et al. 2013). Previous breakout studies mainly focused on the influence of horizontal stress magnitudes while not considering the hole size effect on breakout initiation. This paper thus investigates in detail the effect of hole sizes on breakout behaviours experimentally and analytically. By taking account of the hole size effect, a better understanding of the relationship between breakout geometries and horizontal stress magnitudes can be developed from a theoretical point of view, which can improve the current methodologies of stress estimation using borehole breakout.

2 Experimental Procedures

True triaxial tests were conducted on Gosford sandstone specimens, which were collected from a quarry located in Sydney Basin. According to the rock property testing, the uniaxial compressive strength and Young’s modulus of the specimen are 42.3 MPa and 7.5 GPa, respectively; and the cohesion and internal friction angle are 12.9 MPa and 35°.

To simulate the in situ stress conditions in Australia (\(\sigma_{H} > \sigma_{h} > \sigma_{v}\)), a customized apparatus was designed for this purpose as shown in Fig. 2a. The rock specimen (120 × 120 × 120 mm3) with pre-drilled hole was placed in the middle of the equipment, with the hole aligned in the y-direction. Biaxial stresses (\(\sigma_{h}\) and \(\sigma_{v}\)) were then applied by tightening the nuts shown in Fig. 2a, the stress magnitudes being monitored by the load cells connected between outer and inner plates, as shown in Fig. 2b.

Fig. 2
figure 2

UNSW variable confinement cell

Full size image

Once the desired stress levels were reached, the rock specimen was loaded by the tertiary stress from the MTS machine, see Fig. 3. To ensure the full development and stabilization of the breakout phenomenon, the specimen was held under the same stress condition for another 30 min (Haimson et al. 1991; Haimson and Kovacich 2003; Lee et al. 2016). Rock specimens with three hole sizes (8 mm, 11 mm and 15 mm) were tested under the same stress conditions to observe the influence of borehole size on borehole breakout geometries.

Fig. 3
figure 3

True triaxial test

Full size image

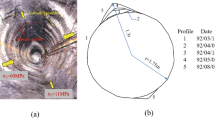
The conventional technique to measure the cross-sectional geometry is with infilled epoxy materials along the length of the borehole (Haimson and Song 1998; Haimson and Lee 2004; Sheets and Haimson 2004; Katsman et al. 2009; Lee et al. 2016). This may, however, not be very accurate considering that the hole size is only 11 mm, where a 1% variation in breakout depth is 0.11 mm and both angular span and breakout depth show some variation along the borehole length. It is important to take account of these variations to obtain precise measurements for later studies. Therefore, the optical scanning technique was implemented to measure breakout geometries with higher accuracy, as displayed in Fig. 4b. The rock specimen was first cut in half along \(\sigma_{H}\) such that the breakout profile would not be damaged, but well preserved. The inner faces were then sprayed to cover shiny particles to ensure the scanning quality. Afterwards, scanning was undertaken to capture the full breakout profile from top to bottom, see Fig. 4a. Subsequently, breakout geometries were obtained by determining the average values of the scanning data along the borehole axis.

Fig. 4
figure 4

Optical scanning

Full size image

3 Results and Discussion

To investigate breakout geometries and the influence of borehole sizes, three sets of experiments with different hole sizes were carried out under various \(\sigma_{H}\) stress conditions, with constant \(\sigma_{h}\) = 10 MPa and \(\sigma_{v}\) = 5 MPa applied. Results showed a good alignment between breakout depth and \(\sigma_{h}\) direction. This confirmed that breakout is indeed a reliable tool for stress orientation determination. Figure 5 presents a clear V-shaped borehole breakout obtained from the experiments, where \(\sigma_{H}\) = 60 MPa and the hole size is 11 mm.

Fig. 5
figure 5

Experimental borehole breakout

Full size image

3.1 Breakout Geometries and Horizontal Stress Magnitudes

Figures 6 and 7 show strong stress dependencies on breakout geometries. For the same hole size, both normalised breakout depth (\(L/R\)) and angular span increase with the increasing horizontal stress ratio, in particular, they both increase with \(\sigma_{H}\), as \(\sigma_{h}\) and \(\sigma_{v}\) were all kept constant during the experiments. Clear linear trends can also be observed based on the figures, in which both parameters increase at relatively steady rates, except for 15 mm hole size, where the gradients for breakout geometries are sharper. Experimental results obtained from this study agree with previous experimental studies conducted by earlier researchers (Haimson and Herrick 1986; Haimson and Herrick 1989; Haimson and Song 1993; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006; Lee et al. 2016), suggesting that there are correlations between breakout geometries and horizontal stress magnitudes.

Fig. 6
figure 6

σH/σh vs θb

Full size image
Fig. 7
figure 7

σH/σh vs normalised depth (L/R)

Full size image

Figure 8 displays the relationships between the two breakout geometries. According to the experimental results, it is noticed that the normalised breakout depth is strongly dependent on the angular span (Gough and Bell 1982; Zheng et al. 1989), the wider breakout always being deeper for the same hole size. This trend can be bounded in a narrow increasing region as shown in Fig. 8. Haimson et al. (1991) observed similar results in their experiments, in which they argued that, due to the dependency between breakout geometries, they are redundant factors for horizontal stress estimation. Therefore, deriving two horizontal principal stresses from two redundant breakout geometries is not viable.

Fig. 8
figure 8

θb vs L/R

Full size image

3.2 Breakout Geometries and Hole Sizes

Previous experiments focus heavily on the horizontal stress magnitudes, the hole size used being quite consistent, with radii in the 10–11 mm range. In this paper, three different hole sizes are studied.

Figures 6 and 7 illustrate that, under the same stress conditions, a larger hole size actually results in a wider angular span and deeper normalised breakout depth. For each hole size, the gradients of the breakout geometries and increasing horizontal stress ratio show similar relationships as observed in previous studies without considering the hole size. The indication here is that hole size is crucial for borehole breakout geometries and has to be explicitly analysed.

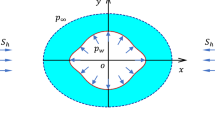
According to the Kirsch solution, the stress concentration around a circular cavity can be calculated from the in situ stress field, given elastic conditions (Jaeger et al. 2009):

$$\sigma_{r} = \frac{1}{2}(S_{H} + S_{h} )\left( {1 - \frac{{R^{2} }}{{r^{2} }}} \right) + \frac{1}{2}\left( {S_{H} - S_{h} } \right)\left( {1 - 4\frac{{R^{2} }}{{r^{2} }} + 3\frac{{R^{4} }}{{r^{4} }}} \right)\cos 2\theta + \Delta P\frac{{R^{2} }}{{r^{2} }}$$
(1)
$$\sigma_{\theta } = \frac{1}{2}(S_{H} + S_{h} )\left( {1 + \frac{{R^{2} }}{{r^{2} }}} \right) - \frac{1}{2}\left( {S_{H} - S_{h} } \right)\left( {1 + 3\frac{{R^{4} }}{{r^{4} }}} \right)\cos 2\theta - \Delta P\frac{{R^{2} }}{{r^{2} }}$$
(2)
$$\tau_{r\theta } = - \frac{1}{2}(S_{H} + S_{h} )\left( {1 + 2\frac{{R^{2} }}{{r^{2} }} - 3\frac{{R^{4} }}{{r^{4} }}} \right)\sin 2\theta$$
(3)

where \(\sigma_{r}\) = radial stress around the circular hole, \(\sigma_{\theta }\) = tangential stress around the circular hole, \(\tau_{r\theta }\) = shear stress around the circular hole, \(S_{H}\) and \(S_{h}\) = maximum and minimum effective horizontal principal stresses,\(R\) = hole size, \(\frac{R}{r}\) = 1/normalised breakout depth, \(2\theta\) = 180 − breakout angular span, and \(\Delta P\) = the difference between fluid pressure and the pore pressure.

The Kirsch solution uses the normalised breakout depth and angular span (\(\theta_{b}\)) as inputs, which mean that the stress concentrations should be identical at a certain location around the borehole regardless of the hole size, and, under the same principal stress conditions, breakout geometries should be the same for any hole sizes. However, the above experimental results show a substantial discrepancy between the breakout geometries for different hole sizes.

Based on the Kirsch solution, Barton et al. (1988) proposed a model which introduced a relationship between horizontal stress magnitudes and angular span. It is the basis of the current stress polygon technique using borehole breakout and has been implemented in numerous field conditions (Barton et al. 1988; Zoback and Healy 1992; Brudy et al. 1997; Lund and Zoback 1999; Zoback et al. 2003; Valley and Evans 2015). The model assumes plane strain, where the borehole wall fracture is due to the horizontal stress concentration. For the sake of simplification, \(\Delta P\) is assumed to be zero. Along the borehole, the stress conditions can be calculated as:

$$\sigma_{r} = 0$$
(4)
$$\sigma_{\theta } = S_{H} + S_{h} - 2\left( {S_{H} - S_{h} } \right)\cos 2\theta$$
(5)
$$\tau_{r\theta } = 0.$$
(6)

The above equations show that, along the borehole, the radial stress and shear stress can be neglected. Therefore, it may be assumed that the tangential stress, \(\sigma_{\theta }\) at the maximum borehole initiation angle (the angular span) should be equal to the UCS (Barton et al. 1988):

$$UCS = \sigma_{\theta } = S_{H} + S_{h} - 2\left( {S_{H} - S_{h} } \right)\cos 2\theta$$
(7)

The breakout angular span hence can be estimated as:

$$2\theta_{b} = 180^\circ - \cos^{ - 1} \left( {\frac{{S_{H} + S_{h} - UCS}}{{2\left( {S_{H} - S_{h} } \right)}}} \right)$$
(8)

in which the angular span, \(2\theta_{b}\) = 180 − 2θ and \(S_{H}\) and \(S_{h}\) are assumed to be equal to \(\sigma_{H}\) and \(\sigma_{h}\).

$$2\theta_{b} = 180^\circ - \cos^{ - 1} \left( {\frac{{\sigma_{H} + \sigma_{h} - UCS}}{{2\left( {\sigma_{H} - \sigma_{h} } \right)}}} \right)$$
(9)

Based on the horizontal stress magnitudes and UCS, angular spans from experiments can be estimated. Given that the analytical solution does not account of the influence of hole size, the angular span it predicts should be the same for any hole size for the same stress conditions. Figure 9 shows the predictions against the experimental results, and it can be seen that the prediction has a less steep gradient compared with experimental results for 15 mm hole size, although they all exhibit an increasing trend with increasing horizontal stress ratio. In addition, a considerable discrepancy between the prediction and the closest set of experimental results can be seen, which again indicates that hole size should be used as a parameter while investigating the breakout geometries under experimental scenarios.

Fig. 9
figure 9

Prediction on experimental results

Full size image

3.3 Hole Size Effect

As observed and demonstrated by many researchers from uniaxial tests on pre-drilled prisms and hollow cylinder tests (Lajtai 1972; Ingraffea 1979; Mastin 1984; Ewy and Cook 1989; Haimson and Herrick 1989; Carter et al. 1991; Elkadi and Van Mier 2006; Dresen et al. 2010; Meier et al. 2013), the hole size has substantial influence on fracture initiation under laboratory conditions. The fracture initiation is detected by strain gauges or acoustic emission and assumed to first occur at the borehole wall along \(\sigma_{h}\), namely, sidewall (\(\theta\) = 90˚).

If the hole size is small, the required stress concentration for fracture initiation at the sidewall was observed to be as large as three times the UCS, in which stress concentration is calculated from Eq. (2) and simplified as \(\sigma_{\theta } = 3\sigma_{H} - \sigma_{h}\). As the hole size gradually increases, the fracture initiation stress decreases dramatically and eventually equals the UCS. Walton et al. (2015) and LeRiche et al. (2017) named this intensification of borehole wall as ‘borehole wall strength (BWS)’. In this paper, as the experiment was under conditions similar to the uniaxial tests, the only difference being the true triaxial loading on rock specimens. This is perhaps the primary reason for discrepancies between the analytical model and experimental observations.

The stress averaging concept was initially proposed by Lajtai (1972) for the explanation of fracture initiation along the maximum horizontal principal stress direction along the borehole (for tensile fracture). The author suggested that even the brittle material can have ‘ductile behaviour’ under high stress gradient. The stress will redistribute and be averaged over a certain distance, \(2d\) (Ortiz 1988). This distance is assumed to be a material property and can be determined based on the data fitting. As the rock around the borehole is subjected to high stress gradient, Lajtai (1972) assumed this gradient to be linear and the average stress is equal to:

$$\sigma_{d} = \sigma_{m} + d \times \left( {\frac{\partial \sigma }{\partial R}} \right)_{R = r}$$
(10)

where \(\sigma_{d}\) = the average stress over the distance, \(\sigma_{m}\) = the maximum tangential stress at the borehole wall, \(\left( {\frac{\partial \tau }{{\partial {\text{R}}}}} \right)_{R = r}\) = the stress gradient at the borehole wall, assumed to be linear over the distance of \(2d\). If \(\sigma_{d}\) = the tensile strength of rock (\(T\)), the fracture will initiate at the point:

$$T = \sigma_{m} + d \times \left( {\frac{\partial \sigma }{\partial R}} \right)_{R = r}.$$
(11)

Based on the Kirsch solution, Eq. (11) can be derived in terms of the horizontal stresses applied:

$$T = \left( {\frac{5d}{R} - 1} \right)\sigma_{H} + \left( {3 - \frac{7d}{R}} \right)\sigma_{h}.$$
(12)

For the uniaxial compressive condition, where \(\sigma_{h}\) = 0, the equation can be rearranged as:

$$P_{T} = \sigma_{H} = \frac{T}{{\left( {\frac{5d}{R} - 1} \right)}}$$
(13)

where \(P_{T}\) is the required uniaxial compressive stress for fracture initiation along the direction of applied stress (\(\theta\) = 0°). Nesetova and Lajtai (1973) implemented the same concept to explain the stress initiation at the borehole sidewall using the Coulomb failure criterion as the stresses at the location are compressive stresses. The same approach was used as discussed above and the equation for the compressive condition derived as:

$$P_{S} = \frac{{2 \times \tau_{s} }}{{3 - 10\frac{d}{R}}},$$
(14)

where \(P_{S}\) = the applied uniaxial stress required for fracture initiation at the sidewall. As the stress concentration around the borehole clearly does not drop linearly, Carter (1992) later considered the true stress gradient over the distance by integrating the Kirsch solution into the gradient calculation and simplified the failure criterion to the uniaxial compressive condition:

$$P_{S} = \frac{d \times UCS}{{\left( {R + d} \right)\left( {1 - \frac{{R^{2} }}{{2\left( {R + d} \right)^{2} }} - \frac{{R^{4} }}{{2\left( {R + d} \right)^{4} }}} \right)}}.$$
(15)

Due to the stress averaging, the stress concentration that rock around the hole is subjected to is considerably lower than predicted by Kirsch solution. This in turn requires more stress to be applied to the rock specimen to induce fracture initiation. The stress concentration around the borehole can be represented by the Kirsch solution and its input is the normalised depth (\(L/R\)). For the stress averaging concept, the stress concentration is averaged in the distance (\(d/R\)). Since \(d\) does not change and \(R\) varies between experiments, a larger \(R\) will lead to a shorter normalised stress averaging distance (\(d/R\)). Consequently, the higher stress concentrates within a shorter averaging distance for a larger hole size compared with a smaller hole size, which eventually results in wider and deeper breakouts. To be more specific, \(d\) is assumed to be 2 mm for the explanation. For the breakout experiment, where \(\sigma_{H}\) = 40 MPa, \(\sigma_{h}\)=10 MPa and \(\sigma_{v}\) = 5 MPa, the tangential stress and the stress averaging values can be calculated based on Eq. (2) and plotted in Fig. 10. From the figure, it is clear that a larger hole size has a higher averaging tangential stress. If the rock strength is the same, the higher tangential stress undoubtedly will produce more fractures, thus larger breakouts.

Fig. 10
figure 10

σθ along the σh direction and stress averaging under σH = 40 MPa, σh = 10 MPa and σv = 5 MPa

Full size image

Bažant et al. (1993) explained this borehole wall strengthening using the principle of conservation of energy, in which the potential energy loss due to breakout formation from a circular borehole is equal to the energy dissipation of rock fracturing which forms breakout. In their study, Bažant et al. (1993) assumed that borehole breakout is formed by parallel and equidistant axial splitting of cracks which undergo the buckling process, see Fig. 11. The potential energy loss is evaluated by Eschelby’s theorem (Eshelby 1957), in which the potential energy can be calculated as the difference between the energies required to generate an elliptical cavity and a circular hole in a vacuum that is subjected to a biaxial stress field; the energy dissipation is calculated by the fracture energy release from vertical cracks within the breakout region.

Fig. 11
figure 11

Illustration of Bažant et al. (1993)

Full size image
$$BWS = \sigma_{ef} \approx C_{1} R^{{ - \frac{2}{5}}} + C_{0}$$
(16)

where \(C_{1} = \left( {\frac{{\pi^{2} 5^{1/2} }}{{48k^{2} }}E'^{3} G_{f}^{2} } \right)^{1/5}\) and \(C_{0} = 3\left( {\frac{{GE'G_{f} }}{5\lambda }} \right)^{{\frac{1}{3}}}\). \(E^{\prime} = E/\left( {1 - v^{2} } \right)\), \(E\) = Young’s modulus and \(\nu\) = Poisson’s ratio, \(G_{f} = K_{IC}^{2} /E^{\prime}\), in which \(K_{IC}\) = fracture toughness, \(k\) = empirical positive constant that is less than 1, and \(\lambda\) = empirical length (material property). According to the equation, it is also clear that as the hole size increases, BWS decreases. Papanastasiou and Thiercelin (2010) proposed a calibration process for Bažant et al. (1993) to determine the parameters required under experimental data.

The aforementioned methods require additional experimental work to determine the BWS for each rock type, which is sometimes difficult to be implemented due to the lack of the experimental data. As the conventional stress estimation from borehole breakout experiences difficulties in obtaining the absolute magnitudes, a machine learning algorithm has been developed by Lin et al. (2018). The model is trained based on the experimental data and validated against field data which are all from literature. The parameters used in the training process include breakout depth, angular span and BWS. Since the previous data are from different rock types and do not contain the information to use the above techniques for BWS, it is not feasible to use either technique for the general determination of BWS. Therefore, Lin et al. (2018) collected existing uniaxial tests data (Haimson and Herrick 1989; Carter 1992) on pre-drilled blocks, see Fig. 12, and derived an empirical relationship between BWS and borehole size:

Fig. 12
figure 12

BWS/UCS vs borehole radius, after Lin et al. (2018)

Full size image
$$BWS = \left( {0.0005R^{2} - 0.0638R + 2.7885} \right) \times UCS$$
(17)

The equation is only applicable for the determination for the experimental cases and primarily for the model training, where the borehole radius is below 15 mm. Due to the similarity of rock properties between our experiment and the collected data, this empirical relationship was used directly for the BWS calculation of Gosford sandstone. The estimated BWS of radii 8 mm, 11 mm and 15 mm are 97.72 MPa, 90.83 MPa and 82.23 MPa, respectively. Equation (9) is again used for the prediction of angular span with the newly estimated BWS, and results are shown in Fig. 13.

Fig. 13
figure 13

Experimental results with predictions including borehole size effect

Full size image

Based on the results, it can be observed that predictions are more reasonable than before. In particular, for a 15 mm borehole size, the prediction is very accurate compared to the experimental results. Barton et al.’s (1988) model overestimated the angular spans for both 8 mm and 11 mm borehole radii, with the 8 mm hole size having the largest discrepancy between predicted and experimental results. This indicates that the larger the hole size, the better the prediction that Barton et al.’s (1988) model would produce. However, the discrepancies may also likely be due to the lack of data for smaller hole sizes. As displayed in Fig. 12, the majority of the data have hole sizes over 10 mm. In this case, the empirical relationship might not yield a very accurate estimation for BWS for hole sizes below 10 mm. It is suggested to collect more BWS data for improvement of the empirical relationship.

3.4 Further Investigations on Breakout Geometries

3.4.1 Breakout Angular Span

Angular span is the most crucial parameter for in situ stress estimation as it is reported to form quickly and not to widen (Mastin 1984; Zoback et al. 1985; Zheng et al. 1989; Schoenball et al. 2014). However, many studies have argued that the breakout angular span increases with \(\sigma_{H}\) for constant \(\sigma_{h}\) and \(\sigma_{v}\) (Haimson and Herrick 1986; Haimson and Herrick 1989; Haimson et al. 1991; Haimson and Song 1993; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006; Lee et al. 2016), and therefore it is considered to be worthwhile to re-investigate the trend of angular span with respect to horizontal stresses.

The model proposed by Barton et al. (1988) is analysed here for the relationship between angular span and horizontal stress ratio in a vertical borehole; for the same rock property, to examine whether the angular span increases with increasing horizontal stress ratio, \(\sigma_{h}\) should be kept as a constant rather than a parameter. Thus, \(\sigma_{H} = a\sigma_{h}\), where a is the horizontal stress ratio, and Eq. (9) can be rearranged as:

$$f\left( a \right) = 2\theta_{b} = 180^\circ - \cos^{ - 1} \left( {\frac{{a\sigma_{h} + \sigma_{h} - UCS}}{{2\left( {a\sigma_{h} - \sigma_{h} } \right)}}} \right).$$
(18)

The first-order derivative of the function with respect to a can indicate the angular span change with respect to the horizontal stress ratio:

$$\frac{df\left( a \right)}{da} = \frac{{UCS - 2\sigma_{h} }}{{2\sigma_{h} \left( {a - 1} \right)^{2} \sqrt {1 - \frac{{(a\sigma_{h} - UCS + \sigma_{h} )^{2} }}{{4\left( {a\sigma_{h} - \sigma_{h} } \right)^{2} }}} }}$$
(19)

Since the horizontal stress ratio, (a) is always greater than 1, \(\left( {a - 1} \right)^{2}\) and \(\sqrt {1 - \frac{{(a\sigma_{h} - UCS + \sigma_{h} )^{2} }}{{4\left( {a\sigma_{h} - \sigma_{h} } \right)^{2} }}}\) should be greater than 0, which means the denominator of Eq. (15) is positive. Thus, the term that defines the relationship between angular span and horizontal stress ratio is the numerator, i.e., \(UCS - 2\sigma_{h}\).

If \(UCS > 2\sigma_{h}\), then the function has a positive first-order derivative, which means the breakout width increases with the horizontal stress ratio and \(\sigma_{H}\). This agrees with the prevailing argument.

If \(UCS = 2\sigma_{h}\), the derivative is zero, which means there is an extremity occurring, which can also be considered as the transitional point.

If \(UCS < 2\sigma_{h}\), a negative derivative is obtained. Given the increase in horizontal stress ratio, the breakout angular span can be narrower at constant \(\sigma_{h}\) and \(\sigma_{v}\). This indicates that there may exist an ‘unconventional trend’ between the angular span and the increasing horizontal stress ratio, which has not been observed in experimental conditions (Haimson et al. 1991; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006; Sahara et al. 2017). Figure 14 shows the previous experimental observations which satisfy this stress–strength condition and constant \(\sigma_{h}\) and \(\sigma_{v}\).

Fig. 14
figure 14

Previous experimental data which UCS < 2σh

Full size image

Interestingly, a growth in angular span with increasing horizontal stress ratio is still observed regardless of the UCS of specimens, which disagrees with the explanation above. Nevertheless, this can be explained by the hole size effect discussed in the previous section, in which the borehole wall strength is significantly amplified for smaller hole size. To take account of the hole size effect, data reported by Lee and Haimson (2006) are carefully analysed. Based on Eq. (17), the BWS of the rock specimen is converted to 75.28 MPa. Thereby, according to Eq. (5), \(\sigma_{\theta }\) along the hole at different angles can be estimated and depicted together with its UCS and BWS in Fig. 15. If \(\sigma_{\theta }\) is greater than the rock strength, breakout should occur at that angle, i.e., the region of the stress curve that is above the UCS or BWS line.

Fig. 15
figure 15

Tangential stress along the borehole, where σh = 20 MPa

Full size image

From Fig. 15, it can be seen that \(\sigma_{\theta }\) is higher for a higher horizontal stress ratio until the angular span is at 120°. After this angle, a reverse trend can be observed such that the increasing horizontal stress ratio will result in a lower \(\sigma_{\theta }\) thus a narrower angular span. At 120°, \(\sigma_{\theta }\) can be expressed from Eq. (5):

$$\sigma_{\theta } = S_{H} + S_{h} - 2\left( {S_{H} - S_{h} } \right)\cos 60^\circ = 2S_{h}$$
(20)

Assuming \(S_{h}\) is constant, \(\sigma_{\theta }\) at 120° should always be the same regardless of \(\sigma_{H}\). This also indicates that if the rock strength is equal to \(2S_{h}\), the breakout angular span produced should be 120°, see Figs. 15 and 16.

Fig. 16
figure 16

Tangential stresses at breakout = 120˚

Full size image

Although the experimental conditions satisfied the unconventional trend requirement, \(UCS < 2\sigma_{h}\), the truth is that the actual hole strength BWS is three times over \(\sigma_{h}\) because of the small hole size tested. As \(BWS > 2\sigma_{h}\), this is still under the conventional scenario in which the higher stress ratio yields a wider angular span, as shown in Fig. 14. In this case, Eq. (9) should be re-expressed in terms of BWS:

$$2\theta_{b} = 180^\circ - \cos^{ - 1} \left( {\frac{{a\sigma_{h} + \sigma_{h} - BWS}}{{2\left( {a\sigma_{h} - \sigma_{h} } \right)}}} \right)$$
(21)

It is also noticed that there is one set of data, \(\sigma_{h}\) = 40 MPa in Lee and Haimson (2006), where \(BWS < 2\sigma_{h}\), but the unconventional trend still is not observed in that data. As discussed earlier, this might be due to the limitation of the empirical relationship, which may underestimate the BWS value for smaller hole sizes. Another possible explanation is the influence of the vertical stress confinement. In their experiment, the strike-slip faulting mechanism (\(\sigma_{H} > \sigma_{v} > \sigma_{h}\)) was considered, to keep \(\sigma_{v}\) as the intermediate principal stress, \(\sigma_{v}\) had to increase with \(\sigma_{h}\) in different tests, which can apply more confinement to the rock around the hole (Song 1998; Chang et al. 2010). It is hence suggested that under experimental conditions for breakout analysis, the influence of BWS and \(\sigma_{v}\) should be considered.

3.4.2 Breakout Depth

Unlike the angular span, breakout depth is rather complicated and difficult to predict by an analytical solution. This is mainly because of its inelastic deformation and time-dependent propagation behaviour observed in the field and numerically (Mastin 1984; Barton et al. 1988; Kessels 1989; Schoenball et al. 2014). Another reason is that the stress condition is not in fact simple in the rock along the borehole wall.

Gough and Bell (1982) attempted to use angular span to compute the breakout depth based on the Mohr–Coulomb criterion. They assumed that breakout commences at the wall and forms into a V-shape by the intersection of two major shear fracture planes at the breakout tip, as shown in Fig. 17. However, since the breakout formation and propagation involve both shear and tensile fractures (Tronvoll and Fjaer 1994; Cuss et al. 2003; Lee et al. 2016), a simple shear failure model does not solve the problem.

Fig. 17
figure 17

Shear fractures from Gough and Bell (1982)

Full size image

Zoback et al. (1985) combined the Kirsch solution and Mohr–Coulomb criterion and postulated a model in which the breakout depth can be calculated with given horizontal stress magnitudes and Mohr–Coulomb parameters. For the same reason as Gough and Bell (1982) and the breakout propagation beyond the elastic condition, the model significantly underestimates the breakout depth. Haimson and Herrick (1986) revealed that although the model underestimates the breakout depth compared with experimental results, the prediction of breakout depth follows a similar trend as what was observed in experiments.

Current analytical solutions cannot effectively predict the relationship between breakout depth and horizontal stress ratio, and it is therefore only possible to determine this relationship from the experimental observations. The experimental results presented in this paper as well as those from previous studies (Haimson and Herrick 1986; Haimson and Herrick 1989; Haimson and Song 1993; Herrick and Haimson 1994; Haimson and Lee 2004; Lee and Haimson 2006) all show that breakout depth increases with the increasing horizontal stress ratio and \(\sigma_{H}\). This indicates that breakout depth should increase with the horizontal principal stress ratio.

3.4.3 The Relationship Between Breakout Geometries

As discussed earlier, some researchers suggest that both breakout geometries are dependent on each other and redundant, and there is an exclusive relationship between the two geometries that is insensitive to the stress magnitudes. In this case, the estimation of two horizontal stress magnitudes using breakout geometries is not viable. Figure 18 shows the relationship between the breakout depth and angular span under various stress conditions and rock types from previous studies. It can be seen that there is an increasing trend between the two geometries although the gradients are very spread out. Perhaps the relationship between the breakout geometries is dependent on the material.

Fig. 18
figure 18

Previous experimental data on breakout geometries after Lin et al. (2018)

Full size image

Figure 19 displays the experimental results from Haimson and Lee (2004). From the illustration, it is clear that the gradients of each set of experiments are different and cannot be constrained in a narrow band although the trends are increasing. A series of very similar breakout depth values (refer to the red dot line in the figure) also have significantly different angular span values. This indicates the relationship between the breakout depth and angular span may not be unique. As the laboratory investigation was performed on the same rock properties, the only factors that changed from test to test are the horizontal stress magnitudes. The change in gradients could only be the results of various horizontal stress magnitudes applied. The results shown here imply that breakout geometries may not be redundant factors for stress estimation, as their relationship is heavily influenced by the horizontal stress magnitudes.

Fig. 19
figure 19

Experimental results on breakout geometries from Haimson and Lee (2004)

Full size image

As discussed in Sect. 3.4.1, the breakout angular span increases with the increasing horizontal principal stress ratio unless the applied minimum horizontal principal stress is over half of the BWS value. This is very difficult to be observed in the experimental conditions due to the hole size effect. On the other hand, the breakout depth increases with the increasing horizontal stress ratio. In fact, this is a rather special case but also shows the non-redundancy between the two breakout geometries and the influence of horizontal stress magnitudes (ratio) on this relationship.

4 Conclusions

In this paper, a set of experimental data on breakout geometries is presented. Results confirm that both angular span and depth are dependent on horizontal stress magnitudes and ratio, which suggest that they can be used for horizontal stress estimation. Under the same stress condition, the comparison between breakout geometries with different hole sizes reveals that hole size has a substantial influence on breakout geometries. The larger hole size tends to yield deeper and wider breakouts, whose effect is not considered by the Kirsch solution nor in Barton et al. (1988).

The primary reason for this discrepancy is the hole size effect, which has been discussed by several researchers. However, the models proposed by Carter (1992) and Bažant et al. (1993) all include empirical parameters which require additional experiments and assumptions. To incorporate this effect in the experimental investigation, this paper used an empirical relationship between hole size and borehole wall strength that was proposed by Lin et al. (2018). After taking account of the hole size effect, the predictions using Barton et al. (1988) are much closer and reasonable to the experimental results. In general, all existing experimental investigations of hole size effect modify the specimen size with the hole size, i.e., the larger the hole size, the larger the specimen. This is not an ideal situation because the scale effect of rock strength also exists due to the change in specimen dimensions, which the previous experimental results do not take account of when studying the hole size effect. The current study has proposed a series of uniaxial compression tests on block specimens with pre-drilled holes while keeping the specimen dimensions the same. This enables the elimination of scale effect on specimen dimension changes, and a focus only on the hole size effect.

Based on the analysis on the previous experimental studies, it was found that the relationship between the breakout depth and angular span is not unique, although they appear to increase with each other. In fact, the relationship between the two geometries is considerably sensitive to the horizontal stress magnitudes. The analysis performed in this study revealed that the breakout angular span may be narrower if the minimum horizontal stress value is lower than half of the BWS value. However, this is difficult to observe in the experimental conditions due to the hole size effect. Nevertheless, this suggests a very special case where the higher horizontal stress ratio could lead to a narrower but deeper breakout under certain stress–strength conditions. Both arguments indicate that the relationship between two breakout geometries is not unique, but is influenced by the horizontal stress magnitudes, leading to a tentative conclusion that they are not redundant factors for stress estimation.