Prediction of Near-Field Wave Attenuation Due to a Spherical Blast Source

Abstract

Empirical and theoretical far-field attenuation relationships, which do not capture the near-field response, are most often used to predict the peak amplitude of blast wave. Jiang et al. (Vibration due to a buried explosive source. PhD Thesis, Curtin University, Western Australian School of Mines, 1993) present rigorous wave equations that simulates the near-field attenuation to a spherical blast source in damped and undamped media. However, the effect of loading frequency and velocity of the media have not yet been investigated. We perform a suite of axisymmetric, dynamic finite difference analyses to simulate the propagation of stress waves induced by spherical blast source and to quantify the near-field attenuation. A broad range of loading frequencies, wave velocities, and damping ratios are used in the simulations. The near-field effect is revealed to be proportional to the rise time of the impulse load and wave velocity. We propose an empirical additive function to the theoretical far-field attenuation curve to predict the near-field range and attenuation. The proposed curve is validated against measurements recorded in a test blast.

1 Introduction

When an explosive detonates, shock waves are generated and propagated from the source. The amplitude of the stress waves quickly decays with the distance from the source. Blast-induced vibration may potentially damage adjacent structures, lifelines, and slopes. There is a clear need to accurately estimate the level of vibration induced by blasting.

A large body of the literature focuses on empirically estimating the blast load. Empirical equations to predict the peak explosion pressure as functions of detonation velocity and explosive density have been proposed by Hino (1956), Konya and Walter (1991), Liu and Tidman (1995), and Siskind (2005). Empirical impulse pressure time histories have also been proposed by Blake Jr (1952), Duvall (1953), Starfield and Pugliese (1968), Jiang (1993), Blair (2003), Saharan and Mitri (2008), and Blair (2015). The Jones–Wilkins–Lee equation (Lee et al. 1968) was used to estimate the dynamic load under detonation in reactive hydro simulations to simulate the thermodynamics of the system.

Numerical analyses have been frequently performed to simulate the blast. The finite element analysis program AUTODYN (2009) has been used to calculate the temporal variation of the detonation pressure, as documented in Ma et al. (1998), Chen et al. (2000), Hao et al. (2002), and Deng et al. (2014). Numerical studies to estimate the size of the fractured zone created by the denotation pressure have also been performed (Cho and Kaneko 2004; Ma and An 2008; Ning et al. 2011; Yilmaz and Unlu 2013). Trivino et al. (2009) perform a combined finite–discrete element method to simulate the single-hole blast-induced damage. This zone can be used to simulate the damage area for a single borehole. However, a study that derives a representative attenuation curve based on numerical simulation results has not yet been performed.

Closed-form equations to calculate the waveform due to an impulse spherical loading were derived by Blake Jr (1952) and Duvall (1953). Jiang et al. (1995) presents rigorous wave equations in both undamped and damped media for a spherical source. For a given impulse load, the near-field region was defined as R/a < 5, where R is the distance from the source and a is the radius of the spherical source. Because a single empirical load was used, the influence of the frequency of the impulse load on the attenuation of the waves was not investigated. Studies have shown that a spherical source, where only compressional waves are generated, is not realistic. A cylindrical source, where both compressional and shear waves are induced, has been reported to be more representative, especially in blasts with high length-to-borehole diameter ratios. Numerous theoretical solutions were derived, which include the studies of Heelan (1953), Tubman et al. (1984), Meredith et al. (1993), Blair (2007), and Blair (2010).

Numerical simulation or an analytical wave equation provides valuable insights into the wave attenuation characteristics, but is not routinely used in practice because of difficulties in their application. In practice, an empirical attenuation curve, which relates peak particle velocity (PPV) with scaled distance (function of separation distance and charge weight), is most often used to predict the amplitude of the vibration (Dowding 1984). The measurements recorded at the far-field surface are used to fit the attenuation curve. A theoretical far-field attenuation curve for a sinusoidal wave has also been derived and used in practice (e.g., Nelson and Saurenman (1983)). Kim and Lee (2000) reported, based on surface measurements, that the theoretical far-field curve can reliably predict the far-field attenuation of blast waves. At near-field, propagation is dominated by a quasi-static or reactive vibration with no resultant transfer of energy (Meyer 1964). The circulating pressure field propagates around the source rather than away from it, and therefore, the attenuation becomes greater than at far-field. The theoretical far-field equation, however, cannot capture this near-field attenuation.

In this study, we perform a series of axisymmetric, dynamic finite difference analyses to model the propagation of stress waves induced by spherical blast source and to derive the near-field attenuation curve. The numerical model is verified against two closed-form solutions. Based on numerical simulations, we propose predictive equations that are additive to a widely used theoretical far-field equation due to spherical source to account for the near-field effect. Because the near-field attenuation is accurately simulated, the newly developed attenuation curve accurately predicts the attenuation from source-to-site. We validate the proposed source-to-site attenuation curve against recordings made in a test blast. A step-by-step flowchart on how to produce a site-specific source-to-site attenuation curve from surface measurements is also presented.

It should be noted that this study is limited to the wave attenuation due to a spherical source, instead of a cylindrical source which was reported to be more realistic. It is because the response due to a cylindrical charge is dependent on numerous parameters including the depth of blast, orientation of the borehole, and length-to-borehole diameter ratios. Therefore, a representative attenuation curve for cylindrical source would be quite complicated in form. To produce simple predictive equations that can be routinely used in practice, we assumed a spherical wave attenuation. However, a comprehensive parametric study using cylindrical source is warranted as a future research.

2 Theoretical and Empirical Attenuation Curves

The amplitude of the stress waves induced by blasting decreases with distance from the source. The vibrational decay is produced by two phenomena—geometrical spreading and material damping (Dowding 1996). The geometrical spreading, also called radiation damping, is caused by the expansion of the surface over which the vibration energy is transmitted. The following theoretical equation for geometrical damping can be used to calculate the decay of the peak amplitude with distance:

$$A_{R} = A_{r} \left( {\frac{r}{R}} \right)^{s}$$

(1)

where A _r is the peak amplitude at a distance r from the source, A _R is the peak amplitude at a distance R from the source, and s is the geometric damping coefficient. Table 1 summarizes values of s for various source and wave types. For spherical wave propagation from an underground source, s = 1. The material damping is caused by the nonlinear hysteretic behavior of the geologic media. The following equation calculates the attenuation of a harmonic vibration due to material damping:

$$A_{R} = A_{r} e^{{ - \frac{{2\pi f_{\text{p}} \xi }}{c}(R - r)}}$$

(2)

where e is the exponential number, c is the wave velocity of the media, f _p is the predominant frequency of blast wave, and ξ is the small strain damping ratio. The theoretical attenuation equation that accounts for both geometrical spreading and material damping can be obtained as the product of geometrical and material damping (Nelson and Saurenman 1983):

$$A_{R} = A_{r} \left( {\frac{r}{R}} \right)^{s} \cdot e^{{ - \frac{{2\pi f_{\text{p}} \xi }}{c}(R - r)}}$$

(3)

In practice, a simpler empirical formula is widely used to predict the surface vibration at far-field (Wiss 1981):

$${\text{PPV}} = K\left( {\frac{R}{{W^{b} }}} \right)^{ - n}$$

(4)

where K and n are empirical parameters, W is the charge weight per delay, and R/W ^b is the scaled distance. Both the square root (b = 2) and cubic root (b = 3) scaling laws are used. In this study, we use the square root scaling law, and therefore, the scaled distance is defined as $R/\sqrt W$.

Table 1 Geometric spreading coefficient (Kim and Lee 2000)

3 Theoretical Wave Attenuation Equation Due to Spherical Source

Various mathematical descriptions of spherically diverging elastic waves instigated by an impulse pressure in spherical source were proposed. Blake Jr (1952) derived closed-form solutions for wave attenuation in elastic full-space subjected to the following power-exponential law pressure function

$$P(t) = P_{0} \cdot e^{ - \beta t}$$

(5)

where P is the pressure, P ₀ is the constant pressure, and β is the decay constant of the pressure pulse. The function, shown in Fig. 1, reaches the peak pressure instantly with no finite rise time. The closed-form equation for the velocity time series at far-field (R ≫ a) is given by:

$$V(R,\tau ) = \frac{{P_{0} a}}{\rho cR}\sqrt {2 - 2\upsilon } \cdot \exp \left( { - \tau \cdot \frac{c}{a}\frac{1 - 2\upsilon }{1 - \upsilon }} \right) \cdot \cos \left( {\omega \tau + \tan^{ - 1} \left( {1 - 2\upsilon } \right)^{1/2} } \right)$$

(6)

where V is the velocity, ρ is the density of the rock, υ is the Poisson’s ratio of the rock, ω is the natural frequency of the oscillating cavity, τ = t − (R − a)/c, and t is the time.

Fig. 1

Time histories of impulse loads

Duvall (1953) proposed an analytical equation to calculate the response of elastic media subjected to the following impulse load:

$$P(t) = P_{0} \left( {e^{ - \alpha t} - e^{ - \beta t} } \right)$$

(7)

where $\alpha = n_{d} \cdot \omega /\sqrt 2 ,\;\beta = m_{d} \cdot \omega /\sqrt 2$, and n _d and m _d are decay constants. The function is an improvement over the power-exponential law function used by Blake Jr (1952) because the rise and decay of the pressure can be simulated and adjusted through the decay constants. The analytical equation to calculate the response of velocity of the elastic media is as follows:

$$\begin{aligned} V(R,\tau ) = & \frac{{3P_{0} }}{{2\rho c^{2} }}\left( {\frac{a}{R}} \right) \cdot f\left( \tau \right) + \frac{{3P_{0} }}{{2\rho c^{2} }}\left( {\frac{a}{R}} \right)^{2} \cdot q\left( \tau \right) \\ f\left( \tau \right) = & \frac{{2n^{2} }}{3}\frac{{e^{{{\raise0.7ex\hbox{${ - n\omega \tau }$} \!\mathord{\left/ {\vphantom {{ - n\omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{3 - 2n + n^{2} }} - \frac{{2m^{2} }}{3}\frac{{e^{{{\raise0.7ex\hbox{${ - m\omega \tau }$} \!\mathord{\left/ {\vphantom {{ - m\omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{3 - 2m + m^{2} }} - \frac{{e^{{{\raise0.7ex\hbox{${ - \omega \tau }$} \!\mathord{\left/ {\vphantom {{ - \omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{\sqrt 2 \sqrt {3 - 2n + n^{2} } }} \cdot 2\sin \left( {\omega \tau + \theta_{1} - 2\theta_{3} } \right) \\ & + \frac{{e^{{{\raise0.7ex\hbox{${ - \omega \tau }$} \!\mathord{\left/ {\vphantom {{ - \omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{\sqrt 2 \sqrt {3 - 2m + m^{2} } }} \cdot 2\sin \left( {\omega \tau + \theta_{2} - 2\theta_{3} } \right) \\ q\left( \tau \right) = & - n\frac{{e^{{{\raise0.7ex\hbox{${ - n\omega \tau }$} \!\mathord{\left/ {\vphantom {{ - n\omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{3 - 2n + n^{2} }} + m\frac{{e^{{{\raise0.7ex\hbox{${ - m\omega \tau }$} \!\mathord{\left/ {\vphantom {{ - m\omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{3 - 2m + m^{2} }} + \frac{{e^{{{\raise0.7ex\hbox{${ - \omega \tau }$} \!\mathord{\left/ {\vphantom {{ - \omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{\sqrt 2 \sqrt {3 - 2n + n^{2} } }} \cdot \sqrt 3 \sin \left( {\omega \tau + \theta_{1} - \theta_{3} } \right) \\ - \frac{{e^{{{\raise0.7ex\hbox{${ - \omega \tau }$} \!\mathord{\left/ {\vphantom {{ - \omega \tau } {\sqrt 2 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 2 }$}}}} }}{{\sqrt 2 \sqrt {3 - 2m + m^{2} } }} \cdot \sqrt 3 \sin \left( {\omega \tau + \theta_{2} - \theta_{3} } \right) \\ \end{aligned}$$

(8)

where θ ₁ , θ ₂ , θ ₃ are the phase angles, $\theta_{1} = \tan^{ - 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\left( {1 - n} \right)}}} \right. \kern-0pt} {\left( {1 - n} \right)}}} \right)$, $\theta_{2} = \tan^{ - 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\left( {1 - m} \right)}}} \right. \kern-0pt} {\left( {1 - m} \right)}}} \right)$, and $\theta_{3} = \tan^{ - 1} \sqrt 2$. f(τ), q(τ) are time history functions of the wave at R. The equation is only applicable to undamped elastic media with υ = 0.25.

Jiang et al. (1995) developed analytical solution for the wave radiation in the elastic full-space due to the following power-exponential law function:

$$P(t) = P_{0} t^{n} e^{ - \beta t}$$

(9)

where n is an integer. The closed-form velocity equation of elastic media is as follows:

$$\begin{aligned} V(R,\bar{\tau }) =& - \frac{a}{R}f(\bar{\tau }) - \left( {\frac{a}{R}} \right)^{2} q(\bar{\tau }) \\ f(\bar{\tau }) =\, & c\frac{{\partial^{2} \phi_{1} }}{{\partial \bar{\tau }^{2} }},\quad q(\bar{\tau }) = c\frac{{\partial \phi_{1} }}{{\partial \bar{\tau }}} \\ \phi_{1} = & \frac{{ - p_{c} }}{{\rho_{d} b_{2d} }}\left\{ {\left( {\bar{\tau } - 2\frac{{b_{1d} }}{{b_{2d} }}} \right)e^{{ - \alpha_{c} \bar{\tau }}} + e^{{ - \alpha_{d} \bar{\tau }}} \left[ {\frac{{b_{1d} }}{{\sqrt {b_{2d} } \omega_{d} }}\cos \left( {\omega_{d} \bar{\tau } - \theta } \right) - \frac{1}{{\sqrt {b_{2d} } }}\sin \left( {\omega_{d} \bar{\tau } - \theta } \right)} \right]} \right\} \\ \end{aligned}$$

(10)

where $\bar{\tau } = \left( {t - \frac{R - a}{c}} \right)\frac{c}{a}$, $p_{c} = \frac{{P_{0} }}{E}\left( {\frac{a}{c}} \right)^{n}$, $\omega_{d} = {{\left( {1 - 2\upsilon } \right)^{1/2} } \mathord{\left/ {\vphantom {{\left( {1 - 2\upsilon } \right)^{1/2} } {\left( {1 - \upsilon } \right)}}} \right. \kern-0pt} {\left( {1 - \upsilon } \right)}}$, $\alpha_{d} = {{\left( {1 - 2\upsilon } \right)} \mathord{\left/ {\vphantom {{\left( {1 - 2\upsilon } \right)} {\left( {1 - \upsilon } \right)}}} \right. \kern-0pt} {\left( {1 - \upsilon } \right)}}$,$\alpha_{c} = \frac{a}{c}\alpha$, $b_{1d} = \frac{a}{c}\left( {\alpha_{0} - \alpha } \right)$, $b_{2d} = \left( {\frac{a}{c}} \right)^{2} \left( {\omega_{0}^{2} + \left( {\alpha_{0} - \alpha } \right)^{2} } \right)$, $\theta = \frac{{b_{1d} }}{{\omega_{d} }}$.

Jiang et al. (1995) also presented an analytical procedure to calculate the response of viscoelastic full-space due to a spherical source. A non-constant Q model was developed to simulate the viscoelastic attenuation. It uses separate mechanisms for geometric and viscoelastic attenuations. The procedure involves Fourier transforms performed in frequency domain.

Trivino et al. (2009) reported that the empirical pressure equation is not typical of experimental data, which typically show shorter rise time. Blair (2015) proposed the following modified pressure time history:

$$P(t) = P_{0} \left( {{\raise0.7ex\hbox{$e$} \!\mathord{\left/ {\vphantom {e n}}\right.\kern-0pt} \!\lower0.7ex\hbox{$n$}}} \right)^{n} \left[ {1 - \left\{ {1 + \frac{1000}{\sqrt m }\left( {\frac{\beta t}{n}} \right)^{m} } \right\}^{ - 1} } \right]\left( {\beta t} \right)^{n} e^{ - \beta t}$$

(11)

where m is an integer that controls the rise time. The function becomes identical to the pressure form of Jiang et al. (1995) for m = 0. The rise time of the pressure function decreases with an increase in m. There is currently no analytical solution for the spherical source (such as those given by Eq. 8 and 10) for the wave radiation produced by the revised pressure function.

The pressure curves of Duvall (1953), Jiang et al. (1995), and Blair (2015) are compared in Fig. 1. All functions are normalized to the peak pressure (P _max). For Duvall (1953)’s function, α = 1200 and β = 2400. Jiang et al. (1995) and Blair (2015) functions use β = 2000 and n = 1. The function of Duvall (1953) is shown to be similar to the curves of Jiang et al. (1995). As noted previously, the curves of Jiang et al. (1995) and Blair (2015) using m = 0 are identical. The curves for m = 8 and 64 are shown to have much shorter rise times compared to other functions.

It should be noted that even though the complete waveform can be predicted from the theoretical solution, a numerical model or an empirical attenuation curve is widely utilized in practice because of the following reasons. Firstly, in many cases only the peak amplitude is required to assess the damage of adjacent structures and facilities. Secondly, the theoretical equations are only compatible with the empirical function used in respective studies. It cannot be used with another form of the blast load. Lastly, the viscoelastic procedure requires calculation in the frequency domain using a dedicated code and, therefore, is difficult to use in practice.

4 Numerical Model

We performed a series of axisymmetric analyses to simulate the spherical propagation of blast-induced waves through elastic and viscoelastic continuum and developed representative attenuation curves. Numerical analyses were performed with FLAC^2D version 7.0 (Itasca Consulting Group 2011), a commercial finite difference analysis program.

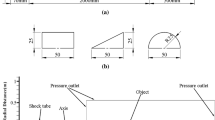
The fracture zone caused by blasting is modeled as a spherical cavity with a radius of a. The rock fracturing process, which requires a hybrid finite–discrete element analysis, was not simulated in this study. The full-space was modeled as an elastic and viscoelastic material. It was assumed that the blast generates stress waves that are imposed at the interface between the fractured zone and the elastic media. The blast load was applied in a normal direction to the cavity surface in the form of a pressure or velocity time series. The rate of attenuation is inversely proportional to the radius of the cavity. The cavity should not be considered as the actual fractured zone. Rather, the size of the cavity should be considered as an effective parameter to control the attenuation rate. We applied a = 1 in the numerical simulations. Figure 2 displays the computational model and boundary conditions. The viscous damper proposed by Lysmer and Kuhlemeyer (1969) was applied at the side, top and bottom boundaries to absorb incident motions. The depths of the blast used were 10, 15, and 20 m. The lateral dimension of the computational domain was 40 m. The size of the element greatly influences the accuracy of the numerical simulation. Kuhlemeyer and Lysmer (1973) proposed the following equation to determine the maximum size of the mesh:

$$\Delta l \le \frac{c}{10f}$$

(12)

where l is the element size. Based on Eq. (12) and a sensitivity study to evaluate the effect of the mesh size, we applied 0.05 m elements in the analyses. The calculated responses were extracted at nine monitoring points within profile and at the surface, respectively. The monitoring points within profile are located at the center depth of the cavity. They are illustrated in Fig. 3. The range of R/a from the source is from 10.5 to 35.80. The incident angle ranges from 5.7° to 65.2°. The Rayleigh damping formulation, defined in Eq. (13), was used to model the small strain damping of the geologic media:

$$[C] = \alpha [M] + \beta [K]$$

(13)

where [C] is the damping matrix, [M] is the mass matrix, [K] is the stiffness matrix, and ξ is the damping ratio. Additionally, α and β are the Rayleigh coefficients that determine the frequency dependence of the damping formulation, where α and β are defined as 4πξ(f ₁ f ₂)/(f ₁ + f ₂) and ξ/[π (f ₁ + f ₂)], respectively, and ξ is the target damping ratio. The formulation matches the target damping ratio only at the frequencies of f ₁ and f ₂ (Fig. 4), which are termed target frequencies. The damping of soils is known to be independent of the loading frequency, particularly in cohesionless soils or rock masses. However, the Rayleigh damping formulation is frequency dependent and introduces numerical damping. To reduce the frequency dependence, the variation of the frequency of vibration is observed in the following section, and a protocol to select the target frequencies is reported in the ensuing section.

Fig. 2

Computational model for the simulation of blast wave propagation

Fig. 3

Monitoring points at the surface and within profile

Fig. 4

Frequency dependence of the Rayleigh damping formulation

5 Verification of the Numerical Model and Generation of Input Motion

To verify the numerical model, the results of the dynamic analyses are compared to the closed-form solutions. For the undamped case, Jiang et al. (1995) represents the correct solution. We verified the undamped model against Jiang et al. (1995)’s analytical equation. Jiang et al. (1995) also proposed analytical solution for wave attenuation in damped full-space. The wave equation can capture the near-field response but assumes that the damping of the media is frequency dependent. However, experimental data reveal that the hysteretic damping of soils and rocks is mostly frequency independent. Because the frequency dependence of the Rayleigh damping formulation used in the numerical simulation is different from the analytical model of Jiang et al. (1995), two solutions are not compared. Instead, the numerical results are compared to the theoretical far-field model applicable for harmonic vibration, even though the impulse load is not a sinusoid.

Figure 5 compares the velocity time history calculated from the numerical simulation and Jiang et al. (1995)’s equation for undamped media. c was set to 4000 m/s and ρ = 2500 kg/m³. The pressure of the loading was set to 1 GPa. It is demonstrated that the numerical model very accurately predicts the wave attenuation, producing almost identical results to the analytical solution.

Fig. 5

Comparison of closed-form solution for undamped elastic space (Jiang et al. 1995) and computed velocity time histories at four distances from the source

Figure 6a compares peak velocity amplitude attenuation in damped media calculated from numerical simulations and the far-field attenuation curve. Figure 6b illustrates the tangent slopes (s’) of the attenuation curves. In all analyses, c = 4000 m/s and ρ = 2500 kg/m³. The damping ratio was set to 5%. The attenuation curves are normalized to peak velocity at R/a = 10 to compare only the far-field response. The target frequencies (f ₁ and f ₂) for the Rayleigh damping formulation were varied. Because the pressure functions have a short rise time followed by a long decaying curve, the predominant frequency (f _p) is not an ideal index to characterize the impulse function. The peak response is dependent on the rise time and not the decay time. Therefore, the rise time was used to select f ₁. We used f ₁ = 1/(4t _r ) in all analyses. For a sinusoid, 1/4t _r is identical to f _p. Three values were used for f ₂, which were 5/(4t _r), 10/(4t _r), and 20/(4t _r). Figure 6a compares the attenuation curves normalized to PPV at R/a = 10 to compare the response only at far-field. Even though the theoretical far-field attenuation curve is only applicable to a harmonic wave, the attenuation curve derived from impulse loading matches well with the theoretical curve. Use of f ₁ = 1/(4t _r) and f ₂ higher than 10/(4t _r) produces results that fit favorably with the theoretical solution, where a frequency-independent damping is used. It is therefore demonstrated that (1) theoretical attenuation curve can be used to estimate the peak amplitude of impulse load and (2) the frequency-independent damping is well approximated with the Rayleigh damping formulation if f ₁ and f ₂ are selected appropriately. In the following analyses, f ₂ = 10/(4t _r) was applied.

Fig. 6

Effect of the target frequencies selected for the Rayleigh damping formulation on attenuation: a normalized attenuation curve and b slope of attenuation curves

6 Source-to-Site Attenuation Curve Accounting for Near-Field Effects

We performed a suite of analyses for a broad range of load frequencies, damping ratios, and wave velocities. We firstly used three pressure time histories, which are the functions of Blair (2015) with m = 0, m = 8, and m = 64, termed Loads A, B, and C, respectively. The pressure functions were applied normally to the wall of the cavity.

Figure 7 illustrates the velocity time histories at R/a = 1, which is the free surface of the cavity, and at R/a = 15. In a numerical simulation, the impulse load can be either applied as a pressure load or an equivalent velocity time history at R/a = 1. The response was reported to be identical whether a pressure function or an equivalent velocity time series is applied (Fan et al. 2004). In the following numerical simulations, the velocity time histories were applied as input motions.

Fig. 7

Velocity times histories of the elastic media at R/a = 1 and 15 subjected to Loads A, B, and C

Figure 8 plots the variation of f _p and 1/4t _r with distance from the source. Both f _p and 1/4t _r of all functions increase with distance from the source. f _p at R/a > 10 for Loads A, B, and C is 600, 658, and 720 Hz, respectively. 1/4t _r is higher, obviously because of the short rise time. 1/4t _r is 1085, 1190, and 1560 Hz, respectively. Although the Blair (2015) m = 8 and m = 64 functions match better with the experimental measurements, it should be noted that in the process of the rock fracturing, the frequency characteristics of the vibration are greatly altered. The predominant frequency of the waves transmitted to the elastic media after fracturing is reported to be in the range of 1–300 Hz (ISO 2000). Because we do not simulate the rock fracturing in our study, the change in the frequency cannot be modeled. Instead of modeling such process, we accounted for it by using elongated time histories. From the velocity functions calculated from Loads A, B, and C, elongated forms of the velocity time histories are generated. The time step (Δt) of the respective motions is increased by factors of 2, 4, and 8. The total number of modified velocity functions used was nine, as shown in Fig. 9. We used both original motions and the modified waveforms to develop the attenuation curve.

Fig. 8

Computed rise time and predominant frequency of Loads A, B, and C with distance from the source

Fig. 9

Input loads modified from Loads A, B, and C by increasing the time step (Δt) to 2Δt, 4Δt, and 8Δt

Figure 10a, b, c shows the normalized attenuation curves, f _p, and 1/4t _r using three velocity time histories derived from Load A. f _p is shown to range from 75 to 300 Hz, whereas 1/4t _r ranges from 136 to 543 Hz. Figure 11 compares selected attenuation curves derived from numerical analyses with theoretical far-field curves calculated for four different wavelengths and c = 4000 m/s. The theoretical curves are positioned such that they intersect with the numerically derived curves at far-field. The slope of the numerically derived curve is shown to decrease with R/a until it becomes identical to the theoretical slope, which is unity for undamped media. Figure 12a and b plots the variation of the tangent slopes of the theoretical and numerically derived attenuation curves subjected to Load A in c = 4000 m/s media for undamped and damped (ξ = 5%), respectively. The scaled distance at which the slope of the numerically calculated curve is within a prescribed threshold level of the theoretical curve (10% in this study) is termed L _NF in this study. We also denote the portion of the attenuation curve with R/a < L _NF as near-field and R/a ≥ L _NF as far-field. Because the slopes of the numerically derived and theoretical far-field attenuation curves are identical at a scaled distance beyond L _NF, we only need to quantify the difference at near-field. We first develop an empirical correlation for L _NF, and second, we propose a function to quantify the difference between the numerical and far-field curve at near-field.

Fig. 10

Dynamic response of the elastic media subjected to motions derived from Load A: a normalized attenuation curves, b predominant frequency with distance from the source, c rise time with distance from the source

Fig. 11

Comparison of theoretical far-field and numerically derived attenuation curves for various wavelengths

Fig. 12

Comparison of the slope (s’) of the attenuation curve with c = 4000 m/s subjected to Load A: a damping = 0%, b damping = 5%

The case matrix of the numerical simulations is summarized in Table 2. We applied a total of twelve input velocity time histories. P wave velocities were set to 3000 and 4000 m/s. The density was set to 2500 kg/m³, and υ was assumed as 0.25. For damped media, we only applied the time histories modified from Load A. Four damping values were 0, 1, 3, and 5%.

Table 2 Case matrix

Figure 13 plots L _NF against the equivalent wavelength (λ) normalized by the radius of the cavity, where the equivalent wave length is defined as 4ct _r. Figure 13a plots the results for all motions in undamped media. Figure 13b compares the results using modified Load A motions and four damping ratios. For all cases, the normalized equivalent wavelength is shown to have a primary influence on L _NF. The damping ratio is shown to have a secondary influence on L _NF and, therefore, is not included in the empirical equation for L _NF. The following predictive equation, derived from regression analysis and conditional only on the normalized equivalent wavelength, is shown to provide a good fit with the calculated L _NF.

Fig. 13

Correlation between L _NF and the normalized equivalent wavelength: a all motions in undamped media, b Load A-derived motions in damped and undamped media

$$L_{\text{NF}} = 1.5 \cdot (\lambda /a)^{0.75}$$

(14)

Next, a functional form for the residual, which represents the difference between near-field and far-field curves, is developed. The residual, shown in common log units (Fig. 14), is shown to be primarily dependent on the wavelength and secondarily dependent on the damping ratio, similar to L _NF. In Fig. 15, the residual is plotted against the scaled distance normalized by L _NF. All residual curves collapse into a narrow band, and a single curve can fit the residuals calculated for a broad range of input parameters considered in this study. A functional form for the residual can be developed based on regression analysis as follows:

$${\text{Residual}} = \left( {\frac{{70\frac{R/a}{{L_{\text{NF}} }}}}{{70\frac{R/a}{{L_{\text{NF}} }} + 1}}} \right)\left\{ {0.055\left( {\frac{R/a}{{L_{\text{NF}} }}} \right)^{ - 1.55} + 1} \right\}$$

(15)

The residual is very practical and easy to use because it is additive to the theoretical far-field curve. The resulting curve, denoted as the source-to-site within the profile curve, can predict the vibration near-field and also estimate the blast load at the source.

Fig. 14

Variation of residual in logarithmic units with scaled distance

Fig. 15

Variation of residual in logarithmic unit with normalized scaled distance

Figure 16 displays the selected source-to-site attenuation relationship from numerical simulations and the source-to-site curves proposed in this study. Notably, the attenuation curves from numerical analyses, which are verified against analytical solutions as presented in the previous section, represent the correct response. For all of the cases, the proposed source-to-site curves are shown to fit quite well with the results of the numerical analysis. At near-field, the attenuation increases with increases in c and f. This is obvious considering that an increase in both c and f induces a corresponding increase in the wavelength, which causes the near-field effect to escalate. At far-field, the damping ratio primarily influences the attenuation of blast waves. With an increase in the damping ratio, the attenuation curve becomes highly nonlinear and results in higher slopes.

Fig. 16

Attenuation curves calculated for various P wave and damping ratios

Notably, a typical attenuation curve presents a relationship between PPV at the surface of a geologic profile and the scaled distance. Because the stress wave is amplified at the free boundary, the attenuation curve at the surface is always larger than the “within-profile” curve. We need to quantify the difference between the surface and within-profile attenuation curves because the measurements are always taken at the surface. It is reported that the amplification at the surface for the spherical blast source is dependent on υ, depth of the source, and incident angle (Jiang et al. 1998). Jiang et al. (1998) calculated the amplification factors for four depths of the source (h/a) and incident angles ranging from zero to 90°. The amplification factor for elastic media with υ = 0.25 ranged approximately from 2.02 to 2.15 for h/a = 6 and 2.0 to 2.05 for h/a = 24 up to an incident angle of 65° (Fig. 17). The amplification factor was shown to quickly decay at higher incident angles. For the range of incident angle simulated in this study, which ranges from 5.7° to 65.2° as shown in Fig. 3, the amplification factor can be considered to be two.

Fig. 17

Peak amplitude ratio of surface to within-profile waves. The amplification factors calculated by Jiang et al. (1998) for ν = 0.25 are also compared

We performed a series of analyses in undamped elastic media to evaluate the amplification factor of the surface motion relative to the within-profile motion. The blast source was located at depths of 10, 15, and 20 m from the surface. Load A with Δt was used as the blast source. c was set to 4000 m/s. The motions were extracted at a total of eighteen points, as illustrated in Fig. 3. The peak amplitude was calculated a plane parallel to the direction of the wave propagation. The peak amplitude ratio of surface to within-profile motions is plotted against incident angle in Fig. 17. The surface motions are larger in magnitude by approximately a factor of two compared with the within-profile motions. The range is consistent with the values calculated by Jiang et al. (1998). The within-profile motion can be taken as the surface motion reduced by a factor of two for an incident angle smaller than 65° and h/a exceeding 6. For cases beyond this range, a site-specific analysis is required to estimate the peak amplitude ratio of surface to within-profile motions.

The full procedure to develop the within-profile source-to-site attenuation curve is shown in Fig. 18. From the slope and amplitude of the surface measurements, the parameters for the far-field attenuation relationship can be determined. f _p is determined from the Fourier spectrum of the recorded motion. The slope of the measured data is used to determine the damping ratio. After fitting the far-field attenuation curve to the surface data, the corresponding within-profile curve is produced by dividing the curve by a factor of two. Because f _p and damping ratio are identical, the slope is parallel to the surface curve. In the next step, L _NF is calculated using Eq. (14). The final step is calculating the residual function from Eq. (15) and adding it to the within-profile far-field curve. The proposed source-to-site attenuation curve can also be used to determine the corresponding source load and input parameter (ξ) for a numerical simulation.

Fig. 18

Flowchart to develop within-profile source-to-site curve and determine the peak amplitude at the source (PPV_source)

7 Validation of Proposed Procedure

Validation of the proposed source-to-site attenuation curve was conducted through comparison with surface recordings measured during a test blast; the schematic plot of which is shown in Fig. 19. Emulsion explosives (ϕ32 mm) were installed at a depth of 28 m from the surface. The charge weight was 0.635 kg. The site was primarily composed of biotite gneiss. The properties of the rock were estimated as c = 2580 m/s, υ = 0.30, and ρ = 2500 kg/m³.

Fig. 19

Schematic plot of test blast

The recorded longitudinal, transverse, and vertical velocity time histories at station S1 are shown in Fig. 20. Also shown is the velocity time history extracted at a plane 22.5° counter-clockwise from the horizontal surface, which is parallel to direction of the incident wave at station S1. 1/4t _r of the velocity time history, as determined from the Fourier spectrum, was 43 Hz. The theoretical far-field equation was fitted to the surface recordings. The equivalent damping ratio that produces most favorable fit with the recordings is 5.5%. The equivalent wavelength was calculated as 75 m, and corresponding L _NF was 38.2. The within-profile far-field curve is parallel to the surface curve but lower by a factor of two. The residual function was calculated using Eq. (15). The source-to-site within-profile curve was developed by adding the residual function to the far-field within-profile curve. The comparison demonstrates that even though the surface far-field curve is higher than the within-profile far-field curve by a factor of two, it still underestimates the vibration within ground at near-field.

Fig. 20

Recorded surface motions at station S1

We performed a dynamic analysis to simulate the test blast. We used the recorded time history at S1 as input load, but the peak amplitude was scaled to the blast load at R/a = 1 of the source-to-site attenuation curve. The radius of the cavity was calculated as 0.8 m. In Fig. 21, the calculated motions at the surface and within profile are shown. The numerically simulated surface motions are shown to provide a favorable match with the recorded motions. We also find good agreement between the calculated within-profile motions and the proposed source-to-site attenuation curve. The comparisons highlight that the proposed procedure provides a reliable estimate of the source load even for field conditions.

Fig. 21

Comparison of recorded data, far-field and source-to-site curves, and numerical results

8 Conclusions

We performed a suite of axisymmetric finite difference analyses to calculate the attenuation of the stress waves induced by a spherical blast source. The fractured zone generated by blasting was modeled as a spherical cavity. The blast load was applied in normal direction to the cavity surface. To verify the numerical model, the results were compared to two theoretical equations. We show that the numerical model can accurately predict the propagation and near-field attenuation only if the element size is considerably smaller than the wavelength. It was demonstrated that the lower target frequency (f ₁) of the Rayleigh damping formulation should be selected as 1/4t _r of the blast wave, where t _r is the rise time. A favorable fit with the theoretical far-field is achieved when the higher target frequency (f ₂) is higher than 10(1/4t _r).

A parametric analysis was conducted to calculate the attenuation of the blast waves for a broad range of loading frequencies, wave velocities, and damping ratios. The attenuation curves derived from numerical analyses were compared with theoretical far-field curves. The difference between two set of curves in logarithmic units was termed the residual. The residual was revealed to be significant and proportional to the equivalent wavelength. We propose two empirical functions to predict the residual. The residual of all analyses collapsed into a narrow band when normalized. The residual function is convenient to use because it can be added to the theoretical far-field curve to predict the near-field attenuation. The resulting curve, termed the source-to-site within-profile curve, can predict the vibration at near-field and also estimate the blast load at the source. The proposed curve was validated against surface recordings measured during a test blast. The blast load at the source was determined from the attenuation curve. Numerically calculated surface motions agreed favorably with the recordings, thereby validating that the proposed attenuation curve is applicable and the source load can be reliably estimated.