1 Introduction

The simulation of hydraulic fracture (hereafter called HF) propagation in subsurface formations with pre-existing mechanical discontinuities (i.e. all kinds of weakness planes: faults, joints, veins, bedding planes or natural fractures, thereafter referred as NF) remains an important challenge. In unconventional reservoirs, such as oil and gas shales, tight gas sandstones, which have typically a few percent porosity and nano-scale permeability, production depends to a large extent on successful hydraulic fracture stimulation in horizontal wells. At the same time, in these formations, the HF propagation can be largely affected by the interaction with NF discontinuities when those are present.

There are two big challenges in performing adequate HF design in naturally fractured reservoirs. First, the natural discontinuities have to be identified and characterized in terms of their geometric properties (location, orientation, spatial density and extent) and their mechanical properties (friction, cohesion, toughness and hydraulic permeability). Second, the understanding and description of HF propagation through NFs remain a scientific challenge even when the NF properties are known. Despite a multitude of laboratory tests, mine-back observations, numerical and analytical studies devoted to HF–NF interaction (Beugelsdijk et al. 2000; Jeffrey et al. 2009; Cipolla et al. 2008), there is currently no HF–NF interaction model that could both be computationally efficient for engineering HF simulators and correctly predict fracture crossing behavior for a wide range of HF and NF fracture properties and pumping conditions.

During the past decade, advanced numerical models of HF–NF interaction have been developed. One of them, developed by the hydraulic fracturing group at CSIRO Melbourne, has focused mainly on the interaction of one HF and one NF (Zhang and Jeffrey 2006, 2008; Zhang et al. 2007, 2009; Chuprakov et al. 2013). This fully coupled 2D plane-strain DDM model of fracture interaction has the advantage of modeling accurately the complex mechanics of the elastic fracture interaction, viscous fluid flow within the fracture and its diversion at fracture junctions, quasi-brittle fracture propagation and initiation, as well as additional mechanical processes (such as history-dependent frictional sliding at the NF, fracture compliance, intrinsic permeability and shear-enhanced dilation). Pseudo-3D models of HF propagation in the presence of NFs extend plane-strain models to account for the effect of fracture height and/or subcritical growth (Olson and Taleghani 2009; Dahi-Taleghani and Olson 2011; Olson and Wu 2012) and simulate fracture complexity due to the interactions with multiple NFs (Wu et al. 2012; Weng et al. 2011; Kresse et al. 2012). Discrete element techniques such as 3DEC have also been developed to predict fully three-dimensional fracturing stimulation in naturally fractured rocks by assessing areas of their tensile and shear failure (Nagel et al. 2011; Gil et al. 2011). All these numerical models have helped the understanding of realistic fracturing processes in the field. However, those simulators do not account for proper mechanics of each particular HF–NF interaction. As an exception, the MineHF2D code by CSIRO (Zhang and Jeffrey 2006, 2008; Zhang et al. 2007, 2009), does that properly, but comes with a computational cost penalty that prevents practical use and limit parametric analysis of the fracture interaction problem (Chuprakov et al. 2013).

Despite the fact that the mechanics of fully coupled fracture propagation in a planar geometry has been thoroughly studied analytically (Garagash 2006; Garagash and Detournay 2000, 2005, 2007; Adachi and Detournay 2002; Detournay 2004), the accurate coupled solution of the equations for the whole process of HF–NF interaction, including HF approach, contacts with the NF, and re-initiation of a secondary HF is computationally prohibitive even in a 2D domain. Previously developed analytical models for this problem have made quite simplistic assumptions that make the models too restrictive (Renshaw and Pollard 1995; Blanton 1986; Warpinski and Teufel 1987; Gu et al. 2011). For example, Renshaw and Pollard (1995) evaluate the new crack initiation at the end of a sliding zone at the NF, whereas it has been shown that the most probable re-initiation location with highest stress concentration is at the end of the open zone of the NF (Chuprakov et al. 2011). Renshaw and Pollard’s model also only considers orthogonal intersection between an HF and a NF, although this model was generalized to non-orthogonal intersection by Gu and Weng (2010). Blanton (1986) makes an assumption for the profiles of the normal and shear tractions generated at the NF when deriving the stress criterion for fracture re-initiation. As a result, his stress criterion also differs from what is observed in accurate numerical solutions of the fracture interaction problem. Warpinski and Teufel (1987) established a criterion for fracture re-initiation solely based on the critical stress and neglecting energy principles of fracture mechanics and is, therefore, limited. Finally, all these previous models omit Griffith’s energy criterion of crack initiation across the NF (Janssen et al. 2004). The fact is the stress criterion used alone can be either inapplicable like in fracture problems, or at least insufficient, as in problems with stress singularities near notches (Leguillon 2002; Leguillon and Murer 2008; Leguillon and Yosibash 2003). An adequate fracture re-initiation mechanism description must honor both strength and energy criteria (also called mixed criterion). Finally, none of the existing analytical criteria takes into account the effect of fluid flow (i.e. rate and fluid viscosity) that is known from experimental and field observations to be crucial in the interaction with hydraulic fractures (Beugelsdijk et al. 2000; de Pater and Beugelsdijk 2005).

The aim of the present paper was to develop a new analytical description of fracture interaction (hereafter called OpenT) that is more consistent with all key recognized parameters. Herein, we concentrate on quantitative description of the NF activation due to the contact with the HF and outline geometric and geomechanical conditions for the HF re-initiation at the NF. This new model includes a dependency on the HF pumping characteristics and the NF permeability missed in previous interaction models. It also enables the prediction of the re-initiated fracture offset and branching, which is not presented in this paper. We validate this new model by comparing the results in terms of crossing/arresting behavior to laboratory observations and numerical results.

2 Model of HF–NF Contact: OpenT

2.1 Problem Definition and Assumptions

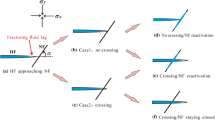
Consider a pressurized HF that is in contact with a pre-existing, initially unpressurized NF in a homogeneous elastic impermeable rock compressed by two principal in situ stress components σ (∞)1 and σ (∞)3 , aligned with Oxy reference plane, such that they are parallel and perpendicular to the HF, respectively. The two contacted fractures form a “slanted” T-shape junction with arbitrary angle β, as shown in Fig. 1.

Fig. 1
figure 1

Problem statement for the NF activation. The two contacted fractures, HF and NF, form a “slanted” T-shape junction with angle β. The stresses σ (∞)1 and σ (∞)3 are, respectively, parallel and perpendicular to the HF. The open zone at the NF is bounded by \(b_{\text{o}}^{( - )}\) and \(b_{\text{o}}^{( + )}\) and the sliding zone by \(b_{\text{s}}^{( - )}\) and \(b_{\text{s}}^{( + )}\)

Full size image

Upon contact, the penetrating fracturing fluid will gradually change the inner fluid pressure inside the NF from the intact formation pore pressure to the fluid pressure inside the HF. Following the elastic perturbation produced by the contact with the HF tip and the local change of effective stress, the NF will be elastically activated in opening and shear close to the fracture junction point (Fig. 1). For convenience the NF activation problem is solved in the local system of coordinates Ox′y′ associated with the NF (and not aligned with principal stresses), where the Ox′ axis is co-directed with the NF, and the negative Oy′ axis corresponds to the direction of new crack growth perpendicular to the NF. The created open zone at the NF is bounded by b (−)o and b (+)o , and the sliding zone is bounded by b (−)s and b (+)s , respectively (Fig. 1).

The activation of the NF is thus a multi-parameter function of the HF aperture at the junction (that depends on the parameters of fluid injection), far-field stresses, the angle of fracture interaction, the inner fluid pressure, the frictional and cohesional properties of the NF.

As a result of the local NF activation, the stress field at the opposite side of the NF will be perturbed. The sufficient spatial concentration of tensile stresses induced in the rock mass close to the activation zone can enable initiation of new tensile cracks at the opposite side of the NF. Initiation of a new crack across the NF implies its subsequent growth into the rest of the rock and further on.

The goal of the work is thus to detect the parametric conditions for initiation and offsetting of a new crack crossing the NF in the framework of the given problem statement.

Here is the list of key model assumptions:

  1. 1.

    The interaction between the HF and the NF is plain-strain. To ensure this, the depth of the contact between the HF and the NF (along the third coordinate) must be at least longer than the lengths of the HF and NF affected by fracture interaction.

  2. 2.

    The height of the growing HF is assumed to be comparable or less than the height of the pre-existing NF, to avoid situation of cutting NF by oversized HF.

  3. 3.

    The rock is elastic, isotropic, impermeable, brittle and homogeneous (without any other pre-existing weakness planes than the NF). The elastic and strength properties of the rock on both sides of the NF are identical.

  4. 4.

    The prescribed far-field stress is local with respect to the considered HF–NF contact. This stress can differ from the stress field far away from the NF because of possible NF slippage, stress influence by the wellbore, perforations, or other pressurized or sliding fractures in the neighborhood of the considered NF, and so on. This local stress change near any particular NF can be calculated using fracture simulation tools (Cipolla et al. 2010; McLennan et al. 2010; Wu et al. 2012).

  5. 5.

    Prior to contact, the NF is stable (non-activated) in the given far-field stress state. According to the Mohr–Coulomb failure criterion, the differential far-field stress is low enough to prevent the NF from sliding at the given stress field, cohesion and friction coefficient of the NF.

  6. 6.

    The NF in consideration does not cross the wellbore and is not directly affected by pressurization of the wellbore. Atkinson and Thiercelin (1995, 1997) have studied this particular situation. Analysis here is designed solely for remote interactions (with respect to wellbore) between the fluid-driven HF fracture and the NF.

  7. 7.

    The NF filling, its mechanical and chemical properties including interaction with fracturing fluid are not explicitly considered. However, we suppose that the NF has uniform hydraulic permeability. The NF is initially pressurized by pore fluid pressure, and fracturing fluid penetrates the NF with time after the contact.

  8. 8.

    Both the HF and the NF at the contact are planar. The HF is aligned with the orientation of the far-field principal stresses (perpendicular to the minimum in situ stress). The NF is inclined and has spatial dimensions exceeding the activation area created nearby the HF–NF contact.

  9. 9.

    The HF tip is blunted (has finite opening) at the contact with the NF. The blunting is a function of contact time, injection rate and fluid viscosity, in situ stress, Young’s modulus, frictional and cohesional properties of the NF.

  10. 10.

    The HF tip propagation before crossing is continuous and quasi-static, which permits the stable state when a HF makes a T-shaped contact with an NF.

The following sign conventions regarding fracture displacements, normal and shear stresses are used throughout the work normal fracture displacements w are positive and equal to the full opening of the fracture. Shear displacements at fracture v are positive when the associated rotation takes place in a clockwise direction. The sign of the normal stress component is positive when it is in compression, and, oppositely, negative, when it is in tension. Shear stress is positive when causing negative shear displacement in a counterclockwise direction.

2.2 Boundary Conditions at the NF Before and After Contact

As per Mohr–Coulomb failure criterion (Jaeger et al. 2007), the stability of the NF before contact with the HF establishes the following relationship for the shear and normal far-field stress components, τ (∞) and σ (∞) n , along the NF:

$$\left| {\tau^{(\infty )} } \right| < C_{0} + \lambda \sigma_{n}^{(\infty )} ,$$
(1)

where \(C_{0}\) is the cohesion and λ is the friction coefficient of the NF. The normal and shear components of far-field stress applied to the NF, inclined by the angle β with respect to the direction of maximum stress σ (∞)1 , are expressed via σ (∞)1 and σ (∞)3 as follows:

$$\sigma_{n}^{(\infty )} = \sigma_{1}^{(\infty )} \,\sin^{2} \beta \,\, + \,\sigma_{3}^{(\infty )} \cos^{2} \beta$$
(2)
$$\tau^{(\infty )} = (\sigma_{3}^{(\infty )} - \sigma_{1}^{(\infty )} )\,\sin \,\beta \,\cos \,\beta$$
(3)

There is symmetry of the problem with respect to angle β. In general, the range of possible angles is changing −π/2 to π/2, but it can be noted that for any negative angle β the considered 2D plane can be flipped to give inclination angle β in the positive range \([0, \pi /2]\) without changing geometry of the fracture. In the work we will consider only positive values of the interaction angle.

Relying on the quasi-static behavior of the NF after the contact with the HF, we write down the total normal stress σ n applied at the open NF zone as a function of the inner fluid pressure p filling the NF:

$$\sigma_{n}^{{}} \left( {x^{\prime} } \right) = p\left( {x^{\prime} } \right), \; b_{\text{o}}^{ - } \le {x^{\prime}} \le b_{\text{o}}^{ + }$$
(4)

In this zone the shear stress τ must disappear, while in the slipping parts of the NF that remain closed τ must follow the cohesionless Mohr–Coulomb law with coefficient of friction λ, so for the shear stress along the entire activated zone of the NF we have

$$\tau \left( {x^{\prime} } \right) =\left \{{\begin{array}{ll} {\lambda \sigma_{n} \left( {x^{\prime} } \right) \text{sgn} (\tau ), \quad b_{\text{s}}^{ - } \le x' \le b_{\text{o}}^{ - } } \\ {0, \quad\quad\quad\quad\quad\quad b_{\text{o}}^{ - } \le x^{'} \le b_{\text{o}}^{ + } } \\ {\lambda \sigma_{n} \left( {x^{\prime} } \right) \text{sgn} (\tau ), \quad b_{\text{o}}^{ + } \le x' \le b_{\text{s}}^{ + } } \\ \end{array} }\right\} ,$$
(5)

where sgn(τ) is the sign of shear stress in this region.

2.3 HF Tip Blunting at the Contact with the NF

A preliminary numerical study revealed that the stresses and energy sufficient for creating a new crack crossing the NF will most likely take place at the moment of T-shaped fracture contact (Chuprakov et al. 2011). When a moving pressurized HF closely approaches a pre-existing discontinuity and intersects it, the fracture tip shape suddenly becomes blunted. The process of tip blunting can be interpreted as the coalescence of a previously isolated HF with another tensile and shear fracture at the NF.

Numerical DDM computation of elastic interaction between a HF and a non-cohesive frictional interface indicates that right after their contact the HF tip becomes blunted at the junction point and has a considerable aperture (Figs. 2, 3).

Fig. 2
figure 2

Fracture opening shape (left) and profiles of opening and sliding at the HF (right) from DDM computation (Chuprakov et al. 2011) of the HF contact with cohesionless and unpressurized NF at 90°. E = 20.4 GPa, v = 0.2, p = 35 MPa, σ 1 = σ 3 = 20 MPa, λ = 0.5

Full size image
Fig. 3
figure 3

Same as in Fig. 2 but for the angle of HF contact with the NF of 45°

Full size image

As a consequence, after the fracture contact the mechanical perturbation of the NF generated by the HF tip is produced by a blunted dislocation rather than elliptically closed fracture tip as supposed in previous studies (Renshaw and Pollard 1995; Gu et al. 2011; Gu and Weng 2010). Accurate numerical simulations show that the stress field perturbation in the vicinity of the HF with blunted tip is complex and cannot be expressed analytically. For the sake of the analytical approach, we approximate the HF at the junction as a slot of uniform aperture w T (a dislocation), for which the solution for stress components are known as (Hills et al. 1996; Barber 2010; Crouch and Starfield 1983).

$$\sigma_{ij}^{{\left( { \sqsupset } \right)}} \left( {r,\theta } \right) = - \frac{{\varOmega_{\text{T}} }}{4\pi } \frac{1}{r} f_{ij}^{{\left( { \sqsupset } \right)}} \left( \theta \right)$$
( 6)

where ΩT = w T E′ is the modified aperture of the fracture slot, E′ = E/(1 − ν 2), E is the Young’s modulus, ν is the Poisson ratio, and the angular functions \(f_{ij}^{{\left( { \sqsupset } \right)}}\) in polar coordinates are \(f_{rr}^{{\left( { \sqsupset } \right)}} \left( \theta \right) = f_{\theta \theta }^{{\left( { \sqsupset } \right)}} \left( \theta \right) = \cos \theta\), \(f_{r\theta }^{{\left( { \sqsupset } \right)}} \left( \theta \right) = \sin \theta\). In particular, the normal and shear components of the HF-induced stress perturbation at the NF inclined at angle β can be written as

$$\left. {\sigma_{n}^{\left( 1 \right)} (x')} \right|_{\theta = \beta ; \beta - \pi } = - \frac{{\varOmega_{{{\text{T}}2}} }}{4\pi } \frac{1}{x'} ,$$
(7)
$$\left. {\tau_{{}}^{\left( 1 \right)} (x')} \right|_{\theta = \beta ; \beta - \pi } = - \frac{{\Psi_{{{\text{T}}2}} }}{4\pi } \frac{1}{x'} ,$$
(8)

where ΩT2 = ΩT cos β is the modified opening of the NF and ΨT2 = ΩT sin β is the modified sliding of the NF at the junction point, as follows from geometrical relationship.

Equation (7) indicates that in the proximity of the fracture junction, the HF creates strong tensile stress (σ (1) n  < 0) along the fracture wing having acute angle with the HF (\(x' > 0\)) and creates a strong compressive field (σ (1) n  > 0) along the other NF wing which has an obtuse angle with the HF (\(x' < 0\)). This means that a certain open zone will be created along the positive wing of the NF (\(x' > 0\)) and can never appear along the negative wing of the NF (\(x' < 0\)). Note also that, in the case of orthogonal fracture crossing, such model of the HF does not produce tensile stress along the NF and the open zone cannot be generated. At the same time, oppositely directed sliding parts of the NF generate the tensile stress at the opposite side of the NF, which can cause new crack initiation.

In order to find the produced opening and sliding at the HF–NF junction point, we need to solve elasticity equations numerically using a DDM scheme with friction logic included (Zhang and Jeffrey 2006; Chuprakov et al. 2011) for Figs. 2 and 3. Before the more accurate model of the elastic fracture contact is built, it is possible to use known estimates for the HF width as a first-order approximation to the HF opening at the HF–NF junction. For the plane-strain KGD fracture with Newtonian fluid of viscosity μ with rate Q and propagating in an impermeable rock along one direction, its average width is estimated as (Valko and Economides 1995), eqn. (9.25).

$$\left\langle w \right\rangle = 2.53 \sqrt[4]{{\frac{{Q\mu L^{2} }}{E'H}}},$$
(9)

where L is the length and H is the height of the HF at contact. A similar estimation for the average width of the fracture propagating with radial symmetry (penny-shaped) is given by (Valko and Economides 1995), eqn.(9.39).

$$\left\langle w \right\rangle = 2.24 \sqrt[4]{{\frac{Q\mu R}{E'}}},$$
(10)

where R is the radius of the fracture. Hereafter, for the interpretation of experiments we will use the averaged width of the HF interacting with the NF from (10) as the estimate of the HF aperture at the junction point.

$$w_{\text{T}} = \left\langle w \right\rangle$$
(11)

2.4 NF Activation in Opening and Shear

In quasi-static condition, the total stress along the NF is a linear combination of (1) the stress induced by the HF, σ (1) ij ; (2) the stress self-induced by the NF activation σ (2) ij ; and (3) the far-field stress σ (∞) n . The solution for the elastic displacements along the NF can be written in terms of spatial gradients, or distributed dislocation densities, as

$$B_{y} = \frac{dw}{dx'}, B_{x} = \frac{dv}{dx'},$$
(12)

where w and v are the opening and sliding profiles of the NF given by (Hills et al. 1996)

$${\mathcal{B}}_{y} \left( {x_{\text{o}} } \right) = - \frac{4}{{\pi \sqrt {1 - x_{\text{o}}^{2} } }}\mathop \int \limits_{ - 1}^{1} \sigma_{n}^{\left( 2 \right)} \left( {x^{\prime} \left( s \right)} \right)\frac{{\sqrt {1 - s^{2} } }}{{x_{\text{o}} - s}} ds$$
(13)
$${\mathcal{B}}_{x} \left( {x_{s} } \right) = - \frac{4}{{\pi \sqrt {1 - x_{\text{s}}^{2} } }}\mathop \int \limits_{ - 1}^{1} \tau_{{}}^{\left( 2 \right)} \left( {x^{\prime} \left( s \right)} \right)\frac{{\sqrt {1 - s^{2} } }}{{x_{\text{s}} - s}} ds$$
(14)

where the normalized open and shear crack coordinates x s (\(- 1 \le x_{\text{s}} \le 1\)), x o (\(1 \le x_{\text{o}} \le 1\)) are

$$x_{\text{o}} = \left( {\frac{2}{{b_{\text{o}}^{ + } - b_{\text{o}}^{ - } }}} \right) x^{\prime} - \left( {\frac{{b_{\text{o}}^{ + } + b_{\text{o}}^{ - } }}{{b_{\text{o}}^{ + } - b_{\text{o}}^{ - } }}} \right)$$
(15)
$$x_{\text{s}} = \left( {\frac{2}{{b_{\text{s}}^{ + } - b_{\text{s}}^{ - } }}} \right) x^{\prime} - \left( {\frac{{b_{\text{s}}^{ + } + b_{\text{s}}^{ - } }}{{b_{\text{s}}^{ + } - b_{\text{s}}^{ - } }}} \right)$$
(16)

Note that the mapping of the normalized coordinates x o and x s onto the dimensional scale x’ is, generally speaking, different, as the open and sliding zone can be different in extent. The unknown partial stresses due to the NF (σ (2) n , τ (2)) can be obtained from the boundary conditions at the NF, far-field stresses and HF-induced stress as found above as

$$\sigma_{n}^{\left( 2 \right)} (x') = \sigma_{n} (x') - \sigma_{n}^{(1)} (x') - \sigma_{n}^{(\infty )}$$
(17)
$$\tau_{{}}^{(2)} (x') = \tau (x') - \tau_{{}}^{(1)} (x') - \tau_{{}}^{(\infty )}$$
(18)

The normal component σ (2) n defines only the normal crack displacement (opening), and the net shear stress τ (2) defines the shear displacement (sliding) at the NF. Once the dislocation densities are found, the profiles of the modified sliding \(\Psi (\bar{x})\) and opening \(\varOmega \left( {\bar{x}} \right)\) are found from

$$\Psi \left( {x_{\text{s}} } \right) = - \left( {\frac{{b_{\text{s}}^{ + } - b_{\text{s}}^{ - } }}{2}} \right)\mathop \int \limits_{{x_{\text{s}} }}^{1} {\mathcal{B}}_{x} (s) ds,$$
(19)
$$\Omega \left( {x_{\text{o}} } \right) = - \left( {\frac{{b_{\text{o}}^{ + } - b_{\text{o}}^{ - } }}{2}} \right)\mathop \int \limits_{{x_{\text{o}} }}^{1} {\mathcal{B}}_{y} (s) ds,$$
(20)

where we take into account that crack lengths are different for the sliding and open crack sections.

The boundaries of the open and sliding zones along the NF \(\left( {b_{\text{o}}^{ + } ,\,b_{\text{o}}^{ - } ,\,b_{\text{s}}^{ + } \,{\text{and}}\,\,b_{\text{s}}^{ - } } \right)\) are still unknown. They can be calculated from the equality of the stress intensity factor at the tips of the activation zones and corresponding fracture toughness (critical stress intensity factor) value. For example, if the tips of the slippage zone along the NF are mechanically closed (pure Mode II crack), the unknown boundaries of the sliding crack b +s and b −s are found from

$$K_{\text{IIC}} ({\text{s}} = \pm 1) = \pm \frac{1}{4}\sqrt {\pi l} \left. {{\mathcal{B}}_{x} \left( {s;b_{\text{s}}^{ + } , b_{\text{s}}^{ - } } \right)\sqrt {1 - s^{2} } } \right|_{{{\text{s}} \to \pm 1}} ,$$
(21)

where K IIC is the Mode II NF toughness, and l = (b +s  − b −s )/2 is the half-length of the sliding crack.

In the more complex case of the mixed mode crack when the tips of the open and sliding zone coincide, one can use the empirically justified F-criterion (Shen and Stephansson 1993, 1994). Substitution of the solutions for the Mode I and Mode II stress intensity factors at the crack tips into the F-criterion results in the following equations for the crack boundaries b − and b +

$$\mathop {\lim }\limits_{s \to \pm 1} \left( {1 - s^{2} } \right)\left[ { \frac{{{\mathcal{B}}_{y}^{2} \left( {s;b_{{}}^{ + } , b_{{}}^{ - } } \right)}}{{K_{\text{IC}}^{2} }} + \frac{{{\mathcal{B}}_{x}^{2} \left( {s;b_{{}}^{ + } , b_{{}}^{ - } } \right)}}{{K_{\text{IIC}}^{2} }} } \right] = \frac{16}{\pi l},$$
(22)

where l = (b + − b −)/2 is the half-length of the mixed-mode crack. The solution of these equations gives the unknown boundaries b − and b + of the crack affected by both modes of fracture toughness.

2.5 Stress Concentration Nearby HF–NF Contact

As mentioned above, the total stress field in the fracture interaction problem can be determined as a superposition of the partial stress contributions from the HF, the NF and far-field stress. One can show that the sum of these stress components can finally be written via complex coordinate z = x + iy as

$$\sigma_{m}^{{}} \left( z \right) = {\text{Im}}\; I_{c} \left( z \right) + \sigma_{m}^{(\infty )}$$
(23)
$$\sigma_{d}^{{}} \left( z \right) = y \frac{{dI_{c} \left( z \right)}}{dz} - i \;I_{\text{s}} \left( z \right) + \sigma_{d}^{(\infty )} ,$$
(24)

where \(\sigma_{m}^{{}} = ( {\sigma_{xx}^{{}} + \sigma_{yy}^{{}} } )/2\) is the mean stress component, \(\sigma_{d}^{{}} = ( {\sigma_{xx}^{{}} - \sigma_{yy}^{{}} } )/2 - i\sigma_{xy}^{{}}\) is the deviatoric component of the stress tensor and \({I_c}\left( z \right)\; = \;{I_s}{z_s}\; + \;i{I_n}{z_0}\) is the complex integral, where \(z_{\text{s}} = x_{\text{s}} + iy_{\text{s}}\) and \(z_{\text{o}} = x_{\text{o}} + iy_{\text{o}}\) are the normalized complex coordinates of the shear and open NF zones, respectively. The shear-induced and opening-induced components of the integral, I s and I n , respectively, are found as follows:

$$I_{\text{s}} \left( {z_{\text{s}} } \right) = - \frac{1}{{\pi \sqrt {z_{\text{s}}^{2} - 1} }}\mathop \int \limits_{ - 1}^{1} \tau^{(2)} \left( s \right) \frac{{\sqrt {1 - s^{2} } }}{{ z_{\text{s}} - s}}ds$$
(25)
$$I_{n} \left( {z_{\text{o}} } \right) = - \frac{1}{{\pi \sqrt {z_{\text{o}}^{2} - 1} }}\mathop \int \limits_{ - 1}^{1} \sigma_{n}^{(2)} \left( s \right) \frac{{\sqrt {1 - s^{2} } }}{{ z_{\text{o}} - s}}ds$$
(26)

2.6 Stress Criterion for the New Tensile Crack

If the surrounding rock is homogeneous, the analysis of new crack initiation must be focused on the points of stress concentration. The locations of the stress concentration along the activated NF correspond typically to the junction point and the tips of the open and sliding zones created at the NF. These tip locations, x′ = x j , are the most probable points of crack nucleation, and their search is, thus, reduced to the inspection of the integrals I k (x q ) for the extremes.

Once x j are detected, we next find the angular orientation of the maximum tensile hoop stress around x j as

$$\theta_{j} = \mathop {\text{argmax}}\limits_{\theta \in [ - \pi ; \pi ]} \left( { - \left. {\sigma_{\theta \theta }^{{}} \left( {x_{j} ;r;\theta } \right)} \right|_{r \to 0} } \right),$$
(27)

where the hoop stress component σ θθ is found from Eqns. (23), (24) as

$$\sigma_{\theta \theta }^{{}} \left( \theta \right) = \sigma_{m}^{{}} \left( \theta \right) - {\text{Re }}\left[ {\sigma_{d}^{{}} \left( \theta \right)\exp \left( {2i\theta } \right)} \right]$$
(28)

In the direction θ j the tensile crack has the highest probability to appear, so it should be selected for evaluation of the stress and energy criterion for crack initiation.

The necessary condition for crack initiation is given by the requirement of critical tensile hoop stress, i.e.

$$\left. {\sigma_{\theta \theta }^{{}} \left( {x_{j} ;r;\theta_{j} } \right)} \right|_{r \to 0} \le - T_{0} ,$$
(29)

where T 0 is the tensile strength of the rock. If this criterion is not met at x j the crack can never be initiated at this point. However, if this condition is satisfied, the possibility of crack initiation is still conditioned by the energy criterion that has to be verified.

If the tensile stress monotonically decays in magnitude with distance from the NF and eventually tends to the compressive far-field stress, one can define the maximum distance r = δ T, where the stress criterion is still satisfied

$$\left. {\sigma_{\theta \theta }^{{}} \left( {x_{j} ;r;\theta_{j} } \right)} \right|_{{r < \delta_{\text{T}} }} \le - T_{0}$$
(30)

The range of potential initiation crack lengths \(r \in (0, \delta_{\text{T}} ]\) will be used to check the energy criterion.

2.7 Energy Criterion for the New Tensile Crack

In quasi-brittle formations, the initiation of a new tensile crack of length δl is possible provided that the release of elastic strain energy δW n because the initiation of the crack exceeds the energy required for the formation rupture. This condition can be written in terms of the energy release rate (ERR) G inc due to incremental creation of a crack with length δl as (Jaeger et al. 2007; Janssen et al. 2004; Leguillon 2002)

$$G_{\text{inc}} (\delta l) = \frac{{\delta W_{n} }}{\delta l} > G_{\text{IC}} ,$$
(31)

where G IC is the critical ERR for Mode I cracks, which is expressed via experimentally measurable Mode I fracture toughness of the rock K IC in plane-strain conditions as follows (Janssen et al. 2004)

$$G_{\text{IC}} = \frac{{K_{\text{IC}}^{2} }}{E'}$$
(32)

For cracks continuously propagating from the tip, the condition (31) is met for infinitesimally small increments δl. However, if the point of crack initiation contains no stress singularity or it is weak, the energy condition of crack initiation (31) is satisfied for the cracks of a finite size δl.

Consider the creation of a tensile crack with a length δl originating at some point x j at the NF as is depicted in Fig. 4. This sketch reflects the particular case of crack initiation at the end of the open NF zone followed by the sliding zone.

Fig. 4
figure 4

Sketch of a crack initiation across the NF. This example is the particular case when a tensile crack is created at the end of the open zone followed by the sliding zone

Full size image

The incremental change in potential elastic energy δW n , is defined as the difference between the energy before and after the incremental crack initiation, is equal to that change if this crack would continuously grow from the infinitesimally small length to the final size δl.

The incremental rate of the energy release G inc can thus be expressed by the integral of differential ERR G I along the whole crack growth history from zero length to δl. Noting that the differential ERR G I is expressed via stress intensity factor (SIF) at the tip of the growing crack as (Janssen et al. 2004)

$$G_{\text{I}} (\delta l) = \frac{{K_{\text{I}}^{2} (\delta l)}}{E'}$$
(33)

we can write, for incremental ERR,

$$G_{\text{inc}} (\delta l) = \frac{1}{{E^{'} \delta l}}\mathop \int \limits_{0}^{\delta l} K_{\text{I}}^{2} \left( l \right) dl$$
(34)

For the ERR evaluation, it is, therefore, necessary to obtain the solution for the SIF at the tip of the crack virtually growing from the NF. Following the mentioned assumptions, it is assumed that this crack is growing as a dry Mode I crack in the direction of a maximum principal tensile stress at this point. The SIF at the tip of the crack of length δl is found as

$$K_{\text{I}} \left( {\delta l} \right) = 2\gamma \sqrt {\frac{\delta l}{\pi }} \mathop \int \limits_{0}^{1} \frac{{ - \sigma_{\theta \theta } (x_{j} ; r\left( s \right), \theta_{j} )}}{{\sqrt {1 - s^{2} } }} ds,$$
(35)

where the factor γ is introduced to correct the mismatch between the solution for the real crack originated at the NF and the hypothetical crack in infinite rock without the NF. This factor is determined by taking the asymptote of the SIF at the infinitesimally short crack growing from the tip of the fracture with known SIF K I0. Requiring that K I(δl → 0) = K I0, we find that \(\gamma = 2^{ - 3/2} \sqrt \pi \varGamma \left( {3/4} \right)/\varGamma \left( {5/4} \right) \cong 0.85\).

Note that (35) has a physical sense only when the value of stress intensity factor K I(δl) is positive. Changing its sign to negative values means that the crack tip must be closed and no longer described by linear elasticity approach. In the considered problem, the initiated crack is growing from the point at the NF having sufficient tensile stress concentration. Moving away from the NF the maximum tensile stress component σ θθ is gradually decreasing and eventually changes its sign from negative (tensile) to positive (compressive) values. As a result, both the opening and the stress intensity factor K I at tip of a new crack must decrease with increase of the crack length. With a sufficiently long length of the crack the crack tip will be closed and stress intensity factor reaches zero. Above that critical distance, (35) is no longer applicable. In other words, this critical distance is the definite upper limit for the energy criterion of crack initiation under the given stress field.

2.8 Joint Stress-Energy Criterion of the Crack Initiation

In addition to the sufficient energy criterion (31), the necessary stress criterion for crack initiation (30) should be complemented. This can be realized by the requirement for the crack to be initiated within the critical stress zone (Leguillon 2002). Taking into account the upper bound of the tensile stress region δ T near the NF mentioned above, the combined stress-energy criterion is written as

$$G_{\text{inc}} \left( {\delta l} \right) > G_{\text{IC}} ,\quad \delta l < \delta_{\text{T}}$$
(36)

which means that the length of the initiated crack δl with sufficient energy release rate should not exceed the boundary of tensile stresses δ T. Rewriting this condition via the representation of the incremental ERR (34) and critical ERR in terms of stress intensity factor K I at the tip of the virtually growing crack and fracture toughness, \(K_{\text{IC}}^{{}}\); according to (36), it becomes

$$\frac{1}{\delta l}\mathop \int \limits_{0}^{\delta l} K_{\text{I}}^{2} \left( l \right) dl > K_{\text{IC}}^{2} , \quad \delta l < \delta_{\text{T}}$$
(37)

This condition requires to inspect the entire range of possible crack lengths, δl, where this condition is satisfied. To make this search efficient we solve for the maximum of the left-hand side of (37) with respect to δl. Taking the derivative with respect to crack length, δl, this equation is reduced to

$$\sqrt { \frac{1}{{\delta l^{*} }}\mathop \int \limits_{0}^{{\delta l^{*} }} K_{\text{I}}^{2} \left( l \right) dl} = K_{\text{I}} \left( {\delta l^{*} } \right),$$
(38)

where δl * is the crack length with the maximum incremental ERR. The next check can be done to make sure that δl * ≤ δ T and

$$K_{\text{I}} \left( {\delta l^{*} } \right) > K_{\text{IC}}$$
(39)

if the crack is to be initiated. If the condition (39) is not satisfied, the initiation criterion is not satisfied.

In the alternative case when the local maximum for the energy criterion lies behind the stress-affected region, i.e. δl * > δ T, the condition for the energy criterion has to be checked at the boundary of stress-affected zone

$$K_{\text{I}} \left( {\delta_{\text{T}} } \right) > K_{\text{IC}}$$
(40)

and the final conclusion about the initiation of the crack has to be made.

The initiation of a tensile crack at all possible crack initiation sites x j can be quantified with the help of the following crossing function:

$$Cr(x_{j} ) = K_{\text{I}} \left( {x_{j} ; \delta l^{*} } \right) - K_{\text{IC}} ,$$
(41)

which takes positive values if the crack is to be initiated or negative values if not.

2.9 Injected Fluid Penetration into the NF

The transient process of fluid penetration into the NF after the contact can be estimated as a gradual increase of the uniform fluid pressure in the NF from the level of pore pressure to the level of fluid pressure in the HF.

First, we evaluate the length of infiltrated zone within the NF, L f, as a function of time. Let us assume that the NF is mechanically closed but has a non-zero hydraulic conductivity, such that the Newtonian fluid propagates along the NF in a closed state. This is possible to quantify by introducing the residual opening of the NF in a closed state as w r. The hydraulic permeability, k, of the NF for fracturing fluid flow is then related to the residual opening as

$$k = \frac{{w_{\text{r}}^{2} }}{12}$$
(42)

The fluid flow within the fracture is described by the continuity and Poiseuille equations, respectively, as follows:

$$\frac{\partial q}{\partial s} + \frac{\partial w}{\partial t} = 0$$
(43)
$$q = - \frac{k(w)}{\mu }\frac{\partial p}{\partial s},$$
(44)

where q is the local flow rate, p is the local pressure of the fluid, μ is the fluid viscosity and s is the current coordinate of the fracture. If the residual permeability is uniformly distributed along the NF, and the NF is kept closed after HF–NF contact, then w r ≡ const, and from (43), we obtain the flow rate along the NF, q, as follows:

$$q = w_{\text{r}} \dot{L}_{\text{f}} ,$$
(45)

where \(\dot{L}_{\text{f}}\) is the velocity of fluid penetration into the NF. From Poiseuille law (44), we find the following equation for the fluid penetration in the NF:

$$\dot{L}_{\text{f}} = \frac{k}{\mu } \frac{{p_{\text{HF}} }}{{L_{\text{f}} }},$$
(46)

where p HF is the excess fluid pressure (fracturing fluid pressure less the pore pressure) at HF tip (junction point). The penetration of the fluid is feasible when the fracturing fluid is not too viscous. In this case once the tip is blunted the pressure may not change with time significantly. Provided that the excess fluid pressure p HF is kept constant during the time t after the contact, the solution for the fluid penetration length L f can be written as follows:

$$L_{\text{f}} (t) = \sqrt { \frac{{2 k \;p_{\text{HF}} }}{\mu } t}$$
(47)

This length gives the extent of the NF zone where the fluid pressure is changed as a result of fluid penetration into the NF. The associated effect of the net normal stress change on the activation of the NF and HF re-initiation will be negligible when L f is small compared to the length of the activated zone b s. In contrast, when L f exceeds the activation zone length, the fluid pressure in the NF can be considered the same as in the HF. It is reasonable to state that it is the following ratio of the fluid penetration length L f and the activation length b s

$$\lambda_{\text{f}} = \frac{{L_{\text{f}} }}{{b_{\text{s}} }} = \sqrt { \frac{{2 k\;p_{\text{HF}} }}{{\mu b_{\text{s}}^{2} }} t}$$
(48)

that governs the state of fluid pressurization within the activated NF zone. Keeping the assumption of the uniform fluid pressure along the activated zone, we prescribe the fluid pressure in the NF \(p_{\text{NF}}\) as

$$p_{\text{NF}} = p_{\text{HF}} \;f(\lambda_{f} ),$$
(49)

where a positive function f(λ f) must be chosen such that f(λ f) ≪ 1 when λ f ≪ 1, and f(λ f) = 1 when λ f ≫ 1. Such functional behavior can be approximated, for example, by a hyperbolic tangent f(x) = th(x) which satisfies the required boundary conditions. With a correcting coefficient ρ, (49) can be written as

$$p_{NF} = p_{\text{HF}} {\text{th}}\left( {\rho \sqrt { \frac{{2 k\; p_{\text{HF}} }}{{\mu b_{\text{s}}^{2} }} t} } \right)$$
(50)

As a starting point, one can use (50) with ρ = 1. More details on the effect of fluid penetration into the NF are discussed in (Kresse et al. 2013).

3 Benchmarking and Discussion

3.1 OpenT vs. Numerical Simulations

We now provide benchmarking results of the OpenT model with the fully coupled DDM scheme of HF–NF interaction implemented in the code MineHF2D (Zhang and Jeffrey 2006; Zhang et al. 2009). The code comprises of elastic interaction, fracture propagation and fluid flow in the fractures in a coupled manner. The comparison of the OpenT model with this numerical model is focused on the sensitivity of the fluid injection rate and the hydraulic permeability of the NF to the crossing vs. arresting HF–NF scenario.

The characteristics of the fluid injection dictate the elastic opening profile of the fracture and, in particular, the resultant blunting of the HF at the contact with the NF. As a first-order approximation of the opening at the junction after the HF–NF contact, the OpenT model used the concept of the average width of the HF as per Eq. (11). To validate this assumption and confirm that the injection rate does increase the opening at the junction and favors crossing behavior when the HF reaches the NF, we conduct several numerical simulations using MineHF2D simulator. In these simulations, only the rate of fluid injection at the inlet of the HF was modified. The HF is propagating up to 1 m length away from the inlet point, where it makes contact with the NF. The results of the fracture interaction observed in all these simulations have been classified into a class of crossing cases when the new fracture has been reinitiated at the back side of the NF and propagated further in rock, and a class of cases when the HF has been arrested at the NF.

Figure 5 shows the results of the numerical study along with the corresponding predictions from three analytical models (OpenT, Renshaw−Pollard or RP and Blanton) for the orthogonal (90°) and two of them (OpenT and Blanton) for tilted fracture intersection (60°) and various far-field stress differences.

Fig. 5
figure 5

Crossing/arresting diagram for fracture intersection angles β = 90° and β = 60° with the cohesionless NF (K (NF)IC  = K (NF)IIC  = 0), λ = 0.68, σ 1 = 5.33 MPa, \(\sigma_{3}\) = 2.67 MPa, E′ = 10 GPa, K IC = 3.6 MPa m1/2, T 0 = 4.95 MPa. Viscosity of the injected fluid μ = 833 cP, the HF length at contact with the NF L = 1 m. The solid lines are the predictions of OpenT model, and the dashed lines are for RP and Blanton criteria

Full size image

As is expected, at sufficiently small injection rates the fracture is arrested at the NF and the fluid penetrates into the NF. For large flow rates, a fracture is re-initiated at the NF a short while after the contact. Note that the results of the OpenT model with its simplified estimation of the blunting at the contact and the results of MineHF2D numerical simulations are in good agreement in Fig. 5. The RP and Blanton models are insensitive to the flow rate and therefore cannot capture this effect.

In this paper, we developed a simple approach to take into account the fluid penetration into the NF after contact. The approach is reduced to adjusting the fluid pressure inside the NF after the contact while preserving its uniform profile along the NF. To validate this approach, we run additional numerical simulations of HF–NF interaction with MineHF2D code, where the finite permeability of the cohesionless NF is prescribed.

In the following comparison, two large-scale simulations are performed where in both, the maximum and minimum far-field stresses are, respectively, 5.33 and 2.67 MPa and the length of the HF at the contact is 100 m. We used a Newtonian fluid with a viscosity of 0.001 Pa s and a rate of 0.001 m2/s. The rock formation has a plane-strain Young’s modulus of E′ = 10 GPa, a tensile strength of 4.95 MPa and a Mode I fracture toughness of 3.69 MPa m0.5. The friction coefficient of the NF is 0.68. The NF is orthogonal to the HF. The permeability of the NF is chosen to be either 3.5 D or 83 mD, which corresponds to, respectively, 6.5 and 1 μm for the residual NF aperture. All other parameters except the NF permeability are identical in these two simulation cases. The modeling examples with large and small NF permeability are intentionally selected to clearly see the effect of fracturing fluid penetration into the NF on the fracture crossing behavior.

It should be noted that, as (50) indicates, the NF pressurization effect does also depend on the viscosity of the fracturing fluid, μ, fluid pressure at the junction point, p HF, as well as the cohesional and frictional weakness of the discontinuity producing the activated zone b s. These parameters should also impact the fracture crossing outcome. Some of these parameters (viscosity and pressure) also increase the aperture of the HF, which magnifies the possibility of crossing even more.

In that sense, selecting only the NF permeability as the variable parameter in our simulations, we concentrate solely on the fluid penetration effect.

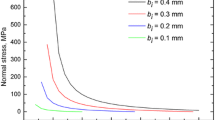
Figures 6 and 7 show the result of fracture interaction in those two cases when sufficient time after the contact has elapsed. This post-contact time is roughly equal to the time of fracture propagation from the inlet to the NF.

Fig. 6
figure 6

The result of HF–NF interaction numerical simulation with a NF permeability of 3.5 D after the fracture contact. The HF opening profile and the slipped (white) and intact (yellow) zones at the NF (left), and the profiles of the penetrated fluid pressure along the NF in MPa (right) are shown

Full size image
Fig. 7
figure 7

Same as in Fig. 6 but for a NF permeability of 83 mD

Full size image

Figures 6 and 7 plot the profile of the fluid pressure along the NF that corresponds to the post-contact fracture configuration depicted in the pictures. One can see that the enlarged fluid penetration in the first simulation case with the high-permeable NF prevents a new crack to be initiated at the opposite side of the NF and, hence, it forms a T-shape arrest of the fracture (Fig. 6). In contrast, the hindered fluid flow into the NF in the second simulation case with the low-permeable NF enables HF blunting at the contact sufficient to initiate a new crack earlier than if the entire activated NF zone is pressurized (Fig. 7).

Along with the parameters of the simulation cases Table 1 summarizes the results of the corresponding calculations for the length of activated zone, b s, fluid penetration into the NF, L f, effective fluid pressure at the NF, p NF estimated from (50) and prediction of fracture interaction outcome given by the OpenT model.

Table 1 Results of calculation of the parameters for the OpenT model related to the effect of fluid penetration on fracture activation and crossing for two simulation cases shown in Figs. 6 and 7
Full size table

From the analysis of these two simulations, we conclude that the introduced correction for the fluid pressure in the NF correctly predicts HF–NF crossing versus arrest outcome of fracture interaction observed in the numerical simulations.

3.2 OpenT vs. Previous Analytical HF–NF Criteria

In the OpenT model developed above, there are parameters included in previously published criteria such as those of Blanton (1986), Renshaw and Pollard (1995) (thereafter called RP) and extended Renshaw and Pollard by Gu and Weng (2010; Gu et al. 2011) (thereafter called eRP), which are the far-field stress difference, friction coefficient and angle of fracture intersection. Let us first compare the OpenT model with the ones of eRP and Blanton.

In Fig. 8, we show the boundary between the HF–NF crossing and arresting areas in the parameter space of the fracture intersection angle β and the dimensionless stress difference Δ = (σ 1 − σ 3)/σ 3. The OpenT model is the only one sensitive to the parameters of the HF such as injection rate, fluid viscosity and length. The crossing curve in Fig. 8 is plotted for three different lengths of the HF and the same injection and in situ parameters. The longer fracture has larger opening and easily breaks the NFs at comparably smaller angles, while for shorter fracture the crossing is not possible even in the case of orthogonal intersection (red curve). In the same graph the crossing criterion of Blanton and eRP are plotted for the same characteristics of the NF, rock and stresses. They give different results preserving only the qualitative tendency of the criteria to large angles and large rock stress difference.

Fig. 8
figure 8

HF–NF crossing criterion plotted as the boundary between the areas of crossing (above the lines) and arresting (below the lines) in the parameter space of intersection angles β and dimensionless stress difference Δ = (σ 1 − σ 3)/σ 3. Friction coefficient λ = 0.5 at the cohesionless NF (K (NF)IC  = K (NF)IIC  = 0), minimum stress σ 3 = 20 MPa, plane-strain Young modulus E′ = 10 GPa, fracture toughness of rock K IC = 1 MPa m1/2, tensile strength T 0 = 6.88 MPa. The solid lines are the predictions of OpenT model, the dashed line is for the eRP criterion, and the dashed-dotted line is for the Blanton criterion. The parameters of the HF used in the OpenT are Q = 10−6 m2/s, μ = 1 cP, L = 1 m (red line), 5 m (green line) and 10 m (blue line)

Full size image

Figure 9 demonstrates the crossing criterion of the three models in the parameter space of dimensionless stress difference and friction coefficient for two angles of fracture intersection 60° and 90°. The minimum stress difference for crossing behavior decreases with friction coefficient and becomes zero for comparably high friction between the NF interfaces.

Fig. 9
figure 9

HF–NF crossing criterion plotted as the boundary between the areas of crossing (above the lines) and arresting (below the lines) in the parameter space of dimensionless stress difference Δ = (σ 1 − σ 3)/σ 3 and friction coefficient λ for the cohesionless NF (K (NF)IC  = K (NF)IIC  = 0), minimum stress \(\sigma_{3}\) = 20 MPa, plane-strain Young modulus E′ = 10 GPa, fracture toughness of rock K IC = 1 MPa m1/2, tensile strength T 0 = 6.88 MPa, and fracture intersection angles 60° (green lines) and 90° (red lines). The solid lines are the predictions of OpenT model, the dashed lines for eRP criterion, and the dashed-dotted lines for Blanton criterion. For the OpenT, the parameters of the HF are Q = 10−6 m2/s, μ = 1 cP, L = 1 m

Full size image

The criteria are not well matched again, but the eRP criterion gives results much closer to the predictions of OpenT model than Blanton model. However, we note that the curves given by OpenT model will be sensitive to the parameters of fluid injection and fracture length, as was already demonstrated above. The larger the HF opening at the contact with the NF, the easier it will be for the crossing behavior.

There is another difference between the OpenT model and previous criteria. The new crack nucleation can appear with some offset with respect to the point of HF–NF contact in the case of an inclined fracture contact. Figure 10 indicates the energetic competition between the two possible cracks, initiated from two positions at the NF. The blue line in Fig. 10 shows the SIF for the crack initiated right from the junction point (non-jogged crossing case). The green line designates the SIF for the initiated crack at an offset (jogged crossing case).

Fig. 10
figure 10

SIF for the cracks initiated from the junction point (blue line) and from an offset point at the end of the open NF zone (green line). The NF is here a cohesionless interface

Full size image

From Fig. 10, it is evident that an inclined HF–NF intersection will favor jogged fracture paths. Only if the angle becomes more than 70° the jogging can be suppressed by the initiation of a crack directly from the junction point.

As a summary, in Tables 2 and 3, we list the total number of input parameters and output characteristics in all the mentioned models.

Table 2 Comparative list of input parameters in HF–NF models
Full size table
Table 3 Comparative list of output parameters in HF–NF models
Full size table

3.3 OpenT vs. Laboratory Experiments

We now compare the OpenT model with three independent laboratory experiments as well as with other analytical criteria (Blanton and eRP) and numerical results from MineHF. All the experiments have been performed with boreholes orthogonal to the minimum principal stress direction, akin to 2D plane-strain conditions found in analytical and numerical models.

3.3.1 Blanton Experiments

Blanton (1982) reported HF–NF crossing laboratory experiments on hydrostone blocks with a pre-existing frictional interface (tensile strength of 1.5 MPa, Young’s modulus of 10 GPa, Poisson’s ratio of 0.22, Mode I fracture toughness of 0.17 Pa m1/2, friction coefficient at the interface of 0.75). The injection rate used was 0.82 cm3/s, but the type of fluid used in these experiments is unknown. The angle between the HF and a pre-interface was from 30° to 90°.

3.3.2 Warpinski and Teufel Experiments

Warpinski and Teufel (1987) performed similar experiments on Coconino sandstone (tensile strength of 6.4 MPa, Young’s modulus of 24.8 GPa, Poisson’s ratio of 0.39, Mode I toughness of 0.93, friction coefficient at the interface of 0.68) under tri-axial conditions. Artificial single joints were made at prescribed angles of 30°, 60° and 90° to the intended direction of hydraulic fracture propagation. The injection fluid was 40-weight oil with viscosity of 0.32 Pa s and constant injection rate 0.1 cm3/s.

3.3.3 TerraTek Experiments

More recently, Gu et al. (2011) also reported HF–NF experiments on Colton sandstone blocks performed in polyaxial stress conditions at TerraTek laboratories (tensile strength of 4.054 MPa, Young’s modulus of 20.4 GPa, Poisson’s ratio of 0.2, Mode I fracture toughness of 1.6 Pa m1/2, friction coefficient between the interface edges of 0.615). A 1-in diameter borehole was drilled in the center of each block, cased with a slotted steel casing to control the hydraulic fracture initiation and propagation. Silicone oil was used as the injection fluid (viscosity of 1 Pa s) with an injection rate of 0.5 cm3/s. The angle between the HF and the interface was varied from 45° to 90°.

Figure 11 presents the results for the three experiments in terms of crossing/arresting diagrams for different angles of intersection and relative stress difference. Experimental results where the HF crossed the NF are represented by black crosses and by black squares when the HF was arrested at the NF. Colored crosses and squares correspond to numerical results from MineHF2D. The three analytical criteria (Blanton in dashed yellow line, Gu and Weng’s eRP in dashed blue line and OpenT in green, light blue and red) show the limits above which there is crossing and under which there is no-crossing. For Blanton’s experiment, the pumping fluid was unknown, so we made a series of computations for different values of fluid viscosities starting from water viscosity, which is 0.001 Pa s (blue lines, crosses and squares) and then viscous fluid with 0.1 Pa s (green lines, crosses and squares) and 1 Pa s (red lines, crosses and squares).

Fig. 11
figure 11

Crossing/arresting diagrams for different angles of intersection and relative difference of applied stresses: (top) TerraTek’s, (middle) Warpinski and Teufel’s, and (bottom) Blanton’s experiments. Symbols are as follows: black cross-square for experimental data, colored cross-square for MineHF2D simulations, and colored lines for analytical criteria

Full size image

We can observe the following situations in Fig. 11: (top) all analytical and numerical results correctly predict the TerraTek HF–NF crossing/non-crossing experimental data (Middle) only Blanton’s model and MineHF2D correctly predict the Warpinski and Teufel data, and (Bottom) only OpenT and MineHF2D for water viscosity and eRP correctly explain Blanton’s data. Overall, we note that the OpenT model is the analytical model that captures injection sensitive behavior (rate and viscosity) and adequately describes two out of three of the experimental data and MineHF2D results. We also note that the eRP criterion coincides with the OpenT for low-viscosity cases. Finally, we observe that as the fluid viscosity increases, the crossing limit for the OpenT (and MineHF2D) becomes less sensitive to the relative stress difference. An additional experimental point was acquired in 2013 for the TerraTek experiment by taking the conditions of the lowest differential stress and 90° intersection point (arresting condition) and by increasing the viscosity from 1 to 2,500 Pa s. The change of viscosity changed the outcome of the experiment from a non-crossing to a crossing situation as predicted by the OpenT model (comparison not shown). This result looks promising but it is clear that the validation of the OpenT for different fluid viscosity and injection rate would require additional experiments. In addition, direct experimental observations of the opening of the HF and interface (shape and values in time) at all stages (approach, intersection, onset of initiation) would greatly benefit our understanding of the elastic and fluid effects and the validity of the assumptions and limitations of the different models.

4 Conclusions

The problem of a hydraulic fracture contact with a pre-existing discontinuity was solved analytically using a blunted dislocation discontinuity approach. This analytical model offers a closed-form elasticity solution of the fracture contact problem and energy-related condition for HF re-initiation across the NF. The model allows all angles of interaction between the HF and the NF and accounts for fluid penetration into the permeable NFs.

The key benefits of the present work can be summarized as follows:

  1. 1.

    We have provided an improved understanding of the mechanisms causing new crack initiation and jogging across the NF in the hydraulic fracture propagation process. We showed that, aside from the far-field stress contrast and cohesional properties of the NF, the fluid injection parameters, such as a product of injection rate and fluid viscosity, Qμ can control the scenario of fracture interaction. This opens a new possibility to control fracture complexity in naturally fractured rocks by selecting an optimum injection schedule.

  2. 2.

    To the best of our knowledge, OpenT is the first quantitative model that describes the NF activation in opening and shear in accordance with accurate numerical simulations of elastic fracture contact. Compared to the other models, the OpenT model predicts locations of fracture re-initiation at the NF, being also coupled with fluid penetration into the NF.

  3. 3.

    The model was compared with three independent laboratory experiments as well as with two other analytical criteria (Blanton and eRP) and fully coupled numerical simulations from MineHF2D. The cross-model comparison indicated a good prediction of the crossing-arresting results by the OpenT model.

  4. 4.

    The relative computational efficiency of the OpenT model (compared to the numerical models) along with the successful validation by advanced numerical tools makes the model attractive for implementation in modern engineering tools simulating hydraulic fracture propagation in naturally fractured environment, such as UFM (Wu et al. 2012; Kresse et al. 2013).