1 Introduction

Seismic events induced by human activities have been a research topic studied extensively for a long time in modern seismology. Nuclear explosion is a source that produces man-made seismic vibrations. Some investigations have been conducted on its destructive power and stress wave propagation since 1960s to meet the needs of national defense or the prohibition of nuclear weapons (Kharin et al. 1966; Bykovtsev and Kramarovskii 1994; Liu and Ahrens 2001). Blasts associated with mining, tunneling, stone crushing, and excavation of deep foundations are another source of man-made seismic events having smaller magnitudes than natural earthquakes or nuclear explosions (Henrych 1979). There are many blasting-induced microseism predictors available suggested by different researchers (Sambuelli 2009; Mesec et al. 2010; Blair 2010; Liang et al. 2011). Their intensity is directly related to source characteristics, the distance between the source and the receiver, as well as geological and geotechnical properties. As compared to natural earthquakes, blasts have a higher stress change and a more rapid energy release in the vicinity of the explosion source, which leads to a higher vibration frequency (Negmatullaev et al. 1999). With the increase in mining depth and with the construction of underground tunnels and radioactive waste disposal systems, more and more deep underground openings are being excavated worldwide. Local elastic strain energy concentration associated with stress redistribution by excavation operations results in the generation and growth of rock cracks and even the movement of nearby geological discontinuities. In this process, the continuing release of strain energy and the stress wave propagation can also induce microseismic events in surrounding rock masses (Kaiser and Tang 1998; Fialko et al. 2002; Kozyrev et al. 2005; Wang et al. 2011). As pointed out by Kaiser and Tang (1998), “excavation-induced seismicity has become an important indicator for assessing the stability of rock excavations, particularly in mining engineering.”

It is generally acknowledged that explosion is the source of blasting-induced microseismic vibrations. It should be noted that, during deep rock mass excavation by blasting, accompanying the process of rock fragmentation and the formation of a new free surface, in situ stress on this boundary is removed instantaneously, which is termed the transient release of in situ stress. The classical elastic rebound theory of earthquakes maintains that an earthquake will occur when stress is released suddenly. In contrast to the conventional quasi-static excavation unloading, studies by Abuov et al. (1988) and Carter and Booker (1990) revealed that the rapid release of stress near the excavation face during construction blasting can produce a dynamic tensile stress in the surrounding rock mass, and its magnitude is proportional to the release rate of stress. Cai (2008) believed that the drill and blast excavation in a deep-buried tunnel would create a huge unbalanced force right at the excavation face, and some of the strain energy would need to be converted into kinetic energy in order to dissipate the unbalance. A true-triaxial rock test was conducted by He et al. (2010) to demonstrate that, accompanying the sudden unloading in one direction of a rock sample, elastic stress waves, which travel from the origin point within the rock to a boundary where they are observed as acoustic emission signals, are generated. In field tests, the stress field is also found to have a guiding effect on the propagation of blasting microseismic waves. Zhang et al. (2005) found that the measured blasting vibration is much greater than that predicted in the direction of the maximum principal stress. The research findings above indicate that, during the deep rock mass blasting, the transient release of in situ stress on the excavation contour occurring with explosion may be another excitation of blasting-induced microseisms.

From the viewpoint of elastic strain energy release, the microseismic events triggered by the transient release of in situ stress behave similarly to mining-induced microseisms and rock bursts. However, it has been rarely studied in previous studies concerning blasting-induced microseisms. Therefore, studying the transient release of in situ stress during the blasting excavation of deep rock masses will be a great help to a better understanding of the mechanism of blasting excavation-induced microseisms and a better control of blasting vibrations by construction operations. Furthermore, establishing a relationship between microseismic vibrations and stress provides an effective way for underground projects to determine the secondary stress distribution and then predict geological hazards. In the present study, in combination with microseismic records in a blast of deep rock masses, microseismic events induced by the transient release of in situ stress are firstly identified by a time–energy density analysis and an amplitude spectrum analysis, and separated from recorded microseismic signals by a digital filter. Then, a case study of bench blast carried out in a deep underground powerhouse is made. The energy release mechanism and the mechanical process of the excavation-induced microseisms are discussed. Finally, a numerical simulation is conducted to demonstrate the microseismic events and their corresponding vibrations induced by the transient release of in situ stress.

2 Transient Release of In Situ Stress Induced Microseism

When deep underground openings are excavated with the method of drill and blast, both explosion shock and detonation gases pressurizing blasthole walls cause fragmentation of surrounding rocks. Accompanied by the throwing of fragments from their initial locations, the in situ stress on the newly formed excavation boundary will be released instantaneously. This unloading disturbance is propagated outside in the form of elastic waves. It is conceivable that, if the in situ stress reaches a considerable magnitude and is removed in a very short period of time, the disturbance of stress release will produce microseismic vibrations in surrounding rock masses.

A simple and vivid spring model shown in Fig. 1 can be used to reveal the microseismic vibrations by the transient release of in situ stress during deep rock mass blasting. Under the stress σ, the flabby spring (Fig. 1a) will be compressed by a certain displacement, and this resembles the initial stress state of rock masses (Fig. 1b). If the stress is slowly removed, the spring will be slowly restored to its original state and stop at the equilibrium position, as the dashed line shows (Fig. 1c). However, if the sudden removal of stress happens, the spring will rebound at a high speed and extend below the equilibrium position due to an inertial force (Fig. 1d) and then vibrate up and down. Compared to the quasi-static unloading, the transient release behaves as if an equivalent tensile stress (σ) is acted on the newly formed excavation boundary.

Fig. 1
figure 1

Schema of the transient release of in situ stress induced microseisms

Full size image

In the field of blasting engineering, the intensity of microseismic vibrations is commonly described by the peak particle velocity (PPV), as it is well correlated with the degree of vibrational damage to structures. On the basis of the elastic unloading theory, the PPV on the excavation face can be expressed in terms of the stress jump at the wave front:

$$ v_{\text{r0}} = \frac{\sigma }{{\rho_{\text{r}} C_{\text{p}} }} $$
(1)

where v r0 is the PPV on the excavation face, σ is the stress jump at the wave front, ρ r is the rock mass density, and C p is the P-wave velocity in the rock mass.

3 Review of Field Data

3.1 Project Background and Field Tests

The Pubugou Hydropower Station is located in the western part of Sichuan Province in China and in the midstream of the Tatu River, a branch of the Yangtze River. Its underground powerhouse consists of a main powerhouse, a main transformer chamber, a gate chamber, diversion tunnels, and tailrace tunnels, as can be seen in Fig. 2. The main powerhouse measures 290.65 × 26.80 × 66.68 m (length × width × height), and the main transformer chamber arranged downstream has a size of 250.30 × 18.30 × 25.58 m. The in situ stress of this region is dominated by tectonic stress and reaches a moderate-to-high magnitude. Both the maximum principal stress σ 1 (21.1–27.3 MPa) and the minimum principal stress σ 3 (10.2–12.3 MPa) are horizontal, with a 20–30° angle between the maximum and the longitudinal axis of the main powerhouse. The intermediate principal stress σ 2 (15.5–23.3 MPa) approaches the vertical direction.

Fig. 2
figure 2

Layout of the underground powerhouse in the Pubugou Hydropower Station

Full size image

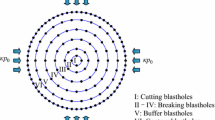
The main powerhouse is excavated in nine horizontal layers and each layer has a height of about 8.0 m, as is shown in the excavation procedure in Fig. 3. In the II–VII layers, a middle cut blast is carried out prior to both sides of protective layers, with a cycle footage of 8.0 m. During the middle cut blast of the IV layer, we monitored blasting-induced microseisms. Figure 4 shows the arrangement of the measurement points and the blasting design, where σ T and σ L are the transversal and longitudinal in situ stresses, respectively. Detailed blasting parameters are listed in Table 1. Here, the blast is divided into eight delays, with 4–5 blastholes detonated in each delay. Odd series of non-electric millisecond delay detonators labeled as MS1–MS15 are adopted. Their delay time is listed in Table 2. The 1#–8# measurement points of vibration sensors are arranged on the floor of the main powerhouse, and the 9# and 10# vibration sensors are located on the side wall of the main transformer chamber directly toward the blasting area.

Fig. 3
figure 3

Diagrammatic representation of the excavation procedure of the underground powerhouse (units: m)

Full size image
Fig. 4
figure 4

Diagrammatic representation of the microseismic monitoring and blasting design (units: m)

Full size image
Table 1 Blasting design parameters of the deep rock mass blast case and the open-pit blast case
Full size table
Table 2 Delay time of the millisecond delay detonators
Full size table

Figure 5 shows typical radial velocity–time histories measured at the 6# and 10# points in the Pubugou Underground Powerhouse. To focus on the influence of the horizontal radial in situ stress on microseismic vibrations, only radial velocity–time histories are presented. Since the vibration signals of the first four delays are not separated clearly from each other, the vibration signals of the MS9, MS11, MS13, and MS15 delays are analyzed in the present study.

Fig. 5
figure 5

Radial velocity–time histories monitored in the Pubugou Underground Powerhouse. a 6# measurement point. b 10# measurement point

Full size image

To better identify microseisms by the transient release of in situ stress during the cut blast of the Pubugou Underground Powerhouse (deep rock mass blast case), a case of open-pit blast with similar rock properties and drilling–blasting parameters is cited from our previous work as a comparison (Lu et al. 2011a). Compared to the blast in the deep rock mass, the initial in situ stress in the open-pit blast can be ignored. This open-pit blast case is taken from the ash storage base excavation of the Huaneng Fuzhou Power Station. The blast is divided into ten delays and a single blasthole is detonated in each delay. The adopted drilling–blasting parameters are also listed in Table 1. Figure 6c, d shows typical radial velocity–time histories (third delay) from site monitoring in the Huaneng Fuzhou Power Station (open-pit blast case). The two measurement points are both on one side of the blasting area and their distances from the source of the blast are 31 and 51 m, respectively.

Fig. 6
figure 6

Microseismic signals of single delay and corresponding time–energy density curves. a 6# measurement point of the deep rock mass blast case. b 10# measurement point of the deep rock mass blast case. c 1# measurement point of the open-pit blast case. d 2# measurement point of the open-pit blast case

Full size image

3.2 Microseismic Signal Analyses

For the blast case of the underground powerhouse, these radial microseismic signals may contain vibrations induced by explosion and the transient release of in situ stress, respectively. Unfortunately, the two different vibrations which overlap with each other have no clear identification points in the recorded velocity–time histories (see Fig. 5). This presents a considerable challenge to distinguishing visually the microseisms induced by the transient release of in situ stress.

3.2.1 Time–Energy Density Analysis of Wavelet Transform

The time–energy density analysis of wavelet transform has recently been introduced by several investigators to process non-stationary random signals of blasting vibrations, as it can detect the signal catastrophe (Ling and Li 2004; Cheng et al. 2005). During a blast of the deep rock mass, both explosion and the transient release of in situ stress are the energy sources of blasting microseisms. Different energy inputs in the mechanism will generate an energy catastrophe. So, peaks in the time–energy density curves allow identification of the transient release of in situ stress induced microseisms.

If f(t) (in our case, the vibration records) is a function belonging to L 2(R), a space of all finite energy functions, the continuous wavelet transform of f(t) is defined as:

$$ W_{f} \left( {a, \, b} \right) = \left\langle {f(t), \, \psi_{a,b} (t)} \right\rangle = \left| a \right|^{{ - \frac{1}{2}}} \int\limits_{R} {f\left( t \right)\psi \left( {\frac{t - b}{a}} \right)} dt $$
(2)

with:

$$ \psi_{a, \, b} \left( t \right) = \left| a \right|^{{ - \frac{1}{2}}} \psi \left( {\frac{t - b}{a}} \right) $$
(3)

where ψ a,b (t) is called the analyzing wavelet or continuous wavelet, ψ(t) is the wavelet basis or mother wavelet, a is a scale parameter which controls the frequency content of the dilated wavelet basis, and b is a time parameter which localizes or centers the wavelet basis at and around t = b.

The wavelet transform of f(t) is energy conservation, and then the following formula holds:

$$ \int\limits_{R} {\left| {f\left( t \right)} \right|^{2} } dt = \frac{1}{{C_{\psi } }}\int\limits_{R} {\frac{da}{{a^{2} }}} \int\limits_{R} {\left| {W_{f} \left( {a, \, b} \right)} \right|^{2} db} $$
(4)

with:

$$ C_{{{\uppsi}}} = \int\limits_{R} {\frac{{\left| {\hat{\psi }(w)} \right|^{2} }}{\left| w \right|}} dw < \infty $$
(5)

where C ψ is taken as the admissibility condition and \( \hat{\psi }(w) \) is the Fourier transform of ψ(t).

\( \left| {W_{f} \left( {a, b} \right)} \right|^{ 2} /\left( {C_{{{\uppsi}}} a^{ 2} } \right) \) can be taken as the energy density function in plane (a, b). That is to say, \( \left| {W_{f} \left( {a, b} \right)} \right|^{ 2} /\left( {C_{{{\uppsi}}} a^{ 2} } \right) \) gives the energy in space (a ± Δa, b ± Δb). Thus, Eq. (4) can be written as:

$$ \int\limits_{R} {\left| {f\left( t \right)} \right|^{2} dt} = \int\limits_{R} {E\left( b \right)db} $$
(6)

with:

$$ E\left( b \right) = \frac{1}{{C_{\psi } }}\int\limits_{R} {\frac{1}{{a^{2} }}\left| {W_{f} \left( {a, \, b} \right)} \right|^{2} da} $$
(7)

where E(b) is called the time–energy density function. It shows the energy distribution of signals at all frequency bands with the change of time parameter b. The following formula gives the energy distribution of signals in an integrating range [a 1, a 2] with the change of time parameter b:

$$ E^{\prime}\left( b \right) = \frac{1}{{C_{\psi } }}\int\limits_{{a_{1} }}^{{a_{2} }} {\frac{1}{{a^{2} }}\left| {W_{f} \left( {a, \, b} \right)} \right|^{2} da} $$
(8)

E′(b) is called the local time–energy density function and it shows all the energy of signals in the range from scale (frequency) a 1 to scale (frequency) a 2. By selecting different values of a 1 and a 2, the distribution of signal energy in different frequency bands can be obtained.

The choice of wavelet basis for a particular application depends on the objectives of analysis and the type of functions analyzed. The Daubechies’ wavelets, which are orthogonal, nearly symmetric, as well as relatively smooth and also allow for compact representation of the original signals and fast algorithm implementation (Daubechies 1988), have been successfully applied to process non-stationary signals, including blasting vibration signals (Iyama and Kuwamura 1999; Ling and Li 2004; Cheng et al. 2005; Amiri and Asadi 2009). Among the wavelet bases, the function that attenuates speedily and whose wave shape is similar to the analyzed signals should be chosen (Ling and Li 2004). According to the requirement, the wavelet function of 8th-order Daubechies (Db8) is employed in the present study. By choosing appropriate scale parameters a 1 = 1 and a 2 = 125 to let the integrating range locate within the frequency bands of the vibration records, the single delay vibration signals are transformed with the Db8 wavelet basis to get local time–energy density distributions, as shown in Fig. 6 (only the MS11 delay of the deep mass blast case is given in the figure).

From Fig. 6c, d, the time–energy density curves of the open-pit blast are mainly composed of three to four peaks, which are centralized and constituted a peak group. In the case of open-pit blast, the initial in situ stress of the rock mass can be ignored. This means that the blasting-induced microseisms result from explosion alone and the peak group corresponds to only one excitation source, the blasting load. However, two distinct peak groups corresponding to two excitation sources can be seen in Fig. 6a, b in the case of deep rock mass blast. It is the authors’ belief that the two excitation sources are the blasting load and the subsequent transient release of in situ stress.

3.2.2 Amplitude Spectrum Analysis

As the blasting design in Fig. 4 shows, blasting conditions related to two adjacent delays are basically identical except for the shot-to-sensor distances and the transversally initial in situ stresses on excavation boundaries. Our numerical simulation reveals that slight differences in shot-to-sensor distances hardly influence the vibration velocities beyond 30 m away from the blasting site. Thus, comparing the vibrations between two adjacent delays enables the further identification of the microseismic events induced by the transient release of in situ stress. Since no clear identification points between these two different vibrations can be observed in the recorded velocity–time histories (Fig. 5), the frequency domain is selected in order to study this problem.

In view of the possibility that there are some overlaps of frequency bands between vibrations induced by the in situ stress release and those of the blast, an amplitude spectrum analysis is made in the present study, as its dominant frequencies allow the detection of signals of different frequency bands to a great extent. After microseismic signals are collected, the amplitude spectrum of signals can be estimated by utilizing the Fourier transform. Its mathematical expression is as follows:

$$ F(\omega ) = \int\limits_{ - \infty }^{\infty } {f(t)e^{ - i\omega t} dt} $$
(9)

where ω is the circular frequency and the function F(ω) is defined as the amplitude spectrum of f(t).

Figure 7 shows the amplitude spectrum comparisons between the MS9 and MS11 delays of the deep rock mass blast, as well as the amplitude spectrum of the single delay of the open-pit blast. For each single delay, microseismic signals in the open-pit blast distribute mainly below 50 Hz and has only one dominant frequency. But for the deep rock mass blast, each single delay vibration has two dominant frequencies, and the frequencies of all inflection points between two peak amplitudes are within a range of 80–90 Hz, without exceptions. This implies that the vibrations which have different dominant frequencies do not originate from some accidental factors, such as the delay errors of detonators, but, instead, come from inevitable excitation sources, say, the blasting load and the transient release of in situ stress.

Fig. 7
figure 7

Amplitude spectrum curves for single delay microseismic signals. a 6# measurement point of the deep rock mass blast case. b 10# measurement point of the deep rock mass blast case. c 1# measurement point of the open-pit blast case. d 2# measurement point of the open-pit blast case

Full size image

During the middle cut blast of the Pubugou Underground Powerhouse, the eight delays shown in Fig. 4 are grouped according to their initiation scheme: MS1, MS5, MS9, and MS13 from the first group and MS3, MS7, MS11, and MS15 from the second group. The results from the finite element method indicate that, corresponding to initiations of the first and second delay detonator groups, the longitudinally initial in situ stresses σ L on the excavation boundaries are 7.6 and 8.6 MPa, respectively, with a percentage difference of only 11.6 %, but the transversally initial in situ stresses σ T are 16.6 MPa (near the longitudinal axis) and 33.0 MPa (near the protective layer), respectively, and have a difference of 49.7 %. Details of the peaks of the amplitude spectrum curves from the deep rock mass blast are listed in Table 3. In the frequency range 0–85 Hz, at the 6# and 7# points where the directions of measured radial vibrations are parallel to the longitudinal axis of the main powerhouse, the amplitude spectrum peaks have a smaller difference between the two adjacent delays, about 9.2 % on average, while at the 9# and 10# points, where the radial vibrations are perpendicular to the longitudinal axis, they differ widely and the average difference reaches up to 42.9 %. In addition, because the initial in situ stress of the first delay group is less than that of the second group, all the differences of the amplitude spectrum peaks at each point are negative. The foregoing quantitative analyses show that, within 85 Hz, the amplitude spectrum peaks correlate well with the in situ stresses on the excavation boundaries. This permits us to conclude that the frequencies of microseismic vibrations due to the transient release of in situ stress are mainly distributed in the range 0–85 Hz. In the relatively high-frequency range of 85–400 Hz, some differences of amplitude spectrum peaks are positive. This is because the delays with five blastholes to be detonated have a larger charge weight and induce stronger vibrations. In other words, the charge weight only affects the vibration amplitudes at high frequency.

Table 3 Amplitude spectrum peaks of the single delay microseismic signals
Full size table

Based on the above qualitative and quantitative analyses, it can be concluded that the microseismic waves induced by the deep rock mass blast are superposition of different vibrations which are produced by the blasting load and the transient release of in situ stress, respectively. The low-frequency component in the recorded microseisms results mainly from the transient release of in situ stress, while the high-frequency component originates primarily from the blasting load. We believe that it is because the blasting load has a shorter rising time and a higher load gradient, while the transient release of in situ stress lasts longer. Details over the load variations will be discussed in the next section. Compared to explosion-induced vibrations having similar PPVs, the low-frequency vibrations associated with the transient release of in situ stress are more adverse to underground structures, as the natural frequencies of engineering structures are relatively low. Investigating the transient release of in situ stress induced microseisms requires an effective identification and separation from recorded microseismic signals. On the basis of the above analyses, the microseismic waves induced by the transient release of in situ stress can be approximately obtained by separating the low-frequency component from the microseismic records with a low-pass filter. The remaining high-frequency signals after being filtered are mostly explosion-induced microseismic waves. In the present study, filtering is carried out by a finite impulse response (FIR) digital filter, which is a stable system and has characteristics of allowing exact linear phases and preventing delay distortion. The window function method is applied to the design of FIR due to its explicit physical meanings. According to the frequencies of the inflection points between two peaks in the amplitude–frequency curves shown in Fig. 7a, b, the cutting frequency is determined as 85 Hz.

4 Mechanism and Mechanical Process

4.1 Energy Release of Deep Rock Mass Excavation

Excavation-related stress paths, stress states, and dynamic responses of rock masses, in the final analysis, are the rock energy accumulation, storage, dissipation, and release. Thus, microseismic vibrations induced by the transient release of in situ stress can be explained from the viewpoint of elastic strain energy release. Assuming that an original rock mass under triaxial stress is in the elastic equilibrium state, in the principal stress space, elastic strain energy density has the following mathematical expression (Solecki and Conant 2003):

$$ e = \frac{1}{2E}\left[ {\sigma_{1}^{2} + \sigma_{2}^{2} + \sigma_{3}^{2} - 2\mu \left( {\sigma_{1} \sigma_{2} + \sigma_{2} \sigma_{3} + \sigma_{1} \sigma_{3} } \right)} \right] $$
(10)

where e is the elastic strain energy density, E is the elastic modulus, σ 1, σ 2, and σ 3 are the principal stresses, and μ is Poisson’s ratio.

For the rock mass containing n elements, its elastic strain energy U is:

$$ U = \sum\limits_{j = 1}^{n} {e_{j} } \cdot V_{{{\text{r}}j}} $$
(11)

where e j and V rj are the elastic strain energy density and volume of the jth rock element, respectively.

When an opening is excavated in the rock mass, the distribution of stress in the remaining rock mass is changed by excavation operations, which alter the geometry of the original rock mass and completely release the normal in situ stress on the excavation boundary. A stress-affected zone is formed in the immediate vicinity of the excavation boundary. Due to deformation and stress adjustment, an amount of energy in this zone is released. Together with the strain energy stored in the rock mass for removal, the sum ΔU is the total energy released in specific excavation footage:

$$ \Updelta U = U_{ 1} + U_{2} - U_{2}^{\prime } $$
(12)

where U 1 and U 2 are the elastic strain energy included in the excavation zone and the stress-affected zone, respectively, before excavation, and U 2′ is the strain energy included in the stress-affected zone after excavation, as shown in Fig. 8.

Fig. 8
figure 8

Diagrammatic representation of the excavation-induced changes of stress and elastic strain energy

Full size image

The deep rock mass under triaxial stress can store tremendous elastic strain energy, and the amount of released energy by excavation considerably exceeds the energy ΔG required to dynamically fracture the rock mass. The excess amount:

$$ \Updelta K = \Updelta U - \Updelta G $$
(13)

in most cases is converted into kinetic energy and released in the form of rock bursts or microseismic vibrations. For a rock mass characterized by elastic modulus E = 20,000 MPa and Poisson’s ratio μ = 0.3, assuming that the vertical and horizontal stresses are 25 and 20 MPa, respectively, the released kinetic energy by excavating 1,000 m3 of the rock mass can reach up to 108 N × m (Zhao et al. 2003). Due attention must be paid to the enormous kinetic energy release by excavation when underground openings are designed and constructed. When the method of drill and blast is adopted in excavation, the energy of explosion, besides being mostly spent in crushing and breaking the rock mass, is also released in the form of kinetic energy and generates microseismic vibrations, which are coupled with the stress release-induced microseismic vibrations in the surrounding rock mass. Thus, Eq. (13) can be rearranged to yield the kinetic energy:

$$ \Updelta K = KU_{\exp } + \Updelta U - \Updelta G $$
(14)

where U exp is the energy of explosion and K < 1.

4.2 Transient Release Process of In Situ Stress

Figure 9a presents a geometrical design of the bench blast used in most underground projects today, where B is the drilled burden and S is the spacing between adjacent blastholes. Compared to open-pit blasts, the major difference is that the rock mass is subjected to longitudinal and transversal stresses. Accompanying the breakage process of the burden, the longitudinal and transversal in situ stresses are simultaneously released. Here, the transient release process of in situ stress will be discussed in the longitudinal direction. For the commonly used hole-bottom initiation, the release process of in situ stress can be divided into three phases, as the diagrammatic representations show in Fig. 9b, c, where L 1 is the charge length, L 2 is the stemming length, D is the velocity of detonation, C p is the P-wave velocity in the rock mass, C f is the average velocity of crack propagation (C f = 0.2−0.3C p), C u1 and C u2 are the average velocities of rarefaction waves in detonation gases, and v g is the gas venting velocity.

Fig. 9
figure 9

Mechanics model adopted to determine the transient release process of in situ stress. a Isometric view. b Vertical section view. c Cross-section view

Full size image

Firstly, after the initiation of the explosive at the blasthole bottom, detonation waves are propagated in the column of the explosive at the velocity of D, and then the initial explosion pressure, which denotes the gas pressure applied to the blasthole wall, rises to a maximum of P b0 in a very short period of time. Shock waves, meanwhile, are produced in the surrounding rock mass and propagated at a velocity higher than the P-wave in the rock mass.

Secondly, detonation gases at high pressure propel the deformation of the rock mass surrounding the blasthole, the generation of cracks and further extension at the velocity of C f, as well as the movement of stemming, which, in turn, cause expansion for the gases and initially reduce the blasting load. At this moment, local in situ stress is released in a small area near blast-induced cracks.

Finally, detonation gases burst out to the atmosphere through the stemming column or the opening of burden. By using the modified DDA-BLAST code, Mortazavia and Katsabanis (2001) simulated the processes of burden breakage, fragment throw, and muck pile formation during a typical bench blast. They conclude that, when a small burden (the distance between the individual rows of blastholes) is employed, the opening of the burden occurs at its mid-point due to a significant bending. However, the pressure has already dropped to zero due to a large expansion at the time of venting. While at a burden greater than 1.5 m, gases try to force a path to the atmosphere through the stemming column rather than opening a path in the burden, owing to the inertial resistance of burden. Therefore, for this bench blast case with a burden of 2.0 m, in the final phase, detonation gases vent to the atmosphere along the blasthole after the ejection of stemming. It produces a group of rarefaction waves propagating in gases from top to bottom at the average velocity C u1. When the down-propagating rarefaction waves arrive at the solid end of the bottom, they are reflected as up-propagating rarefaction waves with an average velocity of C u2, leading to a further decline of the gas pressure. With cracks further developing, the excavation face is subjected to both the gas pressure and the in situ stress. According to stress continuity conditions, only when cracks between adjacent blastholes are interconnected and the gas pressure decays to a level equaling the initial stress on the excavation face, the in situ stress begins to be entirely released along the newly formed excavation face. In most cases, with rarefaction wave reflections reaching the orifice, the gas pressure has declined to the same level of the atmosphere pressure. The process of the in situ stress release simultaneously ends, and normal and shear stresses on the excavation face are completely released.

The whole release process of the in situ stress shown diagrammatically can be plotted in Fig. 10, which is mathematically expressed in the following formula:

$$ P_{\text{r}} (t) = \left\{ \begin{aligned} &\sigma { 0} \quad \le t \le t_{\text{b}} \\ &P_{\text{b}} (t ) \quad { }t_{\text{b}} < t \le t_{\text{d}} \\ \end{aligned} \right. $$
(15)

where P r(t) is the release process of the in situ stress, σ is the initial stress on the excavation face, P b(t) is the blasting load variation versus time, t b is the beginning time of the in situ stress release, and t d is the duration of the blasting load.

Fig. 10
figure 10

Variations of the blasting load and the transient release of in situ stress versus time

Full size image

Obviously, the beginning and variation of the transient release of in situ stress depend on the stress magnitude, on the excavation face, and the blasting load variation versus time. In a millisecond delay blast, the initial stress corresponding to a certain delay time is the secondary stress produced by the blast in the previous delay. The blasting load variation applied to the blasthole wall can be obtained by combined calculations of the blasthole expansion, crack growth, stemming movement, and detonation gas venting. It has been studied in detail by Lu et al. (2011b), as the curve in Fig. 10 shows.

According to the Chapman–Jouguet model for the detonation wave in a condensed explosive, the initial explosion pressure P b0 is guided by the widely known equation (Henrych 1979):

$$ P_{\text{b0}} = \frac{{\rho_{\text{e}} D^{2} }}{2(\gamma + 1)}\left( {\frac{{d_{\text{c}} }}{{d_{\text{b}} }}} \right)^{2\gamma } $$
(16)

where P b0 is the initial explosion pressure, ρ e is the explosive density, d c is the charge diameter, d b is the blasthole diameter, and γ is the ratio of the specific heats for the detonation gases. From experimental results, the constant γ is expected to be in the range 1.2–3.0.

It is assumed that the explosion gases behave ideally and no heat losses occur. The pressure variation P b(t) on the blasthole wall can be obtained through the widely used ideal gas law equation:

$$ P_{\text{b}} (t) = \left( {\frac{{V_{\text{b}} }}{{V_{\text{g}} (t)}}} \right)^{\gamma } P_{{{\text{b}}0}} $$
(17)

where V b is the initial blasthole volume and V g(t) is the gas volume at any time.

The rising time of the blasting load t r can be determined as:

$$ t_{\text{r}} = \frac{{L_{1} }}{D} $$
(18)

The duration of the blasting load can be approximately determined by using the equation:

$$ t_{\text{d}} = \frac{{L_{1} }}{D} + \frac{{\sqrt {\left( {\frac{1}{4}S^{2} + L_{2}^{2} } \right)} }}{{C_{\text{f}} }} + \frac{{L_{1} + L_{2} }}{{C_{\text{u1}} }} + \frac{{L_{1} + L_{2} }}{{C_{\text{u2}} }} $$
(19)

The duration of the transient release of in situ stress is available as:

$$ \Updelta t = t_{\text{d}} - t_{\text{b}} $$
(20)

where Δt is the duration of the in situ stress release.

Bench blasts or full-face blasts in most underground projects in China normally use blasthole diameters from 42 to 110 mm, spacing from 0.8 to 2.5 m, and blasthole lengths from 1.5 to 10.0 m. Propagation velocities of rarefaction waves in the detonation gases of most commercial explosives used in China range from 500 to 1,000 m/s. P-wave velocities in rock masses are assumed to be in the range from 4,000 to 6,000 m/s. If the initial in situ stress reaches a magnitude of 10–50 MPa, it can be estimated by Eqs. (15)–(20) that the duration of the in situ stress release Δt lies in the range 2–10 ms, which is in accordance with the results of high-speed photography and numerical simulations (Preece et al. 1993; Mortazavi and Katsabanis 2001; Zhu 2009). Under such conditions, the strain rate due to the in situ stress release is estimated at a magnitude of 10−1–101 s−1 or higher. It is generally accepted that, when the strain rate caused by loading or unloading exceeds the critical value of 10−1 s−1, the inertial force should not be ignored and the process is a dynamic one (Henrych 1979). However, in previous studies, most researchers tended to take the in situ stress release of rock masses as a quasi-static process without considering the transient release of rock energy and resultant dynamic responses.

The instantaneity of the blasting load determines that the in situ stress release on the excavation face is really a transient process. The enormous elastic strain energy ΔK released in several milliseconds induces microseisms in the surrounding rock mass inevitably. Based on Eqs. (10)–(14), it can be concluded that the intensity of the microseismic vibrations is correlated with the magnitude of the in situ stress and the dimension of the excavation face.

5 Demonstration by Numerical Calculation

5.1 Numerical Model and Parameters

To demonstrate the theory presented in our study, particle vibration velocities in the surrounding rock mass induced by the blasting load, the transient release of in situ stress, and the combined action of both are simulated by employing the dynamic finite element software ANSYS/LS-DYNA. The region of analysis is an underground block (Fig. 11) with dimensions 190 × 130 × 120 m (length × width × height). The main powerhouse and the main transformer chamber are excavated in its middle part. A bench height of 8.0 m, which is the area where the blasting and the transient release of in situ stress are simulated, is located in the upper zone of the main powerhouse. The underground block is granite characterized by elastic modulus E = 20,000 MPa, density ρ r = 2,610 kg/m3, and Poisson’s ratio μ = 0.21. Only the rock mass nearby to blastholes becomes yielded, greater than some distance, the blasting wave does not have enough energy to damage the rock mass, and at long distances, is propagated as an elastic wave (Toraño et al. 2006; Lu et al. 2011b). Therefore, the rock mass is treated as an elastic material in this simulation. It should be noted that, when a deep underground opening is excavated with the method of drill and blast, a fractured zone or an excavation damage zone (EDZ) would be induced close to the surface of the remaining rock mass. Therefore, the rock mass near the excavation perimeter including the wall, floor, and bench face would deteriorate and be different from the virgin rock mass. One approach to accounting for fracturing is to consider the fractured rock mass as an effective elastic medium, in which the elastic constants are related to the density of fracturing. Since only far-field microseismic vibrations are simulated in the present study, in this numerical model, two layers of weak elements, which extend 0–0.5 and 0.5–1.0 m, respectively, from the excavation perimeter into the rock mass, are used to simplify the EDZ according to the study of Martino and Chandler (2004). Because there are no test data available for rock mass properties in the EDZ, numerical tests are carried out by comparing simulated vibrations with recorded data. The elastic modulus of the rock mass in the inner weak layer, close to the excavation perimeter, is reduced by 50 %, and in the outer weak layer, it is reduced by 20 %. The other properties and loads are left equal to those of the virgin rock mass.

Fig. 11
figure 11

Dynamic finite element model used for the calculations

Full size image

The block is divided into a mesh of hexahedron-shaped finite elements, where the eight-node brick element is adopted in the current study. Kuhlemeyer and Lysmer (1973) suggested that the mesh size should be shorter than 1/8th–1/10th of the wavelength in order to reduce properly any wave distortion. According to this requirement, the element sizes in this model vary from 0.5 m near the pressuring point to 2.5 m at the border. The model mesh has 308,904 elements and 324,987 nodes. The time step size corresponds roughly to the time of an acoustic wave propagation through an element using the shortest characteristic length, which is given as the cube root of the element volume. According to the shortest characteristic length of 0.5 m and P-wave velocity of 4,400 m/s, the time step of 0.1 ms is selected in the present simulation. Non-reflecting boundaries are enforced on the exterior faces of the model to prevent artificial stress wave reflections from reentering the model and contaminating the results. The damping in the model is done through the Rayleigh classical approach by making the damping matrix equal to a linear combination of the mass and stiffness matrices. The values used in our case are 4.0 and 0.00007, respectively.

Numerically, the blasthole pressure is usually approximated by the Jones–Wilkins–Lee (JWL) equation of state. It is a simple pressure–volume–energy equation of state developed to predict the adiabatic expansion of detonation products under an effective stemming without taking gas venting into account. Thus, in our calculations, the shape of the pressure pulse shown in Fig. 10 is employed as a direct input of dynamic load. The following explosive properties are considered: explosive density ρ e = 1,000 kg/m3, velocity of detonation D = 3,500 m/s, and ratio of the specific heats γ = 3.0. Substituting these explosive properties and the blast design parameters listed in Table 1 into Eqs. (15)–(20) gives the peak blasting load applied to the blasthole wall P b0 = 338.9 MPa, the rising time of the blasting load t r = 1.8 ms, the duration of the blasting load t d = 8.0 ms, and the duration of the transient release of in situ stress Δt = 4.0 ms. The variations of loads are plotted in Fig. 10. In view of highly complicated stress conditions and changes of the rock mass continuity around a blasthole caused by rock fragmentation, the two dynamic loads are applied to the excavation face rather than the blasthole wall. Our previous study has indicated that this equivalent simulation method is applicable to the prediction of far-field microseismic responses of the ground subjected to blasting loads (Lu et al. 2011b). According to the Saint-Venant’s principle, the equivalent blasting load on the excavation face is given by P be(t):

$$ P_{\text{be}} (t) = \frac{{d_{\text{b}} }}{S}P_{\text{b}} (t) $$
(21)

The peak blasting load on the excavation face is equal to 15.3 MPa. On this non-hydrostatic pressure condition, besides the normal stress, the shear stress is also released, which is difficult to simulate directly in ANSYS/LS-DYNA. In order to implement this release process, the stresses on the excavation face obtained by static calculations are equally converted to nodal forces and then released in the manner described in Eq. (15).

5.2 Results and Discussion

Figure 12 shows the recorded microseismic signals of the single delay, the separated waves by the FIR filter, as well as the simulated waves (only the MS11 delay at the 6# and 10# measurement points is given in the figure), where BL, TRIS, and CA represent the blasting load, the transient release of in situ stress, and the combined action of both, respectively. Comparisons between the separated (or measured) and the computed results, such as peak velocities, frequencies, and duration of the velocity–time histories, show a satisfactory agreement. Table 4 gives the separated and simulated PPVs generated by the two excitations, respectively, in the delays of MS9–MS15. As can been seen, the intensity of the microseismic vibrations due to the transient release of in situ stress is comparable to that of the explosion; the ratio reaches up to 75 % on average in the longitudinal direction of the main powerhouse, and, especially in the transversal direction, the stress release surpasses the blasting load and dominates the vibrations due to excavation-induced stress concentrations. Therefore, during deep rock mass excavation by blasting, the microseisms by the transient release of in situ stress and related structural responses should be considered in blasting design and construction. In simulated waves, the microseismic frequencies by the transient release of in situ stress are significantly lower than those by the blasting load, which demonstrates the correctness of the signal analyses in Sect. 3. At the 6# measurement point on the floor of the main powerhouse, surface waves that arrive at the receiver later are also contained in the measured and computed waves, causing the waveforms to be more complicated and the duration to be prolonged. It should be noted that the frequency bands of the two phenomena have some overlaps and are not separated from each other clearly. The separation of waves in this paper is just an approximation of the two different microseismic vibrations, and the stress release-induced microseismic waves obtained by filtering still contain some low-frequency components of the explosion-induced vibrations. Because of a combination of this factor and others, such as drift errors of monitoring instruments and local rock looseness at measurement points, simulated waves differ somewhat from separated waves, especially at the tail part of waveforms.

Fig. 12
figure 12

Comparisons between the separated and simulated microseismic waves for a single delay. a 6# measurement point. b 10# measurement point

Full size image
Table 4 Separated and simulated peak particle velocities (PPVs)
Full size table

In view of a good agreement with the measured data, the attenuation with distance for microseismic waves in the MS11 delay is given by the numerical results, as plotted in Fig. 13, where the distance on the abscissa refers to the horizontal straight-line distance from the edge of the blasting area. Points of interest in the longitudinal direction are selected from the connecting line between the 1# point and the 6# point, and in the transversal direction from the same elevation with the 10# point. It can be seen from Fig. 13 that, within the distance of 20 m, the stress release-induced PPVs are greater than those by explosion owing to the concentration of stress after the blast in the MS9 delay, and then gradually tend to the other one. Due to amplification effects of the free side wall in the main transformer chamber, local amplification and then decay of the vibration velocities appear near the transversal distance of 40 m.

Fig. 13
figure 13

Attenuation with distance curves of the simulated peak particle velocities (PPVs). a Longitudinal direction of the main powerhouse. b Transversal direction of the main powerhouse

Full size image

Theoretical and experimental analyses show that blasting-induced velocities attenuate with distance as the negative power function. The PPV at any position of the ground subjected to dynamic loads takes the form (Lu and Hustrulid 2003):

$$ v_{\text{r}} = kv_{{{\text{r}}0}} \left( {\frac{{r_{\text{e}} }}{d}} \right)^{\alpha } = k\frac{\sigma }{{\rho_{\text{r}} C_{\text{p}} }}\left( {\frac{{r_{\text{e}} }}{d}} \right)^{\alpha } $$
(22)

where v r is the PPV at an observation point, k is a parameter describing the propagating media, r e is the size of the loading face, d is the distance from the loading face, and α is the attenuation exponent of velocity. For the bench blast in our study, r e and d refer specifically to the length of the bench blasted in a single delay and the distance from the connecting line of an individual row of blastholes.

Because of the free side wall in the main transformer chamber, the velocity variations in the transversal direction become more complex. Thus, only the PPVs in the longitudinal direction plotted in Fig. 13a are carried out the regression calculations as listed in the following formulae.

Transient release of in situ stress:

$$ v_{\text{r}} = 6.60\frac{\sigma }{{\rho_{\text{r}} C_{\text{p}} }}\left( {\frac{{r_{\text{e}} }}{d}} \right)^{1.51} \left( {{\text{Correlation coefficient }} = \, 0. 9 5} \right) $$
(23)

Blasting load:

$$ v_{\text{r}} = 7.74\frac{\sigma }{{\rho_{\text{r}} C_{\text{p}} }}\left( {\frac{{r_{\text{e}} }}{d}} \right)^{1.75 \, } \left( {{\text{Correlation coefficient }} = \, 0. 9 3} \right) $$
(24)

A better correlation coefficient shows that the distance–decay of the transient release of in situ stress induced microseismic velocities also follows the law of a negative power function. But it has a smaller attenuation index than that of the explosion-induced microseisms because the high-frequency component of vibrations decays faster. This regression formula can be used to predict the microseismic intensity by the transient release of in situ stress under similar field conditions and blasting parameters.

6 Conclusions

In this study, the release mechanism of the elastic strain energy and the release process of the in situ stress are discussed for deep rock mass excavation with the method of drill and blast. The release of strain energy around the excavation face is a transient process associated with the development of cracks, the outburst of detonation gases, and the formation of a new free surface. The enormous strain energy of deep rock masses released within several milliseconds in the form of kinetic energy will inevitably induce microseismic vibrations in surrounding rock masses. The blasting excavation-induced microseisms in high-stress rock masses are attributed to both explosion and the transient release of in situ stress. Furthermore, the stress release has the potential for surpassing the blasting load and dominating vibrations, depending on the magnitude of the in situ stress and the dimension of the excavation face. Based on the signal analyses and the comparisons with numerically simulated waves, it can be concluded that, in microseismic signals monitored in a deep rock mass blast, the low-frequency component results mainly from the transient release of in situ stress, while the high-frequency component originates primarily from blasting load. In view of the low natural frequencies of structures, the stress release-induced microseisms would aggravate the vibrational damage to structures in underground projects.

The work presented is just a preliminary identification and separation for the microseismic vibrations induced by the transient release of in situ stress. Some important parameters such as the detailed duration of the release process and the magnitude of stress release-induced vibrations, etc., cannot be directly determined from recorded vibration signals, and the simulation model employed is an equivalent elastic model. Notwithstanding its limitation, this study does provide an insight into the genetic mechanism of the excavation-induced microseisms. Based on the stress release-induced microseisms, further studies are required in order to determine the transient change of secondary stress distribution in surrounding rock masses.