1 Introduction

Hydraulic fracturing was first applied in the petroleum industry in the 1940s to stimulate productivity in low permeability oil-bearing formations. It has been one of the primary engineering tools for waste disposal in drill cuttings re-injection (CRI) and produced water re-injection (PWRI) wells. To successfully inject drill cuttings slurry or produced water under fracturing conditions, it is essential to predict the extent of hydraulic fractures accurately based on understanding the fundamental mechanism(s).

Besides the benefit of waste injection projects, another synergistic application for the hydraulic fracturing is unconventional resources. Hydraulic fracturing makes it possible to produce oil and natural gas in formations where conventional technologies are ineffective. One typical unconventional hydrocarbon source is natural gas produced from shale, termed “shale gas.” Because the shale may have insufficient permeability to allow significant fluid flow to a wellbore, many types of shale are currently not considered as commercial sources of natural gas. Recently, a significant increase in shale gas production has resulted from hydraulic fracturing, which is used to create extensive artificial fractures around wellbores. When combined with horizontal drilling, the hydraulic fracturing may allow formerly unpractical shale layers to be commercially viable. The fracturing process is complicated and needs to be accurately modeled to improve the efficiency of the fracturing.

Over the years research has been conducted on modeling the growth of fractures in various rocks and reservoir formations. Perkins and Kern (1961) performed a fluid mechanics study on the rupture of brittle materials and the theory of elastic deformation of rock. Their results indicated that for a given formation, crack width is essentially controlled by fluid pressure drop. High pressure drops result in relatively wide cracks, while low pressure drops result in relatively narrow cracks.

Rice and Rosengren (1968) investigated the crack-tip strain singularities with the aid of energy line integral exhibiting path independence for all contours surrounding a crack tip in a two-dimensional deformation field. Elastic and elastic/plastic materials were studied. Their study determined that the product of stress and strain exhibits a singularity varying inversely with distance from the tip in all materials.

Nordgren (1972) studied the propagation of hydraulic fractures of limited vertical and elliptic cross-section with the inclusion of fluid loss. His study determined that the fracture length and width grow faster with time in the no-loss than in the large loss case. Leung and Li (1989) developed an experimental technique for indirectly determining a tension-softening curve. The tension-softening curve is suggested to be a size-independent fracture ‘parameter’ for quasi-brittle materials. The technique was based on generating specimens that had a large size and a four-point bending mode.

Martin (2000) developed crack-tip plasticity (CTP) method, which assumed a fracture tip of finite radius, with a zone of plastically deformed material around it. The plastic zone forms when stresses on the rock increase beyond the yield point of the rock, at which point the rock starts to flow plastically. The plastic zone acts to absorb extra energy from the fracturing fluid, making it harder to propagate fractures through formations with significant plastic deformation. This in turn means that, for a given ductile material, fractures will be smaller and less conductive than those predicted by the Linear Elastic Fracture Mechanics (LEFM).

van Dam et al. (2000) performed scaled laboratory experiments of hydraulic fracture propagation and closure in soft artificial rock and outcrop rock samples. Numerical simulations of the fracture behavior in plastic rocks were also performed, using independently measured rock properties. The simulations aided in interpreting the measurements and extrapolating the results to field scale. Plasticity induces a larger width in a fracture for a given net pressure, compared with elastic rock. However, the pressure to propagate fractures was only marginally increased and, in the case of laboratory tests, was actually lower than expected from elastic behavior. The most dramatic effect of plasticity is that closure is much lower than the confining stress due to strong stress redistribution along the fracture.

Recently, Dean and Schmidt (2009) developed a geomechanical reservoir simulator that combined hydraulic fracture growth, multiphase/multicomponent Darcy/nonDarcy porous flow, heat convection and conduction, solids deposition, and poroelastic/poroplastic deformation in a single application. The program contained two separate criteria that could be used to model fracture propagation: a critical fracture-opening criterion based on a stress-intensity factor and a cohesive zone model that used quadrilateral cohesive elements in the fracture. The cohesive zone model includes a cohesive strength and an energy release rate in the calculations at the tip of a propagating hydraulic fracture.

Although research has been performed in the past few decades, the fundamental physics of hydraulic fracture in rocks, especially ductile rock, is still not clearly understood and requires further research. Most of the hydraulic fracture applications in the oil and gas industry still rely on empirical methods or linear elastic fracture mechanics (LEFM)-based numerical tools. Generally, these methods give reasonable predictions for hard rock hydraulic fractures. However, when applied to model long-duration injection in highly heterogeneous subsurface strata or hydraulic fracture in ductile shale and other soft rocks such as clay or weakly consolidated sandstone, LEFM-based methods typically give conservative predictions. One of the reasons for the conservatism is that the fracture process zone ahead of the crack tip is not negligible for ductile rock fracture analysis. For ductile rock (which are quasi-brittle in nature), a cohesive fracture mechanics-based method can be used to simulate the fracture tip effect. A method based on cohesive fracture mechanics is developed in this paper to incorporate the effect of fracture process zone and material softening on the ductile rock fracture.

2 The Basic Equations of Cohesive Fracture Analysis

Figure 1 shows the nonlinear zone ahead of a fracture in materials ranging from brittle to ductile. Generally, the nonlinear zone consists of two zones: the fracture process zone characterized by progressive softening and a nonlinear zone characterized by plastic hardening (Bazant and Planas 1998). Case 1 corresponds to a very brittle material. Since the entire nonlinear zone is small as compared to the structure size, LEFM is applicable to this case. Case 2 corresponds to a very ductile material where the softening zone is still small, but the nonlinear hardening zone is not negligible and dominates the fracture behavior (Yao et al. 2007). In this case, elasto-plastic fracture mechanics such as the HRR theory (Hutchinson 1968; Rice and Rosengren 1968) could be employed. HRR crack-tip field equations provide the theoretical foundation for the J-integral-based fracture criterion in elastic–plastic fracture mechanics, which is outside the scope of this paper. Case 3 corresponds to quasi-brittle material, where a major part of the nonlinear zone undergoes progressive damage with material softening due to micro-cracking and void formation. Here, cohesive fracture mechanics-based theory can be applied. Most of the ductile rocks, such as ductile shale, belong to case 3.

Fig. 1
figure 1

Fracture process zone in different materials

Full size image

Typical computational methods to predict the hydraulic failure of injection wells are linear elastic mechanics-based (Valko and Economides 1995). Recently, the pore pressure cohesive zone model (CZM) has been developed to predict hydraulic failure of different rocks. The cohesive zone method is a numerical tool developed to model crack initiation and growth in quasi-brittle materials (Saouma et al. 2003; Maier et al. 2006; Segura and Carol 2010). This method treats fractures as a gradual process in which separation between incipient material surfaces is resisted by cohesive traction. Compared with the traditional method (Perkins and Kern 1961), the CZM can be applied from micro- to macro-scale, as long as the parameters, cohesive strength and critical separation displacement, are determined by careful fracture experiments. The model can predict the entire fracture process from crack initiation to propagation accurately for any joint geometry and under any applied loads. Crack initiation and propagation are natural outcomes of a CZM analysis and has been adopted in current research through the finite element program, ABAQUS. The damage mechanics are incorporated into the model and the damage initiation and evolution conditions are defined. The model is applied to predict the effects of rock properties and fracture parameters on the hydraulic fracture process.

To incorporate a cohesive zone model into the finite element model, the principle of virtual work can be modified to be (Roe and Siegmund 2003):

$$ \int\limits_{V} {\tilde{P}:\delta \tilde{F}\,{\text{d}}V - } \int\limits_{{S_{\text{i}} }} {\vec{T}_{\text{CZ}} \cdot \delta \Updelta \vec{u}\,{\text{d}}S} = \int\limits_{\partial V} {\vec{T}_{\text{e}} \cdot \delta \vec{u}\,{\text{d}}S} $$
(1)

where \( \tilde{P} \) is the nominal stress tensor which equals \( \tilde{F}^{ - 1} \det (\tilde{F})\tilde{\sigma };\,\tilde{F} \) is the deformation gradient; \( \tilde{\sigma } \) is the Cauchy stress tensor; V is the control volume; \( \vec{u} \) is the displacement vector; \( \vec{T}_{\text{CZ}} \) is the cohesive zone traction vector; \( \vec{T}_{\text{e}} \) is the traction vector on the external surface of the body; S i is the internal boundary; and \( \partial V \) is the external boundary of V.

Figure 2 shows the typical cohesive element traction-separation (T-S) Law used in the model. For a simplest bi-linear traction-separation type cohesive zone model as shown in Fig. 2a, the interfacial stiffness is defined by:

$$ K_{\text{eff}} = \frac{{E_{\text{eff}} }}{{h_{\text{eff}} }} = \frac{{2G_{\text{IC}} }}{{\delta_{\text{ini}} \delta_{\text{fail}} }} $$
(2)

where E eff is the cohesive layer stiffness; h eff is the specific thickness; G IC is the fracture energy and equals to the area under the T-S curve; δ ini and δ fail are the separation at crack nucleation and element failure point, respectively.

Fig. 2
figure 2

Typical cohesive element traction-separation (T-S) Law

Full size image

The maximum traction at the crack nucleation point Tult is defined by (corresponding to stiffness degradation factor SDEG = 1 in ABAQUS):

$$ T_{\text{ult}} = \frac{{2G_{\text{IC}} }}{{\delta_{\text{fail}} }} $$
(3)

From Eqs. 2, 3 and Fig. 2a, \( \delta_{\text{ini}} = \frac{{T_{\text{ult}} }}{{K_{\text{eff}} }} = \frac{{T_{\text{ult}} h_{\text{eff}} }}{{E_{\text{eff}} }}\,{\text{and}}\,\delta_{\text{fail}} = \frac{{2G_{\text{IC}} }}{{T_{\text{ult}} }}. \)

Decreasing h eff or increasing E eff, the value of interfacial stiffness K in the T-S law increases.

In LEFM, when the cohesive zone size is much smaller than the fracture size, the fracture energy of Mode I can be defined by:

$$ G_{\text{IC}} = \frac{{K_{\text{IC}}^{2} }}{E}(1 - \nu^{2} ) $$
(4)

K IC is the fracture toughness; E is Young’s modulus, and ν is the Poisson’s ratio.

The leakoff model in pore pressure cohesive zone model is based on hydraulic fluid continuity. The tangential permeability (in ABAQUS it is actually resistance to fluid flow rather than permeability) k t is defined based on Reynold’s equation (ABAQUS User’s Manual 2011):

$$ k_{\text{t}} = \frac{{d^{3} }}{12\mu } $$
(5)

where μ is the fluid viscosity and d is the gap opening defined by:

$$ d = t_{\text{curr}} - t_{\text{orig}} + g_{\text{init}} $$
(6)

where t curr and t orig are the current and original cohesive element geometrical thicknesses, respectively; and g init is the initial gap opening.

Permeability of reservoir rock, or hydraulic conductivity \( \bar{k} \), is used in the finite element model:

$$ \hat{k} = \frac{\nu }{g}\bar{k} = \frac{\mu }{\rho g}\bar{k} $$
(7)

where ν is kinematic viscosity, μ is dynamic viscosity, ρ is fluid density (=1 for water), and g is gravity acceleration (=9.8 m/s2).

A quadratic nominal stress criterion to predict damage initiation is adopted in the current research. Damage is assumed to initiate when a quadratic interaction function involving the nominal stress ratios reaches unity. This criterion is represented as (ABAQUS User’s Manual 2011):

$$ \left( {\frac{{\left\langle {t_{\text{n}} } \right\rangle }}{{t_{\text{n}}^{0} }}} \right)^{2} + \left( {\frac{{t_{\text{s}} }}{{t_{\text{s}}^{0} }}} \right)^{2} + \left( {\frac{{t_{\text{t}} }}{{t_{\text{t}}^{0} }}} \right)^{2} = 1 $$
(8)

where \( t_{\text{n}} ,\,t_{\text{s}} ,\,t_{\text{t}} \) refer to the normal, the first, and the second shear stress components; and \( t_{\text{n}}^{0} ,\,t_{\text{s}}^{0} ,\,t_{\text{t}}^{0} \) represent the peak values of the nominal stress when the deformation is either purely normal to the interface or in the first or the second shear direction; the symbol \( \left\langle {} \right\rangle \) is the usual Macaulay bracket interpretation, used to signify that a purely compressive deformation or stress state does not initiate damage.

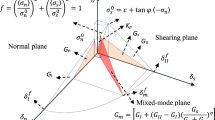
Typically, Mode-I-based fracture criteria are employed in conventional hydraulic fracture numerical models; however, it is not sufficient when a pronounced shear stress component exists. Mode II type fracture can play an important role under certain loading conditions in rock fracture mechanics. For example, the experiments performed by Lim et al. (1994) gave the mixed-mode fracture toughness data for a synthetic soft rock using the SCB specimens; the average of the experimental results for KIIc/KIc is 0.44. Under pure tensile or pure shear loading, the maximum Mode I stress-intensity factor is typically greater than the maximum Mode II stress-intensity factor. For brittle rocks, Mode I fracture toughness is usually smaller than Mode II fracture toughness, which will lead to Mode I fracture. Classical mixed-mode fracture criteria can only predict Mode I fracture but not Mode II fracture.

The damage evolution for mixed-mode failure in the current model is defined based on the Benzeggagh–Kenane fracture criterion (Benzeggagh and Kenane 1996), when the critical fracture energies during deformation along the first and the second shear directions are similar; i.e. \( G_{\text{s}}^{C} = G_{\text{t}}^{C} , \) the criteria is given by:

$$ G_{\text{n}}^{C} + (G_{\text{s}}^{C} - G_{\text{n}}^{C} )\left( {\frac{{G_{\text{S}} }}{{G_{\text{T}} }}} \right)^{\eta } = G^{C} $$
(9)

where the mixed-mode fracture energy \( G^{C} = G_{\text{n}} + G_{\text{s}} + G_{\text{t}} ; \) where G n, G s, and G t refer to the work done by the traction and its conjugate relative displacement in the normal, the first, and the second shear directions, respectively. \( G_{\text{n}}^{C} ,\,G_{\text{s}}^{C}\, {\text{and}}\,G_{\text{t}}^{C} \) refer to the critical fracture energies required to cause failure in the normal, the first, and the second shear directions, respectively. Here, \( G_{\text{S}} = G_{\text{s}} + G_{\text{t}} ,G_{\text{T}} = G_{\text{n}} + G_{\text{S}} , \) and η are material parameters. If a more complicated mixed-mode fracture criterion is required for a shear-dominated case, the user-defined subroutine can be developed to incorporate the specific failure criteria.

3 Simulation Model and Parametric Study

A three-layer 3D pore pressure cohesive element model is developed to predict hydraulic fracture caused by fluid injection as shown in Fig. 3a. The overburden, side burden and pore pressure boundary conditions are applied, as in Fig. 3b. Symmetry boundary condition is applied in the model and half wing of the fracture is simulated. A side burden is applied as a surface pressure along with a pore pressure. The top plane has an overburden pressure applied. The bottom plane is fixed in all three directions. The vertical plane represents the predefined cohesive element layer.

Fig. 3
figure 3

Three layers 3D pore pressure cohesive zone model to predict hydraulic fracture with one perforation zone

Full size image

An orthotropic overburden stress state is imposed with the maximum principle stress in the formation aligned orthogonal to the cohesive element fracture plane. User-defined subroutines were developed and incorporated into the numerical model to simulate leakoff coefficients (Ufluidleakoff), depth dependent realistic initial stresses (SIGINI) and pore pressure boundary conditions (UPOREP). A depth varying initial void ratio is specified using user subroutine VOIDRI. Gravity loading is also specified.

Firstly, a short-term water simplified injection case with zero leakoff has been analyzed to investigate the accuracy of fracture geometry prediction using the developed model. A low-viscosity Newtonian fluid with a viscosity of 1 × 10−6 kPaS (1 centepoise, roughly the viscosity of water) is injected at a surface rate of 2 bbl/min for 30 min. A linear Drucker–Prager model with hardening is chosen for the rock, the elastic modulus, Poisson’s ratio, and critical stress-intensity factor for the rock are 3.45 GPa, 0.3, and 1.1 MPa \( \sqrt m , \) respectively. The injection point (perforation zone) is set at the middle zone (the middle layer). Figure 3c, d show the fracture prediction in cohesive element layer and corresponding fracture schematic.

The predicted fracture length and critical cohesive separation δ fail is given in Table 1. The result shows that, compared with the LEFM-based Pseudo 3D model and the PKN method (Perkins and Kern 1961; Nordgren 1972), the fracture length predicted using the pore pressure cohesive zone model is closer to the analytical solution.

Table 1 Fracture length and critical cohesive separation predicted using different models
Full size table

With similar injection and material conditions, the fracture propagation with two perforation zones is investigated using pore pressure cohesive zone model. The boundary and fracture schematic is shown in Fig. 4a, b. Figure 4c, d show the fracture prediction by defining the same rock properties at the upper and lower layer, when the distance between the two injection intervals is 20 and 40 m, respectively. Similar fracture geometry is observed in both perforation zones. Figure 4e, f show the fracture prediction by defining the upper layer as brittle rock and bottom layer as ductile rock, respectively. It is observed that the fracture in hard rock is longer and narrower compared with the fracture in ductile rock, which matches with the field observations. The shorter fracture in the ductile rock is partially due to the fact that the larger deformation in ductile rock absorbs more energy than hard rock, and less energy is being used to extend the fracture. If the injection intervals are far enough from each other, independent fractures are propagated; if the two injection intervals are close to each other, the fractures will merge and fracture geometry is dominated by the fracture in brittle rock.

Fig. 4
figure 4

Fracture in brittle and ductile rock predict using pore pressure cohesive zone model with two perforation zone

Full size image

The elastic modulus effect on fracture length and width was investigated using the developed finite element model. As shown in Fig. 5, with the decrease of elastic modulus, the fracture length decreases and fracture width increases, this matches the observations in field. Leakoff coefficient is typically used to calculate the time-dependent fluid leakoff velocity and overall fluid loss based on mass conservation; it is a combination of the mechanisms acting to prevent fluid loss to the formation. The leakoff coefficient used in the cohesive fracture model is based on hydraulic conductivity and different from that typically adopted in the oil and gas industry, i.e. the Carter’s leakoff coefficient.

Fig. 5
figure 5

Elastic modulus effect to one wing fracture length and width

Full size image

Since the leakoff coefficient is a function of the permeability of the formation, a parametric study was conducted for various permeabilities from 0.001 to 1,000 mD and leakoff coefficients from 0 to 0.001 m3/(kPa s) in Fig. 6. Generally, the fracture length decreases with increasing permeability and leakoff coefficient. The model has been applied to investigate the fracture behavior in both brittle and ductile rocks. Figure 7 shows a representative prediction of bottomhole pressure (BHP), von Mises stress field, and plastic strain in brittle and ductile rock using the pore pressure CZM. It is observed that for fracture in brittle rock, the pressure increases to breakdown pressure and then decreases to propagation pressure, which is routinely presented in literature, and these is no plastic strain observed. However, for a fracture in ductile rock, the bottomhole pressure keeps increasing and develops serious plastic strain, which can be explained by the major energy consumed by the deformation of the rock, with only a small amount of the energy used to create the fracture surface. The simulation results show that injection in ductile rock could require higher pumping horsepower than conventional design based on hard rock fracture experience.

Fig. 6
figure 6

Permeability and leakoff effect to one wing fracture length

Full size image
Fig. 7
figure 7

Different fracture behaviors in brittle and ductile rock

Full size image

The pore pressure cohesive zone model has been applied to predict the effects of different parameters on fracture geometry, as shown in Table 2. Based on the parametric analysis, under the same fluid injection volume, with the increase of Young’s modulus of the rock, the fracture width decreases, while the fracture length and height increase. With the increase of injection rate, the fracture width, length and height increase. With the increase of leakoff coefficient, the fracture width, length and height decrease. With the increase of injected fluid viscosity, the fracture length decreases, fracture width and height increase.

Table 2 Effects of different parameters to fracture geometry predicted using pore pressure cohesive zone model
Full size table

4 Effective Fracture Toughness for Ductile Rock Fracture Simulation

Based on the size of the fracture process zone ahead of crack tip, a straightforward method can be developed to consider the effect of ductility on fracture parameters. Irwin’s estimate of the effect of crack extension is shown in Fig. 8a (Irwin 1957), where the inelastic zone at the crack tip is assumed to be a finite size R. Irwin retained the value of R by cutting off the singular stress peak, thus,

Fig. 8
figure 8

Estimate of the fracture process zone for ductile rock

Full size image
$$ \sigma_{\text{yy}} = K_{\text{I}} (2\pi x)^{ - 1/2} $$
(10)

The fracture process zone R is:

$$ R = \frac{1}{2\pi }\left( {\frac{{K_{\text{I}} }}{{\sigma_{\text{y}} }}} \right)^{2} $$
(11)

However, for ductile rocks, the nonlinear zone must be larger than Irwin’s prediction, as shown in the softening of the rock material in Fig. 8b.

Applying a similar equivalent area rule and assuming the rock softening curve is parabolic yields:

$$ \int\limits_{r1}^{Rc} {K_{\text{IC}} [2\pi (x - r_{1} )} ]^{ - 1/2} {\text{d}}x = \int\limits_{0}^{Rc} {f_{\text{t}}^{'} \left( {\frac{x}{{R_{\text{c}} }}} \right)^{n} {\text{d}}x} = \frac{1}{n + 1}R_{\text{c}} f_{\text{t}}^{'} $$
(12)

where \( f_{\text{t}}^{'} \) is the rock tensile strength and can be determined from core test.

$$ R_{\text{c}} = \frac{n + 1}{\pi }\left( {\frac{{K_{\text{IC}} }}{{f_{\text{t}}^{'} }}} \right)^{2} = \left( {\frac{{K_{\text{eff}} }}{{f_{\text{t}}^{'} }}} \right)^{2} $$
(13)

The parameter n represents the values of softening parabolic distribution degree as shown in Fig. 8b, which needs to be determined for different rock materials to include the crack-tip effect on the growth of the fracture. The exponential softening of ductile rock is mainly determined by the cohesive fracture energy, which represents the external energy supply required to create fully break a unit surface of cohesive crack. Geometrically, the cohesive fracture energy coincides with the area under the softening curve. For typical quasi-brittle materials such as concrete, the value of n is of the order of 7–14 (Bazant and Planas 1998), thus, the value of \( \frac{n + 1}{\pi } \) usually varies from 2 to 5 for concrete, which leads to \( K_{\text{eff}} = 1.414\sim 2.236K_{\text{IC}} \) based on Eq. 14. For ductile rocks, the value of n can be determined by investigating softening behavior experimentally or computationally. Considering the wide range of brittle to ductile rock properties, a value of \( \frac{n + 1}{\pi } \) varies from 1 to 9 is investigated in the paper. The corresponding effective toughness value varies from 1 to 3 times of the original rock fracture toughness.

The effective fracture toughness can be defined as:

$$ K_{\text{eff}} = \sqrt {\frac{n + 1}{\pi }} K_{\text{IC}} $$
(14)

The idealized characteristic length of fracture is defined by: (Bazant and Planas 1998)

$$ l_{\text{c}} = \left( {\frac{{K_{\text{IC}} }}{{f_{\text{t}}^{'} }}} \right)^{2} $$
(15)

The actual characteristic length of the fracture is:

$$ l_{\text{c}} = \frac{n + 1}{\pi }\left( {\frac{{K_{\text{IC}} }}{{f_{\text{t}}^{'} }}} \right)^{2} $$
(16)

Figures 9 and 10 show the fracture propagation prediction using the pore pressure CZM and pseudo 3D model, respectively. Effective fracture toughness values vary from 1 to 3 times of the original fracture toughness have been applied to the rock of the investigated layer, which corresponds to different parabolic softening curves of ductile rock. The study shows that increasing effective fracture toughness, or more ductile rock, will lead to a shorter fracture length. The fracture toughness effect on the half wing fracture length using pore pressure CZM, LEFM-based pseudo 3D model, and a PKN model is summarized in Table 3 and Fig. 11. With the increase of effective fracture toughness, the predicted fracture length decreases faster by using pseudo 3D model or PKN model than with a pore pressure cohesive zone model.

Fig. 9
figure 9

Cohesive fracture propagation predicted from ABAQUS pore pressure cohesive element model with different effective fracture toughness values

Full size image
Fig. 10
figure 10

Fracture propagation predicted using pseudo 3D model with different effective fracture toughness values

Full size image
Table 3 Fracture toughness effect to one wing fracture length (m) predicted using different methods
Full size table
Fig. 11
figure 11

Fracture toughness effect to one wing fracture length predicted using different numerical methods

Full size image

Figure 12 shows the fracture toughness effect on the half wing fracture length for different leakoff coefficients predicted using a pseudo 3D model. The leakoff coefficient is used in calculating the time-dependent leakoff velocity and overall fluid loss based on mass conservation. For this numerical model, Carter’s Leakoff model is employed (Valko and Economidies 1995)

Fig. 12
figure 12

Fracture toughness effect to one wing fracture length with different leakoff coefficients

Full size image
$$ C_{\text{I}} = C_{\text{v}} = 0.0469\sqrt {\frac{{k_{\text{f}} \Updelta p\varphi }}{{\mu_{\text{f}} }}} $$
(17)
$$ C_{\text{II}} = C_{\text{c}} = 0.0374\Updelta p\sqrt {\frac{{k_{\text{r}} c_{\text{tc}} \varphi }}{{\mu_{\text{r}} }}} $$
(18)
$$ C_{\text{III}} = C_{\text{w}} = \frac{0.0164m}{A} $$
(19)
$$ \frac{1}{{C_{\rm t} }} = \frac{1}{{C_{\rm I} }} + \frac{1}{{C_{\rm II} }} + \frac{1}{{C_{\rm III} }} $$
(20)

where C I is the viscosity control coefficient; Δp is the differential leakoff pressure; k f is the effective permeability to the fracture fluid filtrate; φ is porosity; μ f is the effective viscosity of fracturing fluid; C II is the compressibility control coefficient; k r is the reservoir permeability to reservoir fluid; c tc is the total formation compressibility; μ r is the viscosity of the reservoir fluid; C III is the wall building coefficient; A is the cross-sectional area; m is the slope of a volume versus \( \sqrt {\text{time}} \) plot; and C t is total leakoff coefficient.

Figure 12 shows the facture toughness effect on the one wing fracture length with different Carter’s leakoff coefficients from 0.0001 ft/\( \sqrt {\min } \)to 0.1 ft/\( \sqrt {\min } , \) it is noted that for high permeability formations (leakoff coefficients >0.005 ft/\( \sqrt {\min } \)), the fracture toughness has less effect on the fracture length and the effective fracture toughness is not applicable. However, for most of the low permeability ductile rock with leakoff coefficients less than 0.001 ft/\( \sqrt {\min } , \) effective fracture toughness has a significant effect on the fracture geometry and the effective fracture toughness concept can be applied to simulate the ductile effect on hydraulic fractures. From the numerical analysis, it should be noted that with higher leakoff coefficients, the effect of fracture toughness on the normalized fracture length decreases, and the leakoff phenomenon dominates the hydraulic fracture process. The fracture toughness plays a more important role with higher fracture efficiency (lower leakoff) of the injected fluid. Fracture efficiency is defined as the ratio of the fracture volume to the volume of fluid injected. For higher viscosity fluids with lower leakoff coefficients, fracture toughness can be one of the dominant parameters controlling fracture growth in ductile rock.

Hydraulic fracturing technology is also been widely used for CO2 injection and geothermal extraction. Typically, CO2 injection performance in subsurface formation relies on the ability of the well to maintain high flow rates of carbon dioxide, in lots of these cases the injected CO2 will not fracturing the formation. A user-defined subroutine to accurately predict the fracture initiation will be one of the key issues for CO2 injection modeling. A revised pore pressure cohesive element model can be applied to predict CO2 injection, which is not the focus of this paper. On the other hand, simulation of CO2 injection is more complicated and has other mechanisms to be incorporated in the numerical model. The numerical model developed in currently research focus on hydraulic fracture analysis caused by water, acid, and cuttings slurry injection in different rocks. For these cases, especially cuttings slurry injection, fracture will be initiated relatively easier and fracture geometry and pressure are the key concerns during the injection process. The developed computational model associated with the theoretical derivation gives a more reliable prediction when compared with other conventional methods. It is able to incorporate the fundamental mechanism and explain the field observation of hydraulic fracture in both brittle and ductile rocks.

5 Conclusions

The fundamental difference between LEFM and cohesive fracture mechanics-based methods on prediction of fractures in brittle and ductile rock is discussed in the paper. A full 3D pore pressure cohesive zone model has been developed and applied to investigate the effects of different rock properties and injection parameters on fracture geometry.

The predicted hydraulic fracture of a three-layer water injection case has been compared using pore pressure CZM, LEFM-based pseudo 3D model, a PKN model, and an analytical solution. The result shows that compared with traditional LEFM method, the pore pressure CZM can predict hydraulic fracture geometry more accurately, especially for ductile rock. With the increase of fracture toughness, the pore pressure CZM gives predictions that are more conservative on fracture length as compared with pseudo 3D and PKN models.

Based on cohesive fracture mechanics, a theoretical method has been introduced to calculate the effective fracture toughness for quasi-brittle/ductile rocks. The fracture toughness is found to have significant effect on the fracture characteristics of ductile shale. With a softening model derived either experimentally or numerically, the revised fracture toughness can be determined to include the ductility effect to better simulate hydraulic fracture in ductile rock.