1 Introduction

Dynamic behavior of rock at high strain rates differs considerably from that observed with static or quasi-static tests, and many practical applications require mechanical behavior of rock under dynamic conditions. For example, strain rates ranging from 100 s−1 to more than 104 s−1 occur in many processes or events, such as milling, drilling, blasting, explosion, earthquakes and defensive works. In the past decades, a variety of equipments, including special servo-hydraulic frames, pneumatic-driven loader, drop tower, Split Hopkinson Bar (SHB), spalling and flyer plate, have been utilized to conduct dynamic tests of rock (ASM Int 2000; Field et al. 2004). Among these equipments, Split Hopkinson Pressure Bar (SHPB) of SHB family stands out with the advantages of easy operation, good repeatability and relatively accurate results. Many researchers have used it to conduct tests to give results about dynamic strength, fracture and fragmentation of rocks (Li and Ma 2009; Li et al. 2000, 2005, 2008; Wang et al. 2009; Zhou et al. 2006, 2007).

However, most of the results from SHPB tests were presented with an average strain rate or without mention of the strain rate. By so doing, if the rock under test had no rate effect, the results were correct. But for most rock types, research has shown that their characteristics have a power law or other forms of relationships with strain rate (Cho et al. 2003; Kumar 1968; Li and Meng 2003; Li et al. 2005; Okubo et al. 1990; Tedesco and Ross 1998; Zhou et al. 2007; Zhu 2008). In these cases, strain rate plays a vital role in determining rock behavior. Changes in strain rate would lead to large differences in outcomes. Therefore, results expressed with an average strain rate frequently tend to be inexplicable or self-contradictory. Especially, the obtained stress–strain curves cannot be directly treated as constitutive relationships of rock as in static tests.

To obtain dynamic constitutive curves of rate-dependent rock from SHPB test, efforts must be made to let the specimen deform at a constant strain rate during its deformation. Much research has contributed to this effort in the past years. Among them, two methods deserve to be mentioned. One method is the pulse shaper method, where a thin sheet is put between the striker and the input bar. The method was initially used to reduce wave dispersion effect and overcome premature failure of specimen in traditional SHPB tests (Frantz et al. 1984), and get a constant strain rate of specimen to some extent (Frew et al. 2002; Xia et al. 2008). The other method is the special shape striker method, where a taper-ended striker, instead of a cylindrical striker, is used to produce a half-sine wave (Liu et al. 1998; Li et al. 2005). This method gives results at a constant strain rate with less dispersion and oscillation (Li et al. 2000, 2005, 2008). Despite all these improvements, it is still difficult to obtain a perfect constant strain rate for the specimen within its whole deformation process in SHPB tests.

The objective of the present study is to determine the requirements that can ensure that the specimen deforms at a constant strain rate on SHPB. At the same time, new considerations and an alternative are brought up to get a constitutive relationship for rate-dependent rock.

2 Influence of Strain Rate to Stress–Strain Curves of Rate-Dependent Rock

2.1 SHPB Technique and its Basic Assumptions

The SHPB setup usually consists of a striker, an input bar, an output bar, an absorption bar and other auxiliary components like a gas gun and a data acquisition unit (ASM Int 2000; Li et al. 2000). The specimen is sandwiched between the input and output bars. During a test, the striker is shot out from the gas gun at high velocity and impacts the front end of the input bar. Then an input wave is generated and propagates down the input bar toward the specimen. Once the wave reaches the bar/specimen interface, part of it is reflected, while another part goes through the specimen and transmits into the output bar and absorption bar.

In Fig. 1, the subscript 1 is used to denote the input bar/specimen interface and subscript 2 is used to represent the specimen/output bar interface. ε represents the measured signals on the bars, where the subscripts I, R and T represent incident, reflected and transmitted pulses, respectively. The arrowheads show the direction of wave propagation. According to one-dimensional wave theory, the engineering stress, strain, and strain rate of the specimen can be obtained as:

Fig. 1
figure 1

Wave propagation through bar/specimen interfaces

Full size image
$$ \sigma (t) = {\frac{{A_{\text{e}} E_{\text{e}} }}{{2A_{\text{s}} }}}[\varepsilon_{\text{I}} (t) + \varepsilon_{\text{R}} (t) + \varepsilon_{\text{T}} (t)] $$
(1)
$$ \varepsilon (t) = {\frac{{C_{\text{e}} }}{{L_{\text{s}} }}}\int\limits_{0}^{t} {[\varepsilon_{\text{I}} (t) - \varepsilon_{\text{R}} (t) - \varepsilon_{\text{T}} (t)]} dt $$
(2)
$$ \dot{\varepsilon }(t) = {\frac{{C_{\text{e}} }}{{L_{\text{s}} }}}[\varepsilon_{\text{I}} (t) - \varepsilon_{\text{R}} (t) - \varepsilon_{\text{T}} (t)] $$
(3)

where A e, C e, and E e are the cross-sectional areas, wave velocity, and Young’s modulus of elastic bars. A s and L s are the cross-sectional area and the length of the specimen.

For SHPB test, there are some assumptions to ensure the validity of Eqs. 1–3 in tests:

  1. 1.

    Propagation of elastic waves through the input and output bars can be described by 1D wave theory. This can be fulfilled using big length/diameter ratio bars.

  2. 2.

    Specimen reaches stress equilibrium before failure. Stress equilibrium can be checked by comparing the stresses at two ends of specimen. Premature failure of the specimen can be avoided by non-rectangular incident wave.

  3. 3.

    Friction and inertial effects on the specimen can be ignored. This can be satisfied by using lubricants in the bar/specimen interfaces.

When these assumptions are satisfied, stress, strain, and strain rate can also be expressed as:

$$ \sigma (t) = {\frac{{A_{\text{e}} E_{\text{e}} }}{{A_{\text{s}} }}}\varepsilon_{\text{T}} (t) $$
(4)
$$ \varepsilon (t) = - {\frac{{2C_{\text{e}} }}{{L_{\text{s}} }}}\int_{0}^{t} {\varepsilon_{\text{R}} (t)} dt $$
(5)
$$ \dot{\varepsilon }(t) = - {\frac{{2C_{\text{e}} }}{{L_{\text{s}} }}}\varepsilon_{\text{R}} (t) $$
(6)

2.2 Traditional Result Reporting Method of SHPB Test and its Limitation

Traditionally, the acquired signals of the SHPB test are processed with Eqs. 1–3 or 5–6 to get stress, strain, and strain rate of specimen. Then test results are usually reported as stress–strain curves at an average strain rate. The average strain rate is obtained as the mean value of all the data points of strain rate history from Eq. 3 or 6. This method was supposed to be convenient and simple for result reporting.

However, results by this method frequently tend to be controversial. For example, Fig. 2 shows stress–strain curves of three granite specimens in SHPB tests (parameters of the specimens are shown in Table 1). They have the same average strain rate of 30 s−1 with the traditional results processing method. From Fig. 2, it can be seen that specimens #1 and #2 have similar stress–strain evolution paths at pre-peak stage, but different paths in post-peak part. For specimen #3, it has completely different stress–strain evolution path from specimens #1 and #2. Meanwhile, the dynamic strength values of the three specimens are different, although they have the same average strain rate.

Fig. 2
figure 2

Stress–strain curves of granite specimen #1, #2 and #3

Full size image
Table 1 Parameters of specimens in Fig. 1
Full size table

These phenomena are encountered frequently in SHPB tests. So reason must be found and improvement should be made.

2.3 Influence of Strain Rate to Stress–Strain Curves of Rock

Let us investigate the strain rate histories of the three specimens. Figure 3 shows their strain rate histories. For specimens #1 and #2, their strain rate histories have a similar changing pattern where curves vibrate along 40 s−1 and drop to −20 s−1 and have an average value of 30 s−1. But the strain rate history of specimen #3 has actually a large different pattern from specimens #1 and #2, which rises abruptly and decreases rapidly. The abrupt increasing of the strain rate of specimen #3 leads to stress concentration in it rapidly, which appears as the much higher part of stress in its stress–strain curve.

Fig. 3
figure 3

Strain rate histories of specimens #1, #2 and #3

Full size image

According to the above-mentioned, the average strain rate method tends to conceal the rich information of the strain rate history and may lead to error explanation of the stress–strain results. Much more detailed information of strain rate history should be used for result explanation and reporting in SHPB test.

3 Requirement of Specimen Deformation at a Constant Strain Rate

The strain rate state is vital to the stress–strain performance of the specimen. So factors affecting the strain rate of the specimen must be investigated to give reasonable explanations for SHPB test results.

Resorting to Eqs. 4–6, strain and strain rate of the specimen can be calculated from the reflected wave, and stress of the specimen from the transmitted wave. The stress, strain, and strain rate state of the specimen are all correlated with the incident wave given that the reflected wave and the transmitted wave both originate from the incident wave according to SHPB principles.

3.1 Correlation Analysis Between the Strain Rate and Incident Wave

During the test, the stress wave spreads into the specimen causing an inter-reflection. The specimen is compressed and stress congregates in it. The specimen, with original length of L * and original sectional area of A *, will deform rapidly. After several inter-reflections of the stress wave in the specimen, stress at its both ends will reach equilibrium (Yang and Shim 2005). The stress and strain of the specimen at this moment are marked as σ 0 and ε0.

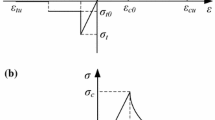
As a general significance, a general constitutive curve as shown in Fig. 4 is supposed for the specimen. In order to facilitate the theoretical analysis, infinitesimal poly-lines are used to approximate the constitutive curve. In segment i, Eq. 7 can be established.

Fig. 4
figure 4

General constitutive curve of specimen

Full size image
$$ \sigma = \sigma_{i - 1} + E_{i} (\varepsilon - \varepsilon_{i - 1} ) $$
(7)

where E is the elastic modulus of rock, which is the function of density, strain rate etc. E i is the modulus of specimen in segment i, which has the same value in each segment.

For brittle material like rock, it is uncompressible. The specimen length and the sectional area at the starting and ending points of each deformation segment are denoted as L n−1, A n−1 and L n , A n . The volume of the specimen is the same during the test.

$$ A^{*} L^{*} = A_{0} L_{0} = AL = AL^{*} (1 - \varepsilon ) $$
(8)

In the first segment, the stress and strain of the specimen have the following relation:

$$ \sigma = \sigma_{0} + E_{1} (\varepsilon - \varepsilon_{0} ) $$
(9)

According to SHPB principles,

$$ \dot{\varepsilon } = {\frac{2}{{\rho_{\text{e}} c_{\text{e}} L_{0} }}}(\sigma_{\text{I}} - \sigma_{\text{T}} ) $$
(10)
$$ \sigma A = A[\sigma_{0} + E_{1} (\varepsilon - \varepsilon_{0} )] = \sigma_{\text{T}} A_{\text{e}} $$
(11)

Then,

$$ \sigma_{\text{I}} = {\frac{{\rho_{\text{e}} C_{\text{e}} L_{0} }}{2}}\dot{\varepsilon } - {\frac{{A^{*} E_{1} }}{{A_{\text{e}} }}} + {\frac{{A^{*} (\sigma_{0} - E_{1} \varepsilon_{0} + E_{1} )}}{{A_{\text{e}} }}}\,{\frac{1}{1 - \varepsilon }} $$
(12)

Expanding Eq. 12,

$$ \sigma_{\text{I}} = {\frac{{\rho_{\text{e}} C_{\text{e}} L_{0} }}{2}}\dot{\varepsilon } - {\frac{{A^{*} E_{1} }}{{A_{\text{e}} }}} + {\frac{{A^{*} (\sigma_{0} - E_{1} \varepsilon_{0} + E_{1} )}}{{A_{\text{e}} }}}\,(1 + \varepsilon + \varepsilon^{2} + \varepsilon^{3} + \ldots ) $$
(13)

For the brittle failure of rock-like material, the maximum failure strain is usually less than 0.01, therefore the high order values of ɛ can be neglected. Then:

$$ \sigma_{\text{I}}\,\dot{ = }\,{\frac{{\rho_{\text{e}} C_{\text{e}} L_{0} }}{2}}\dot{\varepsilon } + {\frac{{A^{*} }}{{A_{\text{e}} }}}[\sigma_{0} + E_{1} (\varepsilon - \varepsilon_{0} )] $$
(14)

Following the same procedure, in the segment n,

$$ \sigma_{\text{I}}\,\dot{ = }\,{\frac{{\rho_{\text{e}} C_{\text{e}} L_{n - 1} }}{2}}\dot{\varepsilon } + {\frac{{A^{*} }}{{A_{\text{e}} }}}[\sigma_{n - 1} + E_{n} (\varepsilon - \varepsilon_{n - 1} )] = {\frac{{\rho_{\text{e}} C_{\text{e}} L_{n - 1} }}{2}}\dot{\varepsilon } + {\frac{{A^{*} }}{{A_{\text{e}} }}}\sigma $$
(15)

That is:

$$ \sigma_{I}\,\dot{ = }\,{\frac{{\rho_{e} C_{e} L}}{2}}\dot{\varepsilon } + {\frac{{A^{*} }}{{A_{e} }}}\sigma $$
(16)

where L changes with the stress state of the specimen and is a function of time.

If the specimen deforms at constant strain rate, then \( \dot{\varepsilon } \) keeps constant with time, whose time derivative is zero.

$$ \ddot{\varepsilon } = 0 $$
(17)

Then:

$$ \dot{\sigma }_{\text{I}} = = {\frac{{A^{*} }}{{A_{\text{e}} }}}\dot{\sigma } + {\frac{{\rho_{\text{e}} C_{\text{e}} }}{2}}\dot{l}\dot{\varepsilon }\dot{ = }\,{\frac{{A^{*} }}{{A_{\text{e}} }}}\dot{\sigma } + {\frac{{\rho_{\text{e}} C_{\text{e}} }}{2}}\varepsilon \dot{\varepsilon }\dot{ = }\,{\frac{{A^{*} }}{{A_{\text{e}} }}}\dot{\sigma } $$
(18)

It indicates that if the specimen deforms at constant strain rate, the incident stress and the deforming stress of the specimen should have the same changing rate.

3.2 Verification of the Requirement with Test Results

In recent years, SHPB tests with the pulse shaper and special shape striker have been reported to be able to carry out tests for specimens at constant strain rates (Li et al. 2005, 2008; Xia et al. 2008). In our laboratory, tests with both methods were also conducted and results were utilized for analysis here. Some basic parameters are listed in Table 2.

Table 2 Parameters in validation tests
Full size table

Figure 5 presents the test data of SHPB test with copper pulse shaper on the front-end of input bar, where the incident, reflected and transmitted waves are exacted and translated together for easy comparison. The time gap between the starting points of incident wave and transmitted wave is the time needed for the wave to propagate through the specimen.

Fig. 5
figure 5

The incident, reflected and transmitted waves in validation test with pulse shaper

Full size image

According to Eqs. 4–6, the strain rate of the specimen can be represented by the reflected wave and the deforming stress of the specimen can be represented by the transmitted wave. From Fig. 5, it can be seen that at time span T 1 between 80 μs and 150 μs, the incident wave and the transmitted wave have the same changing slope, which means that the incident stress and the deforming stress of the specimen have the same changing rate. The reflected wave at this time span turns out to be flat, which indicates the constant strain rate of the specimen. This shows that Eq. 18 is right.

Figure 6 gives the test data of the SHPB test with the special shape striker proposed by Liu et al. (1998). In the figure, t 1 is the time for wave propagating through the specimen with t 1 + t 2 being the time needed for stress equilibrium of the specimen. In time spans t 3 and t 4, the incident wave and the transmitted wave are both linear with the same changing slope, therefore the corresponding reflected wave keeps flat. In time span t 5, the incident wave and the transmitted wave are both curving but with the same changing pattern. The flat reflected wave in this time span again indicates the constant strain rate of the specimen and the correctness of Eq. 18.

Fig. 6
figure 6

The incident, reflected and transmitted waves in validation test with special shape striker

Full size image

Although Eq. 18 points out the requirement for the specimen to deform at a constant strain rate, it should still be noticed that Eq. 18 is a necessary condition rather than a sufficient condition. Without constitutive information of the specimen in advance the stress response of the specimen is unknown. Therefore, it is impossible to accurately determine which incident stress is appropriate for specific rock type or specimen before the test.

Results in Figs. 5 and 6 also show: although both methods can make the specimen deform at constant strain rates to some extent in certain time spans. The perfect constant strain rate state of the specimen during its whole deformation is hard to be realized.

Moreover, getting constant strain rate deformation of specimen with pulse shaper and special shape striker is not an easy thing. Only 1/3 of the specimens have the good luck to experience constant strain rates for short periods according to laboratory records. Most of their strain rates turn out to have histories like that of specimen #3, where almost no flat segments exist.

Additionally, the pulse shaper method has poor repeatability and the deforming behavior of the shaper is difficult to predict. The design and manufacturing of the striker with special shape striker method is also a challenging job. All these limitations need further improvements.

4 Method to Obtain Constitutive Relationship for Rate-Dependent Rock by Data Processing

On the one hand, the stress–stain curve from test is intrinsically the dynamic response of the specimen, regardless of whether the specimen deforms at constant strain rate or not. On the other hand, it is difficult to find a suitable incident wave for the specimen to deform at constant strain rate before the test. And, mechanical improvements such as pulse shaper method and special shape striker method can only get constant strain rates of the specimen partially. Besides, lots of testing data are wasted where constant strain rate is not fulfilled. So, would it be possible to find some way-out other than mechanical improvements that have wider applicability for test data?

4.1 3D Scattergram Method for SHPB Test of Rate-Dependent Rock

Based on previous knowledge, the constitutive relationship of rock can be described with stress, strain and strain rate. The controversial results of SHPB test come from the non-constant strain rate that the specimen is subject to.

In order to discover the overlooked information by the average strain rate method, the 3D scattergram method is brought up over here.

This method is based on the idea that the constitutive relationship is a material property and can be described by function \( f(\sigma ,\varepsilon ,\dot{\varepsilon }) \). The stress–strain curve of the SHPB test represents the dynamic response of the specimen with rich strain rate information. The changing of \( \dot{\varepsilon } \) will lead to different σ − ε curves.

For illustration, test results from a group of 60 granite specimens are used here. The 60 specimens were cored from the same granite block and designed to investigate the dynamic behavior of granite at intermediate strain rates with large diameter SHPB.

First, the SHPB data from an arbitrary specimen #6 are chosen for analysis. Figure 7 gives the acquired signals from strain gauges on the input and output bars. The parameters of the elastic bar and the specimen are shown in Table 3. The non-flat reflected wave shows that the specimen did not deform at constant strain rate.

Fig. 7
figure 7

Test signals of specimen 6# in SHPB test

Full size image
Table 3 Parameters for test of Fig. 7
Full size table

Thereafter, routine jobs like voltage/strain conversion and de-noising are carried out on the above signals. After that σ I(t), σ R(t), and σ T(t + t 0) of the translated σ T(t) are obtained, as shown in Fig. 8, where their absolute values are used for easy comparison; t 0 is the time for wave going through the specimen, which is 6 μs in this case. The sampling rate of the strain gauge is 1 MHz, therefore εT(t) is translated forward by six sampling points.

Fig. 8
figure 8

The incident, reflected, transmitted and unbalance stresses of specimen #6

Full size image

The unbalanced stress of the specimen σ I(t) − σ R(t) − σ T(t + t 0) can be calculated accordingly and is shown in Fig. 8. It gets to be less than 1/10 of the incident stress after 54 μs, which is the time for the wave reflecting nine times in the specimen (Yang and Shim 2005). The σ I(t), σ R(t) and σ T(t) data after 54 μs can be used to calculate σ(t), ε(t) and \( \dot{\varepsilon }(t) \) with Eqs. 4–6.

In succession, instead of being reported and interpreted with stress–strain curve at average strain rate, the \( (\sigma ,\varepsilon ,\dot{\varepsilon }) \) results are put into a 3D Cartesian coordinate system, where strain rate is kept too. Figure 9 presents the \( (\sigma ,\varepsilon ,\dot{\varepsilon }) \) information.

Fig. 9
figure 9

\( (\sigma ,\varepsilon ,\dot{\varepsilon }) \) information of specimen 6# in 3D scatter-gram

Full size image

Following the example, more data of other test sets are processed and used to construct the 3D scatter diagram of the constitutive relationship. Figure 10 is the 3D scattergram with four sets of data. It can be seen that the stress–strain curves usually stride over several strain rate levels. Figure 11 gives the scattergram with all the 60 sets of data. Figure 11b also shows the non-constant state of the strain rate of most specimens.

Fig. 10
figure 10

3D constitutive scatter-gram with four sets of data

Full size image
Fig. 11
figure 11

Overview of the 3D constitutive scatter-gram of granite. a Overview along strain axis. b Overview along the strain rate axis

Full size image

4.2 Explanation of 3D Scattergram Results

The constitutive relationship of rock expressed with 3D scattergram is data set in 3D space. It contains all the constitutive information of the tested rock type. For application in dynamic design or simulation, the conventional constitutive relationship in the form of a stress–strain curve at a specific strain rate may be needed. In such circumstances a planar slice along the specific strain rate can be made in the 3D scattergram space.

Taking the 3D scattergram of Fig. 11 as example, since the tests are mainly conducted at an intermediate strain rate, their strain rates concentrate at the range of (0, 40). Therefore, planar slices along 10, 20 and 30 s−1 are made here. The negative strain rate values in Fig. 11 represent the unloading behavior of granite and are not discussed here.

As stress, strain and strain rate values are all real numbers, the chance for stress–strain values to fall exactly on a specific strain rate plane is relatively low. The planar slices may need to be thicker so as to capture more data. Here planar slices with thickness of two units are used.

Figure 12 gives the (σ, ε) data falling between 9 and 11 s−1 to represent the results on the plane of 10 s−1. It can be seen that the distribution of (σ, ε) data is rather concentrated along the fit line although they are results from different test cases. The absence of data points on some part of the fit line mainly owes to the fact that there are no (σ, ε) data falling on this strain rate for the current specimen group. A larger group of specimens would fill the gap. But it does not affect the analysis here.

Fig. 12
figure 12

Stress–strain date of granite at a strain rate of 10 s−1

Full size image

Figures 13 and 14 give (σ, ε) data of the specimen at the strain rates of 20 and 30 s−1, respectively. Figure 15 puts the fit lines together and shows that:

Fig. 13
figure 13

Stress–strain date of granite at a strain rate of 20 s−1

Full size image
Fig. 14
figure 14

Stress–strain date of granite at a strain rate of 30 s−1

Full size image
Fig. 15
figure 15

Fit lines of stress–strain relationships of granite at strain rates of 10, 20 and 30s−1

Full size image
  1. 1.

    the stress–strain curves differentiate from each other and identify themselves by the strain rate, and

  2. 2.

    the bigger the strain rate, the higher the stress–strain evolution path

4.3 Steps of 3D Scattergram Method

Therefore, the steps of the 3D scattergram method can be concluded as follows:

  1. 1.

    Take out each set of signals acquired from the strain gauges on the input and output bars; extract the incident, reflected and transmitted waves, respectively

  1. 2.

    Check stress equilibrium in specimen with unbalance stress σ I(t) + σ R(t) − σ T(t + t 0). If the unbalance stress is less than 1/10 of the peak value of incident stress, then the specimen can be thought to reach stress equilibrium. Therefore, σ I(t), σ R(t) and σ T(t) after the stress equilibrium of the specimen can be used for calculation; t 0 is the time for the wave to travel through the specimen; t and t 0 in the variables can be substituted by sampling points for convenience. The time between the adjacent two points equals to 1/f, where f is the sampling frequency of the strain meter.

  1. 3.

    Calculate σ(t), ε(t) and \( \dot{\varepsilon }(t) \) with Eqs. 4–6.

  1. 4.

    Put σ(t), ε(t) and \( \dot{\varepsilon }(t) \) into the 3D scattergram, which is a three-dimensional space of \( (\sigma ,\varepsilon ,\dot{\varepsilon }). \)

  1. 5.

    Repeat steps 1–4 till all the data sets are processed. The database should be big enough so that the 3D scattergram becomes more detailed.

Finally, the constitutive relationship of the tested rock type can be produced.

5 Summary and Conclusions

In the prevailing SHPB tests, results are usually reported as stress–strain curves at average strain rates. However, the oscillatory curves frequently make the results inexplicable or self-contradictory. The phenomena are mainly caused by the rich strain rate information that the stress–strain curve contains. The crude results calculated from signals acquired by the strain meter usually stride over several strain rate bands. As shown in Fig. 16, if the solid curves of \( \dot{\varepsilon }_{1} \),\( \dot{\varepsilon }_{2} \),\( \dot{\varepsilon }_{3} \) are intrinsic evolution paths of a certain rock type, then the dashed curve would be the stress–strain curve obtained directly from the test with Eqs. 1–2 where the specimen does not deform at a constant strain rate.

Fig. 16
figure 16

Stress–strain curve striding over several strain rate bands (\( \dot{\varepsilon }_{1} > \dot{\varepsilon }_{2} > \dot{\varepsilon }_{3} \))

Full size image

According to the correlation analysis of the strain rates of specimens, incident stress, reflected stress and transmitted stress, it is found that only when the incident stress and specimen deforming stress have the same changing pattern would the specimen deform at a constant strain rate. This necessary condition was verified with test data with the pulse shaper method and special striker method in the paper. In fact, the double specimen test by Ellwood et al. (1982) gave a good hint for this conclusion, where dummy specimen was used at the front end of input bar so that the incident stress of second specimen was regulated to satisfy Eq. 18 automatically. Tests with other metal materials obtained good constant strain rate results (Tao et al. 2004). But for rock materials, the brittle failure and high energy absorption make the method unavailable.

To obtain constitutive relationships of rate-dependent rock, the perfect condition is to let specimen stay at a constant strain rate during all its deformation process. However, it is still impossible in practice. Methods like the pulse shaper and special shape striker can fulfill this purpose to some extent. But poor repeatability, high manufacturing cost and low success rate of these methods make them need further improvements. 3D scattergram method seems to be a better alternative to get constitutive relationships of rate-dependent rock with fewer requirements. Of course, ways to reduce the required amount of specimens is a challenge for the future.