1 Introduction

Cable-driven parallel robots (CDPRs) are a special class of parallel robots in which the end-effector is actuated by multiple cables. Fixed winches attached to the base frame are used to control the cable length (Gosselin 2014). CDPRs have several significant advantages, such as a large workspace, high payload to weight ratio, and low inertia (Duan et al. 2015; Yuan et al. 2015; Gagliardini et al. 2014). Therefore, CDPRs have been applied in rehabilitation training, large radio telescopes, building cleaning, and 3D printing (Qian et al. 2018).

However, CDPRs still face some limitations owing to cable actuation, which makes it challenging to develop a path planning strategy for practical applications (Wischnitzer et al. 2008). Because multiple cables easily cause interference with obstacles in cluttered environments, it is important to ensure the safety of the robot during the motion of the end-effector (Nguyen and Gouttefarde 2015). The collision phenomenon can cause instability in such robots, causing serious operational problems. In addition, because the cable tension must maintain a positive consistency, the feasible wrenches that the cable can generate are essential for structural stability (Bouchard et al. 2010). The kinematic performance of CDPRs is considered in the proposed path planning method by employing the feasible wrench area and the dexterity indicator (Abdolshah et al. 2017).

Accordingly, researchers have developed different methods for the motion planning of CDPRs. Jiang et al. (2018) proposed dynamic point-to-point trajectory planning for a six-DOF CDPR. More recently, Idà et al. (2019) studied the trajectory planning of CDPRs in the case of rest-to-rest motions, implying that the motion time and path geometry are predefined. However, these studies only considered an underactuated CDPR in an environment without obstacles. Furthermore, the under-actuation of CDPR indicated that there is a unique solution for the cable tension distribution, which easily generates an unbounded oscillatory end-effector (Idà et al. 2021).

In a cluttered environment, path planning is important for CDPRs to avoid obstacles. Lahouar et al. (2009) presented a grid-based path planning method with two modes for a 4-cable-driven parallel manipulator, where the first mode leads the robot to move to the target directly, and the second mode generates a feasible path for the robot to avoid the obstacle. However, the grid cell can reduce the diversity of possible paths. To improve this, Bak et al. (2019) proposed a modified rapidly exploring random trees (RRT) method to generate collision-free paths for CDPRs, which utilized goal-biased sampling and post-processing to reduce the path cost. The RRT method performs well in dealing with various interferences during the path planning of CDPRs by sampling the configuration space (C-space) (LaValle 1998). To improve the conventional RRT method, RRT* is proposed to guarantee optimized results by utilizing neighbor nodes to rewire the tree (Karaman and Frazzoli 2011). Several researchers have also investigated path planning for various types of CDPRs. Bury et al. (2019) developed a continuous collision-checking method for a CDPR mounted on a robotic arm. Rasheed et al. (2019) presented an optimization-based method for a reconfigurable mobile CDPR, but it is time consuming.

Although the above methods enable the CDPRs to avoid obstacles, the kinematic performance of the robot is not included. Owing to the special characteristics of the cable, the stability of the robot depends on the feasible wrenches that the cable can generate (Rasheed et al. 2020). Moreover, the kinematic reliability of the entire workspace must be guaranteed. An important metric for evaluating kinematic stability is the dexterity of the robot, which is denoted by the condition number of the kinematic Jacobian matrix. Zhang et al. (2018) designed a novel cost function based on dexterity, and the collision-free path planning of CDPR is completed by combining the RRT* and potential field guided (PFG) methods. More recently, Mishra et al. (2021) proposed an AFG-RRT* method to generate the optimal path for CDPRs in a cluttered environment. The cited method considered not only the dexterity of the robot but also the wrench capability defined by the capacity margin. However, both methods adopted the conventional goal-biased sampling method, which could reduce the convergence speed by sampling an invalid area.

Based on the above discussion, an adaptively optimal RRT* is developed as an offline path planning for CDPRs in a cluttered environment, which considers the interference among cables, end-effectors, and obstacles. To do so, the kinematic performance index of CDPRs is derived which integrates the dexterity and wrench capability metrics. One should note that although kinematic cost minimization is already widely used in the robotic industry, the wrench capability is not included before. The wrench capability aims to maximize the set of wrenches that can be generated by the cables on the end-effector, it is a unique property of CDPRs caused by the cable tension limitation. Moreover, the adaptive sampling method is proposed in the work to reduce the pathfinding time, which has two main parts: forward and backward sampling. These two sampling methods are adaptively selected based on the total expansion failure rate of the current node. Finally, post-processing was adopted to optimize the planned path.

The remainder of this paper is organized as follows. Section 2 presents the kinematic model of CDPR. Section 3 describes the kinematic performance indices in detail. In Sect. 4, the modified adaptive RRT* method is proposed and explained. The effectiveness of the proposed method is verified through simulations and experiments, as described in Sect. 5. Finally, Sect. 6 concludes the study.

2 CDPRs model

The kinematics analysis of CDPRs is a basic premise for studying the path planning problem. In this section, a general model of an n-DOF CDPR with m cables is established and its position kinematics is analyzed. As shown in Fig. 1a, the corresponding general model is illustrated. To simplify the analysis, the cable mass is neglected. Thus, the cable can be regarded as the straight line segment connected between the end-effector and fixed pully. The global coordinate frame O–XYZ is fixed on the base and the local coordinate frame e-xyz is attached to the center of the end-effector. For the CDPR with m cables, ai (i = 1, 2, …, m) denotes the Cartesian coordinates of the cable exit point Ai expressed in O–XYZ, and ebi denotes the Cartesian coordinates of the end-effector anchor point Bi in e-xyz. The position and orientation of the end-effector described in O–XYZ are represented by \({\varvec{p}} = [x, \, y, \, z]^{T}\) and \({\varvec{\varTheta}}= [\theta_{x} ,\theta_{y} ,\theta_{z} ]^{T}\) repressed by Euler angles, respectively. Thus, the configuration vector of the end-effector can be denoted by \({\varvec{X}} = [{\varvec{p}}, \, {{\varvec{\Theta}}}]^{T}\). The rotation matrix from O–XYZ to e-xyz is denoted as R.

Fig. 1
figure 1

Overview schematic of CDPRs. a Structural diagram of CDPRs; b overview schematic of the proposed method

Full size image

According to Fig. 1a, we select the i-th closed-loop of the CDPR, the cable vector li can be described by

$${\varvec{l}}_{i} = {\varvec{a}}_{i} - {\varvec{p}} - {\varvec{R}} \cdot^{e} {\varvec{b}}_{i}$$
(1)

Equation (1) denotes the position relationship between the end-effector and the cable. Therefore, given a specific position of the end-effector, the state of each cable can be obtained.

The overview schematic of the proposed method in shown in Fig. 1b. This work aims to develop a methodology to efficiently generate an optimal path based on the kinematic performance of CDPR in a cluttered environment from a given starting pose to a given ending pose. To do so, the kinematic performance index of CDPRs is derived which integrates the dexterity and wrench capability metrics. Moreover, the adaptive sampling method is proposed to improve the efficiency of the algorithm. The various constraints such as the workspace, cables/obstacles, and end-effector/obstacles collisions are considered. Finally, the path post-processing method is proposed to smooth the final path.

3 Kinematic performance index generation

3.1 Dexterity index of CDPR

The dexterity of a parallel robot is an important indicator for measuring the accuracy of transmission between cable space and the Cartesian space, and the distribution of dexterity in the workspace plays an important role in the kinematic stability of the CDPR. To detect the dexterity of the CDPR, we differentiate Eq. (1) with respect to time, which gives the following

$$\mathop {\varvec{l}}\limits^{\user2{.}} = - {\varvec{J}}^{T} \dot{\user2{X}}$$
(2)
$${\varvec{J}}({\varvec{X}}) = \left[ {\begin{array}{*{20}c} {{\varvec{u}}_{1} } & \cdots & {{\varvec{u}}_{m} } \\ {{\varvec{u}}_{1} \times ({\varvec{R}} \cdot^{e} {\varvec{b}}_{1} )} & \cdots & {{\mathbf{u}}_{m} \times ({\varvec{R}} \cdot^{e} {\varvec{b}}_{m} )} \\ \end{array} } \right]$$
(3)

where˙ \(\dot{\user2{l}} = [\dot{\user2{l}}_{1} , \ldots ,\dot{\user2{l}}_{m} ]^{T}\) is the velocity vector of the cables, \(\dot{\user2{X}} = [\dot{\user2{p}}, \, {\dot{\mathbf{\Theta }}}]^{T}\) represents the velocity vector of the end-effector, and \({\varvec{u}}_{i}\) denotes the unit vector of the cable. \({\mathbf{J}} \in {\mathbb{R}}^{m \times n}\) is the kinematic Jacobian matrix of the CDPR at a given pose. Therefore, the dexterity of CDPR is denoted by the condition number of the kinematic Jacobian matrix, which is expressed as follows

$$k({\varvec{J}}) = \left\| {\varvec{J}} \right\| \cdot \left\| {{\varvec{J}}^{{ - 1}} } \right\|$$
(4)

It should be noted that k is a number always greater than one, \(k \in [1, \, \infty )\). To facilitate subsequent analysis, the dexterity index of the CDPR \(\gamma_{d}\) is represented by the normalization of k.

$$\gamma_{d} = \frac{{k({\varvec{J}}) - k_{min} }}{{k_{max} - k_{min} }}$$
(5)

where \(k_{max}\) and \(k_{min}\) are the maximum and minimum values of the dexterity of CDPR in the workspace. Thus, a smaller number \(\gamma_{d}\) indicates that a better kinematic performance of the CDPR system at a given pose.

3.2 Feasible wrench set index of CDPR

According to the principle of virtual work, the static equilibrium equation of CDPRs is denoted as follows

$${\varvec{JT}} + {\varvec{w}}_{{\text{e}}} = 0$$
(6)

where \({\varvec{T}} = [t_{1} , \, t_{{2}} {, } \ldots { ,}t_{m} ]^{T}\) represents the cable tension vector. \({\varvec{w}}_{{\text{e}}} = [{\varvec{f}}_{e} , \, {\varvec{m}}_{e} ]^{T}\) denotes the external wrench applied to the end-effector, \({\varvec{f}}_{e}\) is the external force, and \({\varvec{m}}_{e}\) is the external moment. Equation (6) indicates that the CDPR must balance the external wrench to maintain the stability of the system. In practice, the external wrench set (EWS) can be formulated as a set \({\mathbb{R}}^{n}\) expressed by \({\varvec{W}}_{e} = \left\{ { \, {\varvec{w}}_{{\text{e}}} \in {\mathbb{R}}^{n} \, } \right\}\), which can be geometrically represented as a polytope. Consistent with this, owing to the limitation of cable tension, the feasible wrench set (FWS) that the cable can generate is defined as follows

$${\varvec{W}}_{f} = \left\{ {{\varvec{w}}_{f} \in {\mathbb{R}}^{n} | \, {\varvec{w}}_{f} = \sum\limits_{i = 1}^{m} {t_{i} J_{i} } , \, \underline {t}_{i} \le t_{i} \le \overline{t}_{i} } \right\}$$
(7)

Further, Eq. (7) can be rewritten as

$${\varvec{W}}_{f} = \left\{ {{\varvec{w}}_{f} \in {\mathbb{R}}^{n} | \, {\varvec{w}}_{f} = \sum\limits_{i = 1}^{m} {\alpha_{i} \Delta t_{i} J_{i} } + \user2{J\underline {t} },{ 0} \le \alpha_{i} \le 1} \right\}$$
(8)

where \(\Delta t_{i} = \overline{t}_{i} - \underline {t}_{i}\) is the feasible interval of the cable tension, \(J_{i}\) and is the i-th column of the Jacobian matrix. Accordingly, Eq. (8) can be expressed as a zonotope, which can be regarded as a special polytope with central symmetry (Fukuda 2004). However, it came to our attention that \({\varvec{W}}_{f}\) depends on the pose of the end-effector. The convex hull method can be applied to obtain the FWS of the CDPR (Bouchard et al. 2010).

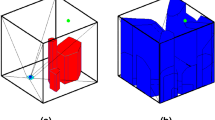
Figure 2a, b shows the EWS and FWS the studied CDPR in this work at a pose [0, 0, 445]T. To simplify the problem and visualize the zonotope in 3D space, the end-effector always remains horizontal in this work. The EWS in this work is a cuboid body due to the external rotational moment around the three axes is neglected. The cable tension was limited to \(\underline {t}_{i} = 0\) and \(\overline{t}_{i} = 100N\). As shown in Fig. 2b, the edge of the zonotope is equal to \(\Delta t_{i} = 100N\). According to the definition of the FWS, the required wrenches in the task can be satisfied if the EWS belongs to FWS, thereby FWS should be as large as possible to balance \({\varvec{W}}_{e}\). Therefore, the feasible wrench index \(\gamma_{f}\) of CDPR is denoted as the normalization of \(1/vol({\varvec{W}}_{f} )\), where \(vol({\varvec{W}}_{f} )\) is the volume of the zonotope of \({\varvec{W}}_{f}\).

Fig. 2
figure 2

Geometrical representation of EWS and FWS. a Polytope representation of EWS; b zonotope representation of FWS

Full size image

4 Formulation of modified adaptive RRT*

4.1 modified adaptive RRT*

In this section, the modified adaptive RRT* is proposed to generate a collision-free path in a cluttered environment based on the kinematic performance of CDPR. The structure of the proposed method is presented in Algorithm 1.

figure a

In the proposed modified adaptive RRT* method, the tree is initialized with the start point xstart, which is then assigned to the first new node xnew. The algorithm proceeds with the distance between the new node xnew and the goal point xgoal larger than a sufficiently small value rg. The AdaptiveSample function generates a random node based on the proposed adaptive sampling method, and then the nearest node xnearest to the tree is found to facilitate the tree growth by the Steer function (line 4–6 of Algorithm 1). The Steer function can be expressed as follows

$${\varvec{x}}_{new} = {\varvec{x}}_{nearest} + \eta ({\varvec{x}}_{rand} - {\varvec{x}}_{nearest} )/\left\| {{\varvec{x}}_{rand} - {\varvec{x}}_{nearest} } \right\|$$
(9)

If the path from xnearest to xnew is collision-free, xnew is inserted on the tree \({\mathcal{T}}\), and the kinematic cost of the new node is obtained based on Sect. 3, which is defined as \(c = \gamma_{d} + \gamma_{f}\) in this work. Subsequently, an optimized strategy similar to RRT* was applied. The neighbors of xnew are obtained with a given radius rc, and the parent of xnew is replaced by the neighbor node with a better kinematic cost (line 10–15 of Algorithm 1). This optimization process is intended to guarantee the kinematic performance of the robot.

4.2 Adaptive sampling

The adaptive sampling method is proposed in this section to reduce the pathfinding time, and the specific process is shown in Algorithm 2.

figure b

The proposed sampling method has two main parts: forward and backward sampling. These two sampling methods are adaptively selected based on the total expansion failure rate of the current node er. rrand is a random number between 0 and 1. Moreover, er can be formulated as the ratio of the number of expansion failures to the number of searches, which reflects the current situation of tree growth. A low er indicates that the influence of the obstacles is not powerful and the adaptive sampling method tends to sample the goal region. Nonetheless, it indicates that obstacles have a considerable impact on tree growth, and the sampling method samples the region far from the center of the tree to guide the tree away from the obstacle area.

4.2.1 Sampling forward

The SamplingForward function uniformly samples inside a hyperspherical cone centered on the goal point. The hypersphere cones in an n-dimensional space can be defined as follows

$$\left\{ \begin{gathered} x_{1} = r\cos (\theta_{1} ) \hfill \\ x_{2} = r\sin (\theta_{1} )\cos (\theta_{2} ) \hfill \\ x_{3} = r\sin (\theta_{1} )\sin (\theta_{2} )\cos (\theta_{3} ) \hfill \\ \vdots \hfill \\ x_{n - 1} = r\sin (\theta_{1} )\sin (\theta_{2} ) \cdots \sin (\theta_{n - 2} )\cos (\theta_{n - 1} ) \hfill \\ x_{n} = r\sin (\theta_{1} )\sin (\theta_{2} ) \cdots \sin (\theta_{n - 2} )\cos (\theta_{n - 1} ) \hfill \\ \end{gathered} \right.$$
(10)

where 0 ≤ r ≤ R, − θ ≤ θ1 ≤ θ, 0 ≤ θ2 ≤ π, …, 0 ≤ θn-2 ≤ π, 0 ≤ θn-1 ≤ 2π. In Eq. (9), the parameters R and θ are determined by the node xc, which has a maximum expansion failure rate, xstart, and xgoal. R and θ can be obtained using the following equations

$$\left\{ \begin{gathered} R{ = }\left\| {{\varvec{x}}_{c} - {\varvec{x}}_{goal} } \right\| \hfill \\ \theta = \arccos ({\varvec{u}}_{s} \cdot {\varvec{u}}_{c} ) \hfill \\ \end{gathered} \right.$$
(11)

where \({\varvec{u}}_{s}\) and \({\varvec{u}}_{c}\) are the unit vectors from xgoal to xstart, and xgoal to xc, respectively. The basic sampling forward process is illustrated in Fig. 3.

Fig. 3
figure 3

Schematic of the proposed adaptive sampling method. a Schematic representation of sampling forward; b schematic representation of sampling backward

Full size image

As shown in Fig. 3a, the forward area is the line between the starting point and the target point, which ensures that the tree grows toward the goal point effectively. After colliding with an obstacle, the forward area is expanded to a cone to continuously guide the tree toward the goal point.

4.2.2 Sampling backward

In this work, the backward region is defined as a hyperball, and the center of the hyperball is the middle point of the current tree denoted by xcenter, which is the mean value of all node coordinates. The radius r is defined as the distance from xcenter to xc. Therefore, the random node xrand in the backward region is limited by the following equation.

$$\left\{ \begin{gathered} {\varvec{x}}_{center} = \sum\limits_{i = 1}^{N} {{\varvec{x}}_{i} /N} \hfill \\ r = \left\| {{\varvec{x}}_{center} - {\varvec{x}}_{c} } \right\| \hfill \\ \left\| {{\varvec{x}}_{center} - {\varvec{x}}_{rand} } \right\| > r \hfill \\ \end{gathered} \right.$$
(12)

Figure 3b represents a Bug trap problem with high planning difficulty (Yershova et al. 2005). where the start point is inside a concave obstacle and cannot directly connect to the goal point. The proposed sampling method makes several unsuccessful attempts in the forward region and then samples the backward region. Thus, the nodes in the area surrounded by obstacles are sparse inside and dense outside. Compared to conventional sampling methods, the proposed sampling method can obtain fewer extensions and collision detections.

4.3 Post-processing

In general, the path generated by the modified adaptive RRT* is not smooth. In this section, post-processing is adopted to optimize the path, which is summarized in Algorithm 3.

figure c

As shown in Fig. 4a, the post-processing starts from the initial node on the initial path σ, and moves to the goal node progressively. Each child node is traversed until a collision-free path with minimum path cost is found. After post-processing, an optimal path σ*is generated, which does not have additional nodes that can be directly connected. As shown in Fig. 4b, the green line indicates the optimized path σ*, it can be seen that the path smoothness is achieved.

Fig. 4
figure 4

Schematic of the path smoothness process. a Schematic diagram of post-processing. b Final optimized path

Full size image

5 Simulation and experimental results

5.1 Consideration

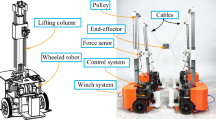
In this section, the proposed modified adaptive RRT* algorithm is simulated and tested on a self-built 8–6 (8 cables with 6 DOF) CDPR, as shown in Fig. 5. The end-effector is a cube with a size of 130 mm × 130 mm × 130 mm and a weight of 0.4 kg. The coordinates of the cable outlet point Ai (i = 1,…,m) are listed in Table 2 (Table 1).

Fig. 5
figure 5

8–6 CDPR prototype

Full size image
Table 1 Coordinates of cable outlet points
Full size table

The workspace is a significant constraint on the end-effector motion. In this work, the typical wrench closure workspace (WCW) is used, which is defined as a set of poses of the end-effector in which the cables can balance any external wrench. The maximum cable tension is the same as that in Sect. 3. For simplification, the cables were pre-tensioned in the initial pose. Thus, the cable tension was not controlled during the motion of the end-effector.

As shown in Fig. 6, the green part represents the WCW and the red line is the frame formed by cable outlet points. In this work, the obstacle/end-effector/cable and the WCW are modeled as the convex body, and the Gilbert–Johnson–Keerthi (GJK) algorithm is applied for the collision detection (Ong et al. 1997).

Fig. 6
figure 6

Wrench closure workspace of the studied CDPR

Full size image

Based on the above analysis, the distribution of kinematic performance indices can be demonstrated in the workspace. From Fig. 7, it can be seen that the cost of the dexterity index gradually decreases as the end-effector approaches the center of the workspace. However, the cost of the feasible wrench set increases under the same conditions. Thus, it is necessary to consider the kinematic cost to balance this contradictory phenomenon.

Fig. 7
figure 7

Distribution of CDPR kinematic performance indexes in the workspace section (z = 445 mm). a Dexterity index. b Feasible wrench set index

Full size image

5.2 Simulation

In this section, several simulations are conducted to demonstrate the proposed path-planning method. The simulation environment was MATLAB 2020a with an Intel i7-9750H processor and 32 GB RAM. The simulation parameters are listed in Table 2.

Table 2 Simulation parameters
Full size table

To validate the proposed method, three environments were designed in which the number of obstacles increased from one to three. These obstacles were modeled as a 3D axis-aligned bounding box, and located in [− 150, 0, 225], [200, − 150, 175], and [− 200, 200, 210], respectively. The closest proximity between the CDPR and the obstacles was defined as 10 mm. For contrasting conditions, the proposed method without adaptive sampling was simulated, in which the goal-biased sampling strategy with 0.5 probability was used to sample the goal point.

Figure 8 shows the simulation results, where the green, red, and blue lines denote the initial path σ, optimized path σ*, and tree, respectively. It is apparent that the proposed modified adaptive RRT* is capable of generating a collision-free path for CDPR, and the post-processing in Algorithm 3 completes the path smoothness with less path cost. It is also clear from the figure that the tree generated using the proposed adaptive sampling method has fewer nodes. Therefore, the computational efficiency of the proposed method is improved.

Fig. 8
figure 8

Simulation results. a Environment 1 with the proposed method. b Environment 1 without adaptive sampling. c Environment 2 with the proposed method. d Environment 2 without adaptive sampling. e Environment 3 with the proposed method. f Environment 3 without adaptive sampling

Full size image

5.3 Evaluation

We should note that comparisons with other advanced methods can only be made if other conditions are consistent, however, computing the kinematic cost during the RRT sampling process is unique in this paper. To evaluate the reliability of the proposed method, 100 simulations were conducted for each environment, as illustrated in Sect. 5.2. These simulations used the same parameters listed in Table. 2. However, we used different start and goal points with the same path length to reproduce the simulation under identical conditions (Xu et al. 2020).

Figure 9a shows the average number of nodes on the tree and the corresponding standard deviation of the simulation evaluation for different environments. It can be observed that the average number of nodes is reduced by 20.5% compared to the goal-biased sampling with a 50% goal probability. Moreover, a lower standard deviation indicates that the proposed method is more stable. To further verify the improvement in kinematic performance, the kinematic cost in Algorithm 1 is replaced by the conventional path length cost, and the comparison result is shown in Fig. 9b. It can be seen that the proposed method obtains a lower kinematic cost, and the average kinematic performance increases by 18.2%. The smaller standard deviation of the kinematic cost with the proposed method can result in a more stable kinematic performance.

Fig. 9
figure 9

Evaluation results. a Number of nodes comparison with different method. b Average kinematic cost comparison with different method

Full size image

5.4 Experimental demonstration

The effectiveness of the proposed method was verified by a real-world experiment. The task was to allow the CDPR to avoid an obstacle with a collision-free path obtained in Fig. 8a. The experimental setup is shown in Fig. 10, which corresponds to environment 1.

Fig. 10
figure 10

Schematic of experiment setup with environment 1

Full size image

We used the April tag to obtain the real position of the end-effector (Olson 2011). Furthermore, the end-effector was maintained at a low speed of 20 mm/s to avoid oscillation. From Fig. 11a, it can be seen that the proposed method generates a collision-free path such that the closest proximity between the CDPR and obstacle is consistently larger than the predefined 20 mm. The end-effector performs obstacle avoidance when the CDPR and obstacle are close to each other, as shown in Fig. 11b. The experimental results are shown in Fig. 12.

Fig. 11
figure 11

Experiment results. a, b Distance change between the CDPR and obstacle. c Position change of the end-effector

Full size image
Fig. 12
figure 12

Experiment visualization. a t = 15 s. b t = 20 s. c t = 25 s, d t = 35 s

Full size image

6 Conclusion

In this study, a modified adaptive RRT* method was developed for CDPRs to find a collision-free path in a cluttered environment while considering the kinematic performance. The proposed method developed an adaptive sampling method, minimized kinematic cost, and achieved fast convergence by utilizing post-processing. The proposed method was simulated in different environments. The simulation results show that the proposed method can generate a collision-free path for CDPRs. Moreover, the average number of nodes on the tree is reduced by 20.5% compared to that without adaptive sampling, and the average kinematic performance increased by 18.2%. Finally, the developed method was fully validated and demonstrated through an experiment using a self-built 8–6 CDPR.