1 Introduction

Reduced order modelling has become a significant area of research in systems engineering since 1960s. Numerous techniques are developed for continuous and discrete time systems (Moore 1981; Aoki 1968; Shamash 1974; Hutton and Friedland 1975; Obinata and Inooka 1983; El-Attar and Vidyasagar 1978; Bistritz 1982; Hwang et al. 1983; Pan and Pal 1995; Sikander and Prasad 2015; Sikander 2016). The influence of discrete time system reduction is increasing day by day due to the fast development of microprocessor and micro-controller based design of control system.

The reduced order modelling techniques are broadly classified into two categories. First is direct reduced order modelling and second is indirect reduced order modelling techniques. The techniques in which the reduced order models are obtained directly in z-domain without using any transformation, comes under the category of direct modelling techniques (Hwang et al. 1983). However, in the second category, the reduced order modelling is based on transformation of discrete time system into continuous time system using different types of transformations such as bilinear, linear transformation, etc. (Chu and Glover 1999; Shih and WD 1973). Finally the reduced order model is achieved using corresponding inverse transformation. In the recent years, artificial neural network (ANN) (Alsmadi et al. 2011), genetic algorithm (GA) (Alsmadi and Abo-Hammour 2015), step response matching (SRM) (Mukherjee et al. 2007) and differential evolution (DE) (Namratha and Latha 2015) based discrete time systems reduction have been introduced.

Telescu et al. (2013) employed an algorithm for reduced order modelling of the systems described by discrete Laguerre functions. Their method is based on minimization of a quadratic error. Singh and Chandra (2012) proposed a composite method for reducing the order of a discrete interval system. They have obtain the coefficients of denominator of lower order system using pole clustering whereas the numerator is synthesized using improved Pade approximation. Various order reduction techniques have also been introduced for controller design. The design of controller for discrete time systems using reduced order modelling is presented by Pal and Pan (1992). Karimaghaee and Noroozi (2011) presented a method to design a four discs system controller using bilinear transformation. Real coded genetic algorithm (Yadav et al. 2010) and differential evolution optimization algorithm (Yadav et al. 2010) is suggested to calculate lower order system and controller design for discrete time systems. These methods are based on the concept of minimizing the integral square error between the responses of higher and reduced order model. Vasu and Sandeep (2012) suggested a method for discrete time system reduction and discrete proportional-integral-derivative (PID) controller design via reduced order modelling which is based on artificial bee colony. This method reduces the complexity involved in the direct design of PID controller.

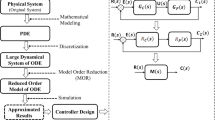
The reduced order model must be achieved by preserving the characteristics of the original model in a realistic manner. Reis and Stykel (2008) suggested a method in which it is shown that structure preservation in the reduced model provides a meaningful physical interpretation. Substructure preservation means to preserve the dominant poles of the original system in the reduced one. In spite of various techniques, no technique always gives the best result for all class of systems. Therefore, this paper contributes a new method for model order reduction (MOR) of discrete time systems by preserving its dominant dynamics in the reduced system. The following covers the major contributions of the present study:

  • First, the Cuckoo Search (CS) algorithm is utilised for the parameter estimation of reduced order model. The numbers of variables of CS are lesser than the variables used in other meta-heuristic techniques, such as, GA, PSO, ant colony (Yang and Deb 2009). Therefore, less variables in CS algorithm leads to the fast convergence.

  • The reduced order system is synthesized by minimizing the summation of square error (SSE) between the responses of higher and reduced order systems.

  • Four benchmark numerical examples of single input single output (SISO) discrete time systems are considered from literature to demonstrate the efficacy and superiority of the proposed method.

  • Also, the step as well as impulse responses of original and reduced order systems are shown.

  • Finally, the results are compared in terms of dominant critical frequency preservation, stability preservation, system responses and performance indices with other renowned techniques and recently published work.

This paper is organized in five sections. Section 1 comprises introduction and the detailed literature review on model order reduction. In Sect. 2, the problem formulation is explained for discrete time single input single output systems and Sect. 3 describe the preliminaries of cuckoo search algorithm. The proposed methodology for system reduction is presented in Sect. 4. The efficacy of the proposed method is depicted in Sect. 5 followed by solved numerical examples considered from literature. Section 6 comprises the conclusion along with the future scope of the presented work.

2 Problem statement

Consider a discrete-time system represented by

$$\begin{aligned} \begin{array}{l} y(k) + {a_1}y(k - 1) + {a_2}y(k - 2) + \cdots + {a_n}y(k - n) \\ = {b_0}u(k) + {b_1}u(k - 1) + \cdots + {b_n}u(k - n) \end{array} \end{aligned}$$
(1)

where y(k) and u(k) are output and input of the system at \(k\text {th}\) sampling instant, respectively. The above system can also be represented by the following pulse transfer function.

$$\begin{aligned} {G_n}(z) = \frac{{Y(z)}}{{U(z)}} = \frac{{{b_0}{z^n} + {b_1}{z^{n - 1}} + \cdots + {b_n}}}{{{z^n} + {a_1}{z^{n - 1}} + \cdots + {a_n}}} \end{aligned}$$
(2)

The objective is to determine the reduced order model of the above system in the following form such as to preserve the essential characteristics like stability, dominant poles and good time/frequency response matching of the original higher order system of Eq. 2 .

$$\begin{aligned} {G_r}(z) = \frac{{Y_r(z)}}{{U_r(z)}} = \frac{{{d_0}{z^r} + {d_1}{z^{r - 1}} + \cdots + {d_r}}}{{{z^r} + {e_1}{z^{r - 1}} + \cdots + {e_r}}} \end{aligned}$$
(3)

where \({U_r(z)}\) and \({Y_r(z)}\) are input and output of reduced order model respectively. \(e_i (i=1,2\ldots r)\) and \(d_i (i=0,1,2\ldots r)\) are unknown coefficients of numerator and denominator polynomial of pulse transfer function of reduced order model.

In order to justify the efficacy and powerfulness of the proposed technique the results are compared in terms of substructure preservation, system responses and performance indices such as summation of square error (SSE) and summation of absolute error (SAE) as given in Eqs. 4, 5 respectively.

$$\begin{aligned} SSE = \sum \limits _{k = 0}^N {{{[y(k) - {y_r}(k)]}^2}} \end{aligned}$$
(4)
$$\begin{aligned} SAE = \sum \limits _{k = 0}^N {\left| {y(k) - {y_r}(k)} \right| } \end{aligned}$$
(5)

where y(k), \({y_r}(k)\) are the outputs of \({G_n}(z)\) and \({G_r}(z)\) at the \(k^{th}\) sampling instant \(t_k\), respectively. N is the number of sampling instances.

3 Cuckoo search algorithm

Cuckoo search (CS) algorithm is based on the natural behaviour of cuckoo birds. They lay their eggs in the nearest nest and destroy other eggs to increase the hatching probability. The algorithm was developed by Yang and Deb (2008). If other birds recognize that the cuckoo eggs, they will throw them outside or simply vacant that place (Yang and Deb 2009). A solution is basically presented by an egg in a nest. Lévy flight (Brown et al. 2007; Viswanathan 2010) is used to form a new nest at new places. The following three rules was suggested by Yang and Deb (2008):

  • Nest must be selected randomly for laying eggs.

  • The nest must be transferred to the next generation if good quality eggs are found in it.

  • \({p_a} \in [0,1]\) is the probability of an alien egg. In that case the eggs may be thrown or the new nest may be form.

The Lévy flight is performed by the following equation to find the new solution \(Y^{(t + 1)}\) of cuckoo i (Yang and Deb 2009):

$$\begin{aligned} {Y_i}^{(t + 1)} = {Y_i}^{(t)} + a \otimes {L \acute{e}vy}(\lambda ) \end{aligned}$$
(6)

where \(a\,(a > 0)\) is a step size which is related to the level of the problem optimized by the technique. The pseudo code and flow chart of Cuckoo search algorithm is depicted in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Pseudo code of cuckoo search algorithm

Full size image
Fig. 2
figure 2

Flow chart of Cuckoo search algorithm

Full size image

Previous study show that CS algorithm perform well as compared to other meta-heuristic algorithms such as GA and PSO. This is because of the lesser number of parameters, such as population size (n) and probability of alien egg (pa), have to be tuned in CS algorithm comparatively. In fact after defining the population size, only one parameter has to be tune in CS algorithm. Also in the CS algorithm the convergence rate is insensitive to the parameter Pa. Therefore, CS is more generic and robust for many optimization problems, comparing with other meta-heuristic algorithms (Yang and Deb 2009).

In CS algorithm, a solution is represented by an egg in a nest whereas each nest represents the set of solutions (parameter set) and a cuckoo egg represents a new solution. The aim is to obtain improved solution by swapping the poor solution with new solution in the nests.

4 Proposed methodology for system reduction

This study present the concept of optimization for discrete time system reduction. The unknown coefficients of the reduced order system represented by Eq. (3) are obtained using the following steps based on cuckoo search algorithm.

Step 1: Consider the fitness function as given in Eq. 4 and the number of selected variables (say q). Initialization of a population of p host nests then the formulation of problem is as follows:

Minimize \(Z=SSE\),

subject to

\({d_{iL}}< {d_i} < {d_{iU}}\);

\({e_{iL}}< {e_i} < {e_{iU}}\).

where \({d_{iL}},{e_{iL}}\) and \({d_{iU}}\), \({e_{iU}}\) are the minimum and maximum values of the selected variables as specified in Eq. (3), respectively and \(i = 0,1 \ldots q\).

Step 2: Calculate the value of \({Z_\alpha }\) for a randomly selected cuckoo (\(\alpha \)), select a nest (\(\beta \)) randomly among p.

Step 3: \(\beta \) is interchanged by the present solution if (\({Z_\alpha } > {Z_\beta }\) ).

Step 4: The calculated solution is the best solution if the stopping condition is arrived.

5 Computational results

In order to show the efficacy of the proposed method, four different SISO systems, namely, supersonic jet engine inlet system, eight order discrete systems and fourth order continuous time system, are taken into consideration.

Example 1

Let us consider a supersonic jet engine inlet system represented by the following transfer function (Alsmadi and Abo-Hammour 2015).

$$\begin{aligned} {G_7}(z&)=\frac{2.043{z^6} - 4.983{z^5} + 6.57{z^4} - 5.819{z^3} + 3.636{z^2} - 1.411z + 0.2997}{{z^7} - 2.46{z^6} + 3.433{z^5} - 3.333{z^4}+ 2.546{z^3} - 1.584{z^2} + 0.7478z - 0.252}\\ \end{aligned}$$

The proposed method is applied on this system and the following reduced third order system is obtained.

$$\begin{aligned} {G_3}(z) = \frac{{0.6232{z^3} - 0.5351{z^2} - 0.2458z + 0.322}}{{{z^3} - 2.26{z^2} + 2.027z - 0.7191}} \end{aligned}$$

while the reduced third order system obtained by using Genetic algorithm based model order order reduction technique (GA-MOR), recently suggested by Alsmadi and Abo-Hammour (2015) is as follows:

$$\begin{aligned} {G_3}(z) = \frac{{1.515{z^3} - 3.124{z^2} + 2.404z - 0.6312}}{{{z^3} - 2.26{z^2} + 2.027z - 0.7191}} \end{aligned}$$

Also, artificial neural network based model order reduction (ANN-MOR) (Alsmadi et al. 2011) is performed on this system which results the following third order model.

$$\begin{aligned} {G_3}(z) = \frac{{1.525{z^3} - 3.125{z^2} + 2.405z - 0.6384}}{{{z^3} - 2.26{z^2} + 2.027z - 0.7191}} \end{aligned}$$

The same discrete time system is reduced by using an algorithm recently developed by Desai (2013) which utilizes the advantages of Eigen spectrum analysis and least square method (ESA & LSM). The resulting reduced third order system is give as follows-

$$\begin{aligned} {G_3}(z) = \frac{{2.185{z^2} - 3.083z + 1.1847}}{{{z^3} - 1.054{z^2} + 0.0808z + 0.0585}} \end{aligned}$$
Table 1 Comparison of different reduction methods for Example 1
Full size table

The responses of original seventh order and reduced third order systems when subjected to unit step and impulse inputs are shown in Figs. 3 and 4 for Example 1, respectively. The advantage of the proposed method is that the response of the reduced third order system, achieved by this method is much closer as the responses of the reduced systems obtained by other methods.

Fig. 3
figure 3

Step responses of original seventh order and reduced third order systems for Example 1

Full size image
Fig. 4
figure 4

Impulse responses of original seventh order and reduced third order systems for Example 1

Full size image

It is observed from Table 1 that the stable reduced order model is achieved by preserving the critical frequencies of the original system. Also, the proposed third order system exhibits the lower values of performance indices such as summation of square error (SSE) and summation of absolute error (SAE) as compared to the reduced systems obtained by other well-known methods available in the literature.

Example 2

As second example, consider the following eight order SISO discrete system which is recently considered by Alsmadi and Abo-Hammour (2015).

$$\begin{aligned} {G_8}(z&)=\frac{{0.1625{z^7} + 0.125{z^6} + 0.0025{z^5} + 0.00525{z^4}- 0.02263{z^3}- 0.00088{z^2}+ 0.003z - 0.000413}}{{{z^8} - 0.6307{z^7} - 0.4185{z^6} + 0.078{z^5} - 0.057{z^4}}{+ 0.1935{z^3} + 0.09825{z^2}- 0.0165z + 0.00225}}\\ \end{aligned}$$

The following reduced second order system is achieved using the proposed technique.

$$\begin{aligned} {G_2}(z) = \frac{{0.01221{z^2} + 0.1405z - 0.07124}}{{{z^2} - 1.7594z + 0.83347}} \end{aligned}$$

whereas, the reduced system achieved by the method based on Genetic algorithm (GA-MOR) suggested by Alsmadi and Abo-Hammour (2015) is as follows.

$$\begin{aligned} {G_2}(z) = \frac{{0.021129{z^2} + 0.12259z - 0.063666}}{{{z^2} - 1.7594z + 0.83347}} \end{aligned}$$

Yadav et al. (2010) suggested a differential evolution (DE) method to obtain a reduced system for the above eight order system and the resulting reduced system is given by

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{ 0}}\mathrm{{.004821z }} - \mathrm{{0}}\mathrm{{.002508}}}}{{0.03046{z^2} - 0.05395z + 0.02563}} \end{aligned}$$

The reduced order modelling based on artificial neural network (ANN-MOR) is suggested by Alsmadi et al. (2011) and the reduced system is given as follows.

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{ 0}}\mathrm{{.1623z + 0}}\mathrm{{.08245}}}}{{{z^2} - 1.7594z + 0.83347}} \end{aligned}$$
Table 2 Comparison of different reduction methods for Example 2
Full size table
Fig. 5
figure 5

Step responses of original eight order and reduced second order systems for Example 2

Full size image
Fig. 6
figure 6

Impulse responses of original eight order and reduced second order systems for Example 2

Full size image

The results are compared in terms of critical frequencies or dominant dynamics of the original system which are preserved by the proposed reduced order system as shown in Table 2. Therefore, the proposed method provides the stable reduced order system for the stable original system. Although the dominant dynamics of the original system are also preserved by GA-MOR and ANN-MOR methods but the proposed system responses exhibits closer approximation and lower values of SSE and SAE comparatively. The closeness of step and impulse responses can be observed from Figs. 5 and 6 respectively. Table 2 depicts the comparative analysis of different reduction methods for Example 2.

Example 3

The following system which is to be reduced is an eight order discrete time SISO system and previously considered by Alsmadi et al. (2011).

$$\begin{aligned} {G_8}(z&)=\frac{0.4209{z^7} + 0.2793{z^6} - 0.0526{z^5} + 0.038{z^4} - 0.1291{z^3} - 0.0656{z^2}+ 0.011z - 0.0015}{{z^8} - 0.4209{z^7} - 0.2793{z^6} + 0.0526{z^5} - 0.038{z^4}+ 0.1291{z^3} + 0.0656{z^2}- 0.011z + 0.0015}\\ \end{aligned}$$

Again the dominant dynamics of the original system are preserved by the proposed reduced order system which is given by

$$\begin{aligned} {G_2}(z) = \frac{{ - 0.05245{z^2} + 0.5894z - 0.3806}}{{{z^2} - 1.5025z + 0.65849}} \end{aligned}$$

The genetic algorithm based model order reduction (GA-MOR) (Alsmadi and Abo-Hammour 2015) is performed on this system which results the following second order model.

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{0}}\mathrm{{.5401z}} - \mathrm{{0}}\mathrm{{.36939}}}}{{{z^2} - 1.5025z + 0.65849}} \end{aligned}$$

whereas Alsmadi et al. (2011) perform artificial neural network based MOR and obtained the following second order reduced model.

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{0}}\mathrm{{.52563z}} - \mathrm{{0}}\mathrm{{.3799}}}}{{{z^2} - 1.5025z + 0.65849}} \end{aligned}$$

Recently, the model order reduction based on least square method and differential evolution (LSM & DE) is suggested by Namratha and Latha (2015) and the following reduced system is achieved when applied on this eight order system.

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{ 0}}\mathrm{{.387715z}} - \mathrm{{0}}\mathrm{{.260852}}}}{{{z^2} - 1.580003z + 0.724034}} \end{aligned}$$

The concept of step response matching in reduced order modelling (SRM-MOR) is introduced by Mukherjee et al. (2007) and obtained the following second order reduced model.

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{0}}\mathrm{{.4923z}} - \mathrm{{0}}\mathrm{{.336}}}}{{{z^2} - 1.5024z + 0.6584}} \end{aligned}$$
Table 3 Comparison of different reduction methods for Example 3
Full size table
Fig. 7
figure 7

Step responses of original eight order and reduced second order systems for Example 3

Full size image
Fig. 8
figure 8

Impulse responses of original eight order and reduced second order systems for Example 3

Full size image

The step and impulse responses of original and reduced order systems, obtained by different techniques are shown in Figs. 7 and 8, respectively from where the closeness among original and reduced order systems can be observed. The comparative analysis of different reduction methods in terms of critical frequencies and performance indices is depicted in Table 3. Therefore, the efficacy and superiority of the proposed method are clearly seen, not only in terms of substructure preservation, stability preservation but also in terms of system output responses and performance indices.

Example 4

The next system is a fourth order continuous time system investigated by Alsmadi et al. (2011) which is given by

$$\begin{aligned} {G_4}(s) = \frac{{{s^3} + 7{s^2} + 24s + 24}}{{{s^4} + 10{s^3} + 35{s^2} + 50s + 24}} \end{aligned}$$

The discretied model of the continuous system with sampling period 0.01s is obtained as follows-

$$\begin{aligned} {G_4}(z&)=\frac{0.0049273{z^4} - 0.0095101{z^3} - 0.00033297{z^2} + 0.0095102z - 0.0045942}{{z^4} - 3.9015{z^3} + 5.7078{z^2} - 3.7112z + 0.90483}\\ \end{aligned}$$

The proposed technique yields the reduced system which is given by

$$\begin{aligned} {G_2}(z) = \frac{{0.005178{z^2} - 0.002317z - 0.002663}}{{{z^2} - 1.97z + 0.9704}} \end{aligned}$$

The conversion of this system to continuous form, produces the reduced second order system in the following from along with the critical financiers \(-1 \) and \(-2\). It means that substructure preservation is achieved by the proposed method.

$$\begin{aligned} {G_2}(s) = \frac{{0.001226{s^2} + 0.7959s + 2.003}}{{{s^2} + 3s + 2}} \end{aligned}$$

The genetic algorithm based model order reduction (GA-MOR) (Alsmadi and Abo-Hammour 2015) is performed on this system which results the following second order model.

$$\begin{aligned} {G_2}(s) = \frac{{0.001228{s^2} + 0.7984s + 2}}{{{s^2} + 3s + 2}} \end{aligned}$$

whereas, Alsmadi et al. (2011) suggested the following reduced order system in the continuous form with critical frequencies \(-1 \) and \(-2\).

$$\begin{aligned} {G_2}(s) = \frac{{ - 0.0040503{s^2} + 0.80006s + 2}}{{{s^2} + 3s + 2}} \end{aligned}$$

The equivalent discrete model of this system is given as-

$$\begin{aligned} {G_2}(z) = \frac{{\mathrm{{0}}\mathrm{{.008079z}} - \mathrm{{0}}\mathrm{{.007882}}}}{{{z^2} - 1.9702z + 0.97044}} \end{aligned}$$

Although Alsmadi’s method also preserves the dominant dynamics of the original system but produces high values of performance indices comparatively as shown in Table 4. On the other hand, the following reduced second order system is obtained by MOR which utilizes the advantages of stability equation method along with particle swarm optimization technique (SE & PSO) (Sikander and Prasad 2015). Although, the stability is preserved in this reduced system but the critical frequencies are completely differs from the original system dynamics as depicted in Table 5. In fact, the critical frequencies of original system are real but in this particular case the critical frequencies of reduced order system comes out imaginary.

$$\begin{aligned} {G_2}(s) = \frac{{\mathrm{{0}}\mathrm{{.7528 s + 0}}\mathrm{{.6952}}}}{{{s^2} + 1.458s + 0.6997}} \end{aligned}$$

The discretized model of this system with sampling period 0.01s is obtained as follows-

$$\begin{aligned} {G_2}(z) = \frac{{0.003754{z^2} + 3.451e - 05z - 0.003719}}{{{z^2} - 1.985z + 0.9855}} \end{aligned}$$
Table 4 Comparison of different reduction methods for Example 4
Full size table
Fig. 9
figure 9

Step responses of original \({4^{th}}\) and reduced \({2^{nd}}\) order systems for Example 4

Full size image
Fig. 10
figure 10

Impulse responses of original \(4^{th}\) and reduced \(2^{nd}\) order systems for Example 4

Full size image

It is also noticed that the values of performance indices of the reduced system obtained by SE and PSO are very high comparatively. The efficacy of the proposed technique is also observed by the system responses with unit step and impulse inputs as shown in Figs. 9 and 10, respectively. The reduced system responses resulting from the proposed technique are much closer to the responses of original system in comparison to the responses of the reduced system provided by the recently published and well-known methods. Here also, stable reduced order system is obtained for given high order stable system as it preserves the dominant dynamics of the original system.

Table 5 Comparison of different reduction methods
Full size table

Additionally, the reduced systems obtained by proposed method are also compared with other existing methods such as ESA and LSM, DE, LSM and DE, SRM-MOR, SE and PSO for all examples. A comparative analysis of these methods is depicted in Table 5. It is found that the proposed method not only preserve the dominant dynamics and stability of the original system but also improve the values of performance indices.

6 Conclusion

A new technique for MOR of discrete time systems using cuckoo search is suggested in this study. The dominant critical frequencies are preserved in reduced order models by minimizing the summation of square error. Four benchmark systems are considered from literature and reduced by proposed method. The simulation results are compared with recently published work, such as GA and ANN based MOR in terms of exact dominant dynamic preservation, stability preservation, step, impulse responses and performance indices. Based on these results, the potential of the new technique is observed as it exhibits the excellent performance comparatively. The linear time interval as well as non-liner system reduction may also be one of the future works.