1 Introduction

Power systems are normally functioned with the maximum probable capacity. Due to various reasons such as deregulation of electricity markets and rapid upsurge of electricity demand affects the stability boundaries. Various instabilities affects the decrement of marginal security in the power system. Under such circumstances, when a circuit breaker is charged, a high transient current flow for a lesser phase of time period until standard flux conditions are recognized. During the most practical system conditions, this transient current is of high values. The harmonics present in transient current has been found to cause wide raging disturbances in power system and power supplies (Brunke and Frohlich 2001). Some solutions are recommended to overcome the problem of Diode Bridge DC reactor (Hoshino et al. 2003) and PWM converter with voltage source are used (TarafdarHagh and Abapour 2007; Madani et al. 2012; Taylor et al. 2012). A few disadvantages like voltage drop, further control circuits, switching devices and bypass or diverted resistances is noted in these previous practices. However, the stability of the system is discussed in no one of the available research methods. This paper is the second part of two-part paper on the topic of TCL based on Thyristor Bridge. The first part (Shrivastav 2015) had presented the mathematical and simulation considerations of transients that occur during closing of circuit breaker and energizing of transformer. Initially two different types of TCL based three-phase 12-pulse and six-pulse converter circuit was proposed. This second part addresses the comparative aspect of stability and the Total Harmonic distortion (THD) between 12-pulse and six-pulse converter based three-phase thyristor bride system.

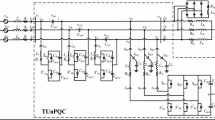
2 TCL connected in series with three-phase circuit breaker

Transient current in circuit breaker occurs due to unexpected change in the magnetizing voltage. The transient current waveform consist a large and long lasting AC component and harmonics (Lian and Perkins 2008) (Fig. 1).

Fig. 1
figure 1

Transient current at 100% nominal volt of circuit breaker

Full size image

To gain better result, a low resistance coil of TCL shown in Fig. 2. The TCL connected in series with three-phase breaker operates in two modes, charging mode and discharging mode (Shrivastav 2015).

Fig. 2
figure 2

Equivalent circuit of three-phase circuit breaker connected with TCL in series

Full size image

The mathematical form, presented in charging mode is expressed as (Shrivastav 2015),

$$\begin{aligned} i(t) = e^{ - (R/L)t} \left( {\frac{ - Vp}{{\sqrt {(R^{2} ) + (wL^{2)} } }}\sin (wt_{1} - \delta ) + \frac{{2V_{TF} }}{R}} \right) \hfill \\ \quad + {\kern 1pt} \,\frac{Vp}{{\sqrt {(R^{2} ) + (wL^{2} )} }}\sin (wt_{2} - \delta ) - \frac{{V_{TF} }}{R} \hfill \\ \end{aligned}$$
(1)

where R = RP + RTCL (Rp is the transformer primary side resistance and RTCL is the resistance of reactor RL), L = Lp + LTCL + Lm (Lp is the transformer primary side leakage inductance and LTCL is the inductance of reactor RL and Lm is the transformer charging inductance), VTF is the thyristor voltage drop in forward conduction mode and Vp is the peak amplitude of the supply voltage.

3 Proposed TCL

As indicated in Fig. 2, (Shrivastav 2015) the transient current of the three-phase transformer can be regulated with the bridge of 12 thyristor, considerably. Although, the substantial amount of current is flowing through these thyristor under loaded condition of transformer. Therefore they are costly as well as system became unstable. Hence to make the system stable and harmonics free, a modified circuit is proposed, as shown in Fig. 3.

Fig. 3
figure 3

Proposed Y-yg transformer connected TCL

Full size image

4 Charging mode

The Fig. 2, depicts the circuit in charging mode with neglecting R1 and L1 is communicated as,

$$V_{LL} \sin (wt - 30) = 2R_{p} i_{1} + 2L_{p} \frac{{di_{1} }}{dt} + 2V_{TF} + L_{TCL} \frac{{di_{1} }}{dt} + R_{TCL} i_{1} + 2\frac{d\varphi }{dt}$$
(2)

Differentiating (2) can be rewritten, as follows

$$wV_{LL} \sin (wt - 30) = 2R_{p} i_{1} + 2L_{p} \frac{{di_{1} }}{dt} + L_{TCL} \frac{{d^{2} i_{1} }}{{dt^{2} }} + R_{TCL} \frac{{di_{1} }}{dt} + 2\frac{{d^{2} \varphi }}{{dt^{2} }}$$
(3)

It is clear that

$$i_{1} (t) = i_{m} (t) + i_{c} (t)$$
(4)
$$\frac{d\varphi }{dt} = R_{c} i_{c}$$
(5)

And

$$\frac{d\varphi }{dt} = \frac{d\varphi }{{di_{m} }}*\frac{{di_{m} }}{dt} = L_{m} \frac{{di_{m} }}{dt}$$
(6)

Applying (4), (5) and (6), can be written as follows

$$i(t) = i_{m1} e^{Ft} + i_{m2} e^{Gt} + i_{m3} \sin (wt + \varphi ) + i_{m4}$$
$$\frac{{d^{2} \varphi }}{{dt^{2} }} = R_{c} \frac{{di_{1} }}{dt} - \frac{{R_{c} }}{{L_{m} }}\frac{d\varphi }{dt}$$
(7)

Supplanting (7) in (3), prompts (8)

$$wV_{LL} \cos (wt - 30) = 2R_{p} \frac{{di_{1} }}{dt} + 2L_{p} \frac{{d^{2} i_{1} }}{{dt^{2} }} + L_{TCL} \frac{{d^{2} i_{1} }}{{dt^{2} }} + R_{TCL} \frac{{di_{1} }}{dt} + 2\left( {R_{c} \frac{{di_{1} }}{dt} - \frac{{R_{c} }}{{L_{m} }}\frac{d\varphi }{dt}} \right)$$
(8)

Comparing (2) with (8) can be rewritten as

$$M\frac{{d^{2} i_{1} }}{{dt^{2} }} + N\frac{{di_{1} }}{dt} + Oi_{1} = P\sin (wt + \alpha ) + Q$$
(9)

where

$$M = L_{m} \frac{{2L_{p} + L_{TCL} }}{{R_{C} }}$$
$$N = L_{m} \left( {\frac{{2R_{p} + R_{TCL} }}{{R_{c} }}} \right) + 2L_{p} + L_{TCL} + 2L_{m}$$
$$\begin{aligned} O = 2R_{p} + R_{TCL} \hfill \\ P = V_{LL} \sqrt {\frac{{R_{c}^{2} + L_{m}^{2} w^{2} }}{{(R_{c} )^{2} }}} \hfill \\ Q = - 2V_{TF} \hfill \\ \alpha = \varphi - 30 \hfill \\ \cos \varphi = \frac{{V_{LL} }}{P} \hfill \\ \end{aligned}$$

Using Laplace transform, (9) leads to the following equation

$$A(s^{2} I(s) - sI(0) - I^{'} (0)) + B(sI(s) - I(0)) + CI(s) = D\frac{s\sin (\alpha ) + w\cos (\alpha )}{{s^{2} + w^{2} }} + \frac{E}{S}$$
(10)

Consequently

$$\begin{aligned} I(s) = D\frac{s\sin (\alpha )}{{(s^{2} + \omega^{2} )(As^{2} + Bs + C)}} + D\frac{\omega \cos (\alpha )}{{(s^{2} + \omega^{2} )(As^{2} + Bs + C)}} + \frac{E}{{s(As^{2} + Bs + C)}} \hfill \\ \hfill \\ \end{aligned}$$
(11)

The transient response of current waveform between 0 and T/4 is illustrated by the following expression using inverse Laplace transform as

$$i(t) = i_{m1} e^{Ft} + i_{m2} e^{Gt} + i_{m3} \sin (wt + \varphi ) + i_{m4}$$
(12)

where

$$i_{m1} = \left( {\frac{E}{F(F - G)} + \frac{DFSin(\alpha )}{{(F - G)(F^{2} + w^{2} )}} + \frac{Dw\cos (\alpha )}{{(F - G)(F^{2} + w^{2} }}} \right)$$
$$i_{m2} = \left( {\frac{E}{G(G - F)} + \frac{DG\sin (\alpha )}{{(G - F)(G^{2} + w^{2} )}} + \frac{Dw\cos (\alpha )}{{(G - F)(G^{2} + w^{2} )}}} \right)$$
$$i_{m3} = \left( {\frac{2wD}{{\sqrt {4w^{4} (F + G)^{2} (2wFG - 2w^{3} )^{2} } }}} \right)$$
$$i_{m4} = \frac{E}{GF}$$
$$F = \frac{{ - B + \sqrt {B^{2} - } 4AC}}{2A}$$
$$G = \frac{{ - B - \sqrt {B^{2} - 4AC} }}{2A}$$
$$\cos (\gamma ) = \frac{{(2wFG - 2w^{3} )\cos (\alpha ) - (2w^{2} (F + G))\sin (\alpha )}}{{\sqrt {4w^{4} (F + G)^{2} + (2wFG - 2w^{3} )^{2} } }}$$

As given in (12), the mode of charging current from 0 to T/4 consist one sinusoidal and two exponential form. Meanwhile, two exponential parts will tend to decay as F and G are negative.

5 Stability analysis

To investigate the stability during the opening and closing of breaker of the above system shown in the Figs. 2 and 3, generally the conventional methods like Bode Plot, Nyquist Plot and Nichols Chart is implemented.

5.1 Bode plot analysis

For defining the stability of a system, this method is very much valuable. It is a logarithmic plot. So, a wide range of gains on the vertical axis collapses with a wide range of frequencies on the horizontal axis. From Eq. (11) Bode analysis is done to check the stability of the system shown in Figs. 2 and 3. The result shows that the preceding system is unstable but the modified system shown in the Fig. 3 is stable considering the same gain margin and other parameters are also constants.

5.2 Nyquist plot analysis

This is basically a parametric plot of a frequency response obtain from Eq. (11), used for assessing the stability of the system shown in the Figs. 7 and 8.

5.3 Nichols plot analysis

In this method from Eq. (11), considering, magnitude loci is constant and phase-angle loci is also constant in the log-magnitude versus phase diagram. The magnitude in dB monotonically decreases with increase in frequency.

6 Total harmonic distortion analysis

In one-phase signals of Figs. 2 and 3 of this paper, harmonic evaluation has been completed by Fast Fourier Transform (FFT) technique. The phase angle and amplitude of harmonic components are separately determined by this fundamental technique. The result shows that the proposed TCL circuit shown in Fig. 3 is more efficient than system shown in Fig. 2.

7 Result and discussion

In a MATLAB platform, the simulation work is carried out. The parameters for simulation and comparative analysis are shown in Tables 1 and 2. Figures 4, 5, 6, 7, 8, 9 and 10 show the close loop stability of Figs. 2 and 3 using conventional methods such as Bode, Nyquist and Nichols etc. As shown in the Figs. 4, 5, 7 and 9, the close loop system becomes unstable without using modified TCL or it can be stable using the conventional TCL shown in the Figs. 6, 8 and 10. Figure 11a–c shows the harmonic distortion of Fig. 2 at different frequency. The harmonic analysis of transient current using conventional TCL of Fig. 3 shown in Fig. 12a–c. The reduction in the amplitude of the THD shown using the proposed TCL. The system harmonic parameters up to 16th order with and without using the proposed TCL are listed in Table 3. This test validates the efficacy of the suggested TCL for limiting the undesirable harmonics. As illustrated in the results, the transient current has been restricted considerably, which will decreases the normal size of all circuit elements remaining to the new current scale. Apparently, this increases the cost of additional TCL circuit, but modified to reduce in inductor size compared to conventional topologies and have fewer number of thyristor.

Table 1 Comparative analysis of parameters
Full size table
Table 2 Parameters for simulation
Full size table
Fig. 4
figure 4

Coil charging mode

Full size image
Fig. 5
figure 5

Bode diagram of Fig. 2

Full size image
Fig. 6
figure 6

Bode diagram of Fig. 3

Full size image
Fig. 7
figure 7

Nyquist diagram of Fig. 2

Full size image
Fig. 8
figure 8

Nyquist diagram of Fig. 3

Full size image
Fig. 9
figure 9

Nichols diagram of Fig. 2

Full size image
Fig. 10
figure 10

Nichols diagram of Fig. 3

Full size image
Fig. 11
figure 11

a FFT output, b THD analysis at 50 Hz, c THD analysis at 60 Hz. For TCL system shown in Fig. 2

Full size image
Fig. 12
figure 12

a FFT output, b THD analysis at 50 Hz, c THD analysis at 60 Hz. For TCL system shown in Fig. 3

Full size image
Table 3 Comparative analysis of harmonic order
Full size table

8 Conclusions

In this paper, a comparative study between two efficient TCL, based on a three-phase thyristor bridge system for the limitation of transient that occurs during the closing of circuit breaker and charging of transformer has been proposed. The main advantage of the suggested limiter is that it can automatically provide high impedance to limit the transient current magnitude. It is not the root cause of distortion in the steady-state load current or voltage waveforms. The proposed TCL has a simple topology, uses fewer thyristor in compare to other TCLs and does not need any controlling circuit. In addition, it effects to minimum harmonic distortion, ripple and lesser voltage drop in the transformers. The simulation results express the efficacy of the proposed TCL. Moreover, this technique shown to be effective in stability analysis of power systems in distribution area.