Design, modeling and test of a novel compliant orthogonal displacement amplification mechanism for the compact micro-grasping system

Abstract

In the compact micro-grasping system, the combination of precisely orthogonal movement transformation, displacement amplification and simple structure is important. The typical solution of the combination issue requires bidirectional symmetric input forces/displacements. However, under a certain driving condition, numerous actuators used in micro-manipulation only supply unidirectional input froce/displacement for the driven mechanism, which makes the typical solution infeasible. In this study, a novel compliant orthogonal displacement amplification mechanism (DAM) is proposed to solve the combination issue for numerous actuators used in micro-grasping. The proposed mechanism is a triangulation amplification-based mechanism with undetermined structural parameters. The number of the undetermined parameters and the solution principle are analyzed. The design process is presented. Finite element analysis (FEA) is used to verify the design method. The FEA results show that, for the design examples, the errors evaluating the orthogonal movement transformation are smaller than 0.56 % and 0.15 % respectively, and the displacement amplification ratios are larger than 4.6. The orthogonal displacement amplification is realized. A precise model of the displacement amplification ratio is derived. The dynamic performances of the proposed orthogonal DAM are modeled and FEA verified. Furthermore, a microgripper utilizing the proposed mechanism is presented. The performances of the gripper, including the displacement amplification and the parallel movement of the jaws, are verified by FEA and experiments.

1 Introduction

Micro-grasping focuses on the grasping of micro-objects ranging from a few to hundreds of micrometers in dimension, which is important in micro-assembly (Woern et al. 2000; Kim et al. 2004; Cecil et al. 2007; Agnus et al. 2013). A micro-grasping system mainly includes the actuator and the end-effector. Generally, the output direction of the actuator is non-collinear with the grasping movement of the end-effector. Meanwhile, the movement of the end-effector needs to be amplified compared with that of the actuator (Millet et al. 2003; Zubir et al. 2009; Hoxhold and Buttgenbach 2010; Kim et al. 2005). The movement direction transformation and displacement amplification should be realized in a compact size. For these reasons, two issues should be considered when designing micro-grasping systems.

One is to precisely transform the movement direction between the actuator and the end-effector. For most of the actuators in micro-manipulation, the output direction is one-dimensional (Bell et al. 2005). A typical case is that the movement of the end-effector should be vertical to the one-dimensional output direction of the actuator, i.e. the orthogonal transformation of the movement direction (Hoxhold and Buttgenbach 2010; Xiao et al. 2011), in which the reduction of the parasitic movement vertical to the desired direction is important. In the recent researches on precision engineering, the analysis, reduction and utilization of the parasitic movement are focused on Lee and Lin (2007), Xiao et al. (2011), Zhao et al. (2012), Huang (2012). Among these researches, symmetric structure is commonly used to reduce parasitic movement. However, symmetric structure can be used to reduce the parasitic movement of orthogonal displacement transformation only when the structure is of bidirectional symmetric input forces/displacements (Xiao et al. 2011; Huang 2012).

The other is the compact displacement amplification mechanism (DAM) with simple structure, especially for the device driven by the actuator without enough output displacement, such as piezoelectric stack actuator (Nah and Zhong 2007), electrostatic actuator (Millet et al. 2003; Bazaz et al. 2011), or chevron electrothermal actuator (Carlson et al. 2007; Shivhare et al. 2015). Being free of clearance, friction and assembly error, flexure-based compliant mechanisms are widely used to construct DAM, such as leverage mechanism (Jouaneh and Yang 2003), bridge-type mechanism (Lobontiu and Garcia 2003), Scott-Russell mechanism (Chang and Du 1998), and topology optimized displacement amplification mechanism (Arunkumar and Srinivasan 2006). Compared with other DAMs, bridge-type mechanism possesses the advantages of compact size, simple structure and large displacement amplification ratio.

The combination of the issues above can be described as: a compact DAM with simple structure which can realize precisely orthogonal movement transformation.

The DAM realizing precisely orthogonal movement transformation can be defined as orthogonal DAM. In the previous researches, the compact orthogonal DAM with simple structure is mainly based on triangulation amplification. In order to reduce the parasitic movement at the output port, typical triangulation amplification mechanism, e.g. bridge-type mechanism, requires the full symmetry of the structure as well as bidirectional symmetric input forces/displacements. The requirement for the bidirectional symmetric input forces/displacements limits the scope of bridge-type mechanism, because in the field of micro-manipulation, most of the actuators with one-dimensional output direction can only supply unidirectional movement under a certain driving condition, such as lateral comb electrostatic actuator (Bazaz et al. 2011), arrays of electrostatic actuators (Bohringer et al. 1996; Millet et al. 2003), and chevron electrothermal actuator. Furthermore, for piezoelectric stack actuator, it is more convenient and stable for preload when fixed at one end, in which the symmetric bidirectional movement is transformed into the unidirectional movement as well (Sun et al. 2014; Liang et al. 2015). Therefore, unidirectional movement is typical for the actuators with one-dimensional output direction.

In this paper, a novel triangulation amplification-based orthogonal DAM with undetermined structural parameters, which can solve the combination problem without requiring bidirectional symmetric input forces/ displacements, is proposed. The principle of the proposed orthogonal DAM is analyzed in Sect. 2. The design process is presented in Sect. 3, where finite element analysis (FEA) is used to verify the effectiveness of the novel design. In Sect. 4, a precise model of the displacement amplification is derived. In Sect. 5, the natural frequency of the proposed orthogonal DAM is modeled and verified by FEA. In Sect. 6, an application of the novel design in micro-grasping is presented and verified by FEA and experiments.

2 Principle of the novel orthogonal DAM

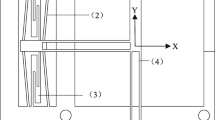
The proposed compliant othogonal DAM is based on triangulation amplification, as shown in Fig. 1a, which is of four kinematic pairs I-IV. The displacement amplification ratio Q is derived by instantaneous center method, as shown in Eq. 1, which is a kinematic model.

$$\begin{aligned} Q = \frac{{{e_\mathrm{out}}}}{{{e_\mathrm{in}}}}\ = \frac{{\left| {\overline{B{o_1}} } \right| }}{{\left| {\overline{A{o_1}} } \right| }} = \cot \alpha \ \end{aligned}$$

(1)

Fig. 1

Principle of the novel orthogonal DAM

In the case that the inclined angle $\alpha$ is in the range of (0, $\pi /4$), the displacement amplification ratio Q is larger than 1, resulting in a displacement amplification mechanism.

In Fig. 1a, rigid body Ao is the input structure. The vertical input force $F_\mathrm{in}$ acts at point o. The output structure BC is restrained by the horizontal sliding pair IV. The displacement boundary conditions of rigid body BC are: $x_\mathrm{C}=0$, $\theta _\mathrm{B}=0$, $\theta _\mathrm{C}=0$, $y_\mathrm{B}=y_\mathrm{C}$. The sliding pair I is designed as symmetric structure to realize grasping movement. The displacement boundary conditions of rigid body Ao are: $y_\mathrm{A}=0$, $\theta _\mathrm{A}=0$. Figure 1b shows the forces and torques acting on rigid body BC, which is in equilibrium. The mark (′) represents reaction forces or torques. When point C is on the left of point $\mathrm C_1$, $l_\mathrm{CC1}>0$. When point C is on the right of point $\mathrm C_1$, $l_\mathrm{CC1}<0$.

Mechanism EABCD is a single loop mechanism. The degree of freedom $DOF_\mathrm{EABCD}$ can be formulated as:

$$\begin{aligned} DOF_\mathrm{EABCD} = \sum \limits _{q = \mathrm I}^\mathrm{IV} {DO{F_q}} - \zeta \end{aligned}$$

(2)

where $DOF_\mathrm{EABCD}$ is required to be one, and $\zeta$ is the rank of the output displacement characteristic equations. For the qth kinematic pair, only one degree of freedom exists. According to Eq. (2), the rank $\zeta$ is three, which equals the rank of the output velocity characteristic equations.

A screw ${\$}$ (Huang and Li 2002) is used to express the relative motion between the fixed ends E and D, where no relative motion exists. Thus, the screw ${\$}$ equals zero.

Furthermore, the rigid bodies E, Ao, AB, BC, D comprise a serial chain. The screw ${\$}$ can be expressed as (Waldron 1967):

$$\begin{aligned} \$=\sum \limits _{i=\mathrm{{I}}}^{\mathrm{{IV}}} {\left( {\begin{array}{lll} {{v_\mathrm{{x}{i}}}}&{}{{v_\mathrm{{y}{i}}}}&{}{{v_\mathrm{{z}{i}}}}\\ {{\omega _\mathrm{{x}{i}}}}&{}{{\omega _\mathrm{{y}{i}}}}&{}{{\omega _\mathrm{{z}{i}}}} \end{array}} \right) } = \left( {\begin{array}{lll} {{v_\mathrm{{xI}}}}&{}{{v_\mathrm{{yIV}}}}&{}0\\ 0&{}0&{}{{\omega _\mathrm{{zII}}} + {\omega _\mathrm{{zIII}}}} \end{array}} \right) \end{aligned}$$

(3)

Denote all the undetermined structural parameters as a vector $\mathbf a =[a_1,a_2,\ldots ,a_\mathrm{m}](\mathrm{m}\ge 1)$. Substituting $\$ =0$ into Eq. (3), the output velocity characteristic equations are obtained:

$$\begin{aligned}&{v_\mathrm{{xI}}} = \mathop{{x_\mathrm{o}}}^{.} ( \mathbf a ,\;{F_\mathrm{in}}) = 0\nonumber \\&{v_\mathrm{{yIV}}} = - \mathop{{y_\mathrm{C}}}^{.} ( \mathbf a ,\;{F_\mathrm{in}}) = 0\nonumber \\&{\omega _\mathrm{{zII}}} + {\omega _\mathrm{{zIII}}} = \mathop{{\theta _\mathrm{C}}}^{.} (\mathbf a ,\;{F_\mathrm{in}}) = 0 \end{aligned}$$

(4)

The rank of Eq. (4) is three, leading to that the equations in Eq. (4) are independent. Three undetermined parameters are needed to make the solution of Eq. (4) feasible.

For bridge-type mechanism, the sliding pair IV is designed to be symmetric to linkage AB and input structure Ao. However, the proposed orthogonal DAM is designed for the actuators with typical one-dimensional output direction. Therefore, the sliding pair IV is designed as elastic support CD with three undetermined structural parameters.

The design of the proposed orthogonal DAM is: (1) design beam AB to make the inclined angle $\alpha$ in the range of (0, $\pi /4$); (2) find three equations $D_n(\mathbf a )(n=1,2,3)$ satisfying all the displacement boundary conditions and the equilibrium equations to solve the undetermined structural parameters a.

For elastic support CD, loads $F_\mathrm{xC}$, $F_\mathrm{yC}$, $M_\mathrm{C}$ are exerted at end C. Considering $x_\mathrm{C}$ = 0 and $\theta _\mathrm{C}$ = 0 as well as the displacement-load relation, the relations among the loads are:

$$\begin{aligned} {M_\mathrm{C}} = f_1 \cdot {F_\mathrm{xC}} + f_2 \cdot {F_\mathrm{yC}} \end{aligned}$$

(5)

$$\begin{aligned} {F_\mathrm{xC}} = g\cdot {F_\mathrm{yC}} \end{aligned}$$

(6)

where the coefficients $f_1$, $f_2$, g are the functions of the compliances of elastic support CD, which are denoted as $\Gamma (\mathbf a )$, as shown in Eqs. (7)–(8).

$$\begin{aligned} f_1=- \frac{{{\Gamma _\mathrm{\theta C - FxC}}(\mathbf a )}}{{{\Gamma _\mathrm{\theta C - MC}}(\mathbf a )}}, \quad f_2= - \frac{{{\Gamma _\mathrm{\theta C - FyC}}(\mathbf a )}}{{{\Gamma _\mathrm{\theta C - MC}}(\mathbf a )}} \end{aligned}$$

(7)

$$\begin{aligned} g=\frac{{[{\Gamma _\mathrm{xC - FyC}}(\mathbf a ) \cdot {\Gamma _\mathrm{\theta C - MC}}(\mathbf a ) - {\Gamma _\mathrm{xC - MC}}(\mathbf a ) \cdot {\Gamma _\mathrm{\theta C - FyC}}(\mathbf a )]}}{{[ - {\Gamma _\mathrm{xC - FxC}}(\mathbf a ) \cdot {\Gamma _\mathrm{\theta C - MC}}(\mathbf a ) + {\Gamma _\mathrm{xC - MC}}(\mathbf a ) \cdot {\Gamma _\mathrm{\theta C - FxC}}(\mathbf a )]}} \end{aligned}$$

(8)

At end C, the relation between y-axis displacement and loads can be expressed as:

$$\begin{aligned} {y_\mathrm{C}} = {\Gamma _\mathrm{yC-FxC}}(\mathbf a ) \cdot {F_\mathrm{xC}} + {\Gamma _\mathrm{yC-FyC}}(\mathbf a ) \cdot {F_\mathrm{yC}} +{\Gamma _\mathrm{yC-MC}}(\mathbf a ) \cdot {M_\mathrm{C}} \end{aligned}$$

(9)

Equations (5)–(9) lead to $y_\mathrm{C}$-$F_\mathrm{yC}$ relation:

$$\begin{aligned} {y_\mathrm{C}} = [{\Gamma _\mathrm{yC-FxC}}(\mathbf a )g + {\Gamma _\mathrm{yC-FyC}}(\mathbf a ) + {\Gamma _\mathrm{yC-MC}}(\mathbf a ){f_1}g+{\Gamma _\mathrm{yC-MC}}(\mathbf a ){f_2}] \cdot {F_\mathrm{yC}} \end{aligned}$$

(10)

For beam AB, considering $\theta _\mathrm{B}$ = 0 and the displacement-load relation, the relation among the loads $F_\mathrm{xB}$, $F_\mathrm{yB}$, $M_\mathrm{B}$ is:

$$\begin{aligned} {M_\mathrm{B}} = {i_1} \cdot {F_\mathrm{xB}} + {i_2} \cdot {F_\mathrm{yB}} \end{aligned}$$

(11)

where the coefficients $i_1$, $i_2$ are related to the compliances of elastic beam AB, which are denoted as S:

$$\begin{aligned} i_1= - \frac{{{S_\mathrm{\theta B - FxB}}}}{{{S_\mathrm{\theta B - MB}}}},\;\;i_2= - \frac{{{S_\mathrm{\theta B - FyB}}}}{{{S_\mathrm{\theta B - MB}}}} \end{aligned}$$

(12)

The mechanism in Fig. 1a is a statically indeterminate structure. Rigid input structure Ao is supported by structure AB-BC-CD and structure oE. The moment $M_\mathrm{A}$ depends on the bending stiffness of structure AB-BC-CD ($K_\mathrm{lef}$) and the bending stiffness of structure oE ($K_\mathrm{oE}$). Due to $K_\mathrm{lef}$ $\ll$ $K_\mathrm{oE}$, the moment $M_\mathrm{A}$ $\rightarrow 0$, which simplifies the rotation-loads relation at point A to: $\theta _\mathrm{{A}}=S_\mathrm{\theta A-FxA}$ $\cdot$ ${F_\mathrm{xA}}+S_\mathrm{\theta A-FyA}$ $\cdot$ ${F_\mathrm{yA}}$. Considering $\theta _\mathrm{A}=0$ and the force equilibrium of beam AB, the relation between the forces $F_\mathrm{xB}$ and $F_\mathrm{yB}$ is:

$$\begin{aligned} F_\mathrm{xB}=jF_\mathrm{yB}= - \frac{{{S_\mathrm{\theta A - FyA}}}}{{{S_\mathrm{\theta A- FxA}}}}F_\mathrm{yB} \end{aligned}$$

(13)

At end B, the relation between y-axis displacement and loads can be expressed as:

$$\begin{aligned} {y_\mathrm{B}} = S _\mathrm{yB-FxB} \cdot {F_\mathrm{xB}} + S _\mathrm{yB-FyB} \cdot {F_\mathrm{yB}} + S _\mathrm{yB-MB} \cdot {M_\mathrm{B}} \end{aligned}$$

(14)

The compliances S are the functions of the dimensions of beam AB and the material. The dimensions of AB should be determined to make $\alpha$ in the range of (0, $\pi /4$). Equations (11), (13) and (14) lead to $y_\mathrm{B}-F_\mathrm{yB}$ relation:

$$\begin{aligned} {y_\mathrm{B}}=q\cdot {F_\mathrm{yB}}=(S_\mathrm{yB-FxB}j + S _\mathrm{yB-FyB} + S_\mathrm{yB-MB}{i_1}j + S_\mathrm{yB-MB}{i_2}){F_\mathrm{yB}} \end{aligned}$$

(15)

With the combination of the displacement boundary condition $y_\mathrm{B}=y_\mathrm{C}$, force equilibrium equation $F_\mathrm{yB}=-F_\mathrm{yC}$ as well as Eqs. (10) and (15), the first equation $D_1(\mathbf a )$ is:

$$\begin{aligned} {\Gamma _\mathrm{yC-FxC}}g + {\Gamma _\mathrm{yC-FyC}} +{\Gamma _\mathrm{yC-MC}}{f_1}g+{\Gamma _\mathrm{yC-MC}}{f_2}=-q \end{aligned}$$

(16)

With the combination of Eqs. (6) and (13), the second equation $D_2(\mathbf a )$ can be obtained as:

$$\begin{aligned} g = - j \end{aligned}$$

(17)

With the combination of the equilibrium of rigid body BC, as well as Eqs. (5), (6), (11) and (13), the third equation $D_3(\mathbf a )$ can be obtained as:

$$\begin{aligned} {f_1} + \frac{{{f_2}}}{{g}} = {l_{CC1}} + \frac{{{l_{BC1}}}}{j} + i + \frac{{{i_2}}}{j} \end{aligned}$$

(18)

3 Design process

Based on the principle in section 2, the design process of the proposed orthogonal DAM can be summarized as:

• (1) set three undetermined structural parameters for elastic support CD, and derive the compliances $\Gamma$;

• (2) design the dimensions of beam AB to make $\alpha$ in the range of (0, $\pi /4$), and derive the compliances S;

• (3) design input structure Ao to make it rigid enough and design output structure BC;

• (4) use $D_n(\mathbf a )$ to calculate the undetermined parameters.

3.1 Design of elastic support CD

Constant cross-sectional elastic beam can be designed as a elastic support with three undetermined structural parameters, which is straightforward and applicable. When elastic support CD is designed as a elastic beam, the schematic illustration of the proposed DAM is shown in Fig. 2a. For being applicable in micro-grasping system, the filleted corners with constant radius $r_\mathrm{d}$ are set. If the undetermined structural parameters are chosen as the length $L_\mathrm{d}$, the width B, and the inclined angle $\gamma$, as shown in Fig. 2b, other structural parameters $r_\mathrm{d}$, h should be assigned as initial design parameters.

Fig. 2

Schematic illustration of the novel orthogonal DAM

Free end C is required to move along $\mathrm y_{\rm C}$ axis towards right. Thereby the $\mathrm x_{\rm C}$-axis movement is the parasitic movement. Castiglianos second theorem describes the generalized displacements of point C in terms of the strain energy $V_\mathrm{CD}$:

$$\begin{aligned} {x_\mathrm{C}} = \frac{{\partial {V_{\mathrm{{CD}}}}}}{{\partial {F_\mathrm{xC}}}}, \quad {y_\mathrm{C}} = \frac{{\partial {V_\mathrm{CD}}}}{{\partial {F_\mathrm{yC}}}}, \quad {\theta _\mathrm{C}} = \frac{{\partial {V_\mathrm{CD}}}}{{\partial {M_\mathrm{C}}}} \end{aligned}$$

(19)

Beam CD is an Euler–Bernoulli beam, for which the sheer strain energy can be ignored. The strain energy $V_\mathrm{CD}$ thereby consists of the axial and the bending deformation terms:

$$\begin{aligned} {V_\mathrm{CD}}= & {} \int _0^{{L_\mathrm{d}}} {\frac{{{{({F_\mathrm{xC}}\cos \gamma + {F_\mathrm{yC}}\sin \gamma )}^2}}}{{2E{A_{\mathrm{{CD}}}}}}} dp \nonumber \\&+ \; \int _0^{{L_\mathrm{d}}} {\frac{{{{[{F_\mathrm{xC}}\sin \gamma (p - {L_\mathrm{d}}) - {F_\mathrm{yC}}\cos \gamma (p - {L_\mathrm{d}}) - {M_\mathrm{C}}]}^2}}}{{2E{I_\mathrm{CD}}}}dp} \end{aligned}$$

(20)

where the cross-sectional area $A_\mathrm{CD}$ and the cross-sectional moment of inertia $I_\mathrm{CD}$ are the piecewise functions of p. Equations (19) and (20) lead to the displacements-loads relation at point C, and the formulation of the compliances $\Gamma (\mathbf a )$ are:

$$\begin{aligned} \Gamma _\mathrm{xC-FxC} &= \frac{1}{E}(G{\cos ^2}\gamma + H{\sin ^2}\gamma )\nonumber \\ \Gamma _\mathrm{xc-FyC} &= \frac{1}{E}(G\cos \gamma \sin \gamma - H\sin \gamma \cos \gamma )\nonumber \\ \Gamma _\mathrm{xC-MC} &= \frac{1}{E}T\sin \gamma \end{aligned}$$

(21)

$$\begin{aligned} \Gamma _\mathrm{yC-FxC}&= \frac{1}{E}(G\cos \gamma \sin \gamma - H\sin \gamma \cos \gamma )\nonumber \\ \Gamma _\mathrm{yC-FyC}&= \frac{1}{E}(G{\sin ^2}\gamma + H{\cos ^2}\gamma ),\;\;\Gamma _\mathrm{yC-MC}=\frac{1}{E}T\cos \gamma \end{aligned}$$

(22)

$$\begin{aligned} \Gamma _\mathrm{\theta C-FxC}&= \frac{1}{E}T( - \sin \gamma )\nonumber \\ \Gamma _\mathrm{\theta C-FyC}&= \frac{1}{E}T\cos \gamma ,\;\;\Gamma _\mathrm{\theta C-MC}=\frac{1}{E}U \end{aligned}$$

(23)

where the integration items G, H, T, U are shown below:

$$\begin{aligned} G&= \int _0^{{L_\mathrm{d}}} {\frac{1}{{{A_{\mathrm{{CD}}}}(p)}}dp}, \quad H = \int _0^{{L_\mathrm{d}}} {\frac{1}{{{I_\mathrm{CD}}(p)}}{{(p - {L_\mathrm{d}})}^2}dp} \nonumber \\ T&= \int _0^{{L_\mathrm{d}}} {\frac{1}{{{I_\mathrm{CD}}(p)}}(p - {L_\mathrm{d}})dp}, \quad U = \int _0^{{L_\mathrm{d}}} {\frac{1}{{{I_\mathrm{CD}}(p)}}dp} \end{aligned}$$

(24)

Considering Eq. (21) and the displacement-loads relation, when $\gamma =0$, $x_\mathrm{C}$ equals $GF_\mathrm{xC}/E$, which is not equal to zero. Therefore, when the inclined angle is zero, the x-axis parasitic movement of beam CD can not be avoided.

Substituting Eq. (23) into Eq. (7) , the coefficients $f_1$, $f_2$ can be further formulated:

$$\begin{aligned} f_1 = \frac{{T \cdot \sin \gamma }}{U}, \quad f_2= - \frac{{T \cdot \cos \gamma }}{U} \end{aligned}$$

(25)

Substituting Eqs. (21) and (23) into Eq. (8), the coefficient g can be further formulated.

$$\begin{aligned} g = \frac{{ - [G - (H - {T^2}/U)]\sin \gamma \cos \gamma }}{{G{{\cos }^2}\gamma + (H - {T^2}/U){{\sin }^2}\gamma }} \end{aligned}$$

(26)

3.2 Design of beam AB

Beam AB is of two elastically translational boundaries, i.e. boundaries A-A and B-B in Fig. 2c. For boundary A-A, the movement along $\mathrm y_B$ axis and the rotation are restrained by the symmetry of the proposed mechanism. For boundary B-B, the movement along $\mathrm x_B$ axis and the rotation are required to be restrained. Beam AB consists of two flexure hinges A, B and a constant cross-section beam L. Theoretically, the amplification ratio of the proposed DAM depends on the ratio $(l_\mathrm{A}/2+L_2+l_\mathrm{B}/2)/t_\mathrm{r}$. Circular notch flexure hinges A, B have the advantage of higher rotation precision, compared with using other notch shape. If Q, t are initially assigned, all the other structural parameters in beam AB can be determined. Figure 2c shows the force analysis of beam AB as well. The force equilibrium leads to that $F_\mathrm{xA}=F_\mathrm{xB}$, $F_\mathrm{yA}=F_\mathrm{yB}$. Beam AB is antisymmetric to its center, and the direction of the loads is antisymmetric to the center of beam AB as well.

The force analysis of beam AB infers that, axial, bending and sheer deformation exist in beam AB. The strain energy $V_\mathrm{AB}$ can be expressed as:

$$\begin{aligned} {V_{\mathrm{{AB}}}}= & {} \int _0^{{L_{\mathrm{{A}}B}}} {\frac{{(F_\mathrm{xB})^2}}{{2E{A_{\mathrm{{AB}}}}}}} \mathrm{d}p \nonumber \\&+ \; \int _0^{{L_{\mathrm{{A}}B}}} {\frac{{{{[-{M_\mathrm{B}}+{F_\mathrm{yB}}({L_\mathrm{AB}} - p)+\lambda {F_\mathrm{xB}}]}^2}}}{{2E{I_\mathrm{AB}}}}\mathrm{d}p} \nonumber \\&+ \; h\displaystyle\iint _\mathrm{AB} {{\frac{{F_\mathrm{yB}^2}}{{8GI_\mathrm{AB}^2}}{{\left(\frac{{1}}{4}\cdot b^2 - {y_\mathrm{B}}\right)}^2}}} \mathrm{d}p\mathrm{d}y_\mathrm{B} \end{aligned}$$

(27)

where the cross-sectional area $A_\mathrm{AB}$, the distance between the point in beam AB and the axis of flexure B: $\lambda$, and the cross-sectional moment of inertia $I_\mathrm{AB}$ are the functions of p. The last term in Eq. (27) is the sheer strain energy item $V_\mathrm{AB-s}$, which can be transformed into a quadratic function of $F_\mathrm{yB}: V_\mathrm{AB-s}=S_\mathrm{s}F_\mathrm{yB}^2$. Similarly, Castigliano’s second theorem can be used to derive the formulation of the compliances S, as shown below:

$$\begin{aligned} S_\mathrm{\theta B-FxB}= \frac{{12{t_\mathrm{r}}}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{-1}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}dp-} \frac{{6{t_\mathrm{r}}{L_2}}}{{Ehb_2^3}} \end{aligned}$$

(28)

$$\begin{aligned} S_\mathrm{\theta B-FyB}&= \frac{{ - 12}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{{{L_\mathrm{AB}} - p}}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}dp} \nonumber \\&+ \; \frac{{ - 12}}{{Ehb_2^3}}\int _{{l_\mathrm{A}}}^{{l_\mathrm{A}} + {L_2}} {({L_\mathrm{AB}} - p)} dp \nonumber \\&\quad+ \; \frac{{ - 12}}{{Eh}}\int _{{l_\mathrm{A}} + {L_2}}^{{L_\mathrm{AB}}} {\frac{{{L_\mathrm{AB}} - p}}{{{{[w - 2\sqrt{(p - {l_\mathrm{A}} - {L_2})({L_{\mathrm{{A}}B}} - p)} ]}^3}}}} dp \end{aligned}$$

(29)

$$\begin{aligned} S_\mathrm{\theta B-MB}& = \frac{{12}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{1}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}dp + }\frac{{12}}{{Ehb_2^3}}{L_2} \nonumber \\&\quad+ \; \frac{{12}}{{Eh}}\int _{{l_\mathrm{A}} + {L_2}}^{{L_\mathrm{AB}}} {\frac{1}{{{{[w - 2\sqrt{(p - {l_\mathrm{A}} - {L_2})({L_\mathrm{AB}} - p)} ]}^3}}}} dp\end{aligned}$$

(30)

$$\begin{aligned} S_\mathrm{yB-FxB}&= \frac{{12{t_\mathrm{r}}}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{{{L_{\mathrm{{A}}B}} - p}}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}} dp + \frac{{6{t_\mathrm{r}}}}{{Ehb_2^3}} \nonumber \\&\quad \cdot \int _{{l_\mathrm{A}}}^{{l_\mathrm{A}} + {L_2}} {({L_\mathrm{AB}} - p)dp} \end{aligned}$$

(31)

$$\begin{aligned} S_\mathrm{yB-FyB}&= 2S_\mathrm{s}+\frac{{12}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{{{{({L_\mathrm{AB}} - p)}^2}}}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}dp} \nonumber \\&\quad+ \;\frac{{12}}{{Ehb_2^3}}\int _{{l_\mathrm{A}}}^{{l_\mathrm{A}} + {L_2}} {{{({L_\mathrm{AB}} - p)}^2}dp } \nonumber \\&\quad+ \; \frac{{12}}{{Eh}}\int _{{l_\mathrm{A}} + {L_2}}^{{L_\mathrm{AB}}} {\frac{{{{({L_\mathrm{AB}} - p)}^2}}}{{{{[w - 2\sqrt{(p - {l_\mathrm{A}} - {L_2})({L_\mathrm{AB}} - p)} ]}^3}}}dp} \end{aligned}$$

(32)

$$\begin{aligned} S_\mathrm{yB-MB}&= \frac{{ - 12}}{{Eh}}\int _0^{{l_\mathrm{A}}} {\frac{{{L_\mathrm{AB}} - p}}{{{{[w - 2\sqrt{p({l_\mathrm{A}} - p)} ]}^3}}}dp} \nonumber \\&\quad + \; \frac{{ - 12}}{{Ehb_2^3}}\int _{{l_\mathrm{A}}}^{{l_\mathrm{A}} + {L_2}} {({L_\mathrm{AB}} - p)dp} \nonumber \\&\quad+ \; \frac{{ - 12}}{{Eh}}\int _{{l_\mathrm{A}} + {L_2}}^{{L_\mathrm{AB}}} {\frac{{{L_\mathrm{AB}} - p}}{{{{[w - 2\sqrt{(p - {l_\mathrm{A}} - {L_2})({L_\mathrm{AB}} - p)} ]}^3}}}} dp \end{aligned}$$

(33)

where $w=2r+t$. Moreover, the structural and loads’ direction antisymmetry of beam AB results in: $S_\mathrm{\theta A-FyA}=S_\mathrm{\theta B-FyB}$, $S_\mathrm{\theta A-FxA}=S_\mathrm{\theta B-FxB}$.

3.3 Design of the output structure BC

The dimensions $l_\mathrm{CC1}$ and $l_\mathrm{BC1}$ characterize the size of output structure BC. The parameter $l_\mathrm{BC1}$, which determines the size of the output port and the stiffness of structure BC, is an initial design parameter.

With the combination of Eqs. (5) and (6), $M_\mathrm{C}$-$F_\mathrm{xC}$ relation can be formulated as:

$$\begin{aligned} {M_\mathrm{{C}}} = \left( f_1+\frac{f_2}{g}\right) {F_\mathrm{xC}} \end{aligned}$$

(34)

where $M_\mathrm{C} >0$ and $F_\mathrm{xC}>0$, leading to that the coefficient $(f_1+f_2/g)$ should be positive. Therefore, the right side of Eq. (18) is positive as well, which determines the relation between $l_\mathrm{CC1}$ and $l_\mathrm{BC1}$:

$$\begin{aligned} {l_\mathrm{CC1}} > -\frac{l_\mathrm{BC1}}{j}-i_1-\frac{i_2}{j} \end{aligned}$$

(35)

3.4 Design examples of the novel orthogonal DAM and its application in micro-grasping

Four design examples are used to verify the design method of the novel compliant orthogonal DAM. The initial design parameters are shown in Table 1. Using the design process summarized in Sect. 3, the dimensions of beam AB and rigid body BC are determined. For reducing the sheer strain energy, the determined dimensions of the flexure hinges should satisfy two conditions: $2r/t\ge 5$ and $2r\ge h$. The undetermined structural parameters of beam CD are calculated. Both the determined parameters and the calculated results of the undetermined parameters are shown in Table 2. A bridge-type mechanism driven by unidirectional input force works as a comparison group. The design examples and the comparison group will be test by FEA in this section.

The movement direction precision of the output structure is evaluated by the errors $\delta$ and $\varsigma$, which are defined as:

$$\begin{aligned} \delta = \left| {\frac{{{x_\mathrm{o}}}}{{{y_\mathrm{o}}}}} \right| \cdot 100\,\%, \quad \varsigma = \left| {\frac{{{y_\mathrm{poi1}} - {y_\mathrm{poi2}}}}{{{y_\mathrm{poi2}}}}} \right| \cdot 100\,\% \end{aligned}$$

(36)

where $x_\mathrm{o}$ is the parasitic x-axis displacement of a point in the output structure and $y_\mathrm{o}$ is the desired y-axis displacement. Points 1 and 2 are two points chosen in the output structure. Error $\delta$ evaluates the translational movement of the output structure along the parasitic direction. Error $\varsigma$ evaluates the rotation of the output structure. If $\delta$ and $\varsigma$ are small enough, the orthogonal movement transformation is well realized.

Table 1 Initial design parameters in the design procedure and the corresponding displacement amplification ratio [according to Eq. (1)]

Table 2 Determined parameters and the calculating results of the undetermined parameters in the design process

Fig. 3

Design example I

Fig. 4

Comparison group

ANSYS workbench 14.5 is used for FEA verification. The input force $F_\mathrm{in}$ is set as 10 N and the material is set as aluminum alloy (Young’s modulus: 71 GPa, Poisson’s ratio: 0.33). The FEA results of design example I and the comparison group are shown in Figs. 3 and 4, in which X axis is corresponding to y-axis desired movement in Fig. 1, and Z axis is corresponding to x-axis parasitic movement in Fig. 1, which is applicative to design example II-IV as well. For the error analysis, points B, C are chosen as “point 1” and “point 2” respectively. The errors $\delta$ and $\varsigma$ of points B, C can effectively evaluate the movement direction precision of rigid body BC.

The values of the errors $\delta$, $\varsigma$ are listed in Table 3. For design examples I to IV, the errors $\delta$, $\varsigma$ are smaller than 0.56 and 0.15 % respectively. The orthogonal movement transformation is well realized. The FEA results of Q are larger than 4.6, which means that the displacement amplification is realized. Equation (1) is a kinematic model, the deformation of beam AB and structure Ao is ignored, which results in the difference between the theoretical and FEA value of Q. For the bridge-type mechanism driven by the unidirectional input force, the errors $\delta$ of points 1 and 2 are 13.64 and 13.71 % respectively, which are much larger than those of the design examples. Therefore, when driven by unidirectional input force, the parasitic movement at the output structure of the bridge-type mechanism can not be avoided, whereas the proposed mechanism can realize orthogonal displacement amplification.

Table 3 FEA values of the errors and the displacement amplification ratio

4 Precise model of Q

In this section, a precise model of Q will be derived considering the static deformation of beam AB and input structure AA′ in Fig. 2a.

The force analysis of beam AA′ is shown in Fig. 5. The input displacement $e_\mathrm{in}$ can be expressed as the sum of the deformation of beam AA′ and the rigid movement of beam AA′:

$$\begin{aligned} e_\mathrm{in}=x_\mathrm{o}=\frac{\partial V_\mathrm{AA'}}{\partial F_\mathrm{in}}+x_\mathrm{oA} \end{aligned}$$

(37)

Fig. 5

Force analysis of structure AA′

The derivation of $V_\mathrm{AA'}$ is similar to that of $V_\mathrm{CD}$ in Sect. 3.1. Therefore, the deformation of beam AA′ is:

$$\begin{aligned} \frac{{\partial {V_\mathrm{AA'}}}}{{\partial {F_\mathrm{in}}}} = \left[ \frac{{{L_\mathrm{AA'}}}}{{4E{B_\mathrm{AA'}}h{{(\frac{{{S_\mathrm{\theta B-FyB}}}}{{{S_\mathrm{\theta B-FxB}}}})}^2}}} + \frac{{L_\mathrm{AA'}^3}}{{4EhB_\mathrm{AA'}^3}}\right] {F_\mathrm{in}} \end{aligned}$$

(38)

where $L_\mathrm{AA'}$ and $B_\mathrm{AA'}$ are the length and width of beam AA′ respectively. The coefficient is the function of the compliance of beams AB and AA′: $fun(S_\mathrm{B},S_\mathrm{AA'})$.

Due to $M_\mathrm{A}$ $\rightarrow$0, the rigid movement $x_\mathrm{oA}$ can be expressed as:

$$\begin{aligned} {x_\mathrm{oA}} = {S_\mathrm{xA-FxA}}{F_\mathrm{xA}} + {S_\mathrm{xA-FyA}}{F_\mathrm{yA}} \end{aligned}$$

(39)

Further considering the force equilibrium of beams AB and AA′ as well as the structural and loads direction antisymmetry of beam AB ,

$$\begin{aligned} {x_\mathrm{oA}} = \left[ {S_\mathrm{xB-FxB}} + {S_\mathrm{xB-FyB}}\left( -\frac{{{S_\mathrm{\theta B-FxB}}}}{{{S_\mathrm{\theta B-FyB}}}}\right) \right] \cdot \frac{1}{2}{F_\mathrm{in}} \end{aligned}$$

(40)

where the coefficient is the function of the compliance of beams AB: $fun1(S_\mathrm{B}$).

Equations (37), (38) and (40) lead to $e_\mathrm{in}$-$F_\mathrm{in}$ relation. The $e_\mathrm{out}-F_\mathrm{in}$ relation can be obtained according to Eq. (15):

$$\begin{aligned} {e_\mathrm{out}} = {y_\mathrm{B}} = \frac{{-q}}{{\frac{{{S_\mathrm{\theta B-FyB}}}}{{{S_\mathrm{\theta B-FxB}}}}}}\cdot \frac{1}{2}{F_\mathrm{in}} \end{aligned}$$

(41)

where the coefficient is the function of the compliance of beams AB: $fun2(S_\mathrm{B}$).

With the combination of $e_\mathrm{in}$-$F_\mathrm{in}$ relation, $e_\mathrm{out}$-$F_\mathrm{in}$ relation and the definition of displacement amplification ratio, the precise model of Q can be derived:

$$\begin{aligned} Q=\frac{{fun2({S_\mathrm{B}})}}{{fun({S_\mathrm{B}},{S_\mathrm{AA'}}) + fun1({S_\mathrm{B}})}} \end{aligned}$$

(42)

Using Eq. (42), the displacement amplification ratio of design example I-IV is calculated, as shown in Table 4. Compared with the FEA results, the errors are smaller than 5.84 %.

Table 4 Theoretical and FEA values of Q

5 Dynamic analysis

The kinematic and static performances of the proposed orthogonal DAM have been designed, modeled and verified by FEA in Sects. 2–4. In this section, the dynamic analysis will be used to evaluate the performance of the proposed mechanism in the situation of fast response.

The proposed DAM has one degree of freedom. If the input displacement is set as the generalized coordinate, the dynamic performance can be described as:

$$\begin{aligned} M\mathop {{x_\mathrm{in}}}\limits ^{..}+K{x_\mathrm{in}} = F \end{aligned}$$

(43)

where M and K are the equivalent mass and equivalent stiffness respectively, and F is the generalized force applied on the DAM.

The Lagrange’s equation of the DAM is:

$$\begin{aligned} \frac{d}{{dt}}\left( \frac{{\partial T}}{{\partial \mathop {{x_\mathrm{in}}}\limits ^. }}\right) - \frac{{\partial T}}{{\partial {x_\mathrm{in}}}} + \frac{{\partial V}}{{\partial {x_\mathrm{in}}}} =F \end{aligned}$$

(44)

where T is the kinetic energy and V is the potential energy. The pseudo-rigid-body model Howell (2001) is shown in Table 6. Flexures GH and G′H′ are added to improve the dynamic performance. When the stiffness of flexures GH and G′H′ is much smaller than structure AA′, the kinematic and static performances of the DAM will not be affected. The kinetic energy T comprises the kinetic energy of structure AA′, AB, A′B′, BC, B′C′. The potential energy V is characterized by the springs in the pseudo-rigid-body model.

Fig. 6

Pseudo-rigid-body model of the proposed orthogonal DAM. (Flexures GH and G′H′ are added to improve the dynamic performance)

Based on Eqs. (43) and (44) as well as the formulation of the kinetic energy of rigid body and the potential energy of spring, M and K can be obtained:

$$\begin{aligned} M= {m_\mathrm{AA'}} + \frac{{2{J_\mathrm{AB}}}}{{t_\mathrm{r}^2}} + \frac{1}{2}{m_\mathrm{AB}}{\left( \frac{{{L_\mathrm{AB}}}}{{{t_\mathrm{r}}}}\right) ^2} + 2{m_\mathrm{BC}}{Q^2} \end{aligned}$$

(45)

$$\begin{aligned} K= 2{k_\mathrm{A}} + 2{k_\mathrm{B}})\frac{1}{{t_\mathrm{r}^2}} + (2{k_\mathrm{F}} + 2{k_\mathrm{E}})\frac{{{Q^2}}}{{{{(\Upsilon {L_\mathrm{CD}})}^2}{{(\cos \gamma )}^2}}}\nonumber \\&+ \; 2{k_\mathrm{lspring}}{(\tan \gamma )^2}{Q^2} \end{aligned}$$

(46)

where m and J are mass and the moment of inertia respectively. The characteristic radius factor of the fixed-guided segment $\Upsilon$ equals 0.8517 (Howell 2001). The stiffness of the torsional springs $k_{\psi }(\psi =\mathrm{A}, \mathrm{B}, \mathrm{E}, \mathrm{F})$ can be obtained from the previous literatures (Howell 2001; Yong et al. 2008), and the stiffness of the linear spring $k_\mathrm{lspring}$ characterize the stiffness of beam CD along x axis at point C.

The principle natural frequency of the DAM is formulated as:

$$\begin{aligned} {f_\mathrm{q}} = \frac{1}{{2\pi }}\sqrt{\frac{K}{M}} \end{aligned}$$

(47)

For design examples I-IV, comparing the theoretical principle natural frequency calculated by Eqs. (45)–(47) with the FEA modal analysis results (as shown in Table 5), the errors are smaller than 8.00 %, which verifies the effectiveness of the dynamic model. Taking design I for example, as shown in Fig. 7, the FEA results show that the principle natural frequency is also the fundamental frequency, which is also applicative to designs II–IV. For design examples I–IV, the fundamental frequency is larger than 1000Hz, which benefits the dynamic performance.

Table 5 Theoretical and FEA results of the principle natural frequency

Fig. 7

FEA modal analysis of design example I

6 Microgripper using the proposed orthogonal DAM

6.1 Design and FEA verification

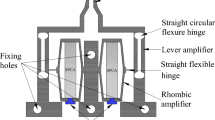
The novel compliant orthogonal DAM can be applied to construct a gripper driven by an actuator with one-dimensional output direction. Figure 8a shows a piezoelectric driven microgripper using the novel mechanism (design example I). The piezoelectric stack actuator is preloaded by tightening the bolt against the base, which is convenient and stable. The gripper arms are connected with rigid bodies BC and B′C′ respectively. Before contacting the micro object, no external force acts at the jaw. Therefore, the stiffness of the rigid bodies will not be affected by the attached gripper arms. The movements of the jaws and the rigid bodies are the same. FEA results (Fig. 8b, c) show that the grasping movements of the jaws are 21.391 and 21.342 $\upmu m$ respectively, and the corresponding parasitic movements are 0.059 and 0.048 $\upmu m$ respectively. The FEA results of the left jaw are slightly different from those of the right jaw, which is due to the slight difference of the mesh in both sides of the gripper. Comparing the vertical input displacement $S_\mathrm{in}=4.733$ $\upmu m$ with the average jaw displacement $S_\mathrm{ave}=21.367$ $\upmu m$, the displacement amplification ratio $Q_\mathrm{gripper}$ is 4.52. Averagely, only 0.25 % parasitic movement is generated at the jaws. The parasitic movement in design I and the compliance of the framework result in the parasitic movement at the jaws. The parallel movement of the jaws is realized without using extra parallelogram mechanism (Wang et al. 2013) or complicated structure (Shie and Huang 2010).

Fig. 8

Piezoelectric driven microgripper using design example I (the crossing over of the gripper arm in and c results from the display amplification of the micro displacement)

6.2 Experiment verification and analysis

In this subsection, optical micro-metrology is used to test the performances of the microgripper. The parallel movement of the jaws will be experimental verified by the optical flow analysis. The left jaw displacement, the right jaw displacement and the input displacement will be measured by template matching method, which can be used to calculate the experimental value of $Q_\mathrm{gripper}$.

The microgripper prototype is shown in Fig. 9a, in which the orthogonal DAM, the gripper arms and the frame are fabricated by wire-electron discharge machining (W-EDM). A polysilicon plate (thickness: 0.5 mm) is bonded with the gripper arms. The jaws clearance in the polysilicon plate is fabricated by laser cutting (initial clearance: 80 $\upmu m$). The gripper prototype and the base are fixed on a $\mathrm x_g$, $\mathrm y_g$-axes motion stage (W2-0-056, itap, Germany) with 0.01 mm motion resolution, which can be used to precisely adjust the position of the gripper. Piezoelectric stack actuator (P-882.11, PI, Germany), which is of one-dimensional output direction, is chosen to drive the gripper. The power system of the actuator comprising a DC power (LSP-1403, Voltcraft, Germany), a voltage amplifier and two programmable powers (GENH-300-2.5, TDK-Lambda, Germany) can supply 0-120V voltage for the piezoelectric stack actuator, as shown in Fig. 9b. The preload bolt (M1.2 $\times$4) is of 0.25 mm pitch, which can supply stable and precise preload. The hardware of the optical micro-metrology consists of a CCD camera (DFK 41AF02, Imaging Source, Germany), a zoom lens (DZ1/L.75-5, Imaging Source, Germany) and a ring LED. The softwares are Piotr’s Computer Vision Matlab Toolbox Dollár (2014) and OFFIS Automation Framework (OFFIS, Germany). Both the x,y-axes motion stage and the hardware of the optical micro-metrology are fixed on a vibration isolation table (Micro 40, Accurion, Germany).

Fig. 9

Experiment setup

In the optical flow analysis, the initial grey image of the jaws and the corresponding image after applying voltage (100 V) are obtained by OFFIS Automation Framework, as shown in Fig. 10a, b. Using optical flow analysis algorithm in Piotr’s Computer Vision Matlab Toolbox, the optical flow value distribution is shown in Fig. 10c, which shows that the $\mathrm x_g$-axis optical flow value of the jaws $OP_\mathrm{xg}$ is around zero. For each jaw, the $\mathrm y_g$-axis optical flow value distribution is uniform. The $\mathrm y_g$-axis optical flow values of both jaws are nearly adverse. Furthermore, the exact $\mathrm x_g$, $\mathrm y_g$-axes optical flow values of six typical points in the jaws are listed in Table 6. The optical flow is corresponding to the movement. Thus, the $\mathrm x_g$-axis parasitic movement of the jaws is smaller than 2.58 % of the $\mathrm y_g$-axis grasping movement, and the grasping movement of the jaws is symmetric. The parallel movement of the jaws is experimentally verified.

Table 6 $\mathrm x_g$, $\mathrm y_g$-axes optical flow value of six typical points in the jaws

Fig. 10

Optical flow analysis

In the experimental test of the displacement amplification ratio, 5$\times$ zoom is used to obtain 0.446 $\upmu m$ pixel resolution. Using the template matching algorithm integrated in OFFIS Automation Framework, sub-pixel resolution can be obtained. The input displacement and the displacements of both jaws are measured. Figure 11 shows the experimental value of $S_\mathrm{in}$ and $S_\mathrm{ave}$. Hysteresis of piezoelectric stack actuator is shown in $S_\mathrm{in}-U$ and $S_\mathrm{ave}-U$ curves respectively. The average experimental displacement amplification ratio of the gripper is 3.24, which verifies the displacement amplification of the gripper. The difference between the simulation value and the experimental value of Q is mainly due to the fabrication error and the error of the material parameters.

Fig. 11

Experimental test of the displacement amplification ratio of the gripper

7 Conclusion

This paper proposes a novel compliant orthogonal DAM without requiring bidirectional symmetric input forces/displacements, which can be used for different kinds of actuators with one-dimensional output direction, such as piezoelectric stack actuator, electrostatic actuator and ribcage electrothermal actuator. The proposed mechanism is a triangulation amplification-based mechanism with undetermined structural parameters. The number of the undetermined parameters and the solution principle are analyzed. The design process is presented. The FEA results of the design examples show that, the errors evaluating the orthogonal movement transformation are smaller than 0.56 % and 0.15 % respectively, and the displacement amplification ratios are larger than 4.6. The orthogonal displacement amplification is realized. A precise model of the displacement amplification ratio is derived. The dynamic performance of the proposed orthogonal DAM are analyzed. The FEA results show that, for the design examples, the errors of the precise displacement amplification ratio model are smaller than 5.84 %, and the errors of the dynamic model are smaller than 8.00 %. A piezoelectric stack driven microgripper utilizing the proposed DAM is presented. The FEA results show that the displacement amplification ratio of the gripper is 4.52, whereas only 0.25 % parasitic movement is generated at the jaws. The experiment tests show that the average displacement amplification ratio of the gripper is 3.24, and 1.67 %−2.57 % parasitic movement is generated at the jaws. The parallel movement of the jaws is realized by the simple structure and verified by FEA as well as experiment. The gripper can be used to fast and stably grasp the micro objects which need high quality of parallel movement, such as microsphere.