1 Introduction

Radio-frequency micro electro mechanical systems (RF-MEMS) technology offers a great future of RF component such as RF-MEMS switches for wireless communication. These RF-MEMS switches are the prime candidate in RF and microwave communication systems as compared to solid state switches because they exhibit low power consumption, low insertion loss, high isolation with high RF power handling capabilities (Balaraman et al. 2002; Goldsmith et al. 1995; Jensen et al. 2003; Yao and Chang 1995). Several researchers have proposed various designs of capacitive RF-MEMS switches to overcome the high actuation voltage requirements (Yao and Chang 1995; Pacheco et al. 1998; Rizk 2000). The use of serpentine suspensions with higher meander sections have been used to achieve lower actuation voltage, which often compromise with space limitation and design complexity (Pacheco et al. 2000). The push pull concept and electromagnetic actuation mechanism have also been proposed to reduce the actuation voltage (Hah et al. 2000). RF-MEMS switches with two actuation mechanism have also been demonstrated but these switches were not used in RF and microwave devices due to their complicated fabrication process with a major challenge of residual stress control (Cho et al. 2005). In addition, recently a new design using a freely moving contact pad has been elaborated but this design suffers with serious limitation of operating angle range, which increases the actuation voltage requirement (Lee et al. 2006). In this paper a simple and effective design concept of non-uniform serpentine flexure suspension has been introduced which lowers the spring constant and actuation voltage.

2 Mechanical design of capacitive RF-MEMS switch

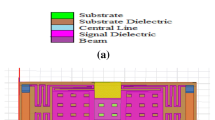
This section describes the actuation voltage calculation for non-uniform serpentine flexure based RF-MEMS switch. This switch beam is suspended at a height of \(g_{0}\) above the dielectric layer on the transmission line as shown in Fig. 1. The actuation voltage for fixed–fixed capacitive RF-MEMS switch can be given as (Rebeiz 2003)

$$V_{p} \,\, = \,\,\,\,\sqrt {\frac{{8K_{z} }}{{27\varepsilon_{0} Ww}}g_{0}^{3} }$$
(1)

where W is the width of the actuation electrode, w is the width of bridge structure, \(\varepsilon_{0}\) is the permittivity of free space, \(K_{z}\) is total spring constant for RF-MEMS switch and \(g_{0}\) is the initial gap between the electrode and MEMS bridge with zero potential.

Fig. 1
figure 1

Sketch of a fixed–fixed beam capacitive RF-MEMS switch

Full size image

So this total spring constant (\(K_{z}\)) will be the sum of all four serpentine spring attached to the flexure, which can be given as:

$$K_{z} \, = \,\,\frac{{4k_{z} }}{N}$$
(2)

where \(k_{z}\) is the spring constant for single spring and N is the number of meander sections. From Eq. 1, it is clear that the actuation voltage can be reduced in three different ways: first by decreasing the height between the bridge and the electrode, secondly by increasing the area of the bridge and lastly diminishing the bridge structure with low spring constant. Out of these possibilities, the third possibility depends on spring constant \(K_{z}\). So actuation voltage can be minimized by using a serpentine spring with less \(K_{z}\). So we propose a non-uniform serpentine spring design to reduce the spring constant of RF-MEMS switches.

3 Non-uniform serpentine flexure design

A schematic of non-uniform serpentine spring with two meander sections is shown in Fig. 2a. Each meander is made of four beam segments, called as connector beams and span beams. These connector beams and span beams are denoted as meander length and meander width with the length of a and b respectively. These beams are having the thickness of t and width of w’. For non-uniform serpentine flexure design the meander width (b) increases in multiples of varying span beam segments. Here for two meander sections for four span beams the meander widths can be represented as b, 2b, 3b and 4b. Non-uniform serpentine spring get their name due their non-uniform meander width. The meanders width can be adjusted to provide the appropriate stiffness ratio with reduced spring constant (Jaecklin et al. 1993). Most of the uniform serpentine springs are designed with constant meander width (Pacheco et al. 2000; Zhang and MacDonald 1991). These developed micromechanical serpentine spring designs exhibit low spring constant, which increases the sensitivity to frictional effects of the beam joints (Pisano and Cho 1989). So we propose a varying meander width concept to reduce the spring constant of RF-MEMS switches. Because of 2-fold flexure symmetry of non-uniform serpentine flexure, the spring constant calculation is done for single spring as shown in Fig. 2b. A perpendicular force \(F_{z}\) is applied in z direction at the end of the beam resulting in a displacement of \(\delta_{z}\). We have chosen the z coordinate direction for spring constant calculation. The guided end has separate \(\varepsilon\) and \(\delta\) coordinate system where \(\varepsilon\) is the coordinate along the beam axis and \(\delta\) is the coordinate normal to the \(\varepsilon\) axis. Here rotational angle of \(\theta_{0}\) and \(\phi_{0}\) are considered from guided end boundary conditions. These boundary end conditions are derived from free body diagram as given for uniform serpentine spring structure (Fedder 1994). Residual stress and extensional stress are neglected in the following analysis. Bending moment and torsion for connector and span beam segments (i, j = 1–2N) have been given in Table 1.

Fig. 2
figure 2

a Schematic of non-uniform serpentine flexure with two meander sections. b RF-MEMS switch beam with non-uniform serpentine flexure

Full size image
Table 1 Bending moment and torsion for connector and span beam segments for two meander sections (N = 2)
Full size table

The total energy for non-uniform serpentine spring is given by

$$U = \,\,\sum\limits_{i = 1}^{2N} {\int\limits_{0}^{a} {\left( {\frac{{M_{a,i}^{2} }}{{2EI_{x,a} }} + \frac{{T_{a,i}^{2} }}{{2GJ_{a} }}} \right)} } \,\,d\varepsilon \, + \sum\limits_{j = 1}^{2N} {\int\limits_{0}^{jb} {\left( {\frac{{M_{b,j}^{2} }}{{2EI_{x,b} }} + \frac{{T_{b,j}^{2} }}{{2GJ_{b} }}} \right)} } \,\,d\varepsilon \,$$
(3)

where E is the Young’s Modulus of elasticity, G is the torsion (or shear) modulus of the elasticity, J is the torsion constant, \(I_{x,a}\) and \(I_{x,b}\) are the bending moment of inertia about x axis for connector and span beam segments respectively. The guided end constraints tilt \(\theta_{0}\) and rotation \(\phi_{0}\) at the end of connector beam segment can be written as follows

$$\theta_{0} = \,\,\frac{\partial U}{{\partial M_{0} }}\, = \sum\limits_{i = 1}^{2N} {\int\limits_{0}^{a} {\left( {\frac{{M_{a,i} }}{{EI_{x,a} }}\frac{{\partial M_{a,i} }}{{\partial M_{0} }} + \frac{{T_{a,i} }}{{GJ_{a} }}\frac{{\partial T_{a,i} }}{{\partial M_{0} }}} \right)} } \,\,d\varepsilon \, + \sum\limits_{j = 1}^{2N} {\int\limits_{0}^{jb} {\left( {\frac{{M_{b,j} }}{{EI_{x,b} }}\frac{{\partial M_{b,j} }}{{\partial M_{0} }} + \frac{{T_{b,j} }}{{GJ_{b} }}\frac{{\partial T_{b,j} }}{{\partial M_{0} }}} \right)} } \,\,d\varepsilon \, = 0$$
(4)
$$\phi_{0} = \frac{\partial U}{{\partial T_{0} }}\, = \,\sum\limits_{i = 1}^{2N} {\int\limits_{0}^{a} {\left( {\frac{{M_{a,i} }}{{EI_{x,a} }}\frac{{\partial M_{a,i} }}{{\partial T_{0} }} + \frac{{T_{a,i} }}{{GJ_{a} }}\frac{{\partial T_{a,i} }}{{\partial T_{0} }}} \right)} } \,\,d\varepsilon \, + \sum\limits_{j = 1}^{2N} {\int\limits_{0}^{jb} {\left( {\frac{{M_{b,j} }}{{EI_{x,b} }}\frac{{\partial M_{b,j} }}{{\partial T_{0} }} + \frac{{T_{b,j} }}{{GJ_{b} }}\frac{{\partial T_{b,j} }}{{\partial T_{0} }}} \right)} } \,\,d\varepsilon \, = 0$$
(5)

The moment and torsion of each beam segment will be calculated as a function of position along the beam’s z axis. We can calculate the resulting moment and torsion for applied unit load at beam segments.

$$M_{0} \,\, = \,\,\,F_{z} \left( {\frac{{G.J8a^{2} + EI_{x} 30ab}}{{G.J4a + EI_{x} 10b}}} \right)\,\, = \,\,F_{z} \,C_{1}$$
(6)
$$T_{0} \,\, = \,\,\, - F_{z} \left( {\frac{{G.J7b^{2} + EI_{x} 2ab}}{{G.J10b + EI_{x} 4a}}} \right)\, = \, - F_{z} C_{2}$$
(7)

where \(\,C_{1} \, = \,\,\frac{{G.J8a^{2} + EI_{x} 30ab}}{{G.J4a + EI_{x} 10b}}\) and \(C_{2} = \frac{{G.J7b^{2} + EI_{x} 2ab}}{{G.J10b + EI_{x} 4a}}\) are the constants, used to simplify the mathematical calculations. Now we substitute \(M_{0}\) and \(T_{0}\) in the equations of bending moment and torsion of connector and span beam segments (Table 1). Now these new equations of bending moment and torsion will be used to obtain the vertical displacement of the serpentine spring in z direction. The unit load method (Castligliano’s second theorem) is employed to determine the deflection of the beam (Timoshenko and Goodier 1970).

$$\delta_{z} = \,\,\frac{\partial U}{{\partial F_{z} }}\,\, = \,\sum\limits_{i = 1}^{2N} {\int\limits_{0}^{a} {\left( {\frac{{M_{a,i} }}{{EI_{x,a} }}\frac{{\partial M_{a,i} }}{{\partial F_{z} }} + \frac{{T_{a,i} }}{{GJ_{a} }}\frac{{\partial T_{a,i} }}{{\partial F_{z} }}} \right)} } \,\,d\varepsilon \, + \,\sum\limits_{j = 1}^{2N} {\int\limits_{0}^{jb} {\left( {\frac{{M_{b,j} }}{{EI_{x,b} }}\frac{{\partial M_{b,i} }}{{\partial F_{z} }} + \frac{{T_{b,j} }}{{GJ_{b} }}\frac{{\partial T_{b,i} }}{{\partial F_{z} }}} \right)} } \,\,d\varepsilon \,_{z}$$
(8)

We can simplify this equation for beam displacement as follows:

$$\delta_{z} \,\, = \,\,\delta_{z1} + \,\,\delta_{z2} \, + \,\,\delta_{z3} \,\, + \,\,\delta_{z4}$$
(9)

where \(\delta_{z1}\) \(\sum\nolimits_{i = 1}^{2N} {\int\nolimits_{0}^{a} {\left( {\frac{{M_{a,i} }}{{EI_{x,a} }}\frac{{\partial M_{a,i} }}{{\partial F_{z} }}} \right)} } \,\,d\varepsilon\),\(\delta_{z2}\) \(\sum\nolimits_{i = 1}^{2N} {\int_{0}^{a} {\left( {\frac{{T_{a,i} }}{{GJ_{a} }}\frac{{\partial T_{a,i} }}{{\partial F_{z} }}} \right)} } \,d\varepsilon\), \(\delta_{z3}\) \(\sum\nolimits_{j = 1}^{2N} {\int\nolimits_{0}^{jb} {\left( {\frac{{M_{b,j} }}{{EI_{x,b} }}\frac{{\partial M_{b,i} }}{{\partial F_{z} }}} \right)} } \,\,d\varepsilon\) and \(\delta_{z4}\) \(\sum\nolimits_{j = 1}^{2N} {\int\nolimits_{0}^{jb} {\left( {\frac{{T_{b,j} }}{{GJ_{b} }}\frac{{\partial T_{b,i} }}{{\partial F_{z} }}} \right)} } \,\,d\varepsilon\) are the displacements for connector and span beam segments because of the bending moment and torsion. The z direction spring constant for two meander based non-uniform spring can be given as:

$$k_{z} = \,\,\,\frac{{F_{z} }}{{\delta_{z1} + \,\,\delta_{z2} \, + \,\,\delta_{z3} \,\, + \,\,\delta_{z3} }}$$
(10)
$$k_{z} \, = \,\left[ {\frac{1}{{EI_{x,a} }}\left( {4C_{1}^{2} a + \frac{64}{3}a^{3} - 16C_{1} a^{2} + 10C_{2}^{2} b - 24b^{3} + \frac{100}{3}b^{3} } \right) + \frac{1}{{GJ_{a} }}\left( {4C_{2}^{2} a + 6b^{2} a - 4C_{2} ba + 10C_{1}^{2} b + 100a^{2} b - 60C_{1} ab} \right)} \right]^{ - 1}$$
(11)

Equation 11 shows the spring constant for two meander based non-uniform serpentine spring. Now this spring constant analysis can also be used to determine the spring constant for different meander based non-uniform serpentine flexures.

4 Results and discussion

Table 2 shows the parameters used for calculating the spring constant and actuation voltage of non-uniform serpentine flexure for RF-MEMS switch. Analytically calculated spring constant is verified by finite element method analysis (FEM). These dimensions of non-uniform serpentine spring were applied to FEM simulation tool (COMSOL Multiphysics version 4.2, http://www.comsol.com/sla) and these results are compared with analytical calculation. We applied a concentrated z direction force of 1 μN at the free end of the non-uniform serpentine spring, which produces the beam displacement of (\(\delta_{z}\)). Here we observed that analytically calculated spring constant is 1–2 % higher than the simulated values due to the absence of residual stress as shown in Fig. 3. This figure also signifies a close agreement between analytical and simulated values of spring constant for single meander non-uniform serpentine flexure. This spring constant analysis is used to achieve low actuation voltage for non-uniform serpentine flexure based RF-MEMS switch. Here the maximum span beam length is restricted only up to 280 μm in order to remove the possibility of system complexity, which may arise due to increase in overall size of the switch. Figure 4 compare the actuation voltage of uniform and non-uniform serpentine flexure based RF-MEMS switches for similar values of span beam length. This plot illustrate that non-uniform serpentine flexure provides actuation voltage of 15–3 V for span beam length from 100 to 280 μm. But the uniform serpentine flexure provides an actuation voltage of 28–8 V for the same span beam lengths (Peroulis 2003). It is also observed that the actuation voltage decreases rapidly for span beam length 100–180 μm but the curve is almost linear from 200 to 280 μm. So the use of span beam with more than 200 μm is not a good decision because it increases flexure’s dimension without affecting the actuation voltage much. Figure 5 illustrates that actuation voltage can be reduced further by increasing the number of meander sections. Here it is not recommended to use more than one meander sections because it will lead to structure complexity with space limitations for RF applications. Hence, it is confirmed that non-uniform serpentine flexure with 200 μm span beam length with single meander section would be a good decision in order to produce an actuation voltage of 5 V.

Table 2 RF-MEMS switch design parameters
Full size table
Fig. 3
figure 3

Comparison of analytically calculated spring constant with FEM simulated values for non-uniform serpentine spring with different span beam lengths (b) ranges from 100 to 280 μm, with one meander section

Full size image
Fig. 4
figure 4

Actuation voltage comparison between uniform and non-uniform serpentine flexure based RF-MEMS switch, with different span beam lengths (b) ranges from 100 to 280 μm, with one meander section

Full size image
Fig. 5
figure 5

Actuation voltage comparison between one and two meander based RF-MEMS switch, with different span beam lengths (b) ranges from 100 to 280 μm

Full size image

5 Conclusion

A non-uniform serpentine flexure design for RF-MEMS switch has been proposed in this paper. This non-uniform serpentine flexure uses a varying span beam length, which results in varying meander width with reduced spring constant. This reduced spring constant is used to achieve low actuation voltage for RF-MEMS switches. RF-MEMS switch with single meander section using a non-uniform serpentine flexure with 200 μm span beam length, offers an actuation voltage of 5 V. This obtained actuation voltage is significantly lower than a RF-MEMS switch using a uniform serpentine flexure with same meander dimensions. Here we also observed that this actuation voltage can further be reduced by using two meander sections with non-uniform serpentine flexure; however it leads with more structure complexity with space limitations.