1 Introduction

Dual stage actuator (DSA) is used in hard disk drives to increase servo control bandwidth to achieve narrower tracks and thus higher storage capacity. A transition from single stage actuator (SSA) or voice coil motor (VCM) to DSA has started in recent years. Although the industry is shipping more DSA drives, DSA design philosophy has not been fully understood by most engineers. Unlike the SSA/VCM for which many engineers in the field can write down its equation of motion in term of the actuator moment of inertia, angular acceleration, VCM Kt and current, few in the field know what the governing equation of motion for DSA is.

The purpose of this paper is to present a simplified analytic dynamic model for DSA to facilitate physical understanding. DSA is approximated as lumped parameter actuators to derive the equation of motion of a DSA suspension. Lumped parameters are then related to suspension dynamic parameters, which is then used to derive the normalized equation of motion. From these equations of motion, key parameters affecting DSA performance are identified. DSA stroke, or the DC gain of the actuator, is derived to relate to geometrical parameters, DSA material properties and suspension dynamics. The results match well with those obtained from complicated finite element models and test data. Much insight is discussed from the model, including lead–zirconium–titanate (PZT) piezoelectric material selection, PZT dimension and placement, and DSA stroke and suspension dynamics tradeoff.

2 DSA design review

This paper focuses on piezoelectric second stage actuator used in recent shipped hard disk drives. Other than first stage VCM, piezoelectric elements integrated on suspensions are used as second stage actuator for fine positioning. Although adopted widely only recently into products, piezoelectric actuator has been considered by the industry for decades for dual stage application.

Mori et al. (1991) applied a second stage piezoelectric actuator with a dual stage control to achieve higher servo bandwidth. Evans et al. (1999) presented a suspension based piezoelectric actuator design. They derived a second order actuator equation of motion based on an equivalent spring–mass model. Tokuyama et al. (2001)developed a DSA suspension concept with PZT installed on a Φ-shaped base plate hinge, which later adopted into multiple products with some variations. Callafon et al. (2006) considered practical manufacture variation of suspension and modeled it as structured and unstructured uncertainties which are identified from frequency domain measurement. Boettcher et al. (2010) obtained a DSA discrete–time model by measuring DSA frequency domain response and compared the performance of two different dual stage controllers. Lengert et al. (2012) used thermal load to simulate voltage applied to PZT and studied DSA stroke sensitivity of two designs, one with PZT installed near suspension base plate and the other near head read/write element for collocated actuation, to key design parameters with FEA.

Dual stage actuators in recent products shipped are generally milli-type actuators. Piezoelectric ceramic patches are attached to suspension base plate structure to create local deformation that leads to amplified slider off-track motion due to geometric effect as the PZT actuator and head read/write element are not collocated. These milli-actuators generally have much larger stroke compared to collocated micro-actuator designs placing the actuators near head element location with limited geometric amplification.

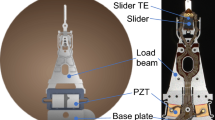
The milli-type DSA shipped so far have two styles, Φ and T styles. Figure 1 is an example of Φ type DSA design. It has one PZT element imbedded, via non-conductive epoxy, in a Φ shape base plate structure. The PZT element is Au plated on the two surfaces in thickness direction and works in “31” mode. One electrode surface is divided into two sections, each grounded to stainless steel structure (SST) via electrically conductive epoxy (ECA). The other electrode surface connects to a flexure Cu pad via ECA. The left and right sections of the PZT element are polarized in opposite directions. When a voltage or electrical field is applied to the element, one side of the PZT expands in plane and the other side contracts in plane to induce slider off track motion. Although one PZT element used in the design shown in Fig. 1, two PZT elements have been used in alternative design with similar Φ stiffener.

Fig. 1
figure 1

Φ type DSA

Full size image

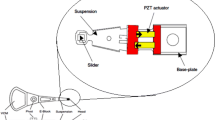
An example of T type DSA designs is shown in Fig. 2. Instead of having a separate stiffener part, the PZT elements, supported on load beam shelves with non-conductive epoxy, are now directly integrated into the base plate with a T shape tip. It has two PZT elements, each grounded to SST using ECA. The driving surfaces of the PZT are connected to flexure Cu pads using ECA. The two DSA traces are then jumped together in flexure.

Fig. 2
figure 2

T type DSA

Full size image

No matter Φ or T type DSA designs, they all rely on the contraction and expansion of PZT elements in 31-mode to create slider off track motion. Since one trace is used to apply common voltage to both elements (or left and right sides), the two PZT elements (or left and right) are polarized in opposite directions to have contraction in one and the expansion in the other. Due to this fundamentally common operation, an analytical model is presented next to derive an equation of motion to study both designs.

3 DSA analytical model

A simplified lumped parameter DSA model is shown in Fig. 3, with following assumptions:

Fig. 3
figure 3

DSA analytical model

Full size image
  1. 1.

    Suspension stiffness that PZT elements need to overcome for stroke generation is represented by two springs with stiffness of k. Other than this stiffness, suspension is assumed rigid. For Φ type design, the spring stiffness comes from the Φ hinges, which is purposely weakened in general for more stroke generation. For T type design, the combined springs are equivalent to a torsional stiffness in the middle of T bar that two PZT elements need to overcome.

  2. 2.

    Suspension base plate is fixed and its movable mass is in front of PZT element with an equivalent moment of inertia as J. Note that the mass of PZT elements and that of stiffener is also combined into J.

  3. 3.

    PZT elements are modeled as two one dimensional bar actuators operating in 31-mode. Note that the left and right sections of the PZT element in Φ type DSA behave like two separate PZT elements in function. One end of the PZT elements is fixed to base plate. The other end is connected to suspension movable mass at the center point of the PZT element in translational degrees of freedom only. The local rational stiffness is neglected and its impact is combined into the two lumped spring stiffness k.

  4. 4.

    Linear piezoelectric material.

Other geometric parameters are defined as shown in Fig. 3. w is PZT element width. l is PZT element length. a is the distance from x axis to the middle width of PZT element. b is the distance from x axis to spring k. h is the distance from y axis to slider trailing edge.

When a voltage is applied to PZT elements, one PZT element shrinks in length and the other expands, which in turn rotates suspension and results in reaction forces from the springs, as shown in Fig. 4. Assume the force generated from the PZT element is F, the equation of motion of the suspension can be written as

$$ \begin{gathered} J\ddot{\theta } + 2kb^{2} \theta = 2aF \end{gathered} $$
(1)

where θ is suspension rotation angle.

Fig. 4
figure 4

DSA analytical model, voltage applied

Full size image

General linear piezoelectric constitutive equations (IEEE Standard on Piezoelectricity, 1987) is

$$ \begin{gathered} S_{p} = s_{pq}^{E} T_{q} + d_{kp} E_{k} \hfill \\ D_{i} = d_{iq} T_{q} + \varepsilon_{ik}^{T} E_{k} . \hfill \\ \end{gathered} $$
(2)

With the one dimensional d31 mode PZT actuator assumption 3, only stress T 1 in x direction and electrical field E 3 in Z direction in PZT elements are considered. The actuator equation, the first equation in (2), can be simplified as

$$ S_{1} = s_{11}^{E} T_{1} + d_{31} E_{3} $$
(3)

where S 1 is the strain in PZT in x direction. \( s_{11}^{E} \) is elastic compliance constant in constant E field. d 31 is piezoelectric constant.

For the bottom extended PZT actuator shown in Fig. 4, Eq. (3) can be expressed as

$$ \frac{\theta a}{l} = s_{11}^{E} \frac{ - F}{wt} - d_{31} \frac{V}{t} $$
(4)

where t is PZT thickness and V is the voltage applied to the element. Negative sign added to force term since PZT is under compression load. From (4), the force F can be written as

$$ F = - \frac{wta}{{s_{11}^{E} l}}\theta - \frac{{wd_{31} }}{{s_{11}^{E} }}V. $$
(5)

In term of moment M created by two PZT elements,

$$ M = 2aF = - \frac{{2wta^{2} }}{{s_{11}^{E} l}}\theta - \frac{{2awd_{31} }}{{s_{11}^{E} }}V. $$
(5a)

Substitute Eq. (5) into (1), the DSA equation of motion (EOM) can be expressed in term of θ as

$$ J\ddot{\theta } + \left( {2kb^{2} + \frac{{2wta^{2} }}{{s_{11}^{E} l}}} \right)\theta = - \frac{{2awd_{31} }}{{s_{11}^{E} }}V. $$
(6)

Note that the rotation angle θ is very small and can be written in term of slider off-track motion y as

$$ \theta = \frac{y}{h} $$
(7)

Substitute (7) into 6, DSA EOM in term of slider off track motion can be derived as

$$ \ddot{y} + \left( {\frac{{2kb^{2} }}{J} + \frac{{2wta^{2} }}{{Js_{11}^{E} l}}} \right)y = - \frac{{2hawd_{31} }}{{Js_{11}^{E} }}V. $$
(8)

Note that above equation can be expanded to add first order damping term, which is generally quantified from experimental data.

4 DSA gain

A key design target of DSA suspension is its stroke capability. Using dynamic terminology, the DC gain of Eq. (8) is the DSA stroke capability. In general, a DSA design with higher gain is preferred.

Using Eq. (8), the DC gain of the DSA suspension can be expressed as

$$ \frac{y}{V} = - \frac{{hawld_{31} }}{{s_{11}^{E} kb^{2} l + wta^{2} }}. $$
(9)

To understand the maximum stroke capability of the design, consider the extreme case that there is no spring connections between load beam and suspension base plate (k = 0), Eq. (9) can be further simplified as

$$ \left( \frac{y}{V} \right)_{\max } = - \frac{hl}{ta}d_{31} . $$
(10)

In this case, there is no force to constrain the PZT motion, all voltage applied to PZT is used to create stroke. The maximum possible stroke is proportional to piezoelectric constant d 31 with a geometric amplification factor hl/ta. In other words, a thinner (t), longer (l) PZT placed closer to x axis and further away from slider has the most stroke generation capability. Take one design with h = 7.64 mm, l = 1.5 mm, t = 0.13 mm, a = 0.775 mm and d 31 = −230 × 10−12 m/V as an example, one can obtain

$$ \left( \frac{y}{V} \right)_{\max } = - 113.7d_{31} = 26.2\;{\text{nm}} $$
(10a)

In reality, unfortunately, maximum stroke in Eq. (10) cannot be obtained due to the suspension stiffness that PZT needs to overcome. In the other extreme case, when the suspension stiffness is infinitely high, a voltage applied to PZT will not create any slider off-track motion. Instead, the PZT generates the maximum force, which is the so called block force, to create a torque (block torque). Using Eq. (5) and assume θ = 0, the block torque M can be expressed as

$$ \left( \frac{M}{V} \right)_{\max } = - \frac{{2awd_{31} }}{{s_{11}^{E} }}. $$
(11)

Note that for larger torque generation capability, the two PZT elements should be placed further away from x axis according to Eq. (11).

Equation (10) is the maximum stroke generation capability and Eq. (11) is the maximum moment generation capability. In real applications, PZT will work somewhere in between the two extreme cases. The off-track stroke and torque are related by Eq. (5a), which is also graphically illustrated in Fig. 5. The stroke at the operation point is shown in Eq. (9) and the moment can be obtained by substitute (9) into (5a). By adjusting the parameters shown in Eq. (9), one can move the DSA operation point along the stroke–torque curve.

Fig. 5
figure 5

DSA stroke vs. torque generation curve

Full size image

5 Determine DSA lumped parameters

In DSA EOM (8), all parameters are well defined except lumped parameters J and k. In this section, EOM (8) is normalized and parameters J and k are connected to suspension dynamic parameters, which can be obtained using FEA or test.

When PZT elements are not present, Eq. (1) can be simplified as

$$ \ddot{y} + \frac{{2kb^{2} }}{J}y = 0 $$
(12)

Define passive suspension sway frequency w p as

$$ w_{p}^{2} = \frac{{2kb^{2} }}{J}. $$
(13)

Equation (12) can be written as

$$ \ddot{y} + \omega_{p}^{2} y = 0 $$
(14)

When voltage is not present, according to EOM (8), the free response of DSA suspension off track motion can be expressed as

$$ \ddot{y} + \omega_{n}^{2} y = 0 $$
(15)

where w n is the suspension sway frequency defined as

$$ \omega_{n}^{2} = \omega_{p}^{2} + \omega_{a}^{2} $$
(16)

w a , or active suspension sway frequency, is the contribution from PZT element to suspension sway frequency, defined as

$$ \omega_{a}^{2} = \frac{{2wta^{2} }}{{Js_{11}^{E} l}} $$
(16a)

From Eqs. (13) and (16), one can obtain

$$ J = \frac{{2wta^{2} }}{{s_{11}^{E} l\left( {\omega_{n}^{2} - \omega_{p}^{2} } \right)}} $$
(17)
$$ k = \frac{{Jw_{p}^{2} }}{{2b^{2} }} $$
(18)

Substitute Eqs. (17) and (18) into (8) and add damping term to make it general, the DSA EOM can be written as

$$ \ddot{y} + 2\eta \omega_{n} y + \omega_{n}^{2} y = - \frac{hl}{at}d_{31} \left( {\omega_{n}^{2} - \omega_{p}^{2} } \right)V $$
(19)

And the DSA DC gain (stroke) can be expressed as

$$ \frac{y}{V} = - \frac{hl}{at}d_{31} \left( {1 - \frac{{\omega_{p}^{2} }}{{\omega_{n}^{2} }}} \right) $$
(20)

Above is a very important result. It relates DSA stroke to geometric parameters, PZT material property and suspension dynamics.

Equations (17) and (18) represent DSA suspension lumped parameters in term of two dynamic properties, w p and w n , which can be obtained by FEA or test. Take Φ style design (Fig. 1) as an example, the suspension sway frequencies without and with PZT installed are obtained from FEA (modal analysis) as shown in Fig. 6. Plug in the numbers of w p (13.5 kHz) and w n (21 kHz) into (20) and considering (10a), the calculated DSA stroke with this design is about 15 nm/V, matching actual test result.

Fig. 6
figure 6

FEA results of DSA suspension sway

Full size image

6 DSA design considerations

Other than the geometric factor and material selection we addressed earlier, Eq. (20) links the DSA stroke capability to its dynamic performance.

For higher stroke capability, w p should be lower. In extreme case that w p is zero, suspension stiffness k is zero per Eq. (13). Physically, this means suspension is broken into two sections from where PZT sits. The base plate part and the front load beam part are disconnected without PZT. The only thing that connects the two sections together is the PZT. Since there is no suspension stiffness for the PZT to overcome, it deforms at its maximum capability with a voltage applied, so called free strain condition. As a result, maximum rotation is generated to create largest slider off track as shown in Eq. (10).

On the other hand, when w p /w n is closer to one, the stroke is close to zero. In this case, the suspension is much stiffer than the PZT element. All the voltage applied to PZT is used to create large stress within PZT itself but not much deformation since it is too soft to push the suspension. For example, the same design with a PVDF strip can hardly generate any stroke.

DSA stroke capability is just one of many suspension design goals. Another important aspect is DSA reliability. Since PZT elements used in these milli-type DSA designs are ceramics that can be cracked easily, parameters in Eq. (20) should be designed to minimize PZT crack possibility. In particular, passive sway frequency w p or suspension stiffness k should be large enough so that much of the external forces applied to suspension is carried by the passive stiffness to prevent large stress generation in PZT element. The design rule is that any external forces applied to suspension, such as windage excitation, vibration load and shocks from external or hitting crash stops, should not create large tensional stress in PZT that leads to cracks. Generally speaking, per Eq. (16), the passive sway frequency term \( (w_{p}^{2}) \) and active sway frequency term \((w _{a}^{2}) \) contribution to the total sway frequency term \( (w_{n}^{2}) \) is roughly same to achieve a balance between the stroke generation and crack prevention.

7 Conclusions

An analytic model is used to drive DSA equation of motion and DC gain. Physical parameters affecting DSA performance are identified and related to suspension dynamic parameters. It is shown that the DSA stroke is determined by its geometric amplification factor, material property and passive and total sway frequencies. A DSA suspension design is a balance between stroke, dynamics and reliability.