1 Introduction

Microcantilevers are considered to be essential elements of many of the current microelectromechanical systems and biosensors (Baller et al. 2000; Lang et al. 2005). The majority of these systems use cantilever-based sensors for detecting signals with wide range of magnitudes. In addition, microcantilevers are recently used to measure the weight of a single cell. The selection of microcantilevers as bio-probing tools is mainly because of their large surface area-to-mass ratio, which provides high sensitivity that can effectively characterize biological cells. Moreover, microcantilevers form a class of biosensors which are sensitive to their mechanical, deformable, and resonant properties, as explained by Sepaniak et al. (2004).

Recent experimental advances in nanotechnology offer the possibility of detecting, characterizing, and manipulating molecules within microfluidic devices. Extensive efforts are focused on the measurement of the physical properties of single cells, which open a new area of research in biological and medical science. For instance, a rectangular gold-coated silicon commercial microcantilever is used to sense mercury in vapor (Xu et al. 2002). Two known techniques are widely used for detection. First, the microbeam is fully coated with gold sputtered along its entire length. Second, gold is deposited only at the microbeam tip. Both cases were tested for mercury detection. Noticeable frequency shifts were attained in thermally induced higher-order modes, as compared to the fundamental mode (Xu et al. 2002). Furthermore, microcantilevers are molecular specific and can be used as chemical sensors by coating a specific chemical recognition agent on one surface. For instance, molecular absorption-induced surface stress on a microcantilever is demonstrated through deflection changes (Kadam et al. 2006).

Recently, experimental studies have demonstrated the use of microcantilevers as bio-sensors to estimate the mass of a single living cell inside a microchannel (Burg et al. 2007; Park et al. 2007). Two novel microfluidic devices are currently used to quantify the properties of cells, such as their sizes and masses (Burg et al. 2007; Park et al. 2007). The first device uses a mechanical resonator as a biosensor to measure the mass of a single molecule with a very high sensitivity. This device is equipped with a suspended microchannel resonator to weigh single nanoparticles, single bacterial cells, and sub-mono-layers of adsorbed proteins in water with very high resolutions (Burg et al. 2007). For a proper operation of this device, the resonator needs to be light and to have a very high quality factor to resolve small mass changes. The second device uses a novel experimental technique to estimate the weight of an adherent cell without removing it from the cantilever array, which is encapsulated in a microfluid device called living cantilever arrays device (Park et al. 2007). The target cell is the HeLa cancer cell, which is injected into a microfluidic channel with a linear array of functionalized silicon cantilevers. The cells were captured on the cantilevers using positive dielectrophoresis techniques and then cultured on the cantilevers in a microfluidic environment. The resonance frequencies of the cantilevers were measured using laser means. The mass of a single HeLa cell was extracted from the resonance frequency shift of the cantilever. The results were compared with the mass of a single living cell obtained by optical con-focal microscopy and flow cytometry devices.

From a theoretical point of view, simplified expressions based on mass-spring models are currently used to relate the cantilever frequency shift and the mass of a single cell, details of these expressions are provided in Jin et al. (2006). In a recent study (Narducci et al. 2009), it was shown that sensitivity of the cantilevers in measuring the cell mass may be increased by using higher-order modes and reducing the cantilevers dimensions. A comparison between the experimental results and the simplified model is given in Narducci et al. (2009). Although these simplified methods can be used to estimate the mass of a single living cell within acceptable accuracy, there is no adequate full theoretical model suitable for direct estimation of the mass of a single adherent living cell. In this work, we develop a simple theoretical model that is capable of estimating the weight of a single cell. The present analysis is mainly motivated by the recent experimental work conducted by Park et al. (2007).

2 Problem formulation

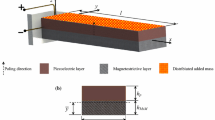
We consider a microcantilever beam placed inside a vacuum microchannel and used as a bio-mass detector. We note that the present microsystem has been used for other applications (e.g., gas sensor) (Nayfeh et al. 2010). The cantilever beam has a tip mass, which is coated with a specific material that can be used as an attractor to a single biological cell of mass m c via a chemical binding effect. The cantilever beam is placed a distance d away from an electrode powered by a DC power supply, as shown in Fig. 1. The basic idea underlying the use of a microcantilever as a mass sensor is the fact that the natural frequency of the beam is slightly modified as a result of depositing the binding cell on the tip. Based on the frequency shift due to the attached cell, the mass can be estimated. A method for detecting the shift in the resonance frequency, once the cell is settled on the tip, is to give the microbeam an intial disturbance, for example a pulse, and then measure the frequency content of the free response. We note that the electric actuation is implemented in the present system to enhance sensitivity of the resonance frequency shift to variations in the added mass. Khater et al. (2009) showed the potential use of an electrostatically actuated microcantilever beam as a mass sensor and proposed a new mass sensing technique which uses the pull-in phenomenon. In this effort, the mass sensing is based on the frequency shift.

Fig. 1
figure 1

Schematic of the bio-mass sensor inside a microchannel: cantilever beam with a tip mass and the attached single cell

Full size image

We model the microbeam using the Euler–Bernoulli beam equation and use perturbation techniques to relate the weight of a single cell attracted by the tip mass of the microcantilever to the shift in its natural frequency. The cantilever microbeam is excited by an external electrode using a DC power supply to enhance its sensing performance. The microcantilever has a uniform square cross section b × h, a length L, and a mass per unit length m and made of polysilicon material. A rigid mass M of finite dimension is attached to the tip of the beam. The detailed dimensions and material properties of the biosensor are given in Table 1.

Table 1 Microsensor specifications
Full size table

3 Mathematical modeling

The general equation and associated boundary conditions that govern the dynamical motion of a microcantilever with a tip mass placed in electrostatic field are based on beam theory. A static analysis is first carried out to derive the maximum cantilever deflection according to the classical pull-in phenomenon. The natural frequencies of the microsystem are then computed by solving an eigenvalue problem. The effect of the DC voltage on the natural frequencies is presented for different tip-electrode spacing distances. Variation of the tip mass as it binds with a single cell is investigated based on the resonance frequency shift. Enhancement of the sensing performance is explored by using higher-order modes. The details of the analysis are given in the following subsections.

3.1 Bio-mass sensor model

We consider the microcantilever shown in Fig. 1. The dimensions and material properties are given in Table 1. The equation of motion governing the transverse deflection w(x, t) of the beam is expressed as (Ghommem 2008; Nayfeh and Pai 2004; Nayfeh et al. 2010)

$$ EI{\frac{\partial^4 w}{\partial x^4}}+ m {\frac{\partial^2 w} {\partial t^2}}-J {\frac{\partial^4w}{\partial x^2 \partial t^2}}=0 $$
(1)

and the associated boundary conditions are at x = 0

$$ w=0, \quad {\frac{\partial w}{\partial x}}=0 $$

and at x = L

$$ EI {\frac{\partial^2 w}{\partial x^2}} = 0, \quad EI {\frac{\partial^3 w}{\partial x^3}} - M {\frac{\partial^2 w} {\partial t^2}} -J {\frac{\partial^3w}{\partial x \partial t^2}}= - {\frac{ \epsilon A V_{\text{DC}}^2} {2(d-w)^2}} $$
(2)

where x is the position along the microbeam length, I is the moment of inertia of the cross-section, J is area moment of inertia of the cross-section, E is Young’s modulus, t is time, A and d are the area and the gap distance of the capacitor, respectively, and ε is the dielectric constant of the gap medium.

For convenience, we introduce the following set of nondimensional parameters:

$$ \begin{aligned} \hat{x}&={\frac{x}{L}}, \quad \hat{w}={\frac{w}{d}}, \quad \hat{t}=\tau t, \quad \hat{J} = {\frac{J}{\text{m\;L}^2}} \\ \alpha &= {\frac{\epsilon AL^{3}}{2 E I d^{3}}}, \quad M_r = {\frac{M}{\text{m\;L}}}, \quad \tau =\sqrt{\frac{EI}{\text{m\;L}^{4}}}\\ \end{aligned} $$

Then, in nondimensional form, the equation of motion and associated boundary conditions become

$$ w^{iv}+\ddot{w}-J\ddot{w}''=0 $$
(3)
$$ w=0,\quad w'=0 \quad \hbox{at} \quad x=0 $$
(4)
$$ w''=0,\quad w'''-M_r\ddot{w}-J\ddot{w}'=-{\frac{\alpha V_{\text{DC}}^2}{(1-w)^2}} \quad \hbox{at} \quad x=1 $$
(5)

where the hat has been removed for notation convenience. We note that, for a microbeam driven in a vacuum microchannel, the damping term is not taken into account in the equation of motion.

3.2 Static deflection

A closed-form solution of the microbeam static defection as a function of DC voltage is derived. The maximum range of the tip displacement and the associated DC-voltage power supplied to the setup are determined.

The static deflection w s (x) of the microbeam subject to an electrostatic force is governed by

$$ w_s^{iv}=0 $$
(6)
$$ w_s(0)=0, \quad w_s'(0)=0, \quad w_s''(1)=0 $$
(7)
$$ w_s'''(1) = - {\frac{\alpha V_{\text{DC}}^{2}}{(1-w_s(1))^{2}}} $$
(8)

The general solution of Eq. 6 can be expressed as

$$ w_s(x)=c_{3}x^{3}+c_{2}x^{2}+c_{1}x+c_{0} $$
(9)

Using the boundary conditions given by Eq. 7 yields

$$ w_s(x)=c_3 x^2(x-3) $$
(10)

We let w s (1) = w M , apply the fourth boundary condition given by Eq. 8, and obtain the following expression relating the maximum deflection of the microbeam tip to the applied DC voltage:

$$ V_{\text{DC}}=\sqrt{\frac{3 w_{M}(1 - w_{M})^{2}}{\alpha}} $$
(11)

When a voltage is applied, the beam restoring force, which is related to the beam stiffness, resists the electrostatic force. As the DC voltage is increased, beyond a critical value known as the pull-in voltage, the restoring force cannot resist the electrostatic force and consequently the beam will pull-in; that is, snaps to the substrate (Abdel- Rahman et al. 2002; Nayfeh et al. 2010).

In Fig. 2a, we depict variation of the maximum static deflection w M with the DC voltage V DC for three gaps d = 1 μm, d = 2 μm, and d = 3 μm. Here, we consider an attractor block attached to the tip having a 5 μm thickness, capacitor surface area A = 400 μm2, and a proof mass of M = m L. The dimensions and material properties of the polysilicon microbeam are given in Table 1. The resulting curves are typical for electrostatic actuators with lower and upper branches of solutions corresponding to stable and unstable equilibria of the microbeam, respectively. The results show that the gap width between the microbeam and the substrate has a significant influence on the voltage-deflection relationship. Increasing the gap width results in an increase in the necessary voltage range to obtain the same level of deflection and the pull-in voltage. Therefore, for a given microcantilever bio-sensor design, to avoid the occurrence of instability and maximize the range of travel requires a bigger gap width. Moreover, the DC voltage supply affects the natural frequencies of the beam as is shown in the following subsection.

Fig. 2
figure 2

The effect of DC voltage on tip deflection and natural frequency: a Variation of the maximum static deflection with DC voltage for the gap widths of d = 1 μm, d = 2 μm, and d = 3 μm. b Variation of the first natural frequency ω0 with the DC voltage V DC for three values of the tip mass \(M_{r_0}\) (d = 2 μm)

Full size image

3.3 Natural frequencies

The natural frequencies of the microbeam with the attached mass M r in the presence of an electrostatic field are computed. A perturbation technique is used to obtain the effect of the binding single cell mass m c to the tip mass on the resonance frequencies. The eigenvalue problem is formulated by assuming that the bio-mass sensor response can be decomposed into static and harmonic components representing its motion in the nth mode as

$$ w(x,t) =w_s(x) + (\phi(x) e^{ i \omega t}+cc) $$
(12)

where cc stands for the complex conjugate of the preceding term. Substituting Eq. 12 into Eqs. 3–5, expanding the result for small motions around w s (x), using Eqs. 6–8, and dropping the nonlinear terms in ϕ, we obtain

$$ \phi^{iv}+J\omega^2\phi''-\omega^2\phi=0 $$
(13)
$$ \phi(0)=0, \quad \phi'(0)=0, \quad \phi''(1)=0 $$
(14)
$$ M_r\omega^2\phi+J\omega^2\phi'+\phi'''={\frac{2\alpha V_{\text{DC}}^2}{(1-w_M)^3}}\phi \quad \hbox{at} \quad x=1 $$
(15)

We let

$$ M_r=M_{r_0}+\delta M_{r_1}+\cdots $$
(16)

where δ is a small nondimensional parameter used as a book keeping device and seek an approximate solution of Eqs. 13–15 in the form

$$ \phi=\phi_{0}+\delta \phi_{1}+\cdots $$
(17)
$$ \omega=\omega_{0}+\delta \omega_{1}+\cdots $$
(18)

Scaling J as δJ, substituting Eqs. 16–18 into Eqs. 13–15, and equating coefficients of like powers of δ, we obtain

Order (δ0)

$$ \phi_0^{iv}-\omega_0^2\phi_0=0 $$
(19)
$$ \phi_0(0)=0, \quad \phi_0'(0)=0, \quad \phi_0''(1)=0 $$
(20)
$$ M_{r_0}\omega_0^2\phi_0+{\frac{2\alpha V_{\text{DC}}^2} {(1-w_M)^3}}\phi_0+\phi_0'''=0 \quad \hbox{at} \quad x=1 $$
(21)

Order (δ)

$$ \phi_1^{iv}-\omega_0^2\phi_1=2\omega_1\omega_0\phi_0-J\omega_0^2\phi_0'' $$
(22)
$$ \phi_1(0)=0, \quad \phi_1'(0)=0, \quad \phi_1''(1)=0 $$
(23)
$$ \begin{aligned} M_{r_0}\omega_0^2\phi_1 + {\frac{2\alpha V_{\text{DC}}^2} {(1-w_M)^3}}\phi_1+\phi_1'''=-M_{r_1}\omega_0^2\phi_0 \\ - 2M_{r_0}\omega_0\omega_1\phi_0-J\omega_0^2\phi_0' \quad \hbox{at} \quad x=1 \end{aligned} $$
(24)

The general solution of Eq. 19 can be expressed as

$$ \begin{aligned} \phi_0(x)&=A_1\cos(\sqrt{\omega_0}x)+A_2\sin(\sqrt{\omega_0}x) \\ &\quad+ A_3\cosh(\sqrt{\omega_0}x)+A_4\sinh(\sqrt{\omega_0}x) \end{aligned} $$
(25)

Substituting Eq. 25 into Eqs. 20 and 21, we obtain a linear system in that A i that can be written in the form

$$ \hbox{M} \left[\begin{array}{llll} A_1 & A_2 & A_3 & A_4 \end{array}\right]^T=0 $$
(26)

where

$$ \hbox{M}= \left[\begin{array}{llll} 1 & 0 & -c\omega_0 & \Lambda c + s\omega_0^{3/2}+M_{r_0}c\omega_0^2 \\ 0 & \sqrt{\omega_0} & -s\omega_0 & \Lambda s -c\omega_0^{3/2}+M_{r_0}s\omega_0^2\\ 1 & 0 & ch\omega_0 & \Lambda ch + sh\omega_0^{3/2}+M_{r_0}ch\omega_0^2\\ 0 & \sqrt{\omega_0} & sh\omega_0 & \Lambda sh -ch\omega_0^{3/2}+M_{r_0}sh\omega_0^2 \end{array}\right]^T $$

and

$$ \begin{aligned} c&=\cos(\sqrt{\omega_0}), \quad s=\sin(\sqrt{\omega_0}), \quad ch=\cosh(\sqrt{\omega_0}), \\& sh=\sinh(\sqrt{\omega_0}), \quad \Lambda = {\frac{2\alpha V_{\text{DC}}^2}{(1-w_M)^3}} \end{aligned} $$

Setting the determinant of the matrix M equal to zero results in the characteristic equation

$$\begin{aligned} \,&\left(\frac{2 \alpha V_{\text{DC}}^{2}}{(1-w_{M})^{3}}+M_{r0}\omega_0^2 \right)(\cos(\sqrt{\omega_0})\sinh(\sqrt{\omega_0})\\ &\quad -\cosh(\sqrt{\omega_0})\sin(\sqrt{\omega_0}))\\ &\quad+\omega_0^{3/2}\left(1+\cos(\sqrt{\omega_0})\cosh(\sqrt{\omega_0})\right)=0\\ \end{aligned} $$
(27)

It should be noted that, in the absence of the tip mass and the DC voltage, Eq. 27 reduces to that of a cantilever beam (Nayfeh and Pai 2004).

Variation of the first natural frequency ω0 with the supplied DC voltage for three different values of the tip-mass M r0, for a gap width d = 2 μm, is given in Fig. 2b. The results show that the natural frequency decreases as the electrostatic force increases and approaches zero as pull-in develops. Thus, the electrostatic force tends to soften the microbeam. The unactuated (V DC = 0) natural frequency of the microsensor decreases and the curvature of the ω − V DC curve increases as the tip mass increases. However, the tip-mass has no effect on the pull-in voltage because it does not contribute to the mechanical restoring force of the beam.

Next, we follow Nayfeh (1983, 1985) to derive an analytical expression for the variation of the shift ω1 in the resonance frequency with the added mass \((M_{r_1}=m_c/(\text{m\;L}))\) on the sensing area. We note that the homogeneous part of Eqs. 22–24 is the same as Eqs. 19–21 and that the latter has a nontrivial solution. Hence, the nonhomogeneous Eqs. 22–24 have a solution only if a solvability condition is satisfied (Nayfeh 1983). To determine this solvability condition, we multiply Eq. 22 with the adjoint ψ(x), which is defined below, integrate the outcome by parts from x = 0 to x = 1 to transfer the derivatives from ϕ1 to ψ, and obtain

$$\begin{aligned} \,&\int\limits_0^1\phi_{1}\left[\psi^{iv}-\omega_0^2\psi\right]dx+ \left[\phi_{1}^{\prime}\psi^{\prime\prime}+\phi_{1}^{\prime\prime\prime}\psi-\phi_{1}\psi^{\prime\prime\prime}-\phi_{1}^{\prime\prime}\psi^{\prime}\right]_0^1\\ & \quad=\int\limits_0^1\left(2\omega_0\omega_1\phi_{0}-J\omega_0^2\phi_{0}^{\prime\prime}\right)\psi dx \end{aligned} $$
(28)

Then, the adjoint equation is determined by setting the coefficient of ϕ1 in the integrand of Eq. 28 equal to zero; that is,

$$ \psi^{iv}-\omega_0^2\psi=0 $$
(29)

To determine the adjoint boundary conditions, we consider the homogeneous problem in Eq. 28, use Eq. 29, and obtain

$$ \left[\phi_{1}'\psi''+\phi_{1}'''\psi-\phi_{1}\psi'''-\phi_{1}''\psi' \right]_0^1 =0 $$
(30)

which, upon using the homogeneous boundary conditions in Eqs. 23 and 24, yields

$$ \psi(0)=0, \quad \psi'(0)=0, \quad \psi''(1)=0 $$
(31)
$$ M_{r_0}\omega_0^2\psi+{\frac{2\alpha V_{\text{DC}}^2} {(1-w_M)^3}}\psi+\psi'''=0 \quad \hbox{at} \quad x=1 $$
(32)

Comparing Eqs. 29, 31, and 32 with Eqs. 19–21, we conclude that the problem is self-adjoint and therefore

$$ \psi(x) = \phi_0(x) $$
(33)

We return to the nonhomogeneous problem and obtain from Eqs. 23, 24, and 28 that

$$ \begin{aligned} &M_{r_1}\omega_0^2\phi_0(1)\psi(1)-2M_{r_0}\omega_0 \omega_1\phi_0(1)\psi(1)-J\omega_0^2\phi_o^{\prime}(1)\psi(1) \\ &\quad=\int\limits_0^1\left(2\omega_0\omega_1\phi_0-J\omega_0^2\phi_0^{\prime\prime}\right) \psi dx \end{aligned} $$
(34)

Using Eq. 25 to substitute for the mode shapes in Eq. 34, we obtain the following solvability condition:

$$ \begin{aligned} &\omega_1\left[2M_{r_0}\omega_0\phi_0(1)^2+ 2\omega_0\int\limits_0^1\phi_0(x)^2dx\right]\\& =-M_{r_1}\omega_0^2\phi_0(1)^2-J\omega_0^2 \left[\int\limits_0^1\phi_0(x)\phi_0^{\prime\prime}(x)dx+\phi_0(1)\phi_0^{\prime}(1)\right] \end{aligned} $$
(35)

The linear variation of the shift ω1 in the natural frequencies with the added mass \(M_{r_1},\) as shown in Eq. 35, is quite encouraging since it indicates that detecting the frequency shift can produce an easy measure of the mass of the single cell settled on the sensing tip.

4 Results

In this section, we explore the parameter space of the bio-mass sensor with a goal of optimizing its performance. To this end, we investigate the effects of variations in the tip mass and capacitor gap width and the use of higher-order modes on the sensitivity of the shift in the resonance frequency to variations in the added mass deposited on the sensing area.

4.1 Single mass detection

In Fig. 3, we show the effect of varying the tip mass on the fundamental resonance frequency. The first natural frequency varies linearly and monotonicly with the added mass. We note that the perturbation analysis predicts well the effect of the added mass on the natural frequency. Decreasing the tip mass increases the resonance frequency and enhances sensitivity of the bio-mass sensor. Based on the present results, one may conclude that the use of a small tip mass in the design of the microsensor might be useful in the sense that it amplifies the slope of variation of the resonance frequency shift with the added mass. This will enable easy detection and measurement of the mass of a single cell deposited on the sensing area. However, the tip mass reduction is limited to the required surface area for attracting the single cell.

Fig. 3
figure 3

Variations of the shift in the first natural frequency with the added mass for M r0 = 0.1, M r0 = 0.2, and M r0 = 0.3 (V DC = 4 and d = 2 μm). The solid line represents the shift obtained from the perturbation analysis. The stars represent the same data obtained by solving the exact eigenvalue problem

Full size image

4.2 Effects of the higher-order modes and the gap width

The effect of using higher-order modes on the sensitivity of a given bio- microcantilever sensor that is used to estimate the mass of a single cell by detecting the shift in resonance frequency is investigated. We consider the first two modes and show variation of the resonance frequency shift with the added mass in Fig. 4a. Clearly, the second-order resonance mode provides a higher sensitivity and, hence, the added mass may be accurately estimated. On the other hand, exciting higher-order modes requires more energy to obtain an output signal with the same amplitude as that obtained by exciting the first mode (Narducci et al. 2009).

Fig. 4
figure 4

a Variations of the shift in the first two natural frequencies with the added mass (VDC = 4, d = 2 μm, and Mr0 = 0.1). b Sensitivity of the resonance frequency shift to variations in the added mass ∂ω1/∂Mr1 versus the gap distance d (VDC = 1 and Mr0 = 0.1)

Full size image

Next, we examine the effect of the gap width on the sensing performance of the present microsystem. Variation of \({\partial \omega_1/\partial}M_{r1},\) which represents sensitivity of the shift in the resonance frequency to variation in the added mass, with the gap width d is shown in Fig. 4b. The results show that sensitivity of the natural frequency to variations in the added mass, \(|\partial \omega_1/\partial M_{r1}|,\) increases nonlinearly with an increase in the gap width. Thus, increasing the gap width does not only increase the pull-in voltage but also provides higher sensitivity, thereby enhancing the performance of the bio-mass sensor. However, increasing the gap width is limited by microfabrication constraints.

5 Conclusion

A bio-mass sensor that has the capability of measuring the weight of a single cell is modeled theoretically in this article. The main component of this microsensor is a cantilever beam with a proof mass attached to its tip. The rigid mass is coupled to an electrode to capacitively drive the beam and is used to bind with a target single cell which eventually changes the sensor resonance frequencies. The operating principle is based on detecting the shift in the resonance frequency to measure the mass of a cell deposited on the sensing tip. A perturbation analysis is performed to investigate sensitivity of the natural frequencies to the added mass. Based on this analysis, we propose an analytical way to measure the mass of a single cell deposited on the tip of the microbeam by detecting the shift in the resonance frequency of the microsystem. We also examine the effect of several parameters, such as the tip mass and the gap width and the order of the used modes, on the sensing efficiency. Such parametric study may provide suggestions for improving the design of the present microsensor.