Single-image super-resolution via joint statistic models-guided deep auto-encoder network

Abstract

Recent researches on super-resolution (SR) with deep learning networks have achieved amazing results. However, most of the existing studies neglect the internal distinctiveness of an image and the output of most methods tends to be of blurring, smoothness and implausibility. In this paper, we proposed a unified model which combines the deep model with the image restoration model for single-image SR. This model can not only reconstruct the SR image, but also keep the distinct fine structures for the low-resolution image. Two statistic priors are used to guide the updating of the output of the deep neural network: One is the non-local similarity and the other is the local smoothness. The former is modeled as the non-local total variation regularization, and the latter as the steering kernel regression total variation regularization. For this unified model, a new optimization function is formulated under a regularization framework. To optimize the total variation problem, a novel algorithm based on split Bregman iteration is developed with the theoretical proof of convergence. The experimental results demonstrate that the proposed unified model improves the peak signal-to-noise ratio of the deep SR model. Quantitative and qualitative results on four benchmark datasets show that the proposed model achieves better performance than the deep SR model without regularization terms.

1 Introduction

Single-image super-resolution (SISR) aims to recover a high-resolution (HR) image from the corresponding low-resolution (LR) image. It is an ill-posed inverse problem because an LR image can be generated by multiple HR images. It is greatly important to restore high-quality images from degraded observations for user’s vision experience or high-level vision task. The learning-based super-resolution (SR) is a hot spot, which learns one mapping function between LR images and its corresponding HR images from external or internal examples in the given datasets. The learning-based SR methods can be further divided into two classes: the traditional learning-based SR methods and the deep learning-based SR methods. The former methods usually need pre-specified base functions; thus, they are limited in the analysis of an image. The latter methods are superior because they optimize the mapping functions of SR in a global way.

Among traditional learning-based SR methods [3, 8, 22, 31], many studies have been designed by using the methodologies such as nearest neighbor (NN), regression and sparse representation. Freeman [8] made a milestone of the NN-based SR methods which transformed the SR problem to the problem of estimating high-frequency details of an interpolating image with the desired scale. The low-frequency patches as input and the output of the corresponding NN patches were resolved by using a Markov model. After that, many improved NN-based methods were developed [3, 22, 31]. Regression-based SR treated SR as a fitting problem. A mapping function from the LR subspace to the HR subspace was learned. Chang et al. [3] adopted local linear embedding (LLE) to solve the SR problem. A high-resolution image patch was the linear combination of its HR nearest neighbors, and the combination weights were corresponding to those of low-resolution patches. Ni et al. [19] utilized support vector regression (SVR) to solve the SR problem in the frequency domain and treated the SR as a kernel learning problem. In [13], a kernel ridge regression was used for SR and achieved promising results. In [16], the SR problem resorted to a Gaussian processing regression. Sparse representation method was very popular in the super-resolution tasks which regularized the reconstruction coefficients with $l_{1}/l_{0}$ norm. Sparse representation-based SR methods usually learn a dictionary, by which an input image patch can be represented. The most representative work among those was [26], where the authors casted the super-resolution problem into a sparse representation problem. Some variants of sparse representation-based SR methods were developed afterward [7, 25].

With the upsurge of deep learning, more and more works resorted to implementing the deep learning on object recognition [29], image retrieval [30] as well as SR. DNN is an end-to-end architecture, and it can be optimized as a whole rather than in a pipeline way. Compared with the traditional SR methods, it is effective and flexible for information processing. There are two important issues of DNN: the neural network architecture and the loss function. The base architecture of the DNN SR methods can be mainly divided into two classes: the convolutional neural network (CNN) and the auto-encoder network. Dong et al. [5] made the beginning of implementing CNN on SR. They trained a CNN with the loss function of the least square error by using the pairs of LR and HR image patches and achieved the breakthrough results on SISR [6]. Then, subsequent CNN SR methods improved the peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) by using robust Charbonnier loss function or $l_{1}$ loss function. Inspired by these impressive works, many CNN-based SR methods are proposed, such as VDSR [11], DRCN [12], ESPCN [20], SCN [24], LAPSRN [14], SRResNet [15], EDSR [17].

As for the auto-encoder, Cui et al. [4] initiatively proposed an SR method based on collaborative local auto-encoder (CLA), where the auto-encoders were stacked and trained layer by layer. The loss function contained three terms: the fidelity, the sparse regularization terms and the non-local similarity-related regularizations. Wang et al. [23] proposed the non-local auto-encoder (NLA) for SR. Similar to CLA, it was trained layer by layer, and then the second auto-encoder was embedded in the first auto-encoder, and so on. The loss function contains the fidelity term, the hidden layer similarity and the hidden layer distribution diversity. Different from the above-mentioned methods, Zeng et al. [27] proposed a coupled deep auto-encoder (CDA) for SR, where LR and SR intrinsic representations were obtained by the LR and SR auto-encoders, respectively. A fully connected neural network was used to convert the LR intrinsic representation into the HR intrinsic representation. And fine-tuning was implemented at the end of the network. In CDA, the least square error was computed as the loss function. The advantage of CDA was that it run fast and stable compared with the other’s auto-encoders. Though deep learning-based SR methods have been widely recognized and succeeded, most outputs of them tend to be blurry, over-smoothed and generally appear implausible.

The previous learning-based SR methods only paid attention to the robust mapping function for SR while neglecting the internal distinctiveness of an image which illustrated the fine structures or textures. To overcome this limit, we utilize the prior knowledge of an image to guide the updating of the output of the deep neural network for SR. It is well known that nature images are of the structure recurrence and the local smoothness, which are applied successfully for image denoising, deblurring and texture synthesis [2, 21]. The non-local total variational regularization (NLTV) [2] and the steering kernel regression total variational regularization (SKRTV) [21] are modeled for the structure recurrence and the local smoothness, respectively. We propose a unified SR model in which the joint statistic models of NLTV and SKRTV guide the CDA model for better SR performance. For the proposed total variation model, we develop a split Bregman iteration (SBI) algorithm. The proposed model can not only reconstruct SR images, but also keep the distinct fine structures.

The main contributions of our algorithm are threefold. First, a unified SR model is established. Our algorithm combines the deep SR model with joint statistic models such as NLTV and SKRTV which preserve the structure recurrence and the local smoothness and make a supplemental constraint on the output of deep SR images. Second, an optimization function is formulated for the unified model under a regularization framework. Third, to make the unified model tractable and robust, a new SBI algorithm is developed to efficiently solve the TV optimization problem associated with the theoretical proof of convergence.

The paper is organized as follows: Sect. 2 briefly introduces NLTV and SKRTV as well as CDA. Section 3 describes the proposed model, which uses two statistic properties to guide the updation of the CDA output. Then, a novel algorithm based on SBI is proposed for solving the TV-based optimization. Experimental results are given and analyzed in Sect. 4. Finally, we conclude that the proposed model is effective for SR.

2 Related work

In this section, we briefly review NLTV [2], SKRTV [21] and CDA [27].

2.1 Non-local statistical modeling for self-similarity

NLTV [2] is effective for image restoration which can be used to regularize the ill-posed deformation removal problem. Under the assumption of non-local self-similarity, the similar patches searched in different locations can be regarded as the multiple observations of the target patch. The NLTV regularization term is formulated as,

$$\begin{aligned} \begin{aligned} \varphi _{nl}(u)&= |\bigtriangledown _{N}u| \\&= \sum _{i}\sum _{j\epsilon P(x_{j})}|u(x_{j})-u( x_{i}) |\sqrt{w_{N}( i,j)} \end{aligned} \end{aligned}$$

(1)

where $w_{N}\left( i,j \right)$ is the similarity weight which measures the similarity between the image patch centered at the pixel position $x_{i}$ and the image patch centered at the pixel position $x_{j}$, and $P\left( x_{j} \right)$ denotes the index set which contains the index of image patches similar to the image patch at the position $x_{j}$. We define the extraction operator as ${\mathfrak {R}}_{x_{i}}u$ representing the patch centered at the pixel position $x_{i}$. The similarity weight between the patches at position $x_{i}$ and $x_{j}$ is defined as,

$$\begin{aligned} w _{N}\left( i,j \right) =\exp \left( -\frac{\left\| {\mathfrak {R}}_{x_{i}}u-{\mathfrak {R}}_{x_{j}}u \right\| ^{2}}{h_{n}^{2}} \right) \end{aligned}$$

(2)

where $h_{n}$ is the global parameter which controls the speed of degradation of exponential function. We reformulate Eq. (1) in a matrix formula as,

$$\begin{aligned} R_{\mathrm{NL}}=\Vert (I-W_{\mathrm{NL}} )X \Vert _1 \end{aligned}$$

(3)

where X is a vector representation of an image, I is a unit matrix, and $W_{\mathrm{NL}}$ is a similarity weight matrix, whose element at (i, j) can be defined as,

$$\begin{aligned} W_{\mathrm{NL}}(i,j)=\left\{ \begin{array}{ll} \frac{\sqrt{w_{N}(i,j)}}{\sum _{j\in P(x_{i})}\sqrt{w_{N}(i,j)}}, &{}\quad j\in P(x_{i}) \\ 0, &{} \quad j\notin P(x_{i}) \end{array} \right. \end{aligned}$$

(4)

where i denotes the ith pixel of an image.

2.2 Steering kernel regression for smoothness

SKR [21] is a locally approximate method, which approximates a point by the means of Taylor expansion. And it can be modeled as a weighted least square method,

$$\begin{aligned} \beta _{i} = \mathop {\arg \min }_{\beta _i}\sum _{i}\left\| y-\varPsi \beta _{i} \right\| _{K_{h_{k}}}^{2} \end{aligned}$$

(5)

where y is the column vector consisting of the neighboring pixels centered at the location $x_{i}$, and $K_{h_{k}}(x_{i}-x)=\frac{\sqrt{{\hbox {det}}(C_{i})}}{2\pi h_{k}^{2}} \exp \left(-\frac{(x_{i}-x)^\mathrm{T}C_{i}(x_{i}-x)}{2h_{k}^{2}}\right)$ is the weight function where $h_{k}$ is a smoothing parameter and the matrix $C_{i}$ is the symmetric gradient covariance at $x_{i}$ in the vertical and horizontal directions. $\varPsi$ is the polynomial basis, which can be defined by,

$$\begin{aligned} \varPsi =\left[ \begin{array}{ccc} 1 &{}\quad (x_{i}-x_j)^\mathrm{T} &{}\quad {\hbox {vech}}^\mathrm{T}(x_{i}-x_{j})(x_{i}-x_j)^\mathrm{T}\\ . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad .\\ . &{}\quad . &{}\quad . \end{array} \right] \end{aligned}$$

(6)

where ${\hbox {vech}}^\mathrm{T}\left\{ {\left[ \begin{array}{cc} a &{}\quad b\\ c &{}\quad d \end{array} \right] } \right\} =\left[ \begin{array}{ccc} a&\quad b&\quad c \end{array} \right].$

The solution of Eq. (5) is

$$\begin{aligned} \hat{\beta _{i}}=(\varPsi ^\mathrm{T}K\varPsi )^{-1}\varPsi ^\mathrm{T}Ky \end{aligned}$$

(7)

where $K=diag\left\{ K_{h_{k}}(x_1-x),K_{h_{k}}(x_2-x),\ldots ,K_{h_{k}}(x_p-x) \right\}$ is a diagonal matrix. The pixel value at $x_{i}$ can be estimated as $R(x_{i})=e_{1}^\mathrm{T}\hat{\beta _{i}}$, where $e_{1}=\left[ \begin{array}{cccc} 1&0&\ldots&0 \end{array} \right] ^\mathrm{T}$ is the first column of identity matrix. We define a weighted vector $W_{S}(i)$ for SKRTV in the ith row as,

$$\begin{aligned} W_{S}(i)&=e^\mathrm{T}(\varPsi ^\mathrm{T}K\varPsi )^{-1}\varPsi ^\mathrm{T}K\\ &=\left[ \begin{array}{cccc}w_{s}(i,1)&w_{s}(i,2)&\ldots&w_{s}(i,P)\end{array}\right] . \end{aligned}$$

Thus, SKRTV regularization term can be formulated as,

$$\begin{aligned} \begin{aligned} \varphi _{l}(u)&= |\bigtriangledown _{S}u| \\&= \sum _{i}\sum _{j\epsilon {\mathbb {N}}(x_{i})}|u(x_{j})-u( x_{i}) |\sqrt{w_{S}( i,j)} \end{aligned} \end{aligned}$$

(8)

where ${\mathbb {N}}(x_{i})$ contains the indices of all ${x_{i}}$’ s neighbors and $w_{S}(i,j)$ is the weight generated by SKR. Similar to the NLTV, we reformulate Eq. (8) in a matrix form as,

$$\begin{aligned} R_{L}=\left\| (I-W_{L})X \right\| _{1} \end{aligned}$$

(9)

$W_{L}$ is defined as,

$$\begin{aligned} W_{L}(i,j)=\left\{ \begin{array}{cc} w_{s}(i,j), &{}\quad j\in {\mathbb {N}}(x_{i})\\ 0, &{}\quad j\notin {\mathbb {N}}(x_{i}) \end{array} \right. \end{aligned}$$

(10)

Note that $\bigtriangledown _{N}u$ and $\bigtriangledown _{S}u$ are vectors which contain all non-local gradients generated by an image.

2.3 Coupled deep auto-encoder for SR

CDA transforms the SR problem into a fitting problem in the feature space. It contains three neural networks: an LR auto-encoder, an HR auto-encoder and a fully connected network. The learned LR and HR features are produced in the hidden nodes in the LR and HR auto-encoders, respectively. A fully connected neural network is constructed between the LR and the HR hidden nodes. An SR fitting function is learned from the LR feature subspace to the HR feature subspace. The fitting error is defined as

$$\begin{aligned} R_{\mathrm{DL}}=\left\| X-X_{_{\mathrm{CDA}}} \right\| _{2}^{2} \end{aligned}$$

(11)

where $X_{_{\mathrm{CDA}}}$ is the output of CDA.

Fig. 1

Reconstruction of the coupled deep auto-encoder

For an LR image, CDA firstly extracts LR features by using the LR auto-encoder. Secondly, the LR features are mapped into the HR feature subspace through the fully connection neural network. Finally, the SR image is reconstructed by decoding the HR features. In this paper, CDA is treated as the deep SR model, because it is simple to use and stable.

3 Modeling joint statistic models-guided CDA

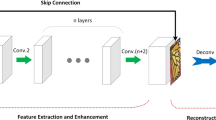
CDA is a simple and effective SR method, but the output also tends to have blurry, over-smoothed details. To overcome this limit, we add a layer to update the output of CDA. The framework is shown in Fig. 1. We firstly pre-train CDA, and then we solve the problem of single-image SR reconstruction, in which there is only one observed LR image for reconstruction. An LR image is regarded as the degeneration of downsampling and blurring from an HR image, and the generation process is formulated as

$$\begin{aligned} Y=DHX+E \end{aligned}$$

(12)

where X and Y are the HR and LR images, respectively. H denotes the blurring operator, D is the downscaling matrix, and E is the noise matrix. As we know, many SR images can be degenerated into the same LR image. It is treated as the inverse problem to estimate the HR image X for SR. We use the three above-mentioned statistic models in Sect. 2 to regularize the SR problem, which is formulated as

$$\begin{aligned} {\hat{X}}= & {} \mathop {\arg \min }_{X}\Bigg \{ \frac{1}{2} \Vert DHX-Y \Vert _{2}^{2}+\frac{1}{2}\lambda _{\mathrm{DL}} \Vert X-X_{\mathrm{CDA}} \Vert _{2}^{2}\nonumber \\&+\,\lambda _{L} \Vert (I-W_{L})X \Vert _{1} +\lambda _{\mathrm{NL}} \Vert (I-W_{\mathrm{NL}})X \Vert _{1}\Bigg \} \end{aligned}$$

(13)

Equation (13) contains four terms: fitting constraint $\frac{1}{2}\lambda _{\mathrm{DL}} \Vert X-X_{\mathrm{CDA}} \Vert _{2}^{2}$, NLTV constraint $\lambda _{\mathrm{NL}} \Vert (I-W_{\mathrm{NL}})X \Vert _{1}$, SKRTV constraint $\lambda _{L} \Vert (I-W_{L})X \Vert _{1}$ and reconstruction constraint $\frac{1}{2} \Vert DHX-Y \Vert _{2}^{2}$. This optimization problem is a TV problem, and we apply SBI [9] to solve it, which is a typical method for $l_{1}$ norm-related minimization problems. SBI can converge fast when it is used in TV-based optimization problem. The basic idea of SBI is to transform an unconstraint optimal problem into a constraint optimization problem.

3.1 SBI for joint TV regularization models

Let us consider a general optimal problem,

$$\begin{aligned} \mathop {\min }_{u}\left| J(u) \right| +H(u) \end{aligned}$$

(14)

which can be converted to a constraint optimal problem,

$$\begin{aligned} \mathop {\min }_{u}\left| d \right| +H(u) \ {\hbox {s.t.}}\ d=J(u) \end{aligned}$$

(15)

SBI is given in Algorithm 1.

Because u is decoupled from the $l_{1}$ portion of the problem, the optimization problem for $u_{k+1}$ in Line 3 is now differentiable. To solve the optimal problem in Line 4 which is coupled with the $l_{1}$ portion of the minimization problem, shrinkage operators are used to compute the optimal value of d,

$$\begin{aligned} d_{j}^{k+1}={\hbox {shrink}}\left( J(u)_{j}^{k+1}+b_{j}^{k},\frac{1}{\lambda }\right) \end{aligned}$$

(16)

where ${\hbox {shrink}}(x,\gamma )=\frac{x}{\left| x \right| }*\max (\left| x \right| -\gamma ,0)$.

According to SBI, we transform Eq. (13) to a constraint optimal problem,

$$\begin{aligned}&\mathop {\min }_{X,d_{\mathrm{NL}},d_{L}} \left( \lambda _{\mathrm{NL}} \Vert d_{\mathrm{NL}} \Vert _{1}+\lambda _{L} \Vert d_{L} \Vert _{1} +\frac{1}{2} \Vert DHX-Y \Vert _{2}^{2}\right. \\ & \left.\qquad + \frac{1}{2}\lambda _{\mathrm{DL}} \Vert X-X_{\mathrm{CDA}} \Vert _{2}^{2}\right) \nonumber \\&\quad {\hbox {s.t.}}\ d_{\mathrm{NL}}=(I-W_{\mathrm{NL}})X, d_{L}=(I-W_{L})X \end{aligned}$$

(17)

We implement line 3 of Algorithm 1 in Eq. (17), and it becomes

$$\begin{aligned} X^{k+1}= & {} \mathop {\arg \min }_{X} \Bigg ( \frac{1}{2}\left\| DHX-Y \right\| _{2}^{2}+\frac{1}{2}\lambda _{\mathrm{DL}}\left\| X-X_{\mathrm{CDA}} \right\| _{2}^{2}\nonumber \\&+\frac{1}{2}\lambda _{\mathrm{NL}}\mu \left\| d_{\mathrm{NL}}^{k}-(I-W_{\mathrm{NL}})X-b_{\mathrm{NL}}^{k} \right\| _{2}^{2}\nonumber \\&+\frac{1}{2}\lambda _{L}\mu \left\| d_{L}^{k}-(I-W_{L})X-b_{L}^{k} \right\| _{2}^{2} \Bigg ) \end{aligned}$$

(18)

According to SBI, Line 4 in Algorithm 1 becomes:

$$\begin{aligned} d_{\mathrm{NL}}^{k+1}= {{\hbox {shrink}}}\left( (I-W_{\mathrm{NL}})X^{k+1}+b_{\mathrm{NL}}^{k},\frac{1}{\mu } \right) \end{aligned}$$

(19)

$$\begin{aligned} d_{L}^{k+1}= {{\hbox {shrink}}}\left( (I-W_{L})X^{k+1}+b_{L}^{k},\frac{1}{\mu } \right) \end{aligned}$$

(20)

Next, Line 5 in Algorithm 1 becomes,

$$\begin{aligned} b_{\mathrm{NL}}^{k+1}= b_{\mathrm{NL}}^{k}+(I-W_{\mathrm{NL}})X^{k+1}-d_{\mathrm{NL}}^{k+1} \end{aligned}$$

(21)

$$\begin{aligned} b_{L}^{k+1}= b_{L}^{k}+(I-W_{L})X^{k+1}-d_{L}^{k+1} \end{aligned}$$

(22)

Equation (18) is a typical quadratic convex optimization problem; it can be solved in a closed form as,

$$\begin{aligned} X^{k+1}&= \eta \left( (DH)^\mathrm{T}Y\right) +\lambda _{\mathrm{DL}}X_{\mathrm{CDA}} \\&\quad +\,\lambda _{\mathrm{NL}} \mu (I-W_{\mathrm{NL}})^\mathrm{T}\left( b_{\mathrm{NL}}^{k}-d_{\mathrm{NL}}^{k}\right) \\ &\quad +\,\lambda _{L}\mu (I-W_{L})^\mathrm{T}\left( b_{L}^{k}-d_{L}^{k}\right) \end{aligned}$$

(23)

$$\begin{aligned} \eta= & {} \left[ (DH)^\mathrm{T}DH +\lambda _{DBN\_SR} \right. \nonumber \\&-\,\lambda _{\mathrm{NL}}\mu (I-W_{\mathrm{NL}})^\mathrm{T}(I-W_{\mathrm{NL}}) \nonumber \\&-\left. \lambda _{L}\mu (I-W_{L})^\mathrm{T}(I-W_{L}) \right] ^{-1} \end{aligned}$$

(24)

The pseudo-code of joint statistic models-guided CDA is presented in Algorithm 2. The parameters $\varepsilon$ and tol are two thresholds set by user. $\varepsilon$ is the threshold to control the fidelity. When the reconstruction error is below $\varepsilon$  the loop will stop. tol is the threshold to control the error of the solution. When the error of the solutions of the two steps before and after is below tol, the loop will stop.

4 Experimental results

4.1 Implementation details

Similar to CDA [27], we extract the Y channel of the image and perform bicubic downsampling. First, CDA is utilized to reconstruct the Y channel of SR image with a specified size. Then, the proposed joint model is utilized to generate the sharper reconstructed image until the reconstruction error of our model becomes minimum and the PSNR of reconstruction result no longer increases. The basic parameters are set as follows. In NLTV, the window size of the similar image blocks is set to $5 \times 5$, the search window size of the non-local similar image blocks is set to $11 \times 11$, and the top 20 similar image blocks are adopted as the reference reconstructed blocks of an image. In SKRTV, the search window size of image blocks is $5\times 5$ . In Algorithm 1, $\mu$ is set to 1.5. In Algorithm 2, tol is set to $1e-5$, and $\varepsilon$ is set to $5e-6$.

The parameters $\lambda _{\mathrm{NL}}$, $\lambda _{L}$, $\lambda _{\mathrm{DL}}$ are chosen as the trade-off among the regularization terms, which are determined experimentally. Actually, we firstly find a better solution of the parameter $\lambda _{\mathrm{DL}}$ when fixing $\lambda _{\mathrm{NL}}$ and $\lambda _{L}$. Later, we update the parameter $\lambda _{\mathrm{NL}}$ when fixing the parameters $\lambda _{L}$ and $\lambda _{\mathrm{DL}}$. After that, we update the parameter $\lambda _{L}$ when fixing the parameters $\lambda _{\mathrm{NL}}$ and $\lambda _{\mathrm{DL}}$. By extensive experiments, ultimately, (0.01, 0.03, 0.001) is assigned to the parameters ($\lambda _{\mathrm{NL}}$, $\lambda _{L}$, $\lambda _{\mathrm{DL}}$) for achieving the better performance of SR. The relationship between results and three parameters is shown in Fig. 2. The three-parameter settings are utilized in the following experiments. We implement our method in MATLAB R2014a. And the CDA source code is provided by the original author.

Fig. 2

Configuration of the parameters: $\lambda _{\mathrm{NL}}$, $\lambda _{L}$ and $\lambda _{\mathrm{DL}}$ for the scale factor of 2, 3 and 4. a–c The curves show how the parameter $\lambda _{\mathrm{DL}}$ affects the SR performance in terms of PSNR when fixing $\lambda _{\mathrm{NL}}=0.25$ and $\lambda _{L}=0.25$, and the PSNR value is the highest when $\lambda _{\mathrm{DL}}=0.001$. d–f The curves show how the parameter $\lambda _{L}$ affects the SR performance in terms of PSNR when fixing $\lambda _{\mathrm{NL}}=0.01$ and $\lambda _{\mathrm{DL}}=0.001$, and the PSNR value is the highest when $\lambda _{L}=0.03$. g–i The curves show how the parameter $\lambda _{\mathrm{NL}}$ affects the SR performance in terms of PSNR when fixing $\lambda _{\mathrm{DL}}=0.001$ and $\lambda _{L}=0.03$, and the PSNR value is the highest when $\lambda _{\mathrm{NL}}=0.01$

To demonstrate our model, we design following experiments. First, the parameters of our model are decided by extensive experiment results. Second, the effects of three regularization terms for SR are analyzed. Third, we also compare our model with the state-of-the-art algorithms on four benchmark datasets: Set5 [1], Set14 [28], BSD100 [18] and Urban100 [10]. Finally, we verify the effects of the joint statistic models combined with LapSRN [14] for SR.

4.2 Ablation analysis

For the convenience of description, let DL denote the deep learning regularization term, NL denote the NLTV regularization term, and L denote the SKRTV regularization term. For example, ${\hbox {CDA}}+{\hbox {DL}}$ means that CDA combined with the deep learning regularization term. The effects of the three regularization terms are investigated. We compared six SR methods: bicubic, CDA, ${\hbox {CDA}}+{\hbox {DL}}$, ${\hbox {CDA}}+{\hbox {DL}}+{\hbox {NL}}$ , ${\hbox {CDA}}+{\hbox {DL}}+L$ and ${\hbox {CDA}}+{\hbox {DL}}+{\hbox {NL}}+L$. Two common metrics PSNR and SSIM are utilized to estimate the performance of SR. Table 1 shows the comparison results for $\times 2$, $\times 3$ and $\times 4$ scaling SR on Set5.

Table 1 Quantitative comparisons: average PSNR/SSIM for scale factors of 2, 3 and 4 on Set5

In Table 1, we observe the joint statistic models-guided CDAs are effective and surpass the original CDA algorithm on Set5 for scale factors of 2, 3 and 4. Particularly, when using three models with CDA, the reconstructed results are the best. Overall, our method achieves 1.31 dB, 1.0 dB and 0.75 dB improvements on Set5 in terms of PSNR with scale factors of 2, 3 and 4, so does it in terms of SSIM.

Visual comparisons among CDA, CDA + DL, CDA + DL + NL, CDA + DL + L and CDA + DL + L + NL are illustrated in Figs. 3 and 4. Here, Fig. 3 shows the visual comparison of the six SR methods on Butterfly image for a scale factor of 3. Figure 4 shows the visual comparison of the six SR methods on Woman for a scale factor of 4. The largest PSNR and SSIM are signed in bold.

Fig. 3

The comparison of visual effects among CDAs with different regularization terms for $\times$ 3 scaling SR on Butterfly of Set5

Fig. 4

The comparison of visual effects among CDAs with different regularization terms for $\times$ 4 scaling SR on Woman of Set5

4.3 Comparisons with the state-of-the-art SR methods

We compare our model (CDA+DL+NL+L) with the state-of-the-art SR methods: A+ [22], SRCNN [5] , SelfExSR [10], SCN [24], CDA [27] and VDSR [12]. For scale factors of 2, 3 and 4, the results of A+, SRCNN and SelfExSR are from the published papers, and we run the public available codes of SCN, CDA and VDSR and get their SR results. We carry out extensive experiments on four benchmark datasets: Set5, Set14, BSD100 and Urban100. To evaluate the quality of reconstructed HR images, PSNR and SSIM are used as criteria.

Table 2 Quantitative comparisons on the average PSNR and SSIM

Table 2 shows the comparison between our method and the state-of-the-art SR methods with average PSNR and SSIM. We observe that our method achieves satisfactory results on Set5, especially for the scale factor of 2; the PSNR and SSIM obtained by our method are the highest. For the scale factors of 3 and 4, VDSR achieves the best PSNR and our method ranks the second. On Set14, our method achieves the best PSNR, and SelfExSR, SRCNN and VDSR get the second best PSNR for the scale factors of 2, 3 and 4, respectively. CDA is superior to our method in terms of SSIM on Set14. On BSD100, our method achieves the best PSNR and SSIM. On Urban100, our method gets the second best PSNR and is inferior to VDSR. Our method achieves the second best SSIM and is inferior to CDA method for the scale factors of 2, 3 and 4. The PSNR obtained by our method is higher, on average, by $+1.02$ dB, $+1.05$ dB, $+0.88$ dB, $+1.28$ dB than CDA on Set5, Set14, BSD100 and Urban100, respectively. The results demonstrate that our method is effective for SR.

From Figs. 5, 6, 7, 8, 9 and 10, we show the visual comparison between our method and the other four SR methods: bicubic, SCN, CDA and VDSR on Set5, Set14, BSD100 and Urban100 for scale factors of 2, 3 and 4 SR images. The best results are marked in bold.

Table 3 Quantitative comparisons: average PSNR/SSIM for a scale factor of 4 on datasets Set5

Fig. 5

Qualitative comparison of $\times 2$ SR on Baby of Set5

Fig. 6

Qualitative comparison of $\times 3$ SR on Bird of Set5

Fig. 7

Qualitative comparison of $\times 3$ SR on Comic of Set14

Fig. 8

Qualitative comparison of $\times 4$ SR on Zebra of Set14

Fig. 9

Qualitative comparison of $\times 4$ SR on an example image of BSD100

Fig. 10

Qualitative comparison of $\times 3$ SR on an example image of Urban100

4.4 Extension: joint statistic models-guided LapSRN

Finally, we combine joint statistic models with LapSRN [14]. LapSRN is constructed by cascading several pyramid deep networks and achieves the best PSNR and SSIM among the above-mentioned methods in Sect. 4.3. As expected, the experimental results show that the average PSNR and SSIM of LapSRN + DL + L + NL for a scale factor of 4 surpass those of the original LapSRN algorithm. In Table 3, we show the average PSNR and SSIM for a scale factor of 4 on the Set5, and LapSRN+DL+L+NL achieves the gain of $+\,0.5$ dB and $+\,0.005$ compared with the original LapSRN algorithm.

5 Discussion and conclusion

In this work, we propose a unified framework encapsulating the reconstruction constraint, fitting constraint, non-local similarity constraint and the steering kernel regression prior terms with CDA. Then, a split Bregman iteration algorithm is developed for optimizing the process. Experimental results on four benchmark datasets show CDA unified with joint statistic models is effective to improve SR performance. The extensive experiments also demonstrate that the joint statistic model is helpful to another deep SR model, LapSRN. Quantitative and qualitative results on four benchmark datasets show that our proposed model obtains the satisfying results in terms of quality and vision.

However, our method has some limitations. Some particles come into being on the edge of an SR image which can be seen when it is enlarged enough. Moreover, our method is computed in a pipeline way rather than in an end-to-end way. In future work, we will apply regularization constraints of NLTV and SKRTV to the deep SR networks in an end-to-end way and further improve the SR performance.