1 Introduction

The quality of electric power has become a pressing concern for electric utilities and their customers over the last decade. This is primarily due to the use of solid-state devices in power control resulting in voltage and current waveform distortions; voltage quality disturbances such as sags, swells, and interruptions; oscillatory and impulsive transients; multiple voltage notches due to solid-state converter switching; generation of harmonics; and the use of renewable energy sources. Therefore, power quality event detection and classification assume considerable importance in determining the sources of these disturbances, thereby making it possible for taking appropriate actions in mitigating them. In the past decade, researchers analyzed the power quality issues with the increasing amount of measurement data from power quality monitors. The time of occurrence and the frequency of power quality disturbances [1–4] are unknown, so the monitoring is often required over an extended period. Further, the power quality disturbances can appear simultaneously as in realistic power networks there are multiple sources of different disturbing events. Till date, most of the power quality analysis techniques have only considered a few power quality simultaneous disturbances namely voltage sags with harmonics, voltage swells with harmonics, and harmonics with interruptions. However, it is not enough in a realistic application scenario when there is a possibility of the occurrences of several simultaneous disturbances creating a more adverse impact on the power distribution network. Thus, it will be desirable to evolve a methodology which will be able to analyze other combinations of two or more power signal disturbances.

According to signal processing point of view, the nonstationary power signal disturbance analysis could be divided into groups such as detection, classification, parameter estimation, and localization. Several authors have presented different signal processing techniques based on discrete wavelet transform (DWT) [5–7], S-Transform (ST) [8–10], in order to identify the type of disturbance present in the power signal more effectively. By this method, it is possible to extract important information from a disturbance signal and determine the type of disturbance that has caused a power quality problem to occur. Although ST is a powerful tool for power signal disturbance assessment, it involves high computational cost. This paper, therefore, considers a computationally simpler technique, which is able to detect, localize, and produce features for robust classification of power signal disturbance events. The proposed procedure is based on a cumulative sum average filter that averages input samples and identifies the multiple changes in the nonstationary power quality waveforms. The filter computes the sum of one cycle data of the original signal. Using this filter, several relevant features such as standard deviation, variance, mean, max, min, entropy, and energy are extracted from the nonstationary power signal data. After the features are extracted, a classification technique is used to classify the data, thereby identifying the nature of the power signal disturbance patterns.

In recent years, the radial basis function neural network (RBFNN) is extensively used for classification and pattern recognition [11–13] in a variety of real-world engineering problems including power quality events. The RBFNN is a feedforward neural network which is faster than the multilayer perceptron (MLP) network in terms of speed of convergence and accuracy. The wavelet neural network (WNN) [14, 15] is another powerful tool to accurately identify various types of power signal disturbances by using time- and frequency-localized nonlinear wavelet basis functions. However, it is difficult to find the proper orthogonal or nonorthogonal wavelet basis functions and to determine the optimal number of hidden layer nodes for the WNN. Another alternative to WNN is the local linear wavelet neural network (LLWNN) [16], where the connection weights between the hidden units and output units are replaced by a local linear combination of weighted inputs to remove redundant nodes in the hidden layer. The advantage of this type network is that the number of neurons in the hidden layers is equal to the number of inputs in the input layer. This architecture thus dispenses the arbitrary choice of neurons in the hidden layer as in the cases of traditional MLP and RBFNNs. However, it suffers from slow convergence speed due to the use of wavelet basis functions in the network. Therefore, in this paper, we have considered an alternative type of RBFNN known as LLRBFNN [17] network in order to take the advantage of the local capacity of the radial basis functions for producing significantly accurate classification. Earlier, LLRBFNN trained with particle swarm optimization (PSO) technique provides good result in financial forecasting in comparison with LLWNN [17]. TLBO algorithm is a new population-based optimization technique proposed in 2011 by Rao et al. [18–24]. Earlier, TLBO algorithm has been applied in constrained mechanical design optimization [21], heat exchangers [22], thermoelectric cooler [23], etc., producing good results.

Therefore, in this paper, the TLBO algorithm is used to train the weights of the LLRBFNN for the classification of power quality events. Also, the optimization of the weights of LLRBFNN model using PSO algorithm is presented in this paper to provide a performance comparison between the TLBO and PSO algorithms. Further to get faster convergence speed and improved classification accuracy, we propose a modified TLBO-based LLRBFNN model for the classification of multiple power signal disturbances. Another powerful learning paradigm is the use of ELM [25–29] for both regression- and classification-type problems. ELM is a much wider type of generalized SLFN (single hidden layer feedforward neural network) whose input weights and offsets of the hidden layer are chosen in a random manner and require no tuning. Architecturally, the ELM is different from traditional learning algorithms for a neural type of SLFN and aims to reach not only the smallest training error but also the smallest norm of output weights. Also, ELM has less computational complexity and provides a unified solution to different practical applications such as regression, binary, and multiclass classifications. It differs from the widely used LS-SVM (least square support vector machines) technique which is computationally far more complex than ELM and necessitates the use of different variants for different problems. On the other hand, ELM provides a unified approach and has only one formulation for different problem types. The ELM completes the whole computation process at once and generates a unique optimal solution without using iterations which provides an ease of parameter selection and fast learning speed. Since practical simultaneous power quality event classification uses a large signal waveform database, it is proposed in this paper to examine the performance of the ELM-trained LLRBFNN classifier in comparison with the modified TLBO-trained LLRBFNN classifier.

This paper has been organized as follows: Sects. 2 and 3 present the cumulative sum average filter (CUSAF) [30–32] for multiple power signal disturbances detection and feature extraction, respectively. Section 4 presents modified TLBO-based LLRBFNN learning, while in Sect. 5, the ELM algorithm is presented. Section 6 outlines the TLBO procedure, and results and discussion are presented in Sect. 7. Laboratory test setup and implementation procedure are described in Sect. 8, while concluding remarks are given in Sect. 9 followed by references.

2 Cumulative sum average filter (CUSAF) for multiple power signal disturbances

The Fourier transforms (FT) and its variants such as STFT (short-time Fourier transform) have been used for power quality assessment without much success. In contrast to Fourier transform-based technologies, the wavelet transform uses short windows at high frequencies and long windows at low frequencies. The poor concentration of energy from wavelet transform leads to ST. The computational complexity of ST involves long calculation time even for short data window. To process large volumes of power signal data, it becomes time-consuming and increases cost overhead. The filter designed here is called cumulative sum average filter (CUSAF) [30–32] which is simple to implement and gives better localization of nonstationary multiple power disturbance signals. The CUSAF averages the input samples and localizes high-frequency components of the nonstationary signal. For a given set of voltage signal samples s(k), the CUSAF can be represented mathematically as

$$ s_{\text{SUM}} (k) = \sum\limits_{{l = k - {\text{NS}} + 1}}^{K} {s(l)} $$
(1)

where k = sample count; NS = number of samples per cycle; K = total number of samples considered for the study, l = an index.

Equation (1) can be written in recursive form as

$$ s_{\text{SUM}} \left( k \right) = s_{\text{SUM}} \left( {k - 1} \right) + s\left( k \right) - s\left( {k - {\text{NS}}} \right) $$
(2)

For sample variation, Eq. (2) can be written as

$$ s_{\text{SUM}} \left( {k_{\text{p}} } \right) = s_{\text{SUM}} \left( {k_{\text{p}} - 1} \right) + s\left( {N_{\text{s}} + k_{\text{p}} } \right) - s\left( {k_{\text{p}} } \right) $$
(3)
$$ {\text{Let}}\;s\left( {N_{\text{s}} + k_{\text{p}} } \right) = g_{\text{sum}} $$
(4)

where N s is the starting sample position, k p is the number of sample variations, and g sum is an array where the filtered data are to be stored.

The amplitude response of the filter is given by

$$ H\left( {{\text{e}}^{j\omega } } \right) = N_{\text{s}} {\text{e}}^{{j\omega \left( {N_{\text{s}} + 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{\text{s}} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] $$
(5)

For multiple sample variation, the filter equation can be written as

$$ \begin{array}{*{20}c} {s_{{1{\text{SUM}}}} \left( {k_{\text{p}} } \right) = s_{1} \left( {k_{{{\text{p}}_{{_{1} }} }} - 1} \right) + s_{1} \left( {(N_{{{\text{s}}_{1} }} ) + k_{{{\text{p}}_{{_{1} }} }} } \right) - s_{1} \left( {k_{{{\text{p}}_{{_{1} }} }} } \right)} \\ {\vdots} \\ {s_{{1{\text{SUM}}}} \left( {k_{{{\text{p}}_{n} }} } \right) = s_{1} \left( {k_{{{\text{p}}_{{_{n} }} }} - 1} \right) + s_{1} \left( {(N_{{{\text{s}}_{n} }} ) + k_{{{\text{p}}_{n} }} } \right) - s_{1} \left( {k_{{{\text{p}}_{n} }} } \right)} \\ \end{array} $$
(6)

As in Eq. (4), let

$$ s_{1} (N_{{{\text{s}}_{n} }} + k_{{{\text{p}}_{n} }} ) = g_{{1{\text{sum}}}} $$
(7)

where \( N_{{{\text{s}}_{n} }} = N_{{{\text{s}}_{1} }} ,N_{{{\text{s}}_{2} }} \ldots \) sample variations, and g 1sum is an array where the filtered data are to be stored.

The amplitude response for the multiple sample variation of the filter is given by

$$ H_{1} \left( {{\text{e}}^{j\omega } } \right) = N_{{{\text{s}}_{n} }} {\text{e}}^{{j\omega \left( {N_{{{\text{s}}_{n} }} + 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{{{\text{s}}_{n} }} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] $$
(8)

2.1 Multiple positional variations in nonstationary power signal disturbance

For positional variation [10], the Eq. (2) can be written as

$$ s_{\text{SUM}} \left( {k_{\text{p}} } \right) = s_{\text{SUM}} \left( {k_{\text{p}} - 1} \right) + s\left( {\left( {N_{\text{p}} - N_{\text{s}} } \right) + k_{\text{p}} } \right) - s\left( {k_{\text{p}} } \right) $$
(9)
$$ s\left( {\left( {N_{\text{p}} - N_{\text{s}} } \right) + k_{\text{p}} } \right) = g_{\text{sum}} $$
(10)

where N s is the starting point of variation, and N p is the end point of variation.

Similarly, the amplitude response for the positional variation in the filter is given by

$$ H_{2} \left( {{\text{e}}^{j\omega } } \right) = N_{\text{L}} {\text{e}}^{{ - j\omega \left( {N_{\text{L}} - 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{\text{L}} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] $$
(11)

where N L = N p − N s

For multiple positional variation, the filter equation can be written as

$$ \begin{array}{c} {s_{{2{\text{SUM}}}} \left( {k_{\text{p}} } \right) = s_{{2{\text{SUM}}}} \left( {k_{{{\text{p}}_{1} }} - 1} \right) + s_{2} \left( {\left( {N_{{{\text{p}}_{1} }} - N_{{{\text{s}}_{1} }} } \right) + k_{{{\text{p}}_{1} }} } \right) - s_{2} \left( {k_{{{\text{p}}_{1} }} } \right)} \\ {\vdots} \\ \end{array} $$
(12)
$$ s_{{2{\text{SUM}}}} \left( {k_{{{\text{p}}_{n} }} } \right) = s_{{2{\text{SUM}}}} \left( {k_{{{\text{p}}_{n} }} - 1} \right) + s_{2} \left( {\left( {N_{{{\text{p}}_{n} }} - N_{{{\text{s}}_{n} }} } \right) + k_{{{\text{p}}_{n} }} } \right) - s_{2} \left( {k_{{{\text{p}}_{n} }} } \right) $$
(13)
$$ {\text{Let}}\;s_{2} ((N_{{{\text{p}}_{n} }} - N_{{{\text{s}}{}_{n}}} ) + k_{{{\text{p}}_{n} }} ) = g_{{2{\text{sum}}}} $$
(14)

where \( N_{{{\text{s}}_{n} }} = N_{{{\text{s}}_{1} }} ,N_{{{\text{s}}_{2} }} \ldots \) sample variations, and g 2sum is an array where the filtered data are to be stored.

The amplitude response for the multiple positional variations is given by

$$ H_{3} \left( {{\text{e}}^{j\omega } } \right) = N_{{{\text{L}}_{n} }} {\text{e}}^{{ - j\omega \left( {N_{{{\text{L}}_{n} }} - 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{{{\text{L}}_{n} }} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] $$
(15)

where \( N_{{{\text{L}}_{n} }} = N_{{{\text{p}}_{n} }} - N_{{{\text{s}}_{n} }} \) and \( N_{{{\text{s}}_{n} }} = N_{{{\text{s}}_{1} }} ,N_{{{\text{s}}_{2} }} \ldots \) starting positions, \( N_{{{\text{p}}_{n} }} = N_{{{\text{p}}_{1} }} ,N_{{{\text{p}}_{2} }} \ldots \) end positions, and g sum is an array where the filtered data are to be stored.

2.2 Combined multiple sample variations with positional variation in nonstationary power signal disturbances

Combining the Eqs. (6) and (13), we get

$$ S_{\text{SUM}} = s_{{1{\text{SUM}}}} \left( {k_{{{\text{p}}_{n} }} } \right) + s_{{2{\text{SUM}}}} \left( {k_{{{\text{p}}_{n} }} } \right) $$
(16)

and

$$ G_{\text{sum}} = g_{{ 1 {\text{sum}}}} + g_{{2{\text{sum}}}} $$
(17)

The combined amplitude response is given by

$$ H\left( {{\text{e}}^{j\omega } } \right) = N_{{{\text{s}}_{n} }} {\text{e}}^{{j\omega \left( {N_{{{\text{s}}_{n} }} + 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{{{\text{s}}_{n} }} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] + N_{{{\text{L}}_{n} }} {\text{e}}^{{ - j\omega \left( {N_{{{\text{L}}_{n} }} - 1} \right)/2}} \left[ {\frac{{\sin c\left( {\omega N_{{{\text{L}}_{n} }} /2} \right)}}{{\sin c\left( {\omega /2} \right)}}} \right] $$
(18)

The CUSAF averages the number of input samples on a cycle-to-cycle basis in a recursive manner and is capable of detecting changes in the power network disturbance signals.

3 Application of CUSAF to nonstationary power signal disturbances

The program for the multiple power disturbance signals such as position and sample variations is written using MATLAB software. Figure 1 shows the localization of different types of multiple nonstationary power signal disturbances using cumulative sum average filter. Referring to Fig. 1a for the case of multiple sample variations, the different notches occur at the 95th, 140th, 170th, and spike occurs at the 340th, 370th, 450th sample points, respectively. After the application of cumulative sum average filter, it is observed that the similar samples in the signal are zero from the beginning of the disturbance and after the completion of the disturbance, and this localizes the fault prominently.

Fig. 1
figure 1figure 1figure 1

(Combined multiple positional and sample variation) Localization of power network disturbance signals using cumulative sum average filter. a Localization of multiple spikes + notch. b (Multiple positional variation) Localization of multiple transient. c Localization of transient + notch. d Localization of multiple transient + notch. e Localization of transient + notch + spike. f Localization of transient + sag. g Localization of voltage sag + harmonic using moving sum average filter. h Localization of voltage swell + harmonic using moving sum average filter

Full size image

In the case of multiple positional variations, for example in the multiple transient case, the first instance started at 129th sample and second instance started at 250th sample, the transient lasts for 60 samples in both the instances. It is observed that after application of cumulative sum average filter from first sample to the starting of transient is zero and after 190th sample all the sample values are zero up to 249th sample and after 311th sample to end of the signal all the sample values are zero as the filter has been designed in one cycle back fashion. For the case of combined multiple positional and sample variation, the transient for first instance started at 129th sample and lasts for 60 samples, second instance started at 250th sample and lasts for 60 samples, and the spike occurs at 340th, 370th, and 450th sample. After application of cumulative sum average filter, it is observed that the similar samples are zero, and thus, multiple faults are localized prominently.

3.1 Feature extraction

The fundamental sinusoidal signal is taken to be of 50 Hz, and it is sampled at 64 samples per cycle with a sampling frequency of 3.2 kHz (50 × 64). Ten categories of multiple power signal disturbances making a total of (200 × 10) 2000 signals are generated using the formulas given in Table 1 from which different statistical features such as standard deviation, mean, max, energy, and entropy have been extracted. Table 2 provides parametric equations for the extraction of the above-mentioned features (shown in Table 3) from the signal samples [x 1, x 2, …, x j , … x N ] obtained from the change detection filter with the help of the cumulative sum average technique. The total number of positional and sample variation disturbance nonstationary power signals used for classification is given below:

Table 1 Power signal disturbance models
Full size table
Table 2 Parametric equations for feature extraction
Full size table
Table 3 Extracted features for multiclass classification
Full size table
  1. 1.

    Multiple notch

  2. 2.

    Multiple spike + multiple notch

  3. 3.

    Multiple transient

  4. 4.

    Transient + multiple notch

  5. 5.

    Swell + multiple spike

  6. 6.

    Sag + multiple notch

  7. 7.

    Transient + notch + spike

  8. 8.

    Sag + harmonics

  9. 9.

    Swell + harmonics

  10. 10.

    Sag + harmonics

The seven extracted features are given as inputs to the TLBO-based LLRBFNN network for classification. A block diagram for multiclass classification of the power signal disturbance events is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram for the power disturbance signal classification

Full size image

4 Proposed TLBO-based LLRBFNN model

In LLRBFNN architecture, a local linear model replaces the connection of weights between the hidden layer and output layer of conventional RBFNN [19]. In comparison with RBFNN (radial basis function neural network), the LLRBFN requires less number of neurons than the RBFNN to approximate the same nonlinear system. In LLRBFNN, the input and number of hidden layer nodes are equal which reduces overall node requirements. The LLRBFN becomes more efficient network because the ability of approximation has been increased by placing a local linear model instead of the hidden layer units. Different optimization algorithms such as PSO with hunter particle [19] and GA [27] have been applied for training the network to have classification accuracy. In this paper, we have proposed a recently developed TLBO-based training algorithm to the LLRBFNN network. Further, the TLBO algorithm has been modified and applied for training to have faster convergence speed and classification accuracy.

4.1 Model description with TLBO-based training

The architecture of the proposed TLBO-based LLRBFNN training is shown in Fig. 3.

Fig. 3
figure 3

Modified local linear RBF neural network

Full size image

In Fig. 3, x = [x 1, x 2, x 3… x n ] are inputs (features); g 1(x), g 2(x), …, g n (x) are the Gaussian activation functions in the hidden units. The hidden layer of the LLRBFNN model takes the local linear weight and computes the output. The activation function of the kth hidden neuron is defined by

$$ g_{\text{k}} \left( x \right) = {\text{e}}^{{\left( { - \frac{{\left\| {x - c_{k} } \right\|^{2} }}{{2\sigma_{k}^{2} }}} \right)}} ,\quad k = 1, 2, \ldots , n $$
(19)

where h k (x) is the activation function of kth node, σ 2 k is the parameter which controls the smoothness of the activation function, c k is the center of the hidden node, and ‖x − c k ‖ indicates the Euclidean distance between the inputs and the function center. The output from the hidden layer kth neuron is obtained by multiplying the activation function of the node with a weighted linear combination of the inputs as

$$ h_{k} (x) = W_{k} g_{k} (x) $$

In expanded form, the output of the kth hidden layer node is therefore obtained as

$$ h_{k} (x) = W_{k} g_{k} (x) = (w_{k0} + w_{k1} x_{1} + w_{k2} x_{2} \ldots w_{kn} x_{n} ).{\text{e}}^{{\left( {\frac{{ - \left\| {\left( {x_{{}} - C_{k} } \right)} \right\|^{2} }}{{2\sigma_{k}^{2} }}} \right)}} $$
(20)

The weight matrix associated with an output node m is thus written as

$$ W_{m} = \left[ {\begin{array}{*{20}c} {W_{m1} } \\ {W_{m2} } \\ \ldots \\ \ldots \\ {W_{mn} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w_{m10} } & {w_{m11} } & \ldots & \ldots & {w_{m1n} } \\ {w_{m20} } & {w_{m21} } & \ldots & \ldots & {w_{m2n} } \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {w_{mn0} } & {w_{mn1} } & \ldots & \ldots & {w_{mnn} } \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} 1 \\ {x_{1} } \\ {x_{2} } \\ \ldots \\ {x_{n} } \\ \end{array} } \right] $$
(21)

The output at the mth node of the output layer is given by

$$ y_{m} = \sum\limits_{k = 1}^{n} {\beta_{mk} h_{k} (x)} ,\quad m = 1,2, \ldots ,M $$
(22)

The next section describes another powerful approach for learning the parameters of the LLRBFNN based on ELM platform for multiclass power signal disturbance pattern recognition.

5 Extreme learning machine (ELM)

ELM is a recently introduced learning algorithm for SLFNs in which the input weights and biases are chosen randomly (weights of connections between the input variables and neurons in the hidden layer) and require no tuning. ELM not only has the capability of extremely fast learning and testing speed and exhibits smallest training error and smallest norm of output weights. Also, ELM has a similar cost function like the LS-SVM but with milder constraints and has been used for the feedforward neural networks, RBFNN, and SVMs. Thus, a robust procedure for both regression and classification results by using ELM approach for updating the weight parameters of the LLRBFNN between the hidden layer and the output layer.

The main advantage of ELM is that the hidden layer of SLFNs can work with a wide range of activation functions including piecewise continuous functions [31]. With a given D-dimensional input data set and N-dimensional hidden layer nodes characterized by a feature space H, the output function of ELM for SLFN can be represented as:

$$ f_{N} (x) = \sum\limits_{i = 1}^{N} {\beta_{i} h_{i} (x)} $$
(23)

and

$$ \beta = [\beta_{1} \, \beta_{2} \ldots \beta_{N} ]^{T} $$
(24)

where h i (x) is the activation function of hidden layer, and β is the weight vector connecting the hidden layer neurons to output layer neuron. If the hidden layer neurons are of the local radial basis function type, the output row vector of the hidden layer is obtained as a function of the inputs as

$$ h(x) = [h_{1} (x),h_{2} (x), \ldots ,h_{n} (x)] $$
(25)

Thus, the hidden layer output matrix is given by the H matrix is obtained as

$$ H = \, \left[ {\begin{array}{*{20}c} {h_{1} (x_{1} )} & {h_{2} (x_{1} ) \ldots } & {h_{n} (x_{1} )} \\ \vdots & {} & {} \\ {h_{1} (x_{n} )} & {h_{2} (x) \ldots } & {h_{n} (x_{n} )} \\ \end{array} } \right] $$
(26)

Equation (25) can be written as

$$ Y = H\beta = T $$
(27)

The training error and the norm of the output weights are minimized by using ELMMinimize ‖\( ||H\beta - T||^{2} \quad {\text{and}}\quad ||\beta || \) to yield

$$ \beta = H^{\varPsi } T = (H^{T} H)^{ - 1} H^{T} $$
(28)

where H Ψ is the Moore–Penrose generalized inverse of matrix H, and T is the target.

The computation of the weight vector of the ELM given in Eq. (28) is done using all the data samples at a time.

5.1 Multiclass ELM classifier output function for classification

Since ELM can approximate any target continuous functions, the output of the ELM classifier Hβ can be as close to the class label of the input data. Thus, in a multiclass classification problem using ELM with a single-output node, the class label closer to the output value is considered to be the predicted class label of the input data. In this case, the classification problem for the proposed constrained-optimization-based ELM (this classification will be termed as ELM1) with a single-output node can be formulated as

$$ {\text{Minimize}}\;L_{\text{P}} = \frac{1}{2}\left\| \beta \right\|^{2} + \frac{1}{2}C\sum\limits_{i = 1}^{N} {\xi_{i}^{2} } ,\quad {\text{subject}}\;{\text{to}}\;h\left( {x_{i} } \right)\beta = t_{i} - \xi_{i} , \quad i = 1, 2, \ldots , N $$
(29)

where C is a parameter to be chosen appropriately, ξ i and t i are the output and the target values at the ith instant; N = number of neurons in the hidden layer. In the case where the training samples are small in number, the above minimization process yields

$$ \beta = H^{T} \left( {\frac{I}{C} + HH^{T} } \right)^{ - 1} T $$
(30)

The output function for the ELM classifier is given by

$$ f(x) = h(x)H^{T} \left( {\frac{I}{C} + HH^{T} } \right)^{ - 1} T $$
(31)

where h(x) is the hidden layer row vector and is obtained as and

$$ h(x) = [h_{1} (x) \, h{}_{2}(x) \ldots h_{i} (x) \ldots h_{\text{L}} (x)] $$
(32)
$$ h{}_{i}(x) = w_{i0} + w_{i1} x_{1} + w_{i2} x_{2} \ldots w_{in} x_{n} ).{\text{e}}^{{\left( {\frac{{ - \left\| {\left( {x - C_{n} } \right)} \right\|^{2} }}{{2\sigma_{n}^{2} }}} \right)}} $$
(33)

Another alternative approach is to consider that there is m number of output nodes pertaining to m-class patterns to be classified. If p signifies the class label of a given set of feature vectors, then the target output vector for the m-nodes becomes t i  = [0, 0, 0…, 1, 0, 0, 0…0]T, and only the pth will have value equal to 1 and all other elements are chosen to be zeroes. In general, the target output for m classes (Fig. 4) is given by

$$ T = \left[ \begin{aligned} t_{1}^{T} \hfill \\ t_{2}^{T} \hfill \\ \vdots \hfill \\ t_{N}^{T} \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}l} {t_{11} } \hfill & \ldots \hfill & {t_{1m} } \hfill \\ {t_{21} } \hfill & \ldots \hfill & {t_{2m} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {t_{N1} } \hfill & \ldots \hfill & {t_{Nm} } \hfill \\ \end{array} } \right] $$
(34)

Since seven classes of power network signals are considered for classification, the target vector becomes

$$ T = {\text{diag}} . { }[1 \, 1 \, 1 \, 1 \, 1 \, 1 \, 1] $$
(35)
Fig. 4
figure 4

Multiclass classification with more than one output neuron using ELM

Full size image

The following optimization equation is solved to train the ELM for multiclass classification (ELMM):

$$ {\text{Minimize}}\;L_{P} = \frac{1}{2}\left\| \beta \right\|^{2} + \frac{1}{2}C\sum\limits_{i = 1}^{N} {\xi_{i}^{2} } ,\quad \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{m} {\lambda_{i,j} } \left( {h\left( {x_{i} } \right)\beta_{j} - t_{i,j} + \xi_{i,j} } \right)} $$
(36)

where \( \beta = [\beta_{1} ,\beta_{2} , \ldots ,\beta_{m} ] \), and β j represents the vector of weights linking the hidden layer to the jth output node. Thus, the output function of the multiclass classifier is obtained as

$$ f_{i} (x) = h(x)H^{T} \left( {\frac{I}{C} + HH^{T} } \right)^{ - 1} T_{i} $$
(37)

where

$$ T_{i} = [t_{i1} , \, t_{i2} , \ldots ,t_{im} ]^{T} $$
(38)

In a multiclass classification, the number of output nodes is equal to m (m > 1), and in such a case, the predicted class label of a given testing sample is the index number of the output node having the highest output value. Thus, the class label of x is given by

$$ {\text{Label}}\left( x \right) = \arg .{\text{Max}}\left( {f_{i} \left( x \right)} \right),\quad i = 1, 2, \ldots , m $$

However, for large number of samples particularly when the tested system has a large dataset, the value of β is given by

$$ \beta = CH^{T} \xi ,\quad {\text{and}}\quad \xi = \frac{1}{C}(H^{T} )^{\varPsi } \beta $$
(39)

and ξ = [ξ 1, ξ 2, …, ξ N ]. Finally, the value of β is obtained as

$$ \beta = H^{T} \left( {\frac{I}{C} + H^{T} H} \right)^{ - 1} H^{T} T $$
(40)

For the ELM classifier, the following equation is used:

$$ f(x) = h(x)H^{T} \left( {\frac{I}{C} + H^{T} H} \right)^{ - 1} H^{T} T $$
(41)

However, an online formulation for ELM for classification known as OS-ELM (online sequence ELM) is given in [29] using each new observation or chunk of observations as

$$ \beta (k + 1) = \beta (k) + P(k + 1)H^{T} (k + 1)[\beta (k + 1) - H(k + 1)\beta^{T} ] $$
(42)
$$ P(k + 1) = P(k) - P(k)H^{T} (k + 1)[I + H(k + 1)P(k)H^{T} (k + 1)]^{ - 1} H(k + 1)P(k) $$

and P(k + 1) = [K(k + 1)]−1, I is an unity matrix of appropriate dimension.

The initial values are obtained using the Moore–Penrose generalized inverse as follows:

$$ \beta (0) = \left[ {\frac{I}{C} + H^{T} (0)H(0)} \right]^{ - 1} H^{T} (0)T(0) $$
(43)
$$ K(0) = H^{T} (0)H(0) $$
(44)

For classification power signal disturbances, the seven features are used as input to the LLRBFNN by using ELM classification algorithm. The weight parameters in the hidden layer are randomly chosen in the range of −1 to +1. The value of C is selected to be equal to 0.5. To study the convergence characteristic of the ELM classifier for power disturbance signals, the objective function to be minimized is chosen as

$$ {\text{Mean}}\;{\text{Square}}\;{\text{Error}}\;{\text{MSE}} = \frac{1}{n}\sum\limits_{k = 1}^{n} {\left( {D_{k} - y_{k} } \right)}^{2} $$
(45)

where “D k ” is the desired vector, y k is the output of the model, and n is the number of data. Another learning scheme used for the LLRBFNN is the teaching–learning-based optimization technique, which is simple to implement for multiclass pattern recognition of power quality disturbances. The next section describes the TLBO algorithm for both the teacher phase and learner phase.

6 Weight update using TLBO algorithm

TLBO algorithm is the recently developed population-based optimization technique applied for mechanical design optimization problems. Teaching–learning-based optimization (TLBO) [20, 21] is basically divided into two parts: The first part is known as the “teacher phase,” while the second part is known as the “learner phase.” The “teacher phase” means learning from the teacher, and the “learner phase” means learners learn through the interaction between themselves.

6.1 Teacher phase

In the TLBO method, the teacher teaches the subject according to his capability and tries to enhance the ability of understanding of all learners to the level of his knowledge in the class, which is practically not possible. Thus, the teacher can only improve the mean level of the learners in a class depending on the capability of the learners. The procedure as to how the teacher improves the mean level of the learners follows a random process depending on different factors such as mean and teaching factor. In this paper, the TLBO technique is applied to train the weights of the LLRBFNN. In the teacher phase, the teacher tries to move the mean M i toward his/her own knowledge level, and so the new mean is designated as M new.

Assuming “W n ” be the number of weights and “n” is the number of learners, the best learner W best i is designated as the teacher in the subject i.

The teaching process is as follows:

$$ W_{i}^{\text{best}} = M_{\text{new}} $$
(46)

The difference between the two mean is given by

$$ D_{f} = {\text{rand}}\left( {W_{i}^{\text{best}} - T_{f} \times M_{i} } \right) $$
(47)

where T f is the teaching factor that decides the value of mean to be changed, and in this program, the value of T f is chosen as 2, and rand provides random number between 0 and 1.

Now adding the difference to the current solution, the update equation becomes:

$$ W_{i}^{\text{new}} = W_{i}^{\text{old}} + {\text{rand}}\left( {W_{i}^{\text{best}} - T_{f} \times M_{i} } \right) $$
(48)

where M i  = mean of the population columnwise, which will give the mean for the particular subject.

Now considering \( M_{{i,{\text{new}}}} = \frac{{W_{i}^{\text{best}} + W_{i}^{\hbox{min} } }}{2} \), and substituting M i  = M i,new in the above Eq. (48), the Eq. (25) becomes

$$ W_{i}^{\text{new}} = W_{i}^{\text{old}} + {\text{rand}}\left( {W_{i}^{\text{best}} - T_{f} \times M_{{i,{\text{new}}}} } \right) $$
(49)

By considering M i,new in the above equation, we do not need to compute the mean value of population in each iteration and the diversity of population increases, because the new mean value M i,new will be different for each individual.

To have fast convergence speed, a new exponential factor \( P_{f} = 0.9 - \exp \left( { - \frac{{W_{i}^{\text{best}} - W_{i}^{\hbox{min} } }}{2}} \right) \) is introduced in the update equation, hence Eq. (49) becomes

$$ W_{i}^{\text{new}} = P_{f} W_{i}^{\text{old}} + {\text{rand}}\left( {W_{i}^{\text{best}} - T_{f} \times M_{{i,{\text{new}}}} } \right) $$
(50)

When the learner finishes learning from the teacher, Eq. (50) is updated, and the solution is accepted provided it is the optimal solution.

6.2 Learner phase

Learners put their efforts to increase their capability of understanding by interaction with each other. A learner learns new knowledge if the other learner has more knowledge than him.

Randomly select two learners W i and W j , where i ≠ j

If objfun(W i ) < objfun(W j ), then the update equation is given by

$$ W_{i}^{\text{new}} = P_{f} W_{i}^{\text{old}} + {\text{rand}}\left( {W_{i} - W_{j} } \right) $$
(51)

Else

$$ W_{i}^{\text{new}} = P_{f} W_{i}^{\text{old}} + {\text{rand}}\left( {W_{j} - W_{i} } \right) $$
(52)

End ifAccept W new i if it gives a better solution.

6.3 Implementation of TLBO algorithm for weight optimization

  • Step 1: Initially, the features are taken as input to the model.

  • Step 2: Initialize the population size according to weights used in the model.

  • Step 3: Teacher phase:

    According to TLBO algorithm in the teacher phase, the weights are selected randomly, and the mean of the population columnwise is calculated as W best i  = M new and then update the weights by using Eq. (26).

  • Step 4: Calculate the mean square error by using \( {\text{MSE}} = \frac{1}{n}\sum\nolimits_{k = 1}^{n} {\left( {D_{k} - y_{k} } \right)}^{2} \)where “D k ” is the desired vector; y k is the output of the model.

    Accept W new i as the optimal solution.

  • Step 5: In the learner phase, randomly select two weights as W i and W j , where i ≠ j, and then calculate MSE(W i ) and MSE(W j ).

If MSE(W i ) is better than MSE(W j )

$$ W_{i}^{\text{new}} = P_{f} W_{i}^{\text{old}} + {\text{rand}}\left( {W_{i} - W_{j} } \right) $$
(53)

Else

$$ W_{i}^{\text{new}} = P_{f} W_{i}^{\text{old}} + {\text{rand}}\left( {W_{j} - W_{i} } \right) $$
(54)

End ifAccept W new i as the optimal solution.

The procedure continues for all data points till the optimal solution for the weights of the LLRBFNN is obtained. It is found from the TLBO algorithm implementation that the teacher phase provides faster convergence speed and less computational time. However, the learner phase requires more computational burden than the teacher phase.

7 Results and discussion

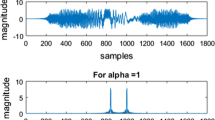
For initial testing, power quality disturbance signals are synthesized using formulas given in Table 1. For the purpose of feature extraction, we have used synthetic signals generated using MATLAB software in a computer system having a configuration of dual core Intel processor, 2.93 GHz speed, and 1 GB RAM. Further, the relevant features are extracted using the cumulative sum average filter, and the statistical formulas are shown in Table 2. The extracted features shown in Table 3 are then fed as inputs to the LLRBFNN network sequentially. For each of the 10 classes of the simultaneous power quality disturbances, 100 data points are used making a total of 1000 for all the classes. In the case of PSO-based LLRBFNN, the error converges after near about 830 iteration steps. In TLBO-based LLRBFNN, it is found that after near about 450 iteration steps, convergence takes place, whereas in the proposed modified TLBO-based LLRBFNN, the error starts converging toward zero slowly after 160 iteration steps. It is found that the computational time for modified TLBO-based LLRBFNN is 11.5367 s. TLBO-based LLRBFNN and PSO-based LLRBFNN involve computational burden as 31.4275 and 43.4538 s, respectively. Table 4 shows the classification accuracy for the different networks. However, using the ELM approach, the mean square error convergences to zero in 300 iterations. Both ELM1- and ELMM-based multiclass classifications were carried out for all the 1000 data points. The convergence characteristic of ELM1 is shown in Fig. 5. Similar characteristic is also obtained for ELMM architecture. The MSE convergence to zero is obtained in nearly 300 iterations. The convergence characteristics for the TLBO and other evolutionary algorithms are shown in Fig. 6.

Table 4 Multiple power signal classification accuracy in percentage
Full size table
Fig. 5
figure 5

Mean square error plot for the ELM

Full size image
Fig. 6
figure 6

Mean square error plot using different evolutionary techniques

Full size image

From Table 4, it is observed that the classification accuracy in the case of PSO-based LLRBFNN, the power signals Swell + Multiple spike and Sag + Multiple Notch is lesser in comparison with both the TLBO-based and LLRBFNN-based models. Modified TLBO-based LLRBFNN model provides good performance in terms of percentage of accuracy than the PSO-based LLRBFNN and TLBO-based LLRBFNN models for different multiple nonstationary power signals.

The accuracies of the proposed method are compared with other widely used power quality classifiers as shown in Table 5. Most of the power quality classifiers considered for comparison are based on time–frequency transforms such as DWT or ST hybridized with either neural network or fuzzy logic systems. Besides, there are a few power quality classifiers which use evolutionary techniques such as decision trees (DT) along with DWT or ST. In comparison with the computationally intensive classifiers studied earlier, the new approach is simple and easy to implement without extensive computations. Also, the accuracy of the proposed LLRBFNN trained by modified TLBO algorithm exhibits superior classification accuracy. The ELM-based LLRBFNN on the contrary produces slightly less accuracy in multiple power signal classification results in comparison with the TLBO approach but requires less computational overhead, thus making it suitable for processing large chunks power quality data. Also, ELMM (multiclass classification with 10 output neurons) produces better classification accuracy in comparison with the ELM1- (one output neuron) and the TLBO-based optimization. Both the algorithms were implemented in a computer with Core 2 Duo processor and 4-GB RAM, and it was found that the execution time for 1000 data points took 13.2 s in the case of TLBO learning-based localized RBF neural network. However, in the case of ELMM-based learning, it was found to be 2.25 s, which is much faster in comparison with the TLBO-based learning paradigm. The next section describes a laboratory implementation of the developed software for power quality disturbance detection. For measuring the learning speed of different algorithms, each of the power quality disturbance test cases comprised 100 specific observations in that class, and the overall speed was ascertained. This study revealed that the proposed ELMM-based learning scheme is nearly six times faster in comparison with the TLBO-based learning scheme for the LLRBFNN classifier.

Table 5 Comparison of proposed classifier performance with existing methods
Full size table

8 Power quality test results from laboratory setup

To further verify the performance of the proposed algorithms, real power signal disturbance patterns are acquired from a test configuration shown in Fig. 7. A three-phase 400 V, 50 Hz power source supplies power to two linear loads comprising resistance and inductance (40 ohms, 70.54 mH) and a nonlinear voltage source-based converter load through two three-phase lines. A three-phase squirrel cage induction motor with a rating of 1.5 kW is also connected across the converter load. Different PQ disturbances were simulated by making faults in the line, additional load switching, and capacitor switching and varying the firing angle of the converter load. The feature extraction and classification algorithms were implemented on a 32-bit floating point digital signal processor from Texas instrument (TMS 320C6713 DSP Starter Kit (DSK) and embedded MATLAB coder. The internal program memory is structured so that a total of eight instructions can be fetched at every cycle. With a clock rate of 225 MHz, the C6713 processor is capable of fetching eight 32-bit instructions every 1/(225 MHz) or 4.44 ns. Real-time classification of PQ waveforms was performed with the DSK using real-time data exchange (RTDX) that allows for data exchange between the host PC and the target DSK, for analysis in real time without stopping the target. RTDX is achieved using the software tools TI C6000 DSP and code composer studio, to provide interface between PC and DSK. The host PC is used to monitor the classification results using the captured discrete data samples of the power quality disturbance signals, showing clearly a little reduction in classification accuracy due to some extraneous noise contaminating the data samples. The real-time data classification accuracy is shown in Table 6 from which it is observed that the TLBO-based classifier when used with practical data gives 97.11 % classification accuracy, while the ELMM-based classifier produced 97.06 % accuracy, which is slightly lower than the former. Further, it can be seen that the classification accuracy gets degraded by nearly 2 % in comparison with the synthetic data. This discrepancy occurs due to the fact that the real-time data contain distortions and noise due to the measuring instruments used for the purpose. However, the classification accuracy is still high for simultaneous power quality disturbances.

Fig. 7
figure 7

A practical laboratory setup for power quality disturbance detection

Full size image
Table 6 Classification accuracy with real-time PQ events
Full size table

9 Conclusion

In this paper, a combination of cumulative sum average filter and modified TLBO-based LLRBFNN model is proposed for the classification of multiple power quality disturbance patterns. The cumulative sum average filter has been designed in a recursive manner for multiple nonstationary power quality disturbance signals for feature extraction. It is found that the filter gives better localization of the power signal disturbances. Unlike the conventional neural architectures, the LLRBFNN requires a small number of nodes and uses a set of local linear models (a linear combination of weighted inputs and a bias) to provide a high-dimensional space for parsimonious interpolation of the nonlinear input–output relationship. The modified TLBO technique is used to adjust the weight parameters of the local linear models associated with radial basis functions and is computationally less involved and straightforward to implement. Mean square error plot shows that the modified TLBO-based LLRBFNN model requires less computation time in comparison with both the TLBO-based LLRBFNN and PSO-based LLRBFNN models. On the other hand, the hybrid LLRBFNN and ELM are slightly less accurate than the TLBO-based LLRBFNN but requires less computation time, thereby making it suitable for large-scale data processing required for power quality disturbances. For better efficiency, it is required that the network should be presented with a particular set of input vectors belonging to the same class for training the network in a class by class manner. However, with multiple output nodes, ELM-based training produces better accuracy in comparison with one output neuron for multiclass classification. Regarding the practical data obtained in a laboratory environment, both the LLRBFNN-TLBO and LLRBFNN-ELMM classifiers perform almost similarly, while the former has a slight advantage in terms of accuracy over the latter. In comparison with the classification of synthetic power quality disturbance signals, the accuracy is found to be degraded by nearly 2 % due to the presence of noise in the signal.