Memristor-based chaotic neural networks for associative memory

Abstract

In chaotic neural networks, the rich dynamic behaviors are generated from the contributions of spatio-temporal summation, continuous output function, and refractoriness. However, a large number of spatio-temporal summations in turn make the physical implementation of a chaotic neural network impractical. This paper proposes and investigates a memristor-based chaotic neural network model, which adequately utilizes the memristor with unique memory ability to realize the spatio-temporal summations in a simple way. Furthermore, the associative memory capabilities of the proposed memristor-based chaotic neural network have been demonstrated by conventional methods, including separation of superimposed pattern, many-to-many associations, and successive learning. Thanks to the nanometer scale size and automatic memory ability of the memristors, the proposed scheme is expected to greatly simplify the structure of chaotic neural network and promote the hardware implementation of chaotic neural networks.

1 Introduction

Chaotic behaviors probably exist in biological neurons. In particular, chaos is considered to play a crucial role in associative memory and learning in human brains. Aihara et al. [1] studied and modeled the chaotic responses of a biological neuron and proposed the concept of chaotic neural network (CNN) in 1990. In the past several decades, chaotic neural networks have been extensively investigated [2–10]. Many characteristics and advantages of CNNs of such as high computation efficiency and adaptability have been explored in a variety of employments, including associative memory [4–10], pattern recognition [2], and combinatorial optimization [3]. However, the continuous development of CNNs has been slowed down for the difficulty in physical implementation. In other words, the complexity of the traditional chaotic neural networks leads to the challenges in hardware circuit implementation and limited network scale, which in turn restricts its information processing capability, thus reducing its practical applications.

The memristor, called the fourth fundamental element, may bring new hope to this canonical research field. In 1970s, Leon Chua explored the missing relationship between flux (φ) and charge (q) of a device based on the symmetry arguments of circuit theory and thus theoretically formulated the memristor [11] and memristive systems [12]. About 40 years later, Williams and his team at the Hewlett-Packard (HP) Labs announced that they experimentally confirmed the existence of the memristor and successfully developed an effective electronic device with nanometer oxides thin film structure [13]. Since the exciting progress, increasingly much attention from academic and industry circles have been paid on the potential element. Gradually, the charming properties of the memristor are explored, including nanometer size, switching mechanism, automatic memory ability, and continuous input/output. As a sequence, memristors have been strongly recommended in many applications such as nonvolatile memory [14–16], chaotic circuits [17, 18], artificial neural network [19], and image processing [20]. In particularly, it is believed that memristor can make progress in the field of chaotic neural networks in terms of greatly simplifying the circuit structure and improving the information processing performance.

In this paper, we propose a memristor-based chaotic neural network model (M-CNN) based on the previous study on memristor and chaotic neural networks (CNNs).It is worth to note that the numerous feedbacks and interactions, that is, the spatio-temporal summations of the external input and neurons, and the interaction between neurons, are achieved automatically by the memristor based on its memory ability. Regarding the structure of the paper, a charge-controlled memristor model with boundary conditions and its working principle based on which the memristor can realize the accumulation are described in Sect. 2. Next, the chaotic neuron model is introduced in Sect. 3. The conventional CNN is also briefly reviewed with the dynamical behaviors of chaotic neuron analyzed. Furthermore, the associative memory scheme of the M-CNN, including separation of superimposed pattern, many-to-many associations and successive learning are presented in Sects. 4 and 5 and followed by a series of simulation experiments illustrated in Sect. 6. Finally, conclusions are drawn in Sect. 7.

2 The HP memristor model

Memristor is a new type of nonlinear electric element whose constitutive relationship is defined by the charge and the flux through the device. The memristive behavior is epitomized by the fact that its resistance changes depending on the history of past current or across voltage [13].

A physical model of the HP memristor is illustrated in Fig. 1. A pure titanium dioxide (TiO₂) layer, a titanium dioxide (TiO_2-X) layer with partial oxygen atoms missing, and two platinum electrodes make up a memristor device. Pure TiO₂ is of high resistivity, while the oxygen vacancies in TiO_2-X render this layer highly conductive. When current flows through the device, the interface between the two layers shifts, thus causing the change in the overall resistance of the device. When the power turns off, the memristor will remain the last resistance state till another external source is applied, which is the so-called memory ability of the memristor.

Fig. 1

HP memristor model

A widely acceptable mathematical model of the HP memristor is described by:

$$ M(t) = M_{\text{ON}} \frac{w(t)}{D} + M_{\text{OFF}} \left( {1 - \frac{w(t)}{D}} \right) $$

(1)

where D is the thicknesses of the film layers (in Fig. 1). $w(t)$ is the time-dependent thickness of the TiO_2-X layer, $M_{\text{ON}}$ and $M_{\text{OFF}}$ are the limit values of the memristor resistance called memristance thereafter.

The change in the state variable $w(t)$ is given by,

$$ \frac{{{\text{d}}w(t)}}{{{\text{d}}t}} = \frac{{\mu_{V} M_{\text{ON}} }}{D}i(t) $$

(2)

Generally, the initial value of the state variable is not zero. Let $w(0)$ be the initial value of $w(t)$, i.e., $w(0) = w(t)|_{t = 0} \ne 0$, the initial value of the memristance is:

$$ M(0) = M_{\text{ON}} \frac{w(0)}{D} + M_{\text{OFF}} \left( {1 - \frac{w(0)}{D}} \right) $$

(3)

Integrating (3) yields:

$$ w(t) = w(0) + \frac{{\mu_{V} M_{\text{ON}} }}{D}q(t) $$

(4)

Hence, (1) can be rewritten as:

$$ M(t) = M(0) + kq(t) $$

(5)

where the constant k equals $\frac{{M_{\text{ON}} - M_{\text{OFF}} }}{{D^{2} }}\mu_{V} M_{\text{ON}} .$

Obey to the physical constructions of a memristor device, one can get that: $0 \le w(t) \le D$, namely, $M_{\text{ON}} \le M(t) \le M_{\text{OFF}}$. Then, the effective charge range in which the memristor exhibits memristive behaviors is obtained.

$$ \frac{{M_{\text{OFF}} - M(0)}}{k} \le q(t) \le \frac{{M_{\text{ON}} - M(0)}}{k} $$

(6)

Let $Q_{\hbox{min} } = \frac{{M{}_{\text{OFF}} - M(0)}}{k},$ $Q_{\hbox{max} } = \frac{{M_{\text{ON}} - M(0)}}{k}$ one gets the charge-controlled memristor model with boundary conditions.

$$ M(t) = \left\{ {\begin{array}{*{20}l} {M_{\text{OFF}} } \hfill & {q(t) < Q_{\hbox{min} } } \hfill \\ {M(0) + kq(t)} \hfill & {Q_{\hbox{min} } \le q(t) < Q_{\hbox{max} } } \hfill \\ {M_{\text{ON}} } \hfill & {q(t) \ge Q_{\hbox{max} } } \hfill \\ \end{array} } \right. $$

(7)

According to (7), memristance varies governing by the amount of the charge flowing through it and also affected by its initial value. Assuming that a constant current pulse $i(t)$ with duration unit 1, is applied in a memristor with known initial value, one can obtain,

$$ \begin{array}{*{20}c} {t = 1,\quad M(1) = M(0) + kq(1);} \\ {t = 2,\quad M(2) = M(1) + kq(2);} \\ {t = 3,\quad M(3) = M(2) + kq(3);} \\ \ldots \\ {t = t,\quad M(t) = M(t - 1) + kq(t)} \\ \end{array} $$

Summing up the above leads to,

$$ M(t) = M(0) + k(q(1) + q(2) + q(3) + \cdots + q(t)) $$

(8)

$$ \sum\limits_{1}^{t} {q(t)} = q(1) + q(2) + q(3) + \cdots + q(t) = \frac{M(t) - M(0)}{k} $$

(9)

In this case, the amount of the charge past the memristor in unit time is equal to the current value numerically, i.e., $q(t) = i(t)$. In this study, the memristor is assumed to work within the normal range, that is, $Q_{\hbox{min} } \le q(t) < Q_{\hbox{max} }$. The summation of all the current pulses can be calculated using (9), which denotes the memristor automatically accomplishes the summation.

Traditional chaotic neural network models achieve the spatio-temporal summation by continuous iterative computations, which results in very complicated network structure. Comparably, the proposed memristive realization scheme can contribute to simpler and compact chaotic neural network architecture.

3 The chaotic neuron model

Chaos and chaotic neural networks have been well studied in mathematic community and engineering community since Lorenz inaugurated the modern chaos theory in 1960s. Here, we briefly review the fundamental knowledge of chaotic neural networks. First of all, the dynamics of a chaotic neuron are described through:

$$ y(t + 1) = ky(t) + \alpha f(y(t)) - a(t) $$

(10)

$$ x(t + 1) = f(y(t + 1)) $$

(11)

where $y(t + 1)$ is the output of the chaotic neuron at time t + 1; $y(t + 1)$ denotes the internal state, and $f( \cdot )$ is an output function in the form of $f(x) = 1/(1 + e^{ - x/\varepsilon } )$ with a steepness parameter $\varepsilon$; $\alpha$, $k$ and $\theta$ are the refractory scaling parameter, the damping factor, and the threshold, respectively.

It is a characteristic of chaotic systems that initially nearby trajectories separate exponentially with time. The Lyapunov exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories.

The Lyapunov exponent λ is defined by [21]:

$$ \lambda = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{n}\sum\limits_{{t = t_{0} }}^{{n + t_{0} - 1}} {\ln } \left| {\frac{dy(t + 1)}{dy(t)}} \right| $$

(12)

The firing rate of a neuron is a fundamental characteristic of the message that conveys to other neurons. It is variable and denotes the intensity of its activation state. Traditionally, it has been thought that most of the relevant information was contained in the average firing rate of the neuron [19].

The firing rate ρ is defined by [21]:

$$ \rho = \mathop {\lim }\limits_{n \to + \infty } \frac{1}{n}\sum\limits_{{t = t_{0} }}^{{n + t_{0} - 1}} {h(x(t))} $$

(13)

where h is a transfer function and assumed to be $h(x) = 1$ for $x \ge 0.5$, and $h(x) = 0$ for $x < 0.5$.

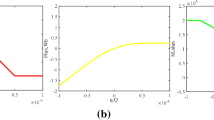
Figure 2 shows the response characteristics of a chaotic neuron coined by (10) and (11) versus increasing bifurcation parameter α. It can be observed that when the value of α increases from 0.8 to 4.0 in the bifurcation diagram, there appear three obvious regions in which the neuron is chaotic, as shown in Fig. 2a. Correspondingly, the Lyapunov exponent has positive value in these chaotic regions, illustrated in Fig. 2b. Finally, the average firing rate is presented in Fig. 2c. Next, a number of chaotic neurons consist of chaotic neural networks.

Fig. 2

Response characteristics of a chaotic neuron versus bifurcation parameter α from 0.8 to 4.0, when k = 0.7, a = 1.0, ε = 0.04: a Bifurcation diagram. b Lyapunov exponent. c Average firing rate

4 The memristor-based associative memory chaotic neural network

The memristor-based chaotic neural networks for associative memory (CAM) are described in this section, including the separation of superimposed patterns and many-to-many associative memory.

4.1 CAM neural network for separation of superimposed patterns

For a chaotic associative memory neural network, when a stored pattern is given as an external input, the network searches around the pattern. Assuming that the training patterns X, Y and Z have been remembered in a chaotic neural network, when X is given to the network as an external input continuously, the network searches around the input pattern, so pattern X can be recalled. When a superimposed pattern (X + Y) is given as the external input, then the network will search around the patterns X and Y. Since the chaotic neurons change their states by chaos, they can separate the superimposed patterns, and thus, X and Y can be recalled in different time.

The dynamics of the ith neuron in the M-CNN can be represented by the following formulas

$$ x_{i} (t + 1) = f\left( {\sum\limits_{j = 1}^{M} {\omega_{ij} } \sum\limits_{d = 0}^{t} {k_{r1} x_{j} (t - d)} + v\sum\limits_{d = 0}^{t} {k_{r2} A_{j} (t - d)} - \alpha \sum\limits_{d = 0}^{t} {k_{r3} x_{i} (t - d)} } \right) $$

(14)

where $\nu$ (constant) is the connection weight between an external input and a neuron. k _r1, k _r2, and k _r3 are decay factors. The $f( \cdot )$ is the continuous output function of the ith chaotic neuron, given by,

$$ f(y) = 2/(1 + e^{ - y/\varepsilon } ) $$

(15)

where $\varepsilon$ is the steepness parameter.

Based on the study in Sect. 2, the summations in (14) can be accomplished with the memristor [refer to (9)]. So the dynamics of the ith neuron in the memristor-based chaotic associative memory neural network can be rewritten as:

$$ x_{i} (t + 1) = f\left( {\sum\limits_{j = 1}^{M} {\omega_{ij} k_{r1} \frac{{M_{1} (t) - M(0)}}{k}} + \nu k_{r2} \frac{{M_{2} (t) - M(0)}}{k} - \alpha k_{r3} \frac{{M_{3} (t) - M(0)}}{k}} \right) $$

(16)

4.2 CAM neural network for many-to-many association

Assuming that a training set (X ₁, Y ₁, and Z ₁) has been stored in a 3-layered CAM neural network, when pattern X ₁ is given to the first layer of the network continuously as an input, the first layer searches and recalls the pattern X ₁; meanwhile, the second and the third layer can search around the pattern Y ₁ and the pattern Z ₁ by chaotic itinerancy, respectively. So, the patterns X ₁, Y ₁, and Z ₁ can be recalled in three layers, respectively. This is so-called one-to-many association. Many-to-many associations refers to the case that if the training sets {(X ₁, Y ₁, Z ₁), (X ₁, Y ₂, Z ₂), (X ₃, Y ₃, Z ₃)} have been stored in a chaotic neural network, when the pattern X ₁ is given to the first layer as an initial input, the composite modes {(X ₁,Y ₁, Z ₁), (X ₁, Y ₂, Z ₂)}that contain a common term X ₁ could be recalled at different time.

In a many-to-many association chaotic neural network, the dynamics of the ith neuron in the αth layer is represented by:

$$ \begin{aligned}x_{i}^{(\alpha )} (t + 1) &= f\left[ \nu \sum\limits_{d = 0}^{t} {k_{s}^{d} A_{i}^{(\alpha )} (t - d)} \right.\\ &\quad+ \sum\limits_{\begin{array}{l} \beta = 1 \\ \beta \ne \alpha \end{array} }^{L} {\sum\limits_{j = 1}^{{N^{(\beta )} }} {\omega_{ij}^{(\alpha \beta )} \sum\limits_{d = 0}^{t} {k_{m}^{d} x_{j}^{(\beta )} } } } (t - d) \\ &\quad+ \sum\limits_{j = 1}^{{N^{(\alpha )} }} {\omega_{ij}^{(\alpha \alpha )} \sum\limits_{d = 0}^{t} {k_{m}^{d} } } x_{j}^{(\alpha )} (t - d) \\ &\quad\left.- \gamma \sum\limits_{d = 0}^{t} {k_{r}^{d} x_{i}^{(\alpha )} } (t - d) - \theta_{i}^{(\alpha )} \right] \end{aligned}$$

(17)

where L is the number of layers, $\theta_{i}^{(\alpha )}$ is the threshold, $\gamma$ is a scaling factor of the refractoriness, $x_{i}^{(\alpha )} (t + 1)$ is the output of the chaotic neuron, $N^{(\alpha )}$, and $N^{(\beta )}$ are the number of chaotic neurons in the αth layer and the βth layer, $\nu$ is the connection weight between the input and neurons, $A_{i}^{(\alpha )}$ is the input of the ith neuron in the αth layer at time t, $\omega_{ij}^{(\alpha \beta )}$ is the connection weight between the ith neuron in the αth layer and the jth neuron in the βth layer, ks, km and kr are external input factor, feedback input factor and factor of the refractoriness, respectively.

Similarly, by using the memristor to realize the spatio-temporal summation, the dynamics of the ith neuron in the network for many-to-many association can be rewritten by:

$$ \begin{aligned}x_{i}^{(\alpha )} (t + 1) &= f\left[ \nu \frac{{M_{1} (t) - M(0)}}{k}\right. \\ &\quad+ \sum\limits_{\begin{array}{l} \beta = 1 \\ \beta \ne \alpha \end{array} }^{L} {\sum\limits_{j = 1}^{{N^{(\beta )} }} {\omega_{ij}^{(\alpha \beta )} \frac{{M_{2} (t) - M(0)}}{k}} } \\ &\quad+ \sum\limits_{j = 1}^{{N^{(\alpha )} }} {\omega_{ij}^{(\alpha \alpha )} \frac{{M_{3} (t) - M(0)}}{k}} \\ &\quad\left.- \gamma \frac{{M_{4} (t) - M(0)}}{k} - \theta_{i}^{(\alpha )} \right]\end{aligned}$$

(18)

5 The memristor-based successive learning chaotic neural network

5.1 Successive learning chaotic neural network (SLCNN)

SLCNN possesses successive learning ability, which can distinguish between known and unknown patterns, and learn the unknown pattern. Furthermore, SLCNN can estimate and learn the correct pattern from a noisy unknown pattern or an incomplete unknown patternmaking use of the temporal summation of the continuous input pattern, which is similar to the physiological phenomenon of a rabbit discovered by Freeman [2]. This section, we also take use of the memory ability of the memristor and propose a memristor-based SLCNN (MSLCNN). The amount of calculation of the network will be greatly reduced, and the network structure can be much simpler.

The model of successive learning chaotic neural network was put forward by Osana and Hagiwara in 1998 [6]. In a successive learning chaotic neural network, the dynamics of the ith neuron is represented by:

$$ \begin{aligned}x_{i}^{(\alpha )} (t + 1) &= f\left[ \nu \sum\limits_{d = 0}^{t} {k_{s}^{d} A_{i}^{(\alpha )} (t - d)} \right.\\&\quad + \sum\limits_{\begin{array}{l} \beta = 1 \\ \beta \ne \alpha \end{array} }^{L} {\sum\limits_{j = 1}^{{N^{(\beta )} }} {\omega_{ij}^{(\alpha \beta )} \sum\limits_{d = 0}^{t} {k_{m}^{d} x_{j}^{(\beta )} } } } (t - d) \\ &\quad+ \sum\limits_{j = 1}^{{N^{(\alpha )} }} {\omega_{ij}^{(\alpha \alpha )} \sum\limits_{d = 0}^{t} {k_{m}^{d} } } x_{j}^{(\alpha )} (t - d) \\ &\quad\left.- \gamma \sum\limits_{d = 0}^{t} {k_{r}^{d} x_{i}^{(\alpha )} } (t - d) - \theta_{i}^{(\alpha )} \right] \end{aligned}$$

(19)

Using memristor to achieve the summations, Eq. (19) can be rewritten as:

$$ \begin{aligned} x_{i}^{(\alpha )} (t + 1) &= f\left[ \nu \frac{{M_{1} (t) - M(0)}}{k} \right.\\ &\quad+ \sum\limits_{\begin{array}{l} \beta = 1 \\ \beta \ne \alpha \end{array} }^{L} {\sum\limits_{j = 1}^{{N^{(\beta )} }} {\omega_{ij}^{(\alpha \beta )} \frac{{M_{2} (t) - M(0)}}{k}} } \\ &\quad+ \sum\limits_{j = 1}^{{N^{(\alpha )} }} {\omega_{ij}^{(\alpha \alpha )} \frac{{M_{3} (t) - M(0)}}{k}} \\ &\quad \left.- \gamma \frac{{M_{4} (t) - M(0)}}{k} - \theta_{i}^{(\alpha )} \right] \end{aligned} $$

(20)

5.2 Distinction between known pattern and unknown pattern

In the MSLCNN, when a known pattern is given to the network, the network searches around the input pattern by chaotic itinerancy. On the other hand, when an unknown pattern is given, the network learns and finally remembers the new coming pattern. This is because of the temporal summation of the continuous pattern input: the influence of the external input $\xi_{i} (t)$ becomes larger than the inter connections $\eta_{i} (t)$ among neurons and the refractoriness $\zeta_{i} (t)$, if the same pattern is given as an external input for a long time [7].

$$ \begin{aligned} &|\xi_{{_{i} }}^{\alpha } (t)| > |\eta_{{_{i} }}^{\alpha } (t) + \zeta_{{_{i} }}^{\alpha } (t)| \hfill \\ &\quad i = 1,2, \ldots N;\;{\kern 1pt} {\kern 1pt} \alpha = 1,2, \ldots ,L \hfill \\ \end{aligned} $$

(21)

where

$$ \xi_{i}^{\alpha } (t) = \nu \frac{{M_{1} (t) - M(0)}}{k} $$

$$ \begin{aligned} \eta_{{_{i} }}^{\alpha } (t) & = \sum\limits_{\begin{array}{l} \beta = 1 \\ \beta \ne \alpha \end{array} }^{L} {\sum\limits_{j = 1}^{{N^{(\beta )} }} {\omega_{ij}^{(\alpha \beta )} \frac{{M_{2} (t) - M(0)}}{k}} } \\ & \quad + \sum\limits_{j = 1}^{{N^{(\alpha )} }} {\omega_{ij}^{(\alpha \alpha )} \frac{{M_{3} (t) - M(0)}}{k}} \\ \end{aligned} $$

$$ \zeta_{i} (t) = - \gamma \frac{{M_{4} (t) - M(0)}}{k} $$

If this inequality is satisfied, the state of the network is regarded as stable, and the time for the network reaching a stable state is denoted by T ^sta, with

$$ \begin{gathered} T^{\text{sta}} = \hbox{min} \left\{ {t\left\| {\xi_{i}^{\alpha } (t)\left| > \right|\left. {\eta_{i}^{\alpha } (t) + \zeta_{i}^{\alpha } (t)} \right|} \right.} \right\} \hfill \\ \forall i,\,i = 1,2, \ldots ,N;\,\forall \alpha ,\,\alpha = 1,2, \ldots ,L \hfill \\ \end{gathered} $$

(22)

Define the following variable V as a criterion of the distinction:

$$ V = \sum\limits_{t = 1}^{{T^{\text{sta}} }} {\sum\limits_{\alpha = 1}^{L} {\sum\limits_{i = 1}^{N} {|x_{i}^{\alpha } (t) - x_{i}^{\alpha } (t - 1)|} } } $$

(23)

Then, if V is larger than the threshold Vth, the input pattern is regarded as an unknown pattern.

5.3 Learn unknown pattern

When an input pattern is regarded as an unknown pattern, the pattern will be remembered in the network. The network learns the new pattern by using Hebbian algorithm. The weight connections are updated according to:

$$ w^{{(\alpha \beta ){\text{new}}}} = w^{{(\alpha \beta ){\text{old}}}} + \lambda x^{\alpha } (T^{\text{sta}} )x^{\beta } (T^{\text{sta}} ) $$

(24)

where $x^{\alpha } (T^{\text{sta}} )$ is the output in αth layer and $\lambda$ is the learning rate.

6 Computer simulations

In order to demonstrate the effectiveness the proposed memristor-based chaotic neural networks, a number of computer simulations are carried out. In the following experiments, the parameters of the memristor are set as: M _ON = 100 Ω, M _OFF = 30 kΩ, M(0) = 15 kΩ, D = 10 nm, and μ _V  = 10⁻¹⁴ m² s⁻¹  V ⁻¹. Besides, the simulation results are presented in output order, that is, from left to right and from row to column.

6.1 Separation of superimposed patterns

According to (16), a memristor-based associative memory chaotic neural network containing 49 neurons has been designed to realize the separation of superimposed pattern. The training patterns are shown in Fig. 3a. The superimposed pattern Z + M is given as the input continuously. The parameters of the network are set as: α = 9.8, k _r1 = 0.1, k _r2 = 0.9, k _r3 = 0.9, and ε = 0.02, $\nu = 200.$

Fig. 3

a Stored patterns in the memristor-based CNN; b output of the memristor-based CNN in separation of superimposed pattern, output of the network in separation of superimposed pattern, in which pattern Z is separated from the superimposed pattern at step 3, 6, 11, 16, and 19, and pattern M is separated at step 4 and 17 successfully

6.2 Many-to-many association

According to (18), a 3-layered 81 × 81 × 81 memristor-based associative memory CNN is designed to deal with many-to-many associations. Here, the parameters are set as: $\nu = 100$, $ks = 0.95$, $km = 0.1$, $kr = 0.95$, $\gamma = 10$, $\varepsilon = 0.015$.

Figure 4 shows the training sets {(Z, M, I), (Z, W, S), (U, C, K)}, which will be learned in the network by Hebbian learning rule. When pattern Z is continuously given to the network as an external input, the training sets (Z, M, I) and (Z, W, S) can be recalled successfully as shown in Fig. 5 at step 10, 11, 12, 24, 25, 26, 27, 28 and 16, 17, 18, 19, 20, 21, respectively.

Fig. 4

Training sets for many-to-many association

Fig. 5

Output of the memristor-based CNN for many-to-many association with pattern Z given as the input

6.3 One-layered MSLCNN

A memristor-based successive learning chaotic neural network in scale of 7 × 7 is designed. The parameter values in the following simulation are set as: $\varepsilon = 0.015$, $ks = 0.99$, $km = 0.1$, $kr = 0.95$, $\gamma = 2.0$, $\nu = 1.0$, $\theta_{{_{i} }}^{\alpha } = 0$, $V{\text{th}} = 50$, $km = 0.1$ $\alpha = 1$. The patterns Z and M are shown in Fig. 6, which has been memorized in the MSLCNN firstly.

Fig. 6

Stored patterns in the MSLCNN

6.3.1 A known pattern was given

Figure 7 shows an association result of the MSLCNN when a known pattern Z was given as an external input. When a known pattern was given, only the input pattern was recalled.

Fig. 7

Output of the MSLCNN when known pattern Z is given as the input

6.3.2 An unknown pattern was given

Figure 8 shows the association results when an unknown pattern I was given as an external input. During steps 1–51, the network cannot recall pattern I because pattern I has not been memorized in the network and shows a chaotic itinerancy. During steps 52–81, patterns I appeared. In this case, the network reached a stable state at step 52, and V was 79. Thus, the pattern I is regarded as an unknown pattern.

Fig. 8

Output of the 3-layered MSLCNN when unknown pattern I is given as the input

6.4 Three-layered MSLCNN

A 3-layered memristor-based chaotic neural network in scale of 81 × 81 × 81 is designed to deal with multilayer successive learning. Figure 9 shows the training sets {(Z, M, I), (Z, W, S), (U, C, K)} stored in the CNN. Here, the parameters of the CNN are set as: $\nu = 100$, $ks = 0.95$, $km = 0.1$, $kr = 0.95$, $\theta_{{_{i} }}^{\alpha } = 0$, $\gamma = 10$, $\varepsilon = 0.015$, $V^{th} = 300$, $\alpha = 3$.

Fig. 9

The training sets

6.4.1 A known pattern was given

Figure 10 shows the result of the 3-layered MSLCNN when a known pattern [e.g., Pattern (Z, M, I)] is given as the input of the network. In this case, the network reaches a stable state at first, and V is 243. Then, the pattern (Z, M, I) is regarded as an unknown pattern, so the network only searches around the input pattern as seen in Fig. 10.

Fig. 10

Output of the 3-layered MSLCNN for successive learning (known pattern)

6.4.2 An unknown pattern was given

When an unknown pattern (e.g., pattern (U, C, K)) was given as the input of the MSLCNN, the network would show a chaotic itinerancy at first and then memorize the pattern as shown in Fig. 11. During steps 1–4, the network could not recall pattern (U, C, K) because it has not memorized. While, during steps 4–81, the input pattern appeared. In this case, the network reaches a stable state at step 4, and V was 371. Then, (U, C, K) is regarded as an unknown pattern.

Fig. 11

Output of the 3-layered MSLCNN for successive learning (unknown pattern)

7 Conclusions

This paper incorporates the memristor into the conventional chaotic neural networks, proposing the memristor-based chaotic neural networks. The automatic memory ability and constantly changeable resistance of memristors have been fully utilized to implement the spatio-temporal accumulations of external input and neurons and between neurons. Specially, two kinds of memristor-based associative memory CNN have been presented for separation of superimposed pattern and many-to-many association, respectively. Similarly, a memristor-based successive learning CNN is also studied. A series of computer simulations have demonstrated the effectiveness of the proposed scheme. Owing to the nanometer scale and automatic memory ability, the proposed memristor-based chaotic neural networks have the advantages in computation complexity and network structure complexity, which is believed to pave the way of hardware implementation of chaotic neural networks.