1 Introduction

Solar thermal power systems utilize the heat generated by a collector concentrating and absorbing the sun’s energy to drive a heat engine/generator and produce electric power. Of the three solar thermal systems, the tower, the trough, and the dish, the dish-stirling systems have demonstrated the highest efficiency [1–3].

Over the last 20 years, eight different dish-stirling systems ranging in size from 2 to 50 kW have been built by companies in the United states, Germany, Japan, and Russia [1]. In principle, high concentrating and low or nonconcentrating solar collectors can all be used to power the stirling engine.

Dish-stirling solar thermal power bases on spot-focused collecting heat and stirling thermodynamics cycle. The concentration ratio of dish concentrator can reach 1,500–3,000, and the operating temperature of the receiver can reach more than 800°C. Reported from literatures, the peak solar-to-electric conversion efficiency of the system has reached 29.4%. Because dish-stirling solar thermal power system adopts the idea of modularity generally, it can be used as scattered power source of electric power system; also it can make up dish field to provide electric power assembly. Just as its high efficiency and flexible combinations, it has been developed quickly in developed countries in the last 20 years, and the output power of unit system ranged from 2 to 50 kWe.

A soft sensor is a conceptual device whose output or inferred variable can be modeled in terms of other parameters that are relevant to the same process [4]. According to Rallo et al. [4], artificial neural network could be used as soft sensor building approach. The ANN is a popular, nonlinear, and nonparametric tool in oil flow rate estimation.

In the present work, HGAPSO is proposed for optimizing the weights of feed-forward neural network. Then, simulation results demonstrate the effectiveness and potential of the new proposed network for power prediction of solar dish-stirling engine that reported in literature in china [5] compared with experimental data.

2 Stirling engine

In order to produce electricity using concentrated solar energy, a proper power cycle that converts the thermal energy to mechanical work is necessary. As well known, stirling engine uses externally supplied thermal energy to make a mechanical motion using repeated heating/cooling of working gas like helium or hydrogen in a closed loop. So the engine could run by any sources of thermal energy as long as the energy is properly transferred into the working gas. Owing to this advantage, Stirling engine has been taken much interest from various renewable energy technologies. Additionally, the engine is known to make relatively low noise compared to the internal combustion engines and also more environmentally friendly in terms of air pollution. Solar application of stirling engine, especially for a small-scale dish-type power system, is one of promising applications, which is already in a commercial stage through over 20 years of R and D efforts [6].

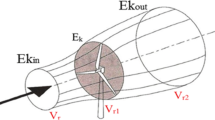
The dish-stirling system, comprising a parabolic dish collector (which is made up a dish concentrator and a thermal absorber) and a stirling heat engine located at the focus of the dish, tracks the sun and focuses solar energy into a cavity absorber where solar energy is absorbed and transferred to the stirling engine to heat its displacer hot-end, thereby creating a solar-powered stirling heat engine, as shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the dish system

Full size image

Figure 2 is a schematic diagram of a stirling heat engine cycle with finite-time heat transfer and regenerative heat losses as well as conductive thermal bridging losses from the absorber to the heat sink. This cycle approximates the compression stroke of real heat engine as an isothermal process 1-2, with an irreversible heat rejection at constant temperature T 2 to the heat sink at constant temperature T L. The heat addition to the working fluid from the regenerator is modeled as isochoric process 2–3. The expansion stroke producing work is modeled as isothermal process 3–4, with irreversible heat addition at constant temperature T 1 from the absorber at constant temperature T H . Finally, process 4–1 closed the cycle, the heat is rejected to the regenerator is modeled as isochoric process 4–1.

Fig. 2
figure 2

Schematic diagram of the stirling heat engine cycle

Full size image

If the regenerator is ideal, the heat absorbed during process 4–1 should be equal to the heat rejected during process 2–3; however, the ideal regenerator requires an infinite area or infinite regeneration time to transfer finite heat amount, and this is impractical. Therefore, it is desirable to consider a real regenerator with heat losses ΔQ R . In addition, we also consider conductive thermal bridging losses Q 0 from the absorber to the heat sink.

3 Methodology

3.1 Finite-time thermodynamic analysis for solar-powered stirling heat engine

Chambadal and novikov first applied finite-time thermodynamics to analyze heat engine in 1975, since then, extensive research have been undertaken on the performance analysis and optimization of stirling heat engines and solar-powered stirling engines based on FTT [7].

A part of the above publications is dedicated to the performance analysis and optimization of low temperature differential stirling heat engines powered by low concentrating solar collectors [8].

3.1.1 Regenerative heat losses of the regenerator

It is important to mention that there also exists a finite heat transfer in the regenerative heat transfer (Q R ) that is given by [9, 10]:

$$ Q_{R} = nC_{V} \varepsilon_{R} (T_{1} - T_{2} ) $$
(1)

where C V is the specific heat of working substance and ɛ R is the effectiveness of the regenerator. Thus, the regenerative heat loss in the two regenerative processes is given by [9, 10]:

$$ \Updelta Q_{R} = nC_{V} (1 - \varepsilon_{R} )(T_{1} - T_{2} ) $$
(2)

In order to calculate the time of the regenerative processes, one assumes that the temperature of the working fluid in the regenerative processes as a function of time is given by [10]:

$$ \frac{{{\text{d}}T}}{{{\text{d}}t}} = \pm M_{i} $$
(3)

where M is the proportionality constant that is independent of the temperature but dependent on the property of the regenerative material. The positive and negative signs correspond to constant volume heating (i = 1) and cooling (i = 2) processes, respectively.

One obtains the time of the two isochoric processes as:

$$ t_{3} = \frac{{T_{1} - T_{2} }}{{M_{1} }} $$
(4)
$$ t_{4} = \frac{{T_{1} - T_{2} }}{{M_{2} }} $$
(5)

3.1.2 The conductive thermal bridging losses from the absorber to the heat sink

The conductive thermal bridging losses from the absorber at temperature T H to the heat sink at temperature T L is assumed to be proportional to the cycle time and given by [10, 11]:

$$ Q_{0} = k_{0} (T_{H} - T_{L} )\tau $$
(6)

where k 0 is the heat leak coefficient between the absorber and the heat sink, and τ is the cyclic period.

3.1.3 The amounts of heat released by absorber and absorbed by the heat sink

For a stirling cycle, the amounts of heat released by the absorber and absorbed by heat sink are as follows [9]:

$$ Q_{1} = [h_{HC} (T_{H} - T_{1} ) + h_{HR} (T_{H}^{4} - T_{1}^{4} )]t_{1} = nRT_{1} Ln\lambda + nC_{V} (1 - \varepsilon_{R} )(T_{1} - T_{2} ) $$
(7)
$$ Q_{2} = h_{LC} (T_{2} - T_{L} )t_{2} = nRT_{2} Ln\lambda + nC_{V} (1 - \varepsilon_{R} )(T_{1} - T_{2} ) $$
(8)

Let Q 1 be the amount of heat absorbed by the working fluid at temperature T 1 from the absorber at temperature T H .

Let Q 2be the amount of heat released by working fluid at temperature T 2 to the heat sink at temperature T L .

Where h HC is high temperature side convection heat transfer coefficient, h HR is high temperature side radiation heat transfer coefficient, h LC is low temperature side convection heat transfer coefficient, Ris the gas constant, and λ is the ratio of volume during the regenerative processes, that is,

$$ \lambda = \frac{{V_{1} }}{{V_{2} }} $$
(9)

Take into account the major irreversibility mentioned above, the net heats released from the absorber Q H and absorbed by the heat sink Q L are given as:

$$ Q_{H} = Q_{1} + Q_{0} $$
(10)
$$ Q_{L} = Q_{2} + Q_{0} $$
(11)

3.1.4 The cyclic period

Using Eqs. 4–8, we get that the cyclic period τ is:

$$ \tau = t_{1} + t_{2} + t_{3} + t_{4} = \frac{{nRT_{1} Ln\lambda + nC_{V} (1 - \varepsilon_{R} )(T_{1} - T_{2} )}}{{\left[ {h_{HC} (T_{H} - T_{1} ) + h_{HR} \left( {T_{H}^{4} - T_{1}^{4} } \right)} \right]}} + \frac{{nRT_{2} Ln\lambda + nC_{V} (1 - \varepsilon_{R} )(T_{1} - T_{2} )}}{{h_{LC} (T_{2} - T_{L} )}} + \left( {\frac{1}{{M_{1} }} + \frac{1}{{M_{2} }}} \right) $$
(12)

3.1.5 Maximum power output and maximum power efficiency of the stirling engine

The power output and the thermal efficiency are given by [7]:

$$ p = \frac{W}{\tau } = \frac{{Q_{H} - Q_{L} }}{\tau } $$
(13)
$$ \eta_{t} = \frac{{Q_{H} - Q_{L} }}{{Q_{H} }} $$
(14)

Using Eqs. 6–14, we have:

$$ P = \frac{{T_{1} - xT_{1} }}{{\frac{{T_{1} + A_{1} \left( {T_{1} - xT_{1} } \right)}}{{h_{HC} \left( {T_{H} - T_{1} } \right) + h_{HR} \left( {T_{H}^{4} - T_{1}^{4} } \right)}} + \frac{{xT_{1} + A_{1} \left( {T_{1} - xT_{1} } \right)}}{{h_{LC} \left( {xT_{1} - T_{L} } \right)}} + F_{1} \left( {T_{1} - xT_{1} } \right)}} $$
(15)
$$ \eta_{t} = \frac{{T_{1} - xT_{1} }}{{T_{1} + A_{1} (T_{1} - xT_{1} ) + [k_{0} (T_{H} - T_{L} )]\left[ {\frac{{T_{1} + A_{1} (T_{1} - xT_{1} )}}{{\left[ {h_{HC} (T_{H} - T_{1} ) + h_{HR} \left( {T_{H}^{4} - T_{1}^{4} } \right)} \right]}} + \frac{{xT_{1} + A_{1} (T_{1} - xT_{1} )}}{{h_{LC} (xT_{1} - T_{L} )}} + F_{1} (T_{1} - xT_{1} )} \right]}} $$
(16)

where

$$ A_{1} = \frac{{C_{V} (1 - \varepsilon_{R} )}}{RLn\lambda } $$

and

$$ F_{1} = \frac{1}{nRLn\lambda }\left(\frac{1}{{M_{1} }} + \frac{1}{{M_{2} }}\right)$$

and

$$ x = {\raise0.7ex\hbox{${T_{2} }$} \!\mathord{\left/ {\vphantom {{T_{2} } {T_{1} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${T_{1} }$}} $$

Therefore, the maximum power output and the corresponding optimal thermal efficiency of the stirling engine are:

$$ P_{\max } = \frac{1 - x}{{\frac{{1 + A_{1} \left( {1 - x} \right)}}{{h_{HC} \left( {T_{H} - T_{1opt} } \right) + h_{HR} \left( {T_{H}^{4} - T_{1opt}^{4} } \right)}} + \frac{{x + A_{1} \left( {1 - x} \right)}}{{h_{LC} \left( {xT_{1opt} - T_{L} } \right)}} + F_{1} \left( {1 - x} \right)}} $$
(17)
$$ \eta_{topt} = \frac{1 - x}{{1 + A_{1} (1 - x) + [k_{0} (T_{H} - T_{L} )][\frac{{1 + A_{1} (1 - x)}}{{\left[ {h_{HC} (T_{H} - T_{1opt} ) + h_{HR} \left( {T_{H}^{4} - T_{1opt}^{4} } \right)} \right]}} + \frac{{x + A_{1} (1 - x)}}{{h_{LC} (xT_{1opt} - T_{L} )}} + F_{1} (1 - x)]}} $$
(18)

3.2 Artificial neural networks

Artificial neural networks are parallel information processing methods that can express complex and nonlinear relationship use number of input–output training patterns from the experimental data. ANNs provides a nonlinear mapping between inputs and outputs by its intrinsic ability [12]. The success in obtaining a reliable and robust network depends on the correct data preprocessing, correct architecture selection, and correct network training choice strongly [13].

The most common neural network architecture is the feed-forward neural network. Feed-forward network is the network structure in which the information or signals will propagates only in one direction, from input to output. A three-layered feed-forward neural network with back propagation algorithm can approximate any nonlinear continuous function to an arbitrary accuracy [12, 14].

The network is trained by performing optimization of weights for each node interconnection and bias terms, until the values output at the output layer neurons are as close as possible to the actual outputs. The mean squared error of the network (MSE) is defined as:

$$ MSE = \frac{1}{2}\sum\limits_{K = 1}^{G} {\sum\limits_{j = 1}^{m} {\left[ {Y_{j} (k) - T_{j} (k)} \right]^{2} } } $$
(19)

where m is the number of output nodes, G is the number of training samples, Y j (k) is the expected output, and T j (k) is the actual output.

The data are split into two sets, a training data set and a validating data set. The model is produced using only the training data. The validating data are used to estimate the accuracy of the model performance. In training a network, the objective is to find an optimum set of weights. When the number of weights is higher than the number of available data, the error in-fitting the nontrained data initially decreases but then increases as the network becomes over-trained. In contrast, when the number of weights is smaller than the number of data, the over-fitting problem is not crucial.

4 Genetic algorithms and particle swarm optimization

4.1 Particle swarm optimization

Particle swarm optimization (PSO) is one of the recent evolutionary optimization methods. This technique was originally developed by Kennedy and Eberhart [15] in order to solve problems with continuous search space. PSO is based on the metaphor of social interaction and communication, such as bird flocking and fish schooling. This algorithm can be easily implemented and it is computationally inexpensive, since its memory and CPU speed requirements are low [16].

PSO shares many common points with GA. It conducts the search using a population of particles that correspond to individuals in GA. Both algorithms start with a randomly generated population. PSO does not have a direct recombination operator. However, the stochastic acceleration of a particle toward its previous best position, as well as toward the best particle of the swarm (or toward the best in its neighborhood in the local version), resembles the recombination procedure in evolutionary computation [17–19].

Compared to GA, the PSO has some attractive characteristics. It has memory, so knowledge of good solutions is retained by all particles, whereas in GA, previous knowledge of the problem is destroyed once the population changes. PSO does not use the filtering operation (such as selection in GAs), and all the members of the population are maintained through the search procedure to share their information effectively.

PSO uses social rules to search in the design space by controlling the trajectories of a set of independent particles. The position of each particle, x i, representing a particular solution of the problem, is used to compute the value of the fitness function to be optimized. Each particle may change its position and consequently may explore the solution space, simply varying its associated velocity. In fact, the main PSO operator is the velocity update, which takes into account the best position, in terms of fitness value reached by all the particles during their paths, P t g , and the best position that the agent itself has reached during its search, P t i , resulting in a migration of the entire swarm toward the global optimum.

At each iteration, the particle moves around according to its velocity and position; the cost function to be optimized is evaluated for each particle in order to rank the current location. The velocity of the particle is then stochastically updated according to

$$ \mathop V\nolimits_{i}^{t + 1} = \omega \mathop V\nolimits_{i}^{t} + \mathop C\nolimits_{1} \mathop r\nolimits_{1}^{t} (\mathop P\nolimits_{i}^{t} - \mathop X\nolimits_{i}^{t} ) + \mathop C\nolimits_{2} \mathop r\nolimits_{2}^{t} (\mathop P\nolimits_{g}^{t} - \mathop X\nolimits_{i}^{t} ) $$
(20)
$$ \mathop X\nolimits_{i}^{t + 1} = \mathop X\nolimits_{i}^{t} + \mathop V\nolimits_{i}^{t + 1} $$
(21)

Equation 2 describes how the velocity is dynamically updated and Eq. 3 is used to update the position of the “flying” particles.

V t i is the velocity vector at iteration t, r 1 and r 2 represent random numbers in the range [0,1]; P t g denotes the best ever particle position of particle i, and P t i corresponds to the global best position in the swarm up to iteration t [17].

The remaining terms are problem-dependent parameters; for example, C1 and C2 represent “trust” parameters indicating how much confidence the current particle has in itself (C1 or cognitive parameter) and how much confidence it has in the swarm (C2 or social parameter), and ω is the inertia weight. The latter term plays an important role in the PSO convergence behavior since it is employed to control the exploration abilities of the swarm. It directly affects the current velocity, which in turn is based on the previous history of velocities. Large inertia weights allow for wide velocity updates providing the global exploration of the search space, while small inertia values concentrate the velocity updates to nearby regions of the design space.

4.2 Genetic algorithm

Genetic algorithm (GA) is a well-known and frequently used evolutionary computation technique. This method was originally developed by John Holland [20] and his PhD students Hassan et al. [21]. The idea was inspired from Darwin’s natural selection theorem that is based on the idea of the survival of the fittest. The GA is inspired by the principles of genetics and evolution and mimics the reproduction behavior observed in biological populations.

In GA, a candidate solution for a specific problem is called an individual or a chromosome and consists of a linear list of genes. GA begins its search from a randomly generated population of designs that evolve over successive generations (iterations), eliminating the need for a user supplied starting point. To perform its optimization like process, the GA employs three operators to propagate its population from one generation to another. The first operator is the “selection” operator in which the GA considers the principal of “survival of the fittest” to select and generate individuals (design solutions) that are adapted to their environment. The second operator is the “crossover” operator, which mimics mating in biological populations. The crossover operator propagates features of good surviving designs from the current population into the future population, which will have a better fitness value on average. The last operator is “mutation,” which promotes diversity in population characteristics. The mutation operator allows for global search of the design space and prevents the algorithm from getting trapped in local minima [21].

4.3 Hybrid genetic algorithm and particle swarm optimization (HGAPSO)

Although GAs have been successfully applied to a wide spectrum of problems, using GAs for large-scale optimization could be very expensive due to its requirement of a large number of function evaluations for convergence. This would result in a prohibitive cost for computation of function evaluations even with the best computational facilities available today. Considering the efficiency of the PSO and the compensatory property of GA and PSO, combining the searching abilities of both methods in one algorithm seems to be a logical approach. In this paper, the hybrid of GA and PSO named HGAPSO, originally presented by Juang [22], is used. The flowchart of the HGAPSO is shown in Fig. 3.

Fig. 3
figure 3

Flowchart of HGAPSO

Full size image

It is obvious that the feasible region in constrained optimization problems may be of any shape (convex or concave and connected or disjointed). In real-parameter constrained optimization using GAs, schemata specifying contiguous regions in the search space (such as 110*…*) may be considered to be more important than schemata specifying discrete regions in the search space (such as (*1*10*…*), in general. Since any arbitrary contiguous region in the search space cannot be represented by single Holland’s schema and since the feasible search space can usually be of any arbitrary shape, it is expected that the single-point crossover operator used in binary GAs will not always be able to create feasible children solutions from two feasible parent solutions.

The floating-point representation of variables in a GA and a search operator that respects contiguous regions in the search space may be able to eliminate the above two difficulties associated with binary coding and single-point crossover.

Hence, a floating-point coding scheme is adopted here for all of the GA, PSO, and HGAPSO. For the frame structures where design variables must have discrete values, the solutions are achieved by rounding the design variables to the nearest permissible integer number.

5 HGAPSO-ANN model results

In this study, an artificial neural network was used to build a model to predict the power of the solar stirling heat engine by using the data set reported in literature of china [5]. Data set that is used in this study is reported in Table 1. Also, statistical properties of data set are shown in Table 2. The best ANN architecture was 3-4-10-1 (3 input units, 4 neuron in first hidden layer, 10 neuron in second hidden layer, and 1 output neuron). ANN model trained with back propagation network was trained by Levenberg–Marquardt to predict power of the solar stirling heat engine using three parameters (effectiveness of the regenerator, absorber temperature, and high temperature of working fluid) as inputs. The transfer functions in hidden and output layer are sigmoid and linear, respectively.

Table 1 T 1opt for different T H and ɛ R
Full size table
Table 2 Statistical properties of data set which used in this study
Full size table

HGAPSO is used as neural network optimization algorithm and the mean square error (MSE) as a cost function in this algorithm. The goal in proposed algorithm is minimizing this cost function. Every weight in the network is initially set in the range of [−1, 1], and every initial particle is a set of weights generated randomly in the range of [−1, 1].

We used 300 data samples that were chosen by a random number generator for network training. The remaining 100 samples were put aside to be used for testing the network’s integrity and robustness.

The power and efficiency of the solar stirling heat engine prediction in the training and test phase are shown in Figs. 4 and 5, respectively. The simulation performance of the HGAPSO-ANN model was evaluated on the basis of mean square error (MSE) and efficiency coefficient R 2. Table 3 gives the MSE and R 2 values for HGAPSO-ANN model of the validation phases. In general, a R 2 value greater than 0.9 indicates a very satisfactory model performance, while a R 2 value in the range 0.8–0.9 signifies a good performance, and value less than 0.8 indicates an unsatisfactory model performance. Figures 6 and 7 show the extent of the match between the measured and predicted power and efficiency of the solar stirling heat engine values by HGAPSO-ANN model in terms of a scatter diagram.

Fig. 4
figure 4

Comparison between measured and predicted power (HGAPSO-ANN): a Training b Testing

Full size image
Fig. 5
figure 5

Comparison between measured and predicted efficiency (HGAPSO-ANN): a Training b Testing

Full size image
Fig. 6
figure 6

R2 HGAPSO-ANN power predicted

Full size image
Fig. 7
figure 7

R2 HGAPSO-ANN efficiency predicted

Full size image
Table 3 Performances of HGAPSO-ANN model
Full size table

6 Conclusions

In this article, we have presented a genetic algorithm evolved neural network. Our methodology presents a hybrid genetic algorithm and particle swarm optimization-based neural network (HGAPSO-ANN), which effectively combines the local searching ability of the hybrid particle swarm optimization and genetic algorithm. The idea of our algorithm is that each initial point of the neural network is selected by a hybrid genetic algorithm and particle swarm optimization, and the fitness of the hybrid genetic algorithm and particle swarm optimization is determined by neural network. The hybrid genetic algorithm and particle swarm parameters are carefully designed to optimize the neural network, avoiding premature convergence. The experimental measurement data have showed that the predictive performance of the proposed model is very well. This has been supported by the analysis of the changes of connection weights and biases of the neural network. One problem when considering the combination of neural networks and hybrid genetic algorithm and particle swarm optimization for prediction of power and efficiency of the solar stirling heat engine is the determination of the optimal neural network topology. Our neural network topology described in this experiment is determined manually. A substitute method is to apply the particle swarm optimization for neural network structure optimization, which will be a part of our future work.