1 Introduction

Feature representation and efficient classification are two important issues in object recognition systems [1, 2]. To achieve the goal of extracting features in a certain scale, Laplacian of Gaussian (LoG) is introduced [3] to simulate the lateral inhibition for edge detection. In order to extract features in certain orientations, oriented filters or steerable filters are introduced by Freeman [4]. However, to be a powerful descriptor, the feature extractor should be anisotropic, which means that it should enhance the feature in a certain scale and orientation simultaneously. Gabor transformation [5] has been widely used as an effective tool in the image processing and pattern recognition tasks. Different from steerable filters [4, 6], Gabor can also include information both in spatial and frequency domains, and it inherits the property of Gaussian, which is a powerful smoothing tool for the image. The derivative of Gaussian is regarded as an important tool to extract the edge feature for images, which is widely used in image processing and computer vision. In face recognition research community, the edge distribution information has been successfully investigated in [7]. In this paper, Gradient Gabor is proposed based on the combination of Fourier transform and the derivative of Gaussian. Gradient Gabor can capture the features in both spatial and frequency domains to deliver orientation and scale information.

In this paper, Kernel Fisher Discriminant Analysis (KFDA) is combined with Gradient Gabor to calculate multiple discriminant subspaces, which can capture nonlinear variations contained in the training database. One problem of the original KFDA lies in that it is defined based on all training samples, which is the curse of the kernel Fisher method when a large training database is available [8–11]. In [11], Liu et al. proposes a method to solve this problem by using kernel trick to select an optimized subset from data and form a subspace of the feature space, however, it is a little complex and not very effective for reducing time consuming or enhancing recognition accuracy according to the reported results [8, 11]. Another problem is that the original kernel fisher method is a global one, which can not exploit the structure information contained in faces. In [10], the KPCA plus LDA framework provides an efficient way to implement KFDA, but it is still global one and need to save all the training samples. In our former work [8], the bagging is used to develop an efficient KFDA, but it still needs to save about half of training samples to get a reasonable performance. Efficient Kernel Fisher (EKF) is proposed based on local kernel mapping and the clustering centers of the training dataset to reserve both local and global information by constructing multiple subspaces. In order to evaluate the performance of the proposed method, we apply it to solve the face recognition problem. Experiments on two face databases, FRGC version 1 and FRGC version 2 [12], are conducted to compare the Gabor and GGabor-based EKF and other kernel fisher methods.

The rest of this paper is organized as follows. The Gradient Gabor filter is proposed in Sect. 2. The recognition method based on Efficient Kernel Fisher (EKF) analysis is described in Sect. 3. The experiments on FRGC version 1 and FRGC version 2 [12] are given in Sect. 4. We conclude the paper in Sect. 5.

2 Motivation of Gradient Gabor filter

In this section, we first briefly review Gabor wavelet, and then define the Gradient Gabor (GGabor) filters. The difference between Gabor and GGabor is then investigated, which shows that GGabor can provide more stable phase information.

2.1 Gabor wavelet

The Gabor wavelets (kernels, filters) can be defined as follows [13]:

$$ \psi_{u,v} (z) = \left( {{{||k_{u,v} ||^{2} } \mathord{\left/ {\vphantom {{||k_{u,v} ||^{2} } {\sigma^{2} }}} \right. \kern-\nulldelimiterspace} {\sigma^{2} }}} \right)e^{{( - ||k_{u,v} ||^{2} ||z||^{2} /2\sigma^{2} )}} \left[ {e^{{ik_{u,v} z}} - e^{{ - \sigma^{2} /2}} } \right], $$
(1)

where \( \mathop {k_{u,v} }\limits^{ \to } = \left( \begin{gathered} k_{v}\; cos\Upphi_{u} \hfill \\ k_{v} \;sin\Upphi_{u} \hfill \\ \end{gathered} \right),k_{v} = {{f_{\max } } \mathord{\left/ {\vphantom {{f_{\max } } {2^{v + 2} }}} \right. \kern-\nulldelimiterspace} {2^{v + 2} }},\Upphi_{u} = u{\frac{\pi }{8}}, \) v is the scale and u is the orientation with f max = π/2. In this paper, 4 scales and 4 orientations are used. Gabor wavelet can enhance the features in certain scales and orientations, which is widely used in image processing and object recognition. The Gabor transformation of a given image is defined as its convolution with the Gabor kernel functions:

$$ G_{{u, v}} (Z) = 1(Z)*\Uppsi_{{ u , v}} (Z), $$
(2)

where z = (x, y), and the symbol * denotes the convolution operator. G u,ν(z) is the convolution result corresponding to the Gabor kernel at scale v and orientation u. The Gabor wavelet coefficient G u,ν(z)is a complex, which can be rewritten as:

$$ G_{u,v} (z) = A_{u,v} (z) \cdot \exp \left( {i\theta_{u,v} (z)} \right), $$
(3)

with a magnitude item A u,v(z), and a phase item θ u,v(z). It is well known that the magnitude varies slowly with the spatial position, while the phases rotate in some rate with positions, even preserving more detailed information. Due to this rotation, the phases taken from image points only a few pixels apart have very different values, although representing almost the same local feature [13]. This can cause severe problems for object (face) matching, and it is just the reason that most previous works make only use of the magnitude for face classification. In the following part, we introduce a new Gradient Gabor filter, which can provide a relatively stable representation of faces.

2.2 Gradient Gabor filters

The Gradient Gabor (GGabor) filters are defined based on the derivative of Gaussian function:

$$ G\psi_{u,v} (z) = - {\frac{{||k_{u,v} ||^{4} }}{{\sigma^{4} }}}\left( {\left( {\cos \left( {\Upphi_{u} } \right)x + \sin \left( {\Upphi_{u} } \right)y} \right)e^{{ik_{u,v} z}} + C} \right)e^{{\left( {{{ - ||k_{u,v} ||^{2} ||z||^{2} } \mathord{\left/ {\vphantom {{ - ||k_{u,v} ||^{2} ||z||^{2} } {2\sigma^{2} }}} \right. \kern-\nulldelimiterspace} {2\sigma^{2} }}} \right)}} , $$
(4)
$$ C = - \left( {{\frac{{\left( {\cos \left( {\Upphi_{u} } \right) + \sin \left( {\Upphi_{u} } \right)} \right)}}{{i\sigma^{2} }}}\left( {k_{v} \cos \left( {\Upphi_{u} } \right) - k_{v} \sin \left( {\Upphi_{u} } \right)} \right)\exp \left( { - {\frac{\pi }{{\sigma^{2} }}}\left( {k_{v} } \right)^{2} } \right)} \right), $$
(5)

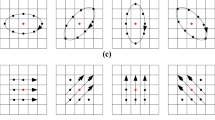
where C is used to make Gradient Gabor DC-free (see the Appendix). Gabor wavelet is modulated by a Gaussian function, which can be regarded as the weighted Fourier transform. The weights for Gabor wavelets are actually exponentially declining with increasing distance. However, Gradient Gabor is defined based on a weighted Gaussian function, which is not declining in an exponential speed as in Gabor wavelets, because it is slowed down by a linear function as shown in Eq. 4 and Fig. 1. Different from original Gabor filters, it can be more stable and provide a robust presentation of the face object by using the multi-scale and multi-orientation local features. Samples of 2D Gabor and GGabor filters are shown in Fig. 2.

Fig. 1
figure 1

Visualization of real parts of 1-D Gradient Gabor and Gabor Filters

Full size image
Fig. 2
figure 2

Visualization of real parts of 2-D Gradient Gabor and Gabor Filters, a is for Gradient Gabor, b is for Gabor (four scales and four orientations)

Full size image

3 Ensemble-based Efficient Kernel Fisher classifier

Face recognition is still an ongoing topic in computer vision research [8–14], because the current systems only perform well under the controlled environment but tend to fail in complex situations with variations in different factors such as pose, illumination, and expression. Major statistics-based approaches for face recognition include Eigenface [14] and Fisherface [14]. Eigenface and Fisherface are the statistical learning methods based on Principal Component Analysis (PCA) and Fisher Discriminant Analysis (FDA), which are well-known linear feature extraction approaches. In recent years, the kernelized feature extraction[15–17] methods have been paid much attention, such as Kernel Principal Component Analysis (KPCA) [10, 17] and Kernel Fisher Discriminant Analysis (KFDA) [8, 9], which are nonlinear extensions to PCA and FDA, respectively. However, one of the problems in KFDA lies in its high dimensionality, when the size of the training database is very large. To solve the problem, we utilize local kernel mapping method to efficiently find discriminant subspaces. As shown in Fig. 3, we divide the face image into several subregions, from which we calculate Gabor and GGabor features to train an ensemble of classifiers. To preserve the global distribution information, the clustering centers are further incorporated into the local kernel mapping scheme, which are the so-called EKF method.

Fig. 3
figure 3

An example of face image divided into 48 subregions

Full size image

3.1 Kernel Fisher discriminant analysis

Kernel Fisher Discriminant Analysis is exploited to calculate a discriminant transformation subspace, and the input data is first projected into an implicit feature space F by a nonlinear mapping \( \Upphi :x \in R^{N} \ge f \in F \). In its implementation, Φ is implicit by just computing the inner product of two vectors in F using a kernel function [8, 9]:

$$ k(x,y) = (\Upphi (x) \cdot \Upphi (y)). $$
(6)

The between-class scatter matrix S b and within-class scatter matrix S w are defined as follows:

$$ {\mathbf{S}}_{b} = \sum\limits_{i = 1}^{C} {p(\varpi_{i} )(u_{i} - u)(u_{i} - u)^{T} } , $$
(7)
$$ {\mathbf{S}}_{w} = \sum\limits_{i = 1}^{C} {p\left( {\varpi_{i} } \right)E} \left\{ {\left( {\left( {\Upphi \left( {x_{i} } \right) - u_{i} } \right)\left( {\Upphi \left( {x_{i} } \right) - u_{i} } \right)^{T} } \right)|\varpi_{i} } \right\}, $$
(8)

where \( u_{i} = \left( {{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n}} \right)\sum\limits_{j = 1}^{{n_{i} }} {\phi \left( {x_{ij} } \right)} \) denotes the sample mean of class i, u is the mean value of all training images, and p(ϖ i )is the prior probability.

In the original kernel fisher method, \( {\mathbf{w}} \in F \) should lie in the span of all the samples in F, named Basis Support Vectors:

$$ {\text{BSVs}} = \left( {\phi \left( {x_{1} } \right),\phi \left( {x_{2} } \right), \ldots ,\phi \left( {x_{N} } \right)} \right), $$
(9)
$$ {\mathbf{w}} = \alpha {\text{BSVs}}^{T} , $$
(10)

where N is the total number of the training samples. The kernel matrices are defined as follows:

$$ {\mathbf{K}}_{w} = \sum\limits_{i = 1}^{C} {p\left( {\varpi_{i} } \right)E\left( {\eta_{j} - m_{i} } \right)\left( {\eta_{j} - m_{i} } \right)^{T} } , $$
(11)
$$ {\mathbf{K}}_{b} = \sum\limits_{i = 1}^{C} {p\left( {\varpi_{i} } \right)\left( {m_{i} - \mathop m\limits^{\_} } \right)\left( {m_{i} - \mathop m\limits^{\_} } \right)^{T} } , $$
(12)

where \( \eta_{j} = \left( {k\left( {x_{1} ,x_{j} } \right),k\left( {x_{2} ,x_{j} } \right), \ldots ,k\left( {x_{n} ,x_{j} } \right)} \right)^{T} ,m_{i} = \left( {{\frac{1}{{n_{i} }}}\sum\nolimits_{j = 1}^{{n_{i} }} {k\left( {x_{1} ,x_{j} } \right)} ,{\frac{1}{{n_{i} }}}\sum\nolimits_{j = 1}^{{n_{i} }} {k\left( {x_{2} ,x_{j} } \right)} , \ldots ,{\frac{1}{{n_{i} }}}\sum\nolimits_{j = 1}^{{n_{i} }} {k\left( {x_{n} ,x_{j} } \right)} } \right)^{T} , \) and \( \mathop m\limits^{\_} \) are the mean vector of all η j .

In [8], we can find that the definition of w based on all training samples is the curse of the kernel fisher method, which requires to save the whole training database. In the following part, we propose a new Efficient Kernel Fisher (EKF) scheme to solve this problem.

3.2 Efficient Kernel Fisher analysis for ensemble-based face recognition

In this part, we try to redefine w by using the local region features and the clustering centers of the training samples. The new Basis Support Vectors are

$$ {\text{BSVs}}^{'} = \left( {\phi \left( {X_{1}^{1} } \right),\phi \left( {X_{2}^{1} } \right),.X_{i}^{j} .,\phi \left( {X_{L}^{{C_{m} }} } \right)} \right), $$
(13)
$$ {\mathbf{w}}^{'} = \alpha^{'} {\text{BSVs}}^{'T} , $$
(14)

where C m is the number of clustering centers, and X is the clustering center calculated from the training data by applying K-means method on the training set with C m  ≪ N. X j i is the Gabor or Gradient Gabor feature extracted from the local region R i , i = 0, 1,…, L − 1 of the jth clustering face image. From Eq. 13, we can see that \( {\mathbf{w}}^{'} \) is based on both training samples and local region features. Each subclassifier can preserve the information about the relationship among local features across the training database by using local kernel method.

In the classification procedure, v 1, v2 are the discriminant feature vectors corresponding to two face images P 1, P 2, the similarity of which can be calculated by using the cosine rule as

$$ d\left( {P_{1} ,P_{2} } \right) = \sum\limits_{i = 1}^{L} {{\frac{{v_{i}^{1} .v_{i}^{2} }}{{||v_{i}^{1} ||.||v_{i}^{2} ||}}}} . $$
(15)

From Eq. 15, we can easily know that the proposed method is based on the sum rule, which actually can exploit the spatial structure information of the face image.

4 Experiments

To validate usefulness of the proposed method, experiments on FRGC version 1 and version 2 databases are conducted. For the experiment 4 on the FRGC version 1, the training set contains 366 images, the target set (Gallery) contains 943 controlled images, and the query set (Probe) has 943 uncontrolled images. For experiment 4 of FRGC version 2, the training set contains 12,776 images, the target set contains 16,028 controlled images, and the query set has 8,014 uncontrolled images. In our study, the polynomial kernel function, k(x, y) = (x.y)2 is used to test the performance of the proposed method.

As shown in [12], the experimental setting is designed for indoor controlled still images versus uncontrolled still images, which is the most challenging FRGC experimental condition. In both experiments, face images are cropped and normalized to the 64 × 72 images, which are further divided into 8 × 12-sized subregion, and the downsample factor for GGabor and Gabor features is 2. In the recognition performance evaluation experiment, we choose features step by step to get the best recognition rates for all comparative methods.

4.1 Comparisons based on FRGC version 1

In this experiment, the mean sample for each class is calculated in the target set. The experiment is conducted to compare the performance of the original Kernel Fisher method and EKF based on Gabor and Gradient features. The P_GGabor or P_Gabor is based on the phase information, M_GGabor or M_Gabor uses the magnitude information, and A_GGabor or A_Gabor exploits both magnitude and phase information. A_Gabor (K) and A_GGabor (K) denote that the methods are based on the original Kernel fisher method, while A_Gabor (E) and A_GGabor (E) are based on the Efficient Kernel Fisher (EKF) method. The Ensemble-GFC method is based on the linear Fisher analysis, details about which can refer to [18, 19]. From Table 1, we can see that A_Gabor (E) and A_GGabor (E) have achieved better performances than the original kernel Fisher method partly for their reserving the structure or local information in faces. While the global information is preserved by using 40 clustering centers. Compared to the original kernel Fisher method using all 366 model samples, EKF is more suitable to the real-world applications. It should be noted that the proposed method achieved a much better performance than the well-known result in [17], which only uses part of FRGC version 1. Compared to the result of LBP (40%) [20], the proposed method also achieves a much better performance as shown in Table 1. The comparative performances of different kernel functions for EKF are also evaluated as shown in Table 2, which shows that the performance of the proposed method is better when the nonlinear kernel is used, because it can capture more complex information contained in the training database.

Table 1 The comparative experiments between original Kernel Fisher and EKF FRGC version 1
Full size table
Table 2 The comparative performances of different kind of kernel functions for EKF on FRGC version 1
Full size table

In Fig. 4, the relationship between the number of clustering centers and recognition rates is depicted, which indicates that the more clustering centers are used, the better performance can be achieved due to more global information reserved. From Fig. 5, we can also find that the phase part of GGabor achieved a better performance than that of Gabor wavelet in terms of rank-1 recognition rates, which confirms that Gradient Gabor can provide more stable information than Gabor. Furthermore, the full magnitude and phase information can be used to enhance the performance of the face recognition system.

Fig. 4
figure 4

Recognition rates of A_GGabor(E) for different numbers of clustering centers on FRGC version 1

Full size image
Fig. 5
figure 5

Recognition rates of the EKF method (40 clustering centers) with different kinds of GGabor and Gabor features on FRGC version 1. P_GGabor and P_Gabor, M_GGabor and M_Gabor, A_GGabor and A_Gabor are base on the phase part, magnitude part, and full part of GGabor and Gabor features, respectively

Full size image

4.2 Comparisons based on FRGC version 2

In this scheme, another bigger database is used to evaluate the performance of the face recognition system. As for the high complexity of the original kernel fisher method for a large training database, we choose a subset of 5,000 samples as basis support vectors to train kernel fisher discriminant subspaces using the bagging-based method as in [8], which are A_Gabor (BK) and A_GGabor (BK). For the EKF method, five subclassifiers are trained for each 100 clustering centers resulting in a total of 500 model size, which greatly decreased the model size with an acceptable performance as shown in Table 3. Therefore, the EKF method is a more promising way for real applications.

Table 3 The comparative experiments between bagging-based Kernel Fisher and the EKF method on FRGC version 2
Full size table

To compare with the results in [17], we conduct another experiment on the FRGC version 2 database. In the experiment, the size of the normalized image is 128 × 144, and the subregion size is 16 × 24. To further increase the performance, we choose five scales and eight orientations for Gabor wavelet. The downsample parameters for x and y directions are set as 2 and 4, respectively. The recognition rate for the GGabor-based EKF is 78.4% when FAR is 0.1%, and the comparative result is 76% in [17], which show that the performance of the proposed method is better.

5 Summary

This paper proposes a new face recognition method based on the Gradient Gabor feature and EKF, in which both magnitude and phase are used to represent the face. The main contributions of the proposed method are (1) A new Gradient Gabor is proposed for face recognition. Different from Gabor phase, the GGabor phase can offer relatively stable information for face recognition. (2) An Efficient Kernel Fisher method based on local kernel mapping and clustering centers of training dataset is proposed to find discriminant subspaces. We have validated the proposed method by conducting the experiments on two face databases, FRGC version 1 and FRGC version 2.

Although the performance of Gradient Gabor and Efficient Kernel Fisher is successfully applied for face recognition, it is interesting to apply the proposed method to other object recognition tasks in future research.