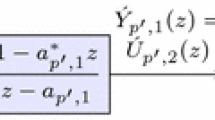
Abstract
This paper presents a neural network-based behavioral model for accurately reproducing the nonlinear and dynamic behavior of new wireless communication devices. Moreover, an efficient procedure to extract a behavioral Volterra model from the parameters of the NN-based model is explained, thus providing a simple way to construct very compact and accurate models, which may provide open information about device performance. Experimental tests try to demonstrate the validity of the proposed approach, for characterization of RF transistors and power amplifiers, showing strong nonlinearities and memory effects in the analyzed bandwidth.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The development of new RF devices for wireless communication systems (i.e., GSM, GPRS, UMTS, WCDMA) needs accurate modeling of its components. Multiple wide-area and local-area wireless systems are now deployed in various places around the world, with a broad combination of constant and envelope-varying signals, different multiplexing schemas and high to very low transmitter output powers. As a result, the design of a RF power amplifier (PA) for such multi-mode applications is a challenge.
A PA efficiency in converting applied DC power to output RF power increases as the amplifier approaches a point named output compression. For maximum efficiency, it is desirable to operate the PA well into compression. When in compression, however, if the input signal has a varying envelope, it results in severe signal distortion and memory effects. To reproduce the envelope-varying input signal with good fidelity, the PA must be operated linearly, at fixed gain. To obtain this, some techniques can be applied, but they also reduce PA efficiency and this is very undesirable for the battery life of a mobile device. Memory effects, in the time-domain, cause the output of the devices to deviate from their usual behavior, therefore behaving nonlinearly. New approaches are needed for new RF devices design, due to the fact that linear RF techniques are unlikely to meet all requirements for near-future mobile terminals [1].
Analysis of nonlinear electronic systems often requires an analytical model for each component that allows drawing conclusions about the system performance. This approach aims to extract (from measurements) a nonlinear relationship in order to build an input/output model (named physical model) able to generalize the nonlinear dynamic behavior of an electronic component and for input waveforms not used in the characterization set. This procedure is based on the known physical behavior of the modeled device that dictates an equivalent-circuit model topology. However, this traditional technique is useful where data trace is known to follow a specific mathematical model. But problems arise when the modeled behavior is previously unknown and so is the model structure.
Since the worldwide wireless communications growth over the last years, measurement-based techniques for PAs modeling has been identified as a particularly critical topic, due to the peculiar features of their nonlinear behavior (such as slow and fast memory effects) and the related impact on the system-level distortion and intermodulation undesired effects [2]. Behavioral modeling is a measurement-based approach that provides a convenient and efficient way to predict system-level performance without the computational complexity of full circuit simulation or physics level analysis of nonlinear systems, therefore significantly speeding up analysis and design processes [3]. In fact, behavioral models have become the object of extensive research during the last few years as a black-box, technology-independent tool to model off-the-shelf PAs, starting from conventional or ad hoc measurements [4]. The model is considered as a black-box in the sense that no knowledge of the internal device structure is required and the modeling information is completely included in the device external response (the measurements).
On the one hand, for development of PA behavioral models, Neural Networks (NNs) have received increasing attention [5, 6]. The question on how to learn the nonlinear behavior response of an amplifier to several input power levels, in order to characterize the memory effects on the device in the time-domain, can be answered with a time-delayed neural network (TDNN) model that can learn a dynamic nonlinear behavior if trained with enough input–output time-domain data samples and their delays, at different power levels, simultaneously [7, 8].
On the other hand, Volterra series models have (traditionally) played an important role in behavioral black-box modeling of dynamic nonlinear elements. Although it has certain popularity, behavioral modeling based on a Volterra series holds their validity only for low dimensional, weak nonlinear systems and requires heavy characterization efforts for Volterra kernels extraction, especially when multi-tone intermodulation is a matter of interest [9].
Our proposal in this work is to combine the best of both worlds, and, using a NN-based behavioral model, obtain an analytical Volterra series model, extracted in function of the network model parameters. This fact can be a great asset for medium-power analysis, because the neural analytical models can be more complex to implement into existing simulation CAD software tools, than compact models based on the Volterra series.
The organization of the paper is as following: Section 2 introduces some concepts regarding behavioral modeling of electronic devices, explaining the importance of the Volterra model. Section 3 explains the proposed procedure for obtaining a Volterra model from a TDNN-based behavioral model. Section 4 presents some experimental results that validate the proposed procedure. Finally, the conclusions are presented in Sect. 5.
2 Behavioral modeling of electronic devices
A behavioral model relates output waveforms y(t) to input waveforms x(t) through an analytical formula, such as y(t) = F[x(t)], which states that the output of a system is an instantaneous function of the input waveforms. Instead, a model that incorporates the notion of memory is shown in Eq. 1, which states that the output is not only an instantaneous function of the input signals, but it also depends on the time-derivatives of the inputs. This concept is called memory
Since the model has to be evaluated on a digital computer, it is convenient to adopt a discrete time representation, such as shown in Eq. 2. It assumes that the time is a succession of (generally uniform) time samples over a convenient sampling period
In order to model the consequences of the memory phenomena within devices behavior, dynamic behavior modeling is required. In fact, it is the incorporation of long-term memory beyond otherwise static nonlinear behavioral models what distinguishes the newest behavioral models for PAs [9].
If the function F[.] in Eq. 2 models a single-input, single-output (SISO) nonlinear dynamical system, it can be represented exactly by a converging finite series of the form of Eq. 3, in discrete time-domain. This equation is known as the Volterra series expansion or power series with memory [10], because the output of the system depends on the actual and also on the past values of the inputs. The series is formed with the sum of terms that have some coefficients h i , with i:1...n, named Volterra kernels [11], where i indicates kernel order
The Volterra approach characterizes a system as a mapping between two spaces, which represent the input and output spaces of that system. The Volterra series is an extension of the Taylor series representation to cover dynamic systems. It is based on a Taylor-series expansion of a device nonlinearity around a fixed bias point or around a time-varying signal. In 1959, Volterra [12] showed that such a series is capable of representing any analytic, time-invariant system. A Volterra series approximation produces an optimal approximation near the point where it is expanded. Therefore, it is known for its good modeling properties of small-signal (or mildly nonlinear) regimes.
Every nonlinear device having a Volterra series expansion has a set of Volterra kernels h 1, h 2, h 3,..., h n about an operating point. The number of terms in the kernels of the series increases exponentially with the order of the kernel. This is the most difficult problem with the Volterra series approach and imposes some restrictions on its application to many practical systems, which are restricted to use second order models because of the difficulty in kernels expression [13].
An effective method of analyzing nonlinear RF/Microwave intermodulation (undesired modulation of one signal by another, caused by nonlinear processing of the signals, which has a direct influence on the system performance) in FET transistors and PAs is through the use of Volterra kernels. A first order kernel describes the linear response of the system, while higher order kernels describe the nonlinear dynamical behavior [14].
The key to a practical use of Volterra series in system design and analysis is finding the values for the kernels or the nonlinear transfer functions. Several methods have been developed for measuring the kernels, in both time and frequency domains [15]. During the last years, several methods have appeared for kernel approximation by interpolation techniques [16], kernel estimation through measurements [17] input–output data statistics [18] or polynomials [19]. Even so, the measurement and identification of the kernels can be very difficult in practice, and this has resulted in the lack of wide practical acceptance of the Volterra approach for nonlinear systems, and its ineffectual use within commercially available circuit simulators.
Back in 1995, for the Biology field, Wray and Green [20] have introduced the idea that the Volterra kernels were related to a neural network model. The basic mathematical relationships between time invariant Volterra models and feedforward ANNs have been addressed in [21], and it has been shown that the two models become equivalent if the activation functions of the single hidden layer are distinct polynomials with trainable coefficients [22]. Those approaches to Volterra kernels’ determination propose proprietary neural network models and learning algorithms and are not easy to use for higher order kernels’ determination. Furthermore, they represent a temporal behavior by means of multi-delayed samples of a unique input/output variable.
This work, instead, proposes a simple and straightforward procedure to extract the Volterra series, directly from a behavioral neural network-based model. The procedure can be applied even in the case of a multivariable nonlinear dependence, for example, input voltages/output current I ds (V gs, V ds) relationship in a PA transistor. A general model can be obtained, independently of the physical circuit under study. The behavioral model proposed is easy to load inside a circuit simulator, Furthermore, an analytical solution derived from the behavioral model, which could be easily implemented inside a commercial circuit simulator, is provided. This fact can be a useful chance when Volterra series analysis is implemented with a commercial RF CAD tool.
The proposed procedure has already been applied for modeling a simple single-input–single-output diode device [23]. With the intention of proving extensibility to the procedure for modeling a multiple-input–single-output relationship, in this paper we have applied the proposed procedure to two completely different case studies: a transistor and a PA, working in RF condition. The procedure is explained in detail in the next section.
3 Volterra identification method neural network-based
An important task when designing an amplifier is the choice of its active component (the transistor). A common choice for PAs is a Field-effect (FET) transistor build on GaAs (Gallium Arsenium), used as high-gain and high-power device. Most of the nonlinear behavior of this device is due to the drain to source output current I ds that depends on the gate and drain voltages V gs and V ds, respectively.
The Volterra series model for the I ds current is shown in Eq. 4, showing up to third order terms, where I ds0 = f (V gs0, V ds0) is the transistor bias point and v gs and v ds are the incremental intrinsic voltages with respect to the bias voltages
The coefficients of the series are the first order (G m1 and G ds), second order (G m2, G ds2 and G md ) and third order (G m3, G ds3, G m2d , G md2) Volterra kernels of the series, which provide information regarding the nonlinear behavior under study. The kernel G m1 is also called transconductance, expression of the performance of the transistor. In general, the larger the transconductance for a device, the greater the gain (amplification) it is capable of delivering, when all other factors are held constant. Similarly, the kernel G ds represents the output conductance.
Figure 1 shows how the Volterra kernels allow identifying multi-tone intermodulation products. When two signals, with frequencies F 1 and F 2, respectively, are introduced into an amplifier bandwidth (dotted line) and increased in power input, the device is pushed into compression, where a nonlinear amplifier generates intermodulation products at frequencies 2F 1 − F 2 and 2F 2 − F 1 (marked with arrows) whose amplitudes (in the frequency-domain) can be determined by the Volterra kernels.
Despite its practical utility, the Volterra kernels calculation or identification is not an easy task. The number of terms in the kernels of the series increases exponentially with the order of the kernel. It imposes some restrictions on its application to many practical systems, which are restricted to use second order models because of the difficulty in kernels expression. In the case of the current/voltages relationships in a transistor, the existing approaches are not useful because the multivariable dependence could not be easily modeled.
In this work, we propose a simple two-step procedure for kernel extraction. Step one creates a neural network-based behavioral model for learning the device nonlinear behavior. After the model has been trained with input/output device measurements, Step two performs a series of calculations that, making use of the neural model parameters, find the desired Volterra kernels.
3.1 Step one
It starts with the definition of an NN-based behavioral model. The neural network used for representing a nonlinear system with dynamic behavior is a feedforward Time-Delayed Neural Network (TDNN) model, shown in Fig. 2.
The inputs to the model are the samples of the independent variables, together with their time-delayed values. In the example presented, input variables are V ds and V gs, and output variable is I ds. The model can be easily extended to more input/output variables.
Each variable can have a delay tap between 0 and N. If we consider two input variables with the same number N of delays, then the total number of input neurons is M (M = 2(N + 1)). In the hidden layer, the number of hidden neurons varies between 1 and H, being H any integer number.
The hidden units have a nonlinear activation function. In our example, we will use the hyperbolic tangent (tanh) because it is a common choice for electronic devices modeling. Initially, H is set to M, but the number of hidden neurons can be changed to improve network accuracy if necessary. The hidden neurons receive the sum of the weighted inputs plus a corresponding bias value each. For bias representation, the hidden neurons receive an input node with fixed value equal to +1. The output neuron has a bias as well.
In the notation used, a super-index in the weights and bias allows identifying to which layer of connections they belong. For example, w 1 ji represents a connection that goes to neuron j at the hidden layer and comes from neuron i at the input layer. Instead, w 2 i represents a connection coming from a hidden neuron i and going to the output layer. In this second group of connection’s weights, the sub-index that indicates the destination neuron has been eliminated because there is only one possible destination neuron (the output).
The TDNN-based behavioral model output is shown in Eq. 5, where x i , i = [1...M] are the inputs to the TDNN model, H is the number of hidden units
Once the TDNN model has been defined, it is trained with appropriate measurements. The input and output waveforms are expressed in terms of their discrete samples in the time-domain. To improve accuracy and to speed up learning, the inputs are normalized to the domain of the hidden neurons’ nonlinear activation functions (in our case, for the tanh, [−1; +1]).
During training, the network parameters are optimized using the Levenberg–Marquardt algorithm [24], which has been chosen due to its good performances and speed in execution. To evaluate learning accuracy, the mean square error (mse) over the normalized training set is calculated.
To avoid overtraining, the total amount of measurement data available is divided into training and validation subsets, all equally spaced, and the “early-stopping” technique [25] has been used as well. The initial weights and biases of the model are calculated using the Nguyen–Widrow initial conditions [26], instead of a purely random initialization, to reduce training time.
3.2 Step two
The output of the TDNN-based behavioral model (Eq. 5) is expanded as a Taylor series around the bias values of the hidden nodes. The hidden nodes’ activation function derivatives with respect to the bias are calculated, yielding Eq. 6, where d means derivative order
Developing Eq. 6 and grouping common terms according to the derivatives order, yields Eq. 7
Equation 8 shows an instance of this formula for the proposed TDNN model with two input variables V gs and V ds, when d = 3 (due to space restrictions, only some third order terms are shown). If this equation (the TDNN-based behavioral model) is compared to Eq. 4 (Volterra series model for a FET transistor), the Volterra kernels h n can be recognized as the terms between brackets in Eq. 8. This step is expressed graphically in Fig. 3.
From this comparison, Eqs. (9)–(13) have been derived which allow the calculation of any Volterra kernel order using the weights and hidden neurons’ bias values of a TDNN-based behavioral model. In the formulas, the derivatives have been developed. Further details on the presented equations can be found on [27].
4 Experimental data
Four experiments with measurement data have been performed for testing the proposed procedure for Volterra kernels and Volterra model extraction from a TDNN-based behavioral model. In any case, good results have been obtained and the proposed procedure has been verified. The figures here reported have been obtained after implementation of both behavioral and Volterra approximation models into a commercial circuit’s simulator.
The first and second test involve a FET transistor, biased at a certain point and working in DC (static behavior), and then at RF (dynamic behavior) compressed at 1 GHz.
The third and fourth experiments are made with measurements from nonlinear PAs, presenting strong nonlinearities and memory effects, working at 1 and 4 GHz, characterized through one-tone and two-tone tests, respectively.
4.1 FET transistor DC behavior
The first test involves DC (static) measurements from a FET transistor, biased at V ds = 3 V, where the following typical parameter values have been used: V gs = [−1;0]V step 0.1 V, V ds = [0;5]V step 0.25 V. A behavioral model such as the one presented in Fig. 2 has been trained with 121 measurements, with N = 0, M = 2, H = 10, until a predefined accuracy has been reached (mse = 1e − 06) after 1,000 training epochs. At the end of the training procedure, the Volterra kernels up to the third order have been extracted from the behavioral model and the Volterra series expansion corresponding to this device has been built. The results are shown in Fig. 4. This figure reports the measurements of the drain current behavior in a FET transistor (dotted line) compared to the TDNN-based behavioral model (dark full line) and Volterra models (gray full line). The approximation of both models to the input/output data is highly accurate.
4.2 FET transistor RF behavior
Concerning the dynamic behavior of a FET transistor, time-domain measurements have been performed to obtain suitable training sets for the behavioral model. The transistor which has been characterized was a medium power GaAs MESFET (10 × 100 mm) transistor, with knee voltage V k = 1.2 V and maximum drain current I max = 180 mA. A drain bias voltage of 5 V has been selected, while −2 V gate bias voltage has been chosen, corresponding to a drain current I dc = 70 mA. Operating frequency (F 0) is 1 GHz and time-domain characterization is performed up to the fourth harmonic.
A behavioral model such as the one presented in Fig. 2 has been trained with 800 data points, with N = 2, M = 6, H = 10, until a predefined accuracy has been reached (mse = 1e − 06) after 1,000 training epochs. Again, using the proposed two-step procedure, the corresponding Voltera model has been built, considering also the delayed samples of the input variables. Results are reported on Fig. 5. The behavioral model correctly reproduces the PA nonlinear dynamic behavior, as well as its corresponding Volterra approximation. However, the last has a higher approximation global error than the TDNN model, certainly due to the fact that it includes only up to third order kernels.
4.3 PA one-tone test
Measurements obtained from a Cernex 2266 PA, with 1–2 GHz bandwidth and 29 dB gain have been used to train the behavioral model, with the parameters: N = 4, M = 10, H = 10. The input–output 200-point data sets have been built with cascading samples obtained from six source power levels, in the entire power range, with 3 dB power step.
The mse associated to this behavioral model is higher than the previous models (1e − 04); however, in this case TDNN and Volterra model are almost indistinguishable one another, as reports Fig. 6.
4.4 PA two-tones test
In this case, measurements from a Cernex 2267 PA have been used, with a 2–6 GHz bandwidth, a 42-dB gain, and 1 dB compression at 32 dBm, stimulated with two tones at center frequency 4.1 GHz and frequency spacing 100 MHz. Each power is swept from −30 to −8 dBm that is 4 dB over the 1-dB compression point for the combined input power. A characterization bandwidth of 22 GHz has been used to calculate the tap delay, in order to take into account fifth order harmonic distortion.
In this case the behavioral model parameters have been setup at N = 4, M = 10 and H = 10. For larger memory duration the neural network tends to become unstable. Results are shown in Fig. 7 for the time-domain. To see the modeling performance in the frequency domain, a Fast Fourier Transform (FFT) has been applied to output waveforms either of TDNN and Volterra model simulation, and compared with spectra measurements made with a Spectrum Analyzer. The results are presented in Fig. 8, where power amplitudes at fundamental, third-order and, only for the TDNN model, fifth-order intermodulation have been plotted against input power. Both models show a good behavior in the full power range and well-matched behavior both in time and frequency domains.
PA 4 GHz time-domain RF measurements (solid line) versus behavioral TDNN-based model (triangle in dotted line) versus Volterra model (inverted triangle in dotted line), for two input tones at 4.05 and 4.15 GHz, for Pout (at f1 = 4.15 GHz), IMD3 (at 2f2 − f1 = 4.25 GHz) and, only for the TDNN model, IMD5 (at 3f2 − 2f1 = 4.35 GHz)
5 Conclusions
Modern communication systems composed by RF/Microwave electronic devices generally have nonlinear behavior, rich in high-frequency dynamics. For analysis and design purposes, they have to be replaced by realistic models, which must take into account this behavior that influences the whole system performance.
The wireless communications market is very important commercially and therefore there is a big interest in finding good suitable models to use in the RF system design process. Lately, behavioral modeling has been identified as a particularly critical issue for simulation time reduction without loosing accuracy. Traditionally, the Volterra series model has been used for this purpose, although more recently, neural networks were proposed.
This work shows a procedure to use the best of both worlds. A procedure to extract a Volterra model in the time-domain from the parameters of a TDNN-based behavioral model has been explained, thus providing a simple way to construct very compact and accurate Volterra models, which provide open and direct information about device performance such as IMD products. Besides, their implementation in circuit simulators is generally less time-consuming than NN-based models.
The experimental test results have demonstrated the validity of the proposed approach, both for transistors and PAs one-tone and two-tones test characterization in RF showing strong nonlinearities and memory effects.
References
McCune E (2005) High-efficiency, multi-mode, multi-band terminal power amplifiers. IEEE Microw Mag 6(1):44–55
Turlington TR (ed) (2000) Behavioral modeling of nonlinear RF and microwave devices. Artech House, Boston
Liu T, Boumaiza S, Ghannouchi FM (2004) Dynamic behavioral modeling of 3G power amplifiers using real-valued time-delay neural networks. IEEE Trans Microw Theory Tech 52(3):1025–1033
Wood J, Root D (eds) (2005) Fundamentals of nonlinear behavioral modeling for RF and microwave design. Artech House, Boston
Jargon J, Gupta KC, DeGroot D (2002) Application of artificial neural networks to RF and microwave measurements. Int J RF Microw CAE 12(1):3–24
Zhang QJ, Gupta KC, Devabhaktuni VK (2003) Artificial neural networks for RF and Microwave design—from theory to practice. IEEE Trans Microw Theory Tech 51(4):1339–1350
Orengo G, Colantonio P, Serino A, Giannini F, Stegmayer G, Pirola M, Ghione G (2007) Neural networks and Volterra-series for time-domain PA behavioral models. Int J RF Microw CAD Eng 17(3):405–412
Stegmayer G, Chiotti O (2006) Neural networks applied to wireless communications. In: Bramer M (ed) Artificial intelligence in theory and practice. Springer, Boston, pp 129–138
Pedro JC, Maas SA (2005) A comparative overview of microwave and wireless power-amplifier behavioral modeling approaches. IEEE Trans Microw Theory Tech 53(4):1150–1163
Boyd S, Chua LO, Desder CA (1984) Analytical foundations of Volterra series. IMA J Math Control Inf 1:243–282
Schetzen M (ed) (1980) The Volterra and Wiener theories of nonlinear systems. Wiley, New York
Volterra V (ed) (1959) Theory of functionals and integral and integro-differential equations. Dover, New York
Giannakis GB, Serpedin E (2001) A bibliography on nonlinear system identification. Signal Process 81:533–580
Rough W (ed) (1981) Nonlinear system theory. The Volterra/Wiener approach. Johns Hopkins University Press, Baltimore
Evans C, Rees D, Jones L, Weiss M (1996) Periodic signals for measuring nonlinear Volterra kernels. IEEE Trans Instrum Meas 45(2):362–371
Nemeth J, Kollar I, Schoukens J (2002) Identification of Volterra kernels using interpolation. IEEE Trans Instrum Meas 51(4):770–775
Wang T, Brazil TJ (2003) Volterra-mapping-based behavioral modeling of nonlinear circuits and systems for high frequencies. IEEE Trans Microw Theory Tech 51(5):1433–1440
Glentis GA, Koukoulas P, Kalouptsidis N (1999) Efficient algorithms for Volterra system identification. IEEE Trans Signal Process 47(11):3042–3057
Franz MO, Schölkopf B (2006) A unifying view of Wiener and Volterra theory and polynomial kernel regression. Neural Comput 18(12):3097–3118
Wray J, Green GGR (1995) Neural networks, approximation theory and precision computation. Neural Netw 8(1):31–37
Marmarelis VZ, Zhao X (1997) Volterra models and three layers perceptron. IEEE Trans Neural Netw 8(6):1421–1433
Iatrou M, Berger T, Marmarelis VZ (1999) Modeling of nonlinear nonstationary dynamic systems with a novel class of artificial neural networks. IEEE Trans Neural Netw 10(2):327–339
Stegmayer G (2004) Volterra series and neural networks to model an electronic device nonlinear behavior. Proc IEEE Int Joint Conf Neural Netw 4(1):2907–2910
Marquardt DW (1963) An algorithm for least-squares estimation of non-linear parameters. J Soc Ind Appl Math 11(2):431–441
Sjoberg J, Ljung L (1995) Overtraining, regularization and searching for a minimum, with application to neural networks. Int J Control 62:1391–1407
Nguyen D, Widrow B (1990) Improving the learning speed of 2-layer neural networks by choosing initial values of the adaptive weights. Proc IEEE Int Joint Conf Neural Netw 3:21–26
Stegmayer G (2006) Nonlinear RF/microwave device and system modeling using neural networks. Ph.D. thesis. Politecnico di Torino, Italy
Acknowledgments
To Professor Pirola (Politecnico di Torino) and Professor Orengo (Università di Roma II) for providing the measurements used in this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Stegmayer, G., Chiotti, O. Volterra NN-based behavioral model for new wireless communications devices. Neural Comput & Applic 18, 283–291 (2009). https://doi.org/10.1007/s00521-008-0180-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00521-008-0180-8