1 Introduction

Environmental problems have increased as a result of the increasing population, living standards, technological developments, industrialization and urbanization in many cities in developing countries. In recent years depending on the economic and technological developments, the amount and the type of both domestic and industrial solid wastes are increasing. Solid wastes can occur in many places in our daily life (Erkut et al. 2008). Particularly in developing countries, improper implementation of solid waste management plans is a problem in terms of transportation, storage and disposal of solid wastes. Because of these reasons, solid waste management has become a very importance issue (Achillas et al. 2013).

Although service levels, environmental impacts and costs that vary significantly, solid waste management is the most important activity that all municipalities around the world are obliged to provide for residents and it serves as a prerequisite for other municipal actions (Abdel-shafy and Mansour 2018).

If we can manage municipal solid waste correctly and intelligently, natural resources are conserved, energy is saved, waste amount is reduced and serious contributions to the economy can be achieved (Sadef et al. 2016). There are many power plants generating energy from waste in the world, but it is not reached the desired level.

Determining the municipal solid waste to energy plant location problem has to be considered from the different aspects as technological, social, economical and environmental. The best alternative should meet all these criteria in the best way. This process is a complex and also time consuming for decision makers with traditional methods (Bilgilioglu et al. 2021). But in the literature, there are very few studies consider this problem under fuzzy conditions (Wang et al. 2018a, b). Fuzzy environment helps eliminate the complexity and vagueness of evaluating these criteria. In this research, we present a hybrid fuzzy multi-criteria methodology for dealing with these complexity and vagueness.

The main objective of this study is to give a perspective that will support and simplify the selection of the most appropriate waste to energy plant location to the decision makers. For each decision, there are too many parameters that affect the decision. All these parameters can be determined essentially based on the experience of the experts; however, there is no concrete approach to the proposed in the literature (Kyriakis et al. 2018). In this paper, site selection problem for the solid waste energy production plant is discussed. A new methodology is recommended for selection of the best place for waste to energy plant location in a small city in Turkey. We integrated the two different methods and also two different fuzzy sets for dealing with the conflicts criteria and the vagueness of the problem. In literature there are many extensions of the fuzzy sets, and these sets are used many different multi-criteria methods in many different areas. But in this study Interval type 2 fuzzy sets and hesitant fuzzy sets are used for evaluation of the criteria numerically. Hesitant fuzzy set can be used where a set of values for membership is possible and Interval type 2 fuzzy sets can be used when membership values are also fuzzy sets. And this situation helps handling with the vagueness and uncertainty.

Interval type 2 fuzzy sets are used for defining the criteria weights with Analytic Hierarch Process (AHP), hesitant fuzzy sets are used for ranking the alternatives with Fuzzy TOPSIS. In this way, proposed methodology provides a multi-criteria evaluation using both continuous and discrete fuzzy sets as well as incorporating different expertise levels of decision makers.

The originality of the paper comes the integration of these fuzzy sets and methods and using for the municipal solid waste energy plant location problem. The proposed methodology is applied for the first time in municipal solid waste management. Also another contribution of the study to the literature is adding the different expertise level of the decision makers to this new methodology. The proposed model is very flexible and practical for the decision makers and gives guidance in solid waste to energy plant location selection.

The rest of the paper is structured as follows; Sect. 2 gives a brief explanation of the literature review, then proposed methodology is explained in Sect. 3, and the case study and scenario analysis are given in Sect. 4. Conclusions of the case study and the future works are discussed in the last section.

2 Preliminaries

2.1 Municipal solid waste management

Selecting the appropriate location and implementing the method, technology and the management program correctly are necessary for carrying out the municipal solid waste in a correct way. It has so many conflicting decision criteria; therefore, it has become an important decision making problem (Achillas et al. 2013). Selecting the best strategy for solid waste management (Vucijak et al. 2016; Jovanovic et al. 2016; Topaloglu et al. 2018; Çoban et al. 2018; Phonphoton and Pharino 2019), determining the waste management facility location or treatment methods, selecting the disposal site (Arıkan et al. 2018; Kahraman et al. 2017; Kamdar et al. 2019) are some of the main decision making problems in this area. In the solid waste management literature the number of papers that apply multi-criteria decision making methods is increased, but in spite of this increase, the studies is still focused on a few themes. The majority of the studies are focus on waste facility location or waste management strategy (Goulart et al. 2017). Santibañez-Aguilar et al. (2013) applied multi-criteria decision making methods for both location and waste management strategy. Ekmekçioğlu et al. (2010) and Perkoulidis et al. (2010) combined location facility and waste allocation problem. Mallick (2021) the integrated GIS-based fuzzy-AHP-MCDA method for solid waste land filling problem in Arabia and Sisay et al. (2020) used the same methods for solid waste land filling problem in Ethiopia. Bilgilioğlu (2021) analyzed the municipal solid waste disposal site selection problem in Turkey.

There are few studies dealing with the solid waste to energy plant location selection problem. Tavares et al. (2011) applied the AHP and GIS for sitting of a municipal solid waste incineration plant. Yap and Nixon (2015) evaluated waste to energy technologies with multi-criteria decision making. Hassaan (2015) compared alternative municipal solid waste incineration power plants with geographic information systems (GIS) approach in Egypt. Wang (2018) combined Fuzzy Analytic Network Process and TOPSIS methods for solid waste to energy plant location selection in Vietnam.

In recent years, multi-criteria decision making methods that use fuzzy sets have been introduced frequently for many solid waste management problems. Kahraman et al. (2017) used Intuitionistic fuzzy sets with EDAS method for ranking the solid waste disposal methods. Topaloglu et al. (2018) applied type-2 Fuzzy TOPSIS method for ranking the alternative waste collection systems in a smart city environment. Wang et al. (2018a, b) are evaluated four solid waste treatment alternatives with combining fuzzy multi-criteria decision making methods. Kharat et al. (2019) combined two fuzzy decision making methods for the selection of the most useful treatment and disposal technology alternative. Abdullah et al. (2019) and Cebi et al. (2020) both used intuitionistic fuzzy sets with different methods. Abdullah et al. (2019) integrated DEMATEL method and Choquet integral for a numerical example for solid waste management. Cebi et al. (2020) applied fuzzy axiomatic design approach for selecting the best the disposal methods.

Since there is few works in the literature for the selection of energy production from municipal solid waste, this issue has been discussed in this paper. Furthermore, sensitivity analysis for multi-criteria methods is an important step, but many of the articles in solid waste management have generally not focused on sensitivity analysis (Goulart et al. 2017). Because of these gaps, our paper focuses on municipal solid waste to energy problem, and we analysis the sensitivity of the criteria.

2.2 Hesitant fuzzy sets

Since Fuzzy Sets is developed by Zadeh (1965), so many extensions are defined by many scholars (Torra 2010). In this paper, one of the newly extensions of fuzzy set is used for ranking of the alternatives in the proposed methodology. Hesitant Fuzzy Sets is introduced by Torra (2010), and these fuzzy sets can handle the hesitancy of the decision makers. The membership degree of an element to a reference set is presented with various possible fuzzy values in Hesitant Fuzzy Sets. This situation helps to remove the decision makers' hesitancy between the alternatives (Khutsishvili et al. 2015). Because of the hesitancy that the most real-life problems have, scientist showed a great interest in Hesitant Fuzzy Sets in a very short time (Rodriguez et al. 2014).

2.2.1 Some basic concepts

In this chapter, we discuss some important definitions about the hesitant fuzzy sets that we use in the proposed methodology.

Definition 1

T is a finite reference set and function \(h_{{\text{H}}} \left( t \right)\) represent a hesitant fuzzy sets H on T and T returns a subset of [0, 1]. Mathematically, it is represented by following expression (Torra 2010):

$$ H = \left\{ {\left\langle {t,\left. {h_{{\text{H}}} (t)} \right\rangle \left| {t \in T} \right.} \right.} \right\} $$
(1)

\(h_{{\text{H}}} \left( t \right)\) shows the membership degrees of the element and also \(h_{{\text{H}}} \left( t \right)\) can get some different values in [0, 1]. For simplify the definition, \(h_{{\text{A}}} \left( x \right)\) \(h_{{\text{H}}} \left( t \right)\) is called a hesitant fuzzy element (HFE) by Xia and Xu (2011).

Definition 2

If we accept h1 and h2 are two different hesitant fuzzy sets, these are the basic operations for h1 and h2 (Torra 2010; Xia and Xu 2011);

$$ {\text{Multiplication}}:\theta h = H\left\{ {\left( {1 - \left( {1 - \gamma } \right)^{\theta } } \right)\left| {\gamma \in h} \right.} \right\}\quad (\theta > 0); $$
(2)
$$ {\text{Complement}}:h^{c} = H\left\{ {(1 - \gamma )\left| {\gamma \in h} \right.} \right\}; $$
(3)
$$ \oplus \,{\text{Union}}:h_{1} \oplus h_{2} = H\left\{ {\left( {\gamma_{1} \, + \,\gamma_{2} - \gamma_{1} \,\,\gamma_{2} } \right)\left| {\gamma_{1} \, \in h_{1} ,\gamma_{2} \in h_{2} } \right.} \right\}; $$
(4)
$$ \otimes \,{\text{Intersection}}:\; h_{1} \otimes h_{2} = H\left\{ {\gamma_{1} \,\gamma_{2} \left| {\gamma_{1} \, \in h_{1} ,\gamma_{2} \in h_{2} } \right.} \right\}; $$
(5)

Definition 3

A Hesitant fuzzy element \(h = h = H\left\{ {\gamma^{\lambda } \left| {\lambda = 1,2, \ldots ,\# h} \right.} \right\};\) and we assume \(\gamma^{ + }\) and \(\gamma^{ - }\) are maximum and the minimum values of hesitant fuzzy set, respectively, then \(\gamma^{*} = \theta \gamma^{ + } + (1 - \theta )\gamma^{ - }\) is an extension value, where \(\theta (0 \le \theta \le 1)\) is a parameter that defines the decision makers risk preference(Xu and Zhang 2014).

2.2.2 Interval type 2 fuzzy sets

In this section type 2 fuzzy sets that is proposed by Zadeh (1975) is introduced. It is considered as an improved version of the type one fuzzy set. It contains more uncertainty with compared to the type one sets (Balin and Baraçli 2017). Because it has primary and secondary membership functions, while type one fuzzy set have only primary membership function (Zhou et al. 2019).

Definition 4

\(\mathop A\limits^{ \approx }\) is a interval type 2 fuzzy set and it can be represented as follows (Zadeh 1975; Mendel et al. 2006):

$$ \mathop A\limits^{ \approx } = \left\{ {((x,u),\mu_{{\mathop A\limits^{ \approx } }} (x,u)\left| {\forall x \in X,\forall u \in J_{x} \subseteq [0,1]} \right.,0 \le \mu_{{\mathop A\limits^{ \approx } }} (x,u) \le 1} \right\} $$
(6)

\(\mu_{{\mathop A\limits^{ \approx } }}\) is the membership function of \(\mathop A\limits^{ \approx }\) and X is the domain of it.

Definition 5

Furthermore \(\mathop A\limits^{ \approx }\) can be shown as in Eq. (7):

$$ \mathop A\limits^{ \approx } = \int\limits_{x \in X} {\int\limits_{{u \in J_{x} }} {\mu_{{\mathop A\limits^{ \approx } }} (x,u)/(x,u)} } \,\,{\text{Where}}\,J_{x} \in [0,1] $$
(7)

Definition 6

In Eq. (7), if all \(\mu_{{\mathop A\limits^{ \approx } }} (x,u) = 1\), \(\mathop A\limits^{ \approx }\) is called Interval Type 2 Fuzzy set (Buckley 1985), and it is a special type of type 2 fuzzy sets, represented as follows (Mendel et al. 2006):

$$ \mathop A\limits^{ \approx } = \int\limits_{x \in X} {\int\limits_{{u \in J_{x} }} {1/(x,u)} } \,\,{\text{where}}\,J_{x} \in [0,1] $$
(8)

Definition 7

In criteria weighting stage of the methodology we preferred trapezoidal interval type 2 fuzzy numbers and it can be shown following;

$$ \mathop A\limits^{ \approx } = \left( {\tilde{A}_{i}^{U} ,\tilde{A}_{i}^{L} } \right) = \left( {\left( {a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ;H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)} \right)\left( {a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ;H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)} \right)} \right) $$
(9)

\(\tilde{A}_{i}^{U}\) is the upper membership function, \(\tilde{A}_{i}^{L}\) is the lower membership function and \(H_{1} \left( {\tilde{A}_{i}^{U} } \right) \in [0,1]\), \(H_{2} \left( {\tilde{A}_{i}^{L} } \right) \in [0,1]\). where \(a_{i1}^{U} ,a_{i2}^{U} ,a_{i3}^{U} ,a_{i4}^{U} ,H_{1} \left( {\tilde{A}_{i}^{U} } \right),H_{2} \left( {\tilde{A}_{i}^{U} } \right)a_{i1}^{L} ,a_{i2}^{L} ,a_{i3}^{L} ,a_{i4}^{L} ,H_{1} \left( {\tilde{A}_{i}^{L} } \right),H_{2} \left( {\tilde{A}_{i}^{L} } \right)\) are all real numbers and \(a_{i1}^{U} \le a_{i2}^{U} \le a_{i3}^{U} \le a_{i4}^{U}\), \(a_{i1}^{L} \le a_{i2}^{L} \le a_{i3}^{L} \le a_{i4}^{L}\), \(0 \le H_{1} \left( {\tilde{A}_{i}^{L} } \right) \le H_{2} \left( {\tilde{A}_{i}^{L} } \right) \le 1\) are satisfied (Zhou et al. 2019).

Let \(\mathop X\limits^{ \approx }\) and \(\mathop Y\limits^{ \approx }\) are two different fuzzy sets as following; \(\mathop X\limits^{ \approx } = \left( {\tilde{X}^{U} ,\tilde{X}^{L} } \right) = \left( {\left( {x_{1}^{U} ,x_{2}^{U} ,x_{3}^{U} ,x_{4}^{U} ;H_{1} \left( {\tilde{X}^{U} } \right),H_{2} \left( {\tilde{X}^{U} } \right)} \right)\left( {x_{1}^{L} ,x_{2}^{L} ,x_{3}^{L} ,x_{4}^{L} ;H_{1} \left( {\tilde{X}^{L} } \right),H_{2} \left( {\tilde{X}^{L} } \right)} \right)} \right)\) and \(\mathop Y\limits^{ \approx } = \left( {\tilde{Y}^{U} ,\tilde{Y}^{L} } \right) = \left( {\left( {y_{1}^{U} ,y_{2}^{U} ,y_{3}^{U} ,y_{4}^{U} ;H_{1} \left( {\tilde{Y}^{U} } \right),H_{2} \left( {\tilde{Y}^{U} } \right)} \right)\left( {y_{1}^{L} ,y_{2}^{L} ,y_{3}^{L} ,y_{4}^{L} ;H_{1} \left( {\tilde{Y}^{L} } \right),H_{2} \left( {\tilde{Y}^{L} } \right)} \right)} \right)\) Some basic operations are shown in the following:

  • Addition

$$ \begin{gathered} \mathop X\limits^{ \approx } \oplus \mathop Y\limits^{ \approx } = ((((x_{1}^{U} + y_{1}^{U} ,x_{2}^{U} + y_{2}^{U} ,x_{3}^{U} + y_{3}^{U} ,x_{4}^{U} + y_{4}^{U} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{U} );H_{1} (\tilde{Y}^{U} )),\min (H_{2} (\tilde{X}^{U} );H_{2} (\tilde{Y}^{U} ))), \hfill \\ \quad (x_{1}^{L} + y_{1}^{L} ,x_{2}^{L} + y_{2}^{L} ,x_{3}^{L} + y_{3}^{L} ,x_{4}^{L} + y_{4}^{L} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{L} );H_{1} (\tilde{Y}^{L} )),\min (H_{2} (\tilde{X}^{L} );H_{2} (\tilde{Y}^{L} ))) \hfill \\ \end{gathered} $$
(10)

  • Subtraction

    $$ \begin{gathered} \mathop X\limits^{ \approx } \Theta \mathop Y\limits^{ \approx } = ((((x_{1}^{U} - y_{1}^{U} ,x_{2}^{U} - y_{2}^{U} ,x_{3}^{U} - y_{3}^{U} ,x_{4}^{U} - y_{4}^{U} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{U} );H_{1} (\tilde{Y}^{U} )),\min (H_{2} (\tilde{X}^{U} );H_{2} (\tilde{Y}^{U} ))), \hfill \\ \quad (x_{1}^{L} - y_{1}^{L} ,x_{2}^{L} - y_{2}^{L} ,x_{3}^{L} - y_{3}^{L} ,x_{4}^{L} - y_{4}^{L} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{L} );H_{1} (\tilde{Y}^{L} )),\min (H_{2} (\tilde{X}^{L} );H_{2} (\tilde{Y}^{L} ))) \hfill \\ \end{gathered} $$
    (11)

  • Multiplication

    $$ \begin{gathered} \mathop X\limits^{ \approx } \otimes \mathop Y\limits^{ \approx } = ((((x_{1}^{U} \times y_{1}^{U} ,x_{2}^{U} \times y_{2}^{U} ,x_{3}^{U} \times y_{3}^{U} ,x_{4}^{U} \times y_{4}^{U} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{U} ),H_{1} (\tilde{Y}^{U} )),\min (H_{2} (\tilde{X}^{U} ),H_{2} (\tilde{Y}^{U} ))), \hfill \\ \quad (x_{1}^{L} \times y_{1}^{L} ,x_{2}^{L} \times y_{2}^{L} ,x_{3}^{L} \times y_{3}^{L} ,x_{4}^{L} \times y_{4}^{L} ; \hfill \\ \quad \min (H_{1} (\tilde{X}^{L} ),H_{1} (\tilde{Y}^{L} )),\min (H_{2} (\tilde{X}^{L} ),H_{2} (\tilde{Y}^{L} ))) \hfill \\ \end{gathered} $$
    (12)

Multiplication with a crisp number t:

$$ \begin{gathered} \mathop X\limits^{ \approx } \otimes t = ((t \times x_{1}^{U} ,t \times x_{2}^{U} ,t \times x_{3}^{U} ,t \times x_{4}^{U} ;(H_{1} (\tilde{X}^{U} ),H_{2} (\tilde{X}^{U} )), \hfill \\ \quad (t \times x_{1}^{L} ,t \times x_{2}^{L} ,t \times x_{3}^{L} ,t \times x_{4}^{L} ;(H_{1} (\tilde{X}^{L} ),H_{2} (\tilde{X}^{L} )) \hfill \\ \end{gathered} $$
(13)

  • Division

$$ \begin{gathered} \frac{{\mathop X\limits^{ \approx } }}{{\mathop {Y}\limits^{ \approx } }} = \left( {\left( {\frac{{x_{1}^{U} }}{{y_{4}^{U} }},\frac{{x_{2}^{U} }}{{y_{3}^{U} }},\frac{{x_{3}^{U} }}{{y_{2}^{U} }},\frac{{x_{4}^{U} }}{{y_{1}^{U} }}} \right)} \right.,\left( {\frac{{x_{1}^{L} }}{{y_{4}^{L} }},\frac{{x_{2}^{L} }}{{y_{3}^{L} }},\frac{{x_{3}^{L} }}{{y_{2}^{L} }},\frac{{x_{4}^{L} }}{{y_{1}^{L} }};} \right. \hfill \\ \quad \left( {H_{1} \left( {\tilde{X}^{L} } \right);H_{2} \left( {\tilde{X}^{L} } \right)} \right) \hfill \\ \end{gathered} $$
(14)

The division operation of \(\mathop X\limits^{ \approx }\) with a crisp number t:

$$ \begin{gathered} \frac{{\mathop X\limits^{ \approx } }}{t} = \left( {\left( {\frac{1}{t} \times x_{1}^{U} ,\frac{1}{t} \times x_{2}^{U} ,\frac{1}{t} \times x_{3}^{U} ,\frac{1}{t} \times x_{4}^{U} ;\left( {H_{1} \left( {\tilde{X}^{U} } \right);H_{2} \left( {\tilde{X}^{U} } \right)} \right),} \right.} \right. \hfill \\ \quad \left( {\frac{1}{t} \times x_{1}^{L} ,\frac{1}{t} \times x_{2}^{L} ,\frac{1}{t} \times x_{3}^{L} ,\frac{1}{t} \times x_{4}^{L} ;\left( {H_{1} \left( {\tilde{X}^{L} } \right);H_{2} \left( {\tilde{X}^{L} } \right)} \right)} \right. \hfill \\ \end{gathered} $$
(15)

where t > 0.

In this paper Interval type 2 fuzzy AHP method is performed, and all the steps of the method are explained in the next section.

3 Methodology

An integrated methodology is introduced and applied for the solid waste energy plant location selection problem. Proposed method consist of three phase, first phase is preparation phase, second phase is Interval type 2 fuzzy AHP Phase and the last one is solution phase which are given in Fig. 1. In Preparation Phase firstly the decision makers are chosen then the alternatives and the criteria that affect the problem and decision makers’ opinion are defined. Before calculating the criteria weights phase, the hierarchy of the problem is defined for using it next phases of the methodology.

Fig. 1
figure 1

The phases of proposed methodology

Full size image

Then hierarchy of the problem as seen in Fig. 2 is checked by the decision makers. The hierarchy of the problem is accepted by the decision makers.

Fig. 2
figure 2

The hierarchy of the problem

Full size image

In second phase of the methodology fuzzy AHP with Interval type 2 fuzzy sets is applied for criteria weightings. All steps of the Interval type 2 fuzzy AHP is described in Sect. 3.1.

The last phase of the methodology is Hesitant Fuzzy TOPSIS method Phase. In this phase, we rank the alternatives locations. All steps of the Hesitant Fuzzy TOPSIS are described in Sect. 3.2.

As far as we know, there is not any work that combines the Interval type 2 fuzzy AHP and Hesitant Fuzzy TOPSIS method for solid waste energy plant location selection problem in literature. This location selection problem consists of many conflicts criteria and these two methods deals with the vagueness and the complexity of the problem.

The proposed methodology helps the decision makers for judgments of the criteria and alternatives by using the interval type 2 fuzzy sets and hesitant fuzzy sets. In preparation phase, the hierarchy of the decision problem is defined from the experts. Four alternative locations and nine criteria are defined with the consensus of the decision makers.

3.1 Interval type 2 fuzzy analytic hierarch process

The AHP is a multi-attribute decision making method that is firstly developed by Saaty (1980). This method helps the decision makers for solving the problem by considering the hierarchy among the criteria (Wheeler et al. 2017). AHP consist of two main stages. In first stage, decision makers (academics, technicians or business people) make judgments about pair wise comparisons for determining the weights for every unique criterion. They give a value for each comparison using 1–9 (Saaty 1980) scale. In the second stage, the weights for each alternative is computed by an algorithm, by this way the alternatives are ranked and quantified (Roberti 2017). This method have three major advantages, one of them is it is so easy to understand and ease of handling multiple criteria, furthermore, the method is useful for qualitative data and also quantitative data (Moeinaddini et al. 2010). But in real life situations, experts may not have enough knowledge or they cannot give a value for each comparison using Saaty scale (Xu and Liao 2014). Besides many advantages of the AHP, due to the weakness of Saaty scale against uncertainty environment, fuzzy AHP is proposed as an extension of the AHP method (Buckley 1985). Fuzzy sets have many extensions in recent years; therefore in literature, there are many papers that apply fuzzy AHP with these extensions of the fuzzy sets.

In this paper, waste to energy plant site selection problem in Kırıkkale city is discussed. In criteria weighting stage, the AHP method with Interval type 2 fuzzy set is applied. The proposed methodology can be seen in Fig. 1. Selecting decision makers, defining alternatives and criteria steps are performed in preparation phase. Therefore the steps of the method are described as follows:

  • Step 1 Firstly the decision makers compare the criteria with each other. And they construct the pair wise comparison matrix is given in Eq. 16.

$$ \mathop A\limits^{ \approx } = \left[ {\begin{array}{*{20}c} 1 & {\mathop {a_{12} }\limits^{ \approx } } & {\begin{array}{*{20}c} \cdots & {\mathop {a_{1n} }\limits^{ \approx } } \\ \end{array} } \\ {\mathop {a_{21} }\limits^{ \approx } } & 1 & {\begin{array}{*{20}c} \cdots & {\mathop {a_{2n} }\limits^{ \approx } } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ {\mathop {a_{n1} }\limits^{ \approx } } \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ {\mathop {a_{n2} }\limits^{ \approx } } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ddots \\ \cdots \\ \end{array} } & {\begin{array}{*{20}c} \vdots \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\, = \left[ {\begin{array}{*{20}c} 1 & {\mathop {a_{12} }\limits^{ \approx } } & \cdots & {\mathop {a_{1n} }\limits^{ \approx } } \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\mathop {a_{12} }\limits^{ \approx } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop {a_{12} }\limits^{ \approx } }$}}} & 1 & \cdots & {\mathop {a_{2n} }\limits^{ \approx } } \\ \vdots & \vdots & \ddots & \vdots \\ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\mathop {a_{n1} }\limits^{ \approx } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop {a_{n1} }\limits^{ \approx } }$}}} & {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\mathop {a_{n2} }\limits^{ \approx } }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathop {a_{n2} }\limits^{ \approx } }$}}} & \cdots & 1 \\ \end{array} } \right]\, $$
(16)

where

$$ \begin{gathered} \frac{1}{{\mathop {a_{{}} }\limits^{ \approx } }} = \left( {\left( {\frac{1}{{a_{14}^{U} }},\frac{1}{{a_{13}^{U} }},\frac{1}{{a_{12}^{U} }},\frac{1}{{a_{11}^{U} }};H_{1} \left( {\tilde{a}_{12}^{U} } \right),H_{2} \left( {\tilde{a}_{13}^{U} } \right)} \right),} \right. \hfill \\ \quad \left. {\left( {\frac{1}{{a_{24}^{L} }},\frac{1}{{a_{23}^{L} }},\frac{1}{{a_{22}^{L} }},\frac{1}{{a_{21}^{L} }};H_{1} \left( {\tilde{a}_{22}^{L} } \right),H_{2} \left( {\tilde{a}_{23}^{L} } \right)} \right)} \right) \hfill \\ \end{gathered} $$

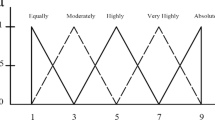
They evaluated the criteria by using linguistic variables that is given in Table 1. For example if an expert think that criterion 1 absolutely strong (AS) then criterion 2, uses (7,8,9,9;1,1) (7.2,8.2,8.8,9;0.8,0.8) Trapezoidal Interval type 2 fuzzy number.

  • Step 2 We aggregated the three decision makes opinion by using geometric mean formula that is given in following equation.

$$ \mathop a\limits^{ \approx }_{ij} = \left[ {\mathop a\limits^{ \approx }_{ij} \otimes \cdots \otimes \mathop a\limits^{ \approx n}_{ij} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 n}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$n$}}}} $$
(17)
Table 1 Linguistic variables in Trapezoidal Interval Type-2 fuzzy number for the assessment of Criteria’s weight
Full size table

  • Step 3 After aggregation of the decision maker’s opinion, Eq. (18) is used for calculating the weights of the all criteria.

    $$ \mathop p\limits^{ \approx }_{i} = \mathop r\limits^{ \approx }_{i} \otimes \left[ {\mathop r\limits^{ \approx }_{1} \oplus ...\mathop r\limits^{ \approx }_{i} \oplus ...\mathop r\limits^{ \approx n}_{n} } \right]^{ - 1} $$
    (18)

  • Step 4 Defuzzify type-2 interval fuzzy weights with DTtrT method (Kahraman et al. 2012).

    $$ DTtrT = \frac{{\left[ {\frac{{(u_{U} - l_{U} ) + (\beta_{U} \cdot m_{1U} - l_{U} ) + (\alpha_{U} \cdot m_{2U} - l_{U} )}}{4} + l_{U} } \right] + \frac{{(u_{L} - l_{L} ) + (\beta_{L} \cdot m_{1L} - l_{L} ) + (\alpha_{L} \cdot m_{2L} - l_{L} )}}{4} + l_{L} }}{2} $$
    (19)

The other steps of the method can be used to rank the alternatives, but in proposed methodology we applied the Hesitant Fuzzy TOPSIS method for ranking the alternatives because of the ability of the method to cope with uncertainties. Therefore, the other steps of the method are not given in this section.

3.2 Hesitant fuzzy TOPSIS method

The TOPSIS is a frequently used multi-criteria decision making method that firstly developed by Huwang and Yoon (1981). After Zadeh (1965) developed the fuzzy sets, TOPSIS method has been used in solving many decision problems. Also there are many articles in the literature that use the TOPSIS method with many different fuzzy sets (Onar 2014). The major contribution of Fuzzy TOPSIS is the usage of fuzzy numbers instead of crisp ones in evaluating alternatives and criteria weights. Chen and Hwang (1992) firstly propose Fuzzy TOPSIS Method.

In Fuzzy TOPSIS method, decision makers use the fuzzy set for evaluating the alternatives but in hesitant Fuzzy TOPSIS method experts use the hesitant fuzzy set. Thus, hesitant fuzzy set allows decision makers to be more flexible while making evaluations about alternatives and helps to eliminate hesitancy of the decision makers.

This section summarizes the steps of the hesitant Fuzzy TOPSIS that we used for ranking the waste to energy production location alternatives. In general, a lot of multi-criteria decision making methods start similar steps as preparation phase, because in preparation phase decision makers, alternatives and criteria are defined. In this paper, Hesitant Fuzzy TOPSIS method is used for ranking the alternatives location. Although there are many versions of Hesitant Fuzzy TOPSIS, in this paper we performed the Onar’s (2014) approach due to its ease of application, the success of the vagueness of expert opinions and allow evaluating with both continuous and discrete fuzzy sets.

As seen in Fig. 1 defining alternatives and criteria, then calculating the weights of criteria steps have also applied in the first two steps of the proposed methodology. After these two steps of the methodology, Hesitant Fuzzy TOPSIS is applied. The steps of the Hesitant Fuzzy TOPSIS method are following;

  • Step 1 Construct the hesitant fuzzy decision matrix \(\Re = \left( {h_{ij} } \right)_{m \times n}\), where \(h_{ij}\) is hesitant fuzzy element, and it demonstrates the rating of alternatives \(A_{i} \in A\) with respect to criterion \(C_{j} \in C\).

  • Step 2 According to the following equations, respectively, calculate the distance between the positive and negative ideal solutions.

$$ {\text{PIS}}\,A^{ + } = \left( {h_{1}^{ + } ,h_{2}^{ + } , \ldots ,h_{n}^{ + } } \right) = \left( \begin{gathered} \left( {H\left\{ {\mathop {\max }\limits_{i} \,\gamma_{ij}^{1} ,\mathop {\max }\limits_{i} \,\gamma_{ij}^{2} , \ldots ,\mathop {\max }\limits_{i} \,\gamma_{ij}^{{\# h_{ij} }} } \right\}\left| {C_{1} \, \in j_{I} } \right.} \right) \hfill \\ or\left( {H\left\{ {\mathop {\min }\limits_{i} \,\gamma_{ij}^{1} ,\mathop {\min }\limits_{i} \,\gamma_{ij}^{2} , \ldots ,\mathop {\min }\limits_{i} \,\gamma_{ij}^{{\# h_{ij} }} } \right\}\left| {C_{1} \, \in j_{II} } \right.} \right) \hfill \\ \end{gathered} \right) $$
(20)
$$ {\text{NIS}}\,A^{ - } = \left( {h_{1}^{ - } ,h_{2}^{ - } , \ldots ,h_{n}^{ - } } \right) = \left( \begin{gathered} \left( {H\left\{ {\,\mathop {\min }\limits_{i} \,\gamma_{ij}^{1} ,\mathop {\min }\limits_{i} \,\gamma_{ij}^{2} , \ldots ,\mathop {\min }\limits_{i} \,\gamma_{ij}^{{\# h_{ij} }} \,\,} \right\}\left| {C_{1} \, \in j_{I} } \right.} \right) \hfill \\ or\left( {H\left\{ {\,\,\,\mathop {\max }\limits_{i} \gamma_{ij}^{1} ,\mathop {\max }\limits_{i} \,\gamma_{ij}^{2} , \ldots ,\mathop {\max }\limits_{i} \,\gamma_{ij}^{{\# h_{ij} }} } \right\}\left| {C_{1} \, \in j_{II} } \right.} \right) \hfill \\ \end{gathered} \right); $$
(21)

\(\,\,\,j_{I}\) refers to the subset of benefit criteria and \(\,\,\,j_{II}\) refers to the subset of cost criteria, and \(\,\,\,j_{I} \cup j_{II} = C\,\,\,j_{I} \cap j_{II} = \phi \,{\text{and}}\,\,\,\,j = \left\{ {1,2, \ldots ,n} \right\}.\)

  • Step 3 There are many distance measures in literature. Calculate the distance measure with the formulas stated below:

$$ d^{h} (A_{i} ,A^{ + } ) = \sum\nolimits_{j = 1}^{n} {\omega_{j} } \sqrt {\frac{1}{{\# h_{ij} }}\sum\limits_{\lambda = 1}^{{\# h_{ij} }} {\left( {\gamma_{ij}^{\lambda } - (\gamma_{ij}^{\lambda } )^{ + } } \right)}^{2} } $$
(22)
$$ d^{h} (A_{i} ,A^{ - } ) = \sum\nolimits_{j = 1}^{n} {\omega_{j} } \sqrt {\frac{1}{{\# h_{ij} }}\sum\limits_{\lambda = 1}^{{\# h_{ij} }} {\left( {\gamma_{ij}^{\lambda } - (\gamma_{ij}^{\lambda } )^{ - } } \right)}^{2} } $$
(23)

\(\# h_{ij}\) is represent the number of elements in Hesitant fuzzy element and \(w_{j}\) is represent the weights of the criteria that calculated by Interval type 2 fuzzy AHP.

  • Step 4 Before the final ranking of the alternatives apply the following formula for the closeness indices; Ai (i = 1, 2,…,m) m = 4.

$$ CC^{h} \left( {A_{i} } \right) = \frac{{d^{h} (A_{i} ,A^{ + } )}}{{d^{h} (A_{i} ,A^{ + } ) + d^{h} (A_{i} ,A^{ - } )}} $$
(24)

  • Step 5 According to the closeness coefficient, rank the alternatives.

4 A real case study

Kırıkkale city is located middle of the Turkey. It is like a connection between the west and the east of the Turkey. This city has a population of 277,984 individuals (based on the latest population census in 2016—www.tuik.gov.tr) and has 183,399 tons/day average solid waste amount. The alternative locations for solid waste energy plant locations are determined with the experts of the Municipality of the Kırıkkale. Alternative one (A1) is Bahşılı-Bedesten location, alternative two (A2) is Çullu location, alterative three (A3) is Aşagı Mahmutlar location and alternative four (A4) is Delice location. Then the criteria are defined with the expert opinion and the literature as seen in Table 2.

Table 2 The Criteria used in the study
Full size table

Nine criteria are defined for the location selection problem from the literature and the expert opinion. Also we assumed that all alternatives have acceptable slope level, all alternatives have nearly the same topography and alternative locations are not near the any historical places or agricultural areas. Therefore we did not add these situations as a criterion.

After defining alternatives and the criteria, we determined the decision matrix from the expert judgments. Decision makers are consisting of three experts from the municipal of the city and the experts have different experience level of the location selection problem. Because of this, we give different importance weights of the experts’ judgments. The weight of the first experts is 0.35; the second one is 0.4, and the last one is 0.25. These weights are determined consensus of the three experts. The judgments of the experts can be seen in Table 3. We used Eq. (13) for aggregation of the decision makers’ opinion. An example for the judgments for C2 to C4 as follows:

$$ \mathop a\limits^{ \approx }_{24} = \left[ \begin{gathered} (0.35 \otimes (0.2,0.25,0.5,1;1,1)(0.2,0.26,0.45,0.83;0.8,0.8)) \otimes \hfill \\ (0.4 \otimes \left( {1,2,4,5;1,1} \right) \, \left( {1.2,2.2,3.8,4.8;0.8,0.8} \right)) \hfill \\ \otimes (0.25 \otimes \left( {1,2,4,5;1,1} \right) \, \left( {1.2,2.2,3.8,4.8;0.8,0.8} \right)) \hfill \\ \end{gathered} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} $$
$$ \mathop a\limits^{ \approx }_{24} = \left( {0.191,0.327,0.654,0.956;1,1} \right), \, \left( {0.219,0.355,0.612,0.876;0.8,0.8} \right) $$
Table 3 Pair wise comparisons for criteria
Full size table

Aggregated evaluations of the experts can be seen in Table 4. But due to the space restriction, we give the three criteria judgments.

Table 4 Aggregated decision matrix
Full size table

After aggregate all the decision makers’ opinion, we calculated the geometric mean of the each row as shown in Eq. (18). Then we defuzzified the Interval type 2 fuzzy sets by using Eq. (19).

After using Eq. (18), we calculate normalized weights of the all criteria as seen in Table 5.

Table 5 Normalized weights of the criteria
Full size table

In the second step of the case study, decision makers make judgments for all alternatives as seen in Table 6.

Table 6 Hesitant fuzzy judgments of the experts for alternatives
Full size table

After using the Eqs. (22) and (23) the positive ideal distance and negative ideal distance for alternatives are calculated.

According to Table 7, the ranking of the alternatives is A1 > A2 > A4 > A3. Bahsılı-Bedesten alternative location is selected the best location for energy plant. The second most appropriate location is Çullu location and, respectively, the others locations are Delice and Asağı-Mahmutlar. This result is shared with the municipality of the city, and the results are endorsed by the decision makers by traditional methods as Delphi method and Brainstorming.

Table 7 Distance measures and the closeness coefficients of the alternatives
Full size table

4.1 Sensitivity analysis

In sensitivity analysis stage, eighth different cases are generated. In first case, all criteria have the current weights. Other seven cases are seen in Table 8.

Table 8 Criteria weights for scenarios
Full size table

In scenario 2, all criteria weights are equal to the highest criterion weight. In scenario 3, all criteria weights are equal to the lowest criterion weight. In scenario 4, all criteria weights are equal to medium weight. The other remaining scenarios are defined according to the characteristics represented by the criteria. For example criterion 1 and criterion 2 are related to the systems cost; therefore, scenario 5 is created for investigating the effect of the cost to the alternative ranking. In this scenario, these criteria weights are equal to the highest criterion weight.

Scenario 6 is created to investigate the effects of environmental criteria on alternatives. In scenario 7 and scenario 8, the effects of distance and social criteria are examined, respectively. All criteria weights can be seen in Table 8.

As seen in Fig. 3, Alternative 1 is ranked in the first place except scenario 5 and scenario 6. In scenario 5, the effect of cost is investigated and alternative 4 has the best performance. In scenario 6, environmental criteria have the highest weight and alternative 2 is ranked first place. Therefore if the municipality makes a decision considering only the environmental criteria, it should choose alternative 2. Similarly, if the municipality makes a decision considering only the cost, it should choose alternative 4. Additionally alternative 3 has the lowest weight in all scenario and ranked last.

Fig. 3
figure 3

Performance of alternatives

Full size image

5 Conclusions

The rapid and uncontrolled growth of the world’s population, technological developments and the increase in social welfare have led to an increase in environmental problems. As a result of increasing environmental problems, solid waste management has become a more important issue day by day. Municipal solid waste, which is the main problem of many countries in the world, is also the most important environmental problems of our country. In addition, as the habits of societies change, the need for energy is increasing. Waste to energy systems play an important role in meeting the energy demand by generating energy and at the same time providing many benefits to the environment by eliminating waste.

In this paper, we discussed municipal waste to energy plant location selection problem in Kırıkkale city which is located in the middle of the Turkey. A new methodology is proposed for dealing with municipal solid waste energy production plant location selection problem. We combined Interval type 2 fuzzy AHP and Hesitant Fuzzy TOPSIS methods for ranking the alternative municipal solid waste energy production plant locations in Kırıkkale. The weights of the criteria are defined with Interval type 2 fuzzy AHP, and the best location is selected with Hesitant Fuzzy TOPSIS Method. To the best of our knowledge, there are not any papers that combines these methods and fuzzy sets for solid waste energy plant location selection problem. The combination of these two methods in the solid waste location selection problem field is thought to make an important contribution to the literature. Interval type 2 fuzzy sets are more powerful for uncertainty of the problem and hesitant fuzzy sets are more powerful for and hesitancy of the experts. By this way, these two methods can deals with the complexity and vagueness of the location selection problem.

In addition, the proposed hybrid model makes an important theoretical and practical contribution, because of the reducing uncertainty in a complex decision problem and also it is quite successful in dealing with the hesitancy of decision makers. In this paper, the methodology does not restrict the decision makers for using continuous or discrete fuzzy sets by using Interval type 2 fuzzy set and hesitant fuzzy set. Thus, proposed model provides a great advantage compared to other studies in the literature. Methodology can be used for many different decision problems, and it provides a guideline for decision makers.

In implementation stage, all analysis is examined by experts from the municipality of the Kırıkkale. We also discussed that the experts have different expertise level by using the different weights for expert opinions. According to the results Bahşılı-Bedesten is determined as the best alternative for solid waste disposal location according to the closeness coefficients. In scenario analysis stage, the effects of cost criteria, environmental and distance criteria on ranking of the alternatives are investigated.

In future studies, newly extensions of the fuzzy sets and different multi-criteria decision making methods can be examined for this problem, maybe this different methods can be compared. Also, any other fuzzy methods can be implemented for selecting waste to energy technology selection problem.

In interval type 2 fuzzy AHP stage, respectively, Investment cost, Distance to Living Areas and Effect of Ecological Environment criteria are calculated as the most important criteria for this problem. Therefore, sensitivity analysis can be performed for these three most important criteria.