MoSSE: a novel hybrid multi-objective meta-heuristic algorithm for engineering design problems

Abstract

This paper introduces a novel hybrid optimization algorithm called MoSSE by combining the features of Multi-objective Spotted Hyena Optimizer (MOSHO), Salp Swarm Algorithm (SSA), and Emperor Penguin Optimizer (EPO). MoSSE uses MOSHO’s searching capabilities to effectively discover the search space, SSA’s leading and selection process to achieve the fittest global solution with quicker convergence technique, and EPO’s effective mover technique for better adjustment of the next solution. The algorithm is tested on ten IEEE CEC-9 standard test functions and compared with seven well-known multi-objective optimization algorithms according to their performance. The experimental results show that MoSSE provides highly competitive outcomes in terms of convergence speed, searchability, and accuracy. Statistical testing is also performed on IEEE CEC-9 test functions. Four performance metrics (i.e., Hypervolume, $\Delta _p$, Spread, and Epsilon) are used to validate the searching capability of the proposed algorithm. MoSSE is further applied to welded beam, multi-disk clutch brake, pressure vessel, 25-bar truss design problems to test its effectiveness. The findings show the utility of the proposed algorithm to resolve the real-life complex multi-objective optimization problems.

1 Introduction

Meta-heuristic optimization approaches take enormous interest from researchers over the past few decades in explaining the search and optimization problems. Such approaches aim to find the solution in computationally traceable ways and are comparatively cheaper and more rapidly than comprehensive searching (Bandarua and Kalyanmoy 2016; Dhiman and Amandeep 2019). Nowadays, researchers are trying to develop the meta-heuristic-based approaches for solving complex problems (Kaur and Gaurav 2019; Garg and Dhiman 2020; Verma et al. 2018; Singh and Gaurav 2017; Garg and Dhiman 2020; Chandrawat et al. 2017; Dehghani et al. 2020). Meta-heuristic optimization techniques can be broadly categorized into two categories such as single-objective and multi-objective (Dhiman and Kaur 2020; Dhiman et al. 2020a, b). Single-objective approaches seek to provide the unique global solution after optimizing the key objective function (Chiandussi et al. 2012; Satnam Kaur et al. 2020). However, most real optimization problems require multi-objective that need to be tackled at the same time. Since these objectives are usually contradictory in nature, finding the optimal solution for all of the objectives is difficult (Dehghani et al. 2019; Dhiman 2019a, b). Multi-objective approaches are also known in these situations, where several objectives need to be reached before some rational conclusion can be drawn (Branke et al. 2004). Multi-objective optimization methods also known as vector optimization approach and involves several competing objects and aim to find the fittest possible solutions (Chiandussi et al. 2012; Coello Coello et al. 2007). The key challenge in multi-objective optimization is to model the preferences of decision-makers in ordering or assessing the relative importance of competing objectives. This problem has three main approaches, specifically priori, posteriori, and interactive (Marler and Arora 2004). Priori approaches employ the scalar function to convert the single-objective problem into multi-objective problem (Konak et al. 2006). Posteriori approaches may not require the user preference information. These methods provide a range of optimal solutions which are mathematically equivalent to Pareto (Dhiman and Kumar 2019). Interactive methods are called as the human-in-the-loop technique, constantly gather decision-makers’ favorites and contain them in the optimization process to find the Pareto optimal solutions (Marler and Arora 2004; Singh et al. 2019; Dhiman 2019).

In 1984, David Schaffer developed Vector Evaluated Genetic Algorithm (VEGA) (Coello Coello et al. 2007). It is the first multi-objective optimization algorithm. Apart from this, various multi-objective algorithms were also developed. These are Non-dominated Sorting Genetic Algorithm 2 (NSGA-II) (Deb et al. 2002), Multi-objective Evolutionary Algorithm based on Decomposition (MOEA/D) (Zhang and Li 2007), Pareto Envelope-based Selection Algorithm 2 (PESA-II) (Corne et al. 2001), Multi-objective Particle Swarm Optimization (MOPSO) (Coello Coello 2002), Strength Pareto Evolutionary algorithm 2 (SPEA2) (Zitzler et al. 2001), Multi-objective Ant Colony Optimization (MOACO) (Angus and Woodward 2009), Multi-objective Brain Storm Optimization Algorithm based on Decomposition (MBSO/D) (Dai and Lei 2019), Modified Multi-objective Self-Adaptive Differential Evolution Algorithm (MMOSADE) (Yang et al. 2019), and Multi-objective Variant of the Vibrating Particles System (MOVPS) (Kaveh and Ghazaan 2019), and Multi-objective Salp Swarm Algorithm (MSSA) (Mirjalili et al. 2017). These algorithms can resolve a variety of multi-objective problems related to several domains, such as software engineering (Mansoor et al. 2017), quantum computing (Singh et al. 2018; Kaur et al. 2018; Dhiman and Kumar 2018), fuzzy systems (Singh and Dhiman 2018a, b; Singh et al. 2018), computer engineering (Chen and Hammami 2015; Jianjie et al. 2017; Hou et al. 2018; Yu et al. 2015), power systems (Dhiman et al. 2018, 2019), industrial problems (Dhiman and Kaur 2019; Dhiman and Kumar 2019; Dhiman and Kaur 2018), civil engineering (Luh and Chueh 2004), mechanical engineering (Mirjalili et al. 2017; Dhiman and Kumar 2017), and so on.

According to No-Free Lunch Theorem (NFL) (Wolpert and Macready 1997), these algorithms are not able to solve all optimization problems. NFL (Wolpert and Macready 1997) has scientifically proved the aforementioned encourages and claim researchers to build new optimization algorithms. There is also space for designing new algorithms with the goal of solving complex problems more efficiently, which are difficult to resolve with present multi-objective approaches. Based on this inspiration, we propose a multi-objective optimization algorithm. This algorithm employs the features of Multi-objective Spotted Hyena Optimizer (MOSHO) (Dhiman and Kumar 2018; Dhiman and Kaur 2017; Dhiman and Kumar 2019), Salp Swarm Algorithm (SSA) (Mirjalili et al. 2017), and Emperor Penguin Optimizer (EPO) (Dhiman and Kumar 2018). It is termed as Multi-objective Spotted hyena, Salp swarm, and Emperor penguin optimizer (MoSSE). MOSHO, SSA, and EPO have proved the effectiveness in resolving various engineering problems. The strengths and drawbacks of these three algorithms are: MOSHO has stronger optimization capabilities and removes the problem of missing selection pressure. But the algorithm has slow convergence speed in its phase of exploitation. On the other hand, SSA and EPO prevent a solution from trapping in local optima. These algorithms provide the optimal solutions with high convergence speed. The main contributions to this work can be summarized as follows:

• The MoSSE algorithm integrates the archive to accumulate all the non-dominated optimal solutions.

• A selection system for replacing and updating the results in the archive with respect to other solution has been implemented.

• MoSSE implements an adaptive grid approach to remove a solution from the most crowded section and increase the variety of non-dominated solutions.

The suggested multi-objective algorithm is evaluated on ten IEEE CEC-9 benchmark test functions including (Zhang et al. 2008), and four real-life engineering design problems. Also, the efficiency of the suggested algorithm is validated by comparing the results with seven well- and widely used multi-objective optimization algorithms, i.e., MOPSO (Coello Coello 2002), NSGA-II (Deb et al. 2002), MOEA/D (Zhang and Li 2007), PESA-II (Corne et al. 2001), MSSA (Mirjalili et al. 2017), MOACO (Angus and Woodward 2009), and MOSHO (Dhiman and Kumar 2018) by using four performance measures.

The remainder section of this paper is presented as follows: Sect. 2 presents a literature review of multi-objective optimization techniques. Section 3 discusses the concepts of MOSHO, SSA, and EPO, and the proposed MoSSE algorithms. The experimental observations and reviews are presented in more detail in Sect. 4. Section 5 assesses the proposed algorithm for four engineering design applications by relating its efficiency with seven well-known multi-objective optimization algorithms. Section 6 eventually completes this analysis and outlines the potential direction for future study.

2 Literature review

Multi-objective optimization provides the correct estimate for the non-dominated Pareto solutions with maximum variation in a single run (Zhou et al. 2011). Because of its numerous advantages such as local optimum avoidance and gradient-free techniques (Mirjalili et al. 2016), academia and the tech industry have attracted considerable interest in solving many real-life problems. Extensive research has also been conducted over the past three decades to develop and test the multi-objective optimization approaches. Some well-established methods of stochastic multi-objective optimization include PESA-II (Corne et al. 2001), NSGA-II (Deb et al. 2002), MOEA/D (Zhang and Li 2007), MOPSO (Coello Coello 2002), SPEA2 (Zitzler et al. 2001), and MOACO (Angus and Woodward 2009).

SPEA2 (Zitzler et al. 2001) is proposed and discussed in 2001. It is the modernized version of SPEA (Zitzler and Thiele 1998) which integrates finest-fitness information, fixed-size external archive to store non-dominated solutions, and upgraded clustering method to remove archive members. PESA-II (Corne et al. 2000) is the newest version of PESA (Corne et al. 2001) algorithm with directed region-based selection method which selects optimal solutions for a hyper-box rather than individual Pareto solutions. The sparse populated hyper-boxes take higher chances of being picked during selection process than crowded hyper-boxes. Instead, individual solutions are randomly selected from the selected hyper-box to achieve crossover and mutation. So, it minimizes the cost of measuring which corresponds to the Pareto rankings.

Another widely used algorithm is NSGA-II (Deb et al. 2002), which is used to resolve the deficiency of elitism, high computational difficulty, and parameter-issue of NSGA (Srinivas and Deb 1994). This algorithm uses a fast, non-dominated sorting method, elitist approach, and niching of operators. First, NSGA-II creates the random population of competing individuals and then uses non-sorting mechanisms to rank and sort each individual. Growing individual will then be assigned a fitness value that is equal to their non-domination level.

MOPSO (Coello Coello 2002) uses an external pool to store and retrieve the Pareto solutions that are more suitable, based on the basic principles of PSO (Eberhart and Kennedy 1995). This algorithm determines the best global particle for each member of the population also known as the best local guide from the set of optimal solutions obtained by Pareto. This procedure improves the variety of solutions and the speed of convergence, especially when dealing with multi-objective problems.

MOEA/D (Zhang and Li 2007) divides the multi-objective problem into a set of single-objective sub-problems. The goal feature for each sub-problem is a weighted combination of all individual goals. However, the weighted sum is one of the approaches used in MOEA/D algorithm. Each sub-problem is optimized by using the current information from its neighboring sub-problems at the same time. The relationship of neighborhood among all sub-problems is defined based on the distance between their aggregated weight coefficient vectors. MOEA/D outperforms NSGA-II in terms of convergence speed and computational complexity. The another multi-objective algorithm based on the concept of the ACO algorithm is MOACO, which Angus and Woodward proposed in 2009 (Angus and Woodward 2009). This algorithm is made up of several elements, including pheromone matrix, solution building, rating and solution evaluation, updating and decay, and Pareto archival. This will improve MOACO with a novel classified strategy to deliver at the nearby solutions and provides an actual balance between exploration capabilities and extraction.

Yu et al. (2016) proposed a priori approach which decomposes the multi-objective problem into a number of scalar problems to find the regions of interest for the decision-maker. This work was further extended to interactively find the regions of interest (Zheng et al. 2017). Yu et al. (2019) introduced the new line of preference-driven optimization method to find the knee regions instead of conventional regions of interest with respect to the preference information the decision-maker gives. In addition to the above algorithms, there are several other methods of optimization such as the Multi-Cat Swarm Optimization (MOCSO) (Pradhan and Panda 2012), Multi-agent Genetic Algorithm (MAGA) (Zhong et al. 2004), Multi-objective Artificial Bee Colony Algorithm (MOABC) (Hancer et al. 2015; Luo et al. 2017), and Multi-objective Flower Pollination Algorithm (MOFPA) (Yang et al. 2014). Although these algorithms can very effectively and efficiently approximate Pareto’s set of optimal solutions, they are not able to solve all NFL theorem optimization problems (Wolpert and Macready 1997). Therefore, a new algorithm is required to be able to resolve problems that was not solved by the existing optimization techniques.

3 Proposed algorithm

In this section, firstly the brief overview of MOSHO, SSA, and EPO algorithms is discussed. Then, the proposed hybrid algorithm is presented by merging the features of these algorithms.

3.1 Multi-objective Spotted Hyena Optimizer (MOSHO)

MOSHO is the multi-objective variant of a newly developed SHO algorithm based on the natural behaviors of spotted hyenas. SHO focuses primarily on attacking, searching, hunting, and encircling actions of the trusted group of spotted hyenas. SHO’s encircling behavior is described by the following equations (Dhiman and Kumar 2017):

$$\begin{aligned}&\vec {X}_h = \mid \vec {A}\cdot \vec {C}_p(x)-\vec {C}(x) \mid , \end{aligned}$$

(1)

$$\begin{aligned}&\vec {C}(x+1)= \vec {C}_p(x)-\vec {B}\cdot \vec {X}_h, \end{aligned}$$

(2)

where $\vec {X}_h$ represents the distance that spotted hyena has to cover to reach the prey. x signifies the running iteration at given instance. The position vectors corresponding to prey and spotted hyena are represented by $\vec {C}_p$ and $\vec {C}$, respectively. $\cdot$ and $\mid \mid$ symbols are used for representing the multiplication vector and absolute value, respectively. In addition, $\vec {A}$ and $\vec {B}$ indicate the coefficient vectors and are computed as follows:

$$\begin{aligned} \vec {A}= & {} 2\cdot \vec {rnd_1}, \end{aligned}$$

(3)

$$\begin{aligned} \vec {B}= & {} 2\vec {h}\cdot \vec {rnd_2} - \vec {h}, \end{aligned}$$

(4)

$$\begin{aligned} \vec {h}= & {} 5 - \Bigg (Itr\times \dfrac{5}{Max_{Itr}}\Bigg ), \nonumber \\&\quad {\textit{where}} \quad {\textit{Itr}}= 0, 1, 2, \ldots , {\textit{Max}}_{Itr}, \end{aligned}$$

(5)

Here, $\vec {rnd_1}$ and $\vec {rnd_2}$ are two random vectors with values in the range of [0, 1]. By changing the values of position vectors $\vec {A}$ and $\vec {B}$, spotted hyenas can reach several different places. Furthermore, the value of $\vec {h}$ is linearly decremented from 5 to 0 over the passage of maximum number of iterations, to maintain a proper balance between exploration and exploitation.

In addition, the spotted hyenas typically live and hunt in groups of trusted mates and have the ability to recognize the prey’s location. The best spotted hyena (search agent), whoever is optimum, knows where the prey and other search agents are located and makes a group of trusted friends and gathers toward the best search agent. The hunting area theoretically is defined using the following equations:

$$\begin{aligned} \vec {X}_h= & {} \mid \vec {A}\cdot \vec {C}_h-\vec {C}_k \mid , \end{aligned}$$

(6)

$$\begin{aligned} \vec {C}_k= & {} \vec {C}_h-\vec {B}\cdot \vec {X}_h, \end{aligned}$$

(7)

$$\begin{aligned} \vec {O}_h= & {} \vec {C}_{k}+\vec {C}_{k+1}+\cdots +\vec {C}_{k+N}, \end{aligned}$$

(8)

where $\vec {C}_h$ and $\vec {C}_k$ signify the location of best search agent and other spotted hyenas, respectively. N represents the number of spotted hyenas and is calculated as follows:

$$\begin{aligned}&N = count_{nos}(\vec {C}_h,\vec {C}_{h+1},\vec {C}_{h+2},\ldots , (\vec {C}_h+\vec {M})), \end{aligned}$$

(9)

$$\begin{aligned}&\vec {C}(x+1) = \dfrac{\vec {O}_h}{N} \end{aligned}$$

(10)

Here, $\vec {M}$ represents a random vector with values in the range of [0.5, 1], nos indicates the number of candidate solutions that are somehow close to the best optimal solution in the search space being considered, and $\vec {O}_h$ is the cluster of optimal solutions. $\vec {C}(x+1)$ determines the best possible solution and helps to update the positions of other spotted hyenas based on the best search agent location.

Spotted hyena discovery is achieved with a vector $\vec {B}$. Vector $\vec {B}$ includes random values that are either > 1 or < 1 and compels the movement of spotted hyenas away from predators. Therefore, $\vec {A}$ ubiquitous aids in discovery and keeps random values within the range of [0, 5], which serves as prey weights. The exploitation of SHO algorithm starts with $\mid \vec {B}\mid <1$, where $\vec {B}$ contains random values lying in the range of $[-1, 1]$.

SHO algorithm optimization cycle starts with the generation of a set of random solutions as the initial population of spotted hyenas. The other search agents form a cluster of trusted friends toward the best search agent within this group, and further update their positions. Finally, the best positions corresponding to the search agents are retrieved as optimal solutions upon completion of the termination criteria. In 2018, the SHO algorithm was further expanded to generate its multi-objective version called MOSHO (Dhiman and Kumar 2018) by adding two new components including archive and group selection mechanism. In subsequent subsections, the brief description of those components is given.

3.1.1 Archive

Also known as an external repository, the archive refers to a storage space that contains archives of all the non-dominated solutions that have been obtained so far. It consists of two main components such as the archive controller and the grid (Coello Coello et al. 2004).

The archive controller monitors the archives when the archive is complete or when a new optimal Pareto solution needs to move into the archive. It compares the non-dominated solutions obtained with the current archive contents at each iteration, and decides whether or not to put a solution in that archive if the following conditions are met:

• If the archive is null, the current solution will be added to the list.

• The solution can only be held in the archive if neither the archive members nor the new solution can win one another in terms of Pareto dominance relationship.

• If the archive has exceeded the maximum permissible size, then adaptive grid mechanism is first invoked to re-organize objective spatial segmentation by omitting one of the most crowded segment solutions. Later, the latest solution will be put in the least crowded section to maximize Pareto’s optimum front diversity (Ruan et al. 2017).

The other part named grid (adaptive grid) is used to distribute the Pareto fronts uniformly (Knowles and Corne 2000). The archive’s objective function space is divided into distinct regions. When an individual put in an external population resides outside the existing grid boundaries, the grid is re-calculated and transferred to each person within it.

3.1.2 Group selection mechanism

Group selection process aims to fit the most recent solution to the existing team members. It chooses the least crowded space search section and recommends one of its non-dominated solutions for the nearby candidate solution cluster. Selection is made using roulette wheel selection method with the following probability:

$$\begin{aligned} U_k=\dfrac{g}{N_k} \end{aligned}$$

(11)

Here, g is a constant variable with value > 1 and $N_k$ indicates the amount of Pareto optimal solutions acquired within the kth row. MOSHO can manage the problems with many computationally low cost constraints.

3.2 SSA Algorithm

SSA is a meta-heuristic optimization algorithm recently proposed by Mirjalili et al. in 2017 (Mirjalili et al. 2017). This algorithm is based on the swarming behavior of salp swarms, which makes a chain of salp when navigating and foraging in the deep sea. The population is divided into two main groups in the salp chain, namely leaders and followers. The leader leads the entire chain from the end, while the followers chase each other. In a n-dimensional search environment, the position of the leader is modified according to the following equation:

$$\begin{aligned} y_k^1= {\left\{ \begin{array}{ll} F_k+a_1((U_k-L_k)a_2+L_k),&{} a_3 \ge 0\\ F_k-a_1((U_k-L_k)a_2+L_k),&{} a_3 < 0 \end{array}\right. } \end{aligned}$$

(12)

where $y_k^1$ is the position of leader in the kth dimension, $U_k$ and $L_k$ signify the upper bound and lower bound of kth dimension, respectively, $F_k$ shows the position of food source,and $a_1, a_2,$ and $a_3$ represent the random numbers.

The position of leader is updated with reference to food source only. The coefficient $a_1$ is responsible for better exploration and exploitation and is defined as follows:

$$\begin{aligned} a_1=2e^{-\Bigg (\dfrac{4x}{Max_{Itr}}\Bigg )^2}, \end{aligned}$$

(13)

where x represents the current iteration and $Max_{Itr}$ indicates the maximum number of iterations. Furthermore, the parameters $a_2$ and $a_3$ are random numbers in range of [0, 1].

The position of followers based on the Newton’s law of motion is updated using the following equation:

$$\begin{aligned} y_k^j=\dfrac{1}{2}AT^2+V_0T,&j \ge 2, \end{aligned}$$

(14)

where $y_k^j$ indicates the position of $j^{th}$ follower, T represents the time, and $V_0$ signifies the initial speed. The parameter A is calculated as follows:

$$\begin{aligned} \begin{aligned}&A=\dfrac{V_{final}}{V_0}, \\&V=\dfrac{y-y_0}{T}, \end{aligned} \end{aligned}$$

(15)

Taking $V_0=0$, Equation (22) can be written as:

$$\begin{aligned} y_k^j=\dfrac{1}{2}(y_k^j+y_k^{j-1}),&j \ge 2. \end{aligned}$$

(16)

3.3 Emperor Penguin Optimizer (EPO)

The main objective of modeling is to identify effective mover (Dhiman and Kumar 2018). L-shape polygon plane is considered as the shape of the huddle. After the effective mover is identified, the boundary of the huddle is again computed.

3.3.1 Generate and compute the huddle boundary

To map the huddling behavior of emperor penguins, the first thing we need to consider is their polygon-shaped grid boundary. Every penguin is surrounded by at least two penguins while huddling, and the huddling boundary is decided by the direction and speed of wind flow. Wind flow is generally faster as compared to penguins movement. The huddling boundary can be mathematically formulated as:

$$\begin{aligned} \chi = \nabla \eta , \end{aligned}$$

(17)

where $\eta$ represents the velocity of wind and $\chi$ indicates the gradient of $\eta$. Furthermore, the complex potential is obtained by integrating vector $\alpha$ with $\eta$.

$$\begin{aligned} G = \eta + i\alpha , \end{aligned}$$

(18)

Here, i represents the imaginary constant and G defines the polygon plane function.

3.3.2 Profile of temperature

Emperor penguins perform huddling to conserve their energy and increase huddle temperature $T=0$ if $X\>0.5$ and $T=1$ if $X<0.5$, where X is the polygon radius. This temperature measure helps to perform exploration and exploitation task among emperor penguins. The temperature is computed as:

$$\begin{aligned} \begin{aligned}&T'=\Bigg (T- \dfrac{Max_{itr}}{y-Max_{itr}}\Bigg ),\\&T= {\left\{ \begin{array}{ll} 0,&{} \text {if } X > 0.5\\ 1,&{} \text {if } X < 0.5 \end{array}\right. } \end{aligned} \end{aligned}$$

(19)

where y represents the current iteration, $Max_{itr}$ indicates the maximum count of iterations, and T defines the time required to identify optimal solution.

3.3.3 Compute the distance

After the huddling boundary is figured out, the distance between the emperor penguin is computed. The current best solution is the solution with higher fitness value than previous optimum solution. The search agents update their positions corresponding to current optimal solution. The position updation can be mathematically represented as:

$$\begin{aligned} \vec {M_{ep}}=Abs\Big (N(\vec {A})\cdot \vec {Q(y)}-\vec {P}\cdot \vec {Q_{ep}(y)}\Big ), \end{aligned}$$

(20)

where $\vec {M_{ep}}$ denotes the distance and y represents the ongoing iteration. $\vec {P}$ and $\vec {A}$ helps to avoid collision among penguin. $\vec {Q}$ represents the best solution, and $\vec {Q_{ep}}$ represents the position vector of emperor penguin. N() denotes the social forces that helps to identify best optimal solution. The vectors $\vec {P}$ and $\vec {A}$ are calculated as follows:

$$\begin{aligned}&\vec {A} = (M\times (T'+ R_{grid}(Accuracy)) \nonumber \\&\quad \times Rand())-T', \end{aligned}$$

(21)

$$\begin{aligned}&R_{grid}(Accuracy) = Abs(\vec {Q}-\vec {Q_{ep}}), \end{aligned}$$

(22)

$$\begin{aligned}&\vec {P} = Rand(), \end{aligned}$$

(23)

where M represents the movement parameter to maintain a gap between search agents for collision avoidance. The value of parameter M is set to 2. $T'$ defines the temperature profile around the huddle, $P_{grid}(Accuracy)$ is the polygon grid accuracy, and Rand() is a random number in range of [0, 1].

The function N() is calculated as follows:

$$\begin{aligned} N(\vec {A})=\Bigg (\sqrt{f\cdot e^{-x/l} - e ^{-x}}\Bigg )^{2}, \end{aligned}$$

(24)

where e is the expression function. f and l are control parameters for better exploration and exploitation. The values of f and l lie in the range of [2, 3] and [1.5, 2], respectively.

3.3.4 Relocation

The best solution (mover) is utilized to update the position of emperor penguins. The selected move leads to the movement of other search agents in a search space. To find next position of a emperor penguins, the following equation is used:

$$\begin{aligned} \vec {Q_{ep}}(y+1)=\vec {Q(y)}-\vec {A}\cdot \vec {M_{ep}} \end{aligned}$$

(25)

where $\vec {Q_{ep}}(y+1)$ denotes the updated position of emperor penguin.

3.4 Proposed MoSSE algorithm

3.4.1 Motivation

Taking inspirations from nature, academics and practitioners conducted extensive research to develop a collection of meta-heuristic optimization algorithms. Such nature-inspired algorithms allow researchers to modify their optimization approaches based on similar algorithms in order to improve the efficacy of the solution and to quickly obtain an optimal solution to solve the complicated problems in large projects effectively. As a result, researchers began using certain algorithms to solve specific engineering problems. But, since they depend heavily on some mathematical formulas, these algorithms expose certain shortcomings and decreases the accurate understanding. Based on this condition, researchers proposed hybrid meta-heuristic optimization algorithms because these algorithms not only avoid the above-mentioned shortcomings, but also increase population diversity and exchange of individual information within the population, thus further enhancing the ability to solve complex engineering problems. Single-solution optimizer often struggles to fulfill the need for precision when solving engineering problems due to the existence of multiple design variables and restricted environments. Therefore, hybrid algorithms prove to be the most efficient methods of achieving such goals (Zhang et al. 2019). Nevertheless, according to the No-Free Lunch Theorem (NFL), these hybrid algorithms cannot solve all optimization problems. NFL (Wolpert and Macready 1997) has scientifically proved the aforementioned claim and encourages academics to build new algorithms for optimization or improve the existing ones. This has encouraged us to project a new algorithm with the aim of solving, more efficiently, many problems with the existing multi-objective solutions that are difficult to solve. In general, the inspiration behind this work can be described as below. The researchers have encountered difficulties with regard to a proper balance between exploration and exploitation characteristics. To address these concerns, it is important to develop an optimization algorithm that maintains this balance in order to enable the proposed approach to find optimal global solutions with greater accuracy (Sree Ranjini and Murugan 2017) for real-life problems. This paper makes use of the process of group selection mechanism used in MOSHO to provide enhanced exploration capabilities. The reasons to prefer the actions of MOSHO over others are as follows:

• This process removes the elimination problem of non-dominated solutions.

• Makes sure that all Pareto optimum objective vectors are found in the approximation set of values.

In addition, MOSHO has fair search capability and therefore stronger exploration capabilities with the group relations and the spotted hyena’s collective behavior. But it endured the disadvantages of slow convergence and lower population density. As a result, it suffers from its robustness, since it can remain stuck in local optima at times. By comparison, the leader and follower selection mechanism is used of SSA algorithm based on salps swarming behavior provides optimal solutions with better convergence. On the other hand, to make sure that the next solution is possible related to previous one, relocation method of EPO algorithm is employed for better positioning the search agents.

3.4.2 Explanation of MoSSE

The MoSSE algorithm integrating the MOSHO, SSA, and EPO algorithms alters the basic structure of the MOSHO algorithm by adding the SSA algorithm’s leader and follower selection function and EPO relocation method to improve the population update process. This integration gives MoSSE more versatility to reinforce the balance between diversity and convergence, as well as to find the optimal solution quickly.

The pseudocode of MoSSE algorithm is given in Algorithm 1. The algorithm starts with the initialization of the spotted hyena population. Then, the efficiency of every search agent is calculated using the feature fitness. A selection of non-dominated solutions is selected based on their fitness. The best search agent is then searched from the search room allocated to the external repository. The next move is to use the leader and followers selection method of the SSA algorithm to re-calculate and further update the positions of the search agents. After that, EPO’s relocation method helps to escape a solution from being stuck in local optima and also increases the solution’s consistency with the highest convergence rate.

Following this process, each search agent’s fitness value is again determined to find the non-dominated solutions and the archive is modified with those newly obtained solutions. If the archive is complete then grid mechanism is executed to delete one of the archived solutions from the highest populated section and add the new solution to the archive. Unless the newly implemented solutions lie beyond the current grid boundaries at each iteration, then grid positions are recalculated to change those solutions. The next step is to update the best search agent if a better solution exists in the database than previous optimal solution and then update the category of spotted hyenas accordingly. The algorithm continues until the conditions for the stoppage are not met.

3.4.3 Computational complexity

MoSSE algorithm’s overall time complexity is ${\mathcal {O}}(Max_{Itr} \times n_o \times (n_p + n_{ns}) \times M \times (S + R))$ because

• 1. MoSSE population initialization requires ${\mathcal {O}}(n_o \times n_p)$ time. Here, $n_p$ reflects the total population size, and $n_o$ indicates the total number of objectives.

• 2. Search agent fitness is measured in ${\mathcal {O}}(Max_{Itr} \times n_o \times n_p)$ time, where $Max_{Itr}$ counts the maximum number of iterations required to simulate MoSSE algorithm.

• 3. The MoSSE search agents takes ${\mathcal {O}}(M)$ time to identify. Here, M stands for the number of spotted hyenas.

• 4. The selection method for the follower and the leader takes ${\mathcal {O}}(S)$ time and relocation method requires ${\mathcal {O}}(R)$ time.

• 5. The proposed algorithm updates the list of non-dominated solutions in ${\mathcal {O}}(n_o \times (n_{ns} + n_p))$ time.

In addition, the MoSSE algorithm’s space complexity is ${\mathcal {O}}(n_o \times n_p)$, because space is needed only during the initialization process.

4 Experimental results and discussions

In this section, we compare the results of MoSSE using four performance metrics to seven well-known algorithms on ten benchmark test functions. The MoSSE algorithm findings are compared with seven well-known multi-objective algorithms, namely MOPSO (Coello Coello 2002), NSGA-II (Deb et al. 2002), MOEA/D (Zhang and Li 2007), PESA-II (Corne et al. 2001), MSSA (Mirjalili et al. 2017), MOACO (Angus and Woodward 2009), and MOSHO (Dhiman and Kumar 2018). In MATLAB R2018b, we implemented these algorithms and executed them in 64-bit Microsoft Windows 10 environment with 2.40 GHz Core i7 processor with 16 GB of Random Access Memory (RAM). From the literature (Katunin and Przystalka 2014), it is evident that the parameter tuning can affect the efficiency of a meta-heuristic strategy, i.e., different parameter values will produce different results. The tuning of the hyperparameters is therefore done carefully, and their values are modified accordingly. The proposed algorithm contains four such parameters and will evaluate their sensitivity by assigning different values to them. We performed experiments for three benchmark test functions, namely UF1, UF3, and UF6.

• 1. Number of iterations: Although we assessed the impact of number of iterations on MoSSE results, we ran the proposed algorithm for 100, 500, 800, and 1000 iterations. The results of experiments reported in Table 1 confirm that MoSSE converges with the increase in the number of iterations toward equilibrium.

• 2. Number of search agents: They also address the effect of population size on MoSSE behavior, taking the various sizes as 50, 80, 100, and 200 into account. Table 2 explains the statistical results of more than 30 experiments on simulation. From the table, it can be observed that with 100 population size, MoSSE produces better optimum solutions, and the value of objective function decreases as more population size increases.

• 3. Influence of archive: To demonstrate the impact of the archive on MoSSE, archive operations on UF1, UF3, and UF6 test functions are shown in Table 3 and Fig. 1 in the form of successive iterations. For these research issues the server size is counted as 10. From Table 3 it can be observed that the proposed algorithm will acquire the optimum values for these test functions over successive generations.

• 4. Influence of selection approach: The proposed algorithm was evaluated using tournament selection and roulette wheel selection strategies for analysis of MoSSE results on UF1, UF3, and UF6 test problems. The selection mechanism convergence analyzes for the above test problems are shown in Fig. 2. Having observed this result, it should be noted that the choice of roulette wheels is better than the tournament selection approach in terms of converging toward the optimal solution.

Table 1 Sensitivity analysis of maximum number of iterations

Table 2 Sensitivity analysis of number of search agents

Table 3 The archive values obtained by MoSSE algorithm using multiple runs

Fig. 1

Effect of archive on a U1, b UF3, and c UF6 test functions

Fig. 2

Effect of selection mechanism on a UF1, b UF3, and c UF6 benchmark test problems

4.1 Benchmark test functions and performance metrics

To demonstrate the efficiency of proposed algorithm, we applied MoSSE on ten IEEE CEC-9 (UF1–UF10) (Zhang et al. 2008) frequently employed test functions with diverse characteristics. The four well-known performance measures are employed, namely Hypervolume (HV) (Zitzler and Thiele Nov 1999; Coello et al. 2010), $\Delta _p (p=1)$ (Schutze et al. 2012; Rudolph et al. Jun 2016), Spread (Coello et al. 2010; Li and Zheng 2009), and Epsilon ($\varepsilon$) (Zitzler et al. April 2003; Knowles et al. 2006) to quantify the convergence and coverage (diversity) of proposed algorithm.

4.2 Evaluation on IEEE CEC-9 test suite

Table 4 lists the performance metrics attained for the MoSSE and the CEC-9 test suite comprising seven aforementioned algorithms. Overall, it is worth noting that for most research problems, MoSSE outperforms other algorithms. In addition, MoSSE provides best performance indicators on fifth, sixth, eighth, and seventh CEC-9 test cases, respectively, in terms of average and SD values of HV, $\Delta _p$, Spread, and Epsilon. For the particular case of UF1 test feature, MoSSE provides best results in terms of all four efficiency measures relative to all other successful algorithms. Subsequently, MOSHO performs better in terms of both SD and mean value. For HV, the average MOEA/D algorithm value is higher, while for MOSHO algorithm, the standard deviation is promising. MoSSE reveals great output in terms of HV, Spread, and Epsilon for UF2 test feature. For UF3 benchmark test issue, in comparison with other multi-objective methods, MOEA/D provides superior results in terms of the average value of $\Delta _p$ and Epsilon metric. But for HV and Spread, respectively, this algorithm falls behind MSSA and MOPSO. In addition, the SD obtained by MOACO and MOPSO is higher compared to the competitor algorithms for the performance metrics. MoSSE produces very positive results compared to the MOSHO algorithm for UF4 and UF5 test functions, and also outperforms it. For UF4, the proposed algorithm produces very promising results for all output metrics considered except for the SD of Spread metric. In comparison, MoSSE obtains the best HV, $\Delta _p$, and Spread values for UF5 test function but does not have better Epsilon metric values. For UF6 and UF7, both MoSSE’s Spread and Epsilon metrics are smaller than MOSHO’s and substantially lower than its competitive algorithms. In addition, MoSSE achieves strong HV but does not achieve better values for UF8 testing as these values have already been bagged by MOEA/D, PESA-II, and NSGA-II algorithms. In addition, the optimal solutions procured by the Pareto are represented in Figure 3. To track the algorithm’s proposed coverage, this figure shows that MoSSE’s optimal Pareto fronts are very similar to the actual optimal front of Pareto. The results described above show that MoSSE can provide impressive coverage and convergence to solve multi-objective problems.

Table 4 Optimization results of multi-objective algorithms on IEEE CEC-9 test suite

Fig. 3

The best Pareto front approximations attained by MoSSE on IEEE CEC-9 (UF1–UF10) benchmark test functions

4.3 Statistical testing

The Mann–Whitney U rank sum test (Mann and Whitney 1947) has been conducted on the average values of IEEE CEC-9 benchmark test functions. Table 5 shows the results of the Mann–Whitney U rank sum test for statistical superiority of proposed MoSSE at 0.05 significance level. First, the significant difference between two data sets has been observed by Mann–Whitney U rank sum test. If there is no significant difference then sign ’=’ appears and when significant difference is observed then signs ’+’ or ’-’ appears for the case where MoSSE takes less or more function evaluations than the other competitor algorithms, respectively. In Table 5, ’+’ shows that MoSSE is significantly better and ’-’ shows that MoSSE is worse. As Table 5 includes 58 ’+’ signs out of 70 comparisons. Therefore, it can be concluded that the results of MoSSE is significantly effective than competitive approaches (i.e., MOSHO, MOPSO, NSGA-II, MOEA/D, PESA-II, MSSA, and MOACO). Overall, the results reveal that MoSSE outperforms other algorithms.

Table 5 Mann–Whitney U rank sum test at 0.05 significance level

5 MoSSE for real-life applications

MoSSE algorithm is applied to four real-life engineering design problems to test the efficacy of the proposed algorithm, namely welded beam design, multiple-disk clutch brake design, pressure vessel design, and 25-bar truss design problems. There are different types of penalty functions to handle these multi-constraint problems. These penalty functions are static penalty, dynamic penalty, annealing penalty, adaptive penalty, co-evolutionary penalty, and death penalty (Coello Coello 2002). However, death penalty function is used to discard the infeasible solutions and does not employ the information of such solutions which are helpful to solve the dominated infeasible regions. Due to low computational cost and its simplicity, MoSSE algorithm is equipped with death penalty function to handle multiple constraints.

5.1 Welded beam design problem

Coello Coello (2000) projected the problem of welded beam, which was also regarded as a traditional benchmark concern in the field of structural optimization. This helps to minimize production costs while reducing the final deflection of welded beams that are subject to four non-linear constraints by optimizing four design parameters, namely welded joint length (l), bar thickness (b), bar height (t), and welding thickness (h). The related other constraints include load buckling, stress bending, deflection of the end beam, and strain of the shear. Figure 4 outlines the welded beam design problem along with its geometrical parameters. Table 6 lists the best MoSSE solutions and other meta-heuristic algorithms. The findings show that the proposed algorithm greatly reduced the cost of manufacturing along with end deflection as compared to the findings of other effective algorithms. The proposed algorithm is also capable of producing a wide variety of optimal and uniformly distributed Pareto solutions (see Fig. 5).

Fig. 4

Schematic depiction of the welded beam design problem

Fig. 5

Obtained Pareto optimal solutions for welded beam design problem

Table 6 Comparison of MoSSE algorithm for welded beam design problem

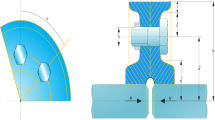
5.2 Multiple-disk clutch brake design problem

Another benchmark problem in the field of multi-objective optimization with the objectives of reducing the mass and stopping time by improving the five design parameters. Such parameters of construction with outer radius, inner radius, number of surfaces, disk thickness, and actuating force are depicted in Fig. 6. The analysis of compared optimal solutions by using the proposed as well as competitor optimization algorithms is tabulated in Table 7. It is seen from this table that MoSSE generates best solutions and improves the overall mass and stopping time. Also, the Pareto optimal fronts are shown in Fig. 7. This figure reveals that the results provided by the MoSSE algorithm are superior than other algorithms.

Fig. 6

Schematic representation of multiple-disk clutch brake design problem

Table 7 Comparison of MoSSE algorithm for multiple-disk clutch design problem

Fig. 7

Obtained Pareto solutions for multiple-disk clutch brake design problem

5.3 Pressure vessel design problem

Kannan and Kramer (1994) suggested a design for a pressure vessel consisting of a cylindrical vessel filled with hemispheric heads at both ends, as shown in Fig. 8. The objective of this problem is to maximize storage capacity and minimize the total cost comprising material, forming and welding costs of the cylindrical vessel. It has four decision variables namely $x_1$, $x_2$, $x_3$ and $x_4$ which represent the shell thickness ($T_s$), head thickness ($T_h$), inner radius (R), and cylindrical section length (L), respectively. It is also known as mixed discrete-continuous optimization problem as the first two variables are integer multiples of 0.0625 inch, whereas the later two are continuous variables.

Fig. 8

Schematic depiction of pressure vessel design problem

Fig. 9

Obtained Pareto optimal solutions for pressure vessel design problem

Table 8 Comparison of MoSSE algorithm for pressure vessel design problem

Table 8 explains the best possible solutions obtained for problem design of pressure vessels by considered algorithms. MoSSE provides effective designs with maximum capacity and low cost compared to the other algorithms. This represents the efficiency and consistency of the suggested algorithm to solve the engineering problem. Further, the ideal non-dominated Pareto optimal fronts are shown in Fig. 9.

Fig. 10

Schematic representation of 25-bar truss design problem

5.4 25-bar truss design problem

The problem is depicted in Fig. 10, which at the same time minimizes vertical displacement at node one and overall structural weight exposed to Euler buckling restriction under two load conditions. This system has 25 cross-area members, each category being divided into eight categories with maximum and minimum allowable limits (also called design variables). Tables 9 to 10 include these classification variables along with the maximum permissible tensile and compressive pressures. Further, these template variables can be picked from set: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.1, 2.2, 2.3, 2.4, 2.6, 2.8, 3.0, 3.2, 3.4.

Table 11 summarizes and compares with other state-of-the-art algorithms as the best possible results. It can be found that when it comes to certain performance metrics, MoSSE competes other algorithms. However, by inspecting Table 11, it can be seen the MoSSE generated better truss design as compared to other competitor algorithms. The obtained best Pareto optimal solutions are given in Fig. 11 which shows that MoSSE convergence is better than other competitor algorithms.

Table 9 Load conditions of issue with 25-bar truss configuration

Table 10 The grouping of 25-bar truss members and their corresponding allowable stresses

Table 11 Comparison of MoSSE algorithm for 25-bar truss design problem

6 Conclusions

This paper introduces a new multi-objective hybrid algorithm called MoSSE to solve real-life problems of engineering design. MoSSE incorporates the quick search and learning method of MOSHO with the leading and follow-up selection process of SSA and relocation method of EPO in order to achieve optimal global solutions. Such integration has helped maintain the suitable balance between the exploration and exploitation of the algorithm in the searching process. The efficiency of proposed algorithm is tested by using the ten standard IEEE CEC-9 test functions, and the obtained results are compared with seven multi-objective algorithms. The result shows that the MoSSE algorithm provides a very good results as compared to other meta-heuristic algorithms and outperformed them in terms of achieving more accurate approximations of Pareto’s optimal, high-convergence solutions, which are distributed equally. Additionally, the proposed algorithm’s ability to solve real-life problems is also demonstrated by evaluating its efficacy on four engineering design problems. The empirical comparisons with well-established optimization algorithms demonstrate the effectiveness of MoSSE in the solution of real-life engineering design problems. The proposed algorithm will be used in future, especially in the cloud computing and medical engineering domains, to solve complex the problems.

Fig. 11

Obtained Pareto optimal solutions for 25-bar truss design problem